Insulin secretion based on the late oral glucose tolerance test period and incident diabetes: the San Antonio Heart Study

Abstract

Aims

The Insulinogenic Index from 0 to 30 min (ΔI _0-30/ΔG_0-30), a measure of insulin secretion derived from the early period of the oral glucose tolerance test, predicts future diabetes. However, there are few data on secretory measures from the late oral glucose tolerance test period. We therefore investigated the association of the ratio of the area under the insulin curve to the area under the glucose curve from 60 to 120 min (I/G_{AUC 60-120}) with incident diabetes.

Methods

Participants were 1540 Mexican Americans and non-Hispanic whites in the San Antonio Heart Study who were free of diabetes at baseline. We analysed indices of sensitivity (Matsuda index) and secretion from the early (ΔI_0-30/ΔG_0-30) and late oral glucose tolerance test periods (I/G_{AUC 60-120}).

Results

A total of 179 participants developed diabetes after 7.5 years. I/G_AUC60-120 was an independent predictor of diabetes [odds ratio × 1 SD unit increase, 0.37 (0.26–0.54)] in a model that also included age, sex, ethnicity, body mass index, family history of diabetes, Matsuda index and (ΔI _0-30/ΔG_0-30) as covariates. I/G_{AUC 60–120} increased the C statistic (a test of discrimination) of the model (0.882 vs. 0.875, P = 0.044). I/G_{AUC 60–120} correctly reclassified one-fifth of individuals with moderate and strong risks of future diabetes. The net reclassification improvement was 0.13 (P < 0.001) and the integrated discrimination improvement was 0.033 (P < 0.001).

Conclusions

An insulin secretory measure derived from the late oral glucose tolerance test period is useful for classifying individuals at risk of future diabetes independently of other risk factors, including insulin sensitivity and a secretory measure from the early oral glucose tolerance test period.

Introduction

First-phase insulin secretion (acute insulin response) derived from the frequently sampled intravenous glucose tolerance test predict conversion to Type 2 diabetes [1,2]. This test is invasive and costly; therefore, simple surrogate indices of insulin secretion have been developed using insulin and glucose concentrations from the fasting state or the early period of the oral glucose tolerance test (OGTT) (e.g. insulinogenic index from 0 to 30 min (ΔI_0–30/ΔG_0–30)]. These surrogate indices are also predictors of future diabetes [3–9]. Another early insulin secretory defect reported in individuals with normal glucose tolerance and a first-degree relative with Type 2 diabetes is reduced second-phase insulin release measured by a clamp technique [10]. Stumvoll et al. [11] described insulin secretory indices derived from the OGTT (S1Ph_OGTT and S2Ph_OGTT) that have strong correlations with first- and second-phase insulin release measured by the hyperglycaemic clamp. However, the ability of these indices to detect individuals at risk of future diabetes has not been explored.

β-Cell dysfunction needs to be interpreted in the context of concomitant insulin resistance [12–14]. We hypothesized that indices of insulin secretion originated from the late OGTT period could add predictive information to ΔI_0–30/ΔG_0–30. We used simple strategies, such as the change in insulin concentration relative to the change in glucose concentration [15] and the insulin area under the curve (AUC) relative to the glucose AUC [16], to generate indices of secretion from the late OGTT period: (1) the ratio of relative change in insulin concentration to relative change in glucose concentration from 60 min to 120 min (ΔI_60–120/ΔG_60–120]; and (2) the ratio of the insulin to glucose concentration areas from 60 to 120 min (I/G_{AUC 60–120}]. The aim of the present study, therefore, was to analyse the association of insulin secretory indices from the early and late OGTT periods with incident Type 2 diabetes.

Patients and methods

Study population

The San Antonio Heart Study is a longitudinal, epidemiological study designed to study Type 2 diabetes and cardiovascular disease among Mexican Americans and non-Hispanic whites living in San Antonio, Texas, USA. Protocols were approved by the Institutional Review Board of the University of Texas Health Science Center at San Antonio. Details of the study design have been previously published [17]. Briefly, all Mexican Americans and non-Hispanic whites (men and non-pregnant women) aged 25–64 years that resided in randomly selected households from low-, middle- and high-income census tracts were invited to participate. All subjects gave written informed consent.

We analysed data from cohort 2 participants, because OGTT sampling times at 30 min and 60 min were not available in cohort 1 participants. Baseline data were collected from January 1984 to December 1988 and follow-up data between October 1991 and October 1996 (mean follow-up of 7.5 years; range 6.3–10.3 years). Incident diabetes was ascertained in 1734 of 2459 [70.5%) participants. Relevant information was missing in 194 participants; therefore, this study presents information on 1540 individuals.

Anthropometric measurements were obtained by trained personnel. Blood specimens were collected before (0 min) and 30, 60 and 120 min after a 75 g oral glucose load (Orangedex; Custom Laboratories, Baltimore, MD, USA) to determine glucose and insulin levels. Serum insulin was measured by a radioimmunoassay (Diagnostic Products Corporation, Los Angeles, CA, USA) that had a high degree of cross-reactivity with proinsulin (70–100%).

We applied the 2003 American Diabetes Association criteria to define diabetes (fasting glucose ≥ 7.0 mmol/l and/or 2-h glucose ≥ 11.1 mmol/l), impaired glucose tolerance (2-h glucose ≥ 7.8 mmol/l and < 11.1 mmol/l), and normal glucose tolerance (2-h glucose < 7.8 mmol/l). Subjects who reported current treatment with glucose-lowering medications were considered to have diabetes.

We used published formulae to calculate homeostasis model assessment of insulin resistance (HOMA IR; basal insulin × basal glucose/22.5) [18] and Matsuda index [10⁴/(basal glucose × basal insulin × mean glucose × mean insulin]^0.5) [19]. In this last formula, mean glucose and mean insulin concentrations indicate average glucose (mg/dl) and insulin concentrations (mU/l) based on sampling times at 0, 30, 60 and 120 min. Glucose values at 90 min were not available in the San Antonio Heart Study; however, the Matsuda index based on 0, 30 and 120 min sampling times and the original Matsuda index had similar relationship with clamp-derived insulin sensitivity [20].

We also used published formulas for ΔI_0–30/ΔG_0–30 (insulin at 30 min − basal insulin/glucose at 30 min − basal glucose) [15], S1PH_OGTT [1283 + 1.829 × insulin at 30 min − 138.7 × glucose at 30 min + 3.772 × basal insulin) [11] and S2PH_OGTT [287 + 0.4164 × insulin at 30 min − 26.07 × glucose at 30 min + 0.9226 × basal insulin) [11]. The parameter I/G_{AUC 60–120} was computed as insulin AUC to glucose AUC from 60 to 120 min. The AUCs were calculated by the trapezoidal method. The parameter ΔI_60–120/ΔG_60–120 was computed as 1 − [(insulin at 60 min − insulin at 120 min/insulin at 60 min)/1 − (glucose at 60 min − glucose at 120 min)/glucose at 60 min]. This formula took into account the negative values resulting from calculating insulin and glucose changes (negative values in 40.3% of the estimates). More importantly, the fit of models with I/G_{AUC 60–120} (C statistic of a model with the Matsuda index as a covariate, 0.833) was better than that of models with ΔI_60–120/ΔG_60–120 (C statistic of a model with Matsuda index as a covariate, 0.785, P < 0.001). Thus, I/G_{AUC 60–120} was used as the index of insulin secretion during the late OGTT period.

Statistical analyses

Statistical analyses were performed with the SAS statistical software (version 9.2; SAS Institute Inc. Cary, NC, USA). Differences in baseline variables by sex and ethnicity were investigated by two-way analysis of covariance for continuous variables or logistic regression for dichotomous variables. Pearson’s partial correlation coefficients were used to analyse the strength of the relationship between variables. Correlation coefficients were compared by the T2 method [21]. The relation of Matsuda index to measures of insulin secretion was also assessed by ordinary least-squares regression as follows: log(secretion measure) = constant + β × log(Matsuda index). We were unable to use a method that accounted for the variability in the measurement of both the dependent and independent variables as previously done for the derivation of both the disposition index (insulin sensitivity index × acute insulin response) on the frequently sampled intravenous glucose tolerance test [13] and insulin secretion-sensitivity index-2 (Matsuda index × insulin AUC to glucose AUC from 0 to 120 min) on OGTT [16]. The risk of future diabetes associated with indices of insulin sensitivity and insulin secretion was determined by logistic regression analysis.

The predictive discrimination was assessed by the C statistic [22]. The C statistic results for different models were compared by bootstrap sampling. We used the Hosmer–Lemeshow goodness-of-fit test, a measure of deviation between observed and expected event rates in deciles of fitted risk values, to assess calibration of a logistic regression model that included age, sex, ethnicity, BMI, family history of diabetes, Matsuda index and ΔI_0–30/ΔG_0–30 before and after the addition of other indices of secretion. Using these two logistic regression models, we examined measures of reclassification, the net reclassification improvement and the integrated discrimination improvement, to analyse the discriminative value of I/G_{AUC 60-120}. The net reclassification improvement takes into account changes in estimated prediction probabilities that involve a change from one category to another [23]. We used clinically relevant a priori categories (< 1%, 1–5.9%, and ≥ 6% yearly risk of diabetes) based on the yearly risk of developing diabetes among San Antonio Heart Study participants who had normal fasting and 2-h glucose concentrations (0.7% per year) or impaired glucose tolerance (6.1% per year). The integrated discrimination improvement evaluates the change in the estimated prediction probabilities for all possible cut-offs [23]. Log-transformed values of insulin levels and indices of insulin resistance/sensitivity and insulin secretion were used to improve discrimination and calibration of the models and to minimize the influence of extreme observations. We considered a P value < 0.050 significant.

Results

Mexican Americans had higher insulin and glucose levels and more adiposity and family history of diabetes than non-Hispanic whites (Table 1). Indices of insulin resistance and secretion were also higher in Mexican Americans. Men had more insulin resistance and central adiposity and higher fasting and 1-h insulin and glucose concentrations than women. Women had more family history of diabetes and higher 2-h insulin and glucose concentrations. Women also had higher insulin secretion, as measured by ΔI_0–30/ΔG_0–30, and similar secretion, as measured by the other secretory indices. Ethnicity had an interaction effect on the relation of sex to HOMA IR, Matsuda index, S1Ph_OGTT and S2Ph_OGTT.

Table 1.

Age-adjusted baseline characteristics by sex and ethnic origin

	Non-Hispanic whites		Mexican Americans		Ethnicity (P)	Sex (P)	Ethnicity × sex interaction (P)
	Men	Women	Men	Women
n	242	268	425	605
Age*	44.1 ± 0.7	43.5 ± 0.7	42.6 ± 0.5	43.7 ± 0.4	0.367	0.360	0.145
BMI (kg/m2)	26.9 ± 0.3	25.5 ± 0.3	28.2 ± 0.2	28.7 ± 0.2	< 0.001	0.637	< 0.001
Waist circumference (cm)	96.0 ± 0.8	81.5 ± 0.8	94.9 ± 0.6	87.2 ± 0.5	< 0.001	< 0.001	< 0.001
Family history of diabetes (%)	14.4 (10.5–19.5)	20.1 (15.7–25.3)	35.1 (30.7–39.7)	42.2 (38.3–46.9)	< 0.001	0.005	0.724
Fasting glucose (mmol/l)	4.82 ± 0.04	4.63 ± 0.03	4.87 ± 0.03	4.72 ± 0.02	0.024	< 0.001	0.516
1-h glucose (mmol/l)	7.55 ± 0.14	6.72 ± 0.13	7.90 ± 0.10	7.23 ± 0.09	< 0.001	< 0.001	0.501
2-h glucose (mmol/l)	5.21 ± 0.11	5.59 ± 0.10	5.69 ± 0.08	6.25 ± 0.07	< 0.001	< 0.001	0.349
Fasting insulin (mU/l)†	9.22 ± 0.52	6.94 ± 0.37	10.83 ± 0.46	10.32 ± 0.46	< 0.001	0.004	0.011
1-h insulin (mU/l)†	81.0 ± 3.7	64.5 ± 2.8	104.8 ± 3.6	90.5 ± 2.6	< 0.001	< 0.001	0.291
2-h insulin (mU/l)†	39.6 ± 2.5	47.9 ± 3.0	60.9 ± 2.5	79.8 ± 3.3	< 0.001	< 0.001	0.432
HOMA IR†	1.96 ± 0.12	1.42 ± 0.08	2.33 ± 0.10	2.15 ± 0.08	< 0.001	< 0.001	0.011
Matsuda index†	4.08 ± 0.20	5.31 ± 0.25	3.16 ± 0.12	3.43 ± 0.11	< 0.001	< 0.001	0.028
ΔI0–30/ΔG0–30†	1.13 ± 0.06	1.30 ± 0.07	1.42 ± 0.06	1.71 ± 0.06	< 0.001	< 0.001	0.628
I/GAUC 60–120†	0.58 ± 0.02	0.56 ± 0.02	0.75 ± 0.02	0.76 ± 0.02	< 0.001	0.924	0.440
S1PhOGTT†	1241 ± 45	1170 ± 40	1451 ± 39	1543 ± 35	< 0.001	0.456	0.046
S2PhOGTT†	331 ± 10	307 ± 9	385 ± 9	397 ± 8	< 0.001	0.777	0.042

Data are n, mean ± standard error or rates ± 95% confidence intervals.

^*Non-adjusted values;

^†Back-transformed from log transformation.

HOMA IR, homeostasis model assessment of insulin resistance; I_0–30/G_0–30, insulinogenic index from 0 to 30 min; I/G_{AUC 60–120}, ratio of area under the insulin curve to area under the glucose curve from 60 to 120 min; S1Ph_OGTT and S2Ph_OGTT, Stumvoll’s first phase and second phase insulin release, respectively.

Correlations between indices of secretion and with other metabolic variables

We found that ΔI_0–30/ΔG_0–30 had a moderate relationship with I/G_{AUC 60–120}. These two indices had strong correlations with S1Ph_OGTT and S2Ph_OGTT (Table 2). In addition, S1Ph_OGTT was very highly correlated with S2Ph_OGTT (r = 0.99) and both had similar relationships with all metabolic variables. We found that ΔI_0–30/ΔG_0–30 was less strongly related to indices of insulin resistance and measures of adiposity than any of the other secretory indices. All secretory indices had direct correlations with insulin levels (moderate for ΔI_0–30/ΔG_0–30, moderately strong for S1Ph_OGTT and S2Ph_OGTT, and strong for I/G_{AUC 60–120}). Secretory indices differed in their relationships with plasma glucose levels (weakly negative for ΔI_0–30/ΔG_0–30 and weakly positive for I/G_{AUC 60–120}).

Table 2.

Pearson’s partial correlations between indices of secretion and with other metabolic variables^*

	ΔI0–30/ΔG0–30†	I/GAUC 60–120†	S1PhOGTT†	S2PhOGTT†
BMI	0.17	0.37‡	0.36‡	0.39‡
Waist circumference	0.13	0.34‡	0.33‡	0.35‡
Fasting glucose	−0.08	0.05‡	−0.02‡	0.03 §
1-h glucose	−0.38	0.16‡	−0.12‡	−0.06‡
2-h glucose	−0.17	0.15‡	0.01‡	0.05‡
Fasting insulin†	0.24	0.58‡	0.62‡	0.67‡
1-h insulin†	0.32	0.83‡	0.61‡	0.65‡
2-h insulin†	0.24	0.70‡	0.49‡	0.53‡
HOMA IR†	0.30	0.63‡	0.64‡	0.69‡
Matsuda index†	−0.31	−0.78‡	−0.68‡	−0.74‡
I/GAUC 60–120†	0.51	−	0.74‡	0.77‡
S1PhOGTT†	0.78	0.74§	-	0.99‡
S2PhOGTT†	0.75	0.77	0.99‡	–

^*Pearson’s partial correlation coefficients were calculated by controlling for age, sex, and ethnic origin;

^†log transformed variables.

HOMA IR, homeostasis model assessment of insulin resistance; I_0–30/G_0–30 indicates insulinogenic index from 0 to 30 min; I/G_{AUC 60–120}, ratio of area under the insulin curve to area under the glucose curve from 60 to 120 min; S1Ph_OGTT and S2Ph_OGTT, Stumvoll first phase and second phase insulin release, respectively. P-value for the test of difference in the correlation of each secretory index with individual metabolic variables relative to the respective correlation of ΔI_0–30/ΔG_0–30;

^‡P < 0.001;

^§P < 0.01

Although curvilinear, the relation of the Matsuda index to ΔI_0–30/ΔG_0–30 and I/G_{AUC 60–120} was not rectangular hyperbolic (exponent parameters differed significantly from −1) using an ordinary least-squares regression (see the Supporting Information, Table S1).

Predictive discrimination of measures of secretion

During a 7.5-year follow-up, 179 of the 1540 (11.6%) participants developed diabetes. The predictive discrimination of the Matsuda index (C statistic = 0.766) was increased by adding to the model any of the indices of insulin secretion: ΔI_0–30/ΔG_0–30 (0.851, P < 0.001), I/G_{AUC 60–120} (0.832, P < 0.001), S1Ph_OGTT (0.850, P < 0.001) or S2Ph_OGTT (0.851, P < 0.001). The predictive discrimination of a model with the Matsuda index and ΔI_0–30/ΔG_0–30 (C statistic = 0.851) was increased by I/G_{AUC 60–120} (0.860, P = 0.016), but not by S1Ph_OGTT (0.853, P = 0.368) or S2Ph_OGTT (0.854, P = 0.250).

The I/G_{AUC 60–120} value increased the C statistic of a model that had the Matsuda index and ΔI_0–30/ΔG_0–30 as independent variables (0.875 vs. 0.882, P = 0.044) (Table 3). Matsuda index, ΔI_0–30/ΔG_0–30, and I/G_{AUC 60–120} were independent predictors even after entering IGT into the model. In contrast, the C statistic was not significantly changed by either S1Ph_OGTT (0.877, P = 0.828) or S2Ph_OGTT (0.877, P = 0.610).

Table 3.

Odds ratio of indices of insulin sensitivity and insulin secretion for predicting the 7.8-year incidence of diabetes by multiple logistic regression analysis

	Matsuda index	ΔI0–30/ΔG0–30	I/GAUC 60–120	S1PhOGTT	S2PhOGTT	C statistic	P
Model 1	0.24 (0.18–0.31)	0.28 (0.22–0.37)	–	–	–	0.875	–
Model 2	0.09 (0.06–0.14)	–	0.21 (0.15–0.28)	–	–	0.858	0.076
Model 3	0.11 (0.07–0.17)	0.41 (0.31–0.54)	0.37 (0.26–0.54)	–	–	0.882	0.044
Model 4*	0.16 (0.10–0.25)	0.43 (0.32–0.58)	0.46 (0.31–0.68)	–	–	0.888	< 0.001
Model 5	0.11 (0.08–0.16)	–	–	0.24 (0.18–0.32)	–	0.873	0.314
Model 6	0.15 (0.10–0.23)	0.50 (0.32–0.79)	–	0.46 (0.28–0.76)	–	0.877	0.792
Model 7	0.10 (0.07–0.14)	–	–	–	0.22 (0.16–0.30)	0.873	0.556
Model 8	0.14 (0.09–0.22)	0.51 (0.33–0.80)	–	–	0.44 (0.25–0.75)	0.877	0.610

Odds ratios expressed for 1 standard deviation unit increase. Age, sex, ethnicity, BMI and family history of diabetes were included as covariates in all eight models.

^*Impaired glucose tolerance (IGT) was also added to Model 4 as a covariate.

I_0–30/G_0–30, insulinogenic index from 0 to 30 min; I/G_{AUC 60–120}, ratio of area under the insulin curve to area under the glucose curve from 60 to 120 min; and S1Ph_OGTT and S2Ph_OGTT, Stumvoll first phase and second phase insulin release, respectively. P-values are for the comparison with Model 1.

Models predicting incident diabetes that contained the product, Matsuda index × I/G_{AUC 60–120} or Matsuda index × ΔI_0–30/ΔG_0–30, had similar predictive discrimination to those that contained the individual components (see the Supporting Information, Table S2).

Heterogeneity analyses

In a model with the Matsuda index, ΔI_0–30/ΔG_0–30 and I/G_{AUC 60–120} as independent variables, we examined effect modification by testing the statistical significance of the interaction of sex, ethnicity, family history of diabetes and glucose tolerance status on the relation of Matsuda index, ΔI_0–30/ΔG_0–30 or I/G_{AUC 60–120} to incident diabetes. All these potential interaction effects had a P-value ≥ 0.16, except for interaction terms ethnicity × ΔI_0–30/ΔG_0–30 (P = 0.041) and ethnicity × I/G_{AUC 60–120} (P = 0.086). Interaction terms Matsuda index × ΔI_0–30/ΔG_0–30, Matsuda index × I/G_{AUC 60–120}, and ΔI_0–30/ΔG_0–30 × I/G_{AUC 60–120} were not significant either (P ≥ 0.35). Matsuda index, ΔI_0–30/ΔG_0–30, and I/G_{AUC 60–120} were independent predictors of future diabetes in varying categories of age, sex, ethnicity, family history of diabetes, BMI and glucose tolerance (Fig. 1). There were, however, two exceptions: confidence intervals crossed 1.0 with I/G_{AUC 60–120} in individuals aged 25–44 years [odds ratio (OR) 0.70 (0.36–1.35)] and with ΔI_0–30/ΔG_0–30 in those with IGT [OR 0.59 (0.34–1.01)].

FIGURE 1.

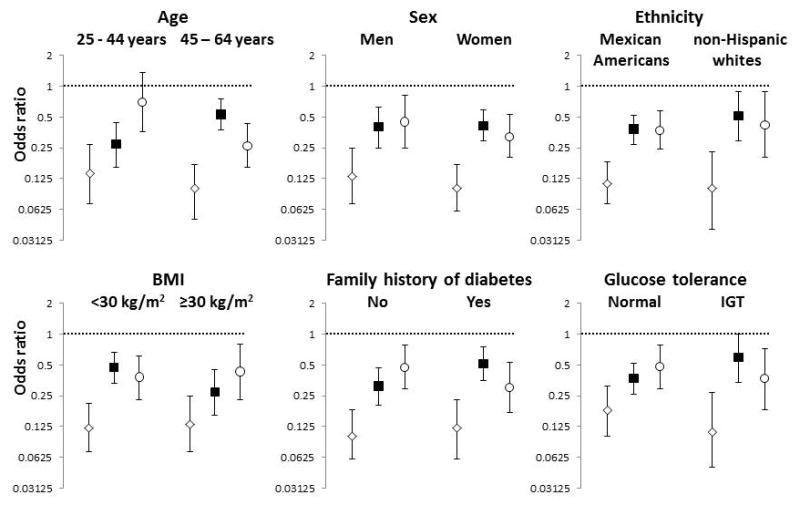
Diabetes risk associated with Matsuda index, ΔI_0–30/ΔG_0–30 (insulinogenic index from 0 to 30 min) and I/G_{AUC 60–120} (ratio of area under the insulin curve to area under the glucose curve from 60 to 120 min) stratified by age, sex, ethnicity, BMI, family history of diabetes and glucose tolerance status. Open diamonds, Matsuda index; closed square, ΔI_0–30/ΔG_0–30; open circle, I/G_{AUC 60–120}. Age, sex, ethnicity, BMI, family history of diabetes, Matsuda index, ΔI_0–30/ΔG_0–30 and I/G_{AUC 60–120} were included in all models. The panels present the odds ratio reflecting the change in risk of future diabetes for one standard deviation unit increase. IGT, impaired glucose tolerance.

Discrimination

The Hosmer–Lemeshow test yielded a chi-square of 16.1 (P = 0.041) for the model without I/G_{AUC 60–120} and 9.1 (P = 0.332) for the model with I/G_{AUC 60–120}. This indicates that the model with I/G_{AUC 60–120} was better calibrated (higher agreement between observed incidence of diabetes and predictions). Almost one-fifth of individuals with moderate and strong risk of future diabetes were reclassified by the addition of I/G_{AUC 60–120} (66 and 98 individuals were properly reclassified to a higher and lower risk category, respectively) (Table 4a). The net reclassification improvement was 0.13 (P < 0.001) after the addition of I/G_{AUC 60–120} and the integrated discrimination improvement was 0.033 (P < 0.001). A statistically significant integrated discrimination improvement indicates that the addition of I/G_{AUC 60–120} improved the discriminatory property of the model with age, sex, ethnicity, BMI, family history of diabetes, Matsuda index and ΔI_0–30/ΔG_0–30.

Table 4.

Comparison of predicted and observed risks of 7.5-year incidence of diabetes in models with and without I/G_{AUC 60–120}

	Model A plus I/GAUC 60–120
(a)	< 1% yearly risk	1–5.9% yearly risk	≥ 6% yearly risk	% Reclassified
(a) Model A*
< 1% yearly risk
Total, n	848	43	0	–
%†	95.2	4.8	–	4.8
Observed yearly risk‡	0.2	1.6	-	-
1–5.9% yearly risk
Total, n	81	408	23	–
%	15.8	79.7	4.5	20.3
Observed yearly risk	0.7	2.9	10.4	–
≥ 6% yearly risk
Total, n	0	17	75	–
%	–	18.5	81.5	18.5
Observed yearly risk	–	2.4	8.4	–
(b)Model B§	Model B and I/GAUC 60–120
< 1% yearly risk
Total, n	907	51	0	–
%†	94.7	5.3	–	5.3
Observed yearly risk‡	0.2	1.3	-	–
1–5.9% yearly risk
Total, n	57	348	15	–
%	13.5	82.9	3.6	17.1
Observed yearly risk	0.7	3.0	8.0	–
≥ 6% yearly risk
Total, n	0	12	105	–
%	–	10.3	81.5	10.3
Observed yearly risk	–	2.4	8.4	–

All estimated and observed risks represent yearly risk of incident diabetes.

^*Model A included age, sex, ethnicity, family history of diabetes, BMI, Matsuda index and ΔI_0–30/ΔG_0–30 (insulinogenic index from 0 to 30 min) as independent variables.

^†Per cent classified in each risk stratum by the model with I/G_{AUC 60–120} (ratio of area under the insulin curve to area under the glucose curve from 60 to 120 min).

^‡Observed proportion of participants developing diabetes in each category.

^§Model B included independent variables of Model A plus impaired glucose tolerance.

The addition of I/G_{AUC 60–120} also had additional value to a different model that included all the independent variables of the previous model plus impaired glucose tolerance (Table 4b). A total of 66 and 69 individuals were correctly reclassified to a higher and lower risk category, respectively. The net reclassification improvement was 0.05 (P = 0.043) and the integrated discrimination improvement was 0.018 (P < 0.001).

Discussion

The Insulinogenic Index, I/G_{AUC 60–120}, predicts incident diabetes independently of ΔI_0–30/ΔG_0–30. The fit of models is excellent across varying categories of age, sex, family history of diabetes and BMI. Equally good fit is demonstrated in both high-risk Mexican Americans and low-risk non-Hispanic whites as well as in individuals with normal glucose tolerance and in those with impaired glucose tolerance. The index I/G_{AUC 60–120} has additional value for predicting incident diabetes beyond the predictive discrimination of Matsuda index and ΔI_0–30/ΔG_0–30.

Most subjects with hyperglycaemia have impaired β-cell function [24]. ΔI_0–30/ΔG_0–30, the capacity for insulin response during the early OGTT period, has shown to correlate weakly with first- and second-phase insulin secretion (r = 0.25 and r = 0.22, respectively) as measured by hyperglycaemic clamp studies [11] and more strongly with first-and second-phase insulin secretion by intravenous glucose tolerance test (r = 0.58 and r = 0.47, respectively) [20]. ΔI_0–30/ΔG_0–30 has been described as a predictor of diabetes in multiple studies [6–8]. The current results indicate that ΔI_0–30/ΔG_0–30 is a strong predictor of incident diabetes independently of a measure of insulin secretion derived from the late OGTT period.

Stumvoll et al. [11] stated that S1Ph_OGTT and S2Ph_OGTT had more robust correlations with first- and second-phase insulin release by the hyperglycaemic clamp technique than did ΔI_0–30/ΔG_0–30 and homeostasis model assessment of β-cell function. In this study, however, both S1Ph_OGTT and S2Ph_OGTT had identical relationships with clamp-derived first phase (r = 0.78) and second phase (r = 0.79) insulin release [11]. This suggests that S1Ph_OGTT and S2Ph_OGTT are highly correlated, as do our results (r = 0.99 for the relationship between S1Ph_OGTT and S2Ph_OGTT). Both indices increase the predictive discrimination of the Matsuda index, but neither of them increases the predictive discrimination of models with ΔI_0–30/ΔG_0–30.

Measured by C statistic [25,26], I/G_{AUC 60–120} increases the predictive discrimination of the Matsuda index and ΔI_0–30/ΔG_0–30. Measures of calibration and reclassification [27,28], which are more sensitive tests of improvement in model discrimination, also indicate that I/G_{AUC 60–120} adds discriminatory value to the Matsuda index and ΔI_0–30/ΔG_0–30. This may be relevant for predicting a future outcome in individuals with a moderate or significant risk. For example, the yearly risk of future diabetes is 1.0% in a hypothetical 50-year-old non-Hispanic white woman who has no family history of diabetes, BMI of 25 kg/m², no impaired glucose tolerance, a Matsuda index of 2 and ΔI_0–30/ΔG_0–30 of 1.5. The addition of I/G_{AUC 60–120} to the prediction model changes the estimated yearly risk of future diabetes to 0.6% if I/G_{AUC 60–120} is 1.5 and to 2.5% if I/G_{AUC 60–120} is 0.5. A much more relevant change occurs in a 50-year-old non-Hispanic white woman who has no family history of diabetes, BMI of 30 kg/m², impaired glucose tolerance, a Matsuda index of 2 and ΔI_0–30/ΔG_0–30 of 1.5. The estimated yearly risk is 4.7% according to the model without I/G_{AUC 60–120}. The addition of this variable changes the yearly risk to 2.3% if I/G_{AUC 60–120} is 1.5 and to 9.9% if I/G_{AUC 60–120} is 0.5. Consequently, I/G_{AUC 60–120} may be useful for the classification of individuals in clinical studies.

The risk estimate that uses I/G_{AUC 60–120} is a more accurate image of actual risk for all 164 reclassified participants. The proportion of reclassified individuals at low risk (< 1% per year) is relatively small, but a more significant proportion occurs in those at moderate (1–6% per year) and high risks (≥ 6% per year). Thus, I/G_{AUC 60–120} would have a significant effect in the stratification of individuals in a hypothetical population. For example, if the prediction model with age, sex, ethnicity, BMI, family history of diabetes, Matsuda index and ΔI_0–30/ΔG_0–30 is applied to a cohort of 100 000 individuals without diabetes from San Antonio, 59 600 of them will be considered at low risk (< 1% yearly risk), 34 200 at moderate risk (1–5.9% yearly risk) and 6200 at high risk (≥ 6% yearly risk) for developing diabetes. The addition of I/G_{AUC 60–120} will reclassify 10 951 individuals: from the low-risk category, 2861 will now be considered at moderate risk; from the moderate-risk category, 5404 will now be at low risk and 1539 at high risk; and from the high-risk category, 1147 will be at moderate risk. Thus, I/G_{AUC 60–120} may have discriminatory value in epidemiological studies.

The relationship between acute insulin response and insulin sensitivity index, two measures derived from the frequently sampled intravenous glucose tolerance test, is hyperbolic [13,16]. A similar relationship has been described between two indices derived from the OGTT, insulin AUC to glucose AUC from 0 to 120 min and Matsuda index [16,29]. The product of these two indices, insulin secretion-sensitivity index-2, has a stronger association with the disposition index than products involving ΔI_0–30/ΔG_0–30 [29]. Unable to take into account the variability in the measurement of Matsuda index and I/G_{AUC 60–120} [13,16], our study cannot determine whether the relationship between these two indices is rectangular hyperbolic. However, our results indicate that the product, Matsuda index × I/G_{AUC 60–120} or Matsuda index × ΔI_0–30/ΔG_0–30, does not improve the ability to predict future diabetes of the individual components, as previously reported using direct measures [30].

In summary, measures of insulin secretion derived from the early and late OGTT periods are independent predictors of Type 2 diabetes. This holds in different subgroups including ethnic and glucose tolerance categories. As the OGTT is relatively easy to perform, insulin secretory indices from the early and late OGTT periods may be useful for understanding the natural history of diabetes.

Supplementary Material

Supp Table S1-S2

Table S1. Relation of Matsuda index to early and late oral glucose tolerance testing (OGTT) measures of β-cell function

Table S2. C statistic of models predicting the 7.8-year incidence of diabetes by multiple logistic regression analysis. Please note: Wiley-Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.