Tuberculosis: Old problems and new approaches

In New York City from 1985 to 1992, reported cases of tuberculosis rose by more than 20%. This followed a 30-year period of decline in the incidence of the disease. The reasons for the reversal are many and include the role of HIV-1 infection in enhancing disease progression and transmission, homelessness in the city, the emergence of multi-drug-resistant strains of the etiological agent (Mycobacterium tuberculosis), and a failing public health infrastructure. Globally, the scale of the tuberculosis problem is enormous, with the World Health Organization estimating that a third of the world’s population is infected with the bacterium and predicting 90 million new cases in the decade up to the year 2000 (1). As the magnitude of the problem continues to grow, the dream of eradication fades into the distant future, despite the fact that the treatment of the disease by mass chemotherapy is a very cost-effective public health intervention. Tuberculosis is likely to remain one of the 10 most important causes of premature mortality worldwide in the coming two decades.

In this issue, Murray and Salomon (2) examine, by the use of a simple mathematical model of transmission, the potential impact of different forms of intervention to control M. tuberculosis. They reach an important conclusion, namely, that active case finding followed by treatment, if orchestrated on a global scale, could save 23 million cases of tuberculosis between 1998 and 2030. Furthermore, they argue that a vaccine of moderate efficacy (e.g., 50%), again used on a global scale, could lower the incidence of disease by 36 million and save 9 million lives over the same time interval. These predictions are likely to be influential. Recent experience suggests that the production of numerical estimates of the burden of morbidity and mortality caused by a given etiological agent confer authority in the process of setting global public health and research priorities. Since the publication of the World Bank report on the global burden of disease (3), it has become fashionable in international health policy circles to wield global estimates of the morbidity and mortality induced by particular diseases, whether it be malaria, HIV, intestinal worms, or tuberculosis. Sometimes, it is difficult not to get the impression that one lobby group is determined to outdo another in terms of quoting disease statistics that suggest that their disease is more prevalent and important than others. The quality of advocacy often seems to be more important than the reliability of the data in determining how international health priorities are set. Once figures are published, their numerical form, and repetition in subsequent publications, confers an aura of scientific validity and robustness. A similar fashion can be observed in health economics, where global estimates of morbidity and mortality underpin the production of figures for the potential cost-benefit of different forms of intervention. Again, numerical estimates, mathematical models, and frequent use typically confer a sense of authority, which in turn plays a key role in advocacy.

How reliable are such studies as guides to the setting of international health priorities and as tools to identify the most cost-effective interventions? It is, of course, easy to be critical in light of the observation that few countries in the world, especially in poor regions, have the appropriate infrastructures to produce reliable statistics on the prevalence or incidence of even the common infectious diseases that are easy to diagnose. Published estimates of global prevalence may be incorrect not just by factors, but perhaps even by orders of magnitude. Some estimates are more reliable than others, particularly if a simple and reliable diagnostic tool (i.e., serology for certain viral infections) has been used extensively in population screening in many different countries. However, this is the exception rather than the rule, and, in most cases, including malaria and tuberculosis, published figures should be interpreted with great caution at present. More emphasis should be placed on acquiring more extensive and reliable data, and published studies should highlight the major areas of uncertainty and try to give some indication of the confidence bounds surrounding any numerical estimate.

In a world in which many countries are subject to an unacceptably high burden of disease caused by treatable infections, action to intervene is clearly a more palatable message than cries for more surveys and more research. Tuberculosis is an example where health professionals may argue about the precise scale of the problem, but all agree that it is large and that the need to do more is urgent. The key issue is, therefore, how best to use limited resources to reduce the burden of disease by different forms of intervention. Here, accuracy is much more important because results can have an immediate effect on policy and subsequent practice. Simple mathematical models often underpin such research because a quantitative template is essential for comparison and prediction. The use of mathematical methods in biomedical research has grown rapidly in the past decade, and applications in epidemiological research have been particularly influential as guides to understanding and templates for parameter estimation and policy formulation (4). However, relatively few health professionals are familiar with the scientific methods used in model formulation and analysis, and, as such, predictions are often accepted with little critical scrutiny.

In some fields, such as the vaccine-preventable childhood viral infections, models have proved to be excellent predictive tools, both in the interpretation of epidemiological pattern and in defining the impact of control interventions. In part, this is caused by the extent of our understanding of the processes that determine the typical course of infection within a patient and those that determine transmission between hosts. It also is caused by the quality of the available epidemiological data (e.g., cross-sectional and longitudinal serological surfaces for a variety of populations) and the care that has been taken to estimate parameters and compare model predictions with observed epidemiological pattern. In contrast, many uncertainties surround key epidemiological processes for M. tuberculosis infection. These include the determinants of observed patterns of the age- and gender-specific incidences of infection and disease (Fig. 1). They also include the factors that lead to disease progression post-infection (only a small fraction of those infected appear to develop serious disease—although this fraction may vary widely between populations) and whether super-infection, reinfection, and reactivation are common events. In particular, much controversy has surrounded the interpretation of the rise in disease incidence in adult age classes after the decay in the teenage years. Is this a consequence of reactivation of infection acquired early in life, or does it reflect new infections?

Figure 1.

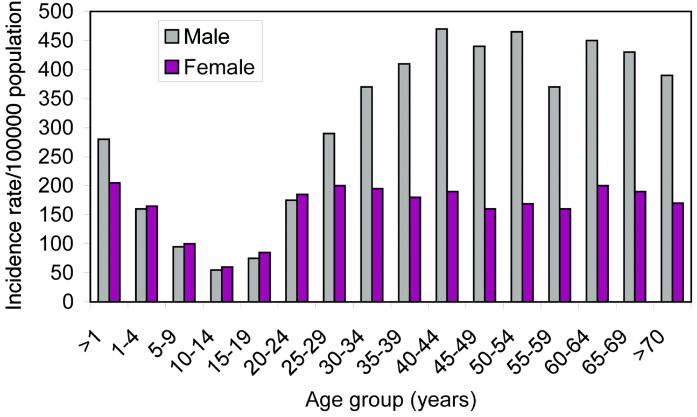
Age- and gender-specific incidence of tuberculosis in South Africa in 1993 (14).

Recent research advances have the potential to shed much light on many of these issues. Of particular note has been the sequencing of the whole genome of M. tuberculosis (the H37Rv genome) by Cole et al. (5). This immediately led to the identification of possible sites of antigenic variation [polymorphic GC rich sequence regions (PGRS) of the genome], which may help explain the persistent nature of the infection plus the ability to super-infect an already infected patient. Other notable advances include the beginnings of the identification of host genes that predispose to infection and disease (6, 7). It seems probable that the traits of susceptibility to tuberculosis and pathogenesis after infection are complex and controlled by many genes. The use of both DNA fingerprinting, plus secondary genotyping using the PGRS regions, in molecular epidemiological studies is also a very useful advance. The techniques can help to ascertain “who acquires infection from whom” and to discriminate between super-infection, reinfection, or reactivation (8, 9). For example, the method has added some support to the argument that much disease in adult age classes may be caused by reactivation as opposed to reinfection (10).

In the construct and analysis of tuberculosis transmission models, two major problems present themselves. First, there are structural issues, such as, what assumptions should be made with respect to the factors that generate the observed age-specific incidence profiles (Fig. 1) (is the key issue reactivation or reinfection?), and how does HIV-1 infection influence pathogenesis and infectiousness? Second, once structure has been decided, what parameter assignments should be made to characterize various biological and epidemiological processes, such as the duration and intensity of the infectiousness of an infected patient? Conventional approaches in the engineering or physical sciences would entail the examination of the sensitivity of model outcomes to key uncertainties. Latin Hypercube Sampling (LHS) would be one option, where ranges, and distributions within the defined range, are set for the uncertain parameters and are used both to examine the diversity of possible outcomes and to define confidence intervals (11). In disease transmission models, a key parameter, in which small changes in value create large differences in disease prevalence or incidence, is that which scales the net rate of transmission (measured in epidemiological terms as the age-specific per capita force or rate of infection). In the case of tuberculosis, the measurement of this parameter is surrounded by much uncertainty, caused in part by the absence of a simple and reliable diagnostic test and in part to uncertainties over reactivation and reinfection. Furthermore, much variability appears to pertain in terms of its magnitude in different locations and even in different communities in defined locations. Analyses of the relative impacts of different interventions will, therefore, often have wide confidence bounds that may overlap in specific cases.

The approach adopted by Murray and Salomon is to stick with one set of assumptions and a range of possible parameter values for five regions of the world (in different simulations, the intensity plus effectiveness of different control interventions are varied). Unfortunately, no attempt is made to gain analytical understanding of the model’s properties (e.g., at equilibrium) and how that varies as a result of different epidemiological assumptions or to define ranges for outcomes related to the degree of uncertainty surrounding key epidemiological parameter assignments. It is, therefore, difficult to establish the reliability of the predictions concerning the relative merits of different forms of intervention, such as active case finding and vaccination with low efficacy products. The key issue here is that the numerical estimates produced by the model are likely to enter the policy arena and influence practice. Researchers who develop these types of simple models, and who use them in a precise numerical predictive mode, ideally should attempt to validate outcomes against different epidemiological databases (e.g., age-specific incidences of infection and associated disease). Second, they also should provide the scientific community and policy makers with some idea of how sensitive predictions are to key assumptions and uncertainties, particularly because the methods used are not familiar to most health professionals.

Confidence in any prediction obviously rises if different analyses using different models come up with the same overall conclusion. A similar study has just been completed by Dye et al. based on a slightly more sophisticated model with crude age structure (12). This study places much greater emphasis on uncertainty but, encouragingly, comes to somewhat similar conclusions. The key messages that can be drawn from the papers by Murray and Salomon and Dye et al. are as follows. First, and most importantly, the work greatly strengthens the message that much more must be done globally to control tuberculosis in poor regions of the world. The problem is likely to get worse rather than better in the coming decade. The burden of disease is very high, even given much frailty in the estimates of global incidence and changes therein over the coming decades. Second, investing huge amounts of money and effort into global tuberculosis programs should not take place without some form of quantitative analysis of the relative benefits of different approaches. Murray and Salomon are to be applauded for their bravery in attempting this difficult task. Someone has to start somewhere, despite the many uncertainties. However, next steps must involve detailed sensitivity and validation analyses and attempts to put the benefits in a cost and practicality framework.

Mathematical model formulation in the biomedical sciences more often acts to tell you what you do not know rather than providing a precise predictive tool. This is clearly the case for tuberculosis, where much uncertainty still surrounds key aspects of transmission and pathogenesis. New molecular and genetic research tools offer much promise in the resolution of many of these unknowns, provided they are used within large-scale and well designed longitudinal epidemiological studies that have relevance in a regional as well as a community setting (13). Finally, in the poorest regions of the world, where tuberculosis is most prevalent, such as sub-Saharan Africa, the epidemic of HIV-1 will complicate severely any predictions involving case finding and chemotherapeutic treatment. What AIDS has taught many clinicians is that most antiinfective agents only work effectively within patients with competent immune systems. In areas of high or rising HIV-1 prevalence, an immediate priority is to attempt to slow the spread of the virus to limit the pathogenesis and transmissibility of infection in the high fraction of people who typically acquire M. tuberculosis. This will help to maximize the benefit accruing from any mass tuberculosis case-finding and treatment program.