The evolution of optimal female mating rate changes the coevolutionary dynamics of female resistance and male persistence

Abstract

Mating decisions usually involve conflict of interests between sexes. Accordingly, males benefit from increased number of matings, whereas costs of mating favour a lower mating rate for females. The resulting sexual conflict underlies the coevolution of male traits that affect male mating success (‘persistence’) and female traits that affect female mating patterns (‘resistance’). Theoretical studies on the coevolutionary dynamics of male persistence and female resistance assumed that costs of mating and, consequently, the optimal female mating rate are evolutionarily constant. Costs of mating, however, are often caused by male ‘persistence’ traits that determine mating success. Here, we present a model where the magnitude of costs of mating depend on, and evolve with, male persistence. We find that allowing costs of mating to depend on male persistence results in qualitatively different coevolutionary dynamics. Specifically, we find that male traits such as penis spikes that harm females are not predicted to exhibit runaway selection with female resistance, in contrast to previous theory that predicts indefinite escalation. We argue that it is essential to determine when and to what extent costs of mating are caused by male persistence in order to understand and accurately predict coevolutionary dynamics of traits involved in mating decisions.

1. Introduction

The outcome of reproductive interactions does not always reflect the best evolutionary interests of both sexes. Accordingly, mating decisions often result in sexual conflict between males and females [1]. A commonly observed example of sexual conflict involves the mating rate, where males generally benefit from increased number of matings, whereas direct and indirect costs of mating [2,3] favour a lower mating rate for females [4,5]. Consequently, females would benefit from traits that limit the mating rate to a value that is closer to the female optimum (referred to as ‘resistance’ or preference [6]), whereas male traits that elevate the mating rate would be favoured in males (referred to as ‘persistence’). Selection for counteracting traits as a result of sexual conflict can lead to a coevolutionary arms race between males and females [1,7].

In contrast to the accumulating evidence from empirical as well as comparative research that coevolutionary arms races may be common in nature [8–12], there has been a relatively limited number of theoretical studies that focus on the coevolutionary dynamics of male and female traits under sexual conflict [13,14]. In a verbal hypothesis, Holland & Rice [7] predicted that sexual conflict over mating rate would result in exaggerated male traits and discriminating females through a chase-away process. This hypothesis was formalized by Gavrilets et al. [15] in a model that examined the coevolutionary dynamics of a male persistence trait and a counteracting resistance trait in females. The model of Gavrilets et al. [15] confirmed the predictions of Holland & Rice [7], and showed that sexual conflict over mating rate would often be expected to result in a coevolutionary arms race between male display trait and female preference. Rowe et al. [16] later extended the model of Gavrilets et al. [15] and found that considering the evolution of the shape of the female preference function (‘sensitivity’) would generally not result in escalating arms races, as previously predicted, but in patterns of escalation, retreat and indifference. Finally, models of Gavrilets et al. [15] and Rowe et al. [16] both concluded that natural selection can prevent further escalation in male and female traits and shut down the coevolutionary arms race.

Theoretical models on the coevolution of male and female reproductive traits under sexual conflict over mating rate assume that significant costs of mating for females result in an optimal mating rate in females that is lower than that of males [15,16]. While mating can be harmful owing to reproductive interactions such as aggressive courtship or harassment by males [17,18], the act of mating per se can also involve costs for females. On the one hand, these costs of mating to females might not depend on male and female reproductive trait values. For example, infection of a female with pathogens transmitted by males [19] or decreased lifespan owing to the presence of gonadotropic substances transferred during copulation [20,21] might decrease female fitness by a constant magnitude per mating, independent of male traits involved in mating. On the other hand, the magnitude of costs of mating might depend directly or indirectly on the value of male ‘persistence’ traits that determine male mating success. For example, male genital structures such as penis spines in the seed beetle Callosobruchus maculatus that increase male mating success by serving as an anchor during copulation might also physically harm females [22]. Similarly, physical traits such as claspers in male water striders [23] and fireflies [24] that improve male mating success might also increase the duration of mating, and consequently, energetic costs [2] and the risk of predation [25] or injury [1] to females. Therefore, costs of mating per se to females and, as a result, the optimal female mating rate may either be constant or may vary with male persistence traits that are involved in mating.

Previous studies that investigated the coevolution of male and female traits under sexual conflict assume that costs of mating to females and the optimal female mating rate are constant over ecological and evolutionary time [15,16]. Here, we extend existing models and investigate the coevolutionary dynamics in biological cases where costs of mating per se to females are not constant, but vary with male traits that determine male mating success. Our analyses show that changes in costs of mating and the optimal female mating rate as a result of the evolution of male traits lead to qualitatively different patterns of coevolutionary dynamics between sexes. For example, in cases where previous theory predicted indefinite exaggeration of the male trait or stable patterns of escalation and retreat [15,16], we find that costs of mating for females can shut down the coevolutionary dynamics or even cause the male persistence trait to disappear from the population. Our results imply that predicting the coevolutionary dynamics of male persistence and female resistance traits will require knowing whether or not the magnitude of the cost of mating for females, and hence the degree of sexual conflict over mating rate is determined by male persistence traits that affect male mating success.

2. The model

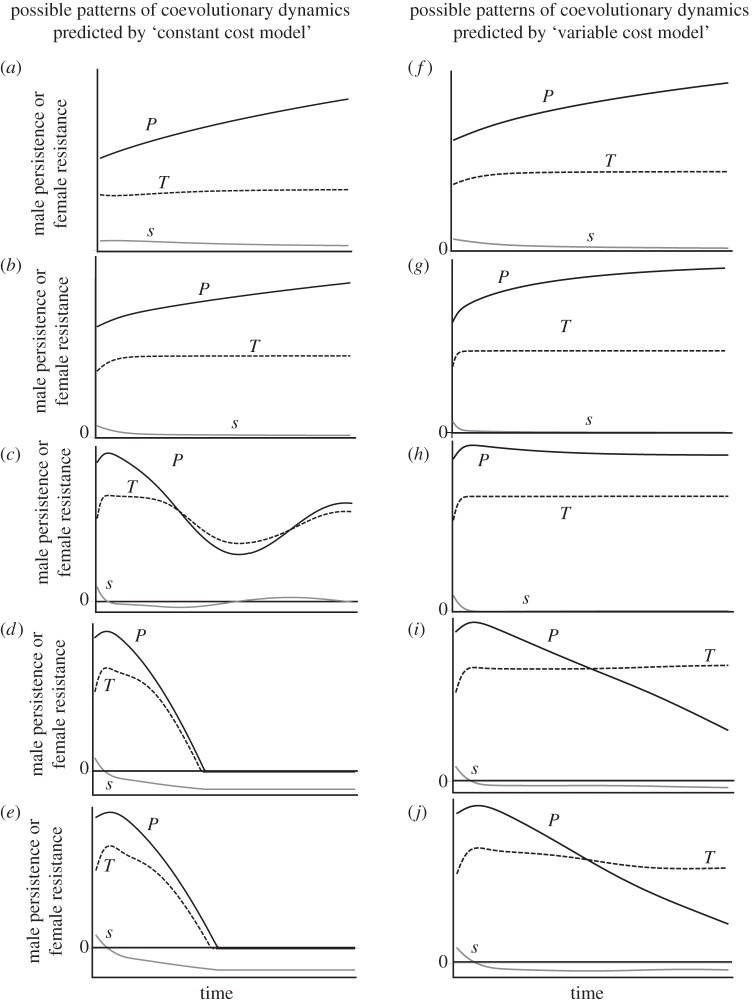
In contrast to previous studies where the optimal mating rate is assumed to be an evolutionarily fixed parameter, our model allows the optimal mating rate to arise dynamically from the interplay between costs and benefits of mating. Accordingly, we develop a fitness function (see later text) that incorporates explicitly the costs and benefits of mating for females. In our model, we assume that mating takes place in discrete reproductive bouts or periods, and the fecundity of females in a given reproductive period depends on the number of matings such that an increase in the number of matings results in greater reproductive success, for example, owing to increased genetic diversity of the offspring. We further assume that a greater number of matings also imposes greater mortality on females (but not on males; hence, sexual conflict over mating rate) and decreases the probability of survival to the next reproductive period. We calculate the expected female lifetime fitness through the sum of expected reproductive success of females in each reproductive period. Following the methodology of previous studies, we analyse this fitness function with a simplified quantitative genetic approach and estimate the coevolutionary change in the male trait and the female preference. In our analyses, we first assume that the cost of mating per se to females does not depend on the male trait that affects male mating success (‘constant cost model’), which is analogous to the assumptions of previous models. We then assume that the cost of mating depends on the male trait value (‘variable cost model’) and investigate if this assumption leads to qualitatively different patterns of coevolutionary dynamics. Our analyses focus particularly on asking whether the predicted qualitative patterns of the coevolutionary dynamics of male persistence and female resistance include indefinite escalation, the loss of either male persistence or female resistance or a stable equilibrium of both traits. Finally, in all of our analyses, we assume a population with discrete, non-overlapping generations.

Previous models of the evolution of female choice under sexual conflict [15,16] focused on the female sensory system and, consequently, on male display traits such as bright coloration or patch size that affect male mating success. In these models, mating decisions are an outcome of the interplay between a male trait P (‘persistence’) and female preference (or ‘resistance’) for the male trait that is determined by two parameters of a sigmoidal function: the threshold T and the sensitivity (or shape) s. The probability of mating between a male with trait value P and a female with preference determined by values of T and s is given as

2.1

It is important to note that, even though we follow the terminology of previous theoretical studies and refer to the male trait and the female preference as ‘persistence’ and ‘resistance’, respectively, our model does not focus on traits that are involved in costly harassment or mating struggles, but on male traits that increase mating success but harm females directly or indirectly during copulation, and female preference or choice traits that affect the outcome of mate competition among males. Accordingly, we adopt the modelling framework described earlier, and investigate the evolution of female preference under biological situations where a trait that affects male mating success also harms females and, therefore, constitutes a cost of mating per se. In our model, we summarize costs of mating per se through their effects on mortality, and assume that female mortality increases with the number of matings. Accordingly, in a population of males with persistence values P, the mortality of a female per reproductive period, μ_f,t, with threshold T and sensitivity s is

2.2

where b_f is baseline female mortality parameter, β is the baseline cost of mating and M_t is the number of males available for mating in a given time period. It is important to note that the number of males available for mating and, consequently, female mortality vary among reproductive periods owing to male mortality (see later text). The parameter γ denotes the degree to which the cost of mating (through mortality) depends on the male trait value. Accordingly, setting γ to zero implies that the cost of mating does not depend on the male trait value and corresponds to the ‘constant cost model’, while positive values of γ correspond to the ‘variable cost model’. Finally, female sensitivity and threshold can be under natural selection towards their respective optima, θ_s and θ_T. Deviations from these optima increase the female mortality rate, depending on the strength of natural selection determined by parameters α_s and α_T.

In contrast, mating is much less costly for males, which underlies the sexual conflict between males and females over mating rate. Accordingly, we assume that males have a mortality rate that does not depend on the number of matings. We give the male mortality rate per reproductive period as

2.3

where b_m is the male baseline mortality parameter. In our calculations of male mortality, we consider the possibility that male persistence is under natural selection towards an optimum given by the parameter θ_P and deviations from this optimum will increase the mortality rate, depending on the strength of natural selection on male persistence given by the parameter α_P.

Finally, we calculate female fitness through discrete reproductive periods, where female reproductive success in a given period increases with the number of matings, owing to, for example, increased genetic diversity of the offspring [26]. We assume, however, that the increase in expected reproductive success of a female with the number of matings is limited by female fecundity. Accordingly, in a single reproductive period (e.g. between times t and t + 1), the number of offspring produced by a female with threshold T and sensitivity s in a population of males with persistence P is

2.4

where f_b is the female fecundity, and ε determines how strongly expected female fitness increases with the number of matings. The assumption of an increasing female fitness with the number of matings, combined with the cost of mating for females, results in an intermediate mating rate that is optimal for females.

Using the equations mentioned earlier, the expected lifetime reproductive success, W_f, of a female with threshold T and sensitivity s in a population of males with persistence P is found as

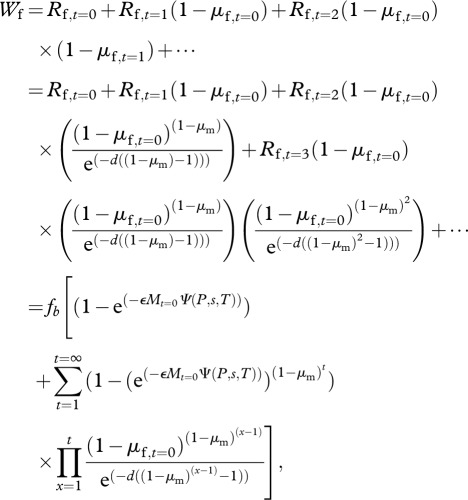2.5

where 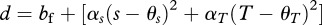from equation (2.2).

The expected lifetime reproductive success of a mutant female with threshold T^* and sensitivity s^*, W_f^*, in a population of males with persistence P is found by replacing s and T with s^* and T^* in equations (2.3)–(2.5).

Assuming that sperm competition among males follows a ‘fair raffle’ principle [27], the expected lifetime fitness of a mutant male with persistence P^*, W_m^*, in a population of males with persistence P and females with threshold T and sensitivity s is found by revising equation (2.5) as

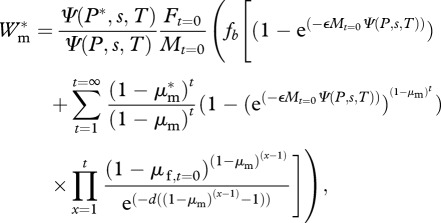2.6

where F_{t =0} and M_{t =0} are the number of females and males in the population, respectively. Equations (2.5) and (2.6) also show that in a population of M_{t =0} males with persistence P and F_{t =0} females with threshold T and sensitivity s, total fitness gained by males is equal to total fitness gained by females, and that our model is self-consistent.

Fitness equations (2.5) and (2.6) incorporate explicitly benefits and costs of mating (i.e. increased reproductive success and mortality, respectively). This approach allows costs of mating and, consequently, the optimal mating rate to vary dynamically with the male trait involved in mating, in contrast to assigning the optimal mating rate as a fixed population parameter. Following Rowe et al. [16], we use equations (2.5) and (2.6) to approximate the coevolutionary dynamics of average values of P, s and T through a simplified quantitative genetic approach [28,29], where the change in average male and female traits is found as

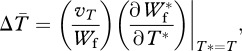2.7

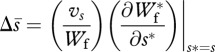2.8

and

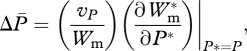2.9

where v_P, v_s, v_T are additive genetic variances of respective traits. In these approximations, we make standard quantitative genetic assumptions of a symmetric unimodal trait distribution and small additive genetic variances [29]. Owing to the complexity of equations that give expected lifetime male and female fitness (i.e. equations (2.5) and (2.6)), we determine the change in average trait values through numerical approximations using Mathematica v. 6.0 [30]. Parameters included in our model are summarized in table 1.

Table 1.

Key variables used in the model.

variable	definition
P	male persistence
s	female sensitivity
T	female threshold
Ψ(P,s,T)	probability of mating between a male with P, and a female with T and s
θP, θs, θT	naturally selected optimum of male persistence, female sensitivity and threshold, respectively
αP, αs, αT	strength of natural selection on male persistence, female sensitivity and threshold, respectively
μf, μm	female and male mortality, respectively
bm, bf	baseline male and female mortality parameter, respectively
Ft =0	number of females in the population
Mt =0	number of males in the population
β	parameter for the baseline cost of mating for females
γ	strength of the effect of male persistence on the cost of mating for females
vP, vs, vT	additive genetic variance in male persistence, female sensitivity and threshold, respectively
Wf, Wm	expected lifetime reproductive success of an individual female and male, respectively
fb	female fecundity
ε	the strength of increase in expected female fitness with the number of matings

3. Analysis of the model

The main question that we are aiming to answer with our model is whether allowing the cost of mating for females to depend on the male trait involved in mating would result in significantly different patterns than indefinitely escalating arms races and stable cycles of escalation and retreat predicted by previous models. In order to address this question in the face of the large number of parameters included in our model, we followed the following analysis strategy. First, we focused on the version of our model that corresponds to a ‘constant cost’ scenario and is analogous to previous models, where the cost of mating and, consequently, the optimal female mating rate do not vary with the male trait involved in mating (i.e. γ = 0). Using this ‘constant cost model’, we imposed various magnitudes of evolutionarily constant costs of mating for females and analysed the coevolutionary dynamics of male persistence and female resistance. This analysis helped us determine whether the ‘constant cost model’ produces the same predictions as previous theory and therefore constitutes a baseline for further analyses. Furthermore, as we consider explicitly costs and benefits of mating for females and allow the optimal mating rate to arise dynamically from our model, in contrast to previous theory where the optimal female mating rate was assumed an evolutionarily constant parameter [15,16], our analyses of the ‘constant cost model’ also helped us determine a baseline range of female mortality values where the baseline model produces the same predictions as previous theory. We then used the ‘variable cost’ version of our model (i.e. γ > 0) and allowed the mortality cost of mating for females to dynamically vary in this baseline range of female mortality values. We compared our analyses of the ‘constant cost model’ and the ‘variable cost model’ to determine whether considering male persistence traits that constitute a cost of mating for females results in novel patterns of coevolutionary dynamics, such as stable equilibria or the loss of male persistence or female resistance traits.

Following previous models, we used this analysis strategy to explore several scenarios of how male persistence and female resistance evolve. We first allowed only one aspect of the female resistance (only T or s) to evolve in the absence of natural selection. We then allowed both the threshold and the sensitivity to evolve. Finally, we considered natural selection on male and female traits and examined the coevolutionary dynamics of persistence and resistance. Using these analyses, we investigated whether considering variable cost of mating and optimal female mating rate results in qualitatively different patterns of coevolutionary dynamics of male persistence and female resistance than predicted by previous models.

4. Results

(a). Case 1: predicted dynamics when only female sensitivity evolves without natural selection

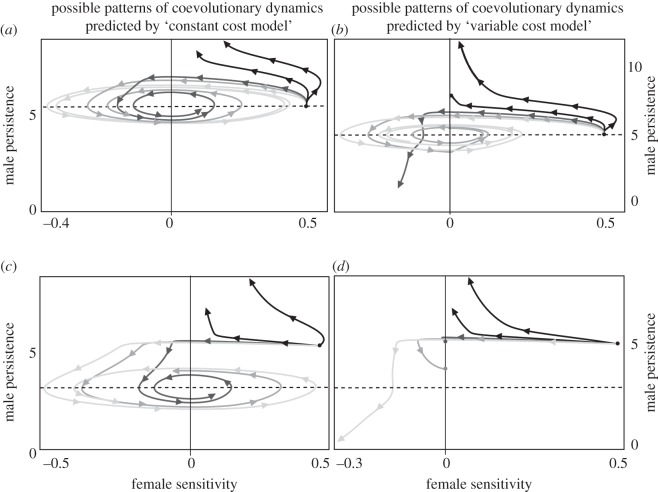
In the case where only female sensitivity and male persistence evolve, but the female threshold is evolutionarily static, our analyses indicate that allowing the cost of mating, and the optimal mating rate, to depend on male persistence trait qualitatively alters predicted coevolutionary dynamics (figure 1). Accordingly, for the baseline range of parameter values where the ‘constant cost model’ (as well as previous models [15,16]) predicts indefinite escalation of the male trait countered by a decreasing sensitivity by females, or a stable cycle of escalation and retreat (figure 1a,c), the ‘variable cost model’ predicts that male persistence traits that harm females during mating would not exhibit indefinite exaggeration, because greater costs of mating with more persistent males would result in selection for decreased female sensitivity and, eventually, female preference for less persistent males, shutting down the coevolutionary arms race (figure 1b,d). Furthermore, in contrast to predictions of previous theory, we found that female resistance may even cause harmful male persistence traits to disappear from the population, where female preference against persistent males would result in a decrease in male persistence, which in turn would decrease the cost of mating for females and further increase female preference for less persistent males (figure 1b,d).

Figure 1.

When only the female sensitivity can evolve, the ‘variable cost model’ gives qualitatively different predictions about the coevolutionary dynamics of male persistence and female resistance. Dashed lines denote the value of the female threshold used in the analyses. The ‘constant cost model’ predicts either a stable cycle of escalation and retreat, or an indefinite exaggeration of male persistence (a,c). The ‘variable cost model’, however, can shut down the exaggeration of male persistence and cause the male trait to disappear from the population (b,d). In (a,c), trajectories coloured black to light grey denote increasing cost of mating for females, given through parameter values β = 10⁻⁵, β = 2 × 10⁻⁵, β = 3 × 10⁻⁵, β = 4 × 10⁻⁵ and β = 5 × 10⁻⁵, respectively. Similarly, in panels b and d, trajectories coloured black to light grey are under increasing cost of mating, through parameter values γ = 10⁻⁶, γ = 2 × 10⁻⁶, γ = 3 × 10⁻⁶, γ = 4 × 10⁻⁶, γ = 5 × 10⁻⁶, with β = 10⁻⁵ across all analyses. Remaining parameter values are: F = M = 1000, v_P = v_S = 0.5, v_T = 0.0, α_P = α_s = α_T = 0.0, ε = 0.005, f_b = 100.

(b). Case 2: predicted dynamics when only female threshold evolves without natural selection

When only female threshold and male persistence evolve, but the female sensitivity is assumed to be evolutionarily static, our analyses show that allowing the cost of mating and the optimal female mating rate to depend on the male persistence trait does not affect qualitatively the predictions about the coevolutionary dynamics. Accordingly, for the same baseline range of parameters, we found that both the ‘constant cost model’ (that is analogous to previous models) and the ‘variable cost model’ predict an indefinitely escalating coevolutionary arms race between males and females (not shown), where increasing male persistence and, consequently, costs of mating are countered by increasing female threshold.

(c). Case 3: predicted dynamics when both female sensitivity and female threshold evolve without natural selection

Similar to the case where only female sensitivity evolves, our analyses show that allowing the cost of mating to depend on the male persistence trait significantly affects the coevolutionary dynamics when both female sensitivity and threshold evolve. Again, for the same baseline range of parameter values where the ‘constant cost model’ predicts indefinite escalation of the male trait (figure 2,b) or stable cycles of escalation and retreat (figure 2c), the ‘variable cost model’ predicts that male persistence traits that harm females during mating would not be infinitely exaggerated, because increasing costs of mating for females would select for decreasing sensitivity and, eventually, female preference against persistent males, shutting down the coevolutionary arms race (figure 2f–h). Furthermore, while the constant cost model predicts that the evolution of female sensitivity can result in the disappearance of both the male persistence trait and the female threshold (figure 2d,e), a significant positive female threshold is always maintained in the population at a stable value under the ‘variable cost model’ where the cost of mating depends on the male persistence trait (figure 2i,j).

Figure 2.

‘The variable cost model’ gives qualitatively different predictions about the coevolutionary dynamics of male persistence and female resistance, when both female threshold and sensitivity evolve. Similar to figure 1, (a–e) and (f–j) denote increasing cost of mating for females, under ‘constant cost’ and ‘variable cost’ models, respectively. The parameter value different from the analyses given in figure 1 is: v_T = 0.5. For the rest of the parameters, refer to figure 1 caption.

(d). Case 4: predicted dynamics when both female sensitivity and female threshold evolve under natural selection

Analyses of the coevolutionary dynamics of female resistance and male persistence become much more complicated when one or more of the traits is considered to be under natural selection. The strength and direction of natural selection influence how much a trait can deviate from a naturally selected optimum owing to sexually antagonistic selection. It is possible, however, to reach some general conclusions about how male persistence and female resistance would be expected to evolve when natural and sexual selection interact. For example, when the female threshold is under strong natural selection, it cannot evolve much from its naturally selected optimum, and the coevolutionary dynamics closely resemble the case where only female sensitivity and male persistence evolve (§4a; [15]). Accordingly, we find that male persistence traits that harm females and constitute a cost of mating are not expected to show indefinite exaggeration and can even disappear from the population owing to the evolution of female resistance. Similarly, if the female sensitivity is under strong natural selection, it is evolutionarily restricted to values close to its naturally selected optimum. Consequently, the coevolutionary dynamics of male persistence and female resistance reduce to patterns we found in our analyses where only female threshold evolves, and predict an indefinitely escalating coevolutionary arms race between male persistence and female resistance (§4b; [16]).

5. Discussion

Evolutionary interests of males and females regarding mating decisions are usually in conflict, where males often benefit from increased number of matings, whereas various costs of mating favour a lower mating rate in females. The resulting sexual conflict over mating rate can drive the evolution of male traits that help males to increase the number of matings (referred to as ‘persistence’ traits), and counteracting female traits that limit the increase in the mating rate (referred to as ‘resistance’ or preference). Previous theoretical studies that examined the coevolutionary dynamics of counteracting male and female traits under sexual conflict over mating rate [15,16] assumed that costs of mating for females result in an optimal female mating rate that is lower than that of males and does not change over ecological or evolutionary time. Costs of mating, however, can often be caused, directly or indirectly, by male traits that increase the mating success of males. Here, we show that the expected coevolutionary dynamics of male persistence and female resistance can change significantly when the costs of mating for females depend on the male trait and, consequently, the optimal female mating rate is not evolutionarily constant. For example, in the case where female resistance evolves only through changes in female sensitivity, natural selection is absent or very weak, and the cost of mating for females does not depend on male persistence and, therefore, is evolutionarily constant, previous theory (as well as our ‘constant cost’ model; §4a) predicts a coevolutionary arms race of indefinitely exaggerated male persistence and decreasing female sensitivity (figure 1a,c; [16]). In contrast, we found that male persistence traits that harm females during mating are not expected to exhibit indefinite exaggeration, because greater costs of mating for females owing to increasing male persistence would result in selection for decreased female sensitivity, and eventually for female preference for less persistent males, shutting down the coevolutionary arms race (‘variable cost model’; figure 1b,d). Similarly, when the female resistance evolves through changes in both female sensitivity and female threshold (§4d), the version of our model where the cost of mating for females does not depend on male persistence (‘constant cost model’) predicts that male persistence could exhibit an indefinite exaggeration countered by decreased female sensitivity (figure 2a,b). In contrast, however, we found that male persistence traits that harm females, and therefore constitute a cost of mating, would not be predicted to show an indefinite exaggeration (‘variable cost model’; figure 2g,h). Furthermore, in contrast to previous theory, we found that male persistence traits that harm females during mating could even disappear from a population owing to female resistance (‘variable cost model’; figure 1b,d), where female preference for less persistent males would result in selection to decrease male persistence and, consequently, the cost of mating, which in turn would cause a greater female preference for less persistent males. In sum, our analyses demonstrate that in order to be able to understand and accurately predict the coevolutionary dynamics of male and female traits under sexual conflict, it is essential to assess explicitly, whether, and to what extent, the costs of mating experienced by females, and consequently the degree of sexual conflict over mating rate, are determined by male reproductive traits that affect male mating success.

An important conclusion of theoretical investigations of the coevolutionary dynamics of male persistence and female resistance under sexual conflict is that the coevolutionary arms races verbally predicted by Holland & Rice [7] may be observed only in some restricted biological circumstances. Gavrilets et al. [15] formalized this verbal argument and showed that the evolution of female choice under sexual conflict results in coevolutionary arms races between male persistence and female resistance. Extending the models of Gavrilets et al. [15], Rowe et al. [16] showed that the evolution of female resistance through changes in female sensitivity, rather than female threshold, can prevent coevolutionary arms races. Results of our analyses suggest that coevolutionary arms races should be even much less common than this previous theory has predicted. For example, in cases where only female sensitivity evolves and previous theory predicted a coevolutionary arms race between male persistence and female resistance, we found that male persistence traits that affect the cost of mating for females, such as penis spikes that physically harm females [22] or claspers that increase the duration of mating [23,24], would not be expected to exhibit an indefinite exaggeration owing to increasing costs of mating and the resulting female preference for less persistent males. Furthermore, while the patterns arising from our model agree with conclusions from previous studies that the strength and direction of natural selection have an important role in shaping the dynamics of male persistence and female resistance and shutting down coevolutionary arms races (§4d; [15,16]), our analyses reveal direct costs of male persistence on females as an equally important but mostly neglected factor in coevolutionary dynamics under sexual conflict. For example, we observe that the exaggeration of a harmful male persistence trait increases the cost of mating for females, which results in a decrease in female sensitivity and, eventually, in female preference for less persistent males, and shuts down the coevolutionary arms race between males and females (figures 1 and 2). We argue that we need further empirical research on the genetic architecture of male persistence and female resistance traits [31], nature of selection on these traits [32], as well as the extent to which costs of mating to females, and the degree of sexual conflict over mating rate, depend on male persistence traits, complemented with theoretical models that explicitly incorporate this information, before we can reach general conclusions about the coevolutionary dynamics of males and females.

Finally, our analyses show that coevolutionary dynamics of male persistence and female resistance strongly depend on parameter values that determine the magnitude of costs of mating for females as a result of male persistence. For example, in the case where female resistance evolves only through changes in the sensitivity (§4a), predicted patterns vary from stable values of male persistence to stable cycles of escalation and retreat or disappearance of male persistence from the population, depending on how costly male persistence is for females (figure 1b,d). Furthermore, in addition to costs of mating per se, females often incur a variety of additional costs, such as injuries sustained owing to harassment [17,18] and increased predation during courtship [33]. We argue that empirically assessing the relative importance and the magnitude of these costs in different mating systems will be essential to understand the coevolutionary dynamics of male and female traits involved in mating decisions, such as persistence and resistance.

Decisions over mating often involve conflict of interests between males and females, where males usually benefit from a greater number of matings, whereas various costs of mating favour a lower mating rate in females. The resulting sexual conflict over mating rate underlies the coevolution of male traits that affect male mating success (‘persistence’) and female traits that regulate the outcome of mating interactions (‘resistance’ or preference). Here, we showed that costs of mating per se to females that are directly or indirectly caused by male traits that determine male mating success lead to qualitatively different coevolutionary dynamics between male persistence and female resistance than predicted by previous theory where costs of mating, and the optimal female mating rate, are assumed to be evolutionarily constant. Specifically, we found that male persistence traits that impose a cost of mating on females are not expected to exhibit indefinite exaggeration, in contrast to escalating coevolutionary arms races predicted by previous theory. Further empirical research that identifies the extent to which various costs of mating for females depend on male reproductive traits and affect the optimal female mating rate, and theoretical studies that explicitly incorporate this information will be critical to predict and understand the evolution of traits involved in reproductive decisions.