On the centrality and uniqueness of species from the network perspective

Abstract

Identifying important species for maintaining ecosystem functions is a challenge in ecology. Since species are components of food webs, one way to conceptualize and quantify species importance is from a network perspective. The importance of a species can be quantified by measuring the centrality of its position in a food web, because a central node may have greater influence on others in the network. A species may also be important because it has a unique network position, such that its loss cannot be easily compensated. Therefore, for a food web to be robust, we hypothesize that central species must be functionally redundant in terms of their network position. In this paper, we test our hypothesis by analysing the Prince William Sound ecosystem. We found that species centrality and uniqueness are negatively correlated, and such an observation is also carried over to other food webs.

1. Introduction

One challenge in ecology is to identify important species [1,2]. Since species are embedded in webs of trophic interactions, one possible approach to importance is to quantify the network centrality of species in a food web [3]. A species with high centrality can affect many others, maybe also more quickly, via strong direct and indirect effects [4,5]. These include vertical effects in the top-down and the bottom-up directions [6], and horizontal effects like exploitive and apparent competitions [7].

Different species have different ecological roles and their network position may reflect these roles [8,9]. For instance, there are producers, top predators and omnivores. Beyond treating centrality as a proxy to species importance, it is also of emerging interest to know how similar the neighbourhoods of species are in a food web [10]. A species can also be important because it has a unique network position with a neighbourhood that poorly overlaps with that of others. As a consequence, species of this kind of importance are not easily replaceable, and their trophic functions are not easily taken over by others.

If an ecosystem is a functioning unit and has only one central species, then intuition suggests that it is prone to failure when such a central species is removed. Therefore, for an ecosystem to be robust, it should have several central species, such that the loss of one can be compensated by others. Thus, we argue that species centrality and uniqueness are two opposing characteristics of existing ecosystems. In this paper, we analyse the Prince William Sound (PWS) ecosystem [11] as an illustrative example and ask, ‘are central species also unique?’, and test the generality of our finding by using other food webs. We note that food webs are dynamic and our analysis only focuses on their topological structure.

2. Material and methods

(a). Data

The food web studied here is derived from the EcoPath with EcoSim [12] mass-balance model of the PWS ecosystem [11]. It is a static representation of a trophic flow network with 48 aggregated trophic groups (electronic supplementary material, S1) and 343 links each representing the trophic flow of carbon between two groups (mass transfers expressed in tC km^–2). Nodes in this type of food web are sometimes highly aggregated trophic groups (e.g. Meiofauna), and for simplicity, we use species and trophic groups interchangeably.

(b). Species importance by centrality

Owing to the structural complexity of networks, there is no unifying approach for quantifying nodal centrality. Different approaches focus on different aspects of network topology and thus provide complementary information. In this paper, we employ some commonly used indices from network science and ecology to measure centrality from the local, global and meso-scale perspectives. Using multiple measures is necessary because a single network index may not reflect fully the biological or ecological importance. Below we describe those indices briefly and refer the readers to electronic supplementary material, S2 for more detail.

Degree centrality (D_i) is a local measure [3], which is the total number of prey and predator species for species i. Eigenvector centrality (E_i) [3] is a weighted version of degree centrality where a neighbour j contributes to species i's centrality, in an amount proportional to j's centrality (i.e. a species is central if it is connected to many central species).

On the global scale, we have closeness centrality (C_i) [3], which quantifies how many steps away species i is from all others in the food web (and then inverses it). A species with high C_i can be important because it can affect others more quickly. Next, betweenness centrality (B_i) [3] measures how frequently species i lies on all shortest paths of interaction between all other species pairs. A species with high betweenness centrality is important because it mediates many indirect interactions between species. Furthermore, we can extend betweenness centrality by considering all paths of interaction between species to obtain information centrality (I_i) [3].

On the meso-scale, TI index quantifies the direct and indirect effects of species i on others up to n steps [5]; these include trophic cascade, indirect food supply and competition. Here, one first determines the probability of species i influencing its neighbour j (i.e. 1/D_j), and then calculates the probability of i influencing j's neighbour k (i.e. 1/D_j × 1/D_k), and so on for neighbours' neighbours up to n steps; and these probabilities are then summed up to give 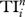for species i. Since earlier literature suggests that indirect effects are on average 3–4 steps long [5], we calculate the case for n up to 5 steps.

(c). Species importance by uniqueness

Quantifying species uniqueness is less well developed in the literature than species centrality. We employ two general measures here; each quantifies uniqueness from different perspective. The first is based on the graph theoretical concept of regular equivalence (RE). Two species i and j are regularly equivalent if they are consumed by predators of similar network positions, as well as if their prey are themselves similar positionally; RE does not necessarily require both species to have the same predator and prey species [9]. For instance, two producer species consumed only by herbivores are more RE than the case where one of them is also consumed by omnivores. The outcome of RE analysis is a REGE matrix with the ijth element representing the positional similarity between i and j; and the sum of the ith row (REGE_i) can be a measure of positional uniqueness of species i; if species i is unique, then this sum should be small because there are not many species of similar network position as i.

The second measure of uniqueness is based on the ecological concept of trophic overlap between species and is related to the TI index [10]. It measures how similar two species are in terms of whether they influence the same other species via direct and indirect effects. First, one determines the effect of species i on species j up to n steps as in TI index; if it is greater than a threshold (T), then we say j is i's strong interactor. Thus, each species has a trophic field containing its strong interactors, and the trophic overlap between species i and all others 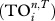is the total number of times species i's strong interactors also appear in other species' trophic fields. If species i is unique, then 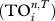should be small as it shares fewer strong interactors with others. Here, we calculate the case up to five steps (as for the TI index), and set T = 0.05 such that there is a reasonable level of variation in 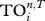values among species (note that if T is set too high then all species' trophic fields will be empty, resulting in 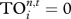; if T is set too low, all species will have the same trophic fields resulting in all 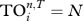, the total number of species).

Indices D_i, E_i, C_i, B_i, I_i and REGE_i are calculated by using UCINET [13], and indices 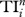and 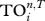can be determined by using CoSBiLab Graph [14].

3. Results

For the PWS food web, we calculated the centrality and uniqueness of individual trophic groups, and then ranked them accordingly (table 1). After pooling the results from the top five ranks for each centrality index, the most central species are (species name followed by its node ID): Pacific cod (no. 11), spiny dogfish (no. 14), deep demersals (no. 18), pollock (no. 19), squid (no. 24), deep epibenthos (no. 27), omnivorous zooplankton (no. 38), shallow small epibenthos (no. 42) and herbivorous zooplankton (no. 45). With the exception of squid, these central species are located in the bottom half of the ranking order according to 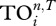. As for REGE_i, these central species are more evenly distributed in the ranking order, but none of them occupies top ranking positions.

Table 1.

Species of the PWS food web ranked (from the top) according to various centrality and uniqueness indices. Here, only node IDs are shown, for actual names see the electronic supplementary material, S1.

Di	Ei	Ci	Bi	Ii		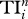	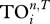REGEi
38	24	38	27	38	38	24	48
11	19	24	42	24	18	28	40
19	38	18	38	19	27	20	47
24	11	11	18	11	11	22	46
14	14	19	45	14	24	13	1
18	34	23	23	18	19	4	26
23	18	14	12	23	14	2	3
34	25	12	11	34	23	10	15
25	28	25	24	25	42	9	4
27	23	27	14	27	34	8	2
12	20	42	19	28	45	30	44
28	32	45	17	32	25	7	45
32	5	34	37	12	12	36	42
42	27	28	34	42	32	21	31
45	12	20	29	45	28	15	39
5	45	32	25	20	5	3	43
20	13	5	33	5	20	31	7
37	42	22	32	37	37	48	6
22	22	17	16	29	29	47	17
29	2	37	5	22	22	40	9
13	37	29	28	13	16	6	14
2	6	16	20	4	17	39	38
4	29	4	39	2	13	1	21
6	4	13	4	17	4	34	37
16	9	2	10	6	33	32	27
17	17	9	22	16	6	44	18
9	30	33	1	9	2	46	24
10	8	6	35	10	10	43	20
33	16	8	6	33	9	41	34
8	10	39	46	30	8	19	12
30	33	30	13	8	30	14	25
44	44	36	2	44	44	25	33
7	36	35	43	36	39	5	32
35	7	10	44	7	35	29	28
36	39	44	9	39	7	35	5
39	35	15	21	35	36	33	11
1	3	7	8	15	1	12	23
3	15	21	30	3	46	11	19
15	21	3	7	21	21	45	29
21	1	1	41	1	15	16	10
46	41	41	31	46	3	26	16
41	46	46	26	41	43	17	22
43	43	43	15	43	41	23	30
26	47	48	36	26	26	42	13
31	48	47	3	48	31	37	8
47	40	26	48	47	48	27	36
48	26	40	47	31	47	38	41
40	31	31	40	40	40	18	35

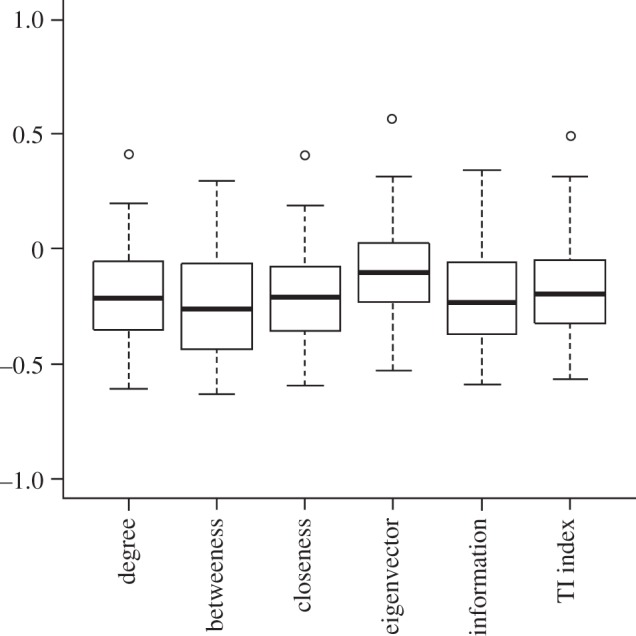
To see the relationship between centrality and uniqueness indices clearly, we calculated Spearman rank correlations between them (table 2). In all cases, there is a negative correlation between each pair of centrality and uniqueness indices. We repeated our analysis with 40 other food webs (electronic supplementary material, S3) to test the generality of our finding; species centrality still correlates negatively with uniqueness in most cases (figures 1 and 2).

Table 2.

Spearman rank correlation coefficient between various centrality and uniqueness indices for the PWS ecosystem.

	Di	Ei	Ci	Bi	Ii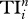
REGEi	−0.40 (p < 0.01)	−0.41 (p < 0.01)	−0.41 (p < 0.01)	−0.27 (p = 0.07)	−0.39 (p < 0.01)	−0.38 (p < 0.01)
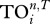	−0.48 (p < 0.01)	−0.36 (p < 0.05)	−0.47 (p < 0.01)	−0.73 (p < 0.01)	−0.46 (p < 0.01)	−0.56 (p < 0.01)

Figure 1.

Distribution of Spearman rank correlation coefficients between uniqueness index REGE_i and different centrality indices when a collection of 40 food webs were analysed.

Figure 2.

Distribution of Spearman rank correlation coefficients between uniqueness index and different centrality indices when a collection of 40 food webs were analysed.

4. Discussion

A pattern has emerged from our analysis which shows that central species are positionally redundant (not unique). As for the PWS ecosystem, it is known to be dominated by the typical phytoplankton–zooplankton–small fish–large predator core pathways [11,15]. Each trophic position in this core is occupied by several trophic groups. For instance, the linkage role in relying trophic flow from basal species to small fishes is shared by zooplanktons and epibenthic groups, while the connection between intermediate trophic levels to top predators is filled by several fish species like cod and pollock. Our analysis identifies those core groups as the most central ones in the PWS system and yet their network positions are not particularly unique.

Central species of the PWS system are those at intermediate trophic levels connecting basal species to top predators; they are also hubs linking several food chains. Our intuition suggests that the observed redundancy in those network positions may ensure safe passages of biomass to species at higher trophic levels if one central species is removed. Thus, we speculate that a food web with many trophic levels should have alternative pathways for maintaining biodiversity at higher trophic levels. Previous studies have demonstrated that food webs are highly reliable as species losses rarely disrupt the passage from basal species to top predators [16,17], and our findings on the positional redundancy of central species may suggest a mechanism that promotes the robustness of food webs.

Our results show the correlation between centrality and uniqueness indices are not perfect, and this implies some species are reasonably central and unique (e.g. squid in the PWS ecosystem). To provide a quantitative assessment of species importance has long been a challenge in ecology [18]. We suggest that species that are both central and unique can also be candidates for important species; and one practical relevance of this is for setting conservation priorities. Moreover, a keystone species is the one that has a disproportionate effect on a community relative to its biomass [1,18]; thus, borrowing this concept, one should also measure species centrality and uniqueness in relation to the biomass of a species and the contribution it makes to systems dynamics.