Biology, not environment, drives major patterns in maximum tetrapod body size through time

Abstract

Abiotic and biological factors have been hypothesized as controlling maximum body size of tetrapods and other animals through geological time. We analyse the effects of three abiotic factors—oxygen, temperature and land area—on maximum size of Permian–Jurassic archosauromorphs and therapsids, and Cenozoic mammals, using time series generalized least-squares regression models. We also examine maximum size growth curves for the Permian–Jurassic data by comparing fits of Gompertz and logistic models. When serial correlation is removed, we find no robust correlations, indicating that these environmental factors did not consistently control tetrapod maximum size. Gompertz models—i.e. exponentially decreasing rate of size increase at larger sizes—fit maximum size curves far better than logistic models. This suggests that biological limits such as reduced fecundity and niche space availability become increasingly limiting as larger sizes are reached. Environmental factors analysed may still have imposed an upper limit on tetrapod body size, but any environmentally imposed limit did not vary substantially during the intervals examined despite variation in these environmental factors.

1. Introduction

Understanding the role of physical and environmental variables in imposing limits on body size is central to understanding the effects of climate change on ecosystems [1–3]. The abiotic environment has been argued to place extrinsic constraints on body size evolution [4–8], as have biological factors both extrinsic (i.e. interspecifically, e.g. ecological incumbency/outcompetition; [9]) and intrinsic (i.e. intraspecifically, e.g. life-history duration [10] and energetic aspects of ecology [11]) to the constrained taxon. Terrestrial tetrapod history is punctuated by major faunal replacement events, where one group expands in taxic and size diversity as another declines. Examples are the rapid replacement of dinosaurs by mammals as the dominant terrestrial tetrapods immediately after the end of the Cretaceous, (approx. 65.5 million years ago (Ma), [10]) and the long-term replacement of therapsids (stem-group mammals) by archosauromorphs (archosaurs, including dinosaurs, pterosaurs and crocodilians, and all species more closely related to them than to lepidosauromorphs) following the Permian–Triassic (P/T, approx. 252 Ma, [12]) extinction event. These events, and associated body size dynamics, provide opportunities to assess the relative importance of abiotic and biological factors in determining the evolution of tetrapod maximum size.

2. Material and methods

Femoral length, as a proxy for body size, was collected for more than 400 Permian–Jurassic archosauromorph and therapsid species, and taxa were dated to geological stage (electronic supplementary material; data from [13]). Oxygen ([O₂]) and carbon dioxide (as a proxy for temperature, [CO₂]) concentration data were taken from the latest GEOCARBSULF model [14,15] data (R. Berner, 2010, personal communication), and non-marine area (NMA) for the Permian–Jurassic from Smith et al. [16]. Size data were sorted into 10 Myr bins centred on GEOCARBSULF midpoints. Mammalian maximum size and Cretaceous–Holocene environmental data (global land area [GLA], δ₁₈O [temperature] and [O₂]) were from Smith et al. [10].

GLS regression was carried out in R v. 2.13.1 [17] using the nlme package, both with a first-order autoregressive model (AR1) to remove serial correlation (the correlation of a variable with itself over successive time intervals, which can inflate type 1 errors), and with no autoregressive model (AR0) for comparison. All combinations of environmental variables were tested as predictors of maximum size (for Permian–Jurassic therapsids and archosauromorphs and for Cenozoic mammals) and mean size (for Permian–Jurassic data). Mammalian data were analysed for Palaeocene–Pleistocene (63.6–0.904 Ma) and Middle Eocene–Pleistocene (42.9–0.904 Ma) timespans. Environmental data series differed in length due to missing data for certain time bins, and therefore analyses were carried out with the full series for each variable and with shortened series to allow different combinations of variables to be examined.

Logistic and Gompertz growth curves were fit to maximum size for Permian–Jurassic data with the nls() function in R (formulae from [10]). In the Gompertz model, the upper asymptote is approached more slowly, indicating greater restriction on body size increase as larger sizes are reached [10]. Curves were fit for Archosauromorpha and three major subclades: Dinosauromorpha, Theropoda and Sauropodomorpha. An archosauromorph curve was also fit beginning at the P/T boundary and using the Permian maximum as initial size. Model fits were compared using the Akaike information criterion for finite sample sizes (AICc).

3. Results

AR1 GLS models were better (had lower AICc values than AR0 models) in all cases, indicating strong serial correlation in all data series. Maximum size for Permian–Jurassic therapsids and archosauromorphs analysed together and separately was best explained by the null model (no relationship between environmental factors and size; table 1; electronic supplementary material), except for archosauromorph maximum size which was explained best by [O₂], but only under AR0 and when the entire available data series was used (preventing comparison with the shorter NMA data series). Mammalian body size was best explained by a null model, except from the Palaeocene to Pleistocene under AR0, where [O₂] + temperature was the best model, and from the Cretaceous to Pleistocene (i.e. the entire GLA series), where GLA also outperformed a null model under AR0 (table 1). The Gompertz equation fitted better (ΔAICc > 30) than the logistic equation for all groups and time periods tested but, for theropod dinosaurs, asymptotic mass was unrealistically large and parameter fits were non-significant (table 2).

Table 1.

Summary of non-null best generalized least squares regression models for Late Permian–Middle Jurassic archosauromorphs and therapsids, and Late Cretaceous–Holocene mammals (data from [10]). Akaike weights are compared with other models for the same clade and time interval.

group	environmental variable	slope	r2	AR order	log likelihood	Akaike weight
Archosauromorpha Permian–Jurassic	[O2]	−0.047	0.407	0	0.179	0.615
Mammalia Palaeocene–Pleistocene	[O2]+ δ18O	0.256, 0.365	0.697	0	−9.942	0.335
Mammalia Cretaceous–Pleistocene	GLA	0.099	0.683	0	−17.409	1.000
Mammalia Cenozoic	[O2]+ δ18O	0.261, 0.347	0.705	0	−10.121	0.656

Table 2.

Results for Gompertz and logistic growth curves fits for maximum size (femoral length) through time for different archosauromorph clades. The Gompertz model was of the form logM = logK−log(K/M₀)e^-αt where M is the maximum size, K the asymptotic maximum size, M₀ the initial maximum size and t the time, and the logistic model was of the form log M = C₀t^γ where C₀ is the initial maximum size, t the time and γ = 0.5 under a random walk. Bold: parameter has significantly good fit (p ≤ 0.05). All maximum size values are in mm.

group	model	AICc	K	M0	α	C0	γ
Theropoda	Gompertz	−11.483	56874.684	346.070	0.003	—	—
	logistic	33.365	—	—	—	89.888	0.098
Sauropodomorpha	Gompertz	−27.674	1665.521	202.577	0.063	—	—
	logistic	29.381	—	—	—	227.788	0.076
Dinosauromorpha	Gompertz	−20.048	1835.675	113.366	0.043	—	—
	logistic	29.548	—	—	—	64.690	0.085
Archosauromorpha	Gompertz	−5.950	1976.697	128.437	0.030	—	—
	logistic	35.698	—	—	—	54.229	0.140
Archosauromorpha from P/T	Gompertz	−16.199	1323.153	72.157	0.112	—	—
	logistic	23.768	—	—	—	159.518	0.085

4. Discussion

Our results indicate a limited role for environmental factors in determining tetrapod maximum body size, and favour instead the importance of intrinsic, clade-specific factors. Although we confirm that all environmental variables tested are apparently good predictors of mammalian maximum size [10], these correlations are only obtained under AR0, and thus probably result from type I error due to serial correlation. Furthermore, a null model outperforms all environmental models for mammalian body size when the exponential change in [O₂] during the Eocene is excluded. Thus, although Eocene and post-Eocene changes in oxygen, temperature and land area followed similar trends to changes in mammalian size, they were unlikely to have been causative (contra to [10]). Although these environmental factors could have played a role in ultimately limiting mammalian size, these limits seemingly did not change during the study interval (see below).

For the Permian–Jurassic data, the association recovered between raw archosauromorph size and [O₂] (table 1, data pictured in figure 1a,b), also probably results from type 1 error due to serial correlation. Lack of robust correlation with environmental factors further weakens evidence that exceptional size in non-avian dinosaurs was facilitated by elevated temperature and oxygen levels [18]. Instead, as discussed previously [18], unique adaptations may have enabled exceptional sizes in non-avian dinosaurs, including pneumaticity and bird-like lung ventilation [18–20] which facilitated cooling [18] and thus circumvented thermal constraints. Flightless birds' failure to reach giant sizes may be explained by competition with mammals or forelimb specialization [18]. Our findings cast doubt on the hypothesis that declining oxygen levels precipitated therapsid decline, enabling archosauromorphs (with more efficient ventilatory anatomy) to diversify [5].

Figure 1.

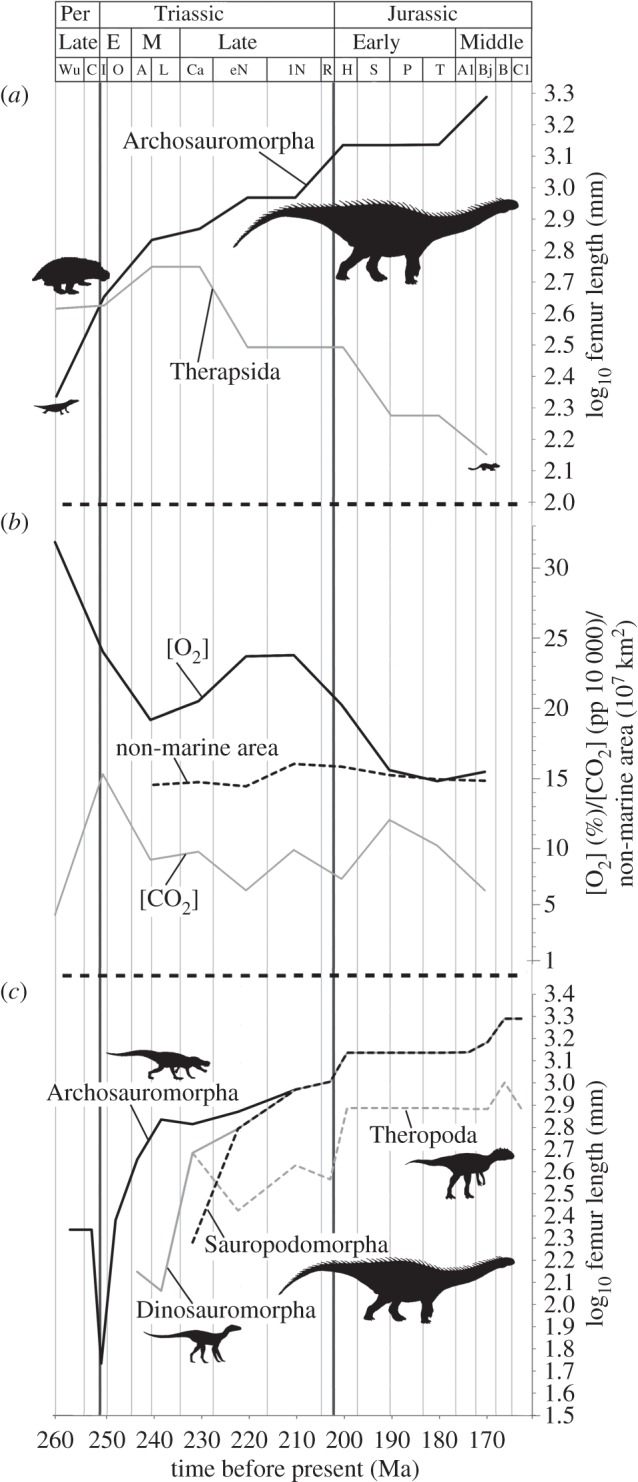
(a) Maximum log femur length (body size proxy) among Late Permian–Middle Jurassic Archosauromorpha (black) and Therapsida (grey). (b) Oxygen (black solid line) and carbon dioxide (grey line) concentrations, and NMA (i.e. land area, black dashed line). (c) Maximum log femur length (body size proxy) for Archosauromorpha (black solid line), Dinosauromorpha (grey solid line), Sauropodomorpha (black dashed line) and Theropoda (grey dashed line). Per, Permian; E, early, M, middle. Stage abbreviations in electronic supplementary material, table S1.

However, inaccuracy and coarseness in body size and environmental data may have contributed to lack of association, and results require reassessment as more refined data become available. The latest GEOCARBSULF model uses the newest isotopic data [15] and accords with the palaeowildfire record [21], but suffers greater inaccuracies than directly measured data and differs markedly from some earlier estimates [22]. Seasonality and other fine-scale aspects, such as within-lineage evolution [23], were not investigated, and our results only apply at large phylogenetic and spatio-temporal scales. Size estimates may be affected by taphonomic and sampling biases. For example, smaller taxa often have low preservation potential (inflating mean estimates), and maximum size may be underestimated during poorly sampled intervals. However, Smith et al.'s [10] finding that sampling just 10 per cent of fossil mammal localities yielded accurate maximum size estimates, and the similarity of our results using mean sizes to those using maxima (electronic supplementary material) suggests that sampling bias is not a major issue.

Fit of Gompertz (as opposed to logistic) models appears to be a widespread feature of maximum body size growth curves in tetrapods, as evidenced by mammals [10] and Permian–Jurassic archosauromorphs (table 2). Lack of robust correlations between archosauromorph, therapsid or mammalian size and environmental variables suggests that biological factors shared by tetrapods (e.g. energetics; [6,11]), not environment, are responsible for decreasing rate of size increase as larger sizes are reached (i.e. the Gompertz pattern). Although some environmental variables may have contributed to imposing an upper limit on tetrapod body size, changes in these variables during the Mesozoic and Cenozoic apparently do not coincide with changes in this body size limit, and did not drive the Gompertz pattern of growth. Although a Gompertz curve was a better fit than a logistic model for Theropoda, it was not a significantly good fit and the asymptotic mass was unrealistic. This may reflect the nesting of the theropod growth curve within dinosauromorphs and the fact that theropods did not exceed their non-dinosaurian forebears in size to the same extent as sauropodomorphs during the study interval, with the shape of the curve thus being much flatter than that for other clades (figure 1c).

Overall, our work casts further doubt on the importance of environmental constraints in determining changes in limits to, and major patterns of, tetrapod maximum body size over large timescales. Instead, we support previous suggestions that maximum size is determined by the biology of particular clades, with prominent roles for constraint in explaining relatively low maximum sizes in mammals, and unique adaptations in explaining exceptional sizes in non-avian dinosaurs.