Abstract
In the previous publications of this series, we presented a set of Thole induced dipole interaction models using four types of screening functions. In this work, we document our effort to refine the van der Waals parameters for the Thole polarizable models. Following the philosophy of AMBER force field development, the van der Waals (vdW) parameters were tuned for the Thole model with linear screening function to reproduce both the ab initio interaction energies and the experimental densities of pure liquids. An in-house genetic algorithm was applied to maximize the fitness of “chromosomes” which is a function of the root-mean-square errors (RMSE) of interaction energy and liquid density. To efficiently explore the vdW parameter space, a novel approach was developed to estimate the liquid densities for a given vdW parameter set using the mean residue-residue interaction energies through interpolation/extrapolation. This approach allowed the costly molecular dynamics simulations be performed at the end of each optimization cycle only and eliminated the simulations during the cycle.
Test results show notable improvements over the original AMBER FF99 vdW parameter set as indicated by the reduction in errors of the calculated pure liquid density (d), heat of vaporization (Hvap) and hydration energy. The average percent error (APE) of the densities of 59 pure liquids was reduced from 5.33% to 2.97%; the RMSE of Hvap was reduced from 1.98 kcal/mol to 1.38 kcal/mol; the RMSE of solvation free energies of 15 compounds was reduced from 1.56 kcal/mol to 1.38 kcal/mol. For the interaction energies of 1639 dimers, the overall performance of the optimized vdW set is slightly better than the original FF99 vdW set (RMSE of 1.56 versus 1.63 kcal/mol).
The optimized vdW parameter set was also evaluated for the exponential screening function used in the Amoeba force field to assess its applicability for different types of screening functions. Encouragingly, comparable performance was observed when the optimized vdW set was combined with Thole Amoeba-like polarizable model, particularly for the interaction energy and liquid density calculations. Thus, the optimized vdW set is applicable to both types of Thole models with either linear or Amoeba-like screening functions.
Keywords: Force field parameterization, van der Waals parameterization, Polarizable force field, Thole’s model, Interaction energy, Density, Heat of vaporization, Hydration energy
1. Introduction
With the growing computer power, there is an increasing desire to develop more accurate molecular mechanical models to study the structures, energies and functions of biomolecules. To this end, various models that take into account the atomic polarization effect have been developed, including force fields that employ the induced dipoles such as OPLS/PFF,1 AMOEBA2,3 and AMBER FF02, FF02EP4 and FF02r1.5 Recently, we have developed a set of induced dipole models based on Thole-screening approach to smooth out the surge of repulsion when two dipoles approach each other (“polarization catastrophe”).6,7 The Thole linear model, which has achieved the best overall performance in our tests, was selected as the base polarization model to parameterize other force field terms. A series of polarizable water models based on the Thole screening functions have also been developed recently.8
In the polarizable model, the non-bonded interactions comprise three integral components: electrostatic, polarization, and van der Waals forces. Van der Waals (vdW) interaction is an important term in a molecular mechanical force field and it is strongly coupled to the electrostatic energy term. For example, in some of widely used force fields including CHARMM9 and OPLS,10 the vdW parameters and atomic charges were tuned simultaneously. With the explicit inclusion of the induced dipoles in the energy function, it thus becomes necessary to refine the van der Waals terms to allow accurate representation of the non-bonded forces.
A major difference between AMBER and other force fields is that the atomic partial charges are derived to reproduce ab initio molecular electrostatic potential (ESP) using a RESP approach. Thus, the atomic charges in AMBER are used for the purpose of representing the electrostatic potential that allows straightforward derivation of atomic charges.11–14 Because the atomic charges are predetermined, the van der Waals parameters need to be tuned more thoroughly to reproduce high-level ab initio or high quality experimental data. This is also true in the polarizable model. Indeed, we found that our Thole polarizable model was unsatisfactory in reproducing the bulk properties with the vdW parameter set that was developed for the additive force fields (FF94,11 FF9915 and FF0313) without adjustment. For a set of 25 pure liquids, the FF99 vdW parameter set has an average percent error (APE) of 6.37% for the densities and a root-mean-square error (RMSE) of 1.47 kcal/mol for the heats of vaporization (Hvap), respectively. Compared to the FF99/GAFF14 additive model, the prediction errors of densities and heats of vaporization were increased 66% and 32%, respectively. The objective of this work is to develop a set of van der Waals parameters in conjunction with our Thole polarizable model to reproduce high level ab initio and high quality experimental data.
In AMBER force fields, the van der Waals term is described by the Lennard-Jones 6–12 potential (Eq. 1). Aij and Bij, the Lennard-Jones parameters for repulsion and attraction can be expressed in terms of effective van der Waals radii and well depths, Rij* and εij (Eq. 1b and 1c), which are further obtained from atomic parameters using the Lorentz-Berthelot mixing rules (Eq. 1d and Eq. 1e), Rij is the distance between atoms i and j.
| (1a) |
| (1b) |
| (1c) |
| (1d) |
| (1e) |
The Lennard-Jones 12-6 potential is widely used by many force fields, which include CHARMM,9 OPLS,10 GROMOS,16 UFF,17 etc. Other popular vdW potentials include the “soft” Lennard-Jones 9-6 potential,18,19 Buffered-14-7 potential,20 among others.
Van der Waals parameterization is regarded as one of the most difficult parts in the development of a molecular mechanical force field. This is particularly true for the general purpose force fields that have broad coverage of the elements, such as UFF,17 ESFF,19 and MMFF.20 For the general-purpose force fields, the vdW parameters are usually obtained using empirical functions. In these force fields the radii and well depths are expressed as functions of ionization energy, electronegativity, hardness, atomic polarizability and Slater-Kirkwood effective numbers of valence electrons.20 For force fields focused on studying biological systems, as is the case in this work, the van der Waals parameters are usually derived to reproduce liquid phase properties. OPLS10 and COMPASS18 belong to this group. For AMBER,11–13 CHARMM9 and GROMOS,16 the van der Waals parameters are also refined to reproduce liquid state properties such as density and heat of vaporization.
There are two complementary approaches in the parameterization of van der Waals parameters. One approach is purely based on condensed phase properties. However, such approach may suffer from parameter correlation problem. For example, Kaminski et al. found that the standard OPLS-AA greatly overestimates the gas phase dimerization energies of methanethiol and ethanethiol, although their liquid state properties are in very good agreement with the experimental results.21 Alternatively, vdW parameterization can also be based on ab initio data. Yet, vdW parameters developed solely based on ab initio data could also be problematic as suggested in many studies.22,23 We also found that adjusting van der Waals parameters can notably improve the interaction energies of the first 673 dimers in Table S1 to achieve respectable results with AUE and RMSE reduced to 0.69 and 1.30 kcal/mol, respectively. Unfortunately, the vdW parameter set obtained this way resulted in notable increase in the densities of 25 pure liquids with an average 14% difference from the experimental values. Therefore a better strategy of vdW parameterization should utilize both the ab initio and experimental data in parameterization.
However, it is a challenging endeavor to design a parameterization protocol to efficiently obtain the data of liquid properties that are typically calculated through molecular simulations. Yin and Mackerell proposed an iterative two-staged procedure to conduct vdW parameterization.23 In their approach, the ab initio interaction energies and geometries are used to optimize the relative magnitude of the vdW parameters. In the second step, the absolute values of the vdW parameters were tuned to reproduce experimental densities and Hvap of pure liquids. Their approach has been applied to produce vdW parameters and atomic charges for single molecular classes.23–25
In this work, we set out to conduct vdW parameterization for the Thole polarizable model to reproduce both high level quantum mechanically derived interaction energies and experimental pure liquid densities using a genetic algorithm. As in a typical GA run, the fitness functions are evaluated more than 100,000 times and it is impractical for us to calculate the densities through molecular simulations during the GA optimization. To tackle this problem, a novel approach is developed to predict the liquid densities from the mean residue-residue interaction energies through interpolation and extrapolation. The final vdW parameter set optimized by GA was thoroughly evaluated in predicting three condensed phase properties including density, heat of vaporization and hydration energy, for 59 small molecules through molecular dynamics simulations.
2. Methods
In this section, we first discuss how to conduct van der Waals parameterization to reproduce both the ab initio interaction energies and experimental liquid densities. Then the MD simulation protocols and an approach to calculate liquid properties are discussed sequentially.
2.1 van der Waals Parameterization
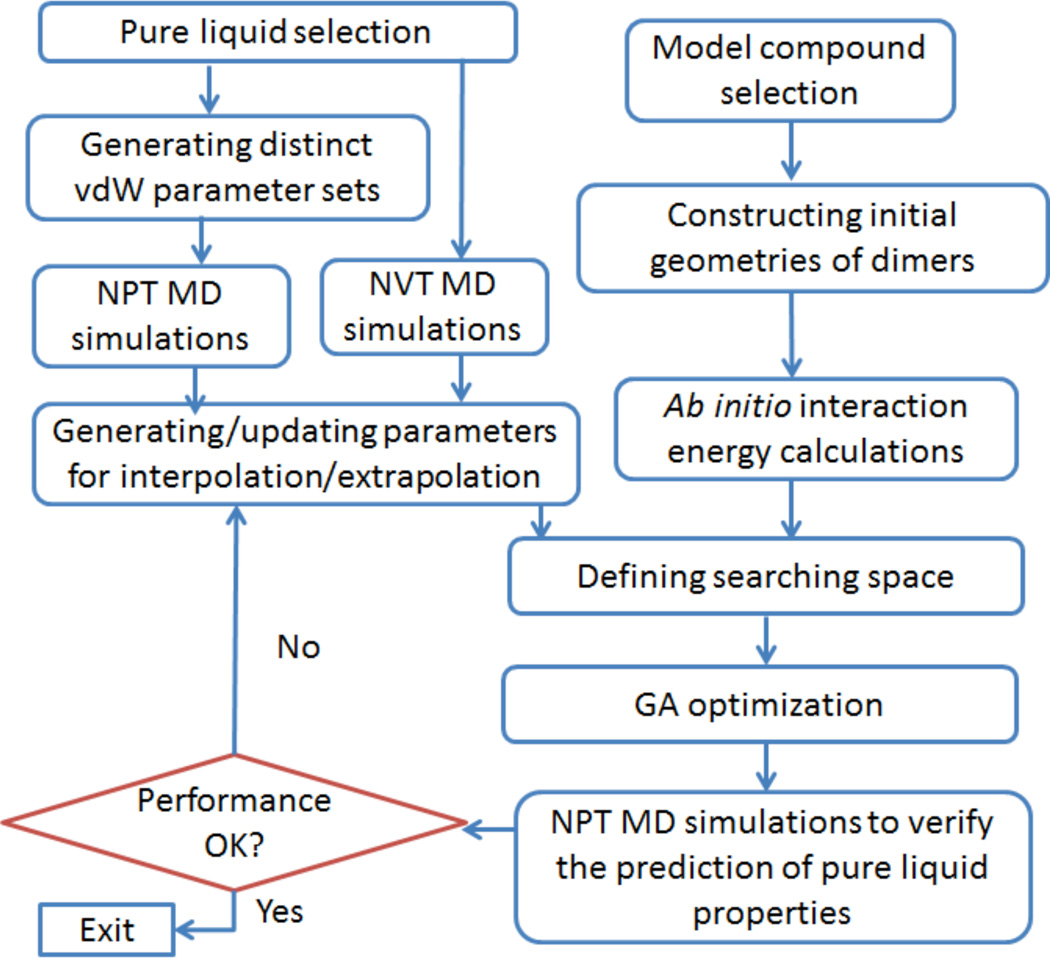
In this work, we propose to predict the liquid densities for an arbitrary vdW set using the mean residue-residue interaction energies. The procedure of vdW parameterization is summarized in Figure 1.
Figure 1.
Procedure of van der Waals parameterization
Before the GA optimization, two types of data need to be prepared. The first type of data includes quantum mechanically derived interaction energies for a set of model compounds that best represent the vdW. In this work, the model compounds are typically the building blocks of amino acids and nucleic acids.
The second type of data is used to predict the densities of pure liquids. For each liquid, a constant volume MD simulation is performed to produce a NVT (canonical) ensemble and the density of the simulation box is set to the experimental value. Secondly, two distinct vdW parameter sets are generated and constant pressure MD simulations are performed for both vdW parameter sets for each liquid. The densities of Liquid i, corresponding to the two vdW parameter sets are obtained from the NPT simulations. Ideally, the experimental density di is between . The mean inter-molecular interaction energies of the two vdW parameter sets, are also calculated using the last snapshot of the NVT MD simulation. The mean inter-molecular interaction energy E is calculated by Eq. 2
| (2) |
where Emol is the energy of entire system and is the intra-molecular potential energy of jth residue, n is the number of molecules in the simulation box. Here a solvent molecule is often a single residue in a pure solvent system.
Rather than running MD simulations to calculate densities, we predict this property through interpolation and extrapolation. For an arbitrary vdW parameter set, mean intermolecular interaction energy of Liquid i, Ei, can be easily calculated using Eq. 2 and its density can be predicted through interpolation/extrapolation using Eq. 3:
| (3) |
It should be noted that the linear relationship of Eq. 3 holds only when are close to the experimental value di. In practice, the van der Waals parameters are refined iteratively and the parameters that fail to make satisfactory prediction should be replaced with new ones.
An in-house generic algorithm (GA) is applied to optimize vdW parameters to maximize the fitness function (Eq. 4) which measures the performance of a vdW parameter set in reproducing the ab initio interaction energies and experimental densities of pure liquids simultaneously.
| (4) |
In equation 4 wIE and wd are adjustable parameters balancing the relative importance of the two properties, interaction energy and density; RMSEIE is the root-mean-square error of the interaction energy calculation and APEd is the average percent error of the density prediction; 0.001 is added to avoid possible numerical overflow. In this work, wIE and wd are set to 1.2 and 2.0, respectively. When RMSEIE approaches 1.2 kcal/mol and APEd approach 2.0%, the two properties contribute equally to the fitness.
Although GA optimization is an automatic procedure, human intuition is needed to adjust the GA searching ranges and redefine atom types. The parameterization procedure is an iterative procedure and a satisfactory vdW parameter set may be obtained only after several GA runs. More details on the algorithm and parameters setting for GA optimization can be found in other publications.6,26–28
2.2 Data Sets
Interaction Energies
In this work, a total number of 1639 dimers were studied and those dimers fall into one of seven categories: (1) amino acid main chain analog dimers, (2) amino acid side chain analog dimers, (3) water – amino acid analog dimers, (4) hydrogen-bonded nucleic acid base pairs, (5) stacked nucleic acid base pairs, (6) nucleic acid base steps, and (7) diverse pairs representing various interaction types.
All the entries of Set 1 are actually the NMA (N-methylacetamide) dimers. The first 31 entries (Nos. 1–31) were taken from our previous publication.7 For Nos. 32–64, the intermolecular distances d between two atoms were constrained during the geometry optimization. Specifically, d are the distances between two amine hydrogen atoms for Nos 32–44, d are the distances between amine hydrogen and carbonyl oxygen for Nos 45–56 and are the distances between two carbonyl oxygen atoms for Nos. 57–64. The exact values of separation distances are indicated by the entry names. For Nos. 65–85, the NMA dimers were generated in the same fashion as already reported except that smaller separation distances were applied.7 Again the separation distances are indicated by the entry names. In Set 2, entries Nos. 536–602 are newly added dimers and the others come from the previous study.7 We added those entries because some interaction types (polar-polar and aromatic-aromatic interactions) were somehow under represented in the initially chosen set of dimers (Nos. 86–535). Again, the same protocol was used to construct the geometries of newly introduced entries. In Set 3, 71 dimers were constructed representing water and amino acid analog interactions. A similar protocol to the one proposed in Ref. 2 was used to generate the geometries of dimers. In brief, dimers that frequently occur in protein crystal structures were selected and clustered; and the representative structures from the top clusters were then selected for ab initio calculations. More details on raw water dimer generation and cluster analysis are presented in our previous work.7
The newly added entries in Sets 1–3 were optimized at MP2/6-311++G(d,p) level. The optimization details on the other entries (Nos. 1–31, 86–535) were described in previous work.7 Single point calculations at MP2/aug-cc-pVDZ (in abbreviation aDZ), MP2/aug-cc-pVTZ (in abbreviation aTZ) were performed for all the 673 dimers. The basis set superposition errors (BSSE) were corrected through the counterpoise corrections.29,30 The interaction energies extrapolated to the complete basis set (CBS) level were calculated using four interaction energies: BSSE corrected interaction energy at the aDZ level , BSSE corrected interaction energy at aTZ level , interaction energy at aDZ level (ΔEaDZ), and interaction energy at aTZ level (ΔEaTZ) using a scheme proposed by Truhlar et al.31,32 All these four interaction energies were calculated by subtracting the monomer energies from the dimer energy computed using the same quantum mechanical model.
Set 4 (Nos. 674–702) come from Šponer, Jurecka, and Hobza’s work.33 Intermolecular hydrogen bonds formed for dimers in this set and their interaction energies were also extrapolated using aDZ and aTZ energies. Set 5 (Nos. 703–948) contains stacked adenine34 and uracil pairs.35 The interaction energies were calculated by extrapolating the aDZ and aTZ energies plus higher-order correlation energy calculated at CCSD(T) level using a small basis set. Set 6 (Nos 949–1048) comes from Svozil, Hobza and Šponer’s work on intrinsic stacking energy calculation for dinucleotide steps in A-RNA and B-DNA duplexes.36 The interaction energies were calculated using RI-MP2 complete basis set limit method augmented with the CCSD(T) correction term derived with smaller basis set. Set 7 (Nos. 1049–1639) contains 66 molecular complexes representing different types of interactions. For each complex, the interaction energies at equilibrium geometry and dissociation curve were calculated at CCSD(T)/CBS level. All the geometric and energetic data come from the recent work of Řezáč, Riley and Hobza.37
Condensed Phase Properties
In total the molecular properties of 59 compounds were studied in this work. Those compounds cover diverse functional groups in organic chemistry, which include hydrocarbons (aliphatic and aromatic, cyclic and acyclic), alcohols, thiol, phenols, ethers, esters, aldehydes, ketones, carboxylic acids, amines, amides, nitriles, nitro-derivatives, disulfides, thiophenes, sulfides, sulfoxides, sulfones, phosphates, halides, and heterocyclic compounds. The experimental densities and heats of vaporization have been already cited in our recent work unless otherwise mentioned in the Tables 7–8.38 The following is additional data resource of densities and heat of vaporizations: Jorgensen et al.,39–42 Lide,43 MacMajer and Svoboda.44 The experimental hydration free energies for 15 compounds in Table 6 come from our previous collection45 and Mobley et al.’s work.46 We divided the 59 compounds into two data sets: 25 compounds that are most relevant to the building blocks of amino acids and nucleic acids are placed in the training set to participate in van der Waals parameterization; the other 34 compounds in the test set are used to objectively evaluate the optimized van der Waals parameters.
Table 7.
Densities of 35 compounds in the test set (gcm−3)
| No | Compound | Expt. | Temp. | Additive | Thole-Linear | Thole-Ameoba | ||
|---|---|---|---|---|---|---|---|---|
| (°C) | GAFF | FF99 vdW | Opt. vdW | FF99 vdW | Opt. vdW | |||
| 1 | 1-butyne | 0.678 | 0 | 0.738±0.000 | 0.748±0.000 | 0.711±0.000 | 0.748±0.000 | 0.711±0.000 |
| 2 | fluorobenzene | 1.023 | 20 | 0.989±0.001 | 1.005±0.000 | 0.989±0.001 | 1.005±0.000 | 0.989±0.001 |
| 3 | propanol | 0.800 | 25 | 0.811±0.001 | 0.821±0.000 | 0.764±0.001 | 0.828±0.000 | 0.770±0.001 |
| 4 | propanethiol | 0.836 | 25 | 0.833±0.000 | 0.835±0.000 | 0.820±0.000 | 0.836±0.000 | 0.820±0.000 |
| 5 | ethyl methyl ether | 0.721 | 7.35 | 0.728±0.000 | 0.741±0.000 | 0.708±0.000 | 0.740±0.000 | 0.708±0.000 |
| 6 | ethyl methyl sulfide | 0.837 | 25 | 0.801±0.000 | 0.818±0.000 | 0.801±0.000 | 0.817±0.000 | 0.802±0.000 |
| 7 | dimethyl disulfide | 1.057 | 25 | 1.019±0.000 | 1.027±0.000 | 1.025±0.000 | 1.028±0.001 | 1.024±0.001 |
| 8 | acetaldehyde | 0.783 | 18 | 0.786±0.000 | 0.800±0.001 | 0.739±0.000 | 0.800±0.000 | 0.740±0.000 |
| 9 | butanone | 0.800 | 25 | 0.784±0.000 | 0.802±0.000 | 0.778±0.000 | 0.802±0.000 | 0.778±0.001 |
| 10 | propanoic acid | 0.988 | 25 | 1.025±0.001 | 1.032±0.001 | 0.939±0.000 | 1.034±0.001 | 0.944±0.000 |
| 11 | N-methylpropanamide | 0.931 | 25 | 0.931±0.000 | 0.963±0.000 | 0.929±0.001 | 0.961±0.001 | 0.929±0.001 |
| 12 | methylacetate | 0.928 | 25 | 0.970±0.001 | 0.989±0.000 | 0.954±0.001 | 0.989±0.001 | 0.953±0.000 |
| 13 | methyl benzoate | 1.089 | 20 | 1.107±0.000 | 1.115±0.001 | 1.090±0.000 | 1.112±0.001 | 1.089±0.000 |
| 14 | nitromethane | 1.140 | 25 | 1.232±0.000 | 1.244±0.000 | 1.205±0.001 | 1.245±0.000 | 1.205±0.001 |
| 15 | benzonitrile | 1.001 | 25 | 1.028±0.000 | 1.040±0.000 | 1.011±0.000 | 1.040±0.000 | 1.012±0.000 |
| 16 | furan | 0.951 | 20 | 0.974±0.000 | 0.983±0.001 | 0.951±0.000 | 0.982±0.000 | 0.952±0.000 |
| 17 | pyridazine | 1.103 | 25 | 1.088±0.000 | 1.131±0.000 | 1.092±0.001 | 1.132±0.001 | 1.092±0.000 |
| 18 | pyrrole | 0.966 | 25 | 1.015±0.000 | 1.037±0.001 | 1.003±0.000 | 1.042±0.001 | 1.006±0.000 |
| 19 | oxazole | 1.080 | 25 | 1.145±0.000 | 1.164±0.001 | 1.125±0.001 | 1.163±0.001 | 1.124±0.000 |
| 20 | toluene | 0.8668 | 20 | 0.855±0.001 | 0.869±0.001 | 0.854±0.000 | 0.868±0.001 | 0.853±0.000 |
| 21 | ethylbenzene | 0.8626 | 25 | 0.844±0.000 | 0.854±0.000 | 0.837±0.000 | 0.853±0.001 | 0.836±0.000 |
| 22 | 2-methyl-1-butene | 0.6623 | 20 | 0.622±0.000 | 0.634±0.001 | 0.640±0.000 | 0.632±0.001 | 0.639±0.000 |
| 23 | butanoic acid | 0.9528 | 25 | 0.995±0.001 | 1.053±0.001 | 1.023±0.001 | - | 1.026±0.000 |
| 24 | 2,3-dimethylbutane | 0.6616 | 20 | 0.662±0.000 | 0.662±0.000 | 0.646±0.000 | 0.662±0.000 | 0.646±0.000 |
| 25 | cyclohexene | 0.811 | 20 | 0.779±0.001 | 0.784±0.000 | 0.776±0.000 | 0.782±0.000 | 0.775±0.000 |
| 26 | tripropylamine | 0.7558 | 20 | 0.768±0.001 | 0.775±0.000 | 0.736±0.000 | 0.777±0.000 | 0.734±0.001 |
| 27 | propylamine | 0.711 | 25 | 0.776±0.000 | 0.813±0.000 | 0.727±0.001 | 0.820±0.000 | 0.756±0.001 |
| 28 | diethylamine | 0.699 | 25 | 0.742±0.000 | 0.749±0.001 | 0.656±0.000 | 0.749±0.000 | 0.657±0.000 |
| 29 | triethylamine | 0.723 | 25 | 0.751±0.001 | 0.751±0.000 | 0.693±0.000 | 0.750±0.000 | 0.689±0.000 |
| 30 | aziridine | 0.831 | 25 | 0.835±0.000 | 0.888±0.001 | 0.805±0.001 | 0.893±0.000 | 0.812±0.001 |
| 31 | azetidine | 0.841 | 25 | 0.827±0.000 | 0.873±0.001 | 0.826±0.001 | 0.879±0.000 | 0.833±0.000 |
| 32 | pyrrolidine | 0.854 | 25 | 0.888±0.000 | 0.902±0.001 | 0.813±0.001 | 0.902±0.000 | 0.817±0.001 |
| 33 | piperidine | 0.857 | 25 | 0.891±0.001 | 0.908±0.000 | 0.842±0.000 | 0.910±0.001 | 0.844±0.001 |
| 34 | dimethyl hydrogen phosphate | 1.3225 | 20 | 1.427±0.001 | 1.448±0.000 | 1.369±0.000 | 1.448±0.000 | 1.383±0.001 |
| APE | 3.46% | 4.56% | 3.17% | 4.50 | 3.26% | |||
| AUE | 0.031 | 0.041 | 0.028 | 0.040 | 0.029 | |||
| RMSE | 0.040 | 0.052 | 0.032 | 0.051 | 0.034 | |||
Table 8.
Heat of vaporization for 34 compounds in the test set
| Temp. | Expt.* | Additive | Thole-Linear | Thole-Amoeba | ||||
|---|---|---|---|---|---|---|---|---|
| No | Compound | (°C) | GAFF | FF99 vdW | Opt. vdW | FF99 vdW | Opt. vdW | |
| 1 | 1-butyne | 25 | 5.58 | 6.58±0.00 | 8.67±0.01 | 7.52±0.00 | 9.02±0.00 | 7.93±0.00 |
| 2 | fluorobenzene | 25 | 8.29 | 5.85±0.01 | 7.86±0.02 | 7.56±0.03 | 7.93±0.02 | 7.60±0.02 |
| 3 | propanol | 25 | 11.35 | 11.65±0.00 | 12.32±0.01 | 12.08±0.01 | 13.04±0.00 | 13.44±0.01 |
| 4 | propanethiol | 25 | 7.62 | 5.01±0.00 | 6.41±0.01 | 6.09±0.00 | 6.43±0.01 | 6.24±0.00 |
| 5 | ethyl methyl ether | 7.35 | 5.91 | 4.17±0.00 | 6.03±0.01 | 5.37±0.00 | 6.02±0.01 | 5.42±0.01 |
| 6 | ethyl methyl sulfide | 25 | 7.61 | 4.50±0.01 | 6.44±0.00 | 6.13±0.00 | 6.45±0.00 | 6.24±0.00 |
| 7 | dimethyl disulfide | 25 | 9.06 | 5.69±0.01 | 7.33±0.00 | 7.28±0.01 | 7.33±0.01 | 7.33±0.01 |
| 8 | acetaldehyde | 25 | 6.24 | 5.21±0.01 | 6.90±0.01 | 5.90±0.01 | 6.99±0.01 | 6.04±0.01 |
| 9 | butanone | 25 | 8.35 | 6.96±0.01 | 9.23±0.02 | 8.42±0.01 | 9.21±0.01 | 8.60±0.01 |
| 10 | propanoic acid | 25 | 13.15 | 14.09±0.01 | 13.77±0.02 | 11.89±0.03 | 14.81±0.03 | 13.16±0.01 |
| 11 | N-methylpropanamide | 25 | 15.5 | 13.64±0.00 | 18.81±0.01 | 17.53±0.02 | 18.80±0.02 | 17.78±0.01 |
| 12 | methylacetate | 25 | 7.72 | 7.86±0.03 | 9.89±0.03 | 8.93±0.04 | 9.90±0.04 | 9.01±0.03 |
| 13 | methyl benzoate | 25 | 13.28 | 12.79±0.01 | 14.85±0.01 | 13.64±0.03 | 14.84±0.02 | 13.62±0.01 |
| 14 | nitromethane | 25 | 9.17 | 11.51±0.02 | 12.15±0.03 | 10.91±0.03 | 12.20±0.03 | 11.14±0.03 |
| 15 | benzonitrile | 25 | 12.54 | 12.48±0.02 | 14.28±0.01 | 13.19±0.00 | 14.27±0.01 | 13.10±0.00 |
| 16 | furan | 25 | 6.62 | 5.26±0.00 | 7.05±0.00 | 6.49±0.00 | 7.12±0.00 | 6.48±0.00 |
| 17 | pyridazine | 25 | 12.78 | 11.20±0.01 | 14.55±0.01 | 13.26±0.01 | 14.60±0.00 | 13.19±0.01 |
| 18 | pyrrole | 25 | 10.84 | 10.39±0.00 | 16.26±0.01 | 15.53±0.00 | 16.39±0.01 | 15.58±0.00 |
| 19 | oxazole | 25 | 7.77 | 8.01±0.01 | 10.01±0.01 | 9.13±0.00 | 10.01±0.01 | 9.07±0.00 |
| 20 | toluene | 25 | 8.84 | 6.92±0.01 | 8.99±0.02 | 8.59±0.02 | 9.09±0.02 | 8.69±0.02 |
| 21 | ethylbenzene | 25 | 10.1 | 7.59±0.01 | 9.64±0.01 | 9.09±0.01 | 9.61±0.01 | 9.13±0.00 |
| 22 | 2-methyl-1-butene | 25 | 6.26 | 3.51±0.01 | 5.71±0.02 | 5.93±0.02 | 5.79±0.03 | 6.09±0.02 |
| 23 | butanoic acid | 25 | 13.86 | 14.37±0.03 | 15.10±0.25 | 16.09±0.03 | - | 17.70±0.03 |
| 24 | 2,3-dimethylbutane | 25 | 7.01 | 5.25±0.00 | 7.09±0.01 | 6.55±0.01 | 7.17±0.01 | 6.62±0.00 |
| 25 | cyclohexene | 25 | 8.02 | 5.78±0.01 | 7.66±0.00 | 7.42±0.00 | 7.72±0.00 | 7.59±0.00 |
| 26 | tripropylamine | 25 | 11.03 | 9.93±0.02 | 12.48±0.01 | 9.76±0.02 | 12.57±0.02 | 9.74±0.01 |
| 27 | propylamine | 25 | 7.47 | 8.91±0.00 | 14.33±0.02 | 10.50±0.02 | 12.79±0.01 | 10.20±0.02 |
| 28 | diethylamine | 25 | 7.48 | 6.79±0.03 | 11.42±0.05 | 8.78±0.04 | 8.21±0.03 | 5.91±0.03 |
| 29 | triethylamine | 25 | 8.33 | 7.33±0.02 | 13.86±0.01 | 11.68±0.01 | 9.05±0.01 | 6.59±0.00 |
| 30 | aziridine | 25 | 8.09 | 7.06±0.01 | 10.94±0.01 | 9.61±0.00 | 9.90±0.01 | 8.48±0.01 |
| 31 | azetidine | 25 | 8.17 | 7.11±0.02 | 11.24±0.04 | 9.11±0.03 | 9.54±0.03 | 9.41±0.02 |
| 32 | pyrrolidine | 25 | 8.95 | 6.58±0.00 | 8.67±0.01 | 7.52±0.00 | 10.70±0.00 | 7.99±0.02 |
| 33 | piperidine | 25 | 9.39 | 5.85±0.01 | 7.86±0.02 | 7.56±0.03 | 11.83±0.03 | 9.28±0.02 |
| AUE | 1.53 | 1.84 | 1.29 | 1.63 | 1.20 | |||
| RMSE | 1.80 | 2.48 | 1.62 | 2.10 | 1.62 | |||
Table 6.
Experimental and calculated hydration energies (kcal/mol)
| No | Compound | Expt.* | Additive | Thole-Linear | Thole-Amoeba | ||
|---|---|---|---|---|---|---|---|
| GAFF | FF99 vdW | Opt. vdW | FF99 vdW | Opt. vdW | |||
| 1 | isobutane | 2.22 | 2.25±0.01 | 1.78±0.03 | 1.99±0.02 | 1.82±0.03 | 2.12±0.02 |
| 2 | benzene | −0.86 | −0.75±0.07 | −2.09±0.11 | −1.90±0.11 | −2.11±0.07 | −1.77±0.09 |
| 3 | ethanol | −5.00 | −4.34±0.07 | −5.78±0.11 | −7.57±0.14 | −6.45±0.12 | −9.04±0.14 |
| 4 | acetic acid | −6.70 | −6.02±0.12 | −1.76±0.16 | −4.30±0.16 | −1.23±0.26 | −5.74±0.21 |
| 5 | methylamine | −4.60 | −4.74±0.06 | −5.27±0.12 | −7.57±0.21 | −5.48±0.13 | −6.90±0.12 |
| 6 | N-methylaceticamide | −10.00 | −7.81±0.09 | −11.13±0.14 | −10.62±0.17 | −10.98±0.12 | −10.59±0.16 |
| 7 | phenol | −6.61 | −4.59±0.07 | −6.31±0.16 | −6.53±0.15 | −6.50±0.20 | −8.05±0.18 |
| 8 | ethanethiol | −1.30 | −0.41±0.03 | −1.25±0.09 | −1.30±0.09 | −1.75±0.07 | −1.58±0.09 |
| 9 | dimethyl ether | −1.91 | −0.47±0.05 | −1.25±0.06 | −0.82±0.08 | −1.28±0.07 | −0.87±0.06 |
| 10 | acetone | −3.80 | −3.52±0.05 | −4.88±0.10 | −4.35±0.08 | −4.72±0.09 | −4.59±0.09 |
| 11 | dimethylamine | −4.28 | −2.54±0.07 | −2.91±0.10 | −3.64±0.15 | −2.94±0.09 | −2.83±0.12 |
| 12 | trimethylamine | −3.23 | −0.32±0.04 | −2.39±0.10 | −2.16±0.09 | −2.56±0.12 | −1.99±0.12 |
| 13 | dimethyl sulfoxide | −8.71 | −8.58±0.11 | −9.46±0.12 | −9.73±0.15 | −9.95±0.15 | −10.01±0.12 |
| 14 | bromomethane | −0.82 | −0.08±0.02 | −0.27±0.03 | −0.11±0.04 | −0.18±0.04 | −0.12±0.03 |
| 15 | pyridine | −4.69 | −3.08±0.05 | −6.34±0.09 | −5.72±0.13 | −6.46±0.08 | −6.17±0.11 |
| Average difference | 1.019 | 0.065 | −0.269 | −0.032 | −0.523 | ||
| Average percent difference | −32.82% | −0.33% | 3.47% | 3.31% | 8.15% | ||
| AUE | 1.04 | 1.10 | 1.07 | 1.21 | 1.24 | ||
| RMSE | 1.35 | 1.56 | 1.38 | 1.72 | 1.54 | ||
2.3 Molecular Mechanical Models
Five molecular mechanical models, namely, the additive using FF9915/GAFF14 (in abbreviation FF99/GAFF), two polarizable models with the FF99/GAFF vdW parameters (in abbreviation TL-FF99vdW and TA-FF99vdW), and two polarizable models with the optimized vdW parameters (in abbreviation TL-OptvdW and TA-OptvdW), were studied in this work. The functional forms of the two Thole polarizable models (TL and TA) are provided in the supporting text. For the additive model, the point charges were derived to fit the HF/6-31G* electrostatic potentials by the RESP program.47 The charges of the four polarizable models were derived to fit the MP2/aug-cc-pVTZ electrostatic potentials by the i-RESP program.48 Unlike RESP, the i-RESP program applies an iterative procedure to determine charges so that the ESP generated by the point charges plus ESP due to self-polarization reproduce the quantum mechanical ESP. The other force field parameters of the three molecular mechanical models come from FF99 and GAFF: whenever possible, the force field parameters in FF99 were adopted and the missing ones come from GAFF. Certainly, in the last two molecular mechanical models, the FF99/GAFF vdW parameters were substituted by the optimized ones.
All electrostatic potentials were generated using the Gaussian 03 software package.49 The residue topology files were prepared using the Antechamber module50 in AMBER 11.51 For each molecule, an internal program was used to generate a rectangular parallelepiped box filled with multiple copies of the monomer, and then the Leap program in AMBER11 was applied to generate the topology files.
2.4 Molecular Mechanical Calculations
An extended version of the Sander program in AMBER11 with implementation of the Thole screening functions was used to calculate the interaction energy and to perform minimizations and molecular dynamics simulations. The 1–4 van der Waals energies were scaled down by 50% for all the molecular mechanical calculations; while the 1–4 electrostatic energies were scaled down by a factor of 1/1.2 only for the additive model (FF99/GAFF). The 1–4 electrostatic scaling factor was set to 1.0 for the polarizable models (TL-FF99vdW, TL-OptvdW, TA-FF99vdW and TA-OptvdW), consistent with the derivation of the charge sets.
The TIP3P water was applied in conjunction with FF99/GAFF and two newly developed POL3 water models that are consistent with the Thole linear and Thole Amoeba-like models were used in conjunction with TL-FF99vdW/TL-OptvdW and TA-FF99vdW/TA-OptvdW, respectively.8 Bond and bond angles in the additive and polarizable water were constrained with a special “three-point” algorithm.52 Except where explicitly stated otherwise, all the degrees of freedom of other molecules were free to change in all the MD simulations.
The interaction energies in GA optimization were calculated using the ab initio geometries and no cutoff was applied. In the control test of studying how minimization affect the interaction energy calculations using a subset of Set 7, steepest descent and conjugated gradient minimizations were performed for each molecule until either the total cycles of minimization exceed 10,000 times or root-mean-square of the gradient is less than 0.001 kcal/mol/Å.
All the liquid phase MD simulations were performed with the periodic boundary condition to produce either canonical or isothermal-isobaric ensembles using the sander program of AMBER11.51 The Particle Mesh Ewald (PME) method53–55 was used to calculate the full electrostatic energy of a unit cell in a macroscopic lattice of repeating images. The non-bonded cutoff of calculating van der Waals and electrostatic energies was set to 9.0 Å, and a continuum model correction term was added to the van der Waals energies. The effect of non-bonded cutoff on the MD simulations was discussed by Shirts et al.56 Temperature was regulated using the Langevin dynamics57 with the collision frequency of 5 ps.58–60 Pressure regulation was achieved with isotropic position scaling and the pressure relaxation time was set to 1.0 picosecond. For the additive model, the integration of the equations of motion was conducted at a time step of 2 femtosecond, while for the polarizable models, the time step was 1 femtosecond and the convergence criterion of induced dipoles was set to 10−6 debye.
There are three phases in a liquid phase MD simulation, namely, the relaxation phase, the equilibration phase and the sampling phase. In the relaxation phase, the main chain atoms were gradually relaxed by applying a series of restraints and the force constants decreased progressively: from 20 to 10, 5 and 1.0 kcal/mol/Å2. For each force constant, the position-restrained MD simulation was run for 20 picoseconds. In the following equilibration phase, the system was further equilibrated for 2 nanoseconds without any restraints and constraints. For the NVT MD simulations, the dimensions of simulation boxes were adjusted so that the density equals to the experimental value, then the system was further equilibrated for another 3 nanoseconds. In the sampling phases of the NPT MD simulations, the snapshots as well as the structural and energy related properties were recorded at an interval of 1 picosecond, and in total 1000 snapshots were saved for further analysis. While for the NVT MD simulations, only 200 snapshots were sampled at an interval of 5 picoseconds.
2.5 Molecular Property Calculations Density Calculations
The average bulk density d was computed from the average volume of the simulation box, <V> using Eq. 5, where Nres is the number of residues in the simulation box, M is molar mass of the molecule in study and NA is the Avogadro constant. The bulk densities were printed out in the output files of MD simulations by sander in default.
| (5) |
Heat of Vaporization
The heat of vaporization ΔHvap can be calculated with Eq. (6),
| (6) |
| (7) |
where are the potential energies in the gas and liquid phases, respectively; is obtained through molecular simulations and is estimated using Eq. (7); is the minimized energy in gas phase; and Natom and Ncons are the number of atoms in the molecules and the number of the constrained degrees of freedom, respectively. The correction term C in Eq. (6) accounts for the difference in vibration energies calculated quantum mechanically and classically, as well as for the polarization and non-ideal gas effects. This term is small and it is neglected in this work.
Solvation Free Energy Calculations
The vdW parameters of ions have been parameterized to reproduce the hydration energies.61 However, solvation free energy is seldom applied to parameterize van der Waals terms of neutral molecules, even though, it is a standard practice to test if a molecular mechanical model is capable to reproduce the experimental solvation free energies of model compounds.
The hydration free energy of a molecule was calculated using thermodynamic integration (TI). In TI calculations, the system evolves according to a mixed potential, V(λ)=(1−λ)kV0+[1−(1−λ)k]V1, where λ and k are mixing parameters and V, V0 and V1 are the mixed, the unperturbed and perturbed potentials, respectively. The free energy change, ΔG, is calculated numerically using Eq. 8.
| (8) |
The solvation free energy of a molecule was calculated by summing up the free energy changes in four perturbations, i.e., the gas-phase and aqueous-phase disappearing of Coulombic interactions and the gas-phase and aqueous-phase disappearing of the van der Waals interactions. For the disappearing of Coulombic interactions, a linear mixing rule was applied (k=1); for the disappearing of the van der Waals interactions, k was set to 6 as suggested by Steinbrecher et al.62 For each of the four free energy perturbations (two in gas phase and two in aqueous solution), 9 windows / free energy simulations were performed in order to numerically estimate the integral in Eq. 8. The free energy change of ith window 〈∂V / ∂λ〉i was weighted by wi. The weight parameters wi, which was obtained to fit the Gaussian quadrature formula, came from Ref. 60. Except that the systems were equilibrated for one nanosecond followed by production for another nanosecond, and the bonds involving hydrogen were constrained, the other MD setting is same to the pure liquid MD simulations discussed above.
Statistical Uncertainty Estimation
The density and most energetic terms in heat of vaporization calculations are ensemble averages. The uncertainty of a term (densities, temperatures and energies) was estimated by the RMS deviation of a serial of accumulated means. For each property, the means were calculated using the first 500, 525, 550, 575, 600…1000 snapshots.
For the hydration energies, the uncertainty of free energy change in each simulation was calculated in a similar way. To calculate the uncertainty of a free energy component, such as charging in aqueous phase, the weighted uncertainty of nine simulations were summed up. The uncertainty of the hydration energy of a compound was obtained by summing up the uncertainties of four free energy components (charges and vdW parameters disappearing in both gas and aqueous phases).
3. Results and discussion
In this section, we first present the efficiency of our iterative procedure in van der Waals parameterization and then discuss the performance of the optimized vdW parameter set in calculating the interaction energies and condensed-phase molecular properties.
3.1 van der Waals Parameterization Using a Genetic Algorithm
As mentioned in the Method section the van der Waals parameterization was performed with the Thole linear polarizable model and the optimized vdW set was also evaluated by the Thole Amoeba-like polarizable model. Atomic coordinates and interaction energies for the 1639 dimers, required for the GA optimization, were derived using high level ab initio models. 25 pure liquids (see Tables 5 and 6) were selected for density prediction. For each liquid, 200 snapshots were obtained from constant volume MD simulations using the FF99/GAFF model. The last snapshot (MD Frame 200) was used to calculate the residue-residue interaction energies for any arbitrary vdW parameter set. It is emphasized that the most time consuming part of GA optimization is to calculate the mean residue-residue interaction energies, therefore, only one NVT snapshot (MD Frame #200) was used in density prediction. The further justification of using one NVT snapshot will be provided below.
Table 5.
Heat of vaporization of the 25 compounds in the training set (kcal/mol)
| No | Compound | Expt. | Temp. | Additive | Thole-Linear | Thole-Amoeba | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (°C) | GAFF | FF99 vdW | Opt. vdW | FF99 vdW | Opt. vdW | ||||||||
| 1 | isobutane | 4.57 | 25 | 3.48±0.02 | 5.28±0.06 | 4.92±0.05 | 5.26±0.06 | 5.00±0.05 | |||||
| 2 | trans-2-butene | 5.15 | 25 | 3.08±0.01 | 4.26±0.00 | 4.62±0.00 | 4.26±0.00 | 4.63±0.01 | |||||
| 3 | benzene | 7.89 | 25 | 6.38±0.02 | 7.44±0.00 | 6.79±0.00 | 7.51±0.00 | 6.84±0.00 | |||||
| 4 | ethanol | 10.04 | 25 | 10.15±0.01 | 12.58±0.02 | 12.71±0.03 | 13.65±0.02 | 14.55±0.02 | |||||
| 5 | acetic acid | 12.33c | 25 | 13.38±0.02 | 13.39±0.10 | 12.68±0.04 | - | 13.63±0.03 | |||||
| 6 | methylamine | 5.59 | 25 | 7.47±0.01 | 7.97±0.01 | 5.54±0.08 | 8.14±0.00 | 5.63±0.01 | |||||
| 7 | N-methyl acetamide | 13.30 | 100 | 12.57±0.02 | 16.73±0.03 | 15.70±0.03 | 16.74±0.00 | 15.90±0.03 | |||||
| 8 | methanol | 8.84 | 25 | 9.72±0.01 | 9.49±0.00 | 9.60±0.00 | 10.25±0.01 | 10.96±0.01 | |||||
| 9 | phenol | 13.82 | 25 | 11.98±0.03 | 13.92±0.02 | 13.77±0.01 | 13.56±0.03 | 14.63±0.01 | |||||
| 10 | ethanethiol | 6.52 | 25 | 4.95±0.01 | 5.66±0.00 | 5.48±0.00 | 5.69±0.00 | 5.64±0.01 | |||||
| 11 | dimethyl ether | 5.14 | −24.6 | 4.64±0.01 | 5.63±0.00 | 5.07±0.01 | 5.62±0.00 | 5.06±0.00 | |||||
| 12 | dimethyl sulfide | 6.61 | 25 | 4.44±0.01 | 5.73±0.01 | 5.56±0.01 | 5.82±0.01 | 5.64±0.01 | |||||
| 13 | acetone | 7.47c | 25 | 7.20±0.02 | 8.53±0.04 | 7.88±0.04 | 8.54±0.04 | 7.99±0.04 | |||||
| 14 | dimethyl amine | 6.08c | 25 | 6.37±0.01 | 6.84±0.00 | 6.43±0.01 | 6.93±0.00 | 5.65±0.01 | |||||
| 15 | trimethylamine | 5.18 | 25 | 4.60±0.02 | 6.90±0.04 | 4.41±0.04 | 6.86±0.04 | 4.38±0.04 | |||||
| 16 | aniline | 12.91 | 25 | 12.16±0.02 | 13.87±0.01 | 12.85±0.02 | 13.88±0.01 | 13.03±0.01 | |||||
| 17 | acetonitrile | 7.87 | 25 | 7.19±0.01 | 10.00±0.02 | 9.13±0.01 | 10.06±0.02 | 9.20±0.01 | |||||
| 18 | N,N-dimethyl acetamide | 11.75 | 25 | 11.13±0.01 | 14.34±0.01 | 13.14±0.01 | 14.34±0.01 | 13.10±0.01 | |||||
| 19 | dimethyl sulfoxide | 10.30 | 189 | 8.84±0.02 | 10.34±0.04 | 9.91±0.04 | 12.71±0.04 | 12.42±0.04 | |||||
| 20 | trichloromethane | 7.48 | 25 | 6.84±0.01 | 7.28±0.00 | 6.77±0.00 | 7.26±0.00 | 6.76±0.00 | |||||
| 21 | tetrachloromethane | 7.75 | 25 | 8.02±0.01 | 8.12±0.00 | 7.59±0.00 | 8.17±0.00 | 7.66±0.00 | |||||
| 22 | bromomethane | 5.45 | 25 | 4.95±0.01 | 5.08±2.00 | 4.88±0.00 | 5.13±0.00 | 4.93±0.00 | |||||
| 23 | tetrahydrofuran | 7.65 | 25 | 7.59±0.02 | 9.65±0.00 | 8.44±0.00 | 9.64±0.00 | 8.59±0.00 | |||||
| 24 | pyridine | 9.56 | 25 | 8.81±0.03 | 10.94±0.12 | 9.99±0.13 | 11.12±0.12 | 10.13±0.12 | |||||
| 25 | quinoline | 14.18j | 25 | 13.18±0.02 | 15.56±0.11 | 14.78±0.10 | 15.72±0.08 | 14.98±0.10 | |||||
| Average difference | −0.572 | 0.884 | 0.208 | 1.073 | 0.540 | ||||||||
| Average percent difference | −7.57% | 9.93% | 0.88% | 12.10% | 3.99% | ||||||||
| AUE | 0.93 | 1.18 | 0.73 | 1.38 | 1.02 | ||||||||
| RMSE | 1.11 | 1.47 | 0.98 | 1.69 | 1.40 | ||||||||
Two distinct vdW parameter sets were needed to interpolate/extrapolate the parameters. Ideally, one vdW set overestimates and the other underestimates the densities of the selected liquids. Since the FF99 vdW set overestimates the densities for most liquids in the training set, it was selected as the first vdW set. To prepare the other vdW set, we adjusted the radii and well depths to scale down the ‘B’ parameters in Eq. 1a by 10% while keep ‘A’ parameters unchanged. This vdW parameter set is referred to as B90 set. As the attraction energies were scaled down, it is expected that the densities predicted by B90 are underestimated. In a few cases where even the B90 set overestimates the densities, the B90 set was replaced with other vdW set which can underestimate the densities. The residue-residue interaction energies were initially calculated for these two distinct vdW parameter sets. The parameters used in density prediction are listed in Table S2. For the tentative new sets of vdW parameters in GA optimization, the densities were predicted through interpolation with Eq. 3. As shown in Table S2, the densities of the two distinct vdW parameter sets are still within small ranges of the experimental values (the mean deviation is 10.5%), which is important to allow the linear interpolation.
GA optimizations were run several times to improve the fitness. The parameters that control GA optimization were set similar to those in our previous work.6 Although GA optimization was automatic, human intuition was needed to redefine atom types and adjust the searching space to improve the fitting performance. The final optimized vdW set is listed in Table 1.
Table 1.
List of the optimized van der Waals parameters
| Atom Type | Definition | Radius (R) | Well Depth (ε) |
|---|---|---|---|
| H | Hydrogen bonded to nitrogen other than HN1 and HN2 | 0.6000 | 0.0157 |
| HN1 | Secondary amine hydrogen | 0.8000 | 0.0100 |
| HN2 | Primary Amine hydrogen | 1.0300 | 0.0100 |
| HO | Hydrogen bonded to oxygen | 0.600 | 0.0007 |
| HS | Hydrogen bonded to sulfur | 0.600 | 0.0157 |
| HC | Hydrogen bonded to sp3 carbon | 1.4164 | 0.0281 |
| HA | Hydrogen bonded to sp2 and sp1 carbon | 1.5738 | 0.0060 |
| H1 | Hydrogen bonded to sp3 carbon with one electron-withdrawing group | 1.3164 | 0.0281 |
| H2 | Hydrogen bonded to sp3 carbon with two electron-withdrawing group | 1.2164 | 0.0281 |
| H3 | Hydrogen bonded to sp3 carbon with three electron-withdrawing group | 1.1164 | 0.0281 |
| H4 | Hydrogen bonded to sp2 carbon with one electron-withdrawing group | 1.5238 | 0.0060 |
| H5 | Hydrogen bonded to sp2 carbon with two electron-withdrawing group | 1.4738 | 0.0060 |
| CT | sp3 carbon | 2.0085 | 0.0591 |
| C | Carbonyl carbon | 1.9600 | 0.0623 |
| CA, C*, CB, CC, CD, CK, CM, CQ, CR, CV, CW | Aromatic sp2 carbon or sp2 carbon in planar ring systems | 1.8807 | 0.1022 |
| C2 | Other sp2 carbon | 1.8372 | 0.1354 |
| CY | sp1 carbon | 1.9275 | 0.1859 |
| OH | Hydroxyl oxygen | 1.8235 | 0.0301 |
| OS | Oxygen in ether and ester | 1.6989 | 0.1526 |
| O | Carbonyl oxygen | 1.6600 | 0.1831 |
| O2 | Carboxyl and phosphate oxygen | 1.4000 | 1.4722 |
| N, NA, N2, N*, NC, NB, NY | Nitrogen other than NT and N3 | 1.8600 | 0.1345 |
| NT, N3 | Amine nitrogen | 1.900 | 0.0500 |
| S,SH | Sulfur | 1.9901 | 0.2653 |
| P | Phosphate | 2.2286 | 0.0980 |
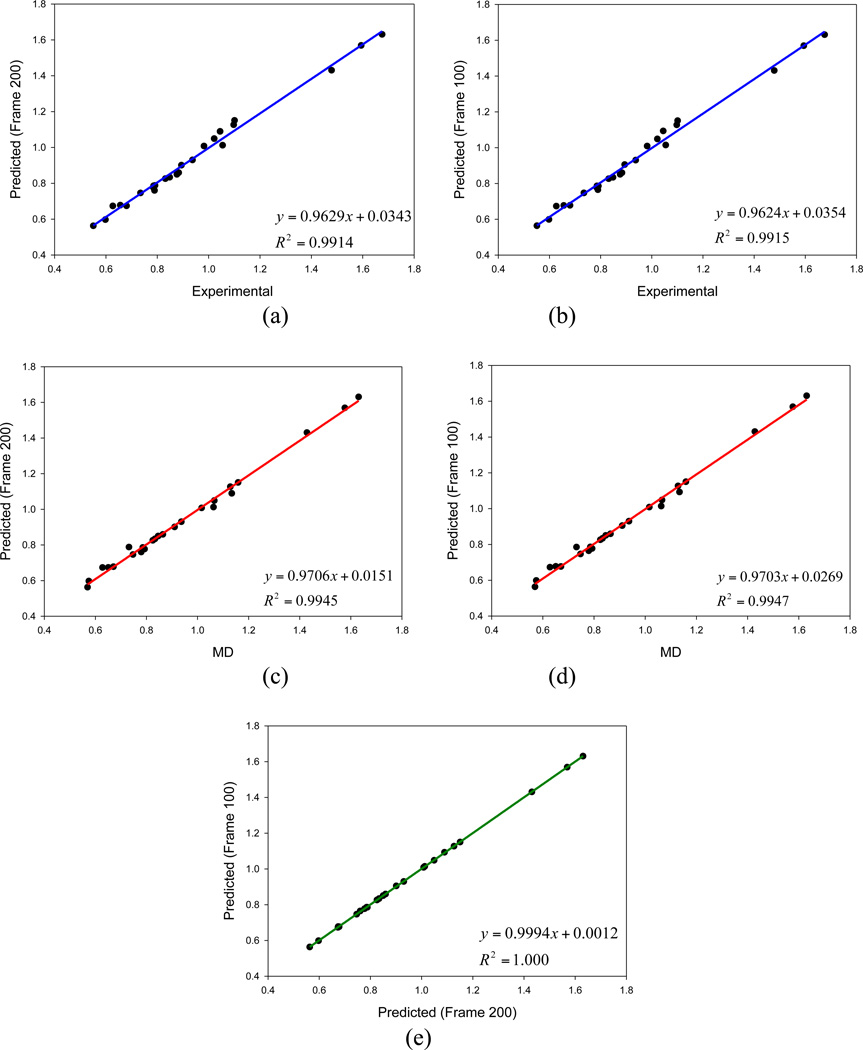
The assessment of the approach to predict liquid densities by interpolating/extrapolating mean residue-residue interaction energies is presented in Figure 2. It demonstrates the comparisons of the experimental, the predicted, and the calculated liquid densities from actual MD simulations. The AUE and APE between predicted and experimental are 0.022 gcm−3 and 2.34%, respectively (Figure 2a); while the AUE and APE between the predicted and the MD densities are 0.015 gcm−3 and 1.80%, respectively (Figure 2c). To justify the use of single NVT snapshot in density prediction, we recalculated the extrapolation/interpolation parameters and predicted the densities using another NVT snapshot (MD Frame #100). As shown in Figure 2e, the predicted densities of the two snapshots are highly correlated: the R2, AUE and APE are 1.0, 0.001 and 0.13%, respectively. The negligible APE between the two sets of predicted densities clearly supports our protocol of using one NVT snapshot in density prediction.
Figure 2.
Comparison of predicted densities (in g/mol) by TL/OptvdW: (a) experimental versus predicted using MD Frame #200, (b) experimental versus predicted using MD Frame #100, (c) MD densities versus predicted using MD Frame #200, (d) MD densities versus predicted using MD Frame #100, and (e) predicted densities using MD Frames #100 and #200.
This vdW parameterization protocol can be expanded to use multiple vdW parameter sets in interpolation/extrapolation, to apply multiple NVT snapshots for more accurate calculation of mean residue-residue interaction energies, and to deal with other liquid properties (such as heat of vaporization) as well.
3.2 Interaction Energies
The interaction energies of 1639 dimers calculated by ab initio and five molecular mechanical models are listed in Table S1. The performance of the five molecular models, namely, FF99/GAFF, TL-FF99vdW, TL-OptvdW, TA-FF99vdW and TA_OptvdW are summarized in Table 2. It is obvious that the polarizable models are much better than the additive one: the RMSE are 2.61, 1.63, 1.56, 1.59 and 1.66 kcal/mol for the above five molecular mechanical models, respectively. Interestingly, all five models achieved similar performance for Set 7 which has 590 dimers representing different types of molecular interactions. If only the amino acid analogs and nucleic acid bases are considered (Sets 1–6), the polarizable models have even bigger advantage over the additive one.
Table 2.
Performance of three molecular mechanical models in interaction energy calculations (kcal/mol)
| Additive | Thole-Linear | Thole-Amoeba | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dimer Class | #data | FF99vdW | Opt. vdW | FF99vdW | Opt. vdW | ||||||
| AUE | RMSE | AUE | RMSE | AUE | RMSE | AUE | RMSE | AUE | RMSE | ||
| Amino acid main chain analog dimers | 85 | 0.70 | 1.18 | 0.37 | 0.64 | 0.42 | 0.71 | 0.37 | 0.62 | 0.42 | 0.70 |
| Amino acid side chain analog dimers | 517 | 2.61 | 4.09 | 1.42 | 1.97 | 1.31 | 1.79 | 1.37 | 1.86 | 1.39 | 2.02 |
| Water amino acid analog dimers | 71 | 1.33 | 2.02 | 1.31 | 2.26 | 1.26 | 1.94 | 1.34 | 2.28 | 1.38 | 2.12 |
| Hydrogen-boned nucleic base pairs | 29 | 1.53 | 2.14 | 1.73 | 2.10 | 1.62 | 2.02 | 1.78 | 2.19 | 1.69 | 2.09 |
| Stacked nucleic base pairs | 246 | 1.27 | 2.10 | 1.29 | 1.90 | 1.25 | 2.06 | 1.29 | 1.89 | 1.25 | 2.06 |
| Nucleic acid base steps | 100 | 0.85 | 1.19 | 1.35 | 1.84 | 0.85 | 1.18 | 1.35 | 1.85 | 0.85 | 1.18 |
| Dimers representing different interaction types | 591 | 0.71 | 1.14 | 0.62 | 0.99 | 0.71 | 1.12 | 0.62 | 0.98 | 0.72 | 1.13 |
| Sum of sets 1–6 | 1048 | 1.86 | 3.15 | 1.30 | 1.89 | 1.19 | 1.77 | 1.28 | 1.84 | 1.23 | 1.90 |
| All | 1639 | 1.44 | 2.61 | 1.06 | 1.63 | 1.02 | 1.56 | 1.04 | 1.59 | 1.05 | 1.66 |
Among sets 1–6, the amino acid side chain analogs (Set 2) showed largest difference. As noted in our earlier work, with FF99vdW set, the AUE reduced from 2.61 in additive FF99 to 1.42 and 1.31 in TL and TA, respectively. The RMSE also reduced from 4.09 in additive FF99 to 1.97 and 1.86 in TL and TA. The optimization of the vdW parameters using TL model further reduced the AUE to 1.31 and RMSE to 1.79. When the optimized vdW was tested on TA model, the AUE was retained at the similar level compared to FF99vdW (1.39 vs 1.37) while RMSE increased from 1.86 to 2.02, by 0.16, understandably, because the optimization was performed on the TL model only. Nevertheless it is clear that the TL and TA models are notably better than the additive model. Notable improvements are seen in nucleic acid base steps, with AUE reduced from 1.35 to 0.85 and RMSE reduced from 1.84 and 1.85 to 1.18 after vdW optimization. Overall, when Sets 1–6 are evaluated, the polarizable models show clear advantages.
Among the four polarizable molecular mechanical models, TL-OptvdW has achieved a marginally better performance than the other three models. However, for the Set 6, the 100 dimers of nucleic acid base steps, the two models utilizing the optimized vdW set notably outperforms the two using the FF99vdW set.
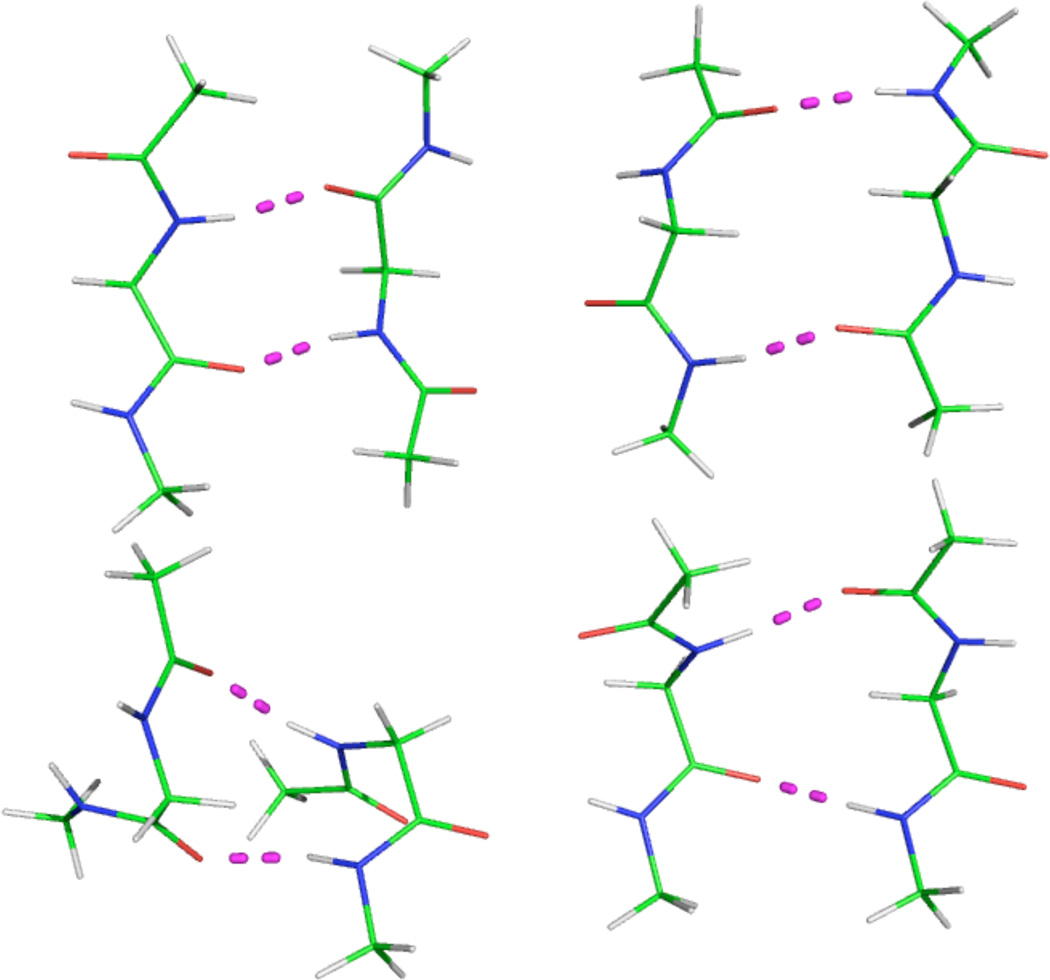
An important practice in protein force field development is to investigate how a force field parameterized using small building blocks of amino acids propagate the calculation errors to larger molecules. However, it is impractical to accurately calculate the energies of large peptides with high level ab initio approaches. Here we calculated the interaction energies of ACE-GLY-NME dimers studied by Wang et al63 using high-level ab initio models. The geometries of the four conformations are shown in Figure 3. The interaction energies in the CBS limit were obtained by extrapolating the interaction energies at MP2/aug-cc-pVDZ, MP2/aug-ccpVTZ, MP2/aug-cc-pVQZ levels with and without BSSE-correction. We consider this comparison a rather critical test because this is the only realistic high level model of the main chain interactions in proteins. Thus, we intentionally excluded this data set in the fitting. Overall, the performance of FF99vdW and the optimized vdW sets are comparable and all polarizable models are significantly better than the additive model as indicated in Table 3. It is not surprising that the AUE and RMSE of the FF99/GAFF additive model are more than two times larger. Such large degree of improvement illustrates the superiority of the polarizable models. It is important to note that all the interaction energy calculations including the ACE-GLY-NME dimers were calculated using the ab initio geometries. This is necessary since the minimized structures depend on both the terms that we intend to test (i.e., non-bonded forces between the peptides) and those that have yet to be refined which would render the QM and MM interaction energies incomparable. Particularly for ACE-GLY-NME dimers, the torsional angle terms, which will be tuned in the final stage according to our force field development process, have significant impact on the minimized structures.
Figure 3.
Ab initio conformations of ACE-GLY-NME dimer63: (1) upper left: abbc5, antiparallel beta C5 conformation; (2) upper right: abbc7, antiparallel beta C7 conformation, (3) lower left: ahh, alpha helical conformation, and (4) lower right: pbb, parallel beta conformation. The hydrogen bonds are shown by dashed lines.
Table 3.
List of the conformational energies of ACE-GLY-NME dimer (kcal/mol)
| Conf. |
Ab Initio* |
Additive | Thole-Linear | Thole-Amoeba | ||
|---|---|---|---|---|---|---|
| FF99 | FF99 vdW | Opt. vdW | FF99 vdW | Opt. vdW | ||
| abbc5 | −14.98 | −13.68 | −15.24 | −14.94 | −15.34 | −15.04 |
| abbc7 | −21.38 | −17.02 | −22.81 | −22.52 | −23.00 | −22.70 |
| ahh | −15.89 | −17.27 | −14.85 | −14.18 | −14.86 | −14.19 |
| pbb | −18.17 | −16.13 | −19.06 | −18.73 | −19.22 | −18.88 |
| AUE | - | 2.27 | 0.90 | 0.86 | 1.02 | 0.95 |
| RMSE | - | 2.59 | 1.07 | 1.07 | 1.11 | 1.13 |
Extrapolated using the BSSE corrected MP2/aug-cc-pVDZ, MP2/aug-cc-pVTZ and MP2/aug-cc-pVQZ energies with CCSD(T)/cc-pVDZ correction. The dimer geometries were optimizaed at MP2/6-311+G** level of theory (see Wang et al63 for detail).
As the interaction energies were calculated using the ab initio geometries without further minimization, it is necessary for us to check if the minimizations significantly distort the ab initio optimized geometries. We selected a subset of Set 7 for this purpose. All the entries in this subset have equilibrium geometries (fully optimized, not in the dissociation curves). Encouragingly, the minimized geometries using the TL-OptvdW model are very close to ab intio ones. The mean and RMS of root-mean-square displacements (RMSD) are 0.222 and 0.277 Å, respectively. To investigate if the two monomers come closer or further away after minimizations, we identified the shortest atomic distances between two monomers based on the ab initio geometries; then the distances of the same atom pairs were calculated for the minimized geometries by TL-OptvdW. Comparing the two sets of distances we found that there is no systematic difference as the mean difference is close to zero (0.029 Å). The AUE and RMSE of the differences are 0.168 and 0.201 Å, respectively. Moreover, compared to the high-level ab initio model, the prediction errors of interaction energies with and without minimization are also very close: the AUE are 0.68 and 0.80 kcal/mol for the ab initio and minimized geometries, respectively; and the RMSE are 0.96 and 1.09 kcal/mol for the two sets of geometries, respectively.
3.3 Molecular Property Calculations
Although the van der Waals optimization was performed on the liquid densities and interaction energies only, improvements on other properties are expected, particularly the heat of vaporization, can also be better predicted, because of the improved interactions. We have found that the densities and heats of vaporization were improved almost simultaneously when we adjust the radius and well depth parameters of several classes of compounds in a recent publication.38
For the 25 molecule training set, the experimental and calculated densities and heats of vaporization of the training set molecules calculated by five molecular mechanical models are listed in Tables 4 and 5, respectively. The average percent errors of the liquid densities are 3.83, 6.37, 2.70, 6.20 and 2.73% for FF99/GAFF, TL-FF99vdW, TL-OptvdW, TA-FF99vdW and TA-OptvdW models, respectively. It is obvious that TL-OptvdW and TA-OptvdW outperform the other molecular mechanical models in density calculations. However, for the heat of vaporization, the best two models are TL-OptvdW and FF99/GAFF, which have achieved an RMSE of 0.98 and 1.11 kcal/mol, respectively.
Table 4.
Densities of 25 compounds in the training set (gcm−3)
| Expt. | Temp. | Additive | Thole-Linear | Thole-Amoeba | ||||
|---|---|---|---|---|---|---|---|---|
| No | Compound | (°C) | GAFF | FF99 vdW | Opt. vdW | FF99 vdW | Opt. vdW | |
| 1 | isobutane | 0.551 | 25 | 0.564±0.004 | 0.587±0.000 | 0.570±0.000 | 0.587±0.000 | 0.569±0.000 |
| 2 | trans-2-butene | 0.598 | 25 | 0.546±0.004 | 0.553±0.000 | 0.575±0.000 | 0.554±0.001 | 0.575±0.000 |
| 3 | benzene | 0.877 | 20 | 0.867±0.006 | 0.877±0.001 | 0.846±0.001 | 0.875±0.001 | 0.845±0.000 |
| 4 | ethanol | 0.789 | 20 | 0.809±0.006 | 0.856±0.000 | 0.780±0.001 | 0.867±0.001 | 0.792±0.000 |
| 5 | acetic acid | 1.045 | 25 | 1.120±0.007 | 1.208±0.002 | 1.134±0.001 | 1.157±0.001 | |
| 6 | methylamine | 0.656 | 25 | 0.773±0.007 | 0.818±0.000 | 0.670±0.000 | 0.826±0.000 | 0.678±0.000 |
| 7 | N-methyl acetamide | 0.894 | 100 | 0.901±0.007 | 0.946±0.001 | 0.910±0.001 | 0.946±0.000 | 0.909±0.001 |
| 8 | methanol | 0.791 | 20 | 0.819±0.007 | 0.854±0.001 | 0.732±0.001 | 0.865±0.000 | 0.750±0.001 |
| 9 | phenol | 1.055 | 45 | 1.051±0.006 | 1.088±0.001 | 1.063±0.001 | 1.090±0.001 | 1.065±0.000 |
| 10 | ethanethiol | 0.832 | 25 | 0.824±0.006 | 0.836±0.000 | 0.825±0.001 | 0.839±0.000 | 0.827±0.000 |
| 11 | dimethyl ether | 0.735 | −24.6 | 0.754±0.005 | 0.780±0.000 | 0.747±0.000 | 0.780±0.000 | 0.747±0.000 |
| 12 | dimethyl sulfide | 0.848 | 20 | 0.804±0.006 | 0.845±0.000 | 0.833±0.001 | 0.845±0.000 | 0.832±0.000 |
| 13 | acetone | 0.785 | 25 | 0.787±0.005 | 0.818±0.000 | 0.793±0.000 | 0.819±0.000 | 0.792±0.000 |
| 14 | dimethyl amine | 0.680 | 0 | 0.741±0.005 | 0.758±0.000 | 0.651±0.001 | 0.761±0.000 | 0.659±0.000 |
| 15 | trimethylamine | 0.627b | 25 | 0.698±0.005 | 0.752±0.000 | 0.628±0.000 | 0.750±0.001 | 0.633±0.000 |
| 16 | aniline | 1.022 | 20 | 1.074±0.006 | 1.090±0.001 | 1.066±0.001 | 1.087±0.001 | 1.069±0.000 |
| 17 | acetonitrile | 0.786 | 20 | 0.731±0.005 | 0.822±0.000 | 0.786±0.000 | 0.821±0.000 | 0.786±0.001 |
| 18 | N,N-dimethyl acetamide | 0.936 | 25 | 0.935±0.005 | 0.965±0.000 | 0.937±0.001 | 0.966±0.001 | 0.936±0.000 |
| 19 | dimethyl sulfoxide | 1.101 | 25 | 1.126±0.006 | 1.170±0.000 | 1.159±0.001 | 1.170±0.000 | 1.159±0.000 |
| 20 | trichloromethane | 1.479 | 25 | 1.448±0.009 | 1.473±0.001 | 1.428±0.001 | 1.471±0.001 | 1.429±0.001 |
| 21 | tetrachloromethane | 1.594 | 20 | 1.607±0.010 | 1.613±0.001 | 1.577±0.001 | 1.612±0.001 | 1.574±0.001 |
| 22 | bromomethane | 1.676 | 20 | 1.642±0.013 | 1.666±0.001 | 1.631±0.001 | 1.664±0.001 | 1.632±0.001 |
| 23 | tetrahydrofuran | 0.883 | 25 | 0.891±0.005 | 0.909±0.001 | 0.864±0.000 | 0.909±0.001 | 0.864±0.000 |
| 24 | pyridine | 0.982 | 20 | 0.992±0.006 | 1.049±0.000 | 1.016±0.000 | 1.053±0.001 | 1.020±0.001 |
| 25 | quinoline | 1.098 | 15 | 1.105±0.005 | 1.145±0.000 | 1.128±0.000 | 1.147±0.000 | 1.131±0.001 |
| Average difference | 0.012 | 0.046 | 0.001 | 0.043 | 0.004 | |||
| Average percent difference | 1.62% | 5.66% | 0.13% | 5.44% | 0.52% | |||
| APE | 3.83% | 6.37% | 2.70% | 6.20% | 2.73% | |||
| AUE | 0.031 | 0.051 | 0.026 | 0.049 | 0.026 | |||
| RMSE | 0.042 | 0.067 | 0.033 | 0.062 | 0.035 | |||
We note that the two polarizable models that utilize the FF99vdW parameter set have the largest prediction errors in both densities and Hvap. This is understandable because the existing vdW parameters, FF99vdW, have been optimized for fixed charge models. Furthermore, the polarizable models include the interactions between the induced dipoles whereas the physical origin of the R−6 dispersion term is the interaction between spontaneous and induced dipoles. Thus, with explicit inclusion of the interactions between the induced dipoles, the models are expected to be more attractive, leading to an overall higher liquid density. This was indeed the case. With FF99vdW, the average densities of the 25 liquids in TL-FF99vdW and TA-FF99vdW models were, respectively, 0.046 g/cm3 (5.7%) and 0.043 g/cm3 (5.4%) higher than the average of experimental densities, whereas the FF99/GAFF fixed charge model was only 0.012 g/cm3 (1.6%) higher. After the optimization, this systematic error was significantly reduced and the average differences were reduced to 0.001 g/cm3 (0.13%) and 0.004 g/cm3 (0.52%) for TL-OptvdW and TA-OptvdW models, respectively.
In addition to the increased densities, the inclusion of the polarizability also has significant impact on the heat of vaporization. In the fixed charge FF99/GAFF model, the heat of vaporization was about 0.57 kcal/mol (7.6%) lower than the average experimental value. However, in the polarizable models TL-FF99vdW and TA-FF99vdW, the average heats of vaporization were 0.88 (9.9%) and 1.07 kcal/mol (12.1%) higher than the average experimental value. After the optimization, these large systematic errors were reduced to 0.21 (0.9%) and 0.54 kcal/mol (4.0%) in TL-OptvdW and TA-OptvdW models, respectively.
Unlike density and heat of vaporization, the solvation free energy is less affected by the van der Waals parameters. Oostenbrink and van Gunsteren pointed out that it was not possible to obtain a set of charges for the polar groups that could simultaneously reproduce the thermodynamic properties of a range of pure liquids and the hydration enthalpy with high accuracy.64 Indeed, the performance of the five molecular mechanical models is very similar in calculating hydration energies of 15 compounds with thermodynamic integration. Encouragingly, the optimized vdW parameter set still outperforms the FF99 vdW parameter set in conjunction with both the Thole linear and Amoeba-like polarizable models, and the RMSE of the four polarizable molecular mechanical models are 1.56, 1.38, 1.72 and 1.54 kcal/mol for TL-FF99vdW, TL-OptvdW, TA-FF99vdW and TA-OptvdW, respectively. The experimental and calculated hydration free energies of 15 compounds are summarized in Table 6. The individual terms of TI calculations as well as their uncertainties are listed in Table S3.
There are 34 molecules in the test set. The experimental and calculated densities and heats of vaporization of the test molecules by three molecular mechanical models are listed in Tables 7 and 8. As expected, the TL-OptvdW and TA-OptvdW achieved a significant better performance than the other three molecular mechanical models in both density and Hvap calculations: for density calculations, the APE are 3.46, 4.56, 3.17, 4.50 and 3.26% for FF99/GAFF, TL-FF99vdW, TL-OptvdW, TA-FF99vdW and TA_OptvdW, respectively; for Hvap, the RMSE are 1.80, 2.48, 1.62, 2.10 and 1.62 kcal/mol for the five aforementioned models accordingly. Compared to the training set, the RMSE of Hvap calculation for the test set are much larger. Even through, it is unreasonable to reach a conclusion that our new van der Waals parameter set is over-fit, as the RMSE of all five molecular mechanical models including FF99/GAFF, TL-FF99vdW and TA-FF99vdW are proportionally increased for the test set.
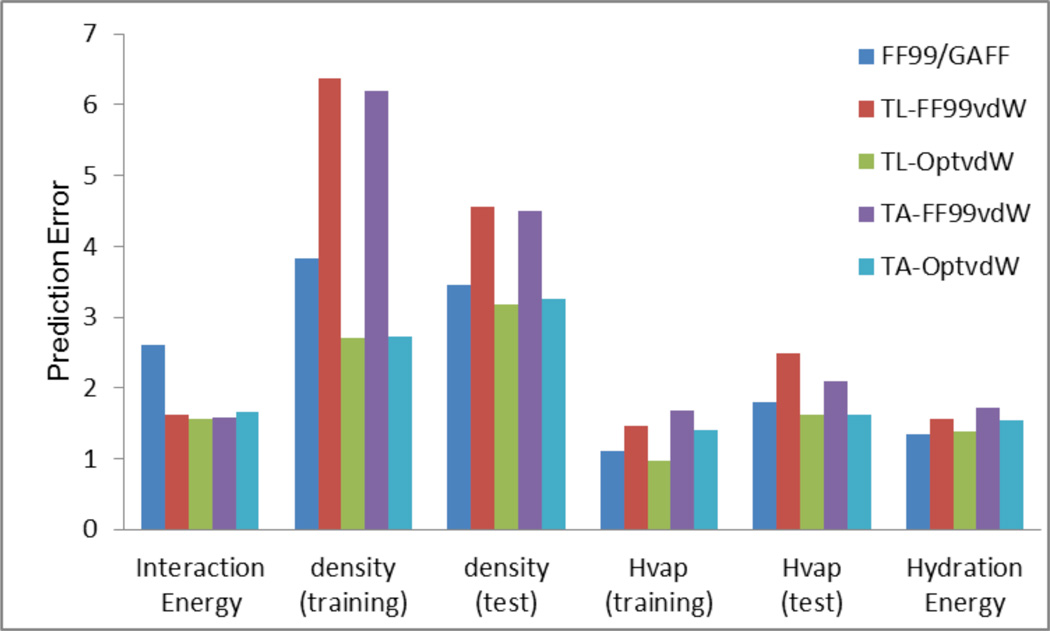
The overall performance of the five molecular mechanical models is demonstrated in the 2D-colum plot of Figure 4. It is shown that the two polarizable models utilizing the optimized van der Waals parameter set outperform the additive model and the two polarizable models utilizing the FF99 van der Waals parameter set. The advantage of polarizable models over the additive one becomes obvious when analyzing the results of the interaction energy calculations. The overall rank of the five molecular mechanical models in condensed property calculations is TL-OptvdW > TA-OptvdW ~ FF99/GAFF > TL-FF99vdW > TA-FF99vdW. In conclusion, the optimized van der Waals parameter set has been successfully developed and it achieves a dramatically better performance than the FF99 vdW parameter set in calculating three condensed-phase properties of a large set of compounds.
Figure 4.
Performance of the five molecular mechanical models: for density, the prediction error is measured as APE (average percent error), for interaction energy, heat of vaporization and hydration energy, the prediction errors are measured by RMSE (root-mean-square error)
It is encouraging that TA-OptvdW has also achieved a satisfactory performance in both interaction energy and bulk molecular property calculations. We further investigated how well the optimized vdW set are transferable among different polarizable models in interaction energy calculations. The results are summarized in Table 9. Encouragingly, the transferability between the Thole linear and Amoeba-like polarizable models is very good as long as the screen factor is not far away from the optimized values (the screening factor is equal to 2.587 for Thole linear and 1.621 for Thole Amoeba-like models). As to the bulk property calculations, in most cases, the predicted densities, Hvap or solvation free energies obtained by TL-OptvdW and TA-OptvdW are comparable to each other (Tables 4–8). However, difference may occur for some molecules that form strong hydrogen bonds in pure solvent or aqueous solution, such as acids and amines. The reason that leads to this difference is that the screening effect of the Thole linear model is stronger than that of Thole Amoeba-like model when the separation distance between two atoms is smaller than 2.5 Å. The screening effect as a function of separation distance for both models is shown in Figure S1. It is expected that the performance of Thole Amoeba-like model can be further improved after we fine tuned the van der Waals parameters that are involved in hydrogen bonding.
Table 9.
Transferability of the optimized van der Waals parameters among different polarizable models in interaction calculation. The performance of each model is evaluated by AUE (average unsigned errors) and RMSE (root-mean-square error) for 1639 dimers listed in Table S1
| Polarizable Model | Screening Factor κ | AUE | RMSE |
|---|---|---|---|
| Thole-Linear Charges and Atomic Polarizabilities | |||
| Applequist | - | 1.229 | 2.953 |
| Linear | 2.587 | 1.015 | 1.562 |
| Linear | 2.441 | 1.036 | 1.619 |
| Linear | 1.662 | 1.202 | 2.558 |
| Amoeba | 1.621 | 1.049 | 1.658 |
| Amoeba | 1.369 | 1.125 | 1.957 |
| Amoeba | 1.330 | 1.136 | 2.018 |
| Amoeba | 1.205 | 1.171 | 2.244 |
| Thole-Amoeba Charges and Atomic Polarizabilities | |||
| Applequist | - | 1.229 | 2.951 |
| Linear | 2.587 | 1.014 | 1.563 |
| Linear | 2.441 | 1.036 | 1.621 |
| Linear | 1.662 | 1.203 | 2.563 |
| Amoeba | 1.621 | 1.048 | 1.660 |
| Amoeba | 1.369 | 1.125 | 1.960 |
| Amoeba | 1.330 | 1.136 | 2.021 |
| Amoeba | 1.205 | 1.170 | 2.247 |
In principle, the approach used in this work can be applied to develop other parameters. For example, Jorgensen et al65 developed OPLS force field by optimizing the parameters, including atomic partial charges, against liquid properties. In AMBER, the partial charges are obtained by fitting the quantum mechanical electrostatic potentials. In which case, adjustment of charges is not recommended. Thus, our adjustments are limited to the van der Waals parameters that are considered more transferable than the partial charges. Nevertheless, a considerably larger data set would be needed if one desires to refine both van der Waals and partial charges.
To improve the quality of our van der Waals parameters further, we plan to introduce more high quality ab initio interaction energy data and experimental density and heat of vaporization data to our training and test sets, and to design better atom type definition schemes to reduce the prediction errors. We will also explore if other molecular mechanical properties have a better relationship to liquid density than residue-residue interaction energy.
4. Conclusions
It is clear that the two non-bonded terms, electrostatic and van der Waals are tightly coupled. The large average percent error of the FF99 vdW set in density calculation strongly suggests that the reparameterization of vdW parameters for the Thole polarizable models is necessary. Owing to the success of density prediction using mean residue-residue energies, we were able to overcome the challenge of calculating densities through molecular simulations and optimize a large set of vdW parameters efficiently using a genetic algorithm.
The optimized vdW parameter set in conjunction with Thole polarization models perform encouragingly better than the FF99vdW parameter set that is coupled with the additive model.
We believe that this vdW parameter set in combination with both the Thole linear and Thole Amoeba-like polarizable models pave a road to parameterization of the bonded terms and enables us to develop a reliable and accurate molecular mechanical model for studying the structures, energies and functions of biomolecules.
Supplementary Material
Acknowledgments
We are grateful to acknowledge the research support from NIH (R01GM79383, Y. Duan, P.I. and R21GM097617, J. Wang, P.I.) and the TeraGrid for the computational time (TG-CHE090098, J. Wang, P.I. and TG-CHE090135, P.Cieplak, P.I.).
Abbreviations
- vdW
van der Waals
- TL
Thole linear polarizable model
- TA
Thole Amoeba-like polarizable model
- GAFF
General AMBER force field
- TL-FF99vdW
Thole linear polarizable model with FF99 van der Waals parameters
- TL-OptvdW
Thole linear polarizable model with optimized van der Waals parameters
- TA-FF99vdW
Thole Amoeba-like polarizable model with FF99 van der Waals parameters
- TA-OptvdW
Thole Amoeba-like polarizable model with optimized van der Waals parameters
- AUE
average unsigned errors
- RMSE
root-mean-square errors
- APE
average percent errors
- R2
correlation coefficient square
- Hvap
heat of vaporization
Footnotes
Supporting Information Available:
The functional forms of Thole linear (TL) and Thole Amoeba (TA) models were provided in the supporting text. The interaction energies calculated by high-level ab initio models as well as the three molecular mechanical models are listed in Tables S1. The individual energetic terms in hydration energy calculation using thermodynamic integration are listed in Table S2. The mean inter-residue energy parameters used in density prediction are listed in Table S3. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Kaminski GA, Stern HA, Berne BJ, Friesner RA. J. Phys. Chem. A. 2004;108:621. [Google Scholar]
- 2.Ponder JW, Case DA. Adv. Protein Chem. 2003;66:27. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- 3.Ren PY, Ponder JW. J. Comput. Chem. 2002;23:1497. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- 4.Cieplak P, Caldwell J, Kollman PA. J. Comput. Chem. 2001;22:1048. [Google Scholar]
- 5.Wang Z-X, Zhang W, Wu C, Lei H, Cieplak P, Duan Y. J. Comput. Chem. 2006;27:781. doi: 10.1002/jcc.20386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang JM, Cieplak P, Li J, Hou TJ, Luo R, Duan Y. J. Phys. Chem. B. 2011;115:3091. doi: 10.1021/jp112133g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang JM, Cieplak P, Li J, Wang J, Cai Q, Hsieh MJ, Lei HX, Luo R, Duan Y. J. Phys. Chem. B. 2011;115:3100. doi: 10.1021/jp1121382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang J, Cieplak P, Cai Q, Hsieh M-J, Wang J, Duan Y, Luo R. J. Phys. Chem. B. 2012 doi: 10.1021/jp212117d. In revision. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comp. Chem. 1983;4:187. [Google Scholar]
- 10.Jorgensen WL, Maxwell DS, TiradoRives J. J. Am. Chem. Soc. 1996;118:11225. [Google Scholar]
- 11.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179. [Google Scholar]
- 12.Wang J, Cieplak P, Kollman PA. J. Comp. Chem. 2000;21:1049. [Google Scholar]
- 13.Duan Y, Wu C, Chowdhury S, Lee MC, Xiong G, Zhang W, Yang R, Cieplak P, Luo R, Lee T, Caldwell JW, Wang J, Kollman PA. J. Comp. Chem. 2003;24:1999. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 14.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA. J. Comp. Chem. 2004;25:1157. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 15.Wang JM, Cieplak P, Kollman PA. J. Comput. Chem. 2000;21:1049. [Google Scholar]
- 16.Oostenbrink C, Soares TA, van der Vegt NF, van Gunsteren WF. Eur. Biophys. J. 2005;34:273. doi: 10.1007/s00249-004-0448-6. [DOI] [PubMed] [Google Scholar]
- 17.Rappe AK, Casewit CJ, Colwell KS, Goddard WA, Skiff WM. J. Am. Chem. Soc. 1992;114:10024. [Google Scholar]
- 18.Sun H. J. Phys. Chem. B. 1998;102:7338. [Google Scholar]
- 19.Shi SH, Yan L, Yang Y, Fisher-Shaulsky J, Thacher T. J. Comput. Chem. 2003;24:1059. doi: 10.1002/jcc.10171. [DOI] [PubMed] [Google Scholar]
- 20.Halgren TA. J. Comput. Chem. 1996;17:520. [Google Scholar]
- 21.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. J. Phys. Chem. B. 2001;105:6474. [Google Scholar]
- 22.Tsuzuki S, Uchimaru T, Tanabe K, Kuwajima S. J. Phys. Chem. 1994;98:1830. [Google Scholar]
- 23.Yin DX, Mackerell AD. J. Comput. Chem. 1998;19:334. [Google Scholar]
- 24.Chen IJ, Yin DX, MacKerell AD. J. Comput. Chem. 2002;23:199. doi: 10.1002/jcc.1166. [DOI] [PubMed] [Google Scholar]
- 25.Feller SE, MacKerell AD. J. Phys. Chem. B. 2000;104:7510. [Google Scholar]
- 26.Wang J, Kollman PA. J. Comp. Chem. 2001;22:1219. [Google Scholar]
- 27.Wang JM, Krudy G, Xie XQ, Wu CD, Holland G. J. Chem. Info. Model. 2006;46:2674. doi: 10.1021/ci060087t. [DOI] [PubMed] [Google Scholar]
- 28.Hou TJ, Wang JM, Chen LR, Xu XJ. Protein Eng. 1999;12:639. doi: 10.1093/protein/12.8.639. [DOI] [PubMed] [Google Scholar]
- 29.Simon S, Duran M, Dannenberg JJ. J. Chem. Phys. 1996;105:11024. [Google Scholar]
- 30.Boys SF, Bernardi F. Mol. Phys. 1970;19:553. [Google Scholar]
- 31.Truhlar DG. Chem. Phys. Lett. 1998;294:45. [Google Scholar]
- 32.Fast PL, Sanchez ML, Truhlar DG. J. Chem. Phys. 1999;111:2921. [Google Scholar]
- 33.Sponer J, Jurecka P, Hobza P. J. Am. Chem. Soc. 2004;126:10142. doi: 10.1021/ja048436s. [DOI] [PubMed] [Google Scholar]
- 34.Morgado CA, Jurecka P, Svozil D, Hobza P, Sponer J. Phys. Chem. Chem. Phys. 2010;12:3522. doi: 10.1039/b924461a. [DOI] [PubMed] [Google Scholar]
- 35.Morgado CA, Jurecka P, Svozil D, Hobza P, Sponer J. J. Chem. Theor. Comput. 2009;5:1524. doi: 10.1021/ct9000125. [DOI] [PubMed] [Google Scholar]
- 36.Svozil D, Hobza P, Sponer J. J. Phys. Chem. B. 2010;114:1191. doi: 10.1021/jp910788e. [DOI] [PubMed] [Google Scholar]
- 37.Rezac J, Riley KE, Hobza P. J. Chem. Theor. Comput. 2011;7:2427. doi: 10.1021/ct2002946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang JM, Hou TJ. J. Chem. Theory Comput. 2011;7:2151. doi: 10.1021/ct200142z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jorgensen WL, McDonald NA. Theochem-J. Mol. Struct. 1998;424:145. [Google Scholar]
- 40.Rizzo RC, Jorgensen WL. J. Am. Chem. Soc. 1999;121:4827. [Google Scholar]
- 41.McDonald NA, Jorgensen WL. J. Phys. Chem. B. 1998;102:8049. [Google Scholar]
- 42.Price MLP, Ostrovsky D, Jorgensen WL. J. Comput. Chem. 2001;22:1340. [Google Scholar]
- 43.Lide DRE. 86th ed. Boca Raton, FL: CRC Press; 2005. p. 4. [Google Scholar]
- 44.Majer V, Svoboda V. Oxford: Blackwell Scientific Publications; 1985. p. 300. [Google Scholar]
- 45.Wang JM, Wang W, Huo SH, Lee M, Kollman PA. J. Phys. Chem. B. 2001;105:5055. [Google Scholar]
- 46.Mobley DL, Bayly CI, Cooper MD, Shirts MR, Dill KA. J. Chem. Theor. Comput. 2009;5:350. doi: 10.1021/ct800409d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bayly CI, Cieplak P, Cornell WD, Kollman PA. J. Phys. Chem. 1993;97:10269. [Google Scholar]
- 48.Cieplak P, Dupradeau FY, Duan Y, Wang JM. J. Phys.-Condens. Matter. 2009;21:333102. doi: 10.1088/0953-8984/21/33/333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JJA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Wallingford CT: Gaussian, Inc; 2004. [Google Scholar]
- 50.Wang JM, Wang W, Kollman PA, Case DA. J. Mol. Graph. Model. 2006;25:247. doi: 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- 51.Case DA, Darden TA, Cheatham ITE, Simmerling C, Wang J, Duke RE, Luo R, Crowley M, Walker RC, Zhang W, Merz KM, Wang B, Hayik S, Roitberg A, Seabra G, Kolossvary I, Wong KF, Paesani F, Vanicek J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Mathews DH, Seetin MG, Sagui C, Babin V, Kollman PA. San Francisco: University of California; 2008. [Google Scholar]
- 52.Miyamoto S, Kollman PA. J. Comput. Chem. 1992;13:952. [Google Scholar]
- 53.Darden T, Perera L, Li L, Pedersen L. Structure. 1999;7:R55. doi: 10.1016/s0969-2126(99)80033-1. [DOI] [PubMed] [Google Scholar]
- 54.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J. Chem. Phys. 1995;103:8577. [Google Scholar]
- 55.Sagui C, Pedersen LG, Darden TA. J. Chem. Phys. 2004;120:73. doi: 10.1063/1.1630791. [DOI] [PubMed] [Google Scholar]
- 56.Shirts MR, Mobley DL, Chodera JD, Pande VS. J. Phys. Chem. B. 2007;111:13052. doi: 10.1021/jp0735987. [DOI] [PubMed] [Google Scholar]
- 57.Uberuaga BP, Anghel M, Voter AF. J. Chem. Phys. 2004;120:6363. doi: 10.1063/1.1667473. [DOI] [PubMed] [Google Scholar]
- 58.Izaguirre JA, Catarello DP, Wozniak JM, Skeel RD. J. Chem. Phys. 2001;114:2090. [Google Scholar]
- 59.Larini L, Mannella R, Leporini D. J. Chem. Phys. 2007;126:104101. doi: 10.1063/1.2464095. [DOI] [PubMed] [Google Scholar]
- 60.Loncharich RJ, Brooks BR, Pastor RW. Biopolymers. 1992;32:523. doi: 10.1002/bip.360320508. [DOI] [PubMed] [Google Scholar]
- 61.Aqvist J. J. Phys. Chem. 1990;94:8021. [Google Scholar]
- 62.Steinbrecher T, Mobley DL, Case DA. The J. Chem. Phys. 2007;127:214108. doi: 10.1063/1.2799191. [DOI] [PubMed] [Google Scholar]
- 63.Wang Z-X, Wu C, Lei H, Duan Y. J. Chem. Theor. Comput. 2007;3:1527. doi: 10.1021/ct700021f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Oostenbrink C, Villa A, Mark AE, Van Gunsteren WF. J. Comput. Chem. 2004;25:1656. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- 65.Jorgensen WL, Maxwell DS, Tirado-Rives J. J. Am. Chem. Soc. 1996;118:11225. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.