Evaluation of a stochastic reconstruction algorithm for use in Compton camera imaging and beam range verification from secondary gamma emission during proton therapy

Abstract

In this paper, we study the feasibility of using the stochastic origin ensemble (SOE) algorithm for reconstructing images of secondary gammas emitted during proton radiotherapy from data measured with a three-stage Compton camera. The purpose of this study was to evaluate the quality of the images of the gamma rays emitted during proton irradiation produced using the SOE algorithm and to measure how well the images reproduce the distal falloff of the beam. For our evaluation, we performed a Monte Carlo simulation of an ideal three-stage Compton camera positioned above and orthogonal to a proton pencil beam irradiating a tissue phantom. Scattering of beam protons with nuclei in the phantom produces secondary gamma rays, which are detected by the Compton camera and used as input to the SOE algorithm. We studied the SOE reconstructed images as a function of the number of iterations, the voxel probability parameter, and the number of detected gammas used by the SOE algorithm. We quantitatively evaluated the capabilities of the SOE algorithm by calculating and comparing the normalized mean square error (NMSE) of SOE reconstructed images. We also studied the ability of the SOE reconstructed images to predict the distal falloff of the secondary gamma production in the irradiated tissue. Our results show that the images produced with the SOE algorithm converge in ~10,000 iterations, with little improvement to the image NMSE for iterations above this number. We found that the statistical noise of the images is inversely proportional to the ratio of the number of gammas detected to the SOE voxel probability parameter value. In our study, the SOE predicted distal falloff of the reconstructed images agrees with the Monte Carlo calculated distal falloff of the gamma emission profile in the phantom to within ±0.6 mm for the positions of maximum emission (100%) and 90%, 50%, and 20% distal falloff of the gamma emission profile. We conclude that the SOE algorithm is an effective method for reconstructing images of a proton pencil beam from the data collected by an ideal Compton camera and that these images accurately model the distal falloff of secondary gamma emission during proton irradiation.

1. Introduction

The use of proton therapy for treating cancer has greatly increased over the past decade, mostly because of the advantageous interaction properties of proton beams. A proton beam initially deposits a relatively low dose upon entering the patient, and the deposited dose rises to a sharp maximum, known as the Bragg peak, near the end of the beam’s range in the patient. The sharp Bragg peak and the finite range of the beam provide the ability to deliver a highly conformal treatment, allowing for dose escalation to the tumor and/or a reduction of exposure to the surrounding healthy tissues. However, errors in patient setup or positioning, day-to-day variations in internal anatomy, anatomical motion, changes to tumor and normal tissue in response to treatment, and other biological factors all lead to uncertainties in the exact position of the distal dose gradient within the patient. Because of uncertainties in the position of the distal falloff, standard proton treatment techniques include the use of large treatment volume expansions to ensure target coverage and to avoid any possible undershoot or overshoot of the beam into nearby critical structures. These large safety margins limit our ability to exploit the steep dose gradients at the distal edge of the Bragg peak, thus reducing the full clinical potential of proton radiation therapy. Therefore, there is a need for a method of verifying the in vivo beam range, to allow for a reduction in necessary treatment margins and to improve our ability to fully exploit the advantages of proton radiation therapy.

One proposed method for in vivo range verification is to measure secondary gamma radiation emitted from the treated tissue (Bennett et al 1978, Paans et al 1993, Min et al 2006). During proton therapy, proton-nucleus interactions produce secondary gamma rays through two distinct methods: (1) by creating positron-emitting isotopes (¹¹C, ¹⁵O, etc.) that produce coincident, 511 keV annihilation gammas (positron annihilation; PA), and (2) by leaving behind an intact, excited nucleus that quickly decays by emitting a characteristic prompt (CP) gamma ray. Because the excited nuclear states are quantized, excited elemental nuclei emit a characteristic CP gamma spectrum.

Many researchers are currently studying the use of PA (Litzenberg et al 1992, Parodi et al 2000, Enghardt et al 2005, Knopf et al 2008) and CP (Min et al 2006, Polf et al 2009a, Testa et al 2009) gamma emission as a method for in vivo dose range verification. In particular, studies of CP emission during proton therapy have shown that it is strongly correlated to the dose deposited in the patient (Min et al 2006, Polf et al 2009a, Polf et al 2009b, Moteabbed et al 2011) and to the composition and density of the irradiated tissues (Polf et al 2009a, Polf et al 2009b). These studies have focused on techniques for measuring the initial energy spectrum and spatial distribution of CP gammas emitted from tissues. However, because of the relatively high energies (2 MeV–15 MeV) of CP emission from tissue, the efficiency of standard gamma detectors and imagers is very low, and standard collimation techniques are ineffective for CP measurements.

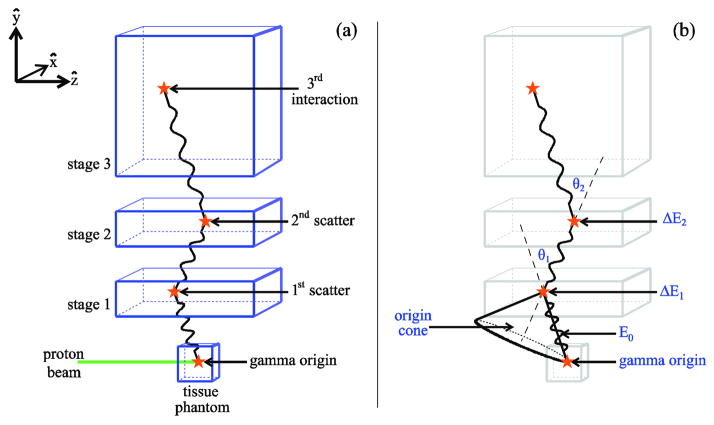
These problems with the standard detectors have led several researchers to study the use of Compton camera imaging (CCI) to measure CP emission during proton irradiation. Compton cameras (CCs) are multistage detectors (typically with two or three stages) that measure the energy deposition and position for each interaction of a gamma as it scatters in the different stages of the camera, as shown for a three-stage CC in figure 1. From the kinematics of the Compton scattering process, the energy deposition and position data for each scatter of the gamma can be used to determine the gamma’s incident energy and the angle of its initial scatter in the detector (Deleplanque et al 1999, Schmid et al 1999). CCs have been used in many applications, including astrophysics (Phillips 1995, Schmid et al 1999) and nuclear medicine (Solomon et al 1988). Because two-stage CCs have low efficiency for gammas with energy greater than ~1 MeV, Kurfess et al (2000) suggested the use of three-stage CCs that do not require the gammas to be completely absorbed. Recent work by Peterson et al (2010) and Robertson et al (2011) has shown that a three-stage CC could provide adequate detection efficiency to allow for measurement and imaging of secondary gammas (both CP and PA) from tissue during proton therapy.

Figure 1.

(a) A gamma ray, produced by a proton beam incident on a tissue phantom, interacts in each of the three detector stages of a CCI system. The gamma origin and three interaction positions are indicated by stars. (b) The origin cone for a gamma ray detected by a three-stage CC. When a gamma produces three interactions in the detector, the scattering angles, θ₁ and θ₂ as well as the initial gamma energy, E₀, can be derived from the interaction positions and the two energies deposited, ΔE₁ and ΔE₂. The CC cannot determine the origin of the gamma ray, but because the scattering angle θ₁ is known, the origin of the gamma ray is restricted to the surface of the origin cone. This cone’s apex is the first scattering position, and its opening angle is 2θ₁.

A variety of approaches for reconstructing images from CC data have been studied. ML-EM (maximum-likelihood expectation-maximization) methods were introduced for CT imaging (Siddon 1985) and adapted for use with CC (Hebert et al 1990). A leading list-mode back-projection algorithm was introduced by Wilderman et al and then improved by Mundy et al (1998, 2010). Kim et al (2007) compared two iterative forward-projection/back-projection algorithms and showed that these algorithms have better resolution than back-projection alone. More recently, Nguyen et al (2011) showed that the COSEM (complete data ordered subsets expectation maximization) algorithm produces qualitatively better image results when optimized using MAP (maximum a posteriori) than maximum-likelihood (ML), since the MAP approach generally allows suppression of the noise in the reconstructed images, whereas all ML approaches fail after a problem-specific number of iterations is completed.

To be useful clinically, the reconstruction algorithm must be both fast (taking a few hours or less) and precise, with resolution on the order of ~1 mm. The stochastic origin ensembles (SOE) algorithm, based on the Metropolis–Hastings algorithm, was originally introduced by Sitek (2008) for use in emission tomography. Andreyev et al (2011) adapted the SOE algorithm to CCI and reconstructed list-mode data from simulated gamma sources embedded in phantoms. They compared their SOE results with the results obtained using the maximum-likelihood expectation-maximization (ML-EM) algorithm (Siddon 1985), designed for CT imaging, and found that SOE was much faster and produced images of similar resolution (Andreyev et al 2011). Here, we apply the SOE algorithm to the problem of reconstructing images of all secondary gamma emission (CP and PA) from tissue during proton therapy.

The purpose of this study was to evaluate the quality of the images (produced using the SOE algorithm) of the gamma rays emitted during proton irradiation and to assess how well the images reproduce the distal falloff of the beam. We investigated how well the SOE reconstructed images can reproduce the distribution of gammas emitted from a tissue phantom that is irradiated with a therapeutic proton pencil beam. We analyzed differences between the SOE reconstructed images and the actual emitted distribution of secondary gamma emission in the irradiated phantom. We determined how these differences change as a function of (1) the number of detected gammas, (2) the voxel probability parameter used during the SOE reconstruction process, and (3) the number of iterations used to reconstruct the image. In addition, we studied the potential clinical applicability of these images by determining how precisely these images can predict the sharp distal falloff of the secondary gamma emission, which is correlated to the proton beam range in the patient.

2. Materials and methods

For this work, we developed software that uses the SOE algorithm to reconstruct 3D images of the secondary gamma emission from tissue irradiated with a therapeutic proton beam. We generated input data to test the SOE-based reconstruction code by using a previously developed Monte Carlo (MC) model that simulates CC measurements of CP gamma emission from tissue irradiated with a proton pencil beam (Peterson et al 2010). In the following sections, we describe the MC model and the SOE implementation as they were used in this work. For a detailed explanation of the SOE algorithm, please see Andreyev et al (2011).

2.1 Generating the input data

To generate the secondary gamma input data, we used an MC model developed with the Geant4 (version 9.4 patch 1) toolkit (Agostinelli et al 2003), as previously used and described by Peterson et al (2010) and Robertson et al (2011). The model consists of a clinical proton beam irradiating a tissue phantom with a three-stage CC positioned above it to measure the production of secondary gammas (see figure 1). The model includes a 110 MeV proton pencil beam with a Gaussian spatial profile (σ= 1 mm) irradiating a 10 × 10 × 10 cm³ soft tissue phantom with composition and density as defined by ICRU Report 49 (1993).

The MC model tracks secondary gammas (CP and PA) produced by nuclear scattering between the proton beam and nuclei in the tissue phantom. When any of these gammas sequentially Compton scatter in the first and second detector stages, followed by a Compton scatter or photoelectric absorption in the third stage (figure 1(a)), the MC model records the position (x_i,y_i,z_i) and energy deposition (E_i) in each detector stage in an output file. Along with the scattering information, the model records the gamma’s initial energy (or “true” energy) and the location at which it was emitted (or “true” origin).

The recorded gamma interaction positions and energy depositions in the CC are used to calculate the initial energy of the gamma (E₀)using the formula (Kroeger et al 2002):

$$E_0=\mathrm{\Delta }{E}_1+\frac{1}{2}\left(\mathrm{\Delta }{E}_2+\sqrt{\mathrm{\Delta }{E}_2^2+\frac{4\mathrm{\Delta }{E}_2{m}_e{c}^2}{1-\text{cos}{\theta }_2}}\right),$$ (1)

where ΔE₁ and ΔE₂ are the energies deposited by the first and second scatters, θ₂ is the second scattering angle (figure 1(b)), m_e is the mass of the electron, and c is the speed of light. After E₀ has been calculated, the initial scattering angle θ₁ is calculated using the Compton scattering formula:

$$\text{cos}{\theta }_1=1+m_e{c}^2\left(\frac{1}{E_0}-\frac{1}{E_0-\mathrm{\Delta }{E}_1}\right).$$ (2)

The detector uncertainties, such as position resolution, energy resolution, and Doppler broadening, are not included in the MC model. Therefore, unless the gamma scatters before reaching the detector, the calculated value for E₀ and the true energy (recorded by the MC model) will be equal. The scattering information does not determine the precise origin of the gamma, but instead restricts the origin to the surface of a half cone, referred to as the origin cone (figure 1(b)). The axis of this origin cone is the line connecting the first two Compton scatters; the cone’s apex is the first scattering position; and its opening angle is 2θ_1.

When a calculation was completed with our MC model, the recorded position and energy deposition of each gamma scatter in the CC, along with the values of E₀ and θ₁ calculated according to equations (1) and (2), were output using ROOT, a C++ based data analysis package (Brun et al 1997). In addition, the true origin of each gamma was included in the ROOT output file so that we could compare the SOE reconstructed images with the MC true origin distributions in the irradiated phantom.

2.2. Reconstructing the gamma origins: SOE algorithm

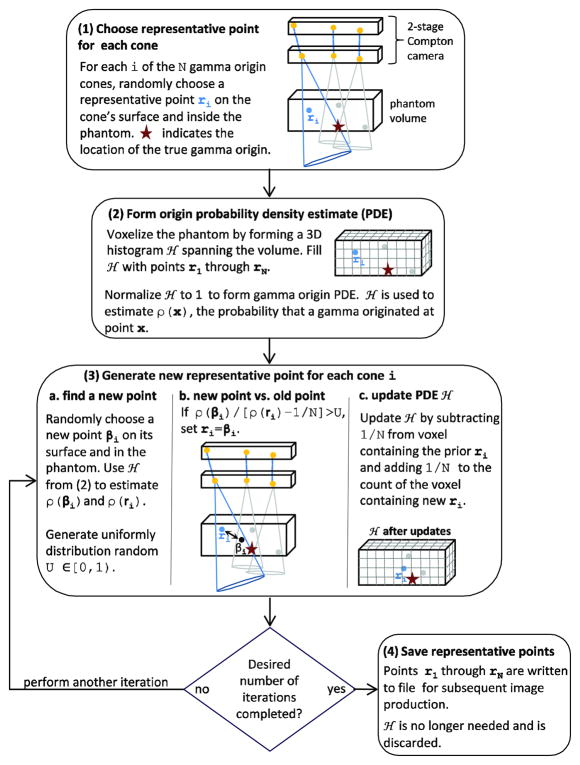
For our SOE reconstruction code, we first implemented the algorithm as described by Andreyev et al (2011) and then made two modifications to its implementation to improve its performance for our specific application. Reconstructing an image from CC data requires combining the information provided by the origin cones corresponding to the detected gammas. Rather than including the entire cone in the reconstruction, the SOE algorithm reproduces the image by considering only a single representative point. The representative points are initially chosen by randomly selecting a point on the cone’s surface and within the phantom volume. Each iteration of the algorithm attempts to improve the reconstruction by exchanging the current representative points with points where the probability of a gamma originating is higher. In this work, we terminate the algorithm after 100,000 iterations although it would also be possible to define a metric of convergence and then terminate the algorithm when a particular metric value has been reached. Figure 2 illustrates the steps of the algorithm for our implementation. The size of the voxels used in step (2) is an algorithm parameter we refer to as the voxel probability parameter (VPP). The pseudo-random numbers in steps 1 and 3 were generated using a combined Tausworthe generator (L’Ecuyer 1996) implemented the ROOT package(Brun et al 1997). For our implementation of the SOE algorithm, it is important that the pseudo-random numbers be equidistributed but not necessarily unique; they are used in different ways and with millions of origin cones which have unique characteristics. The combined Tausworthe generator is maximally equidistributed and relatively fast. We generated an array of 10000019 uniform random numbers between [0, 1) and drew numbers as needed from the list, in order to improve the performance of the algorithm.

Figure 2.

Flow chart for the stochastic origin ensembles reconstruction algorithm. The algorithm is the same for 2-stage (shown) and 3-stage CCs.

When estimating the probability values ρ(r_i) and ρ(β_i) for a detected gamma (step 3b.), we subtract $\frac{1}{N}$ from ρ(r_i) to remove the contribution of the current representative point, r_i, from the probability density estimate; here N is number of gammas detected. This differs from the implementation of Andreyev et al (2011), which includes the contributions of both the new and the representative positions in the origins histogram when calculating ρ(r_i) and ρ(β_i) In most cases, this difference in the calculation is not significant. Because our implementation of the SOE algorithm is less likely to move the representative position from a position with a larger probability to a position with a smaller probability, it may enable more complete convergence. A second difference is that we step through the detected gammas one after another in steps 3a through 3c, whereas Andreyev et al +(2011) select a +detected gamma at random and define an iteration as performing steps 3a through 3c times, where N is the number of detected gammas. Therefore, for a single iteration of Andreyev et al’s implementation, steps 3a through 3c will be performed more than once for some detected gammas and not at all for others. Initial testing indicated that for our application, stepping sequentially through the list of detected gammas and ensuring that each gamma is tested once for each iteration improves the agreement between the MC true origin distribution and the SOE reconstructed origin distribution. We did not formally verify this result.

After the predefined number of iterations, the SOE algorithm records the 3D coordinates of the final representative position of each detected gamma (step 4). The “final images” of the gamma emission are then constructed by binning the final 3D coordinates according to the desired image resolution. Therefore, the resolution of the final images is not determined by the size of the origins histogram voxels used by the SOE algorithm. However, the quality of the final images may be affected by the VPP value. Using a smaller value for the VPP and, therefore, smaller voxels for the origins histogram, may improve the resolution of the reconstructed images. However, using a smaller VPP (i.e. smaller voxels) means there are more voxels in the image field of view (FOV), which in turn means that more detected gammas are needed to fill these voxels and overcome the statistical noise in the origins histogram. To test these effects, we ran the SOE algorithm with the input data containing 1 million (1M) and 4 million (4M) detected gammas using VPP values of 0.5 mm³, 1.0 mm³, and 2.0 mm³. We chose these numbers of gammas on the basis of previous studies, which estimated the number of triple-scattered gammas that can be measured by a CC in a clinical setting to be between 1M and 4M (Peterson et al 2010).

2.3. Quantifying the image quality: normalized mean square error

To compare the images quantitatively, we used the normalized mean square error (NMSE) metric (Andreyev et al 2011). To calculate NMSE, we performed a voxel-by-voxel comparison of the MC gamma origin distribution with the SOE reconstructed distribution. We refer to the MC origins as “true” and the SOE algorithm origins as “reconstructed.” NMSE is given by

$$\mathit{NMSE}=\frac{\mathrm{\sum }{(f_T-f_R)}^2}{\mathrm{\sum }{f}_T^2}\times 100\%,$$ (3)

where f_T and f_R are the true and reconstructed counts of gammas with origin in a voxel. Both summations are performed over all the voxels in the FOV. For a quantitative assessment to be made of the different NMSE values from different SOE reconstructions, the NMSE values must be calculated using the same number of voxels so that they will have the same normalization. For this reason, all of our NMSE values are calculated from 1.4 mm³ voxels regardless of the VPP used by the SOE algorithm during the reconstruction. This voxel size corresponds to 343,000 total voxels and was chosen to be similar but not equal to VPP values used by the SOE algorithm during the reconstruction (0.5 mm³, 1.0 mm³, and 2.0 mm³).

2.4. Predicting the distal falloff

To determine how well the SOE reconstructed gamma origins can predict the shape of the distal falloff of the CP gamma emission, we calculated the differences between the MC true origin distribution and the SOE reconstructed origin distribution in the depth of maximum emission (100%) and the depths of 90%, 50%, and 20% distal falloff. In addition, to estimate the statistical uncertainty in the predicted depths of the distal falloff of the SOE reconstructed gamma emission, we performed 10 trials of the SOE reconstruction algorithm with VPP values 0.5 mm³, 1.0 mm³, and 2.0 mm³ using 10 independent sets of 1M detected gammas each generated from independent MC calculations (for a total of 30 independent reconstructions). For each trial, we calculated the difference between SOE predictions and the MC calculations of the depth of maximum emission and the distal 90%, 50%, and 20% falloff positions of the gamma emission distributions. We then calculated the mean difference in each falloff position for the 10 trials to give us the mean offset, or bias, in the SOE reconstruction predictions. We defined the corrected distal falloff position as the position predicted by the final SOE reconstruction prediction minus the bias. We also defined the uncertainty in the corrected distal falloff position as the standard deviation (1σ) of the 10 differences for the 10 trials.

We modeled both the MC and the SOE reconstructed origin distributions along the depth coordinate ẑ using kernel density estimation (KDE) functions (Rosenblatt 1956, Parzen 1962, Scott 1992). The KDE functions are given by

$$f(z)=\frac{1}{n}{\sum }_{i=1}^n\frac{1}{h\sqrt{2\pi }}exp(-\frac{1}{2}\frac{{({\widehat{z}}_i-z)}^2}{h^2}),$$ (4)

where n is the number of gammas and ẑ_i is the z coordinate of the i^thorigin in the corresponding set of MC or SOE reconstructed gamma origins. The terms in the summation are Gaussian kernels centered at ẑ_i with width h We set the value of h to 0.1 mm so that 95% of the i^th kernel’s contribution to f(z) is within 0.2 mm, or 2σ, of its central value, ẑ_i For each of the MC and SOE reconstructed origin distributions, we calculated the corresponding f(z) for 10,000 evenly spaced depth positions (along z-axis) from 0 to 100 mm. From these 10,000 positions, we determined the depths of maximum emission and the depths of 90%, 50%, and 20% distal falloff for use in the calculations.

3. Results

We applied the SOE algorithm to reconstruct images of CP gamma emission from input datasets containing 1M and 4M gammas. We evaluated the SOE reconstructed images as a function of the voxel probability parameter and the number of iterations performed during the reconstruction.

3.1. Comparison of true and reconstructed gamma origin distributions

3.1.1. Comparison of 2D projections

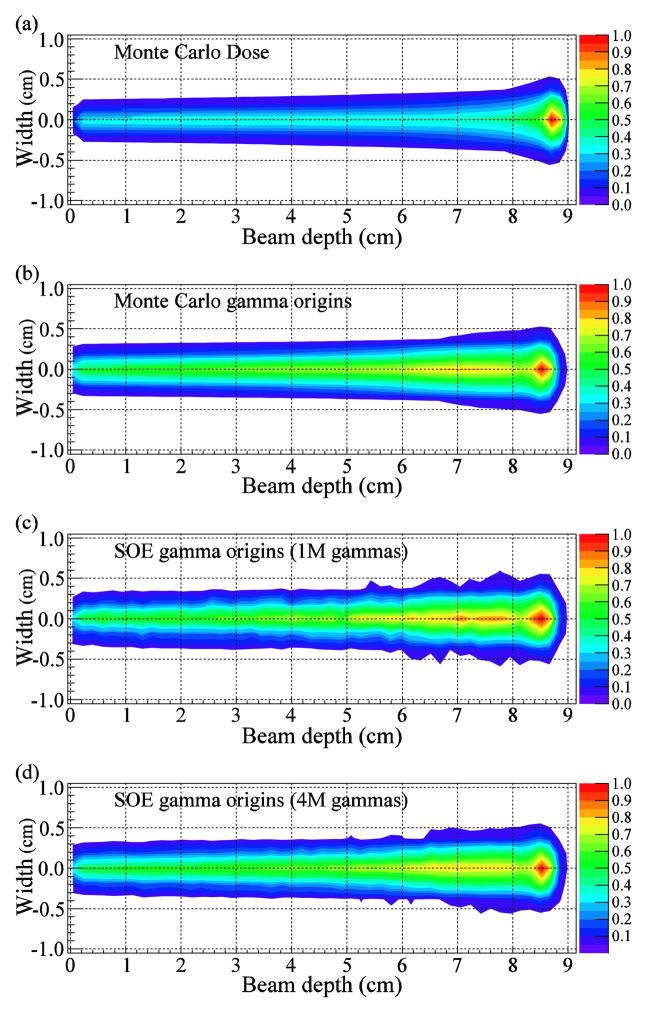
We compared 2D projection images of the MC calculated dose and gamma origin distributions with the gamma emission distributions reconstructed with 10,000 iterations of the SOE algorithm for 1M and 4M gammas using VPP value of 1.0 mm³ (figure 3). The distal edge of the dose (figure 3(a)) extends beyond that of the gamma emission (figure 3(b) (d)), which is consistent with previous results (Kang et al 2009, Moteabbed et al 2011). The distal edges of the reconstructed gamma emission for both 1M and 4M gammas appear to agree well with the distal falloff of the MC gamma emission distributions.

Figure 3.

2D projections comparing the MC dose and gamma origin distributions with the emission distributions reconstructed by the SOE algorithm. (a) Dose density calculated by the MC model. (b) Gamma origin distributions calculated by the MC model. (c, d) Gamma origin distributions reconstructed using 10,000 iterations of the SOE algorithm with (c) 1M and (d) 4M gammas from a simulated CC. The algorithm used VPP value 1 mm³.

3.1.2. Comparison of 1D projection image

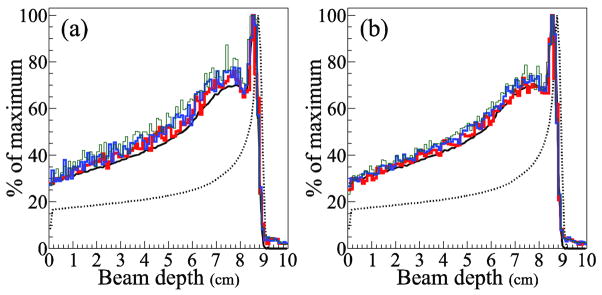
We compared 1D projection distributions of the gamma origins along the beam central axis (figure 4). The reconstructed distributions with 1M and 4M gammas both contain a substantial level of statistical noise, as seen by the spikes in the data along the beam axis. The level of statistical noise increases as the VPP decreases. However, the exact relationship between the VPP and the agreement at the distal edge is unclear in the figure. In addition, comparison of the distributions produced from 1M and 4M gammas shows that increasing the number of gammas decreases the statistical noise of the reconstructed data but does not necessarily improve the agreement at the distal edge. Regardless of the VPP value, there is good agreement between the distal falloff of the images reconstructed using the SOE algorithm and that of true gamma emission.

Figure 4.

1D projections of the gamma origin distribution along the beam central axis for (a) 1M and (b) 4M gammas. The MC dose (dotted line) and gamma origin (solid line) distributions are shown in black. The SOE algorithm reconstructions used 10,000 iterations with VPP value 0.5 mm³ (thin green line), 1.0 mm³ (medium blue line), and 2.0 mm³ (thick red line). All curves and histograms are normalized to their maximum values.

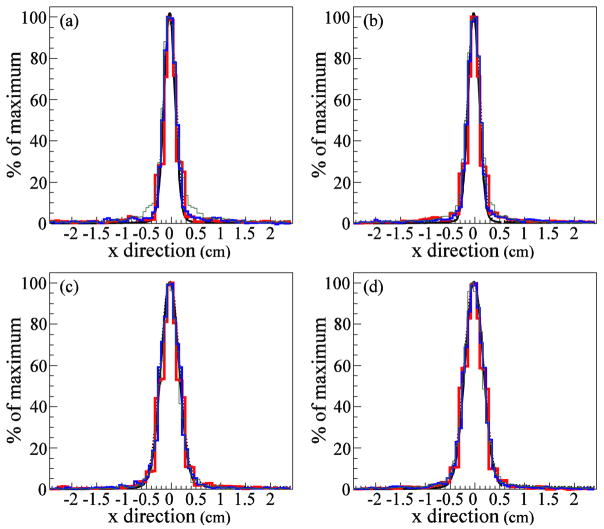
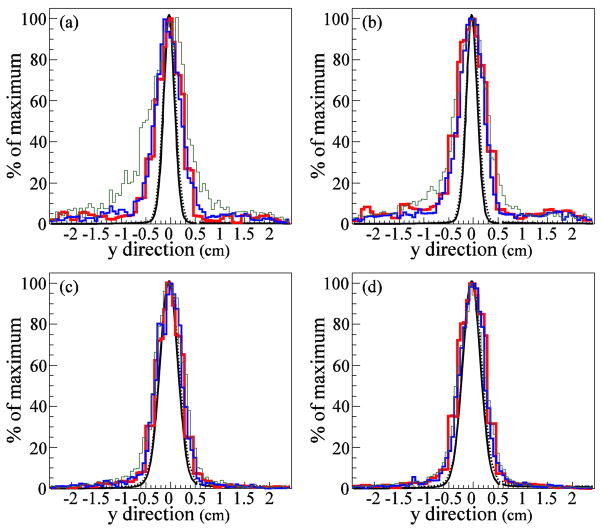
3.1.3. Comparison of 1D profiles

We compared 1D lateral profiles in the x̂ (parallel to the CC detector stages) direction (figure 5) and the ŷ (perpendicular to the CC detector stages) direction (figure 6). As in figure 4, the agreement between the SOE reconstructed images and the MC emission distribution in the x̂ direction (figure 5) is very good. However, in the ŷ direction (figure 6), the SOE reconstructed distributions are much wider than the true origin distributions. CC image resolution in the lateral, x̂ and ẑ, directions is superior to the resolution in ŷ direction, due to the way in which the origin cones and the voxelized phantom intersect. The x̂ and ẑ coordinates are correlated and restricted to ellipses on the ŷ plane. The ŷ coordinate can take on any value from the ŷ position where the origin cone first intersects the phantom to the ŷ position where the origin cone exits the phantom. Thus, the domains of the x̂ and ẑ coordinates are more tightly constrained by the origin cones than is the domain of the ŷ coordinate.

Figure 5.

1D lateral profiles in the direction, parallel to the CC detector stages. (a, b) Gamma origin distributions reconstructed using the SOE algorithm with (a) 1M and (b) 4M gammas at a depth of 5.0 cm, at the center of the tissue phantom. (c, d) Gamma origin distributions reconstructed using the SOE algorithm with (c) 1M and (d) 4M gammas at a depth of 8.5 cm, in the Bragg peak. The SOE reconstructions used 10,000 iterations with VPP values 0.5 mm³ (thin green line), 1.0 mm³ (medium blue line), and 2.0 mm³ (thick red line). The MC gamma origin distributions are shown in black. All curves and histograms are normalized to their maximum values.

Figure 6.

1D lateral profiles in the direction, perpendicular to the CC detector stages. (a, b) Gamma origin distributions reconstructed using the SOE algorithm with (a) 1M and (b) 4M gammas at a depth of 5.0 cm, at the center of the tissue phantom. (c, d) Gamma origin distributions reconstructed using the SOE algorithm with (c) 1M and (d) 4M gammas at a depth of 8.5 cm, in the Bragg peak. The SOE reconstructions used 10,000 iterations with VPP values 0.5 mm³ (thin green line), 1.0 mm³ (medium blue line), and 2.0 mm³ (thick red line). The MC gamma origin distributions are shown in black. All curves and histograms are normalized to their maximum values.

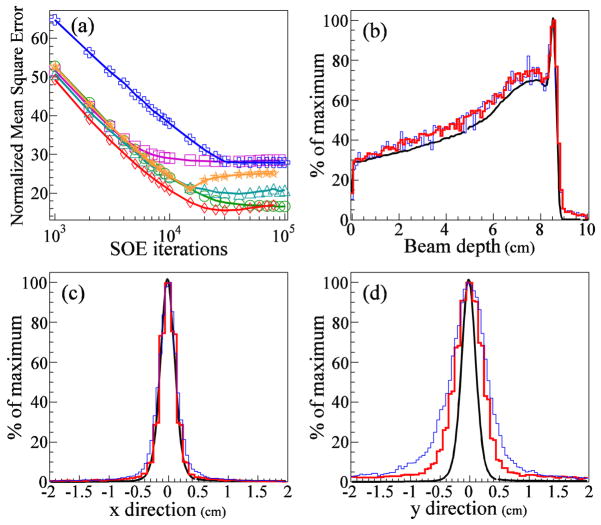
3.2. Quantitative comparisons: NMSE analysis

The calculated NMSE values are shown in figure 7(a) as a function of the number of SOE iterations for six different SOE runs with different combinations of the number of detected gammas and the VPP. In all cases, the NMSE falls rapidly for the first 7000 iterations, after which it either levels off or begins to increase slightly due to an increase in noise inherent to the ML-approach used in our reconstruction. After 10,000 iterations, the SOE run with 1M gammas and VPP value 0.5 mm³ has the largest NMSE value, and the SOE run with 4M gammas and VPP value 1.0 mm³ has the smallest NMSE value. Thus, on the basis of the NMSE metric, these two runs of the algorithm produced the lowest and highest image quality, respectively. This difference in quality is apparent from the 1D projections of the gamma origin distribution from these two runs (figures 7(b)–(d)).

Figure 7.

(a) NMSE values versus number of iterations of the SOE algorithm for sets of 1M and 4M gammas. For each set, the algorithm was run with VPP values 0.5 mm³, 1.0 mm³, and 2.0 mm³. Results are shown for SOE reconstructions using the following numbers of gammas and voxel probability parameters, respectively: 1M and 2 mm³ (green circles), 4M and 2 mm³ (purple squares), 1M and 1 mm³ (cyan triangles), 4M and 1 mm³ (red diamonds), 1M and 0.5 mm³ (blue crosses), and 4M and 0.5 mm³ (orange stars). (b–d) 1D projection of the gamma origin distribution (b) along the beam central axis, (c) in the direction, and (d) in the direction. For (b), (c), and (d), the MC gamma origin distributions are shown in black, and the thin blue lines and thick red lines represent the SOE runs with the largest and smallest NMSE values, respectively, after 10,000 iterations. The SOE reconstruction with 1M gammas and VPP value 0.5 mm³ (thin blue line) has an NMSE value of 38. The SOE reconstruction using 4M gammas and VPP value 1.0 mm³ (thick red line) has an NMSE value of 21.

3.3. Prediction of distal falloff

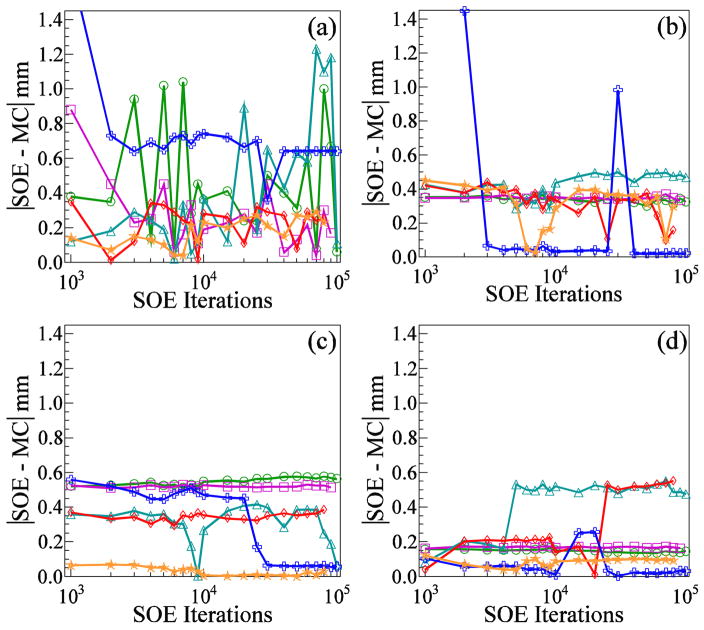
The differences between the SOE algorithm predictions and the MC calculations of the depths of maximum emission (100%) and 90%, 50%, and 20% distal falloff of the gamma emission are shown in figure 8 as a function of the number of SOE iterations. Within 3000 iterations, the SOE predictions of the depth of maximum emission stabilize to within ±1 mm of the MC calculated depths (figure 8(a)). Within 3000 iterations, the SOE depths of the distal falloff stabilizes to within 0.6 mm of the MC calculated depths (figures 7(b)–(d)), with the one exception being the SOE reconstruction which used 1M detected gammas and 0.5 mm³ for the voxel probability parameter. This reconstruction has a statistical fluctuation of slightly less than 10% immediately following the position of maximum emission. After 40,000 iterations, the fluctuation dropped to 90% making it the 90% falloff position and causing the noticeable shift of ~1 mm which can be seen in figure 7(b). After another 10,000 iterations, the fluctuation rose back above 90% and was no longer the 90% falloff position.

Figure 8.

Differences between the SOE algorithm predictions and the MC calculations of the secondary gamma origin emission versus the number of iterations of the SOE algorithm for the positions of (a) the maximum emission, and the falloff to (b) 90%, (c) 50%, and (d) 20% of the maximum. Results are shown for SOE reconstructions using the following numbers of gammas and VPP values, respectively: 1M and 2 mm³ (green circles), 4M and 2 mm³ (purple squares), 1M and 1 mm³ (cyan triangles), 4M and 1 mm³ (red diamonds), 1M and 0.5 mm³ (blue crosses), and 4M and 0.5 mm³ (orange stars).

Table 1 shows the results of the 10 independent trials of the SOE reconstructions, including the bias (mean difference) and uncertainty (1σ standard deviation) in the predicted distal falloff depths of the gamma emission. For 1M gammas using 10,000 iterations and 1.0 mm³ for the voxel probability parameter, we estimate the bias and uncertainty of the SOE reconstructions to be −0.01 ± 0.57 mm, 0.06 ± 0.41 mm, −0.03 ± 0.36 mm, and −0.01 ± 0.35 mm for the depth of maximum emission and the 90%, 50%, and 20% distal falloff positions, respectively. In Table 2, these results are compared with the results for similar SOE reconstructions performed using 10,000 iterations with 1M gammas and VPP values 0.5 mm³ and 2.0 mm³. The larger VPP values, in this case 2.0 mm³, result in increased bias in the reconstructions but reduced uncertainty. For the 90%, 50%, and 20% falloff positions, the corrected distal falloff positions of the SOE images agree with the MC true falloff positions to within an uncertainty of ±0.6 mm regardless of the voxel probability parameter value.

Table 1.

Results of 10 independent trials comparing MC calculations with the SOE algorithm predictions of the beam depths at which the gamma emission reaches a maximum and falls off to 90%, 50%, and 20% of its maximum value. Also shown are the means and sample standard deviations (σ) of the 10 trials. For each trial, the SOE algorithm was run with VPP value 1.0 mm³, 10,000 iterations, and 1M gammas.

Trial	Beam depth (mm) of emission level
	Maximum emission			90% of Maximum			50% of Maximum			20% of Maximum
	MC	SOE	SOE – MC	MC	SOE	SOE – MC	MC	SOE	SOE – MC	MC	SOE	SOE – MC
1	85.62	85.99	−0.37	86.55	86.99	−0.44	87.63	87.89	−0.27	88.48	89.00	−0.52
2	85.62	85.96	−0.34	86.55	86.25	0.30	87.63	87.24	0.39	88.48	88.23	0.25
3	85.61	85.93	−0.32	86.58	86.13	0.45	87.66	87.59	0.07	88.46	88.27	0.19
4	85.62	85.35	0.27	86.55	86.12	0.43	87.63	88.04	−0.42	88.48	88.25	0.23
5	85.70	85.83	−0.13	86.51	86.62	−0.11	87.61	87.97	−0.36	88.46	88.96	−0.50
6	85.65	86.65	−1.00	86.50	87.04	−0.54	87.64	87.29	0.35	88.48	88.26	0.22
7	85.62	84.43	1.19	86.55	86.10	0.45	87.63	87.99	−0.36	88.48	88.32	0.16
8	85.61	85.42	0.19	86.53	86.31	0.22	87.62	87.27	0.35	88.44	88.23	0.21
9	85.62	85.46	0.16	86.55	86.25	0.30	87.63	87.99	−0.36	88.48	88.30	0.18
10	85.56	85.34	0.22	86.49	86.98	−0.50	87.63	87.27	0.36	88.48	88.98	−0.50
Mean	85.62	85.63	−0.01	86.54	86.48	0.06	87.63	87.66	−0.03	88.47	88.48	−0.01
σ	0.03	0.59	0.57	0.03	0.39	0.41	0.01	0.35	0.36	0.01	0.35	0.35

Abbreviations: MC, Monte Carlo; SOE, stochastic origin ensemble.

Table 2.

The bias and uncertainty in the SOE algorithm predictions of the beam depths at which the gamma emission reaches a maximum and falls off to 90%, 50%, and 20% of its maximum value. VPP (voxel probability parameter) refers to the size of the voxel used by the SOE algorithm and does not directly correspond to the precision of the falloff position estimates. For each VPP value, 10 independent trials were performed using 1M gammas and 10,000 iterations. The 1 mm data are repeated from table 1.

VPP value (mm3)	Maximum emission		90% of Maximum emission		50% of Maximum emission		20% of Maximum emission
	Bias (mm)	Uncertainty (mm)	Bias (mm)	Uncertainty (mm)	Bias (mm)	Uncertainty (mm)	Bias (mm)	Uncertainty (mm)
2.0	0.08	0.39	0.33	0.05	−0.52	0.02	0.16	0.01
1.0	−0.01	0.57	0.06	0.41	−0.03	0.36	−0.01	0.35
0.5	0.03	0.43	0.45	0.38	0.17	0.14	0.02	0.10

4. Discussion and conclusions

Our results show that the SOE algorithm can reconstruct images that can be used to predict the distal falloff of the gamma emission distribution with a precision of 1 mm or better. We believe such a capability could be clinically useful if this method were to be fully developed and deployed for in-vivo gamma imaging during proton radiotherapy. Visual comparison of the SOE reconstructed and the true MC origin images shows good agreement in the plane parallel to the CC detector stages. In the plane perpendicular to the CC detector stages, the agreement is noticeably worse. Further study is needed to improve our understanding of the reasons for this difference.

As an objective measure of image quality, we compared the SOE reconstructed and true images using NMSE. The SOE reconstruction obtained with 1M detected gammas and VPP value 0.5 mm³ produced the lowest image quality (the largest NMSE value) after 10,000 iterations. This was expected because, in this case, the SOE algorithm must estimate the origin probability density of 8M voxels with only 1M detected gammas. In contrast, the SOE run with 4M detected gammas and VPP value 1.0 mm³ produced the highest image quality after 10,000 iterations. In this case, the SOE algorithm is estimating the origin probability density of 1M voxels using 4M detected gammas, a factor of 32 larger gamma-to-voxel ratio. However, increasing the ratio further by increasing the VPP value led to a slight increase in NMSE, indicating that the loss of resolution caused by decreasing the voxel size offset the gain from the additional gammas. It is clear that the SOE algorithm’s performance is dependent on the number of detected gammas and the VPP value, but the dependence will change according to the size and distribution of the gamma sources (i.e. the proton beam size) in relation to the FOV used for reconstruction. For these reasons, we made no attempt to identify an optimal gamma-to-voxel ratio that can be generally applied. Similarly, although we have shown NMSE to be a useful measure for comparing the relative quality of different reconstructed images of the same gamma source distribution, we made no attempt to determine a specific value for NMSE that can indicate the quality of a single image or can be used to compare images of different sources.

An alternative quality measure for the reconstructed images is the difference between the positions where the SOE and the true MC origin distributions fall off to some percentage of their maximum value. With this measure, the highest quality images are those that minimize this difference. This figure of merit makes sense because a primary goal of secondary gamma imaging during proton therapy is to verify the proton beam range. Although in this study we considered differences in the depth of maximum emission and the 90%, 50%, and 20% distal falloff positions, a single percentage falloff position or the maximum difference of these three positions could also be used.

Our results show that, after correcting for the bias, the SOE reconstructions consistently predict the distal falloff of the gamma emission to within ±0.5 mm. Because we can correct for the bias by subtracting it from the depth predictions, the best SOE reconstructions for predicting the shape of the distal falloff are those that minimize the uncertainty. Thus, our results showed that the best SOE reconstructions were those that used the largest voxel probability parameter value, 2.0 mm³. In our study, we used an ideal CC which did not include position and energy uncertainties or Doppler broadening. Further studies should include these effects to fully understand the performance limits of the SOE algorithm for data collected from a real CC detector. We would also like to note that in a clinical setting, measuring the bias of the SOE reconstruction distal falloff predictions will be significantly more difficult and, therefore, the best value of the voxel probability parameter might be the one that minimizes the bias rather than the uncertainty.

Our implementation of the SOE algorithm is of order n×m, where n is the number of iterations and m is number of gammas used in the reconstruction. Thus, the runtime is linearly dependent on the number of gammas used in the reconstruction but independent of the VPP used by the SOE algorithm. For the reconstructions presented in this work, 10,000 iterations with 1M gammas were completed in <3 hours on a single AMD Opteron 6128 HE, 2000 MHz CPU running Linux kernel 2.6.18. Improvements in the reconstruction speed could be easily achieved by parallelization of the code and/or implementation on a graphics processing unit (GPU) as shown by Andreyev et al (2011). However, the purpose of this study was not optimization of the reconstruction code, and therefore reconstruction times on the order of ~3 hours were deemed sufficient.

It is important to note that this work attempts to reconstruct the secondary gamma emission distribution. It does not attempt to directly reconstruct the distribution of the dose. Previous studies by Moteabbed et al (2011) and Polf et al (2009b) have shown that the secondary gamma emission distribution is correlated to the dose distribution. However, before any gamma-based imaging system can be used to verify the proton beam range, this correlation needs to be further studied and precisely understood, especially in the case where the beam is irradiating heterogeneous materials.

On the basis of the results of this study, we conclude that (1) the SOE algorithm is an effective method for reconstructing images of a proton pencil beam from the data collected by an ideal CC and (2) the images produced by the SOE algorithm accurately model the distal falloff of secondary gamma emission during proton irradiation. In this study, the images predicted the distal falloff depths to within 0.6 mm³. When CC detector position and energy uncertainties are included, the number of gammas required is likely to increase. However, we believe that further improvements to the algorithm may compensate for some of these effects. We believe that the results of this study justify further investigation of the application of SOE and CCI to in vivo imaging of and verification of the beam range in proton therapy.