Abstract
Children’s (n = 275) use of retrieval, decomposition (e.g., 7 = 4+3, and thus 6+7=6+4+3), and counting to solve additional problems was longitudinally assessed from first to fourth grade, and intelligence, working memory, and in-class attentive behavior was assessed in one or several grades. The goal was to assess the relation between capacity of the central executive component of working memory, controlling for intelligence and in-class attentive behavior, and grade-related changes in children’s use of these strategies. The predictor on intercept effects from multilevel models revealed that children with higher central executive capacity correctly retrieved more facts and used the most sophisticated counting procedure more frequently and accurately than did their lower capacity peers at the beginning of first grade, but the predictor on slope effects indicated that this advantage disappeared (retrieval) or declined in importance (counting) from first to fourth grade. The predictor on slope effects also revealed that from first through fourth grade, children with higher capacity adopted the decomposition strategy more quickly than did other children. The results remained robust with controls for children’s sex, race, school site, speed of encoding Arabic numerals and articulating number words, and mathematics achievement in kindergarten. The results also revealed that intelligence and in-class attentive behavior independently contributed to children’s strategy development.
Keywords: Longitudinal study, central executive, attentive behavior, addition development, intelligence
Introduction
Nationally representative studies conducted in Canada, Great Britain, and the United States suggest the social and individual costs associated with poorly developed mathematical skills are higher than those associated with poor reading skills, in part because more people have difficulty with mathematics than with reading and because of steady increases in the quantitative knowledge needed to function in modern economies (Bynner, 1997; Parsons & Bynner, 1997; Rivera-Batiz, 1992). The studies conducted in Great Britain revealed that while poor reading skills reduced employment opportunities and wages once employed, poor mathematics skills resulted in even dimmer prospects (Every Child a Chance Trust, 2009). The competencies assessed in these studies were basic arithmetic, measurement, and simple algebraic skills, and indicated that a substantial minority (23% in British studies) of adults have not mastered the mathematics expected of a sixth grader, making them functionally innumerate. Similar issues were raised by the National Mathematics Advisory Panel (2008) in the United States. Among their recommendations was that children master whole number arithmetic and fractions during the elementary school years. At the foundation of these competencies is basic addition.
Accordingly, our goal was to determine the cognitive processes that correlate with developmental improvement in children’s use of retrieval-based and counting-based strategies to solve addition problems. Experimental and correlational studies have consistently identified the central executive component of working memory as being involved in the solution of arithmetic problems for children and adults (Ashcraft & Kirk, 2001; Barrouillet & Lépine, 2005; Bull, Espy, & Wiebe, 2008; DeStefano & LeFevre, 2004; Hecht, 2002; Imbo & Vandierendonck, 2007; Lemaire, Abdi, & Fayol, 1996; Noël, 2009; Passolunghi, Vercelloni, & Schadee, 2007). We extend this literature by providing a large-scale (n = 275) longitudinal study of the relation between children’s central executive capacity and their addition strategy development across the grades (first to fourth, inclusive) in which developmental change in strategy usage and accuracy is most common (Ashcraft, 1982; Geary, Bow-Thomas, Liu, & Siegler, 1996).
Moreover, we tested the hypothesis that the relation between the central executive and addition performance is in fact due to two related competencies that have not been as systematically explored in this literature, specifically intelligence and in-class attentive behavior. Intelligence is the single best predictor of academic learning across domains (Deary, Strand, Smith, & Fernandes, 2007; Jensen, 1998), and in-class attentive behavior has been shown to influence mathematics academic achievement above and beyond the influence of intelligence (Duncan, Dowsett, Claessens, Magnuson, Huston, Klebanov et al., 2007). Intelligence and in-class attentive behavior are correlated with the capacity of the central executive, and assess unique competencies (Ackerman, Beier, & Boyle, 2005; Fuchs, Geary, Compton, Fuchs, Hamlett & Bryant, 2010). As a result, the possibilities that the often reported relation between the central executive and addition competence is due to these other competencies or that each of them contributes independently to addition development need to be explored.
Addition Development
By the time they begin formal schooling most children have begun to integrate their understanding of quantity with their counting skills and with an implicit understanding of the effects of addition and subtraction on quantity (e.g., Klein & Bisanz, 2000; Levine, Jordan, & Huttenlocher, 1992; Siegler & Jenkins, 1989). One result is the ability to use counting to solve formal addition problems (e.g., “How much is 3 + 2?”), sometimes using their fingers (finger counting strategy) and sometimes not using them (verbal counting strategy; Siegler & Shrager, 1984). Whether or not they use their fingers, the min and sum procedures are the two most common ways children count (Groen & Parkman, 1972). The min procedure involves stating the larger-valued addend and then counting a number of times equal to the value of the smaller addend. The sum procedure involves counting both addends starting from 1.
The use of counting results in the development of memory representations of basic facts (Siegler & Shrager, 1984), which eventually support the use of memory-based processes for problem solving. The most common are direct retrieval of answers and decomposition. With direct retrieval, children state an answer that is associated in long-term memory with the presented problem, such as stating “eight” when asked to solve 5+3. Decomposition involves reconstructing the answer based on the retrieval of a partial sum; for example, 6+7 might be solved by retrieving the answer to 6+4 and then adding 3. Although use of decomposition is dependent on fact retrieval, it also requires the conceptual insight that numbers can be broken into pairs of smaller numbers that have the same quantity as the original number (Geary, Hoard, Byrd-Craven, & DeSoto, 2004).
The general pattern of developmental improvement is from use of sum counting to direct retrieval (Ashcraft, 1982), but it is not simply a switch from use of the former to the latter. Rather, at any time children can use one of many strategies to solve a given problem. They may retrieve the answer to 3+1 but count to solve 5+8. What changes with learning is the mix of strategies, with sophisticated ones used more often and less sophisticated ones less often (Siegler, 1996), as well as improvement in the speed and accuracy with which each individual strategy is executed (Delaney, Reder, Staszewski, & Ritter, 1998).
Cognitive Correlates
The core component of working memory is the central executive which is expressed as attention-driven control of information represented in two systems (Baddeley & Hitch, 1974; Baddeley, 1986; Cowan, 1995). These are a language-based phonological loop (Baddeley, Gathercole, & Papagno, 1998), and a visuospatial sketch pad (Logie, 1995). It has been well established that the higher the capacity of the central executive the better the performance on measures of cognitive arithmetic (Barrouillet & Lépine, 2005; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Hecht, 2002; Imbo & Vandierendonck, 2007; Klein & Bisanz, 2000; Lemaire et al., 1996; Mazzocco & Kover, 2007; Noël, 2009; Passolunghi et al., 2007; H. L. Swanson & Sachse-Lee, 2001). The independent contributions of the phonological loop and visuospatial sketch pad to arithmetic learning are not as well established (DeStefano & LeFevre, 2004) and thus are not considered in this study, although they are used as control variables.
Barrouillet and Lépine (2005) found that third and fourth graders with higher central executive capacity used direct retrieval more frequently to solve simple addition problems (e.g., 6+3) than did their lower capacity peers. They hypothesized that capacity affects the ease of forming associations between problem stems (e.g., 6+3) and answers generated by means of counting (e.g., 9). Once associations are formed in long-term memory, capacity affects their activation and inhibits the activation of related but incorrect associations during problem solving. In a related study of fourth to sixth graders, Imbo and Vandierendonck (2007) used a dual task procedure to experimentally increase load on the central executive, which functionally results in lowered capacity, while the children solved simple addition problems. The increase in capacity load resulted in slower retrieval of facts from memory and slower execution of the decomposition and counting strategies, but did not affect strategy selection, that is, the processes that result in use of one strategy (e.g., retrieval) or another (e.g., counting). In a study of adults, Hecht (2002) also experimentally manipulated load on the central executive and confirmed that this does not affect strategy selection. Capacity load did not affect speed of retrieval (but see Lemaire et al., 1996), but did slow the speed of executing the decomposition and min counting strategies. The across-study differences for retrieval speed may reflect a decrease in the demands on the central executive with the automatization of fact retrieval. Indeed, frequent use of any addition strategy should, in theory, result in more efficient execution and thus reduced demands on the capacity of the central executive.
The correlational and experimental studies provide a coherent and theoretically plausible view of the relation between the central executive component of working memory and developmental change in the frequency and efficiency of fact retrieval and execution of the decomposition and min counting strategies. However, as noted, other conceptually and empirically related competencies may explain some of these observed relations, or independently contribute to skill development. Intelligence is a prime candidate, as it predicts ease of learning in all domains and is moderately to strongly correlated with the capacity of the central executive (Ackerman et al., 2005; Conway, Cowan, Bunting, Therriault, & Minkoff, 2002; Engle, Tuholski, Laughlin, & Conway, 1999). Attentive behavior in the classroom also affects learning and is moderately correlated with measures of the central executive (Fuchs et al., 2010). Evidence for the apparently critical role of the central executive for addition learning would be strengthened if this relation holds when intelligence and attentive behavior are controlled.
In one such study, Fuchs et al. (2006) demonstrated that the relation between the central executive and individual differences in third graders’ paper-and-pencil arithmetic computational skills was not significant, once their in-class attentive behavior was controlled. They also demonstrated that intelligence was not related to computational skills, once attentive behavior was controlled. These findings, nonetheless, do not address the possibility that the central executive contributes to the early phases of addition learning, given that the third graders in the Fuchs et al. study already had several years of practice solving these types of problems. The findings for intelligence are not conclusive either, because intelligence predicts ease of learning new material and is less predictive of individual difference in highly practiced domains (Ackerman, 1986). Although computational tests are excellent measures of individual differences in overall arithmetic skills, they do not provide information on how the problems are solved and thus cannot be used to determine if central executive contributes to execution of some problem solving strategies but not others, as suggested by Hecht’s (2002) study.
Current Study
The current analyses are based on a larger-scale prospective study of children’s mathematical development and risk for learning disabilities (Geary, 2010). The first of two previous five year longitudinal analyses assessed the relation between beginning of first grade performance on mathematical cognition tasks (e.g., frequency of correct addition fact retrieval) and growth in mathematics achievement through the end of fifth grade (Geary, 2011). The second examined the mathematical cognition development of groups of typically achieving, low achieving, and learning disabled children from first to fifth grade (Geary, Hoard, Nugent, & Bailey, 2012). The current study supplements the first two by providing a detailed analysis of the relation between children’s central executive capacity, intelligence, and in-class attentive behavior and their first to fourth grade growth in the use of direct retrieval, decomposition, and min counting to solve addition problems. The study allowed us to determine if the central executive remains important to skill development, controlling for intelligence and attentive behavior, and to simultaneously determine if these three competencies are independently or differentially related to increases in the correct use of direct retrieval, decomposition, and min counting.
We included several control variables to further strengthen the rigor of the assessment. The first was sex, based on the well documented findings that boys use retrieval and decomposition more than girls when solving addition problems whereas girls use counting more than boys (Carr & Alexeev, 2011; Carr & Davis, 2001; Carr & Jessup, 1997; Imbo & Vandierendonck, 2007; Royer, Tronsky, Chan, Jackson, & Marchant, 1999). The second was race based on racial differences in mathematics achievement (Geary, Boykin, Embretson, Reyna, Siegler, Berch, & Graban, 2008), and the third was mathematics achievement at the end of kindergarten. The latter is an important control because children who have an early advantage in mathematics tend to maintain this advantage throughout their schooling (Duncan et al., 2007); in other words, prior mathematical knowledge may affect addition strategy development in school. We also included school site and speed of number word articulation as controls. Speed of encoding Arabic numerals and articulating number words are of course basic number processes that may affect children’s skill at solving addition problems, and controlling for them allowed us to rule out these processes to primary determinants of skill development (Imbo & Vandierendonck, 2007).
Method
Participants
All kindergarteners from 12 elementary schools in the same school district that serve children from a wide range of socioeconomic backgrounds were invited to participate. Parental consent and child assent were received for 37% (n = 311) of these children, 288 of them completed the first year of testing, and 249 remained in the study through the end of fourth grade). Of this cohort, 275 children completed the majority of assessments and composed the current sample. Across the four years of data analyzed here, 6.1% of the 6600 observations were missing. Missing observations were estimated (maximum likelihood estimates with 5 imputations) using the multiple imputations program of SAS (SAS Institute, 2004).
At the end of kindergarten, their standardized mathematics achievement scores were average (M = 101, SD = 13), based on national norms (Wechsler, 2001), as was their end of end of first grade IQ scores (M = 99, SD = 15; Wechsler, 1999). The mean age was 74 (SD = 4) and 117 (SD = 4) months, respectively, at the times of the first (spring, Kindergarten) and last (fall, fourth grade) assessments. Girls composed 53% of the sample, and 71% were White; most of the remaining children were Black (12%), Asian (4%), or more than one race or unspecified (13%). The mathematics curriculum when the children began the study was Investigations in Number, Data, and Space (Scott Foresman, 1999), and they continued with this curriculum throughout the grades analyzed here. We did not have information on parental socioeconomic status, but we did have information on the percentage of children eligible for free or reduced price lunches at the 12 schools from which the initial sample was drawn; 36% of children attending these schools were eligible.
Standardized Measures
Intelligence
The children were administered the Raven’s Coloured Progressive Matrices (CPM; Raven, Court, & Raven, 1993), a non-timed test that is considered to be an excellent measure of fluid intelligence, and the Vocabulary and Matrix Reasoning subtests of the WASI (Wechsler, 1999). The CPM scores were standardized based on the 287 who were administered the test (M = 100, SD = 15), and the WASI standard scores were converted to the same metric. For preliminary analyses, the Vocabulary subtest was used as a measure of verbal IQ and the mean of the CPM and Matrix Reasoning tests as a measure of non-verbal IQ. A full IQ score (i.e., mean of the three tests, α = .65), however, provided better and more parsimonious fits to the data than separate verbal and non-verbal scores and thus was used in the analyses.1
Achievement
Mathematics achievement was assessed using the Numerical Operations subtest from the Wechsler Individual Achievement Test-II-Abbreviated (Wechsler, 2001). The easier Numerical Operations items assess number discrimination, rote counting, number production, and basic addition and subtraction.
Addition Strategy Choices
Fourteen simple addition problems and six more complex problems were horizontally presented, one at a time, at the center of a computer monitor. The simple problems consisted of the integers 2 through 9, with the constraint that the same two integers (e.g., 2+2) were never used in the same problem; ½ of the problems summed to 10 or less and the smaller valued addend appeared in the first position for ½ of the problems. The complex problems were six double-digit/single-digit pairs; 16 + 7, 3 + 18, 9 + 15, 17 + 4, 6 + 19, 14 + 8.
The child was asked to solve each problem (without pencil-and-paper) as quickly as possible without making too many mistakes. It was emphasized that the child could use whatever strategy was easiest to get the answer, and was instructed to speak the answer into a microphone that was interfaced with the computer which in turn recorded reaction time (RT) from onset of problem presentation to microphone activation. After solving each problem the child was asked to describe how they got the answer. Based on the child’s description and the experimenter’s observations, the trial was classified based on problem solving strategy; the four most common were counting fingers, verbal counting, retrieval, and decomposition. Counting trials were further classified as min, sum, or other. The combination of experimenter observation and child reports immediately after each problem is solved has proven to be a useful measure of children’s strategy choices (Geary, 1990; Siegler, 1987). The validity of this information is supported by findings showing that finger counting trials have the longest RTs, followed respectively by verbal counting, decomposition, and direct retrieval (Siegler 1987). As an example, for second grade, Geary, Hoard, and Bailey (2012) found mean RTs for correct retrieval trials were 2789 (SD = 1892) ms and those for counting fingers trials were 6662 (SD = 4153) ms; means for verbal counting (4980, SD = 3928) and decomposition (4152, SD = 2784) were in between these. All pair-wise comparisons of correct mean RTs were significant (|t|s > 7.49, ps < .05).
Four variables were used to represent children’s competence in solving addition problems. These were the frequency with which children used direct retrieval to solve simple problems, and the frequency with which they used decomposition to solve both simple and complex problems; direct retrieval was not a common strategy for solving complex problems. The fourth variable indexed the frequency and accuracy with which the min procedure was used to solve complex problems, whether or not the children used their fingers. Min counting is the most sophisticated counting procedure that can be used to solve these problems and thus across-grade increases in its use reflect important improvements in problem solving competence. To keep the scores on the same scale across children who used counting with different frequencies and for grade-related changes for individual children, scores were adjusted based on the percentage of problems solved with counting and for counting errors; specifically, [(frequency of min counts) – (frequency of counting errors)]/(percentage of counting trials). The result is that for any of the four grades a score of 6 means that when the child used counting to solve these problems, they always used the min procedure and never committed a counting error. Lower scores indicate counting errors. We did not create a corresponding variable for simple addition, because the sample approached ceiling by the beginning of second grade.
Working Memory
The Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) consists of nine subtests that assess the central executive, phonological loop, and visuospatial sketchpad. All of the subtests have six items at each span level. Across subtests, the span levels range from one to six to one to nine. Passing four items at one level moves the child to the next. At each span level, the number of items (e.g., words) to be remembered is increased by one. Failing three items at one span level terminates the subtest. Working memory spans for the central executive (α = .61), phonological loop (α = .75), and visuospatial sketch pad (α = .51) were the mean span scores for the corresponding subtests.
Central executive
The central executive is assessed using three dual-task subtests. Listening Recall requires the child to determine if a sentence is true or false, and then recall the last word in a series of sentences. Counting Recall requires the child to count a set of 4, 5, 6, or 7 dots on a card, and then at the end of the series, to recall the number of counted dots on each card. Backward Digit Recall is a standard format backward digit span.
Phonological loop
Digit Recall, Word List Recall, and Nonword List Recall are standard span tasks with differing content stimuli; the child’s task is to repeat words spoken by the experimenter in the same order as presented. In the Word List Matching task, a series of words, beginning with two words and adding one word at each successive level, is presented to the child. The same words, but possibly in a different order, are then presented again, and the child’s task is to determine if the second list is in the same or different order than the first list.
Visuospatial sketch pad
Block Recall is another span task, but the stimuli consist of a board with nine raised blocks in what appears to the child as a “random” arrangement. The blocks have numbers on one side that can only be seen from the experimenter’s perspective. The experimenter taps a block (or series of blocks), and the child’s task is to duplicate the tapping in the same order as presented by the experimenter. In the Mazes Memory task, the child is presented a maze with more than one solution, and a picture of an identical maze with a path drawn for one solution. The picture is removed and the child’s task is to duplicate the path in the response booklet. At each level, the mazes get larger by one wall.
In-Class Attention
The Strength and Weaknesses of ADHD-Symptoms and Normal-behavior (SWAN) measure of in-class attentive behavior was used (J. M. Swanson, Schuck, Mann, Carlson, Hartman, Sergeant et al., 2008). The measure includes items that assess attentional deficits and hyperactivity but teachers are asked to rate the behaviors relative to that of a typical child in their classrooms. The nine item (e.g., “Gives close attention to detail and avoids careless mistakes”) measure was distributed to the children’s second, third, and fourth grade teachers who were asked to rate the behavior of the child relative to other children of the same age on a 1 (far below) to 7 (far above) scale. Scores across grades were highly correlated, rs = .70 to .72, and thus we used their mean (α = .88). On the basis of the high correlations across different teachers and grades, we assumed that individual differences in SWAN scores across second to fourth grade also captured individual differences in first grade.
Control Variables
As noted, the five control variables were sex, race, school, number naming RT, and raw Kindergarten Numerical Operations scores. The race variable provided separate contrasts of White children with Black, White children with Asian children, and White children with all remaining children. The school variable included the 12 original schools for the sample, and contrasted each of 11 schools with the school with the largest initial sample. The Numerical Operations score controlled for basic mathematics skills before entry into first grade.
To control for speed of number encoding and articulation (Imbo & Vandierendonck, 2007), we used a rapid automatized naming (RAN) task (Denckla & Rudel, 1976; Mazzocco & Myers, 2003). The child is presented with 5 numbers to first determine if the child can read the stimuli correctly. After these practice items, the child is presented with a 5 × 10 matrix of incidences of these numbers, and is asked to name them as quickly as possible without making any mistakes. RT is measured via a stopwatch, and were highly correlated across grades, rs = .58 to .79, p<.0001, and thus the score was the across-grade mean (α = .90).
Procedure
Assessments
The CPM and Numerical Operations were administered in the spring of kindergarten, the WASI (Wechsler, 1999) in the spring of first grade, and the WMTB-C (Pickering & Gathercole, 2001) during the summer preceding first grade, during the first grade, or the summer after first grade (mean age = 84 months, SD = 6). The addition tasks were administered in the fall of first to fourth grade, inclusive, as was the RAN. The majority of children were tested in a quiet location at their school site, and occasionally on the university campus or in a mobile testing van. Testing in the van occurred for children who had moved out of the school district and for administration of the WMTB-C (e.g., on the weekend or after school). The mathematical cognition and achievement assessments required between 20 and 40 min and the WMTB-C about 60 min.
Analyses
First to fourth grade retrieval, decomposition, and min counting scores were analyzed using multilevel modeling; specifically, PROC MIXED (SAS Institute, 2004). Linear and quadratic (grade2) slopes for grade and intercept values were random effects and the predictors were intelligence, span scores for the central executive, and mean SWAN scores; control variables were included in all analyses. The intelligence, central executive, and SWAN scores were moderately correlated, r s = .40 to .55, ps<.0001, indicating they assessed overlapping as well as unique competencies. To control for this shared variance, residual values for each variable, controlling for the two other variables and controlling for phonological loop and visuospatial sketch pad span scores were computed and used in the analyses.
To produce unbiased estimates of interactions, all of the predictor variables were standardized (M = 0, SD = 1). To put the continuous control variables (i.e., Numerical Operations scores and RAN RTs) on the same scale as the predictors, these were also standardized, and RAN RTs were reversed so that higher values indicate better performance. The slope variable was coded 0 to 3 for first to fourth grades, respectively. Positive predictor on intercept effects mean that higher scores on the predictor are related to higher levels of competence on the addition variable at the beginning of first grade. A positive coefficient for a predictor on linear slope interaction means that higher scores on the predictor are associated with consistent across-grade gains in the addition competence, controlling for all other variables in the model. A positive predictor on intercept effect combined with a negative predictor on linear slope effect means that higher scores on the predictor are associated with higher addition competence at the beginning of first grade, but that the importance of this predictor declines across grades. A positive predictor on linear slope effect with a negative predictor on quadratic slope effect means that higher scores on the predictor are associated with across-grade gains in the addition competence, but the magnitude of the advantage becomes smaller across grades.
The first analytic step was to specify a full model that included all predictors and their interactions with the linear and quadratic slope (grade) variables. The corresponding negative log likelihood, Bayesian Information Criterion (BIC), and t tests for the maximum likelihood estimates for individual predictors were used in model selection (for review, Luke, 2004; Raftery, 1995). Differences in the negative log likelihood values for nested models can be evaluated using the χ2, with the change in the number of predictors as the df. BIC values can be derived from the negative log likelihood; specifically, with a correction factor that evaluates model fit in terms of the overall number of parameters. The BIC values favor parsimonious models. The second step was to drop all quadratic slope by predictor effects with non-significant t tests and evaluate change in overall model fit using the χ2 and change (Δ) in BIC. A non-significant χ2 indicates the trimmed model fits the data as well as the model with more parameters, and a lower BIC indicates better overall fit, given the number of parameters. The Δ BIC is not evaluated using p values, but differences > 10 are considered very strong evidence for the model with the smaller BIC and differences > 3 are considered positive evidence (Raftery, 1995). The odds that the lower valued BIC provides better estimates for the data can be estimated by e.5(Δ BIC), such that a Δ BIC of 10 yields 150:1 odds that the model with the lower valued BIC provides better estimates. The third and fourth steps involved dropping non-significant predictor by linear slope effects and non-significant predictor on intercept effects, respectively, resulting in a final set of predictors of start point and competence growth.
Results
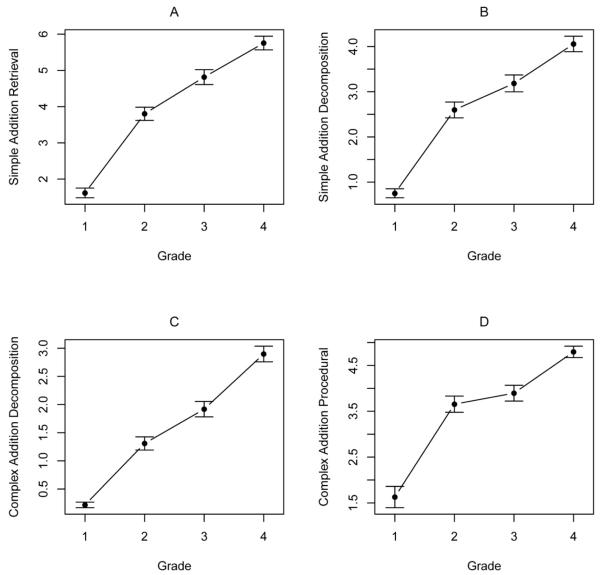
Grade-related changes in the frequency with which direct retrieval (Panel A) or decomposition (Panel B) were used to correctly solve simple addition problems (out of 14 possible) are shown in Figure 1. Also shown are grade-related changes in the frequency with which decomposition (Panel C) was correctly used to solve complex problems (out of 6 possible). Panel D shows the frequency with which min counting was used to solve complex addition problems; these scores are adjusted for overall counting frequency and counting errors.
Figure 1.
Number of simple addition problems (out of 14 possible) correctly solved with direct retrieval of the answer (Panel A) or with use of the decomposition strategy (Panel B). Number of complex addition problems (out of 6 possible) solved with use of the decomposition strategy (Panel C), and the min counting procedure minus the number of counting errors (Panel D). For the latter, score is adjusted based on the number of problems solved with counting. The maximum score of 6 indicates that when the child used counting to problem solve, they always used the min procedure and never committed an error. Figure produced with R (R Development Core Team, 2008).
Simple Addition
Retrieval
The top section of Table 1 shows the summary indexes for the multilevel models. For the full model, none of the predictor by quadratic slope interactions were significant and dropping them resulted in a non-significant increase in the χ2 value (p=.13) and a substantive reduction in the BIC value (i.e., Δ 11.2), indicating better model fit. Examination of the predictor on linear slope effects in the resulting model (Model 2) revealed the effect for the central executive variable was not significant. Dropping this resulted in a non-significant change in the χ2 value (p=.75) and a better (i.e., lower) BIC value. Comparing this final model to the full model indicated no significant difference in the negative log likelihood values, χ2(4) = 3.7, p=.21, as well as a substantial Δ BIC (16.6) favoring the final model.
Table 1.
Fit Indexes for Multi-Level Models
| Model | Negative Log Likelihood |
χ 2 | Para- meters |
p | BIC | Δ BIC |
|---|---|---|---|---|---|---|
| Simple Addition: Retrieval | ||||||
| 1: Full | 5005.1 | --- | 16 | --- | 5201.7 | --- |
| 2: Drop CE, SWAN, and IQ on quadratic slope effects |
5010.8 | 5.7 | 13 | .13 | 5190.5 | 11.2 |
| 3: Drop CE on linear slope effect | 5010.9 | 0.1 | 13 | .75 | 5185.1 | 5.4 |
| Complex Addition: Min Counting Procedure | ||||||
| 1: Full | 5204.3 | --- | 16 | --- | 5406.5 | --- |
| 2: Drop CE, SWAN, and IQ on quadratic slope effects |
5205.0 | 0.7 | 13 | .87 | 5390.4 | 16.1 |
Note: BIC = Bayesian Information Criterion; IQ = full scale intelligence; CE = central executive; SWAN = in-class attention.
The estimates for this final model are shown in the second column of Table 2. Three of the control variables were significant and indicated that girls correctly retrieved fewer answers than boys, Asian children correctly retrieved more answers than White children, and higher mathematics achievement in kindergarten was associated with more frequent correct retrieval in later grades. All of the predictor variable effects shown in Table 2 are significant (ps<.05) except for the intelligence on intercept effect, which was retained because of its interaction with the linear slope variable. The significant SWAN on intercept and central executive on intercept effects indicate that higher scores on these variables were independently associated with more correct fact retrievals at the beginning of first grade. To illustrate, holding all other variables constant, the central executive on intercept effect means that for each 1 SD change in this variable, there was a 0.52 change in the number of facts correctly retrieved, such that children who were 1 SD above average correctly solved an average of 3.21 (2.69 intercept value + 0.52 central executive on intercept value) problems by means of direct retrieval at the beginning of first grade, whereas their peers who were 1 SD below average solved 2.17 problems.
Table 2.
Maximum Likelihood Estimates for Developmental Change in Use of Retrieval and Decomposition for Solving Simple Addition Problems
| Retrieval | Decomposition | |||||
|---|---|---|---|---|---|---|
| Effect | Final Model |
t | p | Final Model |
t | p |
| Intercept | 2.69 | 8.23 | .0001 | 2.14 | 8.57 | .0001 |
| Control Variables | ||||||
| Girls contrasted with boys | −1.41 | −6.51 | .0001 | −0.88 | −5.36 | .0001 |
| Mixed race contrasted with White | −0.21 | −0.64 | .5246 | −0.32 | −1.29 | .1974 |
| Black contrasted with White | −0.20 | −0.52 | .6014 | −0.66 | −2.26 | .0245 |
| Asian contrasted with White | 1.66 | 3.15 | .0018 | 0.085 | 0.20 | .8403 |
| Number Processing Speed | 0.13 | 1.05 | .2931 | −0.04 | −0.48 | .7042 |
| Kindergarten Number Operations | 0.43 | 3.34 | .0010 | 0.30 | 3.14 | .0001 |
| Predictor Variables | ||||||
| Linear Slope (Grade) | 2.28 | 11.27 | .0001 | 1.78 | 9.04 | .0001 |
| Quadratic Slope (Grade2) | −0.31 | −4.78 | .0001 | −0.24 | −3.96 | .0001 |
| Intelligence on Intercept | 0.19 | 1.22 | .2221 | 0.20 | 1.55 | .1229 |
| SWAN on Intercept | 0.53 | 3.17 | .0017 | 0.29 | 2.06 | .0399 |
| Central Executive on Intercept | 0.52 | 3.04 | .0026 | 0.11 | 0.68 | .4959 |
| Intelligence on Linear Slope | 0.15 | 2.16 | .0315 | 0.89 | 3.62 | .0004 |
| SWAN on Linear Slope | 0.19 | 2.72 | .0070 | 0.66 | 2.48 | .0138 |
| Central Executive on Linear Slope | --- | --- | --- | 0.80 | 2.62 | .0093 |
| Intelligence on Quadratic Slope | --- | --- | --- | −0.30 | −3.89 | .0001 |
| SWAN on Quadratic Slope | --- | --- | --- | −0.17 | −2.07 | .0395 |
| Central Executive on Quadratic Slope | --- | --- | --- | −0.24 | −2.53 | .0120 |
Note: Mixed race includes participants identified by their parents as biracial or unspecified; SWAN = in-class attention. Contrasts for the School variable are not shown and the overall effect was not significant for retrieval (p=.36), but was for decomposition (p=.03). For retrieval, variances for intercept (0), linear slope (0.96, se = 1.09, z = 0.88, p=0.1883), and quadratic slope (0.12, se = 0.12, z = 1.02, p=0.1539). For decomposition, variances for intercept (0), linear slope (3.96, se = 0.98, z = 4.03, p=0.0001), and quadratic slope (0.35, se = 0.10, z = 3.63, p=0.0001).
Decomposition
All of the interactions were significant for the full model and thus all effects were retained. The corresponding estimates are shown in the fifth column of Table 2. The control variables indicate that girls used decomposition less frequently than boys, Black children used it less frequently than White children, and that higher mathematics achievement in kindergarten was associated with more frequent use of decomposition in later grades. The overall contrast for school site was also significant (p=.03) but is not shown in the table. The non-significant intelligence on intercept and central executive on intercept effects were retained because of the significant interactions involving these variables. The critical finding is that the across grade increases in the correct use of decomposition were independently related to intelligence, SWAN scores, and capacity of the central executive. The advantage of being above average in these competencies was found in all grades, but the relative magnitude of this advantage declined across grades.
To illustrate, children who were 1 SD above average on the central executive correctly solved 2.10 more problems using decomposition in second grade than in first, whereas their average peers solved 1.54 more problems, on average, a relative advantage of 0.56 problems. This advantage increased to 0.64 problems in third grade and then declined to 0.24 problems in fourth. The average children in turn had the same estimated magnitude of advantages (i.e., 0.56, 0.64, 0.24, respectively, for second to fourth grade) relative to children 1 SD below average on the central executive. These estimates are obtained using the equation below, where change (c) is the number of additional problems solved from one grade (g) to the next (recall for first to fourth grade the g codes are 0 to 3, respectively), and ce is the standardized scores (M = 0, SD = 1) for the central executive variable.
| (1) |
Complex Addition
Decomposition
All of the interactions were significant for the full model and thus all effects were retained. The corresponding estimates are shown in the second column of Table 3. The control variables indicate that girls used decomposition less frequently than boys, and that higher mathematics achievement in kindergarten was associated with more frequent use of decomposition in later grades. The overall contrast for school site was also significant (p=.02) but is not shown in the table. The non-significant predictors on intercept effects reflect the infrequent use of decomposition to solve these problems at the beginning of first grade. The significant predictors on linear slope and on quadratic slope effects show the same pattern as found for use of decomposition to solve simple problems. Above average intelligence, SWAN scores, and capacity of the central executive were independently associated with larger than average grade-to-grade increases in the correct use of decomposition, but the magnitude of these advantages declined across grades.
Table 3.
Maximum Likelihood Estimates for Developmental Change in Use of Decomposition and Min Counting Procedure for Solving Complex Addition Problems
| Decomposition | Min Counting Procedure | |||||
|---|---|---|---|---|---|---|
| Effect | Final Model |
t | p | Final Model |
t | P |
| Intercept | 1.07 | 7.06 | .0001 | 1.82 | 5.69 | .0001 |
| Control Variables | ||||||
| Girls contrasted with boys | −0.58 | −5.72 | .0001 | 0.40 | 2.19 | .0292 |
| Mixed race contrasted with White | −0.28 | −1.84 | .0669 | −0.24 | −0.87 | .3865 |
| Black contrasted with White | −0.21 | −1.18 | .2391 | −0.41 | −1.29 | .1977 |
| Asian contrasted with White | 0.05 | 0.22 | .8261 | 0.20 | 0.46 | .6462 |
| Number Processing Speed | −0.04 | −0.72 | .1039 | 0.53 | 5.21 | .0001 |
| Kindergarten Number Operations | 0.31 | 5.27 | .0002 | 0.49 | 4.59 | .0001 |
| Predictor Variables Linear Slope (Grade) | 0.95 | 7.33 | .0001 | 1.83 | 6.55 | .0001 |
| Quadratic Slope (Grade2) | −0.03 | −0.70 | .4873 | −0.28 | −3.41 | .0007 |
| Intelligence on Intercept | −0.06 | −0.70 | .4816 | 0.57 | 2.88 | .0043 |
| SWAN on Intercept | 0.03 | 0.35 | .7285 | 1.07 | 5.00 | .0001 |
| Central Executive on Intercept | 0.04 | 0.38 | .7010 | 0.66 | 2.70 | .0074 |
| Intelligence on Linear Slope | 0.94 | 5.86 | .0001 | −0.25 | −3.09 | .0022 |
| SWAN on Linear Slope | 0.69 | 3.96 | .0001 | −0.41 | −4.77 | .0001 |
| Central Executive on Linear Slope | 0.81 | 4.04 | .0001 | −0.26 | −2.56 | .0111 |
| Intelligence on Quadratic Slope | −0.25 | −5.03 | .0001 | --- | --- | --- |
| SWAN on Quadratic Slope | −0.15 | −2.73 | .0068 | --- | --- | --- |
| Central Executive on Quadratic Slope | −0.21 | −3.40 | .0008 | --- | --- | --- |
Note: Mixed race includes participants identified by their parents as biracial or unspecified; SWAN = in-class attention. Contrasts for the School variable are not shown and the overall effect was significant for decomposition (p=.02), but not for procedural competence (p=.62). SWAN = in-class attention. For decomposition, variances for intercept (0), linear slope (2.17, se = 0.43, z = 5.11, p=0.0001), and quadratic slope (0.19, se = 0.04, z = 4.75, p=0.0001). For procedural, variances for intercept (5.02, se = 1.03, z = 4.90, p=0.0001), linear slope (7.46, se = 2.17, z = 3.43, p=0.0003), and quadratic slope (0.47, se = 0.20, z = 2.32, p=0.0101).
Min counting procedure
The second section of Table 1 shows the summary indexes for the multilevel models. None of the predictor on quadratic slope effects were significant, and dropping them resulted in a non-significant increase in the χ2 value (p=.87) and a substantially better BIC value (Δ BIC = 16.1). The three predictors on linear slope effects and the three predictors on intercept effects were significant and thus retained in the final model. The estimates for this model are shown in the fifth column of Table 3. The control variables indicate that girls used min counting more frequently than boys, and that faster speed of number word articulation and higher mathematics achievement in kindergarten were associated with more frequent and accurate use of min counting in later grades. The predictor on intercept effects indicate children who were above average in intelligence, SWAN scores, and capacity of the central executive used min counting more frequently and accurately at the beginning of first grade than did their lower scoring peers. The predictors on linear slope effects indicate that this advantage declined after first grade for each of the three predictors.
Discussion
The study provided the first large-scale longitudinal investigation of the independent contributions of the capacity of the central executive, intelligence, and in-class attentive behavior on children’s developing use of direct retrieval, decomposition, and min counting to solve addition problems, while controlling for the effects of sex, race, school site, prior mathematics achievement, and speed of Arabic numeral encoding and number word articulation. The use of multilevel models revealed that the central executive, intelligence, and in-class attentive behavior were independently associated with individual differences in the sophistication and accuracy of children’s problem solving strategies at the beginning of first grade (i.e., predictor on intercept effects). The central executive, intelligence, and in-class attentive behavior were also related to grade-related changes in strategy use (i.e., predictor on slope effects), but the relative contributions of these factors varied across strategy and grade.
Central Executive
The results confirm the importance of individual differences in the capacity of the central executive for skilled execution of each of these three strategies (Barrouillet & Lépine, 2005; DeStefano & LeFevre, 2004; Geary, 1993; Geary et al., 2004; Hecht, 2002; Imbo & Vandierendonck, 2007; Lemaire et al., 1996), but at the same time suggest the relative importance of this capacity varies across strategies and grades. With the control of intelligence, in-class attentive behavior, and phonological loop and visuospatial sketch pad spans, the capacity of the central executive was predictive of correct use of retrieval and min counting to solve addition problems at the beginning of first grade, but did not appear to be important for use of these strategies in later grades. Individual differences in central executive capacity, in turn, were not related to correct use of decomposition to solve simple or complex problems at the beginning of first grade, in part due to the low overall use of this strategy, but were predictive of increased use of this strategy in later grades.
Although our results for retrieval of simple addition facts are consistent with the general findings of Barrouillet and Lépine (2005), that is, children with higher central executive capacity retrieve facts more frequently than their lower capacity peers, the grade-related patterns differed. Barrouillet and Lépine found that third and fourth graders with higher capacity retrieved more addition facts than their lower capacity peers, at least for sums < 10. After first grade, our results suggest that the central executive is not related to frequency of fact retrieval, once the contributions of intelligence and in-class attentive behavior are controlled. Our results do not rule out the possibility that capacity affects retrieval frequency for subsets of problems, as found by Barrouillet and Lépine, but does suggest that future studies should include intelligence and in-class attentive behavior as measures of alternative influences on the development of retrieval usage.
The primary findings of Barrouillet and Lépine (2005) and Imbo and Vandierendonck (2007) indicated that the higher the capacity of the central executive the faster third to sixth graders retrieved simple addition facts from long-term memory. Our results cannot address this relation because different children used retrieval to solve different problems within grades, and because the same children used retrieval to solve different subsets of problems across grades. In this situation, the relation between the central executive and individual differences in mean retrieval RTs would be difficult to assess without the serious confound of retrieval being used to solve different subsets of problems across and within children. The assessment of this relation will require tasks that instructed children to only use retrieval, as done by Imbo and Vandierendonck and Hecht (2002), across the grades and thus control for intelligence and in-class attentive behavior. Our interpretation of the assessed here, and to simultaneously assess literature, at this time, is that the capacity of the central executive likely does affect the speed of addition fact retrieval in children across grades. Whether capacity is an important influence on speed of fact retrieval in well-practiced adults remains to be determined, as current results are mixed (Hecht, 2002; Lemaire et al., 1996).
Experimentally increasing load on the central executive has been found to slow speed of executing the decomposition and min counting strategies in children (Imbo & Vandierendonck, 2007) and adults (Hecht, 2002). Again, our addition task does not allow for an unconfounded assessment of individual or grade-related differences in associated RTs, but our results do indicate that capacity of the central executive is related to individual differences and grade-related changes in the frequency with which children use these strategies, controlling for intelligence and in-class attentive behavior. Individual differences in capacity were associated with more frequent and accurate use of min counting at the beginning of first grade, but the importance of capacity declined in later grades. Use of decomposition to solve simple and complex problems was uncommon in first grade. After first grade, children with higher central executive capacity showed more rapid adoption of decomposition for solving both simple and complex addition problems, but the magnitude of their relative advantage declined by fourth grade. Integrating our findings with those of Imbo and Vandierendonck and Hecht suggests that early in addition skill development individual differences in the capacity of the central executive are particularly important for understanding variation in the rate of learning to accurately use decomposition and min counting, whereas once these strategies have been learned capacity largely affects rate of executing them (Geary, 1994).
Intelligence and In-Class Attentive Behavior
Although intelligence and in-class attentive behavior were not the focus of our study, the corresponding results do contribute to our understanding of children’s strategy development above and beyond the contributions of the central executive. The relation between working memory, especially the attentional and inhibitory control subcomponents of the central executive, and intelligence is vigorously debated, with some theorists arguing they are one and the same (Conway et al., 2002; Engle et al., 1999), and others arguing they assess overlapping and independent competencies (Ackerman et al., 2005; Embretson, 1995). The results of Embretson’s study suggest the independent component of intelligence is the ability to think systematically and logically.
The design of our study does not allow for a replication of this aspect of Embretson’s (1995) findings but the results are consistent with a component of intelligence that is independent of in-class attentive behavior and central executive, phonological loop, and visuospatial sketch pad spans. This independent component was not strongly related to use of direct retrieval, but did contribute to first graders’ use of min counting and the frequency with which they used decomposition in later grades. Geary et al. (2004) proposed that children’s accurate use of min counting and decomposition are dependent in part on the conceptual insight that larger-valued numbers are composed of sets of smaller-valued numbers that can be independently manipulated. We did not directly assess this conceptual knowledge, but its understanding does seem to be consistent with the logical abilities isolated by Embretson. At the very least, the pattern leads to the testable hypothesis that the relation between children’s in telligence and their strategy development documented here is mediated by their conceptual understanding of numbers.
In-class attentive behavior has been found to be related to performance on mathematics achievement tests above and beyond the influence of intelligence (Duncan et al., 2007) and to performance pencil-and-paper tests of computational arithmetic above and beyond the influence of intelligence and working memory (Fuchs et al., 2006; Fuchs et al., 2010). However, previous studies of cognitive influences on grade-related change in children’s strategy choices have not included assessments of in-class attentive behavior (Barrouillet & Lépine, 2005; Geary et al., 2004; Imbo & Vandierendonck, 2007). The current study did so and revealed that independent of intelligence and spans for the central executive, phonological loop, and visuospatial sketch pad, in-class attentive behavior contributes to individual differences in first graders’ use of min counting and their use of decomposition in later grades. As with intelligence, the study design does not allow us to determine which aspects of classroom behavior assessed by the SWAN, such as attention to detail, organization of class work, or impulsiveness (J.M. Swanson et al., 2008), independently contributed to children’s strategy development. Our findings, nevertheless, indicate that at least some aspects of in-class attention and behavior are just as important as the capacity of the central executive and intelligence in explaining individual differences in first graders’ min counting and their later use of decomposition and may be more important than either of these for understanding individual differences in use of direct retrieval.
Control Variables
The contrast of boys and girls and kindergarten mathematics achievement were the only control variables that were consistently related to children’s strategy usage and development. The results for the former are consistent with previous studies that have found that boys use retrieval and decomposition more than girls to solve addition problems and that girls use counting more than boys (Carr & Alexeev, 2011; Carr & Davis, 2001; Carr & Jessup, 1997; Imbo & Vandierendonck, 2007; Royer et al., 1999). Bailey, Littlefield, and Geary (2012) provide a first to sixth grade, inclusive, analysis of this pattern as related to mathematics achievement for the current longitudinal project and thus we do not provide further comment here, but do note that the findings for the central executive, intelligence, and in-class attentive behavior control for these sex differences and control for kindergarten mathematics achievement. The relation between early and later mathematics has also been documented elsewhere (Duncan et al., 2007). Our findings contribute to these by showing that early achievement predicted later skilled use of all of the strategies assess here.
The results for school site and race were inconsistent across strategies and not the focus of our analyses, but controlling for them still contributed to the rigor of the results. The results for speed of Arabic numeral encoding and number word articulation were also inconsistent across strategies. Imbo and Vandierendonck (2007) found that a measure of speed of encoding and comparing Arabic numerals was correlated with use of retrieval, decomposition, and min counting but was not a significant predictor of strategy usage, once age and load on the central executive were controlled. Our results for retrieval and decomposition are consistent with these findings, but also indicated that faster processing of Arabic numerals and articulation of number words was related to more frequent and accurate use of min counting. Again, we cannot be certain which component was more important, but favor speed of number word articulation because articulation is a core component of implicit counting (Logie & Baddeley, 1987) and speed of implicit counting is related to skilled use of counting procedures to solve addition problems (Ashcraft, Fierman, & Bartolotta, 1984; Geary & Brown, 1991).
Conclusion
Children with a higher capacity of the central executive component of working memory had advantages over their lower capacity peers in the adoption and use of the min counting and decomposition strategies to solve addition problems, independent of intelligence, in-class attentive behavior, spans for the phonological loop and visuospatial sketch pad, sex, race, school site, speed of Arabic numeral encoding and number work articulation, and mathematics achievement. The advantage for min counting was evident in first grade, and for decomposition in later grades. Although the results are necessarily correlational, the prospective design and extensive controls, along with consistency with previous studies (Barrouillet & Lépine, 2005; Geary et al., 2004; Hecht, 2002; Imbo & Vandierendonck, 2007; Lemaire et al., 1996), suggest the patterns found in this study are likely to be robust. The results also highlight the independent contributions of intelligence and in-class attentive behavior for understanding individual differences in children’s strategy development, and illustrate the need to include these in future studies of this development.
We studied developmental change in the strategies children use to solve addition problems
Children with higher working memory capacity use more sophisticated strategies
Intelligence and in-class attentive behavior also influence strategy development.
Working memory, intelligence, and in-class behavior influence strategy development differently
Acknowledgements
Institute of Child Health and Human Development. We thank Kendra Anderson Cerveny, Drew Authors acknowledge support from grants R01 HD38283 and R37 HD045914 from the National Bailey, Jennifer Byrd-Craven, Rachel Christensen, Nick Geary, Larissa Haggard, Rebecca Hale, Patricia Hoard, Stacey Jones, Mary Lemp, Patrick Caitlin Cole, Mike Coutts, Sara Ensenberger, Maloney, Rehab Mojid, Cy Nadler, Chatty Numtee, Amanda Shocklee, Jennifer Smith, Ashley Stickney, Jonathan Thacker, Leah Thomas, Jasmine Tilghman, Erin Twellman, Katie Waller and Alex Wilkerson for help on various aspects of the project.
Footnotes
The Bayesian Information Criterion (BIC) was used to compare the fit of models that included separate verbal and nonverbal IQ measures to models that included a single full scale IQ measure. These were the models in which all variables were estimated to predict frequency of correct fact retrieval and use of decomposition for solving simple addition problems, and frequency with which decomposition and min counting were correctly used to solve complex addition problems. In all cases, the differences in model fit were not significant (ps>.05), and the BIC values were smaller (Δ BIC = 9.7 to 12.2), indicating better fit, for the model that included full scale IQ.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ackerman PL. Individu al differences in information processing: An investigation of intellectual abilities and task performance during practice. Intelligence. 1986;10:101–139. doi:10.1016/0160-2896(86)90010-3. [Google Scholar]
- Ackerman PL, Beier ME, Boyle MO. Working memory and intelligence: The same or different constructs? Psychological Bulletin. 2005;131:30–60. doi: 10.1037/0033-2909.131.1.30. doi:10.1037/0033-2909.131.1.30. [DOI] [PubMed] [Google Scholar]
- Ashcraft MH. The development of mental arithmetic: A chronometric approach. Developmental Review. 1982;2:213–236. doi:10.1016/0273-2297(82)90012-0. [Google Scholar]
- Ashcraft M, Fierman B, Bartolotta R. The production and verification tasks in mental addition: An empirical comparison. Developmental Review. 1984;4:157–170. doi: 10.1016/0273-2297(84)90005-4. [Google Scholar]
- Ashcraft MH, Kirk EP. The relationships among working memory, math anxiety, and performance. Journal of Experimental Psychology: General. 2001;130:224–237. doi: 10.1037//0096-3445.130.2.224. doi:10.1037/0096-3445.130.2.224. [DOI] [PubMed] [Google Scholar]
- Baddeley AD. Working memory. Oxford University Press; Oxford: 1986. doi:10.1016/S0764-4469(97)89817-4. [Google Scholar]
- Baddeley A, Gathercole S, Papagno C. The phonological loop as a language learning device. Psychological Review. 1998;105:158–173. doi: 10.1037/0033-295x.105.1.158. doi:10.1037//0033-295X.105.1.158. [DOI] [PubMed] [Google Scholar]
- Baddeley AD, Hitch GJ. Working memory. In: Bower GH, editor. The psychology of learning and motivation: Advances in research and theory. Vol. 8. Academic Press; New York: 1974. pp. 47–90. doi: 10.1016/S0079-7421(08)60452-1. [Google Scholar]
- Bailey DH, Littlefield A, Geary DC. The co-development of skill at and preference for use of retrieval-based processes for solving addition problems: Individual and sex differences from first to sixth grade. 2012. Submitted. [DOI] [PMC free article] [PubMed]
- Barrouillet P, Lépine R. Working memory and children’s use of retrieval to solve addition problems. Journal of Experimental Child Psychology. 2005;91:183–204. doi: 10.1016/j.jecp.2005.03.002. doi:10.1016/j.jecp.2005.03.002. [DOI] [PubMed] [Google Scholar]
- Bull R, Espy KA, Wiebe SA. Short-term memory, working memory, and executive functions in preschoolers: Longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology. 2008;33:205–228. doi: 10.1080/87565640801982312. doi:10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bynner J. Basic skills in adolescents’ occupational preparation. Career Development Quarterly. 1997;45:305–321. doi:10.1002/j.2161-0045.1997.tb00536.x. [Google Scholar]
- Carr M, Alexeev N. Fluency, accuracy, and gender predict developmental trajectories of arithmetic strategies. Journal of Educational Psychology. 2011;103:617–631. doi:10.1037/a0023864. [Google Scholar]
- Carr M, Davis H. Gender Differences in Arithmetic Strategy Use: A Function of Skill and Preference. Contemporary educational psychology. 2001;26:330–347. doi: 10.1006/ceps.2000.1059. doi:10.1006/ceps.2000.1059. [DOI] [PubMed] [Google Scholar]
- Carr M, Jessup DL. Gender differences in first-grade mathematics strategy use: Social and metacognitive influences. Journal of Educational Psychology. 1997;89:318–328. doi:10.1037/0022-0663.89.2.318. [Google Scholar]
- Conway ARA, Cowan N, Bunting MF, Therriault DJ, Minkoff SRB. A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence. 2002;30:163–183. doi:0.1016/S0160-2896(01)00096-4. [Google Scholar]
- Cowan N. Attention and memory: An integrated framework. Oxford University Press; New York: 1995. doi:10.1023/A:1007932721290. [Google Scholar]
- Deary IJ, Strand S, Smith P, Fernandes C. Intelligence and educational achievement. Intelligence. 2007;35:13–21. doi:10.1016/j.intell.2006.02.001. [Google Scholar]
- Delaney P, Reder LM, Staszewski J, Ritter F. The strategy specific nature of improvement: The power law applies by strategy within task. Psychological Science. 1998;9:1–7. doi:10.1111/1467-9280.00001. [Google Scholar]
- Denckla MB, Rudel R. Rapid automatized naming (RAN): Dyslexia differentiated from other learning disabilities. Neuropsychologia. 1976;14:471–479. doi: 10.1016/0028-3932(76)90075-0. doi:10.1016/0028-3932(76)90075-0. [DOI] [PubMed] [Google Scholar]
- DeStefano D, LeFevre J-A. The role of working memory in mental arithmetic. European Journal of Cognitive Psychology. 2004;16:353–386. doi:10.1080/09541440244000328. [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, et al. School readiness and later achievement. Developmental Psychology. 2007;43:1428–1446. doi: 10.1037/0012-1649.43.6.1428. doi:10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Embretson SE. The role of working memory capacity and general control processes in intelligence. Intelligence. 1995;20:169–189. doi:10.1016/0160-2896(95)90031-4. [Google Scholar]
- Engle RW, Tuholski SW, Laughlin JE, Conway ARA. Working memory, short-term memory, and general fluid intelligence: A latent-variable approach. Journal of Experimental Psychology: General. 1999;128:309–331. doi: 10.1037//0096-3445.128.3.309. doi:10.1037//0096-3445.128.3.309. [DOI] [PubMed] [Google Scholar]
- Every Child a Chance Trust [Retrieved August 14, 2009];The long-term costs of numeracy difficulties. 2009 http://www.everychildachancetrust.org/counts/index.cfm.
- Foresman, Scott . Investigations in number, data, and space. Author; Glenview, Il: 1999. [Google Scholar]
- Fuchs LS, Fuchs D, Compton DL, Powell SR, Seethaler PM, Capizzi AM, et al. The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology. 2006;98:29–43. doi:10.1037/0022-0663.98.1.29. [Google Scholar]
- Fuchs LS, Geary DC, Compton DL, Fuchs D, Hamlett CL, Bryant JD. The contributions of numerosity and domain-general abilities for school readiness. Child Development. 2010;81:1520–1533. doi: 10.1111/j.1467-8624.2010.01489.x. doi:10.1111/j.1467-8624.2010.01489.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC. A componential analysis of an early learning deficit in mathematics. Journal of Experimental Child Psychology. 1990;49:363–383. doi: 10.1016/0022-0965(90)90065-g. doi: 10.1016/0022-0965(90)90065-G. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin. 1993;114:345–362. doi: 10.1037/0033-2909.114.2.345. doi:10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC. Children’s mathematical development: Research and practical applications. American Psychological Association; Washington, DC: 1994. doi:10.1037/10163-000. [Google Scholar]
- Geary DC. Missouri longitudinal study of mathematical development and disability. British Journal of Educational Psychology Monograph Series II. 2010;7:31–49. [Google Scholar]; Cowan R, Saxton M, Tolmie A, editors. Understanding number development and number difficulties. No. 7. British Psychological Society; Leicester, UK: (British Journal of Educational Psychology, Monograph Series II: Psychological Aspects of Education - Current Trends). doi: 10.1348/97818543370009X12583699332410. [Google Scholar]
- Geary DC. Cognitive predictors of individual differences in achievement growth in mathematics: A five year longitudinal study. Developmental Psychology. 2011;47:1539–1552. doi: 10.1037/a0025510. doi:10.1037/a0025510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Boykin AW, Embretson S, Reyna V, Siegler R, Berch DB, Graban J. National Mathematics Advisory Panel, Reports of the task groups and subcommittees. United States Department of Education; Washington, DC: 2008. Report of the task group on learning processes; pp. 4-i–4-221. http://www.ed.gov/about/bdscomm/list/mathpanel/report/learning-processes.pdf. [Google Scholar]
- Geary DC, Bow-Thomas CC, Liu F, Siegler RS. Development of arithmetical competencies in Chinese and American children: Influence of age, language, and schooling. Child Development. 1996;67:2022–2044. doi:10.1111/j.1467-8624.1996.tb01841.x. [PubMed] [Google Scholar]
- Geary DC, Brown SC. Cognitive addition: Strategy choice and speed-of-processing differences in gifted, normal, and mathematically disabled children. Developmental Psychology. 1991;27:398–406. doi:10.1037//0012-1649.27.3.398. [Google Scholar]
- Geary DC, Hoard MK, Bailey DH. Fact retrieval deficits in low achieving children and children with mathematical learning disability. Journal of Learning Disabilities. 2012 doi: 10.1177/0022219410392046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Desoto M. Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology. 2004;88:121–151. doi: 10.1016/j.jecp.2004.03.002. doi:10.1016/j.jecp.2004.03.002. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78:1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. doi:10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L, Bailey DH. Mathematical cognition deficits in children with learning disabilities and persistent low achievement: A five year prospective study. Journal of Educational Psychology. 2012;104 doi: 10.1037/a0025398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groen GJ, Parkman JM. A chronometric analysis of simple addition. Psychological Review. 1972;79:329–343. doi:10.1037/h0032950. [Google Scholar]
- Hecht S. Counting on working memory in simple arithmetic when counting is use for problem solving. Memory & Cognition. 2002;30:447–455. doi: 10.3758/bf03194945. doi:10.3758/BF03194945. [DOI] [PubMed] [Google Scholar]
- Imbo I, Vandierendonck A. The development of strategy use in elementary school children: Working memory and individual differences. Journal of Experimental Child Psychology. 2007;96:284–309. doi: 10.1016/j.jecp.2006.09.001. doi:10.1016/j.jecp.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Jensen AR. The g factor: The science of mental ability. Praeger; Westport, CT: 1998. doi:10.1038/381729b0. [Google Scholar]
- Klein JS, Bisanz J. Preschoolers doing arithmetic: The concepts are willing by the working memory is weak. Canadian Journal of Experimental Psychology. 2000;54:105–115. doi: 10.1037/h0087333. doi:10.1037/h0087333. [DOI] [PubMed] [Google Scholar]
- Lemaire P, Abdi H, Fayol M. The role of working memory resources in simple cognitive arithmetic. European Journal of Cognitive Psychology. 1996;8:73–103. doi:10.1080/095414496383211. [Google Scholar]
- Levine SC, Jordan NC, Huttenlocher J. Development of calculation abilities in young children. Journal of Experimental Child Psychology. 1992;53:72–103. doi: 10.1016/s0022-0965(05)80005-0. doi:10.1016/S0022-0965(05)80005-0. [DOI] [PubMed] [Google Scholar]
- Logie RH. Visuo-spatial working memory. Erlbaum; Hove, UK: 1995. [Google Scholar]
- Logie RH, Baddeley AD. Cognitive processes in counting. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1987;13:310–326. doi:10.1037//0278-7393.13.2.310. [Google Scholar]
- Luke DA. Multilevel modeling. Sage Publications; Thousand Oaks, CA: 2004. [Google Scholar]
- Mazzocco MMM, Kover ST. A longitudinal assessment of executive function skills and their association with math performance. Child Neuropsychology. 2007;13:18–45. doi: 10.1080/09297040600611346. doi:10.1080/09297040600611346. [DOI] [PubMed] [Google Scholar]
- Mazzocco MMM, Myers G. Complexities in identifying and defining mathematics learning disability in the primary school-age years. Annals of Dyslexia. 2003;53:218–253. doi: 10.1007/s11881-003-0011-7. doi:10.1007/s11881-003-0011-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Mathematics Advisory Panel . Foundations for Success: Final Report of the National Mathematics Advisory Panel. United States Department of Education; Washington, DC: 2008. http://www.ed.gov/about/bdscomm/list/mathpanel/report/final-report.pdf. [Google Scholar]
- Noël M-P. Counting on working memory when learning to count and to add: A preschool study. Developmental Psychology. 2009;45:1630–1643. doi: 10.1037/a0016224. doi:10.1037/a0016224. [DOI] [PubMed] [Google Scholar]
- Parsons S, Bynner J. Numeracy and employment. Education & Training. 1997;39:43–51. doi:10.1108/00400919710164125. [Google Scholar]
- Passolunghi MC, Vercelloni B, Schadee H. The precursors of mathematics learning: Working memory, phonological ability and numerical competence. Cognitive Development. 2007;22:165–184. doi:10.1016/j.cogdev.2006.09.001. [Google Scholar]
- Pickering S, Gathercole S. Working Memory Test Battery for Children (WMTB-C) Manual. Psychological Corporation Ltd; London: 2001. [Google Scholar]
- R Development Core Team . Rl: A language and environment for statistical computing. R foundation for Statistical computing; Vienna, Austria: 2008. ISBN 3-900051-07-0, URL http://www.R-project.org. [Google Scholar]
- Raftery AE. Bayesian model selection in social research. Sociological Methodology. 1995;25:111–196. doi: 10.2307/271063. [Google Scholar]
- Raven JC, Court JH, Raven J. Manual for Raven’s Progressive Matrices and Vocabulary Scales. H. K. Lewis & Co; London: 1993. [Google Scholar]
- Rivera-Batiz F. Quantitative literacy and the likelihood of employment among young adults in the United States. Journal of Human Resources. 1992;27:313–328. doi:10.2307/145737. [Google Scholar]
- Royer JM, Tronsky LN, Chan Y, Jackson SJ, Marchant H., III Math-fact retrieval as the cognitive mechanism underlying gender differences in math test performance. Contemporary Educational Psychology. 1999;24:181–266. doi: 10.1006/ceps.1999.1004. doi:10.1006/ceps.1999.1004. [DOI] [PubMed] [Google Scholar]
- SAS Institute . Statistical analysis system 7.5. Author; Cary, NC: 2004. [Google Scholar]
- Siegler RS. The perils of averaging data over strategies: An example from children’s addition. Journal of Experimental Psychology: General. 1987;116:250–264. doi:10.1037//0096-3445.116.3.250. [Google Scholar]
- Siegler RS. Emerging minds: The process of change in children’s thinking. Oxford University Press; New York: 1996. [Google Scholar]
- Siegler RS, Jenkins E. How children discover new strategies. Erlbaum; Hillsdale, NJ: 1989. [Google Scholar]
- Siegler RS, Shrager J. Strategy choice in addition and subtraction: How do children know what to do? In: Sophian C, editor. Origins of cognitive skills. Erlbaum; Hillsdale, NJ: 1984. pp. 229–293. [Google Scholar]
- Swanson HL, Sachse-Lee C. Mathematical problem solving and working memory in children with learning disabilities: Both executive and phonological processes are important. Journal of Experimental Child Psychology. 2001;79:294–321. doi: 10.1006/jecp.2000.2587. doi:10.1006/jecp.2000.2587. [DOI] [PubMed] [Google Scholar]
- Swanson JM, Schuck S, Mann M, Carlson C, Hartman K, Sergeant J, et al. [Retrieved September 17, 2008];Categorical and dimensional definitions and evaluations of symptoms of ADHD: The SNAP and the SWAN rating scales. 2008 from http://www.adhd.net/SNAP_SWAN.pdf. [PMC free article] [PubMed]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. PsychCorp, Harcourt Assessment, Inc.; San Antonio, TX: 1999. [Google Scholar]
- Wechsler D. Wechsler Individual Achievement Test –II-Abbreviated. The Psychological Corporation, Harcourt Brace & Co; San Antonio, TX: 2001. [Google Scholar]