3D structures by 2D vibrational spectroscopy

Conspectus

The development of experiments that can generate molecular movies of changing chemical structures is a major challenge for physical chemistry. But to realize this dream, we not only need to significantly improve existing approaches, but we also must invent new technologies .. Most of the known protein structures have been determined by X-ray diffraction and to lesser extent by NMR. Though powerful, X-ray diffraction presents limitations for acquiring time dependent structures. In the case of NMR, ultrafast equilibrium dynamics might be inferred from lineshapes, but the structures of conformations interconverting on such time scales are not realizable.

This Account highlights two dimensional infrared spectroscopy (2D IR), in particular the 2D vibrational echo, as an approach to time resolved structure determination. We outline the use of the 2D IR method to completely determine the structure of a protein of the integrin family in a time window of few picoseconds. As a transmembrane protein, this class of structures has proved particularly challenging for the established structural methodologies of x-ray crystallography and NMR.

We describe the challenges facing multidimensional spectroscopy and compare it with some other methods of structural biology. Then we succinctly discuss the basic principles of 2D IR methods as they relate to time domain and frequency domain experimental and theoretical properties required for protein structure determination. By means of the example of the transmembrane protein, we describe the essential aspects of combined carbon-13 oxygen-18 isotope labels to create vibrational resonance pairs that allow the determination of protein and peptide structures in motion. Finally, we propose a three dimensional structure of the αIIb transmembrane homodimer that includes optimum locations of all side chains and backbone atoms of the protein.

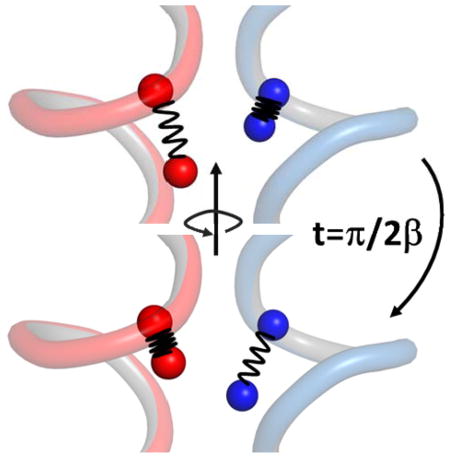
Delocalization among ¹³C=¹⁸O residues on different helices. The vibrational excitation is transferred between modes on different helices on the coherent energy transfer time π/2β.

Motivation and introduction

While we physical chemists like to conjure up scenarios of experiments that generate molecular movies we nevertheless would need to develop new technologies and significantly improve existing methods in order to realize this dream. The methods must make strong connections between structures at atomic resolution and the large nuclear motions of complex molecules during processes of biological importance. The changing structure might be that of a protein from an experimentally prepared point on a free energy surface towards an equilibrium state or it might involve the exchange between small groups of structures present in the equilibrium distribution in solutions or in living cells. To realize these objectives methods are required that determine not just coordinates [x,y,z] of each unit of the biomolecule but instead measure the values of [ x(t−t₀), y(t−t₀), z(t−t₀)] where the delay time t is progressing from an initial structure at t =t₀: this procedure requires a non-equilibrium dynamics experiment, but the method must also be able to determine the structures that are exchanging in the equilibrium distribution.

Most of the known protein structures have been determined by X-ray diffraction and to lesser extent by NMR Though powerful, X-ray diffraction faces challenges in acquiring time dependent structures. Structure distributions are seen in electron density maps, but distinguishing static disorder from rapidly interconverting structures even in conventional diffraction experiments with samples at equilibrium is tricky. Experiments with pulsed X-rays can expose small amplitude synchronized structural dynamics in a crystal lattice or solution phase (1) The free electron laser tunable femtosecond x-ray sources have a beam focus so small that tiny crystals may be studied and a pulse can record the diffraction data before the crystals are irreversibly damaged(2). These femtosecond x-ray pulses also have the potential to record a sequence of molecular images (3). In the case of NMR, while ultrafast equilibrium dynamics might be inferred from lineshapes, the structures of conformations interconverting on such time scales are not realizable.

While there many other techniques in the race to make molecular movies of condensed phase (4) and of gaseous reactions (5, 6) the method highlighted in the present article is two dimensional infrared spectroscopy (2D IR), in particular the 2D vibrational echo, a technique that has been used recently to solve a protein structure(7) and that continues to yield many very novel and exciting applications.(8–15) Certain molecular vibrational modes provide strong measures of local chemical bonding and the extra dimension of 2D IR exposes the coupling between these modes, leading to a three dimensional structure if the number of constraints is sufficient. The extra dimension of 2D IR permits much more robust interpretations than was possible with conventional infrared spectroscopy. The 2D IR also has intrinsically high time resolution that could range from subpicosecond to picoseconds dependent on the required spectral resolution. Therefore 2D IR contains the ingredients that are essential to obtaining structural constraints as a function of time along with an intrinsically short measurement time (16).

The multidimensional spectroscopies in the radiofrequency, microwave and IR ranges as well as x-ray and electron diffraction all provide structural information but their utility in making real molecular movies is limited by the microscopic time of forming the spectrum needed for the analysis. The time scale for 2D IR is set by the properties of the vibrational resonances which enable the measurements of nonequilibrium and equilibrium processes when the system is undergoing picosecond time scale dynamics. Quantitatively, the spectral distinction of two vibrational bands separated by 10 cm⁻¹ requires only 0.5 ps of measurement time. The frequency separations between vibrational modes of peptide links and peptide isotopomers are in the range of 1 to 50 cm⁻¹ which establishes the time limitations of nonequilibrium kinetic measurements by 2D IR. The extremely high structural resolution of NMR comes at the expense of the ability to identify structure evolution. For example to resolve NMR transitions separated by the large chemical shift of 2 MHz requires at least 3ms of measurement time. If the exchange between two conformations is fast compared with the energy difference of the two transitions they cannot be resolved and the result is a transition at an average frequency(17). Furthermore, the structural characterization of species in chemical exchange requires a time resolution faster than that of the exchange rate. The time resolution of 2D IR guarantees that even structures involved in rotations about single bonds could be isolated and assigned. The X-ray or electron diffraction time resolution would be even shorter because they might commonly involve a non-resonant scattering process that will track the probing laser pulse width.

There are many examples of conformational exchange in biological systems where it may be adequate as a first step to obtain knowledge of the time dependent coordinates of only a few critical atoms or chemical bonds that are parts of large macromolecules undergoing conformational changes. An improved understanding of the energy landscape around an equilibrium conformation is an expected result of such investigations. The 2D IR methods also can be applied to non-equilibrium (15, 18–21) experiments where correlated spatial and temporal resolution track the system moving towards equilibrium. This Account outlines how the 2D IR method is used to determine the structure of a trans membrane protein of the Integrin family, representing a class of structures that the established structural methodologies have found challenging. The constraints measured in the example given would have been obtained in the identical manner as described below if proteins with identifiable vibrational transitions were undergoing ca 1ps timescale equilibrium kinetics or non-equilibrium kinetics induced by a trigger pulse.

Peptide vibrations reveal protein structure

The infrared spectra of the protein backbone in the region currently accessible are dominated by the amide A, I, II and III vibrational modes.(22) Each peptide link has its own characteristic amide modes involving the motions of –C(α)-CO-NH-C(α) atoms. The strong amide-I, composed of mostly C=O stretching and a small fraction of C-N stretching and N-H deformation motions, is highly sensitive to the secondary structure of the backbone, partly from electrostatic interactions between amide units. This sensitivity extends also to the tertiary structure. The delocalized vibrational states (excitons) formed by these interactions are unique to the three dimensional structure of the protein(23, 24). When the distance between the peptide links becomes larger than the dimension of the amide group, such as for modes on different helices, the electrostatic effect is approximated by the dipole-dipole interaction. The grand challenge is to determine the structures from the properties of these excitations. We show here how this challenge can be met by 2D IR spectroscopy.

As a practical basis for structure determination a method of identifying and characterizing the various delocalized states must be found. Yet for proteins these vibrational transitions are generally not resolved by infrared spectroscopy. Small peptides sometimes have separate amide I transitions from each amide but when the complexity of the system increases, spectral overlap of different amide I modes is inevitable and the presence of line broadening impedes the resolution of the underlying delocalized transitions. Nevertheless, specific residues or groups of residues can be independently recognized and studied through site specific isotopic substitution of either carbon or carbon and oxygen of the backbone carbonyl by their heavier chemically equivalent isotopes. The amide I transitions having either ¹³C=¹⁶O or ¹³C=¹⁸O labels are downshifted from their unlabeled equivalents by ca. 35 cm⁻¹ and ca. 65 cm⁻¹ respectively. The spectra of these labeled modes of peptides (see for example ref(25)) has assisted the interpretation of 2D IR investigations of small peptides(26) and to probe localized regions in much larger proteins(27) but isotope labeling was only recently configured to obtain structures of proteins(7).

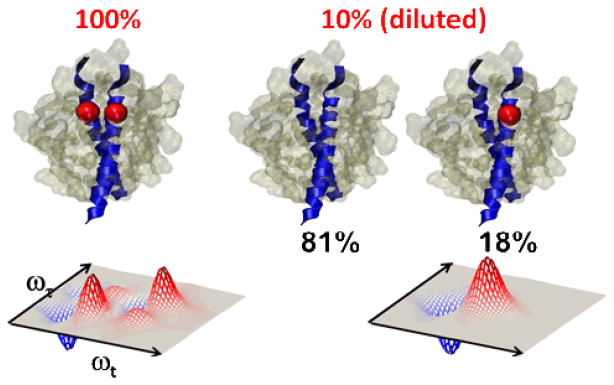
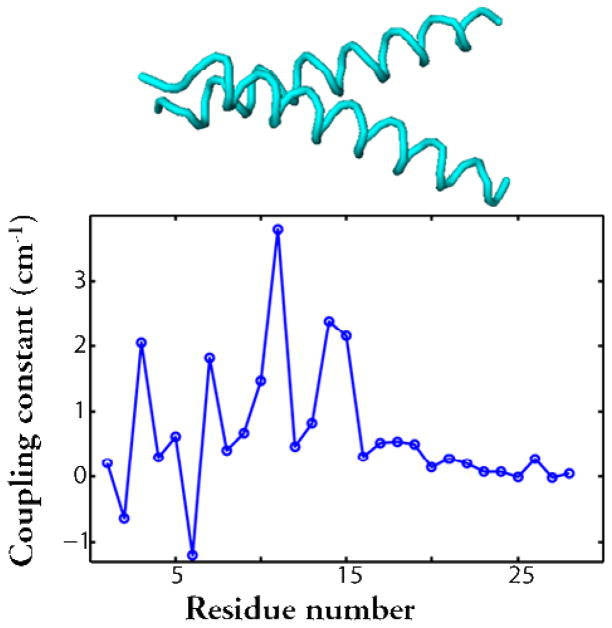
The successful strategy for structure determination involves multiple isotope substitution. The idea is that the interactions between a few isotopically selected residues, spectrally well separated from the transitions of the unlabeled modes, will be interpretable and hence will provide the required structural constraints for the labeled region. More than one isotopically selected residue per protein can be achieved using a variety of methods. Often a peptide synthesizer could be used to obtain the appropriate sequence with two of its peptide links substituted with ¹³C=¹⁸O. The linear and nonlinear infrared spectra will then indicate whether there is coupling between the two modes. While there are $\frac{N(N-1)}{2}$ possible pairs to choose from in a given sequence of N amino acids most of these possibilities can be eliminated by reasonable guesses based on other types of measurement or simulations. Alternatively it has been useful to employ natural assembly to bring together isotope labeled regions, such as in our work on amyloid fibrils(28). A specific residue of a strand was isotope edited such that on aggregation to form fibrils these isotopomers were distributed throughout the structure in a known composition so that their specific inter-residue interactions could be used to establish parameters of a three dimensional structure. The example that is discussed in detail here, concerns a transmembrane helix dimer where isotopomers of individual helices were assembled into dimers as cartooned in Figure 1. These operations allow key inter-residue couplings to be obtained that assist in the determination of the tertiary structure as exemplified by the simulations in Figure 2 for Glycophorin A.

Figure 1. The isotope dilution experiment.

(left) 100% labeled samples have one residue of the sequence fully labeled with ¹³C=¹⁸O. (right) Dilution results in 10% of peptides having one residue isotopically substituted. Nearby ¹³C=¹⁸O labels form excitons.

Figure 2.

The Glycophorin A dimer presents significant coupling only in the crossing region. The upper portion sketches the helix dimer with the spacing of the residues matching the scale on the bottom portion. The lower portion indicates the residue dependence of the tertiary coupling constants obtained by methods described in the text.

Stretching infrared spectroscopy

The 2D IR spectra of the isotopically substituted peptides are understood as measuring the correlations between two coherences created by coupling the amide-I modes to three infrared pulses.(29–31) The signal from the spatial component of the polarization corresponding to the photon echo, was recorded as a function of the pulse intervals. The coherences between the zero and one vibrational quantum states that are excitable within the pulse bandwidth undergo free evolution for times fixed experimentally at τ by a second pulse after which a waiting period (T) allows for the intermediate states to evolve. A third pulse at T+τ drives the system to another group of one and two quantum coherences that span the same frequency range as during τ. It is the polarization from this second set of coherences that generates the echo field during the detection interval (t). Since the phases of the pulses are locked, the free evolution in τ influences the signal at t for sufficiently small values of T, with the result that the 2D IR spectrum of ω_τ versus ω_t does not have a circular contour as would be expected for uncorrelated frequencies but instead has a more elliptical shape that is exclusively determined by the correlations and couplings between the vibrational modes.

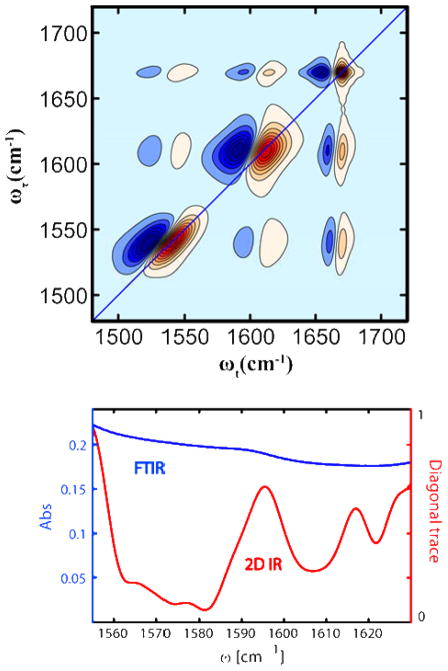
2D-IR spectra always present two types of features, diagonal and cross peaks that are illustrated in Figure 3 (upper panel) for a system of three coupled oscillators with different dynamics and correlations. The diagonal positive peaks represent probe molecules forced to undergo pathways in which the coherence produced during τ and t involves the same one quantum transitions. Their negative counterparts, downshifted by the diagonal anharmonicity, involve coherences in t between two quanta and one quantum states. As for the cross peaks, they correspond to pathways that involve coherences of different oscillators in τ and t. The coupling between these two modes determines the shift of the combination band from the sum of the two frequencies. The vibrational frequency distribution is the same for each of the modes depicted in Figure 3 but the correlation time of the frequency fluctuations is much longer than T in the lowest frequency mode and much shorter for the high frequency mode as indicated by the amount of tilting of the transitions towards the vertical as time advances.

Figure 3.

Typical 2D IR spectral properties:

Upper panel: the 2D IR for three coupled transitions. The red shaded contours are positive, the blue are negative.

Lower panel: trace of linear and 2D IR spectra in the region of the probe.

For resonance pairs of ¹³C=¹⁸O labeled modes with equal unperturbed site energies (ω₀) the transitions to the mixed sates should appear on the diagonal at ω_±0 = ω₀ ± β and if they are different (ω_i, ω_j), at $\left({\omega }_i+{\omega }_j\right)/2\pm 1/2\sqrt{{\left({\omega }_i-{\omega }_j\right)}^2+4{\mid \beta \mid }^2}$. (here the coupling β is given in angular frequency units whereas in the experiments and discussion we use cm⁻¹,ω / 2πc) This result has the well-known time domain interpretation that if an amide on one helix is initially vibrationally excited with the other being in its ground state, then the growing probability that the excitation will be found on the selected ¹³C=¹⁸O mode on the other helix is given by the Rabi formula: $(4{\mid \beta \mid }^2/{[{\left({\omega }_i-{\omega }_j\right)}^2+4{\mid \beta \mid }^2]}^{1/2}){\mathit{sin}}^2{[{\left({\omega }_i-{\omega }_j\right)}^2+4{\mid \beta \mid }^2]}^{1/2}t/2$. However in reality there is severe damping of this motion appearing as line broadening in the frequency domain, which we needed to incorporate in order to obtain reliable values of the peak separations needed for the structure determination.

Quantitative summary of 2D IR method

Recent literature such as ref.(16), provides analytic forms for the 2D IR signals that need not be repeated here. In our experiment we measure a field E_z which is generated by the sample becoming polarized when the amide-I groups are driven into vibrationally coherent states by three pulses (with labels 1, 2 and 3). The polarization P_z is obtained from the reduced density matrix expanded to third order, ρ⁽³⁾:

$${\mathit{P}}_{\mathit{z}}=[Tr\{{\rho }^{(3)}(\tau ,T,t){\mu }_z\}]$$ (1)

The measured field electric field E_z is in quadrature with P_z. The pulses arrive at times 0, τ and τ +T and the signal field is measured at time τ +T +t. In our experiments we chose to observe the signal field in the so-called echo direction k_s = −k₁ +k₂ +k₃ over the range of frequencies ω₁ − ω₂ − ω₃. The pulse spectra were much wider than the bandwidths of the relevant transitions so that a set of real impulse response functions R_total or their Fourier transforms R(ω_τ,ω_t;T) provide a complete description of the signal, where:

$$R_{\mathit{total}}=\langle {\mu }_z(t+T+\tau )[{\mu }_z(T+\tau ),[{\mu }_z(\tau ),[{\mu }_z(0),{\rho }_{eq}]]]\rangle$$ (2)

with all time intervals greater than or equal to zero. We could vary the polarization of the pulses to be ZZXX instead of ZZZZ if needed. The angle brackets imply a trace over all the variables but the system bath interaction is classical with Gaussian frequency fluctuations(32). The choices of amide-I mode v=0, 1 and 2 matrix elements of the dipole operators in each of the terms of 1.2 form the paths of excitation. The number of these paths needed to fit the experimental data was greatly reduced by the rotating wave approximation and exclusion of certain time orderings for practical reasons.

Vibrational transitions of peptide links are diffuse

The vibrational transitions of amide-I modes are modified both by spontaneous relaxation and by the distribution and dynamics of frequencies arising from the structural heterogeneity. The amide v=1 mode vibrational relaxation time is in the range 0.5–1.0 ps and there is no systematic variation with amino acid residue. The spontaneous relaxation alone would imply an amide-I transition width of ca 7 cm⁻¹ whereas the amide-I bandwidths in proteins are generally in the range of 15 cm⁻¹ implying, by deconvolution, that the mean square deviation of the Gaussian frequency distribution (i.e. half the width at the 1/e height) needs to be at least ca. 5 cm⁻¹. The dynamics of this heterogeneous component in proteins ranges over many orders in time, from the millisecond reorganizations of the secondary structures to the femtosecond/picosecond effects of local fluctuating charges on side chains and water molecules. Therefore there is almost always a component of the linewidth that is static on the picosecond timescales and often also a part where the vibrational frequency correlation relaxes quickly enough to be captured by 2D IR. However, in the case of membrane or micelle bound helical proteins the vibrational frequency correlation times are much slower than the 2D IR measurement. There may be only few charged side chains and no water molecules close to the labeled peptide link in middle of a bilayer whose nearest neighbor interactions are weak and not sensed by the amide vibration. Thus the main effect of the environment is to bring about frequency shifts that are different for each micelle and thus to create a quasi-static distribution of frequencies on the 2D IR time scale. This condition appeared to describe the αIIb3 homodimer in micelles that was examined in this work.

Isotope dilution removes the coupling and provides the baseline

In a sample where each helix has a critical ¹³C=¹⁸O substitution dimerization will generate a resonance pair spectrum from which coupling parameters can be obtained. An appropriately diluted sample is one where most of the helices are not labeled and thus they form dimers that have mainly either zero or one ¹³C=¹⁸O mode. Comparison of the spectra where the coupling is present and absent allow accurate coupling parameters to be obtained from the difference spectrum. These principles are widely applicable and Figure 2 shows computations of the tertiary coupling constants for Glycophorin-A, a transmembrane helix dimer whose 2D IR spectra were previously found to exhibit tertiary coupling of amide-I modes in the helix crossing region.(33) The variations of coupling with residue in the calculations of Figure 2 strongly suggest how 2D-IR isotope dilution experiments might be configured. Transmembrane helix dimers in which residues of the sequence are individually labeled with a ¹³C=¹⁸O substitution(7) exemplify the foregoing discussion. Delocalization of the vibrational excitation between the transmembrane helix dimer components takes place when the dipoles of samples prepared with 100% ¹³C=¹⁸O substitutions are nearby. However the excitation is localized in the 10% ¹³C=¹⁸O substituted samples, the dilute case. The effect of dilution is illustrated for a glycine residue of αIIβ3 in Figure 4 which shows a significant reduction in bandwidth as the isotope is diluted. Those residues that have the amide units in close tertiary contact exhibit symmetric and asymmetric transitions caused by a through space coupling that appears as a splitting or broadening of the diagonal 2D-IR peaks.

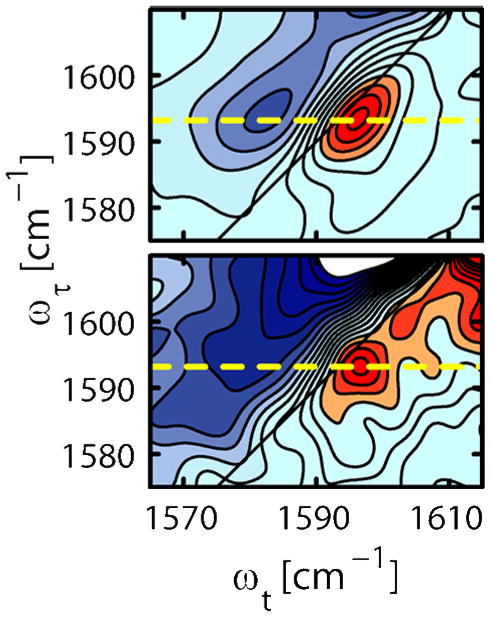
Figure 4.

2D-IR of the TM domain of αIIb dimer: The dilution (lower) of the ¹³C=¹⁸O labeled peptide (G12) narrows the transition significantly from the 100% sample (upper). For details see reference (7).

While in principle these structure related coupling patterns are also contained in the linear FTIR spectra, the 2D IR spectra have distinct advantages, one of which is the diminished contribution from the background. This amazing property (see Figure 3, lower part) derives from the 2D IR signal being proportional to the fourth power of the transition dipole instead of the more familiar squared dependence of linear spectroscopy. Since the extinction coefficient of the background is so low, the signal is dominated by the dilute solution of a high extinction label even at 10% dilution.

The waiting time dependence of the spectral shapes allowed determination of the optimum dynamical model for the frequency correlation. This was an essential input to the numerical simulations of the lineshapes needed for structure determination. The dependence confirmed that the contribution of a distribution of frequencies that is static on the experimental time scale dominates the shape indicating that the time dependence of the frequency correlation function just consists of an immeasurably fast drop to a constant value. The contribution of each protein complex to the signal at each point in the 2D IR spectrum is easily found as a set of two dimensional Lorenzian response functions (7) of the eigen modes one of which is:

$$R_1({\omega }_{\tau },{\omega }_t)=Re\langle \frac{e^{-T/T_1}{\left|{\overrightarrow{\mu }}_{0+}\right|}^4}{\left[i({\omega }_{0+}-{\omega }_{\tau })+{\gamma }_{+0}\right]\left[i({\omega }_{+0}-{\omega }_t)+{\gamma }_{+0}\right]}\rangle$$ (3)

The total signal is obtained from contributions of all resonance pairs in the inhomogeneous distribution through the inclusion of diagonal disorder of the eigenvalues represented by the brackets. We assumed the frequency distribution to be Gaussian. The angular dependence of the transition dipole moment magnitudes to the symmetric and asymmetric resonance pair states has the form:

$$\frac{{\left|{\mu }_{0+}\right|}^2}{{\left|{\mu }_{0-}\right|}^2}=\frac{1+cos\phi sin\theta cos{\alpha }_{ij}}{1-cos\phi sin\theta cos{\alpha }_{ij}}$$ (4)

Here α_ij is the angle between the transition dipoles, tan θ =2|β|/ω₁₂, β = |β|e^iϕ with ω₁₂ the site frequency gap. Equation 4 represents the ratio of peak amplitudes from symmetric and asymmetric transitions in the FTIR spectra and its square gives the ratio of the diagonal peaks in the 2D-IR spectra. The polarization conditions (e.g. zzxx) establish additional constraints and can significantly improve the contrast of exciton transitions.

The dipole-dipole coupling is very sensitive to the direction of the ¹³C=¹⁸O amide transition dipole in the frame of the planar peptide link. While this vector is known for an isolated amide mode, we needed to know it for an isolated ¹³C=¹⁸O mode (n) in a sea of ¹²C=¹⁶O modes (m) from other peptide links. Since the isotope shift of 65 cm-1 is large compared with coupling between modes, the effect of the unlabeled ¹²C=¹⁶O residues of a typical helix estimated from a perturbation expansion yielded:

$$cos\theta =1-\frac{1}{65}\sum _m{\beta }_{nm}cos{\theta }_{nm}$$ (5)

Where β_nm is the dipole-dipole interaction and θ_nm the angle between the transition dipoles of labeled and unlabeled modes. For a long α-helix, the probe transition dipole rotates by less than 3°. On this basis we assumed that the transition dipole vector fixed in the amide group is insensitive to isotope replacement of the carbon or oxygen. Although the dielectric response of the surrounding and intervening media is not fully considered in any of our calculations some of the local field effect is incorporated by our use of the transition dipole from the integrated absorption coefficient.

Use of structural constraints to derive the protein structure

The next step was to relate the spectral features arising from coupling in the 2D IR spectra or the vibrational constraints derived from them, to sets of specific distances and angles characteristic of three dimensional structures. In an early attempt to assess structural constraints from infrared spectra and vibrational frequency dynamics the distributions of vibrational frequencies were computed from instantaneous force fields of peptides(34). More recently, maps that allow vibrational frequencies to be correlated with the classical electric fields obtained from MD simulations have been developed to predict infrared spectra of proteins(35). In the present work we related the experimental spectra to simulated ones by an iterative procedure in which molecular dynamics simulations with different starting structures and 2D-IR spectral fits were used in a closed loop to obtain find optimum structure and dynamics consistent with experiment(36). This approach permitted the inclusion of the time evolution of the coupling constants given by the time evolution of structures. In the process of this work we designed a module that uses vibrational dipole-dipole couplings as constraints in simulated annealing runs for the software Xplor-NIH(37, 38), a standard tool used in structural determination with NMR experiments.

The transmembrane (TM) homodimer from a chain of the integrin aIIbb3 forms in micelles and bacterial membranes(39). The processing of multiple residue labels located in the interaction sites of these TM helices required significant synthetic effort through a collaboration with W.F DeGrado and Ivan Korendovych(7). Our 2D IR experiments on the TM dimer clearly showed the variation of the nonlinear spectra with the position of the residue in the sequence. The shapes of the ¹³C=¹⁸O transitions also alternate with residue number clearly showing the variations of exciton interactions with probed residue. It was very evident from the raw data that these couplings exhibit a repeat pattern of three to four residues characteristic of alpha helices.

Even in the 10% samples there was an alternation in the signal width indicating a sequence location sensitivity of the inhomogeneous width of the spectral transitions. Comparable variations have been reported for individual labels in some other peptides.(40) However the differences between 2D-IR spectra at different isotope dilutions was essential to obtaining the electrostatic interaction of the transition charge distributions associated with the two amide I mode excitations. A model with two local ¹³C=¹⁸O sites on each helix coupling through space to form linear combinations of the local ones, was used. The data for G12 illustrates the typical 2D-IR spectra at different isotope dilutions (Figure 4). The 2D-IR spectral shapes were the same at T = 300 and 1500 fs consistent with the Bloch frequency correlation function required for the computation of the spectra which, along with the coupling between the amide oscillators was fed into computations of the protein structure(7).

In TM structures it can be expected that the peptide links in different helices of a dimer are on average separated by ~6 Å: the shortest separation for the very stable dimer glycophorin A dimer (34) is 4 Å. Hence, the 100% and 10% spectra should differ only by the electrostatic interaction of the transition charge distributions of the two amide I modes. This interaction causes the two local ¹³C=¹⁸O sites to couple and form superpositions of the local ones. The dynamics of these delocalized states are determined by their population and pure dephasing relaxation. The signals are represented by Lorentzian functions averaged over fixed distributions. The absence of ps dynamics strongly suggested there are no mobile associated water molecules nearby to any residue exhibiting properties comparable to those found for proton channels (27, 41) or amyloid fibrils (28). Our prescriptions of the dynamics for predicting the 2D IR spectra are consistent with vibrational frequency domain studies of other transmembrane amide-I transitions (42).

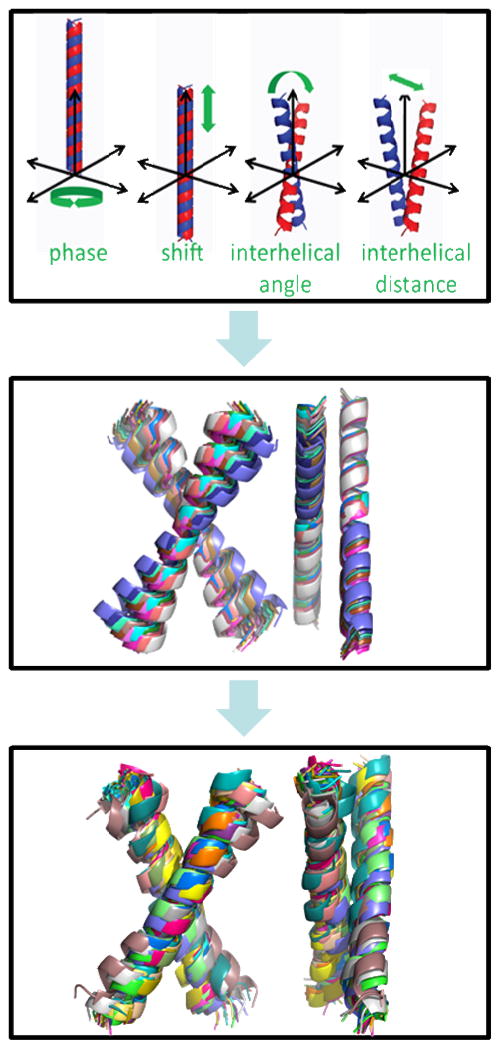
A group of structures consistent with the experiments was first found by sampling the whole space of pairs of helices to identify those most consistent with the distribution of 2D-IR coupling constants. We assumed that the helices were interchangeable by a two fold axis. As indicated in our paper(7) the first tests revealed 48 structures that were consistent with the experiment within a 75% confidence interval.(Figure 5 top and middle) The structure with an interhelical distance of 8.5Å and crossing angle of −60° showed the best agreement with the experiments.

Figure 5. The process of structure determination.

A group of ideal α-helical symmetric dimer structures with coupling consistent with experiment is the starting point for simulated annealing runs with XPlor-NIH (37, 38) with a module that incorporates vibrational dipole-dipole couplings as constraints.

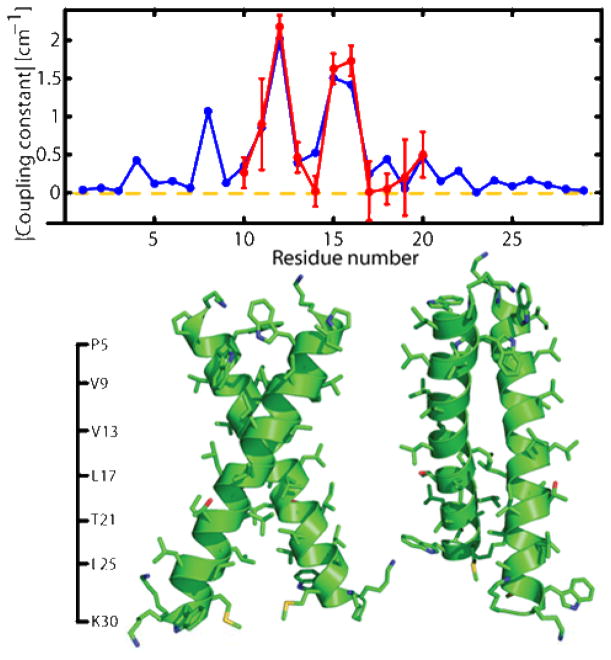
The model including side chains was further refined by a “constrained simulated anneal” with Xplor-NIH(37, 38). All 48 structures were used as starting points for 100 structures. As described in our paper(7), every structure was first minimized by 500 steps to remove unacceptable contacts, bathed at a high temperature (3000 K) for 1000 steps, followed by cooling to a low temperature (10 K) for another 1000 steps and was subjected to standard minimization procedures for the final 2000 steps. This simulated anneal including the dipole-dipole interaction constraints minimizes the energy and accommodates the side chains and the backbone consistent with 20 parallel right-handed helix dimers with crossing angles of −58° +/− 9° and interhelical distances of 7.7 +/− 0.5Å.(Figure 9, bottom) The residues G12, G15, and G16 form the tertiary contact and present the highest coupling magnitudes. The transition dipoles of residues G15, L19, and V11 were found to have negative coupling constants. The energy-minimized structure is shown in Figure 6 where the coupling constant magnitudes for one of the structures are compared with an experimental result.

Figure 6.

Comparison of calculated and observed couplings: (bottom) Lowest energy structure from simulated annealing runs with XPlor-NIH and (top) comparison between calculated and experimental coupling constants.

The peptide sequence G-XXX-G motifs are believed to drive dimerization of helices in cell membranes and lipid micelles (14). The computed structural model for the αIIb homodimer differs from the original canonical motif seen in glycophorin, which has a somewhat smaller crossing angle, interhelical distance, and rotation of each helix about its axis (helical phase). Instead, the computed structure fits to a related right-handed motif, cluster #10 of (43), which has an average crossing angle of −60° +/− 15° and interhelical distances of 8.6 +/− 1.0 Å. This difference can be caused by αIIb having a GxxGG sequence with a third Gly residue which is absent in GPA. This interaction is clearly seen in the spectral widths and couplings at positions 15 and 16 in Figure 4 and data from reference (7). These are the first ‘structural biology’ results from 2D IR.

Some of the significant uncertainties in the coordinates have been addressed previously(7) and we hope that the accuracy will be improved with developments in 2D IR and with increases in the number and types of constraints. We also require an improved understanding of systematic errors such as those introduced from polarizability effects on the inter-mode coupling across the helix interface. These are important subjects for future 2D IR research.

Concerning the time resolution, the group of tertiary constraints measured in the example given here of aIIb3 would have been obtained in the identical manner for a transient population undergoing either equilibrium or non-equilibrium kinetics where the latter would be induced by a trigger pulse on the few ps time scale or longer. In addition, many other constraints could have been used for further refinement. We included only two-fold symmetric dimers having the same residue replaced in each helix. But mixtures of helices with the two isotope edited residues being different would provide independent constraints. Other constraints could be obtained from mixtures of ¹³C=¹⁶O and ¹³C=¹⁸O probes and our previous studies of these interactions(33) prove that it is not necessary to have resonance pairs in order to deduce robust constraints.

Summary and Prospects

Although this Account has focused on the method of 2D IR and how it is applied to structure determination, the ultimate aim of this research is to contribute to elucidating structure –function relations for trans membrane proteins. The approach we describe can be widely applied and be immediately useful in structures known to be built from α-helices which is the case for hundreds of transmembrane proteins. The next challenge for 2D IR is to establish structural parameters for helix oligomers that have highly specific functions or act as channels. The example of a helix homo dimer has simplifying features, but with the addition of secondary structure input from other techniques, PDB mapping and theory, as is the custom with other methods in structural biology, 2D IR is predicted to be a successful approach to obtaining snapshot structures of other less symmetric transmembrane proteins. It can be imagined that the equilibrium structural dynamics revealed by 2D IR will contribute significantly to finding the mechanisms of action of integral membrane proteins.

Biographies

Amanda Remorino earned a B. SC. in chemistry from The School of Science (Facultad de Ciencias Exactas y Naturales) University of Buenos Aires, Buenos Aires, Argentina in 2004. She graduated Ph.D. from Penn in December 2011 with a thesis entitled “Determination of protein structures by two dimensional vibrational spectroscopy isotope dilution experiments.”

Robin Hochstrasser received his B.Sc. from Heriot-Watt University and his Ph.D. from the University of Edinburgh in 1955. In 1958 he moved to the University of British Columbia and then to the University of Pennsylvania in 1963 where he is the Donner Professor of Physical Sciences and Director of the Ultrafast Laser Research Resource (NIH-BTRC).