Chemical Recognition and Binding Kinetics in a Functionalized Tunnel Junction

Abstract

4(5)-(2-mercaptoethyl)-1H-imidazole-2-carboxamide is a molecule that has multiple hydrogen bonding sites and a short flexible linker. When tethered to a pair of electrodes, it traps target molecules in a tunnel junction. Surprisingly large recognition-tunneling signals are generated for all naturally occurring DNA bases A, C, G,T, and 5-methyl-Cytosine. Tunnel current spikes are stochastic and broadly distributed, but characteristic enough so that individual bases can be identified as a tunneling probe is scanned over DNA oligomers. Each base yields a recognizable burst of signal, the duration of which is controlled entirely by the probe speed, down to speeds of 1 nm/s, implying a maximum off-rate of 3 s^-1 for the recognition complex. The same measurements yield a lower bound on the on-rate of ~1 M^-1s^-1. Despite the stochastic nature of the signals, an optimized multi-parameter fit allows base-calling from a single signal peak with an accuracy that can exceed 80% when a single type of nucleotide is present in the junction, meaning that recognition-tunneling is capable of true single-molecule analysis. The accuracy increases to 95% when multiple spikes in a signal cluster are analyzed.

1. Introduction

Further reducing the cost of present “next generation” DNA sequencing techniques will probably require the replacement of expensive optical equipment and biochemical methods (with associated reagent costs).^{1, 2} Electron tunneling across a DNA molecule has been proposed³ and demonstrated^{4, 5} as a candidate base reading system. It is a possible alternative to ion-current sensing where individual nucleotides are readily distinguished by the size induced current blockade in a protein nanopore⁶, but reading single bases embedded within a polymeric DNA molecule is still challenging⁷. Another approach, yet to be demonstrated in practice, is electronic modulation of the conductance of a graphene nano-ribbon containing a nanopore. This might generate microamp signals, leading to very rapid sequencing.⁸

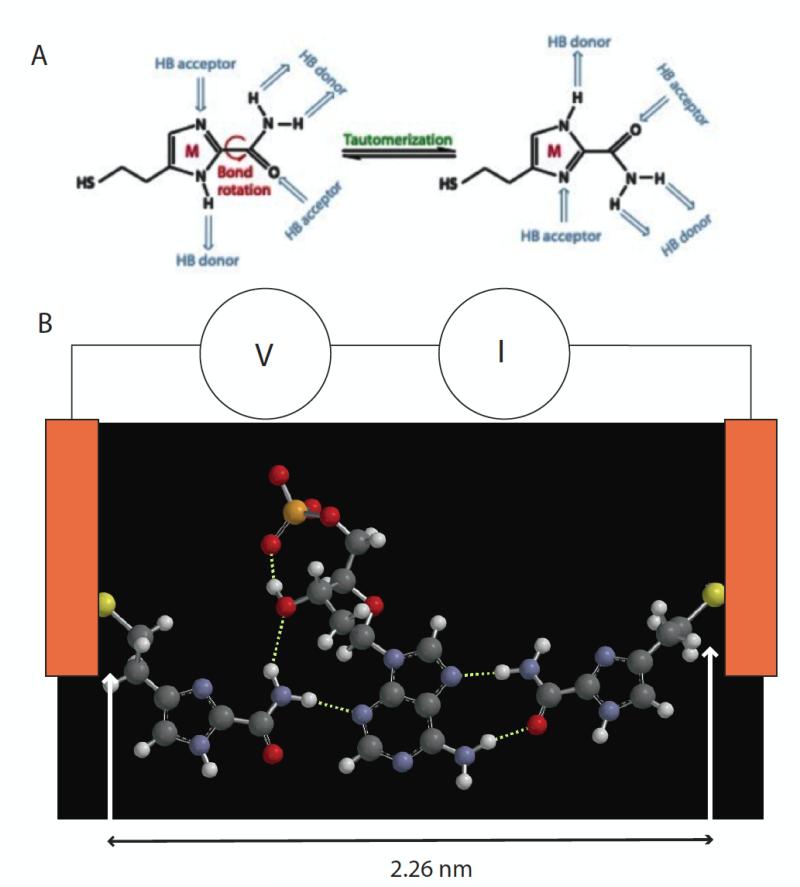
Tunneling readout with bare metal electrodes requires a small gap (on the order of 0.8 nm) and the distribution of signals is very large.⁴ We have proposed an alternative we call recognition-tunneling^{2, 9}. In recognition-tunneling, electrodes are functionalized with adaptor molecules, chemically-bonded to the metal electrodes at one end, and non-covalently interacting with target molecules at the other end. This permits much larger tunneling gaps (2.5 nm for the molecule described here¹⁰) and reduces the signal distrbution considerably¹¹. Using 4-mercaptobenzamide as the adaptor molecule, we were able to identify single bases embedded within a DNA oligomer, thus demonstrating the ability of recognition-tunneling to resolve single bases.¹² 4-mercaptobenzamide produced no signals from thymine, so we developed a new adaptor molecule, 4(5)-(2-mercaptoethyl)-1H-imidazole-2-carboxamide (hereafter “M”) containing multiple hydrogen bonding sites presented in different conformations (Figure 1A). The synthesis and characterization of this molecule is described elsewhere.¹³ We show here that signals are generated by all four bases as well as 5-methyl cytosine using this new molecule. We also introduce a new approach to analyzing stochastic tunneling signals.

Figure 1.

(A) 4(5)-(2-mercaptoethyl)-1H-imidazole-2-carboxamide adaptor molecules (referred to as “M” in the text) showing how tautomerization presents different arrangements of hydrogen bond donors and acceptors. (B) This adaptor molecule (left and right side) trapping dAMP (middle) via a network of hydrogen bonds (dotted white lines). The sulfur atoms are bonded to gold electrodes, and current, I, is read as a bias, V, is applied across the tunnel gap. Individual 2D chemical structures were exported to Spartan’10 (Wavefunctions Inc.) to generate corresponding 3D structures that were energy minimized using the built-in MMFF molecular mechanics prior to the DFT calculation. All the structures were first calculated using B3LYP with /6-31G* in vacuum (structures for all four nucleotides are shown in Fig. S1). The gap size is set by the tunnel conductance and either maintained under servo control or left uncontrolled (but monitored via the baseline current).

An energy minimized structure for a junction containing a dAMP target trapped by two adaptor molecules is shown in Figure 1B. When the Au-S bond distances of about 0.23 nm are added to the S-S distance of 2.26 nm, the resulting structure fits quite well into the ~2.5 nm gap size used in the current work¹⁰. That said, it is important to emphasize that water plays an explicit role in bonding, so “vacuum” models like these serve as little more than a qualitative guide. Energy minimized structures for the other bases are given in Fig. S1 (supporting online information).

Theoretical simulations^{14, 15} of currents in recognition-tunneling have been carried out in “vacuum” at zero degrees Kelvin and they predict fixed current levels that signal the identity of a DNA base trapped in the junction in some fixed geometry. In reality, thermal fluctuations and the active intervention of water molecules generate a stochastic signal train.^{9, 11, 12, 14} In addition, we will show here that signals are probably further complicated by nucleotide-nucleotide interactions when free nucleotide targets are used. To a first approximation, the tunneling signals are “random noise” and we showed (in the supplement to the paper by Huang et al.¹²) how random thermal motion, as sampled by an exponential matrix element, can generate signals that look similar to those we observe. Of course, truly random noise would be useless for sequencing and we will show here how the signals are indeed not random. We will also show how diverse signals can be classified in terms of the chemical identity of the analyte that produced the signal. In this paper, we begin by analyzing aspects of the signals in a subset of the data selected to show features that clearly reflect the identity of the analyte. We identify signal characteristics that could be used to call bases and show how some bases are readily identified in the presence of signals from others, at least in the case of DNA oligomers. This analysis allows us to interpret trains of signal that are generated by sweeping a functionalized STM probe over a functionalized surface in the presence of some simple DNA oligomers. By measuring the duration of the burst of signal that is produced as the probe sweeps over each base, we are able to set some limits on the on- and off-rates for binding of DNA bases in the recognition-tunneling junction.

Finally we turn to the remainder of the data – signals that are clearly generated by binding of nucleotides, but that do not obviously signal a chemical identity. By keeping all of the data collected in each run, and parameterizing each pulse (pulse height, pulse shape, time interval to neighboring pulses) we find surfaces in a hyperspace (whose coordinates are vectors composed of the parameters) that give optimum separation of the pulses according to the identity of the nucleotide that generated them. We are able to achieve better than 80% accuracy in assigning each peak to a base. Thus each peak generally carries useful chemical information, rendering recognition-tunneling a truly single molecule technique. Application of this method requires that the analytes be spatially separated (i.e., by sequential passage through a nanopore) as mixtures of nucleotides that are free to interact in the tunnel junction produce new signals that can be different from those produced by isolated nucleotides or bases separated in a polymer chain.

2.0 Results and Discussion

We begin with a discussion of the controls that establish the baseline above which nucleotide and DNA signals are measured, looking particularly at the differences between measurements made with a stationary and moving probe. Our goal is to simulate the sample motion that would occur were these measurements to be made in a nanopore through which the DNA was translocating. For this reason, we have extended our instrumentation to allow collection of signals from nucleotides as the probe is scanned over them. The second part of the paper analyzes data taken as the probe is scanned over DNA oligomers, showing clear sequential resolution of single bases. The time-dependence of the signal bursts can be used to set limits on on- and off-rates for the formation of the recognition complex.

In the final section of the paper, we turn to a multidimensional analysis of the signal peaks, an analysis that allows accurate base-calling on even a single signal peak, rendering recognition-tunneling a truly single molecule analytical technique (as opposed to a tool for statistical identification by means of repeated reads). We have subjected data taken by slightly different methods to this analysis to test how transferrable the analysis is. Specifically, we have taken data with a stationary probe, and with a moving probe not under servo control, in addition to the data taken with a moving probe under servo control. This latter set of experiments was made in order to examine the effect of having the gap under servo control in the standard STM measurement – a large signal leads to some probe displacement, altering the gap in a way that would not occur in a fixed-gap nanopore device. By comparing the effect of analyzing each data set with an individually-optimized assignment algorithm vs. using just one set of parameters for all the different experimental conditions, we gain some insight into the robustness of the method.

2.1 Control Experiments

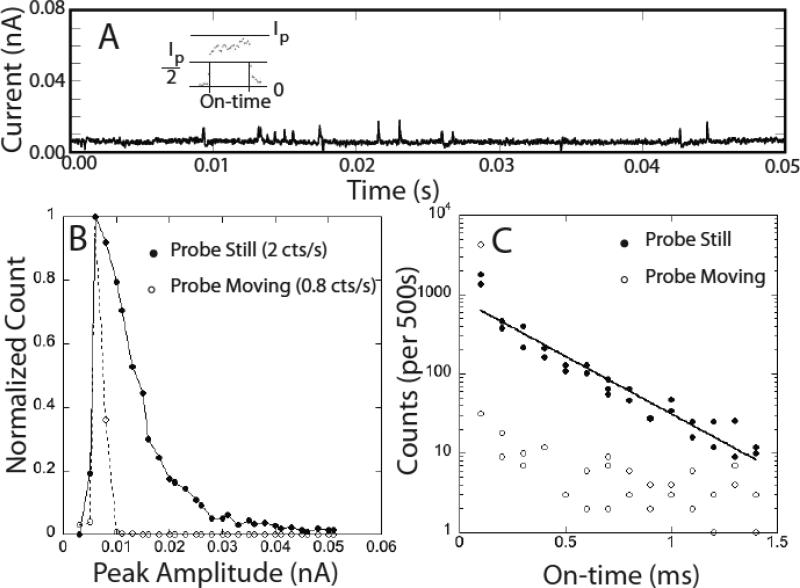
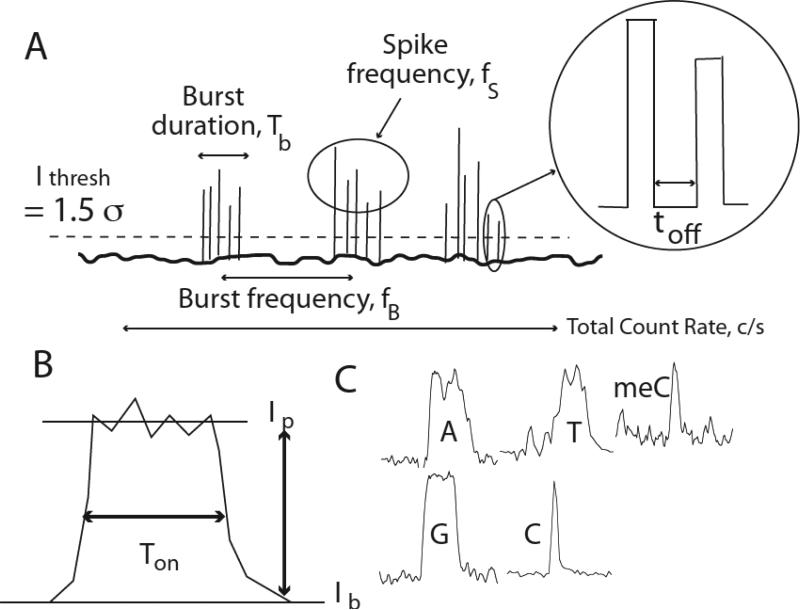
Gold probes and Au(111) substrates were functionalized with M and characterized as described in the experimental methods section. Our yield of functionalized probes is now quite high¹⁶ and is characterized by comparing the signals generated in a tunnel junction to the control signals described here. Since junctions lacking the adaptor molecule on one electrode give a characteristic signal that is different from that obtained when both electrodes are functionalized, we are able to test whether or not we have successfully functionalized probes. Figure 2A shows small signals generated when the tunnel junction is set to a conductance of 12 pS (0.5V, 6pA) in a 1mM phosphate buffered solution (pH 7.0) containing no nucleotides. In contrast to the mercaptobenzamide adaptor molecules¹² the signal in the absence of nucleotides is not clean. This background disappears as the tunnel current is lowered (it is essentially gone at 4 pA) but so does the signal generated by DNA bases. Interestingly, the distribution of pulse heights (Fig. 2B) depends on whether the probe is stationary or moving. The open circles in the figure are taken with a probe that is scanned at 2 nm/s and almost all of the data points lie below 0.01 nA in peak amplitude (and occur with half the frequency of the signals generated by the stationary probe). These peaks are also short-lived on the whole. Fig. 2C shows the distribution of peak widths (“on-time”) and most of the data taken with a scanning probe lie at the limit of the time resolution of the current-to-voltage converter (~0.1 ms). The stationary probe gives a broader distribution of peak heights and an exponential distribution of on-times (solid line in Fig. 2C). The absolute count-rate (Table 1) for this water background is comparable to the signal rates obtained with nucleotides, so an algorithm was developed to remove it (see below).

Figure 2.

Signals generated by 1 mM phosphate buffer (pH = 7). (A) typical trace showing peaks taken with the probe scanning at 2nm/s (probe bias = 0.5V, current set point = 6 pA). The inset shows how the on-time is defined by the duration of a peak at half height. (B) Peak height distribution of pulses for (open circles) the probe scanning at 2 nm/s and (closed circles) a stationary probe. The distributions are normalized to 1 at the highest points and the total count rates are listed on the figure. (C) Distributions of on-times for the spikes.

Table 1.

Overall read frequencies with the probe scanning at 2 nm/s. The Table lists the signal frequencies (Avg. peaks/s) defined as the total number of counts in an experimental run) divided by the duration of the run (usually ~10s ).

	dAMP	dCMP	dGMP	dTMP	dmeCMP	Control
Avg. peaks/s	41.4	20.6	1.1*	11.4	827.5	5.75
Nucleotide signal fraction	0.86	0.72	1**	0.50	0.99	0
Peaks/s post-Filtering	5.98	2.23	0.97	4.45	27.77	0.015
Fraction passed by filter	0.14	0.11	0.88	0.39	0.03	0.003

^*dGMP produces a lower count than the control alone, implying that the water signals are blocked by the presence of this nucleotide. The second row lists the fraction of signals due to nucleotides if the water signal were constant

^**(clearly not true for dGMP). The last two rows list the peak frequency and fraction of peaks passed by the “squareness” filter.

We do not understand why moving the probe makes such a difference to this background signal. One possibility is that the stationary probe concentrates low-level contaminants over time by dieletrophoresis.

The effects of probe or surface functionalization on signals obtained in the presence of nucleotides are shown in Figure S2. When neither probe nor substrate are functionalized with M, 10 βM dAMP in 1 mM phosphate buffer produces only small current spikes (Figs. S2A, B). A similar distribution is produced when only the substrate is functionalized (Figs S2C,D). When the substrate is functionalized with M and the probe with a thiophenol molecule, the peaks are even smaller and less frequent (Figs. S2E and F). This latter measurement underscores the role that hydrogen bonding plays in generating the recognition signal.

2.2 Nucleotide Signals

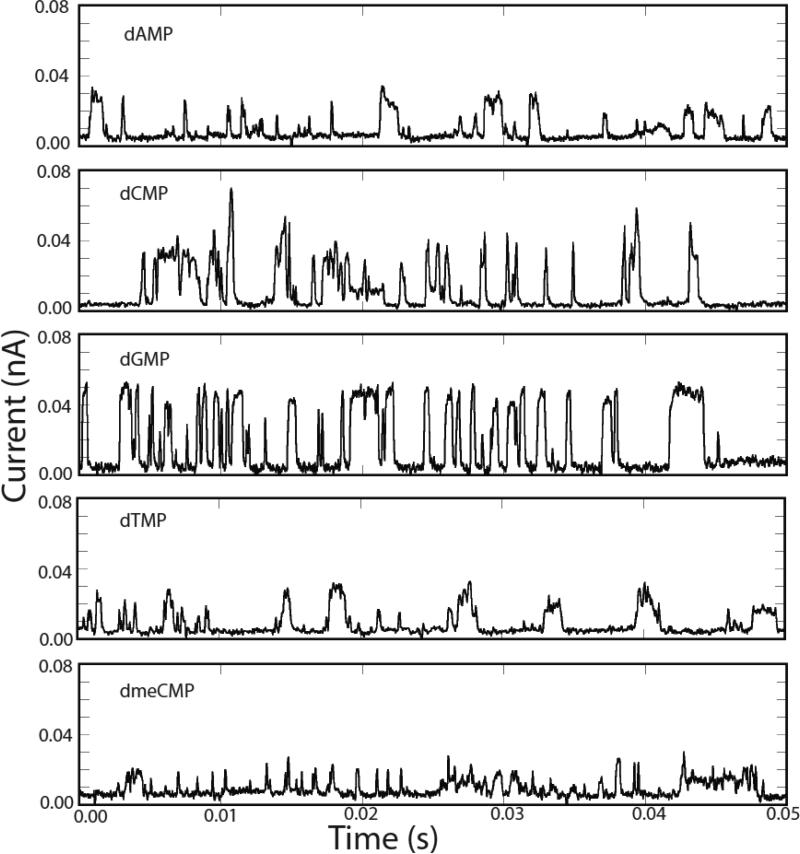
Figure 3 shows typical current vs. time traces for all 4 naturally occurring deoxynucleotides and d(5-methyl CMP) (hereafter d^meCMP) taken with functionalized probes and substrates. These are clearly quite different from the signals generated by the aqueous buffer alone, and, while signals like this are not observed in the absence of nucleotides, there are many “water-like” spikes in the signals obtained with nucleotides present. Examination of typical nucleotide signals in Figure 3 shows that they look like classic “telegraph noise” – on/off signals with a rapid rise, a roughly flat top and a rapid fall. We defined a “squareness” filter as follows: (1) We require a sharp rise-time, the onset of a peak being marked by a first point (the time step between data points is 0.02 ms) within 3pA above the average background, and a second point at least 8 pA above the first point (the first criterion eliminates peaks that do not start at the baseline – for example a second peak superimposed on a first peak). (2) We require a rapid fall time with the data points on the falling edge following the same criteria in reverse. (3) We require a flat top to the signal; that is at least 10 data points before the fall, with a variance such that the variance divided by the average (this average is the quantity we report as peak current) of these high current points in less than 2. Since the onset of the peak has to be between 8 and 11 pA, this filter also rejects all peaks of less than about 10 pA in height. When applied to the raw data, almost all of the water signals are removed from the controls. However, a significant fraction of the nucleotide signal is taken out too (Table 1). This effect is extreme for 5-^meC where over 90% of what are presumably nucleotide-generated signals are removed by the filter. We will address these problems when we discuss the multiparameter analysis, but, for now, the filtered data represents signals that are clearly generated by a nucleotide and not by water alone.

Figure 3.

Representative signals for the four nucleotides and d^meCMP after removal of the water signal. 10 μM nucleotide was dissolved in 1 mM phosphate buffer (pH=7) and the probe, functionalized with M scanned at 2nm/s over an Au(111) surface also functionalized with M. The tunnel gap was set under servo control to a baseline current of 6pA with a probe bias of 0.5V. The slew rate of the servo is much slower than the ms timescale of the pulses observed here. Approximate overall count rates are listed in Table 1 – these are much smaller than the pulse rates observed within the signal bursts shown here because the signals occur in clusters.

The first, really striking aspect of these data is the size of the signals that are generated – tens of picoamps with 0.5V bias and a 6 pA set point current. This is very surprising, because our adaptor molecule (M) contains an ethylene linker, in contrast to our earlier mercaptobenzamide adaptor molecule where the thiol tether was connected directly to the benzene ring. With the mercaptobenzamide adaptor molecules, peak signals were about 20 pA¹², and, since the electronic transmission decay caused by introducing methyl groups is approximately a factor 1/e per methyl group¹⁷, we might expect the signals produced by M to be a factor 10 lower. One possible explanation of the large currents is that the energy level of the HOMO or LUMO of the heterocycle is closer to that of the DNA bases than is the case for the benzene ring in the mercaptobenzamide adaptor molecule.

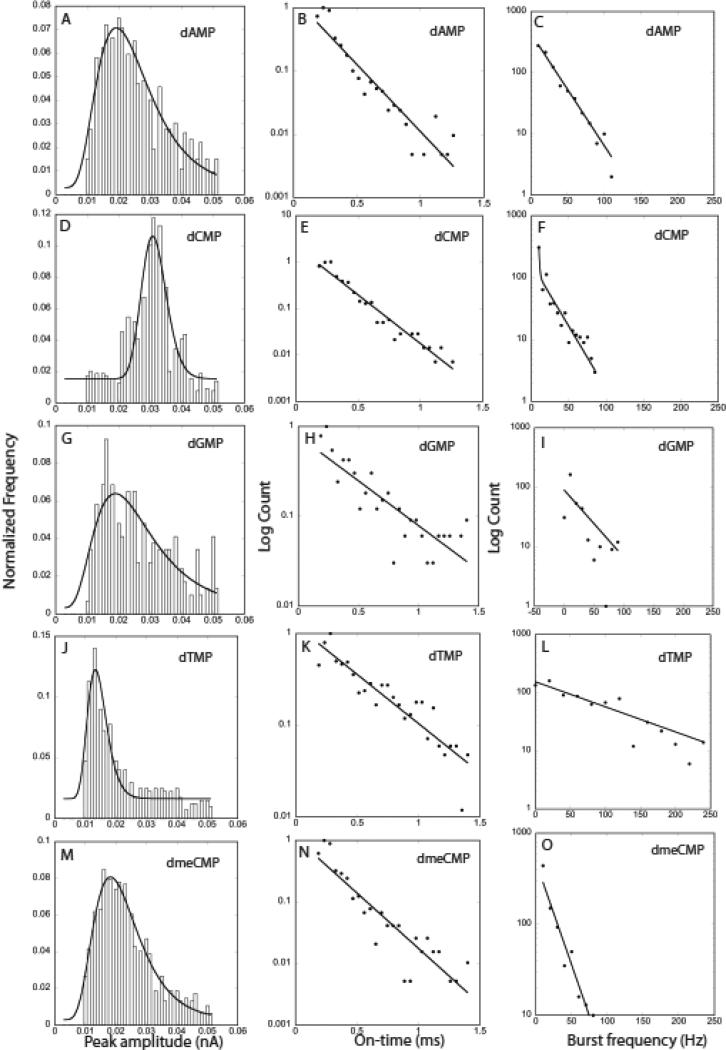
Figure 4 shows a statistical summary of the pulses produced by each of the four nucleotides and d^meCMP. The first column gives the peak amplitude distributions. dCMP gives the largest peak amplitudes and dTMP gives the smallest, while the dGMP, dAMP and d^meCMP distributions are largely overlapped and lie between these extremes. We fitted these distributions in earlier work with a Gaussian distribution in the logarithm of the current^{11, 12} arguing that the bond distances are probably distributed in a Gaussian manner while the currents will vary exponentially with these distances. While this might be true, the log-normal distribution is a more general function describing the random distribution of positive quantities:

$$N\left(i\right)=N_b+\frac{N_0}{\sqrt{2\pi }wi}\text{exp}\left(\frac{-\ln {\left(\frac{i}{i_p}\right)}^2}{2w^2}\right)$$ (1)

Here, N_b is a constant background, N₀ a quantity that controls the height of the distribution, w a parameter that controls its width and i_p is the peak current in the distribution. This function is essentially equivalent to the Gaussian distribution in the logarithm of the currents used previously, since the skew introduced by the multiplicative term in 1/i outside the exponential is small. Peak currents obtained from these fits are listed in Table 2, showing how dCMP and dTMP are characterized by high and low currents respectively.

Figure 4.

Amplitude distributions, (A, D, G, J, M), on-time distributions (B,E,H,K,N) and burst-frequency distributions (C,F,I,L,O) for dAMP (top row), dCMP (second row), dGMP (third row), dTMP (fourth row) and d^meCMP (bottom row). Solid lines are the fits described in the text.

Table 2.

Characteristics of the nucleotide signals for the probe scanning at 2 nm/s.

Nucleotide	Ip (nA)	On-time (ms)	Burst favg (Hz)	Burst f1/e (Hz)
dAmp	0.023±0.001	0.17±0.03	32±21	24±1.6
dCMP	0.031±0.0005	0.21±0.03	25±17	21±6.6*
dGMP	0.024±0.003	0.27±0.03	25±22	39±25
dTMP	0.014±0.0003	0.44±0.06	76±59	101±15
dmeCMP	0.021±0.0005	0.19±0.03	25±16	11±1.2

^*Fits to the burst frequency distribution were single exponentials with the exception of data for dCMP that included a second slow component.

A second obvious characteristic lies in the “on-time” for each pulse. Inspection of Figure 3 shows that dTMP appears to produce longer pulses. The distributions of on-times are given in the second column of Figure 4 and they are quite well fitted by exponentials, $N\left(t_{on}\right)=A\text{exp}\left(\frac{-t_{on}}{t_{1∕e}}\right)$ as would be expected for a Poisson process (solid lines on the figures). Values for t_1/e are listed in Table 2 also. Clearly, dTMP signals are distinguished by longer on-times.

Another parameter is the frequency of signal spikes in a cluster (Fig. 8). These spike clusters are obvious for oligomers (see Fig 6) and are defined operationally by a sliding average over the data stream. When a peak is detected, the number of other peaks within 2000 data points each side (40 ms each side) is counted and a frequency calculated. The frequency is recalculated for each point in the data in turn, and the resulting distribution of frequencies recalculated. Isolated peaks (more than ± 40 ms from a neighbor) produce values of zero. The averages for each nucleotide are listed in Table 2. The frequencies themselves are exponentially distributed (third column of Figure 4) according to $N\left(f\right)=B\text{exp}\left(\frac{-f}{f_{1∕e}}\right)$ and the corresponding values of f_1/e are listed in the last column of Table 2. dGMP and dTMP are characterized by high burst frequencies.

Figure 8.

Showing some characteristics of the tunneling signals. (A) Some properties of signal clusters. Spikes are first located by a point 1.5 standard deviations above the background noise. (B) Pulse height and on time. (C) Pulse shape. This is quantified using Fourier and wavelet components.

Figure 6.

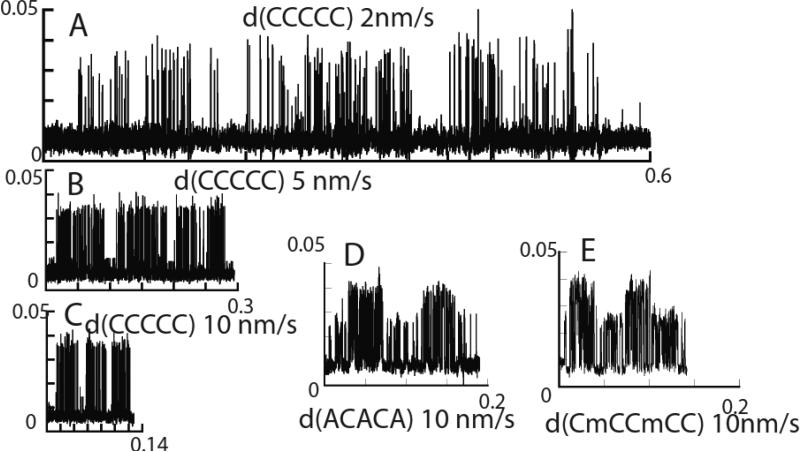
“Clock-scans” over DNA oligomers with the compositions listed. Oligomers were dissolved to a final concentration of 2 μM (intact oligomer) in 1 mM phosphate buffer (pH=7). Scan speeds are as listed on the figure. The burst time changes with scan speed according to equation 2. Homopolymers always give regular bursts and alternating polymers always give alternating bursts when periodic signals are recorded.

Thus it appears that C, T and G can be distinguished from A and ^meC. However A and ^meC in this data set (which has much of the ^meC data removed by the water filter) are not easily separated. These issues are resolved by the multiparameter analysis, but it is clear that we can use this simple analysis to interpret at least a fraction of the data.

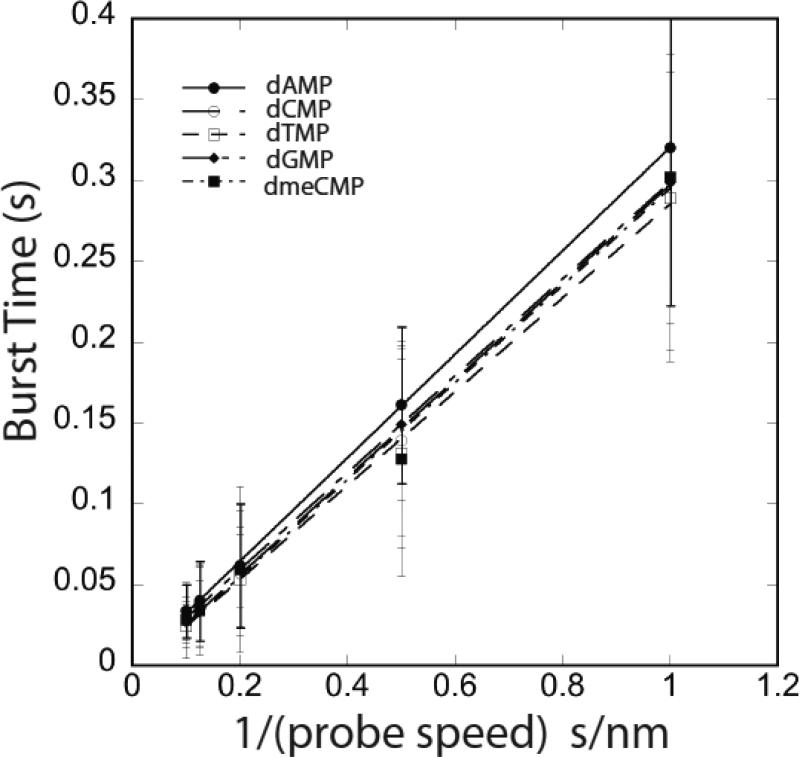
One last parameter is the duration of the signal bursts themselves. The burst-frequency algorithm described above also identifies the duration of closely spaced clusters of signal peaks. This quantity is entirely controlled by the speed with which the probe is scanned, and Figure 5 shows data for all four dNMPs and d^meCMP taken at tip speeds of 10, 8, 5, 2 and 1 nm/s. Plotted as burst time vs. 1/(tip speed) the data are linear, implying that the burst time corresponds to a constant distance traveled by the probe as signal spikes are generated. The slopes of these lines are listed in Table 3 and it is clear that the spatial extent of the signal burst is about 0.3nm, corresponding approximately to the size of a DNA base. These data are discussed further in the following section.

Figure 5.

Burst time (see Fig. 8) vs. 1/tip speed, for scan speeds (L to R) of 10, 8, 5, 2 and 1 nm/s for each of the five nucleotides as listed on the legend. Lines are regression fits using equation 2.

Table 3.

Slope (d) and intercept of the plots of T_b vs 1/(scan speed]

Base/Nucleotide	d (nm)	Tinter (ms)	Possible Kon M-1s-1
dAmp	0.32±0.002	-0.34±1.2	-
dCMP	0.30±0.006	4.2±3.2	1.2
dGMP	0.30±0.002	0.61±0.9	8.2
dTMP	0.29±0.008	4.9±4.2	1.0
dmeCMP	0.3±0.015	5.2±7.5	5.0
A in d(AAAAA)	0.27±0.02	-16±10	-
C in d(CCCCC)	0.24±0.03	-18±18	-

2.3 Oligomer Signals and binding kinetics

In our previous study of recognition-tunneling signals from DNA oligomers¹² molecules were allowed to drift into the gap randomly, so there was no control of the motion of the DNA relative to the tunnel gap, or of the timing of the reads. Attempts to image DNA on surfaces under solution show that it is nearly impossible unless the DNA is strongly tethered to a surface¹⁸ so diffusive motion is always present. We found that we were able to generate a small number of sequential reads using a scanning format we call “clock scanning” (Fig. S3). The scanning tunneling microscope was placed under the control of a field programmable gate array (see experimental methods) and the scan adjusted to be parallel to the surface by recording the surface topography in two orthogonal directions on an atomically-flat Au(111) terrace, and then adding a corrective ramp signal to the probe height so that motion was parallel to the surface without the need of servo control. In a clock-scan, the servo is engaged at the center of the field of data acquisition, then disengaged, and data collected at the probe is scanned out (typically 10 nm) from the center. The servo is then re-engaged at the end of the sweep and the height reset, if needed, for a return sweep. Sweeps in which the height changed significantly (10% change in background tunnel current) were rejected. A second sweep was then commenced, but rotated by 3° with respect to the first sweep. The process was repeated until the scan returned to the origin. Noise-bursts signaled the presence of DNA. Interestingly, these usually occurred at angular intervals of 60°, presumably a reflection of the underlying Au(111) symmetry (Fig. S3). Once a noise burst was detected, the program determined the most likely orientation of the scan on which a molecule might lie by interpolation between neighboring scans that contained a given noise-burst, and the probe was then scanned along that direction while data was acquired. In about 10% of these scans, two or more sequential bursts of signal were observed (Figure 6, Figures S4 and S5). It appears likely that these signals are generated from sequential base-to-base motion of the tunneling probe. While these sequential bursts are relatively rare, they occur much more often than might be expected from an entirely random scans over the DNA on the surface. One possible explanation of this unexpected orientation of the scan direction along the DNA axis (suggested by the 2D noise distribution, Fig. S3) is that the probe-sweep tends to “comb” the DNA on the substrate.

Evidence that these periodic bursts of signal (Fig. 6, Figures S4 and S5) originate with a base-to-base sweep of the scan is:

1. Periodic signals like these are never observed when nucleotides (as opposed to logomers) are examined in a ‘clock-scan’.

2. The spatial separation of bursts is a little over 0.3nm in all samples, the spacing of bases in DNA.

3. Homopolymers produce only one kind of burst in periodic signals (Fig. 6 A-C, Figure S4).

4. Polymers with an alternating composition (Fig. 6D,E, Figure S5) produce only alternating types of burst signal in periodic signals.

The signals produced by scanning oligomers are similar (but not identical) to those produced by scanning nucleotides. Figure S6 shows measured spike-amplitude distributions for d(AAAAA) and d(CCCCC) over which the distributions for the corresponding nucleotides are plotted (differences may reflect the effects of servo control, present for the nucleotides, absent for the oligomers, and also nucleotide-nucleotide interactions that are not possible for nucleotides embedded in a polymer).

The scans in Figure 6 are plotted on approximately the same time-axis scale, and it is clear that faster scanning produces shorter bursts, recapitulating the behavior observed for nucleotides (Fig. 5). If the probe adaptor molecule remains bound to the target as the probe moves over a distance d, then the duration of a burst of signal, T_b will be given by

$$T_b=\frac{d}{V}-T^{on}$$ (2)

where V is the probe speed and T^on is the time required for the recognition complex to form (note we use T^on here to distinguish this binding time from the on time of the pulses, T_on). Thus, the slope of a plot of T_b vs. $\frac{1}{V}$ yields d while the intercept, T_inter, could yield T^on if it was long enough to be resolved in this measurement (Figure 7). The measured values of d together with values for T_inter are listed in Table 3 for both oligomers and nucleotides. d is approximately 0.3 nm in every case while T_inter is small and takes on both positive and negative values. Thus, it is most likely that T^on is too small to be determined in these experiments. Taking the largest positive value (4.9 ms for dTMP) and assuming a sample concentration of 0.2M (one molecule in a volume 2.5 nm × π×(0.5 nm)²) yields the smallest value for K_on as ~1 M^-1s^-1. This is encouraging, in as much as it suggests that binding kinetics are unlikely to limit read speed up to the 20 nm/s (approximately 60 nucleotides/s) used here.

Figure 7.

Burst time vs 1/tip speed, for scan speeds (L to R) of 20, 10, 5, 2 and 1 nm/s for d(CCCCC) and d(AAAAA). Lines are regression fits using equation 2.

At the other end of the scale, the linear relationship (eqn. 2) holds down to scan speeds of 1 nm/s, suggesting that the off-rate, K_off, is less than 3 s^-1 (the inverse of the slowest burst time of ~0.3s). This is in agreement with our measurements of the lifetime of similar complexes using atomic force microscopy, where we have observed that the zero-force lifetime of hydrogen-bonded complexes tethered in a nanogap is on the order of seconds.^{12, 19} Thus, recognition-tunneling may also provide a tool for slowing DNA transport in a nanopore reader.

2.4 Using multiple parameters to call bases

Each of the parameters analyzed thus far (signal amplitude, on-time, burst frequency) is widely distributed, so it appears that many repeated reads would be required to make an accurate base-call. However, the existence of characteristic trends suggests that there is not an unlimited set of random configurations for the system, but rather a finite number of configurations that reflect specific bonding arrangements for each base in the recognition-tunneling junction. Is there some combination of signal characteristics that is more accurate for calling bases than any one of the parameters considered to date?

To investigate these issues, we wrote a program that derived the following parameters for every single signal spike in each experimental run (Figure 8):

2.4.1 Spike Amplitude

This is the average peak amplitude (in picoamps) as defined above.

2.4.2 Spike width

This is the full width of the peak at half the average peak height (analyzed here in terms of the number of 0.02 ms sample points).

2.4.3. Spike Fourier Component N

Each spike is amplitude-normalized and embedded into a data array of a fixed length (4096 points) and the power spectrum $\left(\sqrt{{\mathrm{Re}}^2+{\mathrm{Im}}^2}\right)$ obtained (by FFT) out to the Nyquist limit. This frequency interval is divided into 4 bins and the average value of the power density in each bin (N=1 to 4) recorded. The process for obtaining Fourier components is illustrated in Figure S7.

2.4.4. Spike Phase Component N

The FFT also produces a phase, ϕ, that can also be averaged over the four frequency intervals. The phase is obtained from

$$\varphi ={\text{tan}}^{-1}\left(\frac{\mathrm{Im}}{\mathrm{Re}}\right)$$

where Im is the imaginary value of the FFT and Re the real part. The average is calculated from all of the phase values in each of the four frequency blocks between zero and the Nyquist limit.

2.4.5. Spike Wavelet Component N

This is the Nth component (N = 1 to 9) of a decomposition of the spike into Haar wavelet components as illustrated in Figure S8 (for a description of the Haar Wavelet see Matlab Toolbox, URL: http://matlab.izmiran.ru/help/toolbox/wavelet/ch06 a32.html.). The whole dataset has the background removed, then is processed by the Haar wavelets. At the location of each peak, the wavelet coeffients are extracted and averaged for the duration of the peak. The first wavelet component is obtained by applying the Haar transform to each point to generate a series of 4096/2 differences, Δ(1)_n = I_2n–1 – I_2n. These differences are squared, summed and divided by N_d=2 to produce an average value for Wavelet(1).

At higher levels, N > 1, the Nth wavelet component is produced using the average of M_N = 2^N–1 consecutive points,

$${\overline{I\left(N\right)}}_m=\frac{1}{M_N}\sum _{i=1}^{M_N}{I}_{m{M}_{N^{+i-1}}}$$

to produce the differences,

$$\Delta {\left(N\right)}_n={\overline{I\left(N\right)}}_{2n-1}-{\overline{I\left(N\right)}}_{2n}$$

The Wavelet(N) is then calculated by averaging these difference values. Given the limited time response of the current recording system, only the larger wavelet components are useful.

2.4.6 Number of Peaks In a Cluster

Clusters are defined operationally using the algorithm illustrated in Figure S9. The location of the center of each peak is identified with a 1 in an otherwise null array (Fig. S9A). Each point is then convolved with a Gaussian of unit height and a full width at half height of 4000 0.02 ms sample points (Fig S9B). The Gaussians are summed (Fig S9C) and the boundaries of a cluster defined by the points at which this sum falls below 0.1 (“Threshold” on the Figure). This point is somewhat arbitrary, but values in this range (0.01 to 0.25) work well.

Once clusters are identified, the number of peaks in a cluster is a parameter assigned to each peak in that cluster.

2.4.7 Cluster on time

This is the ratio of the sum of the full widths of all peaks in a cluster to the total duration of the cluster, expressed as a percentage in the code used here. Each peak in a cluster is assigned the value calculated for the cluster.

2.4.8 Spike Frequency

This is calculated independent of the cluster definition and is the number of peaks found within ± 2000 0.02 ms sample points of the center of a given peak. The value is assigned to the peak about which the value was calculated. The calculation is carried out in the following way: Each spike is represented by a 1 at its center location. A Gaussian of unit height and 4000 points full-width at half-height is centered at each 1 in the array. For each spike location, all the Gaussians in the array are summed according to their value at that point, generating a number that reflects the spike frequency in the neighborhood of each spike.

2.4.9 Cluster Frequency N

Each cluster is loaded into an array of 4096 points and the FFT calculated for the entire cluster as described above for spikes. It is resolved into 9 bins covering the frequency range up to the Nyquist limit.

2.4.10 Cluster Phase N

This is calculated analogously to spike phase, but for the whole cluster. This parameter set was not used in the analysis discussed here.

We searched for optimal combinations of this large set of parameters by randomly selecting a number of them, training a support vector machine (SVM)²⁰ (http://www.csie.ntu.edu.tw/~cjlin/libsvm) with 200 spikes randomly selected from a file containing 600 spikes, and then scoring the performance of the SVM with the remaining 400 spikes. The SVM was trained with water signals and the signals for each of the 5 bases in turn, and then fed the remainder of the data (the SVM works by finding N-1 dimensional surfaces that optimally partition an N dimensional space so as to separate each training data set by the largest possible amount). We compiled a cumulative accuracy as follows: We summed up all of the errors in assignment of a data set for any one base (i.e., all the A's called as C's, G's, T's or methyl C's) subtracted from the total number of spikes and then divided the result by the total number (× 100 to get a percentage). We list the parameter combinations that gave the highest percentage of correct calls in Table 4 (this is from a total of 4,157 combinations that were examined). There are a number of combinations that give an 80% accuracy call for each spike in the file. This is remarkable given the obviously stochastic nature of the data. Interestingly, all of the best calling combinations include contextual information (i.e., data derived from the cluster in which the spike lies). The distributions of base-calling accuracies with various combinations of single-peak parameters and cluster parameters are shown in Figure S10. Amplitude data, the obvious choice at the start of this project, does not figure prominently.

Table 4.

The top nine parameter combinations together with the SVM setting.

Cumulative Accuracy (%)	SVM setting	Parameters Used
84	Unsealed	ClusterOnTime(%) clusterfreq3 clusterfreq8 clusterfreq9
80.8	Unsealed	Spike Amplitude (pA) NumPeakslnCluster ClusterOnTime(%) freq3 clusterfreq1 clusterfreq2 clusterfreq3 clusterfreq5 clusterfreq6 clusterfreq7 clusterfreq8 wavelet5 wavelet7
80.7	Easy	NumPeakslnCluster ClusterOnTime(%) freq2 clusterfreq2 clusterfreq7 clusterfreq8 wavelet2
80.7	Easy	NumPeakslnCluster clusterfreq1 clusterfreq4 clusterfreq5 clusterfreq7 waveletl wavelet3 wavelet7
80.7	Unsealed	Spike Amplitude (pA) Spike Frequeney (spikes per 4000 samples) NumPeakslnCluster ClusterOnTime(%) clusterfreq2 clusterfreq3 clusterfreq4 clusterfreq5 clusterfreq7 wavelet2 wavelet4 wavelet7 wavelet9
80.5	Unsealed	NumPeakslnCluster ClusterOnTime(%) freq2 clusterfreq2 clusterfreq7 clusterfreq8 wavelet2
80.5	Easy	Spike Amplitude (pA) NumPeakslnCluster ClusterOnTime(%) freq3 clusterfreq1 clusterfreq2 clusterfreq3 clusterfreq5 clusterfreq6 clusterfreq7 clusterfreq8 wavelet5 wavelet7
80.3	Unsealed	Spike Amplitude (pA) NumPeakslnCluster ClusterOnTime(%) freq1 freq4 clusterfreq1 clusterfreq2 clusterfreq5 clusterfreq7 clusterfreq8 clusterfreq9 wavelet2 wavelet3 wavelet5
80.1	Easy	Spike Width (Samples) ClusterOnTime(%) freq1 freq2 freq4 freq7 clusterfreq2 clusterfreq4 clusterfreq5 clusterfreq6 clusterfreq7 waveletl wavelet2 wavelet3 wavelet4 wavelet6

The SVM settings are as follows: Easy: Easy.py is a predefined python script that is distributed with LIBSVM to automatically determine a few of the adjustable parameters of the SVM. The script iteratively searches the SVM parameters (gamma, C) to specify the most accurate kernel. Scaled: Before training, both the training and testing datasets are scaled so all the parameters range from -1 to 1. This helps to prevent one parameter from overwhelming the SVM data. Unsealed: The SVM is trained with data that has not been scaled.

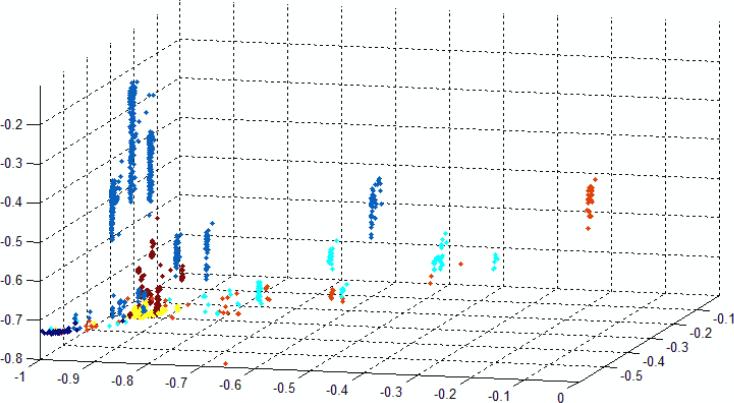
We have attempted to display the separation of data that is achieved by selecting a 2D projection of a 3D plot (Fig. 9) of an example of 12D data. The three axes were constructed as follows: Vector X: Spike Freq, Cluster Length, Freq 5, Cluster Freq 3, Cluster Freq 8; Vector Y: Cluster on Time, Freq1, 2, 4,6 ClusterFreq 5, ClusterFreq 9; Vector Z:; ClusterFreq 1, ClusterFreq 4, ClusterFreq 7). A 2D view was then chosen such that much of the separation can be visualized. The data are separated well at the 80% level, but multiple views are required to show this. Nonetheless, even in this 2D projection, the data are quite well separated. Inspection of many such plots (using axes that separate the data well) show the following common characteristics:

1. Data for A,C and T are widely spread.

2. The spread data tend to form multiple clusters, suggesting that there are several distinct binding motifs responsible for the signal for a given base.

3. Data for G and water tend to be localized.

4. Data for 5-methylC tend to be surrounded by A data points, recapitulating the similarities observed in the simple analysis of peak characteristics (Fig. 4).

Figure 9.

2D projection of a 3D plot in which the axes are linear (orthogonal) combinations of 14 spike parameters showing one view of the separation of the 5 bases and water into distinct clusters (overlapped somewhat in this 2D projection). With the exception of the G and water signals, data are spread out in distinct groups suggesting that discrete sets of configurations are sample in the recognition-tunneling gap. (Water signals were not removed from this data set by prefiltering.) Color code: Blue = dAMP, Red = dTMP, Turquoise =dCMP, Brown = dmeCMP, Yellow = dGMP, Black = water.

Thus far, the analysis has been restricted to the one data set taken with a moving probe (2 nm/s) and servo control on. We went on to analyze the other two different experiments: Data acquired with a stationary gap (which contained a large fraction of “water signals”) and data taken with the current servo off (which is complicated by the presence of occasional probe-crashes). We trained the SVM on mixed pools of training data from all three experiments, and then tested the code on data from all three experiments analyzed with the same set of support vectors used for all three sets of data. The results are summarized in Table 5 which shows the top 5 parameter combinations. Remarkably, the base calling accuracy is still close to 80% despite the fact that the same support vectors were used to analyze all three data sets.

Table 5.

Cumulative accuracies for three data sets obtained in three different experimental conditions. Only one set of Support Vectors was used for all three data sets.

Cumulative Accuracy (%)	SVM Setting	Parameters Used
79.6	Unsealed	ClusterOnTime(%) clusterfreq1 clusterfreq6
78.9	Unsealed	ClusterOnTime(%) freq2 freq3 freq4 clusterfreq2 clusterfreq5 clusterfreq6 clusterfreq7 clusterfreq9 wavelet5
78.4	Unsealed	clusterfreq1 clusterfreq3 clusterfreq4 clusterfreq8 clusterfreq9 wavelet8
77.9	Unsealed	Spike Amplitude (pA) NumPeakslnCluster freq2 freq3 freq5 clusterfreq1 clusterfreq5 elusterfreq8 elusterfreq9 wavelet4 wavelet5
76.9	Unsealed	clusterfreq1 clusterfreq2 clusterfreq8 clusterfreq9
76.5	Unsealed	clusterfreq2 clusterfreq7
76.4	Unsealed	Spike Amplitude (pA) NumPeakslnCluster freq1 freq3 clusterfreq2 clusterfreq3 clusterfreq4 clusterfreq9 wavelet4 wavelet5

As pointed out earlier, much of the data consists of repeated reads on the same base. The distribution of the number of spikes in a cluster follows a heavily damped log-normal distribution. An example of such a distribution (for dAMP with the probe scanned at 5 nm/s) is given in Figure S11. Most of the data contains two or more spikes with clusters of up to 13 spikes being quite common. We set the SVM code to report probabilities for the call for each base and then tabulated these along with the data generated for each spike. As expected, spikes within the same cluster were often called as the same base and we used this repeated data to enhance the accuracy of the calls. In the simplest case, we counted votes within a cluster calling the base by the majority vote. Thus an AACAC read within a cluster is called an A. We also used the probabilities reported by the SVM code, adding each probability and calling the winner from the largest sum (this differs from the vote in biasing the call towards assignments made with the larger probabilities). In both cases, the accuracy, determined by comparison with the frequency of correct calls given the known identity of the target moved up to >95% compared to ~80% that was obtained without the use of cluster voting algorithms (Figure S12). Some calls exceed 99% accuracy (as reported by the SVM). Examples of calls with associated probabilities as a function of cluster size are given in Table S1.

The SVM as currently implemented by us suffers a drawback, however. When presented with new types of signal, it will call the new points as one of the bases it was trained on, regardless of how far they lie from the training data, according to the support vectors they lie behind. Thus, while blind trials with a single nucleotide support the 80% base calling accuracy, data obtained with mixtures of nucleotides are much less accurate (failing extremely in some cases – for example, an equimolar mix of dAMP, dTMP and dGMP was analyzed has having no T's). In all likelihood, the source of the problem is internucleotide interactions in the tunnel junction, with hydrogen bonds between nucleotides replacing interactions with water molecules and the adaptor molecules. If this is the case, then these interactions probably also occur when only a single type of nucleotide is used. Since inter-nucleotide interactions will be more limited when the bases are incorporated into an oligomer, this may account for the differences between the distributions measured for nucleotides and for the corresponding oligomers (Figure S6). Clearly, a DNA sequencing device would be better trained on homopolymers than with nucleotides.

3.0 Conclusions

4(5)-(2-mercaptoethyl)-1H-imidazole-2-carboxamide generates surprisingly large recognition-tunneling signals, despite incorporating an additional two methylene groups in the linker to the electrode. This demonstrates how the electronic states of the adaptor molecule can be engineered to increase the level of tunneling signals. Signals are obtained from all four bases and 5-methylC, though the distributions of peak amplitudes are overlapped significantly. Nonetheless, the signals are distinctive enough that trains of signal bursts can clearly be recognized when a tunneling probe is scanned over DNA oligomers. The burst time is inversely proportional to the probe speed and corresponds to a spatial distance of 0.3 nm (i.e. about the size of a base). These scanning data can be used to set limits on the on- and off-rates for the complex of adaptor molecules with the targets. The off-rates are slow (corresponding to lifetimes of seconds) consistent with AFM measurements of the lifetimes of hydrogen-bonded complexes in a nanogap. ^{19, 12} This behavior has recently been explained as a consequence of the bond confinement in the gap.²¹ The on-rates are fast, probably too fast to be measured with the techniques used here, but certainly consistent with DNA sequencing speeds of many tens of bases per second.

The wide distributions of measured parameters are inconsistent with base calling from single molecule reads, but a multiparameter analysis shows that most signal spikes contain chemical information if analyzed appropriately. Base-calling accuracies can exceed 90% if use is made of repeated reads within a signal cluster. The distribution of data points in hyperspace clusters in a way that suggests a number of different binding motifs in the tunnel gap. Failures of the technique point to complications owing to internucleotide interactions when free nucleotides are used. These difficulties do not appear to be insurmountable and we expect that recognition tunneling will become a useful single molecule analytical technique.

Our kinetic data imply that DNA sequencing in a nanopore reader equipped with a tunnel junction should be possible. The recognition complex forms quickly enough to allow sequencing up speeds that might reach 100 bases/second. On the other hand, the long off times may prove useful in controlling the speed with which DNA translocates through a nanopore, though this remains to be demonstrated in a nanopore device. Of particular note is the ability to directly resolve all four bases, and the epigenetic modification, 5-methyl C. The recently announced success of sequence read out by means of ion current blockade²² shows how single base resolution may be extracted by a clever deconvolution of an ion current signal that is influenced by several bases in the nanopore when only the four natural bases need to be called. The process becomes much more complicated for a fifth base, so the sensitivity of the tunneling readout may prove of value if devices can be manufactured reliably. For both types of readout, the accuracy is at the mid 90% level for each single molecule read. Greater accuracy will require repeated reads, not a significant burden given the single molecule capability of the nanopore methods.

4.0 Experimental Methods

Nucleoside 5’-monophosphates (from Sigma-Aldrich) were used as supplied. HPLC purified DNA oligomers were purchased from IDT. Tunneling measurements were carried out using gold probes and gold substrates. Gold probes were etched as described previously¹¹ and coated with high-density polyethylene^{16, 23} to leave a fraction of a micron of exposed gold. These probes gave no measureable DC leakage, important as this can be a source of distortion of the tunneling signal.¹¹ Capacitative coupling of 120 Hz switching signals was a problem minimized by careful control of the coating profile. It was also diminished by functionalization of the probes.

Gold (111) substrates²⁴ were annealed with a hydrogen flame and then immediately immersed in a 2 mM ethanol solution of 4(5)-(2-thioethyl)-1H-imidazole-2-carboxamide¹³, where they were left for a minimum of 2h (usually overnight), then rinsed in ethanol and blown dry with nitrogen before immersion in the phosphate buffer solution. Characterization of the resulting monolayers is described in Figure S13. Insulated probes were cleaned prior to functionalization by rinsing with ethanol and H₂O, blown dry with nitrogen gas, and then immersed in a 1mM methanolic solution of 4(5)-(2-thioethyl)-1H-imidazole-2-carboxamide¹³ in methanol for 1h. We were able to test the efficiency of the functionalization process by making recognition tunneling measurements on a functionalized gold surface, and comparing the tunneling data to controls in which the probe was functionalized, but the substrate was left bare. The resulting tunneling signals showed clearly whether or not functionalization was successful (Fig S2).

Current signals were recorded using an Agilent PicoSPM (Agilent Chandeler, AZ) together with a digital oscilloscope controlled by a custom Labview program. The servo response time was set to about 30 ms as described previously.¹¹ This places an upper limit on undistorted measurements of pulse widths of a few ms.

The “clock-scanning” system was developed around a Field-Programmable Gate Array (FPGA). A computer running LabView (Version 8.5.1, National Instruments) controlled the FPGA as well as issued API calls to PicoView (Version 1.8, Agilent, Chandler, AZ) via PicoScript (Beta Version, Agilent, Chandler, AZ). For experiments where the tip was moving at a specified speed the tip was set to an initial location from the LabView interface. A radius around this position was set along with a desired tip speed. The tip was then moved in a spoke pattern around the initial point changing by a user specified number of degrees, by issuing tip movement commands to PicoView. The FPGA (PCIe-7842R, National Instruments) contains a built in A/D that enabled the tunneling signal to be recorded at 50kHz from the breakout box. The position of the tip was also recorded by using a voltage divider and reading the piezo voltages for the x and y directions from the breakout box. Provision was made in the code for enabling and disabling the servo at selected point on the scan, and for leveling the orientation of the scan with respect to the substrate as described above.