The Quadratic Hazard Model for Analyzing Longitudinal Data on Aging, Health, and the Life Span

Abstract

A better understanding of processes and mechanisms linking human aging with changes in health status and survival requires methods capable of analyzing new data that take into account knowledge about these processes accumulated in the field. In this paper, we describe an approach to analyses of longitudinal data based on the use of stochastic process models of human aging, health, and longevity which allows for incorporating state of the art advances in aging research into the model structure. In particular, the model incorporates the notions of resistance to stresses, adaptive capacity, and “optimal” (normal) physiological states. To capture the effects of exposure to persistent external disturbances, the notions of allostatic adaptation and allostatic load are introduced. These notions facilitate the description and explanation of deviations of individuals’ physiological indices from their normal states, which increase the chances of disease development and death. The model provides a convenient conceptual framework for comprehensive systemic analyses of aging-related changes in humans using longitudinal data and linking these changes with genotyping profiles, morbidity, and mortality risks. The model is used for developing new statistical methods for analyzing longitudinal data on aging, health, and longevity.

1. Introduction

Age patterns of human mortality rates demonstrate remarkable regularities in different populations: they decline in childhood, exponentially increase in adult ages, and tend to decelerate and level off at the oldest-old ages. Demographers have developed a number of parametric descriptions of mortality curves capturing all aspects of their variation with age [1-4]. Biodemographers and gerontologists have aimed to explain observed features of mortality curves using emerging theoretical concepts [5-12]. Since the chances of death are affected by internal and external stresses challenging deteriorating defense mechanisms in an aging body, the shape of the age trajectories of mortality curves is likely to reflect the average effects of such deterioration, as well as external influences. In other words, if one wants to make conclusions about the aging process developing in individuals comprising the population under study by investigating the age pattern of the corresponding mortality curve, one has to develop a description of such a curve in terms of parameters characterizing the processes which are likely to contribute to the shape of this curve. Such a description can be done using models of aging-related changes represented in longitudinal data merged with data on health and survival events.

Statistical methods for joint modeling of longitudinal and survival (time-to-event) data have been developed during the past several decades using both frequentist and Bayesian approaches (see recent reviews in [13-16] and references therein). Commonly, time-to-event data are analyzed using the proportional hazards model and the usual approach to modeling longitudinal data involves a mixed effects model [17] with the assumption that the random effects or individual-specific parameters are normally distributed, see [18-21] among others). Several papers have developed semiparametric approaches that do not rely on normality of the distribution for the random effects or individual parameters (see, e.g., [22-26]). Further developments include modeling longitudinal data using a stochastic process, either an (integrated) Ornstein-Uhlenbeck or Wiener process, that allows a more flexible description of individual longitudinal dynamics and provides a better fit compared to the usual random effects model (see, e.g., [27-32]).

To be useful as a tool for extracting new information, models of longitudinal data have to be based on realistic assumptions and reflect knowledge and evidence accumulated in the field. Epidemiological studies of risks of disease and death show that the conditional hazards of such events considered as functions of given risk variables often have U- or J-shapes [33-43], so the model of aging-related changes has to take this reality into account. The risk variables as well as their effects on the risks of corresponding events experience aging-related changes (different for distinct individuals) and are measured with certain periodicity in longitudinal studies of aging, health, and longevity. Such data make it possible to evaluate regularities of aging-related changes and their effects on health and survival. An important class of models for joint analyses of longitudinal and time-to-event data incorporating a stochastic process for description of longitudinal measurements is based on this biologically-justified assumption of a quadratic hazard (i.e., U-shaped in general and J-shaped for variables that can take values only on one side of the U-curve) considered as a function of risk factors (i.e., physiological variables). Quadratic hazard models have been developed and intensively applied in studies of longitudinal data [44-48]. The advantage of this approach is that it allows for incorporation of new insights and ideas appearing in the course of research on aging. The prototype of a model discussed in this paper was suggested in [44]. Yashin [45, 49] investigated conditions for preserving a Gaussian distribution property of the stochastic covariates under the operation of conditional averaging, and found that model [44] satisfies these conditions. An important property of this model is that the age trajectory of the total mortality rate can be explicitly represented in terms of the first two moments of the conditional distribution of the processes involved in the description of the conditional mortality risk. This property, as well as its flexibility in describing age trajectories of factors affecting conditional risk, make this model a valuable tool for studying aging, health, and longevity using longitudinal data.

Despite the availability of efficient statistical methods for analyzing longitudinal data, and considerable progress in understanding various aspects of human aging, health, and longevity, many facts and research findings remain largely disconnected. Researchers working with data on aging usually deal with small portions of information used for addressing specific research question using standard statistical methods. Such methods, however, largely ignore available knowledge, new research findings, and emerging theoretical concepts about aging in the process of data analyses. As a result, the potential of many large longitudinal datasets, as well as the knowledge accumulated in the field, remains underused.

Progress in this area would be substantially facilitated if researchers had a tool for analyzing the wealth of available data and were able to incorporate important facts, research findings, and emerging theoretical concepts in the analyses. Several such concepts capable of capturing fundamental features of aging-related changes are currently under development. They are related to the notion of allostatic load [50], the decline in adaptive capacity (homeostenosis) [51-54], the decline in resistance to stresses [5, 55-57], aging-related physiological norms, and heterogeneity in longitudinal data.

In this paper, we describe a mathematical model for analyzing longitudinal data on aging, health, and mortality that incorporates the four concepts of aging described above (i.e., the notions of age-dependent physiological norms, allostatic load, adaptive capacity, and resistance to stress), review applications of this model to analyses of longitudinal data, and investigate its potential for performing more comprehensive analyses of such longitudinal data.

An initial version of such a model was suggested in [58]. Its various extensions have been applied in different contexts to investigate mechanisms of aging-related changes in connection with morbidity/mortality risks. This includes analyses of age trajectories of different physiological indices (such as blood glucose, body mass index, cholesterol, diastolic blood pressure, hematocrit, pulse pressure, and pulse rate) in relation to mortality/morbidity risks [59-62]; applications to “indices of cumulative deficits,” which have proved to be useful for analyses of a wide spectrum of information in relation to health- and aging-related changes and better characterize the aging phenotype than chronological age [63]; and analyses of trajectories of medical costs in relation to mortality risks [64]. Extended versions of this model also have been used in analyses of dependent competing risks [65, 66], heterogeneity in longitudinal data [67], analyses of genetic effects on age trajectories of physiological indices [68], joint analyses of individual health histories and physiological aging [69], and joint analyses of data collected using different observational plans [70].

2. Model

2.1. General description

To analyze longitudinal data on age-dependent changes in physiological states, we propose a dynamic model describing the trajectories of the individual physiological variables and their influence on mortality risks, which have the J-, or U-shape considered as a function of risk factors [71]. Let Y_t (where t is age) be a k-dimensional stochastic process describing a continuously changing vector of risk factors/covariates (e.g., physiological variables), and Z be a vector of time-independent observed covariates (e.g., person’s genetic background). We specify the risk function or conditional hazard of death in the form

$$\mu (t,Y_t,Z)={\mu }_0(t,Z)+{(Y_t-f_0(t,Z))}^{T}Q(t,Z)(Y_t-f_0(t,Z)).$$ (1)

Here μ₀(t, Z) is a background hazard characterizing the mortality rate that would remain if the vector of covariates Y_t followed the optimal trajectory coinciding with f₀(t,Z). “T” in (1) and in formulas below denotes the transposition of the noted vectors or matrices. The matrix Q(t,Z) is a non-negative-definite symmetric matrix of dimension k × k. We use column vectors throughout; thus, the transposition to row vectors in (1) is needed to produce a scalar quadratic term in the hazard rate. The one-dimennsional version of (1) is

$$\mu (t,Y_t,Z)={\mu }_0(t,Z)+{\mu }_t(t,Z){(Y_t-f_0(t,Z))}^2,$$ (2)

μ is some non-negative function of age, t. The U-shape of the risk function may change with increasing age. This is important because the narrowing of the U-shape for some risk factor with age captures the age-related decline in resistance to stresses associated with changes in this factor.

The age trajectory of a physiological variable, for which the minimum value of the risk function is reached, is called the physiological norm. We allow for the norm to be a function of age.

Temporal changes in the vector of risk factors Y_t are described by a diffusion type stochastic differential equation:

$$d{Y}_t=a(t,Z)(Y_t-f_1(t,Z))dt+b(t,Z)d{W}_t,$$ (3)

with intial condition Y₀. Here W_t is specified as a vector Wiener process with independent components, which describes exogenous challenges affecting these covariates. The process W_t is assumed to be independent of the initial vector Y₀ and covariate Z with normally distributed components. Note that such a model preserves the Gaussian property: in the case of an initial Gaussian distribution for Y₀, i.e., in the case that the vector of risk factors observed/measured at the initial wave of a longitudinal study is distributed as a Gaussian random variable, the distribution of Y_t among survivors is also Gaussian [45, 46, 49]. Thus, our assumption of a Gaussian initial distribution defines the structure of the entire process Y_t. The strength of disturbances of W_t is characterized by a matrix of diffusion coefficients b(t,Z).

The vector-function f₁(t,Z) (with the same dimension as the vector Y_t) describes a trajectory of physiological states that organisms subject to allostasis [72] are forced to follow by the process of adaptive regulation at age t. Allostasis is the process of individual adaptation to persistent external disturbances aimed at achieving stability, or homeostasis, through physiological or behavioral change.

The trajectory of Y_t reflects aging-related changes in the organism’s functioning due to the average effects of a complicated interplay among the ontogenetic program, senescence, and environmental stresses. Persistent external or internal disturbances affect age trajectories of the physiological indices. This is called the effect of allostatic adaptation. Taking into account this effect is especially important in analyses of longitudinal data in which measurements of external disturbances are absent or limited. The effects of allostatic adaptation produce deviations from the norm in the trajectories of the process Y_t. The magnitudes of such deviations for each physiological index will be associated with components of allostatic load.

Homeostatic regulation plays a fundamental role for living organisms and such regulation needs to be included in the equation describing physiological changes. The dynamic model (3) includes a description of negative feedback mechanisms with coefficients of homeostatic regulation given by a matrix a(t,Z). According to (3), the age trajectory of physiological variables Y_t will tend to follow the function f₁(t,Z), i.e., adapt to changes in f₁(t,Z) (the absence of such negative feedback mechanism would allow the trajectories to deviate from f₁(t,Z) indefinitely, which is biologically implausible). The ability to adapt depends on the absolute values of the coefficients that are components of the matrix a(t,Z). Age-related changes in these coefficients characterize changes in adaptive capacity with age. Specifically, the elements of the matrix a(t,Z) regulate the age trajectories of the components of the physiological state approximated by the vector Y_t, i.e., they characterize the rate of the adaptive response for any deviation of a physiological index from the state f₁(t,Z) which an organism tends to follow. An important feature of aging – the decline in adaptive capacity – has never been measured directly in longitudinal studies of aging, health, and longevity before. The use of the matrix a(t,Z) in our model allows us to evaluate this effect. For example, in a simplified one-dimensional case, when b(t,Z)=0, for all t, in equation (3), and constant negative a(t,Z)= a for all t, the parameter a is the coefficient of negative feedback in the equation for Y_t, which keeps the trajectory Y_t close to f₁(t,Z). When f₁(t,Z)= f₁, constant for all t and Z, the value of Y_t asymptotically approaches f₁. In the case of non-zero disturbances, the higher the absolute value of a, the closer Y_t is to f₁, and the faster Y_t tends to f₁. That is why the value a(t,Z) characterizes adaptive capacity. When the absolute value of the coefficient a(t,Z) declines with age, more time is needed for the trajectory of Y_t to approach f₁(t,Z) at old ages compared to younger ages. Practical estimation of the changes in adaptive capacity with age involves maximization of the likelihood function (6) below, in which coefficients of matrix a(t,Z) are described as parametric functions of age.

The vector-function f₀(t,Z) in (1) (or, correspondingly, the scalar function f₀(t,Z) in (2)) is introduced to explicitly characterize age-related changes in the “optimal” physiological state corresponding to the minimum hazard at a given age. It represents the age-dependent norm for a given functional state. It may differ from f₁(t,Z) since the process of allostatic adaptation does not necessarily result in the optimal physiological state. Thus, the difference between f₁(t,Z) and f₀(t,Z) provides a measure of the allostatic load.

2.2. Estimation procedure

The model can be estimated using the maximum likelihood method. The survival function associated with the life span distribution is $P(X>t\mid Z)=\text{exp}(-{\int }_0^t\stackrel{‒}{\mu }(u,Z)du)$, where the marginal (unconditional) hazard $\stackrel{‒}{\mu }\left(u\right)$ has the form (see [47, 65, 73]):

$$\stackrel{‒}{\mu }(u,Z)={\mu }_0(u,Z)+{(m(u,Z)-f_0(u,Z))}^{T}Q(u,Z)(m(u,Z)-f_0(u,Z))+Tr\left(Q(u,Z)\gamma (u,Z)\right)$$ (4)

where Tr(·) denotes the matrix trace operator and m(u, Z) and γ(u, Z) satisfy the following system of ordinary nonlinear differential equations:

$$\begin{array}{cc}\hfill \frac{dm(t,Z)}{dt}& =a(t,Z)(m(t,Z)-f_1(t,Z))-2\gamma (t,Z)Q(t,Z)(m(t,Z)-f_0(t,Z)),\hfill \\ \hfill \frac{d\gamma (t,Z)}{dt}& =a(t,Z)\gamma (t,Z)+\gamma (t,Z)a{(t,Z)}^T+b(t,Z)b{(t,Z)}^T-2\gamma (t,Z)Q(t,Z)\gamma (t,Z),\hfill \end{array}$$ (5)

with m(0, Z) and γ(0, Z) being the mean and the variance/covariance matrix of the conditional normal distribution of the initial vector Y₀, given Z. Note that in such a model the conditional distribution of Y_t among survivors is also Gaussian at any age t [45, 46, 49]. The mean and the variance/covariance matrix of this distribution at age t are given by m(t, Z) and γ(t, Z ,), respectively.

Let the sequence $y_{t_o^i}^i,y_{t_1^i}^i,\dots ,y_{t_{n_i}^i}^i,{\tau }_i$ represent the results of measurements of the process Y_t and the life span (which may be censored) related to the i^th individual. The conditional likelihood function for N individuals is (see [47, 65, 73]):

$$\begin{array}{cc}\hfill & \prod _{i=1}^N{\stackrel{‒}{\mu }}^i{({\tau }_i,Z)}^{{\delta }_i}\text{exp}\left\{-{\int }_0^{{\tau }_i}{\stackrel{‒}{\mu }}^i(u,Z)du\right\}\prod _{j=0}^{n_i\left({\tau }_i\right)}{\left(2\pi \right)}^{-\frac{k}{2}}{\mid {\gamma }^i(t_j^i-,Z)\mid }^{-\frac{1}{2}}\hfill \\ \hfill & \times \text{exp}\left\{-\frac{1}{2}{(y_{t_j^i}^i-m^i(t_j^i-,Z))}^T{\gamma }^i{(t_j^i-,Z)}^{-1}(y_{t_j^i}^i-m^i(t_i^j-,Z))\right\}.\hfill \end{array}$$ (6)

Here the superscript “i” denotes respective characteristics for i^th individual, δ_i is a censoring indicator, mⁱ(t, Z) and γⁱ(t, Z) satisfy equation (5) at the intervals $[t_0^i,t_1^i);[t_1^i,t_2^i);\dots ;[t_{n_i-1}^i,t_{n_i}^i);[t_{n_i}^i,{\tau }_i)$ with the initial conditions $y_{t_0^i}^i,y_{t_1^i}^i,\dots ,y_{t_{n_i}^i}^i$, respectively. Here $m^i(t_j^i-,Z)=\underset{t\uparrow t_j^i}{\text{lim}}{m}^i(t,Z)$, and ${\gamma }^i(t,Z)=\underset{t\uparrow t_j^i}{\text{lim}}{\gamma }^i(t,Z)$, and $t_{n_i}^i$ is the age of the latest measurement of a functional state before death/censoring at τ_i.

Maximization of this likelihood function is computationally extensive, because it involves solution of the systems of ordinary differential equations (ODE) (5) for each measurement, for each individual, and at each step of the likelihood optimization procedure. However, our experience with these models is that such solutions are feasible on modern computers and using modern statistical and technical software, e.g., MATLAB’s Optimization Toolbox and ODE solvers, or SAS PROC NLP, implementing different optimization algorithms (such as the Newton-Raphson or trust-region methods) and the Runge-Kutta method for the ODE solution. The parameter estimates then characterize the dynamics of the stochastic process Y_t describing the trajectories of physiological aging, as well as changes in mortality risk over age.

Note that the observed values $y_{t_0^i}^i,y_{t_1^i}^i,\dots ,y_{t_{n_i}^i}^i$ are used as initial conditions for differential equations (5) at the beginning of subsequent intervals between the observation times. Therefore, the individual trajectories of mⁱ(t,Z) and γⁱ(t, Z) differ even for individuals having the same values of Z. Consequently the estimates of the chances of death for individuals having different observed values of the respective covariates also differ.

In this version of the model, we assume that observations $y_{t_0^i}^i,y_{t_1^i}^i,\dots ,y_{t_{n_i}^i}^i$ do not contain measurement errors. This assumption is not a serious problem when the model’s parameters are used to characterize the entire population of study participants. In this case one random process describes age trajectories of functional state in the population. The individual trajectories are just sampling paths of this process, so the differences among individuals are generated by the Wiener process and difference in values at the age at entry into the study. This rough approximation is appropriate for evaluating and predicting population characteristics (e.g., changes in distributions of aging, health, and survival indices in the population in response to changes in health care policy, modification in Medicare services, etc.). It, however, may be unsatisfactory in applications dealing with “personalized” analyses when one is more concerned about the response of individual characteristics to preventive measures or medical interventions. In this situation, one has to “track” individual age trajectories of physiological states, i.e., use different model parameters to describe the age trajectories of the functional states for different individuals. In such individualized applications, taking the measurement error into account could be an important issue. The model can easily be extended to this case. The random process described by equation (3) can be personalized, i.e., (ideally) each individual can be characterized by his/her own stochastic process independent of the processes describing the other individuals.

Since the conditional distribution of Y_t among survivors is Gaussian, whereas most of physiological indices that can be represented by Y_t are positive, and because the model’s characteristics have to be biologically interpreted, appropriate constraints on the parameters of the model are necessary in the estimation procedure. In particular, a) the distribution of Y₀ should guarantee a negligible probability of negative values; b) the functions f₁(t,Z) and f₀(t,Z) should have non-negative values for each age; c) the absolute values of feedback coefficients in the matrix a(t,Z) in (3) should not become too small for the trajectories of Y_t to tend to f₁(t,Z)); d) the background hazard μ₀(t, Z) should have non-negative values for each age and a non-decreasing age pattern; and e) the matrix Q(t,Z) should remain non-negative definite for each age. Our practical experience with these models shows that such constraints usually do not impose limitations in applications of models to real data. An alternative approach would involve the use of the geometric Brownian motion (GBM) for description of trajectories of physiological variables. GBM is, for example, the most popular model used in financial mathematics for description of stock price dynamics (see, e.g., the works by Samuelson [74], Black and Scholes [75], and Merton [76], and numerous developments and applications of this theory in the later decades). GBM ensures that the modeled trajectories are non-negative, which is the desired property for trajectories of physiological variables. Such considerations, however, are beyond the scope of this paper.

2.3 Simulation studies

We generated 100 datasets with data on life spans and a hypothetical physiological index (mimicking pulse pressure) for 5,000 individuals in each dataset. We followed individuals for 56 years with 28 biennial observations of physiological indices, with ages at entry to the study uniformly distributed over the age interval [30, 60]. Individuals with life spans exceeding the age at entry plus duration of the follow-up period (56 years) were considered censored at this age. Such a data structure is similar to the Framingham Heart Study original cohort data [77, 78]. We estimated the one-dimensional version of the model (equations (2), (3)) with a constant diffusion coefficient (function b), σ₁, linear functions of age (t) for the quadratic hazard term (function μ₁), the adaptive capacity (i.e., the negative feedback coefficient a), and the physiological “norm” (function f₀): μ₁(t) = a_μ1 + b_μ1t, a(t) = a_Y + b_Y(t - 30), f₀(t) = a_f0 + b_f0(t - 30), and a Gompertz function for the baseline hazard: ln μ₀(t) = ln a_μ0 + b_μ0(t - 30) (note that for simplicity all these characteristics are assumed independent of covariates (Z)). The “allostatic trajectory” (function f₁) was assumed dependent on age (t) and a dichotomous covariate Z (Z = (0, 1); P(Z = 1) = 0.5): f₁(t, Z) = a_f1 + b_f1(t - 30) + β_f1 Z. The initial value of the diffusion process for Y_t, Y₀, was assumed normal, Y₀ ~ N(f₁(t₀, Z), σ₀), where t₀ is the age at the baseline exam for the respective individual. Initial values of the parameters are given in Table 1 in the row labeled True Values.

Table 1.

Means, standard deviations (St. Dev.) and minimal and maximal values of parameter estimates in 100 simulated data sets

	ln aμ0	b μ 0	aμ1 · 104	bμ1 · 105	aY	bY · 103	σ 0	σ 1	a f1	b f1	a f0	b f1	β f1
Mean	−7.009	0.080	1.486	0.305	−0.200	0.990	6.008	5.001	54.986	0.201	50.016	0.200	4.992
St. Dev.	0.144	0.003	0.364	0.062	0.004	0.142	0.060	0.016	0.136	0.005	0.393	0.013	0.137
Min	−7.321	0.074	0.583	0.169	−0.212	0.671	5.856	4.961	54.617	0.189	49.044	0.156	4.673
Max	−6.705	0.087	2.256	0.468	−0.188	1.432	6.168	5.042	55.287	0.211	51.156	0.232	5.441
True Values	−7.0	0.08	1.5	0.3	−0.2	1.0	6.0	5.0	55.0	0.2	50.0	0.2	5.0

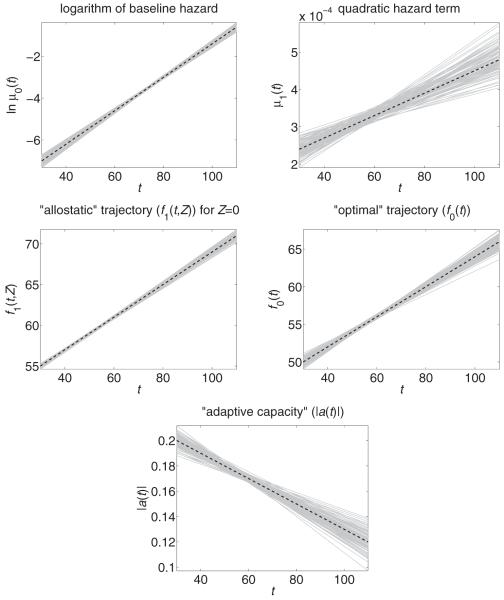
The results of simulations are summarized in Table 1 and Figure 1. The simulations confirm that the parameters of the models can be estimated with reasonable accuracy for a sample size of this magnitude.

Fig. 1.

Estimated (solid grey lines) and true (dashed black lines) trajectories in 100 simulated data sets

3. Discussion

In experimental studies of aging using populations of laboratory animals, the sensitivity of the individual aging process to external disturbances (e.g., medical interventions), or genetic manipulations often is evaluated by comparing empirical survival functions (or mortality rates) constructed for populations in the experimental and control groups. Similarly, the slope of the logarithm of the mortality curve at the adult and old ages often is interpreted as the aging rate [79]. The limitations of such an interpretation have been discussed in a number of papers. Yashin et al. [80] argued that the use of such a measure of the aging rate may be misleading: the changes in the slope of the mortality curve may occur for many other reasons having little to do with the aging process. For example, the slope could change as a result of changes in the heterogeneity distribution (e.g., distribution of frailty [81, 82]), saving individuals’ lives by providing necessary medical help in cases of emergency, etc. Analyzing changes in mortality rates in developed countries, Rozing and Westendorp [83] came to the conclusion that recent progress in mortality reduction does not affect the slope of the logarithm of the mortality curves (see also [80] and references therein for similar observations). Koopman et al. [84] criticized the use of the slope of the logarithm of the mortality curve as a measure of the aging rate and proposed, instead, the use of the age derivative of the mortality rate as such a measure. Although the use of the derivative overcomes some limitations of the slope measure, it could also be criticized because it does not link changes in mortality with biological changes in the aging human body. Data on many such changes affecting health and survival events are collected in longitudinal data. That is why in situations characterized by the wide spectrum of longitudinal data and findings on aging, focusing solely on the properties of the mortality curve and ignoring the presence of other relevant information about aging-related changes affecting survival chances is scientifically incomplete.

The need for the development of new models of aging, health, and mortality and for describing their connection with traditional demographic models has been emphasized by Manton and Yashin [48]. The connection between the Gompertz model of the mortality curve with the model describing longitudinal data played an important role in better understanding forces and mechanisms shaping the age pattern of the demographic mortality rate (see [48] and references therein). This connection is described by the conditional mortality rate in the form of a generalized Gompertz model:

$$\mu (t,Y_t)={\tilde{Y}}_t^T\tilde{Q}{\tilde{Y}}_t{e}^{\theta t},$$ (7)

where ${\tilde{Y}}_t^T=(1,Y_t^T)$ is a vector of covariates Y_t (e.g., physiological indices), t is age, $\tilde{Q}$ is a (constant) matrix, and θ is the Gompertz exponential growth parameter [48]. In applications of this model to longitudinal data, the estimated value of the parameter θ has always been smaller than the corresponding parameter in a Gompertz model that does not include information on covariates. The reduction of the exponential growth parameter has been interpreted as an effect of measurements: the new (reduced) value of the parameter θ characterized the unexplained component of aging-related increase in the mortality rate. Versions of this model have been applied to several datasets.

For example, Manton et al. [71] applied the generalized Gompertz model in (7) to longitudinal data from the first 18 biennial examinations of the Framingham Heart Study (FHS) and compared the results with those obtained from the first 3 waves of the National Long Term Care Survey (NLTCS: 1982, 1984, and 1989). The use of 10 cardiovascular covariates in the FHS model reduced the θ-parameters from 9.4% to 8.1% for males and from 10.0% to 8.1% for females. The FHS study population ranged from 30 to 60 years at the start of the 34-year observation period; hence, the reduced θ-parameters implied that the FHS mortality rates would double every 8.6 years if one were to hold the observed covariates constant at their age-30 values.

The use of 27 ADL, IADL, and physical performance covariates in the NLTCS model reduced the θ-parameters from 8.2% to 5.3% for males and from 9.1% to 4.8% for females. The NLTCS study population was 65 years or older at each wave; hence, the reduced θ-parameters implied that the mortality rates would double every 13.1 or 14.6 years (males, females) if one were to hold the observed covariates constant at their age-65 values. The relative reductions in θ and the corresponding increases in the doubling times were larger for the NLTCS model, indicating that the NLTCS covariates explained more of the age-dependence of mortality than the FHS covariates explained. The differences were attributable, in part, to the age patterns of several FHS covariates which reached peak values near age 60, followed by declines at older ages [61].

The conditional hazard rate (7) in the one-dimensional version of the original model can be represented as follows:

$$\mu (t,Y_t)=({\mu }_0+{\mu }_1{(Y_1-c)}^2)e^{\theta t}={\mu }_0{e}^{\theta t}+{\mu }_1{e}^{\theta t}{(Y_t-c)}^2,$$ (8)

where μ₀, μ₁ and c are constants. The term (μ₀ + μ₁(Y_i - c)²) in (8) describes one of the parameters of the Gompertz mortality model explained by observations Y_t. Thus, equation (8) can be interpreted as providing a more detailed description of the Gompertz mortality curve widely used in demography. In another interpretation, the term μ₀e^θt is interpreted as the “optimal” Gompertz mortality rate which would be observed in an ideal situation when Y_t ≡ c. This representation clearly shows the limitations of the original version: (i) the exponential multipliers in both components of the risk function are the same; (ii) the minimum of the second (quadratic hazard) term is reached at a constant level of the observed covariates.

In the generalized hazard model (1) described above, the covariates’ values minimizing the risk function can change over age. This is a more realistic assumption since in epidemiologic and medical practice specialists often use the notion of physiological “norm”, specific to a given age. This age-dependent norm is explicitly included in the description of age trajectories of mortality risk (compare equations (1), (2), and (8)). This allows one to statistically test hypotheses about age dependence of physiological norms and verify such dependence from available data. The modified hazard model (1) includes the earlier version (8) as a particular case.

In the generalized model, the term μ₀(t) can differ from the multiplier of the quadratic hazard μ₁(t) (we omit dependence of these functions on Z to make this case comparable with (8)) which results in a completely new interpretation of these coefficients. The hazard rate μ₀(t) is associated with death from unmeasured factors. The risk μ₀(t) must be smaller than the total (demographic) mortality risk $\stackrel{‒}{\mu }\left(t\right)$ calculated in the absence of observations on risk factors. Therefore, μ₀(t) characterizes the mortality remaining after all observed covariates follow the “optimal” trajectory and its interpretation remains similar to that used in the original model. In case of a Gompertz specification, both Gompertz parameters in μ₀(t) can be evaluated and compared with their values in $\stackrel{‒}{\mu }\left(t\right)$. This model allows for evaluating the gain in life expectancy when observed covariates follow normal age trajectories.

The term μ₁(t) clarifies the connections between senescence, longevity, and stress-resistance. Indeed, the increasing pattern of μ₁(t) indicates that the branches of the respective U-shaped risk function get steeper, and the range of tolerant deviations of the resultant risk factor from its “optimal” value becomes narrower with age, reflecting the decline in stress resistance with age. Although many aspects of such connections have been investigated in experimental animal studies [56], they have never been adequately addressed in studies of human longitudinal data. Since the decline in stress resistance is an important indicator of aging (senescence), the rate of increase in μ₁(t) (not the slope of the logarithm of the mortality curve) may characterize the rate of aging. More generally, the increasing role of senescence in mortality risk could be captured by the widening pattern of the U-shape of the relative risk, which would indicate a faster increase in μ₀(t) compared to μ₁(t). An important methodological advance of the extended model is that it is transformed to a form where effects of senescence on survival, longevity, and disease development may be evaluated from longitudinal data.

Taking into account the age dependence of the functions f₁(t,Z), f₀(t,Z), and a(t,Z) allows for testing hypotheses about factors and mechanisms affecting the dynamic properties of the age trajectories of physiological states. For example, one could test whether f₁(t,Z) coincides with f₀(t,Z). The difference in these functions means that the processes of allostatic adaptation in response to persistent external disturbances do not tend to minimize mortality risk. One can also test the hypothesis about declines in “adaptive capacity” in the aging human body and evaluate patterns of such declines. All such hypotheses can be tested using the likelihood ratio test. For example, to test the hypothesis about the decline in adaptive capacity with age, one needs to estimate the model first with a decline (say, a linear decline with age in a(t,Z)) and then the model without such a decline (i.e., a(t,Z) is independent of age), where all other functions (except a(t,Z)) are specified similarly in both models, and compare the likelihood functions in these two models using the likelihood ratio test.

The use of observed fixed covariates Z in the functions f₀(t,Z), Q(t,Z), a(t,Z), b(t,Z), and f₁(t,Z) makes the model more personalized. The notion of the “norm” may differ for individuals carrying different alleles or genotypes, or having different histories of events and processes experienced by an individual during the life course (e.g., diseases, environmental exposures), etc. These indicate the need for developing a more general methodology, which could incorporate individualized notions of “norms” and adaptive responses.

An important feature of the model discussed above is the preservation of the Gaussian property in the operation of conditional averaging. If the distribution of risk factors at the initial wave of observations, Y₀, is Gaussian, the distribution of Y_t among survivors is also Gaussian. This allows for describing the probability distributions of dynamic covariates in terms of the first two moments which satisfy ordinary non-linear differential equations. Note that the Gaussian distribution allows for negative values of the risk factors to occur with positive probability. Our studies show that in practice this property does not limit the analyses. The model can also be used as two-moment approximation for the age trajectories of covariates which follow non-Gaussian dynamics. In non-Gaussian cases, the model could also be extended to include higher order moments (e.g., conditional semi-invariants).

Highlights.

• An approach to analyses of longitudinal data on aging, health, and longevity.

• Stochastic process models of human aging, health, and longevity is suggested.

• Incorporating state of the art advances in aging research into the model structure.

• Model deals with resistance to stresses, adaptive capacity, and physiological norms.