Stochastic model search with binary outcomes for genome-wide association studies

Abstract

Objective

The spread of case–control genome-wide association studies (GWASs) has stimulated the development of new variable selection methods and predictive models. We introduce a novel Bayesian model search algorithm, Binary Outcome Stochastic Search (BOSS), which addresses the model selection problem when the number of predictors far exceeds the number of binary responses.

Materials and methods

Our method is based on a latent variable model that links the observed outcomes to the underlying genetic variables. A Markov Chain Monte Carlo approach is used for model search and to evaluate the posterior probability of each predictor.

Results

BOSS is compared with three established methods (stepwise regression, logistic lasso, and elastic net) in a simulated benchmark. Two real case studies are also investigated: a GWAS on the genetic bases of longevity, and the type 2 diabetes study from the Wellcome Trust Case Control Consortium. Simulations show that BOSS achieves higher precisions than the reference methods while preserving good recall rates. In both experimental studies, BOSS successfully detects genetic polymorphisms previously reported to be associated with the analyzed phenotypes.

Discussion

BOSS outperforms the other methods in terms of F-measure on simulated data. In the two real studies, BOSS successfully detects biologically relevant features, some of which are missed by univariate analysis and the three reference techniques.

Conclusion

The proposed algorithm is an advance in the methodology for model selection with a large number of features. Our simulated and experimental results showed that BOSS proves effective in detecting relevant markers while providing a parsimonious model.

Introduction and background

Many of the advances in genome-wide association studies (GWASs) are based on the analysis of case–control data. The goal of such studies is usually to correlate a phenotype, often coded as a binary variable, with genetic markers such as single nucleotide polymorphisms (SNPs). The outcomes of GWASs are increasingly integrated with next-generation sequencing results for SNP validation and disease marker extraction. Therefore, GWASs are powerful tools for the identification of interesting regions at the genome-wide level for further investigation by high-definition procedures.¹

Regrettably, achieving the promising goals mentioned above is hindered by the technical difficulties accompanying GWASs. Recent genotyping technologies allow the extraction of millions of genetic measurements, but the number of subjects is smaller by several orders of magnitude. In the literature, this is known as a ‘p>n’ problem. The key task is to reduce the dimensionality of the problem by identifying the optimal subset of predictors that are informative with respect to the outcome variable. Widely used techniques such as univariate or stepwise regression, are recognized as insufficient to fully address the above issues. Advanced multivariate methods are therefore required in order to determine the biological truth.^2–4

Recently, a number of model search algorithms have been proposed, with particular emphasis on sparse linear models based on regularization methods^{5 6} and naive-Bayes techniques.⁷ Furthermore, Bottolo and Richardson designed a new method for Bayesian model selection for linear regression with continuous outcomes.⁸ Unlike regularization analysis, this method performs a model search by sampling the predictors on the basis of a general and efficient Markov Chain Monte Carlo (MCMC) technique that exploits the conjugacy structure of data and parameters.

In the case of binary outcomes, however, easy analytical tractability is only partially possible, mainly because of the non-linear link between the observed variables and the underlying predictors. Although a detailed Bayesian analysis for binary and categorical responses is available,⁹ model search techniques for binary data have only been explored in a limited number of cases.^10–12

Objective

In the present paper, we propose an innovative stochastic model search technique for binary outcomes. The relationship between the observed responses and the available predictors is described by a latent variable model with a probit link,⁹ rather than resorting to Gaussian approximations.¹² Prior distributions are assigned both to the regression coefficients and the model size, therefore allowing the user to specify a prior belief on the model complexity. A computationally efficient Metropolis-Hastings sampling algorithm⁸ is adopted. Our method extensively explores the model space to identify the important predictors.

Materials and methods

Latent variable model for binary data

Denote with Y the vector of the observed individual binary responses Y_i, where i=1…n and n is the number of subjects. The Y_i are assumed to be the results of independent Bernoulli trials with success probability π_i. Let x_i=(x_i1, …, x_ip)^T be the covariate vector associated with response Y_i, where p is the total number of predictors. Additionally, let β=(β₁, …, β_p)^T be the vector of regression coefficients for the p predictors.

The relationship between observed binary responses and covariates is usually modeled with a link function g, which expresses the dependency of the success probabilities π_i on the linear regressor x_i^Tβ. Taking g as the standard normal distribution Φ yields the probit model:

$${\pi }_i=\Phi \left({\mathbf{x}}_i^T\mathit{\beta }\right)={\displaystyle {\int }_{-\mathrm{\infty }}^{{\mathbf{x}}_i^T\mathit{\beta }}N(0,1)du}$$ (1)

where β, in a Bayesian perspective, can be assigned a multivariate normal prior. Unfortunately, the resulting posterior density of β is not analytically tractable,⁹ although approximations are available in the literature.

In order to circumvent the above issue and obtain the posterior of β, one can resort to a data augmentation approach as described by Albert and Chib.⁹ The idea is to introduce n independent latent variables Z=(Z₁, …, Z_n)^T such that each Z_i ∼ N(x_i^Tβ, 1), letting Y_i=0 if Z_i≤0 and Y_i=1 if Z_i>0. Equation 2 summarizes the latent variable model:

$$Y_i=\{\begin{array}{cc}0& Z_i\le 0\\ 1& Z_i>0\end{array}\mathbf{Z}=\mathbf{X}\mathit{\beta }+\mathit{\varepsilon }$$ (2)

where X is the n×p design matrix with i-th row equal to x_i^T and ɛ is a vector of independent normal errors with zero mean and unit variance.

Of course, if the Z_i were known, and if β were assigned a multivariate normal prior, the posterior of β would be obtained through usual Bayesian linear regression results. Although the Z_i are actually not known, their distribution conditional on the data Y_i is a truncated normal with mean x_i^Tβ and unit variance, the side of truncation depending on the value of Y_i. One could therefore resort to Gibbs sampling to iteratively sample Z and β, thus obtaining the required posteriors.

Variable selection

The goal of variable selection is to model the dependency of Y (or equivalently Z) on a subset of the predictors x₁, …, x_p. However, there is uncertainty about which subset to use. In this work, we follow the approach of Bottolo and Richardson⁸ and introduce a latent binary vector γ=(γ₁, …, γ_p)^T such that γ_j=0 if β_j=0 and γ_j=1 if β_j≠0. The model space is therefore given by the 2^p possible combinations of the indicator variables γ_j. Given γ, the Gaussian linear model in equation 2 can therefore be modified as:

$$\mathbf{Z}=\alpha \mathbf{1}+{\mathbf{\text{X}}}_{\mathit{\gamma }}{\mathit{\beta }}_{\mathit{\gamma }}+\mathit{\varepsilon }$$ (3)

that also accounts for the intercept α. The symbol 1 denotes a column vector of ones. The vector β_γ includes only the coefficients corresponding to γ_j=1. Its length is denoted by p_γ. Similarly, the n×p_γ matrix X_γ is obtained from X by taking the columns for which γ_j=1. The columns of the design matrix are assumed to be centered around zero.

The intercept α is assigned a flat prior, f(α)∝1, whereas the prior distribution for β_γ is taken as a multivariate normal:

$$f\left({\mathit{\beta }}_{\mathit{\gamma }}\right|\mathit{\gamma },{\sigma }^2)=N(0,{\sigma }^2{\Sigma }_{\mathit{\gamma }})$$ (4)

Moreover, the error variance σ² is equal to 1 by definition.⁹ The matrix Σ_γ can be expressed as τI, where τ controls the degree of coefficient shrinkage and I is the identity matrix. Other specifications of the prior covariance matrix in equation 4 are covered by Bottolo and Richardson.⁸ The prior for the indicator vector γ is defined as in Kohn et al¹³:

$$f\left(\mathit{\gamma }\right)=\frac{B\left(p_{\mathit{\gamma }}+a,p-p_{\mathit{\gamma }}+b\right)}{B(a,b)}$$ (5)

which gives rise to a beta-binomial distribution on the model size p_γ. Parameters a and b can be elicited based on prior knowledge on the model size, for example, expected value and variance of p_γ.^{8 13}

In order to obtain γ, observe that, if Z were known, one could write its associated marginal likelihood by integrating out α and β_γ:

$$f\left(\mathbf{Z}\right|\mathit{\gamma })={\displaystyle \int f\left(\mathbf{Z}\right|\mathit{\gamma },\alpha ,{\mathit{\beta }}_{\mathit{\gamma }}\left)f\right({\mathit{\beta }}_{\mathit{\gamma }}\left|\mathit{\gamma }\right)f\left(\alpha \right)d{\mathit{\beta }}_{\mathit{\gamma }}d\alpha }$$ (6)

where the dependence on σ² has been dropped since it is fixed to 1. The term f(Z | γ, α, β_γ) is the multivariate normal density arising from the distribution of ɛ. Note that, up to a normalizing factor, equations 5 and 6 together yield the conditional density f(γ | Z). Also observe that such density does not depend on Y since Z is given. Additionally, observe that, if Z were known, the posterior of β_γ would follow from the usual Bayes formula for linear Gaussian regression.

The model specification is completed by defining the full conditional for Z. As stated in the previous paragraph, conditional on Y_i and β_γ, the densities of Z_i are independent truncated normals:

$$f\left(Z_i\right|Y_i,{\mathit{\beta }}_{\mathit{\gamma }})=\{\begin{array}{cc}T{N}^{-}\left({\mathbf{x}}_{i,\mathit{\gamma }}^T{\mathit{\beta }}_{\mathit{\gamma }},1\right)& Y_i=0\\ T{N}^{+}\left({\mathbf{x}}_{i,\mathit{\gamma }}^T{\mathit{\beta }}_{\mathit{\gamma }},1\right)& Y_i=1\end{array}$$ (7)

where TN⁻ and TN⁺ denote right- and left-truncated normal densities respectively, and x_i,γ^T is the i-th row of X_γ.

Sampling algorithm: Binary Outcome Stochastic Search (BOSS)

Equations 4–7 allow devising a sampling scheme to obtain the posterior density of the latent binary vector γ, which is the main goal of the model search procedure. Our algorithm is based on an efficient Fast Scan Metropolis-Hastings (FSMH) sampler introduced by Bottolo and Richardson⁸ and generalized here to account for binary responses.

The key idea of our algorithm is that, if Z is assumed known, the variable selection problem for binary outcomes reduces to one for continuous outcomes. In such a case, efficient algorithms are available to sample from the conditional density of γ.^{8 12} As shown by Bottolo and Richardson,⁸ sampling γ can be achieved through the FSMH sampler using equations 5 and 6. Once a sample of γ is available, a new value of Z is then sampled from its full conditional distribution and the process is iterated.

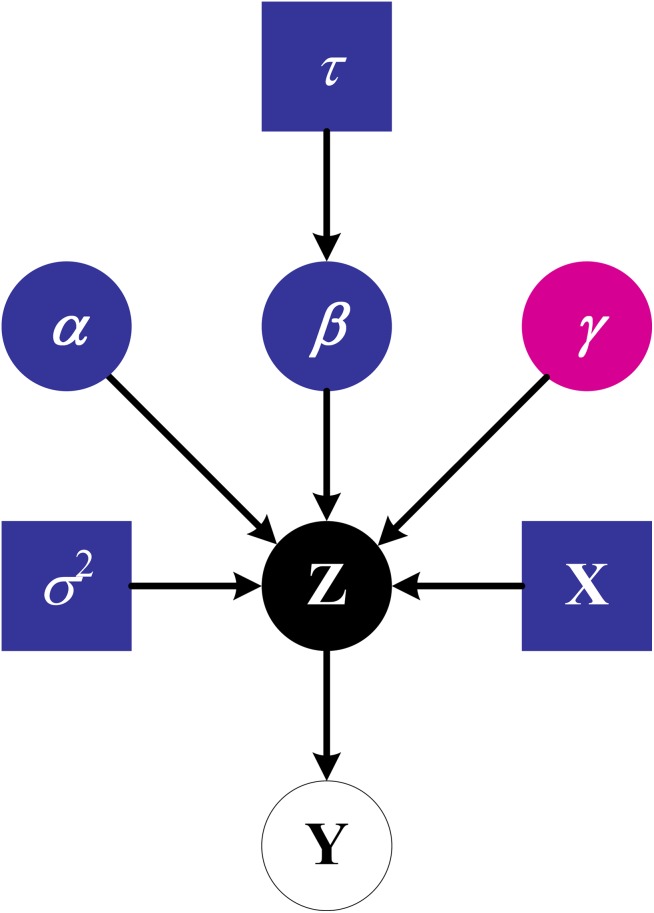
The sampling scheme, depicted in figure 1, is implemented as follows:

Figure 1.

Relationships among the stochastic nodes sampled by BOSS. Squares denote constants (eg, the design matrix), and circles denote random variables.

1. Choose a random initialization for Z (positive or negative according to its corresponding Y_i, see equation 7);

2. Sample γ through the FSMH sampler, using the prior model size in equation 5 and the marginal likelihood of Z in equation 6;

3. Given Z and γ, sample β_γ through the standard Bayesian linear regression. Note that, given Z, such density does not depend on Y;

4. Given β_γ and Y, sample Z from equation 7;

5. Restart from step 2 until a pre-determined number of iterations is reached.

Experimental data and software implementation

The proposed approach has been applied to a first GWAS on the genetic bases of longevity,¹⁴ and a second GWAS aimed at the genetic dissection of the type 2 diabetes (T2D) trait.¹⁵ The latter dataset has been provided by the Wellcome Trust Case Control Consortium (WTCCC) after data access approval.

Individual and marker-level data quality control, inbred patients, and genetic outliers removal have been described by Malovini et al¹⁴ and the WTCCC.¹⁵ A preliminary feature selection has been performed based on the results from univariate Pearson's χ² tests with 2 degrees of freedom comparing genotype distributions between cases and controls. Only SNPs characterized by complete genotype data, passing the significance threshold (p<0.40 for the longevity dataset and p<0.01 for the T2D dataset) and featuring at least five counts per cell have been retained. Missing values in the T2D dataset were imputed to the modal value for each SNP. The above statistical analyses have been performed with PLINK.¹⁶ BOSS was implemented in MATLAB 7.5.0 R2007b¹⁷ together with the RANDRAW routine¹⁸ to sample from the truncated normal density.

Results

Simulated benchmark

A simulation study was performed to assess the performances of BOSS, stepwise regression (stepwisefit function in MATLAB¹⁷), and two state-of-the-art methods, logistic lasso and elastic net¹¹ (package glmnet in R V.2.13.1¹⁹). Our benchmark featured simulated scenarios of varying complexity, according to the following characteristics of the design matrix X:

• Uncorrelated or correlated columns (pairwise correlation of 0.5);

• Percentage of explained variance (ie, proportion of variance of Z explained by the predictors).

Therefore, we simulated 2×3=6 scenarios, labeled as follows:

• A₉₀: uncorrelated X, 90% explained variance;

• A₇₀: uncorrelated X, 70% explained variance;

• A₅₀: uncorrelated X, 50% explained variance;

• B₉₀: correlated X, 90% explained variance;

• B₇₀: correlated X, 70% explained variance;

• B₅₀: correlated X, 50% explained variance.

We set n=200 and p=300, so that p>n. Synthetic datasets were generated by simulating a design matrix X according to the characteristics described above, and a vector of independent normally distributed errors ɛ with zero mean and unit variance. Only the first 10 parameters of the vector β were set to a non-zero value, so as to yield 10 true predictors. The module of such parameters was set so as to obtain the given percentage of explained variance. The 10 true parameters were assigned alternating signs. The values of Z_i so generated were then binarized according to their sign to obtain Y_i (equation 2). Each dataset featured an approximately equal number of cases and controls. For each scenario, 50 simulated datasets were generated.

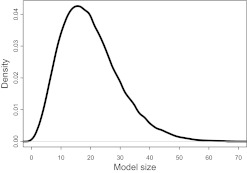
BOSS was run for 6000 iterations (first 1000 of burn-in). The prior model size p_γ was specified by E[p_γ]=20 and Var[p_γ]=100, which elicited the values a=4.52 and b=63.26. Parameter τ was fixed to 1, as done by Bottolo and Richardson⁸ and Hans et al,¹² except in scenarios A₅₀ and B₅₀ where a value of 0.1 proved more suitable. In principle, one could additionally sample τ to actually optimize the algorithm performances. The prior mean and variance were chosen so as to cover a reasonable range of plausible model sizes. The resulting prior density for p_γ is depicted in figure 2.

Figure 2.

Prior density of model size p_γ used for BOSS in the simulation benchmark.

Logistic lasso and elastic net were run with the ‘one-standard-error rule’ to choose the penalty parameter.¹¹ The elastic net method was executed with equal lasso and ridge-regression penalties. Stepwise regression was performed using the default settings of the stepwisefit function.

The goal of the simulated benchmark was to assess the capabilities of BOSS, logistic lasso, elastic net, and stepwise regression to capture the true predictors used to generate the data, while discarding useless predictors. For this purpose, we evaluated precision, recall, and F-measure relative to the number of predictors correctly/incorrectly identified as true/false. In the case of BOSS, a predictor was deemed ‘true’ if its marginal posterior probability of inclusion^{8 12} was at least 50%.

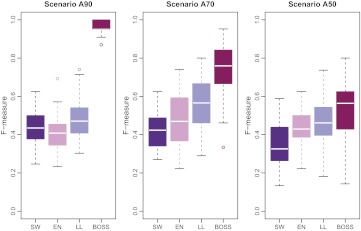
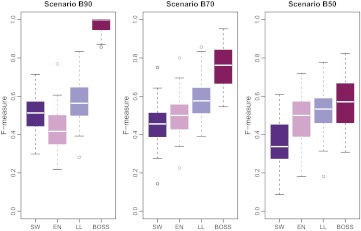
Results of the comparison are reported in figure 3 for uncorrelated predictors (A₉₀, A₇₀, and A₅₀) and in figure 4 for correlated predictors (B₉₀, B₇₀, and B₅₀). The two figures show the distribution of F-measure values obtained with BOSS, logistic lasso, elastic net, and stepwise regression in each scenario. Average numerical values are also reported in table 1 for precision and recall.

Figure 3.

F-measure comparison in scenarios A₉₀, A₇₀, and A₅₀ (uncorrelated predictors). EN, elastic net; LL, logistic lasso; SW, stepwise regression.

Figure 4.

F-measure comparison in scenarios B₉₀, B₇₀, and B₅₀ (correlated predictors). EN, elastic net; LL, logistic lasso; SW, stepwise regression.

Table 1.

Comparison of precision, recall, and F-measure obtained with stepwise regression (SW), elastic net (EN), logistic lasso (LL) and BOSS

Scenario	Average precision				Average recall				Average F-measure
	SW	EN	LL	BOSS	SW	EN	LL	BOSS	SW	EN	LL	BOSS
A90	0.29	0.26	0.33	0.93	1	0.99	0.99	1	0.44	0.40	0.49	0.96
A70	0.28	0.35	0.45	0.78	0.93	0.89	0.89	0.80	0.42	0.48	0.57	0.75
A50	0.23	0.40	0.52	0.68	0.73	0.54	0.50	0.46	0.34	0.44	0.46	0.53
B90	0.35	0.28	0.39	0.95	1	1	1	0.98	0.52	0.43	0.56	0.96
B70	0.31	0.35	0.44	0.78	0.82	0.95	0.93	0.77	0.45	0.50	0.59	0.76
B50	0.26	0.48	0.59	0.83	0.63	0.68	0.61	0.47	0.36	0.49	0.52	0.58

Each value is the average across the 50 datasets simulated in each scenario. In terms of F-measure, BOSS performed better than the three reference methods (p<0.01, one-sided paired t test).

In most scenarios considered here, BOSS outperformed the three reference methods in terms of F-measure. Although BOSS achieved generally lower recall rates, it attained higher values of precision and a better overall tradeoff. Larger priors on the model size and a larger number of iterations did not substantially affect the results obtained with BOSS.

Interestingly, the performances of the four methods did not degrade if predictors were correlated. Overall, logistic lasso proved superior to the traditional stepwise regression and comparable to the elastic net.

Furthermore, we assessed the ability of the four methods to correctly predict newly observed binary responses that were not used for parameter estimation. For this purpose, 50 additional datasets-per-scenario were simulated. The new outcomes were then predicted using the features selected by each method. Prediction performances were evaluated in terms of correctly/incorrectly predicted positive/negative responses. A new outcome was predicted as positive (y=1) if the corresponding probability, reconstructed with the selected features, was greater than a given threshold. We then evaluated specificity, sensitivity, and prediction accuracy for thresholds from 0.05 to 0.95, with steps of 0.05. In order to obtain summary statistics, we computed the area under the receiver operating characteristic (ROC AUC) using mean specificity and sensitivity for a given threshold. Additionally, we calculated the average prediction accuracy across all thresholds.

Table 2 shows the results of our predictive analysis. In most cases, the AUC obtained with BOSS is only slightly greater than with the other three methods. In terms of accuracy, however, BOSS achieves a substantial improvement.

Table 2.

Comparison of prediction performances on new data using the selected features

Scenario	ROC AUC				Average accuracy
	SW	EN	LL	BOSS	SW	EN	LL	BOSS
A90	0.86	0.92	0.93	0.96	0.60	0.66	0.71	0.85
A70	0.78	0.82*	0.82*	0.82	0.59	0.60	0.61	0.70
A50	0.64	0.65	0.66	0.67	0.54	0.53	0.53	0.57
B90	0.87	0.92	0.93	0.94	0.60	0.68	0.71	0.80
B70	0.70	0.77*	0.78*	0.77	0.54	0.57	0.58	0.64
B50	0.64	0.68*	0.67*	0.68	0.54	0.54	0.54	0.56

Except where indicated (*), BOSS improved on the three reference methods (p<0.05, one-sided paired t test).

EN, elastic net; LL, logistic lasso; ROC AUC, area under the receiver operating characteristic; SW, stepwise regression.

Experimental case studies

This section reports the results obtained by BOSS and the three reference methods on the two experimental GWASs.

GWAS on exceptional longevity

A total of 410 long aged individuals (cases), 553 average living controls and 290 364 autosomal SNPs passing data quality control underwent a feature selection pre-processing phase. A subset of 5707 SNPs, selected according to the inclusion criteria reported in the Materials and methods section, were then considered for subsequent analyses. BOSS was run for 20 000 iterations (first 5000 of burn-in; running time of about 4.5 days). The prior model size p_γ was specified by E[p_γ]=20 and Var[p_γ]=100, so as to encompass a range of plausible model sizes without being overly restrictive.

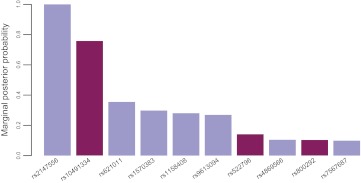
Our analysis allowed the identification of several relevant markers. In particular, the intergenic SNP rs2147556 achieved a 100% probability of inclusion, while rs10491334, mapping to CAMK4 and previously identified as strongly associated,¹⁴ achieved a probability of about 76%. Moreover, BOSS was able to identify rs522796 (KL gene) as mildly associated with the outcome (probability of 14%). This SNP was reported to be related to non-diabetic end-stage renal disease²⁰ and preterm birth.²¹ SNP rs800292, mapping to CFH and known to be associated with age-related macular degeneration,²² was also identified, although with a relatively low probability of inclusion (10%). Posterior probabilities of SNPs obtained with BOSS are shown in figure 5. We limited the plot to the top 10 SNPs in order to summarize the most relevant findings only.

Figure 5.

Marginal posterior probabilities of the 10 top single nucleotide polymorphisms (SNPs) identified by BOSS in the longevity dataset. Darker bars denote SNPs previously reported in the literature.

In order to further evaluate the results obtained by the proposed model search technique, we additionally fitted a multivariate logistic regression model on the top 10 predictors of figure 5. Results are summarized in table 3.

Table 3.

Summary of results from logistic regression on the top 10 predictors identified by BOSS in the longevity dataset

SNP	Chr	Position (bp)	Gene	OR (95% CI)	p Value
rs2147556	13	72010472		0.58 (0.46 to 0.72)	1.8×10−6
rs10491334	5	110800303	CAMK4	0.58 (0.45 to 0.76)	5.3×10−5
rs621011	11	78294837		1.52 (1.24 to 1.87)	7.4×10−5
rs1570383	6	126241555		0.61 (0.47 to 0.78)	1.1×10−4
rs1158408	4	67799134		1.55 (1.21 to 1.99)	5.0×10−4
rs9613094	22	24788388		0.58 (0.44 to 0.75)	6.0×10−5
rs522796	13	32528055	KL	1.36 (1.12 to 1.67)	2.5×10−3
rs4869566	5	38165184		0.67 (0.54 to 0.84)	4.5×10−4
rs800292	1	194908856	CFH	1.53 (1.19 to 1.97)	9.7×10−4
rs7567687	2	129750796		0.69 (0.56 to 0.85)	4.1×10−4

Chr, chromosome; Position (bp), physical position on the chromosome expressed in terms of base pairs; SNP, single nucleotide polymorphism.

It is interesting to observe that the minor allele of rs800292 has a predisposing additive impact on longevity (OR=1.53): this is in accordance with the results obtained by Yang et al, who showed a significant association of rs800292 with a reduced risk for exudative age-related macular degeneration.²²

As a further step, we ran logistic lasso, elastic net, and stepwise regression on the longevity data to assess possible differences with the results obtained by BOSS. The three algorithms were run with the same settings described in the Simulated benchmark section of the Results section. In our analysis, the logistic lasso included most of the features reported in figure 5, but failed to detect rs800292. The elastic net yielded a more parsimonious model, which included four SNPs (rs2147556, rs10491334, rs621011, and rs522796). Stepwise regression selected a large number of features (891): all SNPs in figure 5 were included except rs522796.

GWAS on T2D

A total of 1924 T2D patients, 1458 UK Blood Service (UKBS) controls and 456 856 autosomal SNPs (mapping to chromosomes 1–22) passing data quality control¹⁵ underwent a features selection phase (see Materials and methods section). A total of 4102 markers were then considered for subsequent analyses. We ran BOSS for 700 iterations (first 200 of burn-in; running time of about 1 day). Increasing the number of iterations did not yield appreciably different results. The prior model size p_γ was specified by E[p_γ]=4 and Var[p_γ]=4, in order to allow BOSS identify only the most relevant genetic features.

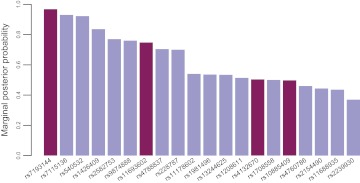
Our analysis detected several SNPs mapping to gene regions which have been previously associated with metabolic syndromes or other disease classes. In particular, the top ranked SNP rs7193144 is an intronic marker mapping to FTO, a gene that has been already associated with T2D and obesity conditions in several European cohorts.^{15 23–25} Moreover, rs4132670 and rs10885409 map to TCF7L2, previously reported to be associated with T2D.^{15 26 27} Last, rs11693602 is localized within the RBMS1 gene, which has been associated with T2D by Qi et al.²⁸ Posterior probabilities of SNPs obtained with BOSS are shown in figure 6. We limited the plot to the top 20 SNPs in order to summarize the most relevant findings only.

Figure 6.

Marginal posterior probabilities of the 20 top single nucleotide polymorphisms (SNPs) identified by BOSS in the type 2 diabetes (T2D) dataset. Darker bars denote SNPs previously reported in the literature.

Additionally, we performed further model evaluation by fitting a multivariate logistic regression on the genetic markers reported in figure 6. Results are reported in table 4.

Table 4.

Summary of results from logistic regression on the top 20 predictors identified by BOSS in the T2D dataset

SNP	Chr	Position (bp)	Gene	OR (95% CI)	p Value
rs7193144	16	53810686	FTO	1.25 (1.13 to 1.39)	2.4×10−5
rs7115136	11	98935203		0.79 (0.71 to 0.89)	4.1×10−5
rs540532	2	30954621		1.38 (1.20 to 1.59)	8.3×10−6
rs1426409	4	37173944		0.78 (0.69 to 0.88)	3.6×10−5
rs2582753	2	191216109		1.34 (1.18 to 1.52)	4.7×10−6
rs9874888	3	60016317		0.76 (0.67 to 0.85)	5.3×10−6
rs11693602	2	161224658	RBMS1	0.74 (0.65 to 0.84)	4.0×10−6
rs4788837	17	72466219		0.78 (0.70 to 0.88)	2.2×10−5
rs228787	17	42099488		1.36 (1.18 to 1.57)	1.7×10−5
rs11178602	12	71491505		1.18 (1.04 to 1.34)	1.1×10−2
rs1981496	14	106645846		0.71 (0.60 to 0.84)	1.1×10−4
rs13244625	7	2206690		1.30 (1.13 to 1.49)	1.5×10−4
rs1208611	10	38160499		1.56 (1.29 to 1.89)	6.5×10−6
rs4132670	10	114767771	TCF7L2	1.36 (1.16 to 1.59)	2.0×10−4
rs1708558	6	67049406		0.75 (0.65 to 0.87)	1.6×10−4
rs10885409	10	114808072	TCF7L2	0.90 (0.77 to 1.04)	1.6×10−1
rs4760786	12	71446789		0.86 (0.75 to 0.98)	2.5×10−2
rs2154490	21	30915962		1.26 (1.12 to 1.43)	1.7×10−4
rs11688935	2	189175905		1.26 (1.13 to 1.41)	4.4×10−5
rs2239930	17	10558733		1.26 (1.12 to 1.43)	2.0×10−4

Chr, chromosome; Position (bp), physical position on the chromosome expressed in terms of base pairs; SNP, single nucleotide polymorphism.

We also performed logistic lasso, elastic net, and stepwise regression on the T2D data. All three algorithms identified more than 600 features each. However, stepwise regression and logistic lasso detected none of the four SNPs introduced above. The elastic net missed rs10885409, but captured rs7193144, rs11693602, and rs4132670.

Discussion

The results obtained offer an interesting insight into our new model search technique and its performances relative to three established methods for feature selection.

In the simulated benchmark, stepwise regression captured many features, including important ones, although at the cost of reduced precision. Logistic lasso performed better than stepwise regression and comparably to the elastic net, although both techniques attained relatively low precisions (0.26–0.59; see table 1). By contrast, as far as this simulation study is concerned, BOSS was able to discover true signals even in difficult scenarios with as low as 50% of explained variance. Note that, even if the prior model size allowed for possibly large models (up to about 60 predictors, see figure 2), BOSS was able to identify a small subset of key features that correlated well with the data, while discarding unimportant predictors. Interestingly, BOSS compared favorably with the reference methods in terms of prediction performances. Our analysis suggests that the greater ability of BOSS to detect the true predictors entails increased prediction accuracy on newly observed data.

It is worth remarking that, in principle, BOSS is also capable of handling interactions between features. Although this was not extensively explored, a preliminary simulated analysis (similar to the A₉₀ scenario) showed that BOSS successfully captured both the main and interaction effects between pairs of features.

In the longevity study, BOSS effectively accomplished variable selection with many possible predictors (about 5700 SNPs) and a smaller number of observations (n=963). BOSS successfully identified relevant genetic markers and yielded a parsimonious model, which can be used for predictive purposes. In particular, rs10491334 has been previously associated with longevity in the same population,¹⁴ while rs800292 has been previously associated with age-related macular degeneration in a cohort of Han Chinese individuals.²² Moreover, rs522796 has been reported both in relation to non-diabetic end-stage renal disease²⁰ and preterm birth.²¹

The results from logistic lasso, elastic net, and stepwise regression obtained on the longevity data were comparable, although neither the lasso nor the elastic net were able to detect rs800292. Stepwise regression yielded an overly parametrized model, with almost as many features (891) as subjects (963), but missed the association of rs522796.

In the T2D study, BOSS identified SNPs mapping to genes known to be associated with diabetes or other metabolic syndromes.^{15 23–28} Further, BOSS identified functionally relevant variants that would have been discarded by standard univariate association tests: for example, the top SNP detected by BOSS, rs7193144, achieved a univariate p value of 2.61×10⁻⁵ (χ² distribution with 2 degrees of freedom), which is greater than usual significance thresholds, for example, 1×10⁻⁵ or less. A direct comparison of our findings with those reported by the WTCCC¹⁵ is only partially feasible, since our research group has no access to the WTCCC 1958 British Birth Cohort, which was included in the original analyses as the control group. Locus-based analyses will allow identification of structural correlations and/or potential interactions between the selected SNPs and other functionally relevant unobserved variants.

Interestingly, stepwise regression and logistic lasso were able to detect a large set of features, but failed to identify the four SNPs reported in the Results section. This may be explained by convergence to a local optimum for the stepwise regression, and excessive coefficient shrinkage for the lasso. The elastic net did not detect rs10885409 but found the other three markers described above.

The computational efficiency of our approach deserves one last remark. It is a known in the literature that advanced sampling-based techniques for model selection may be computationally demanding (see, for example, O'Hara and Sillanpää²⁹), especially if compared to lasso-based methods.¹¹ In the two experimental studies, we preliminarily filtered the genetic features to approximately the same number (about 4000 and 6000), so as to demonstrate the effectiveness of our approach while keeping the computational complexity reasonable. Nonetheless, our results showed that the detection of relevant makers was not hindered. Of note, variational Bayes approaches (see, for example, Girolami et al³⁰) could be adapted for model selection to further speed up the model search.

Conclusion

The algorithm presented in this paper represents a step forward in the statistical methodology for variable selection. Binary outcomes have traditionally received less attention than continuous outcomes, mainly because of their lower analytical tractability. Moreover, the ‘p>n’ problem requires advanced techniques that allow discovery of important features without yielding overparametrized models. We tackled such challenges using a Bayesian paradigm and developed a general MCMC framework for variable selection in the presence of binary responses. The exact formulation of the likelihood paves the way to generalizations such as multinomial responses that cannot be handled simply by Gaussian approximation. The results obtained from our simulated benchmark and the two experimental case studies suggest that BOSS is an effective and reliable tool for model selection when the number of features is very large.