Abstract
Objective
Several studies have shown how sets of single-nucleotide polymorphisms (SNPs) can help to classify subjects on the basis of their continental origins, with applications to case–control studies and population genetics. However, most of these studies use dimensionality-reduction methods, such as principal component analysis, or clustering methods that result in unipartite (either subjects or SNPs) representations of the data. Such analyses conceal important bipartite relationships, such as how subject and SNP clusters relate to each other, and the genotypes that determine their cluster memberships.
Methods
To overcome the limitations of current methods of analyzing SNP data, the authors used three bipartite analytical representations (bipartite network, heat map with dendrograms, and Circos ideogram) that enable the simultaneous visualization and analysis of subjects, SNPs, and subject attributes.
Results
The results demonstrate (1) novel insights into SNP data that are difficult to derive from purely unipartite views of the data, (2) the strengths and limitations of each method, revealing the role that each play in revealing novel insights, and (3) implications for how the methods can be used for the analysis of SNPs in genomic studies associated with disease.
Conclusion
The results suggest that bipartite representations can reveal new patterns in SNP data compared with existing unipartite representations. However, the novel insights require multiple representations to discover, verify, and comprehend the complex relationships. The results therefore motivate the need for a complementary visual analytical framework that guides the use of multiple bipartite representations to analyze complex relationships in SNP data.
Keywords: Visualization of data and knowledge, human-computer interaction and human-centered computing, networks, systems to support and improve diagnostic accuracy, linking the genotype and phenotype, discovery, text and data mining methods, uncertain reasoning and decision theory
Background and significance
Because more than 99% of the 3 billion base pairs in the human genome are identical across all humans,1 the remaining <1% contains crucial information about how humans vary. This variation, resulting from millennia of natural selection and random drift, is coded in ∼20–30 million locations on the human genome, commonly referred to as single-nucleotide polymorphisms (SNPs). High-throughput genotyping technologies have helped identify SNPs that are associated with the risk of developing specific diseases2 and SNPs that are highly associated with continental origins. For example, several studies have identified SNPs that have large differences in genotype frequencies between two or more ancestral populations such as Africans and Europeans.3 Identification of such SNPs (referred to as ancestry informative markers or AIMs) have important implications for research in risk assessment, diagnosis, prognosis, and treatment of common diseases. For example, because African Americans have ∼10–15% European admixture,4 AIM SNPs can be used to select or assign subjects to subpopulations in case–control studies, with the potential of reducing confounding based on ancestral origins.5
To the best of our knowledge, the methods used in the above studies rely on a unipartite view (either SNPs or subjects) of the data. For example, studies that identify AIM SNPs typically use dimensionality-reduction methods, such as principal component analysis (PCA), or clustering methods, such as k-means. Such methods aim to identify a parsimonious set of SNPs that separate the data into distinct population clusters, in addition to revealing admixture. The output of these methods typically includes a plot of subjects (eg, scatter plot, dendrogram) to show how they relate to each other on the basis of appropriate distance measures. However, as discussed below in a brief survey of existing methods, such methods cannot directly reveal which clusters of subjects are related to which clusters of SNPs, nor can they reveal the nature of their membership on the basis of the proportion of genotypes.
Overview of current methods
Several detailed reviews of methods used to analyze SNP data exist.6 7 The current methods can be broadly classified into univariate and multivariate methods.
Univariate analysis of SNPs and subjects
Most analyses of SNP data use the univariate χ2 test to identify which SNPs are the most significant across the populations being studied (eg, subjects from different ancestries or between diseased and healthy populations). This method compares for each SNP the proportion of genotypes between the two or more groups being studied, and outputs the significance for each SNP. Because of the large number of SNPs being tested, the results are adjusted for false discovery using methods such as the Bonferroni correction. Researchers then use the most significant SNPs for further analyses. Although this method is powerful, it is limited because it treats each SNP independently, when SNPs could in fact be working in groups.
Multivariate analysis of SNPs and subjects
Multivariate methods that are applied to SNP data can be broadly classified into two categories: (1) distance-based, and (2) model-based.
The distance-based methods typically consist of two steps.3 6 The first step performs dimensionality reduction to project the data into a lower dimensional space. For example, PCA identifies the dimensions (referred to as components) that describe maximum variability in the data, and model them as linear combinations of the SNPs. PCA also outputs each subject's (or SNP's) coordinates along the identified components,6 and plots them in two dimensions using pairs of components as axes. This plot visually suggests how many clusters exist in the data. The second step attempts to find boundaries for clusters in the data. For example, k-means takes as input the coordinates generated from PCA, along with the inferred number of clusters, and generates the cluster boundaries for the subjects (or SNPs). Finally, to test the significance of the identified SNPs, researchers often use Wright's F statistic,8 which measures the diversity of the randomly chosen SNPs within the same subpopulation relative to that found in the entire population.
In contrast to the above distance-based methods, model-based algorithms such as STRUCTURE9 and ADMIXMAP10 assume an underlying probabilistic model, and estimate the parameters in the model from the data using maximum-likelihood or Bayesian estimation. In addition to clustering subjects in the data, these algorithms can estimate ancestral information in admixed subjects.11 12 Given that the data consist of K different populations, these algorithms output a vector of K values for each subject in the data, where the vector values correspond to the ancestry proportion in a subject's genome content that is derived from each population.
Objective
Although the above methods are powerful in separating subjects on the basis of continental origins and disease subtypes, or in identifying the important SNPs, they are based on a unipartite view of the data: they can be used to analyze either SNP clusters based on subjects or subject clusters based on SNPs. For example, they cannot directly reveal which clusters of subjects are related to which clusters of SNPs, nor can they reveal the nature of their membership based on the proportion of genotypes. To address these limitations, we explored the use of bipartite visual analytical representations to analyze SNP data. Such representations enable the simultaneous view of (1) subjects and SNPs, and (2) the type and frequency of genotype associations between subjects and SNPs. We therefore posed the research question: what is the bipartite relationship between subjects (from different continental origins) and SNPs (known to code for ancestry information)?
Methods
Data
To address the research question, we used SNP data from the phase 2 HapMap (release 23) database.13 Because prior research has identified14 and verified15 that 128 AIM SNPs contain strong signal related to ancestry, we extracted genotype data for these 128 SNPs for 60 unrelated subjects from Ibadan, Nigeria (henceforth referred to as ‘Yoruba Africans’) and 60 unrelated subjects from Utah-resident Americans with ancestry from northern and western Europe (henceforth referred to as ‘Utah Americans’). Of the 128 SNPs, 78 had complete data, and the remaining 30 had missing data for <5% of the subjects; the latter 30 SNPs were excluded from the analysis. The final dataset contained genotype data for 78 SNPs and 120 subjects and had no missing genotypes.
A SNP typically has only two possible bases (eg, A or G), one of which is less common in the population (‘minor allele’), and the other is more common (‘major allele’). Because humans carry two copies of the genome, SNPs that have bases A and G can have three combinations across the two copies of the genome: AA, AG and GG. These three combinations are referred to as the ‘genotypes’ of the SNP. For each SNP, we coded the three genotypes as 0, 1, or 2 denoting whether a subject was a ‘major homozygote’ (having two copies of the major allele), a ‘heterozygote’ (having one copy of each allele), or a ‘minor homozygote’ (having two copies of the minor allele), respectively. The minor allele of a SNP was determined to be the one that had the lower frequency in the data. This encoding is referred to as the ‘additive genetic model’,2 and is typically used in many genetic analyses, including in the analysis of AIM SNPs.
Experimental methods
Our analysis consisted of two steps: (1) ‘exploratory visual analysis’ through the use of three bipartite visual representations chosen to identify emergent bipartite relationships between subjects and SNPs; (2) ‘quantitative analysis’ through the use of methods suggested by the emergent visual patterns. This two-step method was motivated by our earlier studies16–18 that used a similar approach, and which have revealed that bipartite relationships can exhibit in different patterns (eg, nested clusters, disjoint clusters), each prompting the use of quantitative methods that make the appropriate assumptions about the underlying data.
Exploratory visual analysis
We selected bipartite networks as our primary method for analyzing the relationship between subjects and SNPs because they (1) are based on a simple but expressive graph-based visual representation to display both subjects and SNPs simultaneously, and (2) can be interactively manipulated to explore emergent patterns, which can be quantitatively verified through a wide range of graph-based and other quantitative methods. However, as described below, because the bipartite network representation was not adequate for our analysis, we used two other complementary bipartite visual representations that are well known in the bioinformatics community, but not often used in combination.
Bipartite networks
Networks provide a powerful approach for representing and analyzing complex relationships. They are increasingly being used to analyze a wide range of molecular measurements related to gene regulation,19 disease–gene associations,20 and disease–protein associations.21 A network (also called a graph) consists of a set of nodes, connected in pairs by edges; nodes represent one or more types of entities (eg, subjects and SNPs). Edges between nodes represent a specific relationship between the entities (eg, a homozygote relationship between a subject and a SNP). Figure 1 shows a sample bipartite network where edges exist only between different types of entities22 such as subjects and SNPs. The network was created using Pajek23 (version 1.23).
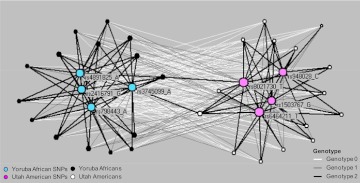
Figure 1.
A sample bipartite network showing 15 subjects (black and white nodes) and eight SNPs (colored nodes), and their connecting edges representing genotypes 0 (white), 1 (gray), and 2 (black). The nodes are sized on the basis of the sum of the weights of their connecting edges, and laid out using the Kamada–Kawai algorithm, which helps to reveal the relationship between the nodes and the nature of cluster memberships. This figure is produced in colour in the online journal-please visit the website to view the colour figure.
Edge weights in the network were used to represent the genotype (0, 1, or 2). Node diameter was used to represent the sum of weights on the edges connected to that node. This enabled rapid visual inspection to determine, for example, which subjects have overall high aggregate genotype values, and how such subjects relate to the rest of the network.
Global patterns in the network were visualized and analyzed using the Kamada–Kawaii layout algorithm,24 which is well suited for small to medium sized networks (50–1000 nodes).25 The application of this algorithm results in nodes that are connected by high edge weights to be pulled together, and those with low edge weights to be pushed apart. As shown in the sample network in figure 1, the result is that nodes with a similar pattern of edge weights (eg, black nodes on the left-hand side) are placed close to one another.
Network analyses provide two advantages for analyzing complex relationships. (1) They do not require a priori assumptions about the relationship of nodes within the data, such as the hierarchical assumption of hierarchical clustering or disjoint clusters of k-means. Instead, network layouts enable the identification of multiple structures (eg, hierarchical, disjoint, overlapping, nested) in a single representation,25 but often do reveal disjoint clusters. Therefore, while layout algorithms such as Kamada–Kawai depend on the force-directed assumption and its implementation, such algorithms do not impose a structure such as a particular type of clustering on the data, often leading to the identification of more complex structures in the data.17 (2) Networks also enable the simultaneous visualization of multiple raw values (eg, subject–SNP associations, subject attributes), aggregated values (eg, sum of edge weights), and emergent global patterns (eg, clusters) in a uniform visual representation. The network representation therefore enables the rapid generation of hypotheses based on complex multivariate relationships, and enables a more informed approach for selecting quantitative methods to verify the patterns in the data.
Heat maps
Although networks provide a powerful method for visualizing data, the edges can often get very dense, making it difficult to analyze the edges and their weights connected to specific nodes. We therefore used a second bipartite representation called a bipartite heat map.26 Here, instead of using Euclidean distances and edge weights to represent relationships between nodes (such as in the bipartite network), the heat map uses a color grid to represent such relationships. As shown in figure 3B, the rows represent subjects, the columns represent SNPs, and the cells represent genotypes: white=0, gray=1, and black=2.
Figure 3.
(A) The bipartite network without the non-discriminating single-nucleotide polymorphisms (SNPs); (B) the associated heat maps with dendrograms, which were used to determine the boundaries of the SNP and subject clusters. This figure is produced in colour in the online journal-please visit the website to view the colour figure.
Circos ideograms
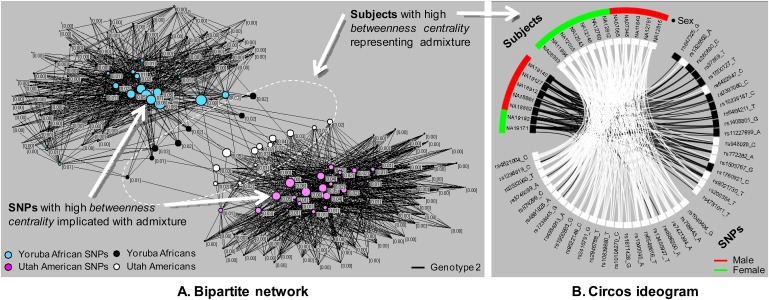
Although heat maps enable inspection of subjects and their relationship to each SNP, they cannot simultaneously represent attributes of the entities, such as the sex of subjects, nor do they allow interactive exploration of the relationship between subsets of the data, such as subjects who have high admixture (resulting from mating between subjects from reproductively isolated ancestral populations3). We therefore used a third bipartite representation called a Circos ideogram.27 As shown in figure 4B, the Circos ideogram represents the bipartite network of subjects and SNPs in an inner circle, and attributes of subjects such as sex in the outer rings.
Figure 4.
(A) The bipartite network with nodes sized based on the betweenness centrality measure; (B) the Circos ideogram showing the relationship of the admixed Utah Americans to the SNPs of both clusters (Utah American and Yoruba African SNP clusters), and the sex of the subjects (outer ring). (The betweenness centrality measure for each node has been multiplied by 10 000 to enable Pajek to display them to the maximum two decimal places.) This figure is produced in colour in the online journal-please visit the website to view the colour figure.
Quantitative analysis
The insights derived from the three bipartite visualizations were analyzed using three quantitative methods, which were selected based on their appropriateness to the emergent patterns in the network.
Agglomerative hierarchical clustering
Because the network analysis suggested the existence of disjoint clusters, we used agglomerative hierarchical clustering to verify the number of clusters and to identify the boundaries of the clusters. The clustering was performed using Manhattan distance (to handle the 0, 1, and 2 edge weights representing the genotype) with the Ward linkage function.27 The number of clusters and their boundaries were determined on the basis of natural breaks in the SNP, and in the subject dendrograms. The dendrograms were used in conjunction with the heat maps to aid visual analysis of the results.
Betweenness centrality
To identify subjects with high admixture of SNPs from the two ancestries, we calculated the betweenness centrality23 for each node in the network. In a unipartite network, this measure is defined as the fraction of the shortest paths between every pair of nodes in the network that pass through the node of interest. When there exist several clusters in a network, nodes that have high betweenness centrality values tend to be located between clusters because they act as ‘bottlenecks’ or ‘bridges’ for the shortest paths that start from one cluster and end in another cluster. For our analysis, we used the bipartite version of the betweenness centrality measure developed by Borgatti and Halgin.28
Clusteredness and bipartite modularity
To test the statistical significance of clusteredness in the network, we compared the variance, skewness, and kurtosis of the dissimilarities in the HapMap data, to 1000 random permutations of these data. For each network permutation, we preserved the size of the network and the edge weight distribution of each SNP when analyzing the SNP dendrogram, and the edge weight distribution for each subject when analyzing the subject dendrogram. Significant breaks in the HapMap's subject or SNP dendrograms would result in a significantly larger variance, skewness, and kurtosis of the dissimilarity measures, compared with the same measures generated from the random networks.
We also computed the modularity of the bipartite network. Modularity29 quantifies the notion that there are more edges between nodes in a cluster than can be expected by random chance, and fewer edges between nodes across clusters than can be expected by random chance. Modularity values range from −1 to +1, where high values (>0.3) represent substantial clustering.29 For our analysis, we used the RGraph algorithm30 to compute the modularity of two unweighted bipartite networks of the data: (a) a network where the edge represents the presence of one or more copies of the minor allele (the ‘dominant’ genetic model), and (b) a network where the edge represents the presence of two copies of the minor allele (the ‘recessive’ model).
Results
The bipartite visualizations and quantitative analysis revealed distinct SNP and subject clusters, in addition to a subset of subjects that represents an admixed population. For each outcome, we describe the results of the visual analysis, followed by their quantitative verification.
SNP and subject clusters
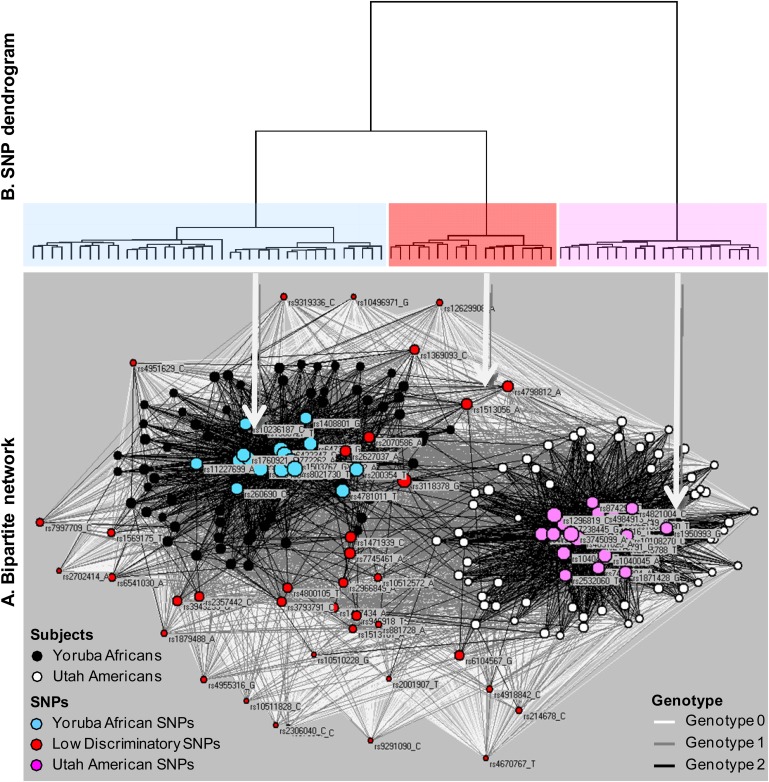
The bipartite network visualization of 120 subjects and 78 SNPs revealed a complex but understandable clustered pattern. As shown in figure 2A, there are two major clusters of SNPs and subjects, one to the left and another to the right. The SNPs are connected to subjects via white, gray, and black edges denoting genotype values 0, 1, and 2, respectively. The left cluster (shown in blue) consists of SNPs that have predominantly the minor homozygote genotype (genotype 2) for the Yoruba African subjects (black nodes), whereas the right cluster (shown in pink) consists of SNPs that predominantly have the minor homozygote genotype for the Utah American subjects (white nodes). Henceforth, for brevity, we refer to the left SNP cluster as ‘Utah American SNPs’ and to the right SNP cluster as ‘Yoruba African SNPs’. There also appear to be additional SNPs that circle mainly the Yoruba African SNPs. These SNPs have weaker connections to both the Yoruba African subjects and the Utah American subjects, as shown by their fewer black edges.
Figure 2.
(A) The bipartite network showing the subjects (black and white nodes), ancestry informative marker (AIM) single-nucleotide polymorphisms (SNPs) (colored nodes), and their connecting edges representing genotypes 0 (white), 1 (gray), and 2 (black). (B) The SNP dendrogram was used to determine the boundaries of the SNP, and a similar dendrogram determined the boundaries of the subject clusters. This figure is produced in colour in the online journal-please visit the website to view the colour figure.
To quantitatively verify the above visual result, we used agglomerative hierarchical clustering. As shown in figure 2B, the SNP dendrogram shows a substantial break at three as well as two clusters. Because the three clusters corresponded well to the three distinct topologies of the SNPs, we colored the SNP nodes in the bipartite network on the basis of the boundaries of the three clusters identified by the SNP dendrogram. A dendrogram of the subjects showed that the subject clusters perfectly match the two ancestries defined a priori. It is important to note that the dendrogram alone did not provide an explanation for the nature of the third less dominant SNP cluster (colored red). The nature of the third cluster was more apparent in the network based on its ring topology, and its genotype pattern with the other two dominant SNP clusters. The two methods therefore together provided an explanation for the overall topology of the bipartite network and its subparts, in addition to the quantitative verification of its boundaries.
To generate a network based on a parsimonious subset of the SNPs, and to examine the admixture based on the dominant SNP clusters (blue and pink), we removed the center SNP cluster (red nodes) from the network, and re-laid the network using the Kamada–Kawai algorithm. Figure 3A shows the result of this transformation on the network. As shown, the original Yoruba African and Utah American subjects continue to be strongly clustered around their respective SNPs. The network also revealed a subset of subjects between the two clusters that appeared to have an admixture of SNPs because the members of this subset have genotype 2 associations with some Utah American SNPs, and also with some Yoruba African SNPs.
The clusteredness of the subjects in the HapMap data was statistically significant when compared with 1000 random networks based on variance of the dissimilarities (HapMap =74822.5, random mean =1023.6, p<0.001, two-tailed test), skewness of the distribution of dissimilarities (HapMap =10.56, random mean =4.3, p<0.001, two-tailed test), and kurtosis of the distribution of dissimilarities (HapMap =114.01, random mean =24.28, p<0.001, two-tailed test).
To compute modularity, we generated unweighted bipartite networks representing the dominant and recessive genetic models as described in the methods section. For the recessive network shown in figure 3A, the modularity was above 0.3 (subjects =0.47, SNPs =0.49), indicating that the clustering of the subjects, and of the SNPs, was substantial compared to random chance.23 In both cases, the highest modularity was achieved with the same clusters identified by the hierarchical clustering. For the dominant network (not shown), the modularity was lower (subjects =0.25, SNPs =0.26), suggesting that in this dataset, the recessive model discriminates between the two ancestral populations more strongly compared to the dominant model.
Subjects with ancestry admixture
To analyze the admixed subjects who are located in the center of the network, we used the betweenness centrality measure. Because genotype 2 appeared to be the main determinant of the clusters, we used the recessive model to conduct this analysis. As shown by the enclosed dotted line in figure 4A, the betweenness centrality measure correctly identified 12 Utah Americans and seven Yoruba Africans who have genotype 2 relationships with SNPs in both clusters.
The betweenness centrality also identified SNPs that have strong connections to the admixed subjects, and therefore are implicated in the admixture. However, owing to the density of black edges in the network, it was difficult to determine which SNPs from each cluster were connected to subjects from the opposite cluster. Furthermore, the admixed subjects were scattered across the heat map (rows containing dark cells representing genotype 2 in the upper right and lower left areas of figure 3B) because they do not form a cluster based on their membership to the same SNPs.
To address this limitation, we used the Circos representation for a closer inspection of this subset of subjects across all the SNPs. Figure 4B shows the Circos ideogram where the edges and SNP nodes can be highlighted on the basis of one or the other cluster of subjects to which they are connected. Therefore, as shown in figure 4B, we highlighted all edges that were connected to the Utah American nodes (white nodes), to explore which Yoruba African nodes were, and were not, connected to them. As shown, the representation revealed eight SNPs (colored white on the right hand side of the diagram) that accounted for the admixture of the Utah Americans, and the remaining 10 SNPs (colored black) were not involved in that admixture. Similarly, the Circos ideogram enabled the identification of SNPs that were involved in the admixture of the Yoruba Africans, and those that were not. The Circos ideogram therefore helped to closely examine the admixture on the basis of the inter-cluster relationship, which was neither directly possible in the network, nor in the heat map representations. In addition, the outer ring of the ideogram shows the sex of the subjects (red = male, green = female), revealing how their proportion varies across the admixed subjects in the two ancestral groups. The Circos ideogram therefore enabled the exploration of the three-way association between SNPs, subjects, and their attributes.
Discussion
Our goal was to explore the role of bipartite visual analytical representations in the analysis of SNP data. Although the results matched many of the results from earlier AIMs studies,14 15 they provided a richer understanding of the associations in the data. First, while the larger set of 128 SNPs that we used to seed our study were clearly discriminatory for subjects from a large number of ancestral origins, the network analysis helped to identify a smaller set of 40 SNPs that is possibly sufficient to form strong clusters of Utah Americans and Yoruba Africans.
Furthermore, this smaller set also enabled us to closely examine the admixed subjects, and which SNPs were involved in that admixture. The results therefore provided a richer understanding of the association between the SNP and subject clusters, in addition to the nature of the cluster memberships. These in turn enabled us to understand the complementary role that each bipartite representation played in revealing the associations as discussed below.
Relationship between clusters
The bipartite network of 78 SNPs in figure 2A revealed (1) SNPs that were highly discriminatory of the two ancestries, (2) SNPs that were not discriminatory of the two ancestries, and (3) the relationship of the SNP and subject clusters. Because the weakly connected SNPs formed a ring-like structure around the Yoruba African SNP cluster, it suggested a weak but nonetheless relatively strong relationship with that cluster compared with the Utah American cluster. This pattern was difficult to discover from the heat map because of a fundamental difference in the two representations: two-dimensional network layouts have two degrees of freedom in laying out the nodes, and therefore can show multiple adjacency relationships; in contrast, dendrograms have only one degree of freedom because nodes can be located along either the x or y axis, restricting the number of adjacencies that can be represented simultaneously. These adjacencies have to be inferred by inspecting the color gradations in the heat map, which is perceptually more difficult to comprehend, compared with layouts that use distance to show similarity. However, although these relationships are difficult to discover from heat maps and dendrograms, we used them to confirm those patterns after the fact. In contrast, the network layout, although suggesting distinct SNP and subject clusters (whose significance was verified through comparison with random networks, and through modularity), cannot on its own discover the boundaries of the clusters, and therefore we used the dendrograms and modularity to discover those boundaries, which we then confirmed by overlaying them as similarly colored nodes in the network. The two representations therefore together enabled the discovery and confirmation of the relationship between the clusters.
Nature of cluster memberships
In addition to the identification of the cluster boundaries, and the relationship between the clusters, the bipartite representations also revealed the nature of the cluster memberships. Unlike unipartite representations used by methods such as PCA, k-means, and unipartite networks, bipartite networks through weighted edges explicitly show the nature of the relationship between a subject and a SNP. This feature, along with the overall topology of the network, revealed insights such as what kind of relationship is responsible for the formation of the clusters. For example, the two dominant clusters in our dataset were mainly held together because of the genotype 2 relationships from their respective subject populations. This might not necessarily be the case in other datasets. For example, clusters could be held together with very few genotype 2 relationships, and be dominated instead with many genotype 1 relationships. One might argue that such information can be extracted directly from the raw data, but the power of the bipartite visual analytical representations is that they can suggest patterns that the researcher might not otherwise think about analyzing.
Similar to the inadequacy of any single representation to enable the comprehension of the clusters and their relationship to each other, networks and heat maps were also unable to provide a more complete view of the admixed population. While the network helped to identify the existence of the admixed population, the density of the edges did not allow a direct inspection of the nature of their admixture, and which SNPs in both clusters were responsible for that admixture. Furthermore, these admixed subjects were spread out in the heat map, as their discovery is based on a network-based relationship which is not the basis of the clustering algorithm. In contrast, the Circos representation enabled the selection of edges on the basis of the subject cluster to which they were connected, which helped to quickly identify which nodes were, or were not, implicated in the admixture. Therefore, although the Circos representation is not designed to identify clusters, it enabled the inspection of the admixture in a much more effective way compared with networks and heat maps.
Methodological and theoretical implications
The results have methodological and theoretical implications. From a methodological perspective, the bipartite representations intuitively show a researcher studying the data from a case–control study, not only which subjects have high admixture, but also the reason for that admixture based on the type and nature of SNP cluster membership. For example, if SNPs are the focus of the study, then the bipartite representation can reveal important information for making critical decisions to prevent confounding experimental results. Furthermore, when studying SNP data beyond AIMs, researchers can use the identity of the SNP membership to rapidly derive data-driven hypotheses for disease causation. For example, we used the Genetic Association Database31 to analyze the known association of the 18 Yoruba African SNPs and the 22 Utah American SNPs with diseases. We found that the Yoruba African SNPs were associated with hypertension, schizophrenia, prostate cancer, Parkinson's disease, and autoimmune inflammatory diseases. In contrast, the Utah American SNPs were associated with osteoporosis, schizophrenia, bipolar disorder, and multiple sclerosis. These associations demonstrate a differential prevalence of diseases in the two populations based on the SNPs with which they were associated. In case–control SNP data, such differential prevalence of SNP–disease associations provides a starting point for elucidating the associations between the disease under study, and with other diseases.
From a theoretical perspective, we have demonstrated that the network representation enabled us to rapidly explore the effect of different genetic models (eg, recessive, dominant) on the SNP and subject clustering, and how the emergent patterns were detected and quantitatively verified through network measures such as modularity and betweenness. We have also elucidated the limitations of networks, and how to overcome them through the use of multiple bipartite visual representations. The results show that each representation provides different affordances, and therefore plays the role of enabling discovery, confirmation, explanation, and inspection for different tasks. This understanding has inspired us to explore the development of a complementary visual analytical framework, which could explain and guide the use of multiple visual analytical representations for rapidly enabling discoveries in complex SNP data.
Although we have focused on separately identifying SNP and subject clusters to understand how they are related, biclustering methods are designed to identify clusters that allow membership of both types of node (eg, SNPs and subjects). Indeed, our use of biclustering32 put into separate clusters the Utah American and their SNPs, and the Yoruba subjects and their SNPs. However, this method does not appear to help identify subjects with high admixture, which motivated the use of betweenness centrality, as we have demonstrated.
Limitations
There are three main limitations to our study. (1) Because it was designed as a proof-of-concept for the application of multiple visual analytical representations to comprehend the relationship between subjects and SNPs, we focused on the use of existing visual analytical methods that are well known in the bioinformatics community. However, there exist several other visual analytical representations, such as TreeMap33 and CateRank,34 which should be analyzed for their affordances, and for their complementary potential to bipartite networks. Furthermore, several researchers have proposed the use of advanced interactive methods for exploring bipartite networks,35 and for linking multiple representations,36 which should enable the rapid comprehension of such complex data. (2) SNP datasets typically are high dimensional, with a large number of SNPs—potentially in the millions—which require visualization methods that scale up computationally and perceptually. In our future research, we therefore plan to develop methods that exploit advanced computing resources, such as large memory resources and parallel computing capabilities, which should enable the analysis of such ‘big data’, in addition to interactive methods that help to rapidly filter out biomarkers that are not discriminatory for the phenotype of interest. (3) We have demonstrated the use of three bipartite visual analytical representations on only one SNP dataset, and the generality of our approach needs to be tested in additional datasets, particularly in ones where little is already known about the significant SNPs.
Conclusion
Although there exist powerful methods for analyzing SNP data, to the best of our knowledge they rely on unipartite representations of the data. Here we explored the use of three bipartite visual analytical representations and associated quantitative methods to enable a richer understanding of the relationships in SNP–subject data. The results suggest that bipartite representations of AIM SNPs data can provide not only an understanding of the SNP and subject clusters based on different models, but also how the clusters are related to each other, and the nature of the membership of the subjects to different SNP clusters.
Although we have demonstrated the value of bipartite representations in only one SNP dataset, our ongoing research suggests that the approach is more general. For example, we have begun to use the same approach to analyze a dataset of SNPs related to Alzheimer's disease. The results are revealing complex patterns of bipartite clustering, which have the potential to lead to a deeper understanding of the underlying genetics in Alzheimer's disease. Furthermore, we are investigating how to extend bipartite modularity to handle weighted edges, which will enable us to additionally analyze SNP–subject bipartite networks with all three genotypes simultaneously.
Finally, we believe we have only scratched the surface in understanding the complementary role of multiple bipartite visual analytic representations. While the development of new methods holds a high premium in the informatics field, we believe that there is much to be understood in how to strategically combine existing visual analytical methods to reveal new insights in a domain. Accordingly, in our future research, we hope to develop a comprehensive framework that integrates current methods with bipartite visual analytical representations, with the goal of helping researchers to rapidly identify complex SNP-related phenomena and unravel the mysteries related to the genetic causes of complex diseases.
Acknowledgments
We thank G Vallabha, V McMicken, M Abbas, J Tupa, and S Trevino III for their contributions.
Footnotes
Contributors: SKB and SV conceived the idea, SV extracted and formatted the data, SKB designed and performed the network analysis, KEB conducted the modularity analysis, GB and SV assisted in the quantitative analysis, SKB wrote the manuscript, and all the authors provided editorial advice.
Funding: SKB was supported in part by a Clinical and Translational Science Award (UL1RR029876) from the National Center for Research Resources, National Institutes of Health, and a grant from CDC/NIOSH # R21OH009441-01A2; SV was supported by NLM grant HHSN276201000030C, and KEB was supported by NSF grant DMR-0908286.
Competing interests: None.
Patient consent: We used publicly available data from the International HapMap Project.
Provenance and peer review: Not commissioned; externally peer reviewed.
Data sharing statement: The data we used are all publicly available.
The Kamada–Kawai layout algorithm is approximate because it does not guarantee a globally optimal layout. The method is therefore used to explore the data using different starting conditions, and the observed topology verified using appropriate quantitative methods. Layouts generated using the Fruchterman–Reingold algorithm produce similar topologies to Kamada–Kawai, but with a different node layout because it uses a different layout algorithm.
References
- 1.Kreuzer K, Massey A. Molecular Biology and Biotechnology: A Guide for Teachers. 3rd edn Washington, D.C: ASM Press, 2007 [Google Scholar]
- 2.Lewis CM. Genetic association studies: design, analysis and interpretation. Brief Bioinform 2002;3:146–53 [DOI] [PubMed] [Google Scholar]
- 3.Tang H, Quertermous T, Rodriguez B, et al. Genetic structure, self-identified race/ethnicity, and confounding in case-control association studies. Am J Hum Genet 2005;76:268–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Parra FC, Amado RC, Lambertucci JR, et al. Color and genomic ancestry in Brazilians. Proc Natl Acad Sci U S A 2003;100:177–82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Paschou P, Lewis J, Javed A, et al. Ancestry informative markers for fine-scale individual assignment to worldwide populations. J Med Genet 2010;47:835–47 [DOI] [PubMed] [Google Scholar]
- 6.Patterson N, Price AL, Reich D. Population structure and eigenanalysis. PLoS Genet 2006;2:e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Witherspoon DJ, Wooding S, Rogers AR, et al. Genetic similarities within and between human populations. Genetics 2007;176:351–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nassir R, Kosoy R, Tian C, et al. An ancestry informative marker set for determining continental origin: validation and extension using human genome diversity panels. BMC Genet 2009;10:39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics 2000;155:945–59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hoggart CJ, Shriver MD, Kittles RA, et al. Design and analysis of admixture mapping studies. Am J Hum Genet 2004;74:965–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Aldrich MC, Selvin S, Hansen HM, et al. Comparison of statistical methods for estimating genetic admixture in a lung cancer study of African Americans and Latinos. Am J Epidemiol 2008;168:1035–46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tsai HJ, Choudhry S, Naqvi M, et al. Comparison of three methods to estimate genetic ancestry and control for stratification in genetic association studies among admixed populations. Hum Genet 2005;118:424–33 [DOI] [PubMed] [Google Scholar]
- 13.International HapMap Consortium The international HapMap project. Nature 2003;426:789–96 [DOI] [PubMed] [Google Scholar]
- 14.Kosoy R, Nassir R, Tian C, et al. Ancestry informative marker sets for determining continental origin and admixture proportions in common populations in America. Hum Mutat 2009;30:69–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kidd JR, Friedlaender FR, Speed WC, et al. Analyses of a set of 128 ancestry informative single-nucleotide polymorphisms in a global set of 119 population samples. Investig Genet 2011;2:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bhavnani SK, Abraham A, Demeniuk C, et al. Network analysis of toxic chemicals and symptoms: implications for designing first-responder systems. AMIA Annu Symp Proc 2007:51–5 [PMC free article] [PubMed] [Google Scholar]
- 17.Bhavnani SK, Bellala G, Ganesan A, et al. The nested structure of cancer symptoms: implications for analyzing co-occurrence and managing symptoms. Methods Inf Med 2010;49:581–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bhavnani SK, Carini S, Ross J, et al. Network analysis of clinical trials on depression: implications for comparative effectiveness research. AMIA Annu Symp Proc 2010:51–5 [PMC free article] [PubMed] [Google Scholar]
- 19.Albert RK. Boolean modeling of genetic regulatory networks. In: Complex Networks editors: Ben-Naim E, Frauenfelder H, Toroczkai Z, eds. Berlin: Springer-Verlag, 2004:459–79 [Google Scholar]
- 20.Goh KI, Cusick ME, Valle D, et al. The human disease network. Proc Natl Acad Sci U S A 2007;104:8685–90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ideker T, Sharan R. Protein networks in disease. Genome Res 2008;18:644–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Newman M. Networks: An Introduction. New York, NY: Oxford University Press, 2010 [Google Scholar]
- 23.Batagelj V, Mrvar A. Pajek - analysis and visualization of large networks. In: Jünger M, Mutzel P, eds. Graph Drawing Software, Berlin: Springer, 2003:77–103 [Google Scholar]
- 24.Kamada T, Kawai S. An algorithm for drawing general undirected graphs. Inf Process Lett 1989;31:7–15 [Google Scholar]
- 25.Nooy W, Mrvar A, Batagelj V. Exploratory Social Network Analysis with Pajek. New York, NY: Cambridge University Press, 2005 [Google Scholar]
- 26.Johnson RA, Wichern DW. Applied Mutlivariate Statistical Analysis. Upper Saddle River, NJ: Prentice-Hall, 1998 [Google Scholar]
- 27.Krzywinski M, Schein J, Birol I, et al. Circos: an information aesthetic for comparative genomics. Genome Res 2009;19:1639–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Borgatti SP, Halgin D. Analyzing affiliation networks. In: Carrington P, Scott J, eds. The Sage Handbook of Social Network Analysis. Thousand Oaks, CA: Sage Publications, 2011 [Google Scholar]
- 29.Newman ME, Girvan M. Finding and evaluating community structure in networks. Phys Rev E Stat Nonlin Soft Matter Phys 2004;69:026113. [DOI] [PubMed] [Google Scholar]
- 30.Guimera R, Sales-Pardo M, Amaral LA. Module identification in bipartite and directed networks. Phys Rev E Stat Nonlin Soft Matter Phys 2007;76:036102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Becker KG, Barnes KC, Bright TJ, et al. The genetic association database. Nat Genet 2004;36:431–2 [DOI] [PubMed] [Google Scholar]
- 32.Barber MJ. Modularity and community detection in bipartite networks. Phys Rev E Stat Nonlin Soft Matter Phys 2007;76:066102. [DOI] [PubMed] [Google Scholar]
- 33.Johnson B, Shneiderman B. Tree-Maps: a space-filling approach to the visualization of hierarchical information structures. Proc. of the 2nd International IEEE Visualization Conference (San Diego, Oct. 1991) 284–91 [Google Scholar]
- 34.Filippova D, Shneiderman B. Interactive exploration of multivariate categorical data: exploiting ranking criteria to reveal patterns and outliers, Human-Computer Interaction Lab, University of Maryland, Technical Report # HCIL-2009-38. 2009.
- 35.Schulz HJ, John M, Unger A, et al. Visual Analysis of Bipartite Biological Networks. Proc of Eurographics Workshop on Visual Computing for Biomedicine, Delft, Netherlands. October 2008., pp. 135–42 [Google Scholar]
- 36.Stolte C, Tang D, Hanrahan P. Polaris: a system for query, analysis, and visualization of multidimensional databases. IEEE Trans Visual Comput Graph 2002;8:75–84 [Google Scholar]