A simple indentation device for measuring micrometer-scale tissue stiffness

Abstract

Mechanical properties of cells and extracellular matrices are critical determinants of function in contexts including oncogenic transformation, neuronal synapse formation, hepatic fibrosis and stem cell differentiation. The size and heterogeneity of biological specimens and the importance of measuring their mechanical properties under conditions that resemble their environments in vivo present a challenge for quantitative measurement. Centimeter-scale tissue samples can be measured by commercial instruments, whereas properties at the subcellular (nm) scale are accessible by atomic force microscopy, optical trapping, or magnetic bead microrheometry; however many tissues are heterogeneous on a length scale between micrometers and millimeters which is not accessible to most current instrumentation. The device described here combines two commercially available technologies, a micronewton resolution force probe and a micromanipulator for probing soft biological samples at sub-millimeter spatial resolution. Several applications of the device are described. These include the first measurement of the stiffness of an intact, isolated mouse glomerulus, quantification of the inner wall stiffness of healthy and diseased mouse aortas, and evaluation of the lateral heterogeneity in the stiffness of mouse mammary glands and rat livers with correlation of this heterogeneity with malignant or fibrotic pathology as evaluated by histology.

1. Introduction

Several recent studies have highlighted the role of physical environmental factors as vital regulators of cell and tissue function. Specifically, the stiffness of cellular substrates has been implicated in controlling a variety of cell behaviors, including but not limited to proliferation, migration (in the context of invasion and metastasis), synapse development, growth rate, cytokinesis and stem cell differentiation (reviewed in Discher et al 2005, Discher et al 2009b, Janmey and McCulloch 2007, Lopez et al 2008, Wells 2008). Whole tissue stiffness has been shown to be a risk factor for the development of cancer (Lopez et al 2008) as well as an important diagnostic read-out in pathologic processes involving tissue injury and fibrosis, including cancer (Krouskop et al 1998) and liver disease (Georges et al 2007, Ziol et al 2005), while tissue density has long been recognized as a risk factor in breast cancer (Boyd et al 2009, McCormack and dos Santos Silva 2006).

These results, which have demonstrated unequivocally the relevance of mechanical stimuli in biological function, have established the need for accurate and high resolution characterization of the elasticity of biological tissues. Although several methods are currently available for this application, these typically measure mechanical properties either at a global scale (i.e. whole tissue tensile, compression, or magnetic resonance elastography (Manduca et al 2001) and mechanical rheometry analysis (Georges et al 2007)) or at a cellular level (e.g. atomic force microscopy (Engler et al 2007, Solon et al 2007) or micropipette aspiration (Byfield et al 2004)). Although nanoindentation measurements of some soft biological tissues have been carried out (Franke et al 2007, Gentleman et al 2009), variation in tissue stiffness on an intermediate (i.e. hundreds of micrometers to millimeter) length scale, where heterogeneity would be expected in both normal and diseased soft tissue, has yet to be extensively explored because of a lack of widely employed experimental tools available for such an application.

In parallel with studies of intact tissues, the response of cultured cells to the stiffness of their substrate is increasingly well documented, and different cell types have been shown to respond to different ranges of stiffness (Discher et al 2009a, Engler et al 2006, Georges and Janmey 2005, Levental et al 2007), sometimes with strong cellular changes triggered by relatively small changes in substrate elasticity (Mammoto et al 2009). Matrix stiffness cannot be inferred simply from the concentrations of biopolymers or synthetic polymers used to prepare hydrogel or other flexible substrates, but needs to be tested directly, since matrix elasticity is often very strongly dependent on the precise concentration of active crosslinkers, filament length, network architecture, and other factors that vary from one experiment to another. Moreover, the traction forces that cells apply to their matrix can themselves alter matrix stiffness for biopolymer networks like collagen and fibrin that exhibit strain-stiffening behavior, and recent studies show that cells can alter substrate stiffness hundreds of micrometers away from their edges (Winer et al 2009). These studies demonstrate a need for direct measurement of matrix elasticity, ideally on a length scale over which structural and mechanical heterogeneity can affect cell response.

To enable rapid elasticity measurements of soft materials on a scale of hundreds of micrometers adapted to samples that can also be visualized or probed by light and atomic force microscopy, we have combined a micronewton resolution force probe and a nanometer resolution micromanipulator using commercially available equipment with relatively low cost. The method is amenable to a variety of applications and sample preparations, including both fully hydrated and dry samples as well as microscopic and whole tissue samples. Assembly and calibration of the device is rapid and simple, as are data gathering and interpretation, allowing quantitative determination of the viscoelastic properties of tissues with minimal time and capital investment. This device has been validated by measuring the elasticity of well-characterized polyacrylamide gels and verifying good agreement with both macroscopic rheometry and nanoscopic AFM measurements. The device and some of its potential applications are described in this contribution.

2. Device description and characterization

2.1. Tension probe and micromanipulator

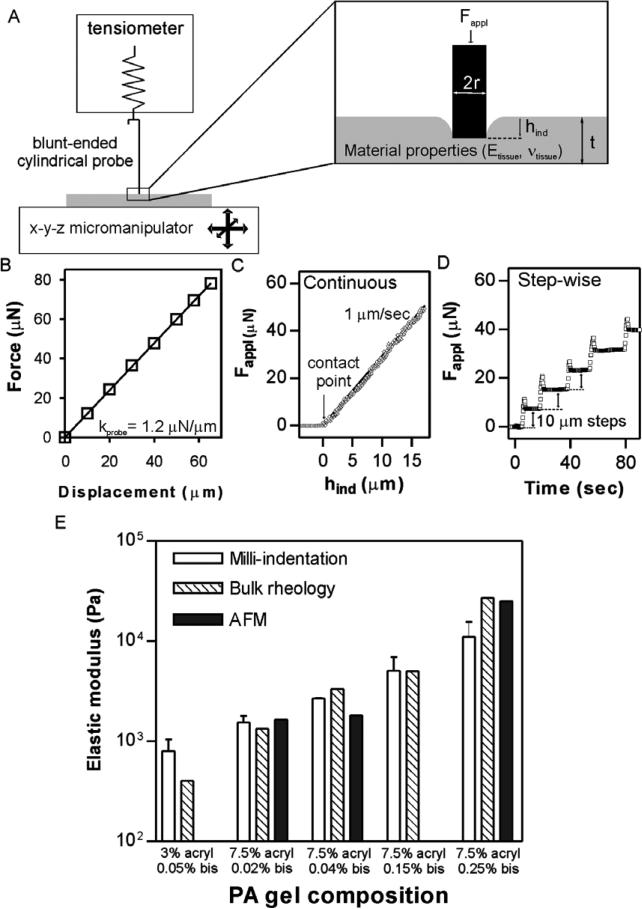
The device described in this contribution combines two existing, commercially available technologies for the measurement of biological sample mechanical properties: (1) a μN-resolution tensiometric force probe adapted from the surface tension measurement apparatus of a Langmuir monolayer trough (MicroTrough X, Kibron Inc, Helsinki, Finland), consisting of a 0.255 mm radius blunt-ended cylindrical tungsten wire hung from a digital microbalance; and (2) a 40 nm resolution hydraulic micromanipulator (MLW-3, Narishige, Tokyo, Japan) (figure 1(A)) (although a 3-axis manipulator was used, only one-dimensional displacement is necessary to obtain stiffness information). The force–displacement relationship was found to behave as a Hookean spring (force linearly related to displacement—k_probe ~ 1.2 N m^–1) with spring constant calibrated prior to each measurement. Spring constant calibration was done by bringing the probe in contact with a non-compliant surface (glass coverslip), displacing the probe by precise translation of the surface using the micromanipulator and measuring the resulting changes in force (a representative calibration is shown in figure 1(B)).

Figure 1.

Method description and validation. (A) Schematic representation of the stiffness measurement device with a zoom on the region of interface with the sample. (B) A sample calibration of the probe spring constant (k_probe). (C) An example of stiffness measurement of a 7.5% acrylamide/0.02% bis polyacrylamide gel by continuous indentation at 1 μm s^–1. The bold line is a fit to equations (3) with E = 2162 Pa. (D) An example of step-wise stiffness measurement of the same gel with successive 10 μm displacements of the gel upwards into the probe. (E) Comparison of measured stiffnesses of PA gels between the indentation technique described here (white bars), bulk rheological measurements (striped bars; taken from Yeung et al (2005) and Solon et al (2007)), and nanoscopic AFM measurements (solid bars; taken from Solon et al (2007)).

For all measurements, samples were placed on the micromanipulator stage, which was manually positioned under the free-hanging probe, followed by upward micromanipulator displacement of the stage and sample toward the probe until contact occurred between the probe and sample. For macroscopic samples, contact between the sample and probe was determined by a consistent change in measured force upon repeated indentation (usually occurring within 10 μm of displacement after an initial change in force), while for microscopic experiments, the contact point was fitted to the force–displacement data. Following establishment of contact between probe and sample, the sample was indented by micromanipulator translation upward into the probe, either at a continuous rate (figure 1(C)) or in successive stepwise indentations (figure 1(D)). These translations resulted in decreases in voltage collected by the Filmware software package (Kibron) which could be converted into decreases in force measured by the probe (equally, an increase in force on the sample-F_appl) and upward displacement of the probe:

$$\Delta z_{\text{probe}}=\frac{F_{\text{appl}}}{k_{\text{probe}}}.$$ (1)

Subtracting the displacement of the probe from the known vertical displacement of the sample yielded the indentation of the probe into the sample:

$$h_{\text{ind}}=\Delta z_{\text{sample}}-\Delta z_{\text{probe}}$$ (2)

The force–indentation relationship of a soft homogeneous material on a hard surface is given by:

$$E_{\text{tissue}}=\frac{G_{\text{tissue}}^{\prime }}{2^{\ast }(1+{\upsilon }_{\text{tissue}})}=\frac{F_{\text{appl}}^{\ast }(1-{\upsilon }_{\text{tissue}}^2)}{h_{\text{ind}}^{\ast }{\kappa }^{\ast }2r}$$ (3)

where r is the radius of the indenter, E_tissue and $G_{\text{tissue}}^{\prime }$ are the elastic and shear storage moduli, respectively, υ_tissue is Poisson's ratio and κ is the Hayes correction factor for finite sample thickness (Hayes et al 1972). More complete treatments of thickness correction have been developed (Cheng et al 1999, Zhang et al 2004) and could be applied in cases where the sample thickness is precisely known.

For macroscopic samples (sections 2.2, 3.2 and 3.3) 7–10 successive step-wise indentations at each spot were averaged by taking the instantaneous change in force upon indentation (neglecting the initial overshoot) to obtain the measured E_tissue. Indentation-to-indentation variation was minimal (figure 1(D)) and no sample conditioning by indentation was observed, likely due to the small indentation relative to the sample thickness (less than 5%). Spatial variability was interpreted as representing material heterogeneity since measured values for homogeneous materials were highly laterally reproducible. The samples were either measured while submerged in saline solution, or the saline solution was aspirated, leaving only enough to keep the sample moist (spring constant was calibrated in the wet or dry configuration used for experiments).

2.2. Polyacrylamide gel validation

This device and technique were validated by comparing stiffness measurements of polyacrylamide hydrogels to measurements obtained using other, more established methods. Polyacrylamide hydrogels have long been used as a biochemical separation tool, but recent interest in the substrate elasticity dependence of cell behavior has led to extensive characterization and modulation of their material properties (Engler et al 2004, Pelham and Wang 1997, Yeung et al 2005). Polyacrylamide gels of known compositions were prepared as described (Pelham and Wang 1997), indented as above, and the resulting elastic moduli compared with published bulk rheological (Yeung et al 2005) and nanoscopic (Solon et al 2007) measurements (figure 1(E)). From this comparison, it is clear that there is good agreement between the technique described here and other techniques for samples from several hundred Pa up to approximately 10 kPa. Stiffer materials (>10 kPa) are not measured well by this technique because the low spring constant of the probe does not induce significant indentation of stiff samples, leading to large errors in elastic modulus calculations (see section 4).

3. Applications to biological materials

The intermediate length scale and high force and displacement resolution of the milliprobe technique suggest a broad range of possible applications in measuring the mechanical properties of biological tissues. These applications include evaluating the global stiffness of microscopic objects, measuring the wall stiffness of very thin and very soft tissues, and determining the lateral heterogeneity of macroscopic tissue samples. We illustrate this point in this section by describing a variety of distinct experiments that have been performed using the described apparatus.

3.1. Global stiffness of microscopic objects

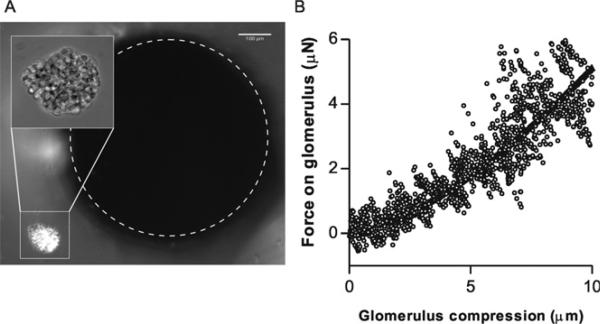
While nanoscopic techniques like AFM are applicable to microscopic samples, these probe the sample at the maximal length scale of several cells, and often subcellularly. A unique functionality of the milliprobe apparatus is the ability to measure the global mechanical properties of very small biological samples, as illustrated by measurement of the stiffness of isolated, intact mouse glomeruli. The glomeruli were deposited as a dilute suspension on a glass coverslip, which was mounted (using an extension arm) onto the hydraulic micromanipulator. The extension arm was configured to allow suspension of the coverslip above an objective of an inverted microscope. The probe was positioned above the coverslip and lowered until both the glomeruli and the probe were visible in the field of view under 10× magnification (figure 2(A)). The manipulator was then used to position the glomerulus to be measured directly under the probe, and then manually translated up towards the probe at a constant rate (200 nm every 5 s). The Hertz model describes the deformation of a sphere by a flat surface, taking into account the increased contact area as the sample is compressed (Sneddon 1965):

$$F_{\text{appl}}=\frac{4\sqrt{R_{\text{sample}}}}{3\pi }\left(\frac{E_{\text{tissue}}}{1-{\upsilon }_{\text{tissue}}^2}\right)h_{\text{ind}}^{\frac{3}{2}}$$ (4)

where R_sample is the radius of the glomerulus, approximated in our measurement as 100 μm. Figure 2(b) shows the force–compression behavior of a single isolated glomerulus along with the model fit to the data with a shear modulus of 3.0 kPa. The measured stiffness corresponds well to previous measurements generated using micropipette aspiration (not shown) and derived from measurements of glomerular capillary pressures by micropuncture and pathological glomerular capillary dilation in rats with reduced renal mass and hyperfiltering glomeruli (Dworkin et al 1984, Hostetter et al 1981, Nagata et al 1992).

Figure 2.

Quantitative compression of microscopic objects. (A) A single isolated mouse glomerulus (imaged at 40× in inset) positioned near the tip of the milli-indenter. (B) Force–compression behavior of a mouse glomerulus compressed at 0.04 μm s^–1. Fit is a Hertz model fit (equation (4)—glomerulus is simplified as a 100 μm solid sphere with ν = 0.5) with $G_{\text{glomerulus}}^{\prime }=3.0\mathrm{kPa}$.

3.2. Local elasticity of very thin samples

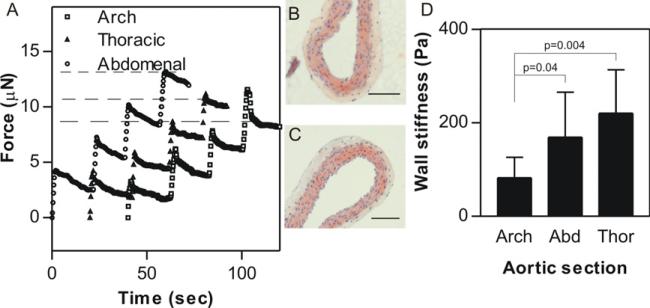
Using the corrections outlined (Hayes et al 1972), the apparatus described here can be used to measure samples whose thickness is on the order of the tip diameter (here, 255 μm), provided the sample thickness is well characterized. To demonstrate this capability, the wall stiffness of transected mouse aorta sections was determined as a function of the distance from the heart. Aortic wall thickness was quantified by microscopic examination of histological sections (figures 3(B) and (C)) and found to be relatively independent of location (thoracic aorta—84.9 ± 9.8 μm; aortic arch—98.2 ± 20.5 μm) so a simplifying assumption of 100 μm for all aortic sections was made for all measurements.

Figure 3.

Stiffness quantification of very thin tissues. (A) Sample traces from four successive indentations (by 5 μm displacements of the probe into the sample) into explanted mouse aorta sections from various regions of the aorta (circles—abdominal; triangles—descending thoracic; squares—aortic arch). Representative images of transverse sections of a longitudinally dissected thoracic aorta (B) and aortic arch (C) section. The wall thickness calculated from these images (~100 μm) was used to correct for the sample thinness in the stiffness calculation. (D) Aortic wall stiffness as a function of the region of the aorta. Mean ± SD from 7 to 9 samples. There appears to be a clear dependence of aortic wall stiffness on the section tested.

Aortic wall stiffness was quantified by successive 5 μm indentations of the probe into the sample (figure 3(A)). The indentations were reduced from the usual 10 μm to avoid sample compression that might lead to errors in the estimated wall thickness. Comparison of figure 3(A) with the PA gel indentation in figure 1(D) clearly shows that the aortas are both softer and more viscous than the elastic PA gels, as evidenced by the significant exponential stress relaxation observed after the initial indentation. Additionally, the total force on the probe after 4 successive indentations (dashed lines) was dependent on the section of the aorta being indented (curves have been offset for clarity). Quantification of the instantaneous stiffness of the aortas revealed that the average stiffness was a function of location, with the arch being the softest (G′ = 82 ± 44 Pa) followed by the abdominal (169±69 Pa) and the thoracic aorta (220 ± 93 Pa).

3.3. Micrometer-scale variation in whole tissue stiffness

The microscopic dimensions of the indenter probe allow for measurement of tissue mechanical properties at a level relevant to both natural and pathological biological variation. To demonstrate this capability, we used the device described above to characterize mesoscale (i.e. hundreds of micrometer to tens of millimeter) variation in two distinct pathophysiological scenarios, early hepatic fibrosis in CCl₄-treated rats and malignancy in mouse mammary glands.

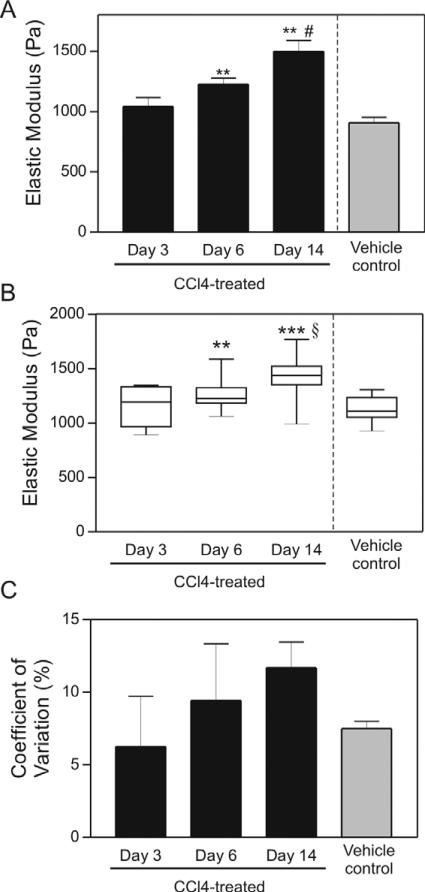
We observed a CCl₄ treatment time-dependent increase in local liver stiffness, both by rheology (figure 4(A)) and with the milliprobe indentation apparatus (figure 4(B)). Significant differences in CCl₄-treated livers compared to oil-treated controls were initially observed at six days following toxin-treatment and became more significant with increasing time (figures 4(A) and (B)), mirroring our previous rheological measurements (Georges et al 2007). Interestingly, we found that the difference between treated animals and controls were more significant using the indentation technique, likely because local differences in tissue stiffness can be accounted for in the indentation measurements.

Figure 4.

Micrometer-scale variation of normal and fibrotic liver tissue. (A) Average elastic modulus from bulk rheological measurements of liver tissue after treatment with CCl₄ or vehicle for indicated time. Data are represented as mean ± SD. These bulk rheometry measurements are a subset of those described in Georges et al (2007) and are shown here for comparison with indentation measurements. (B) Box plot of elastic modulus measurements determined by indentation of tissue from the same livers showing mean values and variance increase with time of CCl₄ treatment. (C) Quantification of COV of liver tissue after treatment with CCl₄ or vehicle for indicated time. Data are represented as the mean ± SD. ** p ≤ 0.01, *** p ≤ 0.001 comparing 3-day to 6- and 14-day CCl₄-treated tissues. ^# p ≤ 0.01 comparing to vehicle to CCl₄-treated tissues. ^§ p ≤ 0.001 comparing to vehicle to CCl₄-treated tissues. With the exception of one liver from an oil-injected animal which was measured in three regions, all liver slices were measured in five different regions. Numbers of livers per time point ranged from 2 to 4.

Using the indentation device, we saw a large variation in local tissue stiffness even in the livers from oil-injected rats (all of which were Metavir stage F0), as might be expected given the structurally different regions of the liver on this scale (i.e. central, portal, parenchymal).

Similarly, calculations of the coefficient of variation (COV—standard deviation of various spots within a single sample normalized by the average), measurable only with the indentation apparatus, illustrated a time-dependent increase in liver stiffness heterogeneity (figure 4(C)), suggesting that the CCl₄-induced liver stiffening was not occurring throughout the tissue uniformly, but rather through focal regions of increased stiffness, as suggested by histological analysis showing heterogeneous matrix deposition throughout the tissue (not shown).

Both the variability in normal liver tissue and the increased variability in the CCl₄-treated livers were striking. Although we were unable to identify the region of the liver (central, parenchymal, or portal) probed in individual measurements, and although we have shown previously that liver stiffness and fibrosis are not linearly related (Georges et al 2007), the increasing variability in the day 14 livers likely reflects increasing periportal fibrosis. These regional variations in stiffness in the injured liver may prove important in driving the architectural rearrangements that are typical of more advanced disease (Stopak and Harris 1982).

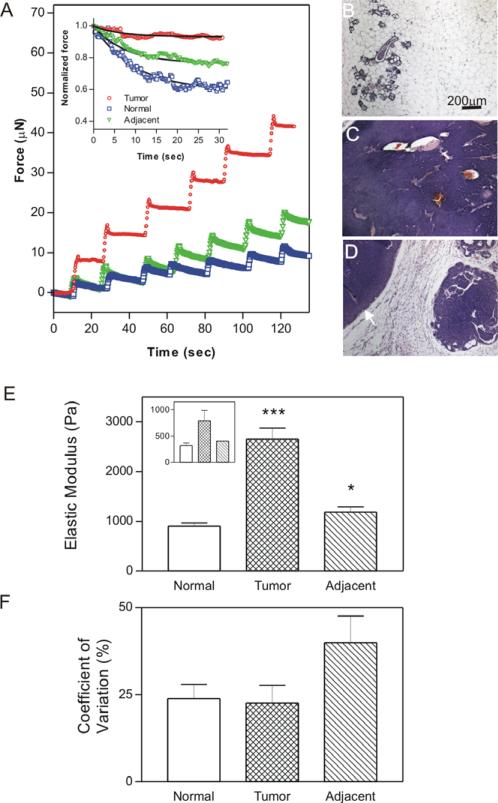
As an additional validation of the applicability of the indentation device, the mechanical properties of murine mammary glands at various stages of tumor progression were determined. Obvious differences between tumor and non-tumor regions could be detected both in the total force applied to the sample following successive 10 μm displacements (figure 5(A)) and the degree of stress relaxation observed (figure 5(A) inset).

Figure 5.

Micrometer-scale variation of mammary gland tissue stiffness in relation to pathology. (A) Sample traces from successive indentations (by 10 μm displacements) into explanted mouse mammary gland tissues from tissues of various histological characterizations (squares—normal; circles—tumor; triangles—tissue directly adjacent to tumor). Inset shows sample stress-relaxation curves with fits to data using equations (5). ((B), (C), (D)) Representative hematoxylin and eosin images of normal (B), tumor (C), and adjacent (D) tissues (arrowhead marks the visible tumor). (E) Average elastic modulus of mammary tissue determined by indentation; mean ± SD of 2–8 measurements for each of a total of 24 mammary glands from 7 mice. Inset shows bulk rheological measurements of the same tissues for comparison. (F) Quantification of coefficient of variation (COV; SD/mean) in the three different tissue types. Data are represented as the mean ± SD COV of at least 6 glands per pathology from at least 5 mice. * p value of ≤ 0.05, *** p value of ≤ 0.001.

Quantification of instantaneous elastic moduli of 24 glands from seven mice (from five independent experiments) shows significant differences in tissue elastic moduli between all tissue types (figure 5(E)). Tumor samples were significantly stiffer than either of the non-tumor samples (p < 0.001), confirming measurements by bulk rheology (figure 5(E) inset) as well as previous observations (Paszek et al 2005, Levental et al 2009). Additionally, the tumor-adjacent tissue (i.e. tissue that was within 10 mm of a macroscopic tumor) was significantly stiffer than the normal regions (p = 0.017), illustrating the unique advantage of this technique, namely the ability to measure tissue mechanical properties on a microscopic scale where important biological variability occurs. The increase in stiffness of tumor-adjacent tissue confirms recent macroscopic observations and suggests an important physiological role for tumor associated changes in the surrounding stromal tissues (Levental et al 2009). Analysis of the coefficient of variation confirms that by using this method we can measure tissue-level heterogeneity, as evidenced by significantly higher lateral heterogeneity of tumor-adjacent samples (as might be expected from the variety of biochemical and biophysical effects of malignancy) than either the tumors or normal tissue (figure 5(F)).

Furthermore, the indentation technique presented in this work allows for the determination of a tissue's viscoelastic mechanical properties. In a subset of the above glands, individual relaxation curves (figure 5(A) inset) were fitted to a simple two-component stress-relaxation model:

$$G\left(t\right)=1-G_{\infty }(1+{\mathrm{e}}^{-t∕\tau })$$ (5)

where G(t) is the reduced relaxation function and G_∞ and τ are the fitting constants for the equilibrium modulus and relaxation time constant, respectively. Fitting eight curves from each tissue type (one representative curve per sample), significant changes in viscoelastic properties between tumor and non-tumor samples were observed in the equilibrium modulus but not in the relaxation time constant (table 1). Although these measurements do not allow any direct assignment of the structural determinants for the observed differences in material properties, it is possible that τ reflects the movement of fluid through tissue, while G_∞ is a quantification of the ‘interconnectedness’ of a tissue. Significant variation in one, but not the other, of these properties suggests that while factors determining fluid movement (e.g. tissue pore size) are unaffected at the relevant scales, tissue crosslinking is significantly increased in tumors, consistent with recent biochemical observations (Levental et al 2009). Most importantly, these measurements demonstrate the utility of our device in measuring not only the instantaneous elastic behavior of tissue samples but also the micrometer-scale heterogeneity of time-dependent viscoelastic/poroelastic (Galli et al 2009) tissue material properties.

Table 1.

Equilibrium moduli and relaxation times for normal and malignant murine mammary tissues.

Tissue type	G ∞	τ
Normal	0.36 ± 0.14	6.4 ± 3.2
Tumor-adjacent	0.43 ± 0.26	7.8 ± 5.6
Tumor	0.18 ± 0.11	7.6 ± 7.1

4. Advantages and shortcomings compared to available technologies

The recent dramatic increase in interest regarding mechanical effectors of biological processes has stimulated the development of novel cell culture techniques (Johnson et al 2007) to measure the interactions of cells and multi-cellular structures with new biocompatible materials possessing controllable mechanical and bioactive properties (e.g. Freudenberg et al 2009). Despite these in vitro advances, there remains a dearth of information regarding the mechanical properties of soft biological tissues at the level of biologically relevant variation.

The measurement apparatus and techniques described in this contribution constitute a simple, commercially available and cost-effective method for measuring tissue mechanics with sub-millimeter lateral spatial resolution. The main advantage of the described device is the intermediate length scale of measurement enabled by the micrometer-scale probe; it is also important to note that spatial resolution of the device can be varied using different diameter probes. Compared to bulk material property methods (e.g. macroscopic tensiometry or rheometry), our device allows resolution of biological structures well below the organ level as demonstrated by the measurement of an intact glomerulus (figure 2), an order of magnitude improvement on previous measurements of kidney mechanical properties (Nasseri et al 2002). The glomerulus measurement also emphasizes the unique stiffness resolution available with the milliprobe indentation device described here. From the graph in figure 2 it is clear that μN force resolution is readily achievable with the commercial tensiometric probe, suggesting a stiffness resolution well below 0.1% (probe area ~0.2 μm²).

Several technologies have recently been developed to measure the mechanical properties of biological samples with nano-microscopic resolution. These devices (the most widely used of which is the atomic force microscope) have enabled investigations of subcellular mechanics (Sen et al 2005, Solon et al 2007) and even the mechanical properties of single proteins (Rief et al 1997). However, because of the minute probe sizes required for such high resolution measurements, these techniques are limited to exploring structures of at most several cells, and usually on the level of a single cell. While important and interesting insights have been gained with these approaches, questions of tissue physiology cannot be addressed at this level. Although commercial instruments have been employed to measure stiffness of relatively soft samples by indentation (reviewed in Ebenstein and Pruitt 2006), these instruments probe size scales that are typically an order of magnitude smaller (Gentleman et al 2009, Kaufman et al 2008) and samples that are several orders of magnitudes stiffer (Ebenstein and Pruitt 2004, Franke et al 2007) compared to the measurements described here.

A device with comparable capabilities to the one described here was recently developed and characterized (Jacot et al 2006). This technique is a novel and useful method for measuring of mechanical properties with sub-millimeter resolution, and the alternative technique reported here offers some advantages, including cost (under $5,000), ease of assembly, and ease of use; the Jacot device requires highly accurate microscopic quantification of indentation, which is inherently subject to error.

The device and technique we describe here are readily amenable to automation, potentially allowing the generation of 2D stiffness maps of cross-sections of tissues and whole organs. More precise control of indentation rate and direction would allow direct quantification of time-dependent visco/poroelastic mechanical properties (e.g. the relaxation parameters determined in table 1) by dynamic control of stress and strain. Since the samples can remain in aqueous media, they can be chemically stimulated by adding solutes to the medium, and spatial heterogeneity of millimeter size samples can be investigated by cutting sections at different angles. These extensions have not yet been undertaken in this initial study.

Despite the advantages offered by the device described here, there are some inherent limitations. Probably the most significant is that our technique only allows probing of surface mechanical properties and so is limited to providing two-dimensional stiffness information, in contrast to recently developed 3D methodologies, such as ultrasound elastometry. An additional limitation is that all the calculations used here to determine tissue moduli assume the material to be homogeneous and isotropic, while biological materials are inherently heterogeneous, with significant compositional and directional variability. A problem inherent to measuring stiffness of soft materials by continuously increasing indentation (as in figures 1(c) and 2) is that significant errors in measured moduli can be induced by small inaccuracies in quantification of the contact point (Kaufman and Klapperich 2009). This is particularly problematic for very compliant samples where changes in force upon initial compression are small and within the error of the experiment; however, methods are available to accurately determine contact points (Deuschle et al 2007).

Another disadvantage of the described device is that while the stiffness of the probe allows accurate determination of stiffness in the range of many biological tissues (100 Pa–10 kPa), it precludes measurement of stiffer materials as these no longer indent under the relatively small loads applied by the probe. In our observations, experimental errors begin to diverge as sample stiffness exceeded 10 kPa. Finally, a significant limitation is the thickness of the sample that can be accurately measured with this technique. Although there are no equipment constraints prohibiting measurement of thin samples, the correction factor used to correct for sample thickness diverges exponentially when the probe radius is thicker than the sample (Hayes et al 1972). Hence, very small errors in assumed sample thickness can lead to large errors in calculated stiffness. This limitation can be overcome by accurate quantification of sample thickness, although this can be difficult in heterogeneous biological samples.

The device and technique presented in this contribution provide an easy-to-use, inexpensive and versatile platform for the quantification of the mechanical properties of biological tissues. The intermediate length scale probed by this technique is ideally suited for measuring the biological heterogeneity that would be expected both in healthy tissues and a variety of disease states. We believe the use of techniques such as the one described here will enable the quantification of relevant tissue material properties at a mesoscale and further exploration of the role of mechanics in physiological function and disease.

5. Sample preparation

All animals were maintained in specific pathogen-free conditions in accordance with the guidelines of the Laboratory of Animal Research at the University of Pennsylvania, and experiments were performed with the approval of the University of Pennsylvania Institutional Animal Care and Use Committee (IACUC).

5.1. Microscopic tissues: glomeruli

Glomeruli were prepared using a standard sieving method (Schlondorff 1990). The glomeruli were deposited as a dilute suspension on a glass coverslip which was mounted for microscopic observation as described in more detail in section 3.1.

5.2. Thin samples: rat aorta

Aortas were isolated from 4-to-6-month old C57BL/6 mice and attached to 35 mm culture dishes by placing small amounts of adhesive on the two ends of approximately 5 cm transected sections. Samples were kept submerged in PBS during indentation.

5.3. Whole tissue stiffness: Fibrosis progression in CCl₄-treated livers

Male Sprague-Dawley rats were treated with CCl₄, and livers were harvested on the indicated day post-treatment as previously described (Georges et al 2007). Livers were stored in Hank's buffered saline solution (HBSS) on ice until analysis. Prior to indentation testing, uniform 3 mm slices from the left lobe of each liver were prepared, placed in a 35 mm tissue culture dish, and measured as above.

5.4. Whole tissue stiffness: Malignant progression in mammary glands

Female FVB-TgN MMTV-neu mice (Jackson Laboratory) exhibiting varying stages of mammary gland tumor progression were sacrificed, the abdomens shaved, and mammary glands excised intact (i.e. attached to the underlying dermal layers). The samples were adhered to 35 mm tissue culture dishes using industrial strength adhesive (Krazy Glue™) such that the gland was positioned face-up. The samples were temporarily stored in PBS on ice until analysis and were probed in the PBS solution using the technique described above. Several points were probed on each gland. Each indentation position was characterized by visual inspection and post-measurement fixation and histological examination as normal, tumor, and tumor-adjacent (the area of the tissue that lies within 10 mm of the visible tumor; figures 5(B)–(D)).