Biophysical characterization of a relativistic proton beam for image-guided radiosurgery

Abstract

We measured the physical and radiobiological characteristics of 1 GeV protons for possible applications in stereotactic radiosurgery (image-guided plateau-proton radiosurgery). A proton beam was accelerated at 1 GeV at the Brookhaven National Laboratory (Upton, NY) and a target in polymethyl methacrylate (PMMA) was used. Clonogenic survival was measured after exposures to 1–10 Gy in three mammalian cell lines. Measurements and simulations demonstrate that the lateral scattering of the beam is very small. The lateral dose profile was measured with or without the 20-cm plastic target, showing no significant differences up to 2 cm from the axis A large number of secondary swift protons are produced in the target and this leads to an increase of approximately 40% in the measured dose on the beam axis at 20 cm depth. The relative biological effectiveness at 10% survival level ranged between 1.0 and 1.2 on the beam axis, and was slightly higher off-axis. The very low lateral scattering of relativistic protons and the possibility of using online proton radiography during the treatment make them attractive for image-guided plateau (non-Bragg peak) stereotactic radiosurgery.

INTRODUCTION

Proton therapy is now a well-established method in treatment of cancer [1] and noncancer [2] diseases. The rationale of using protons with energies between 60 and 250 MeV is based on the favourable depth–dose distribution, so that the targets can be located on a spread-out Bragg peak while the normal tissue is exposed in the plateau region [3]. These favourable ballistic properties produce high target conformality and reduce the risk of effects on normal tissue, including secondary cancers [4]. However, the proton beam is broadened by multiple scattering in the beam-line materials and in the patient's body. This broadening produces a ‘dose halo’ in the treatment plan which reduces the dose gradient between the target volume and organs at risk [5]. For a charged particle with atomic number z and mass number A, the lateral scattering is roughly proportional to z/Aβ², where β = v/c is the particle speed. Therefore, the lateral scattering can be reduced either by using heavy ions such as carbon [6], or by increasing the particle velocity. In the latter case, using protons in the GeV region, the targets cannot be exposed on the Bragg peak (for instance, the range of 1-GeV protons is ∼3.2 m in water), which means various beams need to be cross-fired to the target from different angles, in a similar manner to X-ray therapy.

The advantage of ‘plateau’ (non-Bragg peak) radiotherapy is that there is a stable beam profile providing very sharp dose contours allowing critical organs to be spared. For this reason, relativistic protons hav already been proposed for plateau stereotactic radiosurgery in Berkeley [7]. The only clinical experience comes from St. Petersburg in Russia: more than 1000 patients have been treated with 1-GeV protons at the Petersburg Nuclear Physics Institute (PNPI) since 1975 [8].

A major advantage of relativistic protons is that the beam crossing the patient can be exploited for proton radiography. Proton radiography has been investigated since the early 1970s because of its low radiation dose, high density resolution and ability to measure directly proton stopping power, but spatial resolution is still a limiting factor precluding most practical applications [9]. However, proton radiography with high-energy protons reaches unprecedented spatial resolution, as proved with the 800-MeV beam in Los Alamos National Laboratory for imaging explosives [10]. A project for proton microscopy at the new Facility for Anti-proton and Ion Research (FAIR) in Darmstadt plans to exploit a 4.5-GeV proton beam for radiography, reaching spatial resolutions below 10 μm and a time resolution below 10 ns [11]. This high precision in beam delivery combined with online high-resolution imaging and dose verification leads to reduced target margins and improves image-guided stereotactic radiosurgery for cancer (e.g. small brain metastasis, pituitary adenoma, vestibular Schwannoma) and noncancer (e.g. arteriovenous malformations, trigeminal neuralgia, epilepsy, intracranial aneurysm, macular degeneration) lesions [7–9].

Notwithstanding their clinical use at PNPI [8], relativistic proton beams have been poorly characterized for their radiobiological properties. In space radiation research relativistic light and heavy ions are often used, but normally at low doses and measuring late stochastic endpoints, relevant for risk assessment in human space missions [12, 13]. Here we have performed a full physical and biological characterization of the 1-GeV proton beam at the NASA Space Radiation Laboratory (NSRL) in the Brookhaven National Laboratory (Upton, NY), including dose measurements in a plastic (PMMA) target, lateral scattering Monte Carlo simulation, and survival of three different cell lines.

MATERIALS AND METHODS

Accelerator

Details of the experimental setup at NSRL have been described elsewhere [14, 15]. Briefly, the 1-GeV proton beam at NSRL was extracted in air and directed perpendicular to a 20 × 20 cm multi-layer lucite target (PMMA; ρ = 1.16 g/cm³). Dose was measured using a Far West thimble ionization chamber in different positions on the target and at various lateral off-axis distances corresponding to the positions of the cell samples (see below). The incident beam full width at half maximum (FWHM) was measured with radiographic films and a pixel camera and was 1.79 ± 0.03 cm. Dose rate ranged from 0.5 to 20 Gy/min. The highest dose rates were used for experiments at large distances from the beam axis. In cell experiments without the PMMA block, a broad beam of 15 × 15 cm was used. For comparison, cells were also exposed to a ¹³⁷Cs γ-ray source in the Medical Department of the Brookhaven National Laboratory at a dose rate of approximately 1 Gy/min.

Simulations

Beam simulations were performed using SRIM2011 [16] or the GEANT4 Monte Carlo package [17]. For comparison, lateral scattering was also calculated using theMolière theory, which describes very well the lateral spread of proton beams used in Bragg peak therapy [18]. For small angles, the higher order terms in the Molière theory can be neglected, and the beam at a depth d into a material of radiation length L_rad can be described as a Gaussian distribution with standard deviation:

Cells and survival assay

Three different cell lines were use for radiosensitivity measurements. Two cell lines were derived from human epithelial tumours of the tongue (SCC25) and the larynx (SQ20B). Both cell lines were kindly donated by Dr Eleanor Blakely (LBNL, USA). Cells were grown in D-MEM:F12 (75:25) supplemented with 0.4 μg/ml hydrocortisone and 20% foetal calf serum. Plating efficiency was ∼30% for SCC25 and ∼60% for SQ20B, and the doubling time was ∼24 h for both. These cell lines were selected as representative of cancers of the same histological type but with different radio-sensitivity: in fact, SQ20B cells are more radio-resistant to γ-rays than SCC25 cells [19]. As a standard control cell line we used the common Chinese hamster ovary V79 cells, kindly provided by Dr Antonella Tabocchini (ISS, Rome). V79 cells were grown in Eagle's minimum essential medium (MEM) (10% foetal calf serum) with a plating efficiency of ∼90% and a doubling time of ∼13 h. Cells were exposed in a monolayer in log phase in Lab-Tek chamber tissue culture slides (Nalgene). The distance from the axis was measured from the centre of the beam spot to the centre of the slide, positioned along the major axis. Irradiations were performed at room temperature, and 10–15 min after exposures cells were trypsinized, counted with a Coulter counter, diluted and seeded at low density in 100-mm Petri dishes for colony-forming assays as described elsewhere [20].

Data analysis

Surviving fractions were calculated by colony counting, dividing the plating efficiency of the irradiated population by the plated efficiency of the controls, measured in the same experiment. Standard errors were calculated using the distribution of counts in five dishes for each test point (10 dishes were used for the controls). Errors were eventually enlarged using the robust fitting procedure to account for systematic errors in the colony assay measurements [21]. Weighted fits on experimental survival measurements S were performed using the usual linear quadratic formula:

Fitting parameters α and β were calculated by the weighted χ² minimization and their uncertainties corresponding to a χ² variation of 1. The relative biological effectiveness (RBE_α) was calculated as the ratio of the α coefficients of the proton and γ-ray curves and uncertainty estimated from the errors on α and β. RBE₁₀ is the ratio of the doses of γ-rays and protons producing 10% survival. These doses were interpolated from the best fits and uncertainties on interpolated values calculated considering the exponential function and the 95% confidence interval (α = 0.05). Fits and data analysis were performed with the SigmaStat® software (Jandel Scientific).

RESULTS

The main advantages of the relativistic protons in radiosurgery are the high precision and low lateral scattering. Simulations are shown in Fig. 1. The beam's eye view of the 1-GeV beam after 20 cm in PMMA has been simulated with SRIM2011 [16], and the FWHM spread as a function of the target density either calculated using Molière's formula [18] or simulated by GEANT4 [17]. The advantage of relativistic protons over conventional therapy energy is clearly shown: at 1-GeV, the lateral spread is reduced to almost 90% of the spread at 200 MeV. The simulations have been extended to 2- and 4.5-GeV protons, which will be used in the radiography project at FAIR [11]. Simulations and calculations show a good agreement at high energy.

Fig. 1.

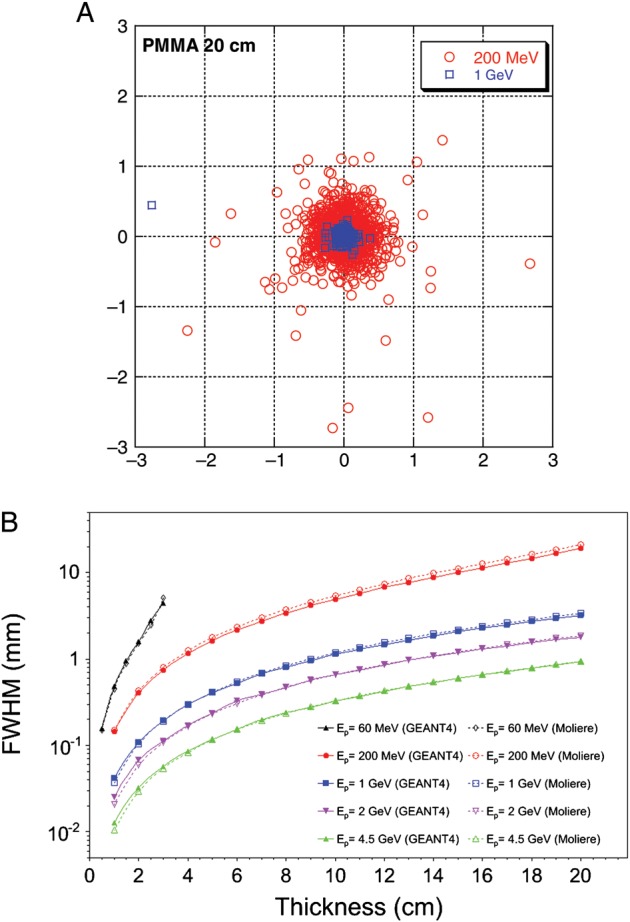
Simulations of the lateral straggling of the proton beam used in our experiments. Left, a beam's eye view of the position of single protons after traversal of 20-cm PMMA. Simulations by SRIM 2011 [16] at two different energies: typical therapeutic 200-MeV beam, and the 1-GeV beam used in the experiments described here. Right, calculations of the beam shape's FWHM for a monoenergetic incident proton beam in PMMA using Molière's formula [18] or simulated by GEANT4 [17]. The FWHM spread is calculated for beams accelerated at 60 MeV (used in eye therapy), 200 MeV (deep protontherapy), 1 GeV (these experiments), 2 and 4.5 GeV (future FAIR facility).

The dose as a function of the target thickness shows a clear increase as a function of depth up to 40% at 20 cm in PMMA (Fig. 2). These measurements are reasonably reproduced by the GEANT4 simulation, which shows that the increase is caused by the production of secondary protons (Fig. 2). Some discrepancies between measured and simulated doses are significant, and this is probably caused by the partial simulation performed here. We did not fully simulate the beam-line taking into account all scatterers, exit windows, air, monitors, ionization chamber shape, etc. This is probably the cause of some of the quantitative discrepancies in Fig. 2, while the trends remain the same. Simulations predict that the contribution from other ions (deuterons, tritons, helium and lithium) is negligible.

Fig. 2.

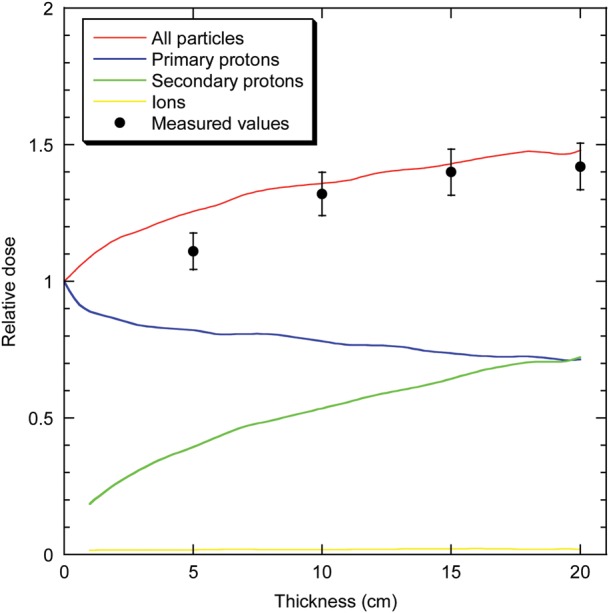
Dose of a 1-GeV proton beam measured along the beam's axis after PMMA blocks of increasing thickness. Dose is normalized to the entrance value measured by a monitor chamber in front of the target. Measurements are pooled from experiments at seven different dose values (ranging from 2–10 Gy), and bars are standard errors of the mean values. Curves are interpolations of GEANT4 simulations. The contributions of primary protons, secondary protons and other ions (neutrons, deuterons, tritons, helium and lithium) are plotted in different colours.

The energy spectrum after 20 cm is simulated in Fig. 3. According to the SRIM2011 simulation, the energy of the beam after the 20-cm PMMA block is reduced to 957 MeV, and the linear energy transfer in water is only slightly increased from 0.222 to 0.224 keV/μm [16]. Whilst the primary protons lose relatively little energy in the target, resulting in a small energy straggling (red curve), the spectrum of the secondary (target-emitted) protons extends to low energies (blue curve) and is almost flat. The slow protons in the spectrum are caused by target nuclear evaporation emission [14]. Some of the secondary protons are generated by neutrons, which are emitted with approximately the same frequency as knock-out protons. However, GEANT4 simulations predict that only 4% of the dose is caused by neutrons, because neutrons release a much smaller dose per particle than charged particles. The neutron spectrum is also shown in Fig. 3.

Fig. 3.

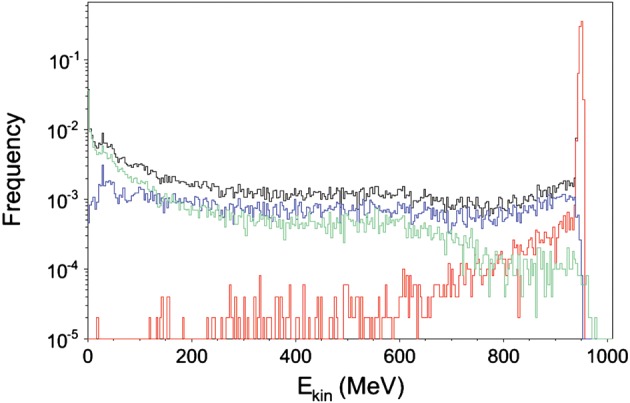
Simulated energy spectrum of the 1-GeV proton beam after traversal of 20-cm PMMA. Simulation was performed with 50 000 protons using GEANT4. Red, primary protons; blue, secondary protons; green, neutrons; black, total.

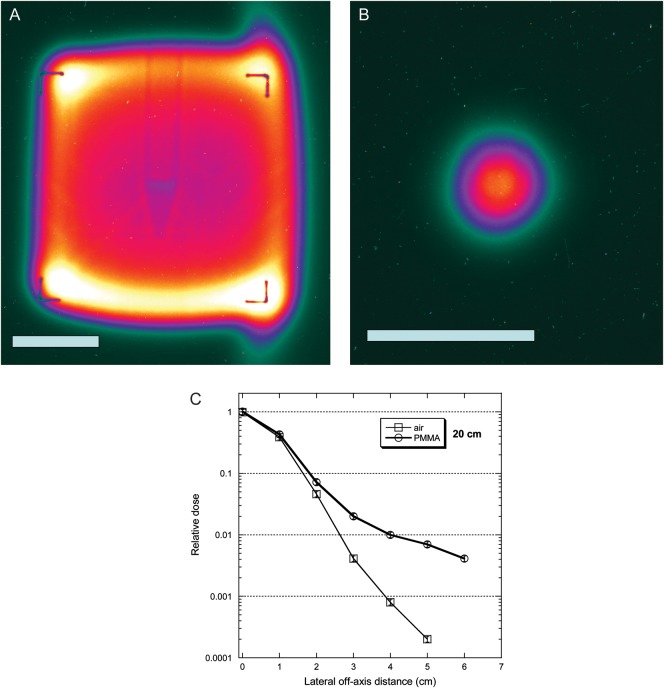
The secondary knock-out protons are mostly emitted in a forward direction [14, 15], but they have a larger spread and contribute to increasing the dose lateral spread as a function of the depth. Images of the actual beam with 1.79 cm FWHM and broadened to 15 × 15 cm are shown in Fig. 4 using the pixel camera. The potential for radiography is shown: the image of a Falcon tube containing tissue culture medium is clearly visible. The measured lateral dose after 20 cm in air or PMMA is shown in Fig. 4C. The long tail of for the beam going through the lucite target is caused by secondary protons, mostly knock-out protons, since evaporation protons are slow and are generally stopped within the target.

Fig. 4.

Lateral straggling of the beam as visualized by a pixel camera for a broad beam (A) and the actual small beam (B) used in our experiments. White bar is 5 cm. The plot (C) shows the measured dose after 20 cm air or PMMA on the beam axis and at different lateral distances.

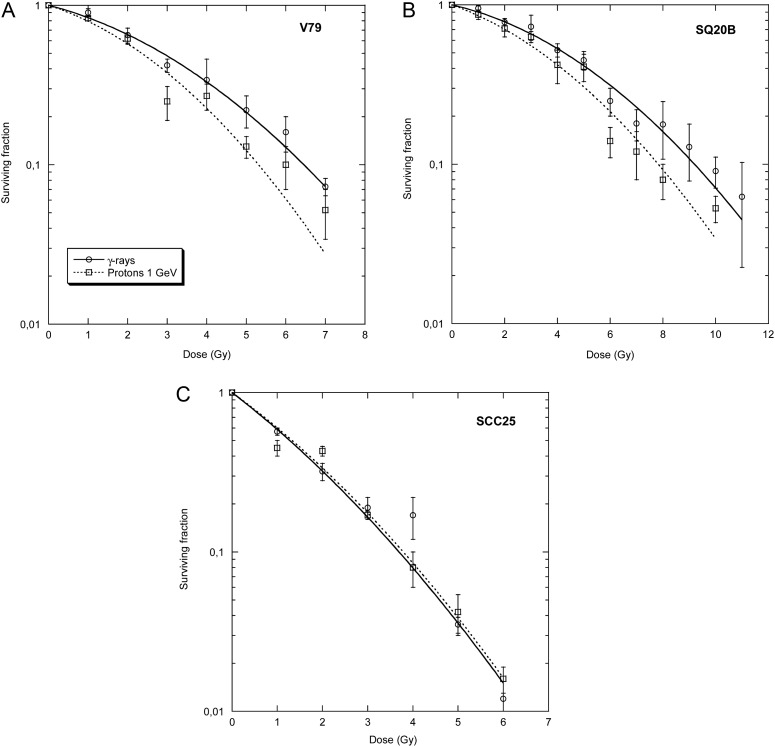
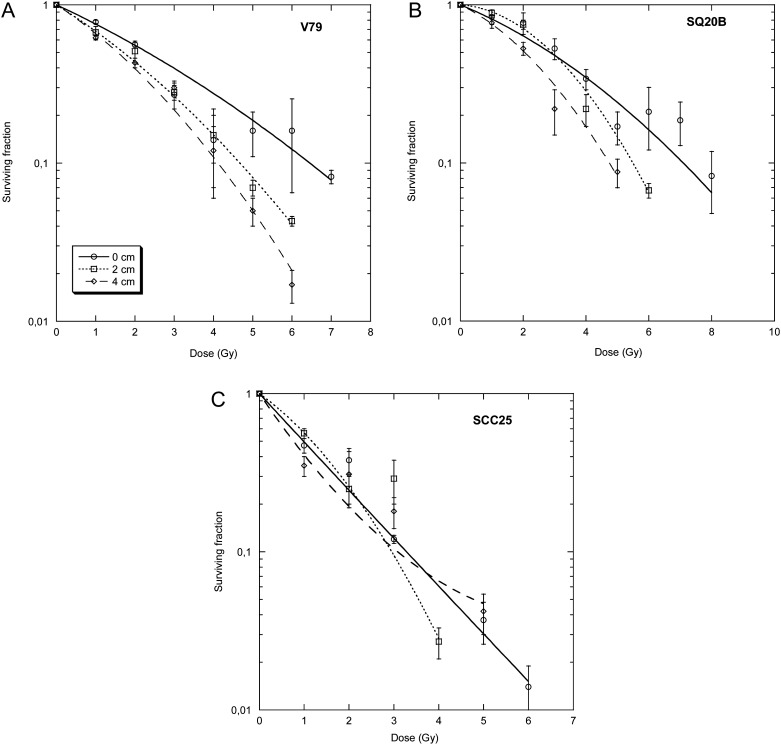
Survival of the three different cell lines of graded doses of γ-rays and 1-GeV protons is shown in Fig. 5. SQ20B cells are more radio-resistant than SCC25 cells [19, 20, 22]. The RBE is higher for radio-resistant than radio-sensitive squamous cell carcinoma. Cell samples were also exposed to the proton beam after 20 cm PMMA at different lateral distances (0, 2, and 4 cm) from the beam axis. Survival curves are shown in Fig. 6. The RBE of the proton beam compared with γ-rays is always small, and bearing in mind the uncertainties in the RBE estimates it is around 1 on the axis, and 1.2–1.4 off-axis (Table 1). For radio-resistant cells (V79 and SQ20B), an increase in the α/β ratio was observed in the survival curves after the shielding, while for the radio-sensitive SCC25 tumours no significant differences were observed between γ-rays and protons at all angles and depths (Table 1).

Fig. 5.

Survival curves of V79, SQ20B and SCC25 cells after exposure to γ-rays or protons at 1 GeV. Bars are standard errors of the mean values. Lines are best fits using the linear-quadratic model (see Table 1 for the fitting parameters).

Fig. 6.

Survival curves of V79, SQ20B and SCC25 cells after exposure to protons behind the 20-cm PMMA block. The flasks were exposed either on the beam axis, or at 2 or 4 cm from the main axis. Bars are standard errors of the mean values. Lines are best fits using the linear-quadratic model (see Table 1 for the fitting parameters).

Table 1.

Parameters of the linear-quadratic cell survival fits shown in Figs 5 and 6

Cell	Radiation	Absorber thickness (cm)	Lateral spread (cm)	α (Gy−1)	β (Gy−2)	α/β (Gy)	RBEα	RBE10
V79	γ-rays	0	0	0.15 ± 0.03	0.033 ± 0.009	4.5 ± 0.5	–	–
	Protons 1 GeV	0	0	0.18 ± 0.07	0.047 ± 0.022	3.9 ± 0.6	1.2 ± 0.6	1.2 ± 0.3
		20	0	0.20 ± 0.02	0.044 ± 0.004	18.7 ± 0.3	1.8 ± 0.4	1.0 ± 0.3
		20	2	0.32 ± 0.05	0.036 ± 0.008	12.1 ± 0.3	2.4 ± 0.7	1.4 ± 0.3
		20	4	0.38 ± 0.03	0.043 ± 0.0007	8.3 ± 0.2	2.6 ± 0.7	1.6 ± 0.3
SQ20B	γ-rays	0	0	0.087 ± 0.022	0.017 ± 0.004	4.9 ± 0.3	–	–
	Protons 1 GeV	0	0	0.13 ± 0.03	0.020 ± 0.006	6.7 ± 0.4	1.5 ± 0.5	1.23 ± 0.24
		20	0	0.07 ± 0.06	0.05 ± 0.01	9.7 ± 0.7	2.1 ± 0.9	1.3 ± 0.5
		20	2	0.03 ± 0.04	0.070 ± 0.007	0.4 ± 1.2	0.4 ± 0.4	1.7 ± 0.5
		20	4	0.22 ± 0.06	0.054 ± 0.018	4.1 ± 0.4	2.5 ± 1.0	1.9 ± 0.7
SCC25	γ-rays	0	0	0.50 ± 0.05	0.033 ± 0.011	15.1 ± 0.4	–	–
	Protons 1 GeV	0	0	0.47 ± 0.04	0.036 ± 0.010	13.2 ± 0.3	0.94 ± 0.12	0.9 ± 0.3
		20	0	0.71 ± 0.06	–0.0013 ± 0.016	–	1.41 ± 0.18	1.1 ± 0.6
		20	2	0.47 ± 0.09	0.11 ± 0.03	4.4 ± 0.3	0.93 ± 0.20	1.2 ± 0.4
		20	4	0.96 ± 0.13	–0.07 ± 0.03	–	1.9 ± 0.3	1.2 ± 0.3

Weighted fits on experimental survival data were performed using the Levenberg–Marquardt algorithm and the uncertainties correspond to a χ² variation of 1. All fits used both α and β parameters reported below and plotted in Figs 4 and 5, even though some of the parameters were not significant. The RBE_α was calculated as the ratio of the α coefficients of the proton and γ-ray curve. RBE₁₀ is the ratio of the doses of γ-rays and protons producing 10% survival. These doses were extrapolated from the best fit curves and uncertainties calculated.

DISCUSSION

Recent progress in proton radiography makes the use of relativistic protons appealing for radiosurgery. Although the ballistic advantages of Bragg peak therapy are lost, with plateau protons the lateral scattering is reduced compared with Bragg peak ions (see Figs 1 and 4), and online radiography allows an ‘aim-and-shoot’ treatment method, which may be very useful for selected clinical cases [9]. A systematic biophysical characterization of the beam is necessary for a detailed treatment plan. We have shown here that the lateral straggling is indeed very small (about 0.7 mm after 20 cm in lucite) and produces very small off-axis doses (Fig. 4), i.e. a much reduced ‘dose halo’ compared with conventional proton therapy [5]. However, we measured a significant increase in the dose along the beam axis at increasing target depth in the target, up to 40% after 20 cm. This dose build-up is caused mostly by knock-out secondary protons emitted from target atoms by nuclear spallation with the primary beam (Fig. 3). The RBE at 10% survival for Chinese hamster fibroblasts and two human squamous cell carcinomas ranges between 1 and 1.2, much lower than the RBE values for these same cells relative to low-energy protons [20] or heavy ions [22], but similar to the value of 1.1 normally used in Bragg peak proton therapy [23] and measured in radiobiological experiments [24–26]. Similarly low RBE for 1-GeV protons has been also measured for white blood cell loss in mice [27]. The RBE is higher for radio-resistant than for radio-sensitive cells (Table 1), which is consistent with experience in high-linear energy transfer radiobiology [3, 12]. RBE and α/β ratio increase with target depth and off-axis for radio-resistant cells, most likely because of the production of slower protons at higher linear energy transfer (Fig. 3). This is consistent with the recent observation that secondary protons produced by the primary 1-GeV proton beam induce DNA damage in human keratinocytes positioned at 90° from the beam axis, even though the measured dose in that position was only a few mGy [28].

Our measurements and simulations support further developments of relativistic protons for image-guided plateau proton radiosurgery. In silico comparisons of treatment plans with stereotactic radiosurgery or stereotactic body radiation therapy will allow a selection of those cases where proton radiosurgery may be competitive with X-rays. The increase in dose along the target should be carefully considered in the treatment plan, whereas the RBE can be dealt with in a similar way to Bragg peak radiotherapy.