A comparison of two theories of perceived distance on the ground plane: The angular expansion hypothesis and the intrinsic bias hypothesis

Abstract

Two theories of distance perception—ie, the angular expansion hypothesis (Durgin and Li, 2011 Attention, Perception, & Psychophysics 73 1856–1870) and the intrinsic bias hypothesis (Ooi et al, 2006, Perception 35 605–624)—are compared. Both theories attribute exocentric distance foreshortening to an exaggeration in perceived slant, but their fundamental geometrical assumptions are very different. The intrinsic bias hypothesis assumes a constant bias in perceived geographical slant of the ground plane and predicts both perceived egocentric and exocentric distances are increasingly compressed. In contrast, the angular expansion hypothesis assumes exaggerations in perceived gaze angle and perceived optical slant. Because the bias functions of the two angular variables are different, it allows the angular expansion hypothesis to distinguish two types of distance foreshortening—the linear compression in perceived egocentric distance and the nonlinear compression in perceived exocentric distance. While the intrinsic bias is proposed only for explaining distance biases, the angular expansion hypothesis provides accounts for a broader range of spatial biases.

1. Background

Distance perception has been extensively studied for centuries. Many different sources of information for estimating depth and distance have been identified, and it has been suggested that different sources of perceptual information have different effective ranges and that their reliabilities vary across viewing conditions (Cutting and Vishton 1995). One type of information that is of particular interest is information about direction of gaze. In principle, gaze direction toward a point on level ground can be used to measure egocentric distance if eye-height is known. Gibson (1950, 1979) emphasized that the ground plane provides a great deal of important visual information about distance, including optical flow, angular declination, and texture gradients. These ground-based sources of information are particularly useful for locomotor space (ie, what Cutting and Vishton called “action space”). However, even when it comes to ground distance in locomotor space, both empirical data and theoretical accounts of perceived distance remain difficult to integrate across various paradigms and theorists. For example, some evidence suggests that perceived ground distance in locomotor space is increasingly compressed at greater distances (eg, Gilinsky 1951; Ooi and He 2007) while some evidence suggests that it is roughly constantly compressed (eg, Foley et al 2004), and yet other evidence suggests it is essentially accurate (eg, Loomis et al 1992).

Recently, two theories have been proposed, which have the potential to explain a number of empirical findings concerning the perception of ground extents in locomotor space. One theory is the intrinsic bias hypothesis (Ooi et al 2006). The other theory is the angular expansion hypothesis (Durgin and Li 2011; Li and Durgin 2010). Although the two theories are similar inasmuch as they both attribute the misperception of distance to biases in perceived slant, the fundamental assumptions of the two theories are very different. In the present paper, we will review and compare how the two theories explain some empirical findings in distance perception.

2. Fundamental geometrical assumptions of the two theories

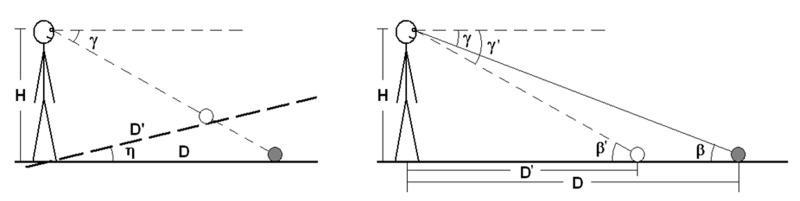
The fundamental assumption of the intrinsic bias hypothesis is that there might be a default representation of space when no visual information is available. This default representation (or intrinsic bias) biases the perceived geographical slant of the ground plane (by an additive constant, η), which in turn results in biases in perceived distance, as shown in the left side of Figure 1.

Figure 1.

Diagrams depicting the fundamental geometrical assumptions of the intrinsic bias hypothesis (left) and the angular expansion hypothesis (right).

In contrast, the angular expansion hypothesis assumes that the perceived gaze declination γ′ and the perceived optical slant β′ are systematically biased (by a multiplicative factor of about 1.5), so that the perceived distance D′ is foreshortened but the perceived geographical slant of the ground plane is largely unchanged, as shown in the right side of Figure 1.

3. Evidence and predictions of the intrinsic bias hypothesis

The evidence of the assumption in the intrinsic bias hypothesis originally came from experiments using a blind walking and gesturing paradigm (Ooi et al 2001; see also Loomis 2001) conducted in a dark environment. When participants were asked to perceive the 3D location (ie, distance and height) of a dim target light in the dark and to indicate it by walking blindly to the perceived distance of the target and gesturing the perceived height with the hand, the indicated location always lay on an implicit surface slanted upward despite the variant physical locations of the target light (Ooi et al 2001, 2006).

As shown in Figure 1, left, if the perceived ground plane is tilted upward by a constant angle η, the perceived egocentric distance D′ (which can be expressed by Equation 1, see Ooi and He 2007) would be compressed relative to the physical distance D′,

$${\displaystyle D^{\prime }=\frac{H\cos (\gamma )}{\sin (\gamma +\eta )}}$$ (1)

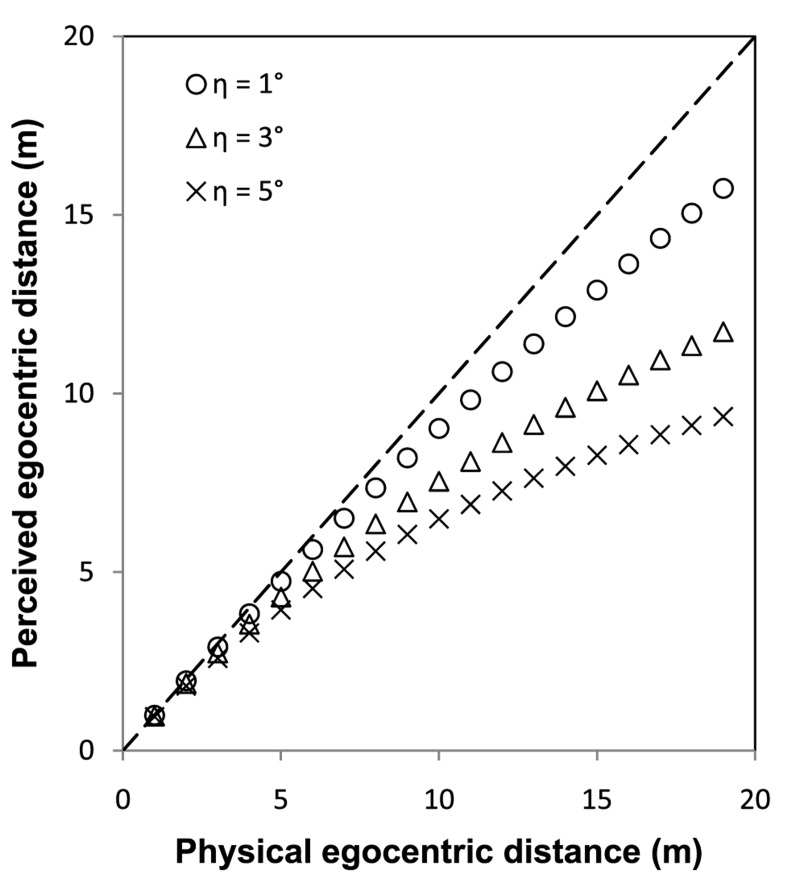
Figure 2 shows the perceived egocentric distance D′ as a function of the physical distance D, based on the prediction of Equation 1 for three possible values of η. We can see the predicted perceived egocentric distance is increasingly compressed when the physical egocentric distance increases. Moreover, even small changes in η result in substantial differences in distance compression, especially for long distances. This pattern of egocentric distance foreshortening is consistent with Gilinsky's (1951) observation of accelerating distance compression using an equal apparent interval procedure.

Figure 2.

Predicted perceived egocentric distance foreshortening based on the intrinsic bias hypothesis for various values of η. η is the assumed bias in the perceived geographical slant of the ground plane.

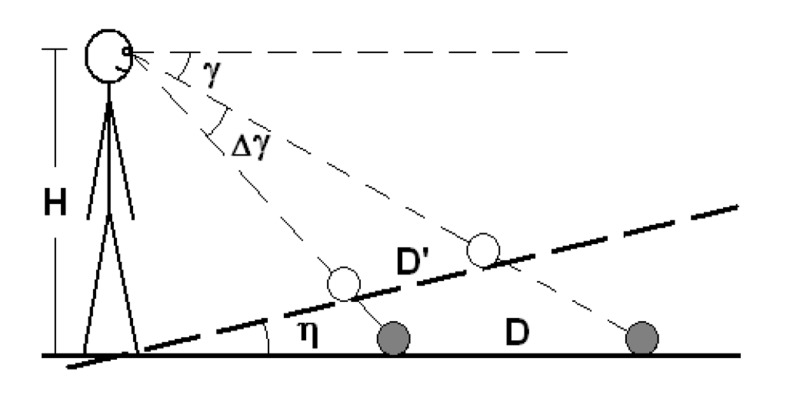
The intrinsic bias hypothesis predicts that perceived exocentric sagittal distance would also be foreshortened. As shown in Figure 3, if the perceived geographical slant of the ground is tilted up by an angle of η (due to the intrinsic bias), the perceived exocentric sagittal distance D′ can be expressed as,

$${\displaystyle D^{\prime }=\frac{H\cos (\gamma )}{\sin (\gamma +\eta )}-\frac{H\cos (\gamma +\Delta \gamma )}{\sin (\gamma +\Delta \gamma +\eta )}}$$ (2)

Figure 3.

Diagram depicting the perceived exocentric sagittal distance foreshortening predicted by the intrinsic bias hypothesis.

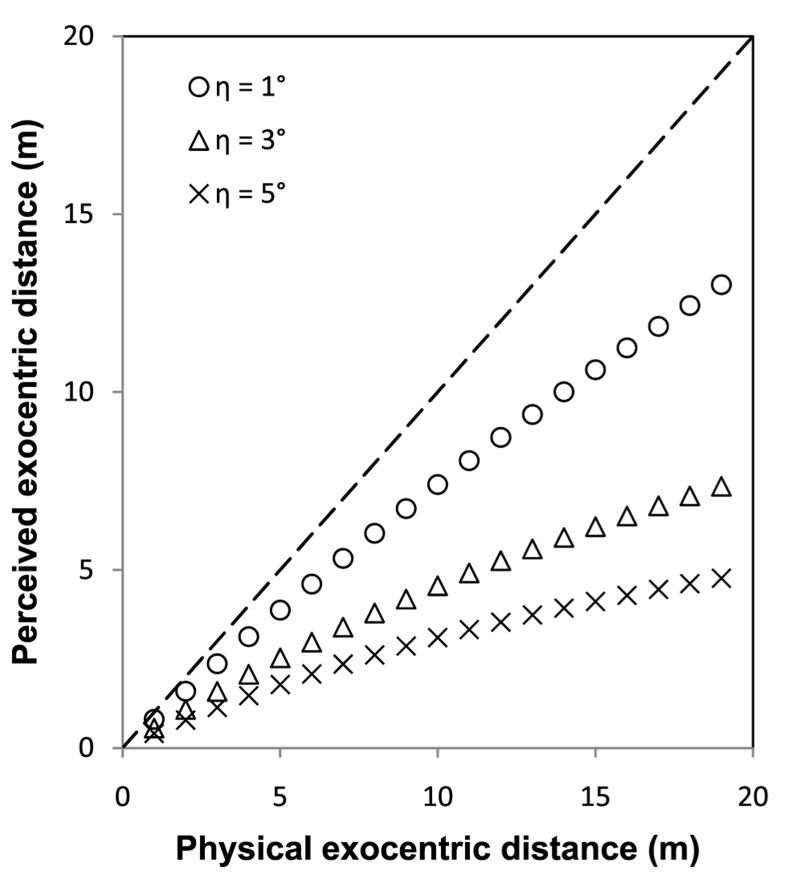
Figure 4 shows the perceived exocentric distance D′ (based on the prediction of Equation 2) as a function of the physical distance D, when the near end of the physical sagittal extent is fixed at 10 m from the observer. We can see the predicted perceived exocentric distance is also increasingly compressed when the physical exocentric distance increases. Moreover, even small changes in η would result in substantial difference in the distance compression especially for long distances. This pattern of exocentric distance foreshortening is consistent with Li et al's (2011) observation with an aspect ratio task.

Figure 4.

Predicted perceived exocentric distance foreshortening based on the intrinsic bias hypothesis. η is the assumed bias in the perceived geographical slant of the ground plane. In this simulation, the near end of the exocentric extent is fixed at 10 m from the observer.

Although the intrinsic bias hypothesis provides plausible explanations for perceived distance foreshortening, it fails to predict the observed results in the distance fractionation experiments. For example, Purdy and Gibson (1955) showed that participants could bisect or trisect large egocentric distances fairly accurately. Lappin et al (2006) reported reliable but small errors (3% to 13% of the total bisected distance) in a distance bisection experiment, in which their participants always set the middle point too far from themselves.

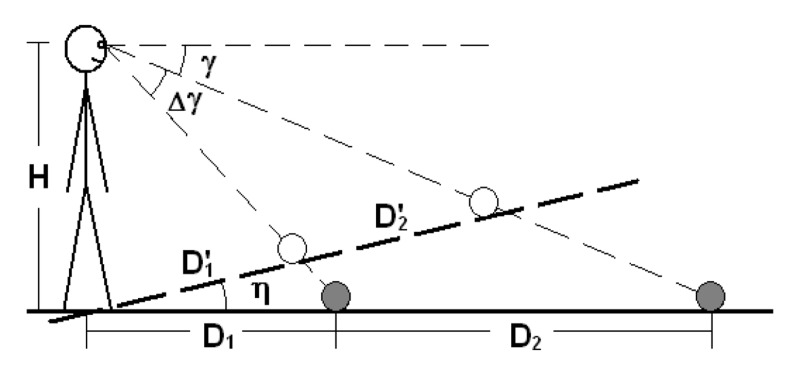
In contrast, the intrinsic bias hypothesis predicts that the middle point should be set much too close to the observer (Figure 5). The perceived distance ratio D₂′/D₁′ can be expressed by Equation 3,

$${\displaystyle D_2^{\prime }/D_1^{\prime }=\frac{D_1+D_2}{D_1}·\frac{\sin (\gamma )·\sin (\gamma +\Delta \gamma +\eta )}{\sin (\gamma +\eta )·\sin (\gamma +\Delta \gamma )}-1}$$ (3)

Figure 5.

Diagram depicting the performance in the distance bisection task based on the assumption of the intrinsic bias hypothesis.

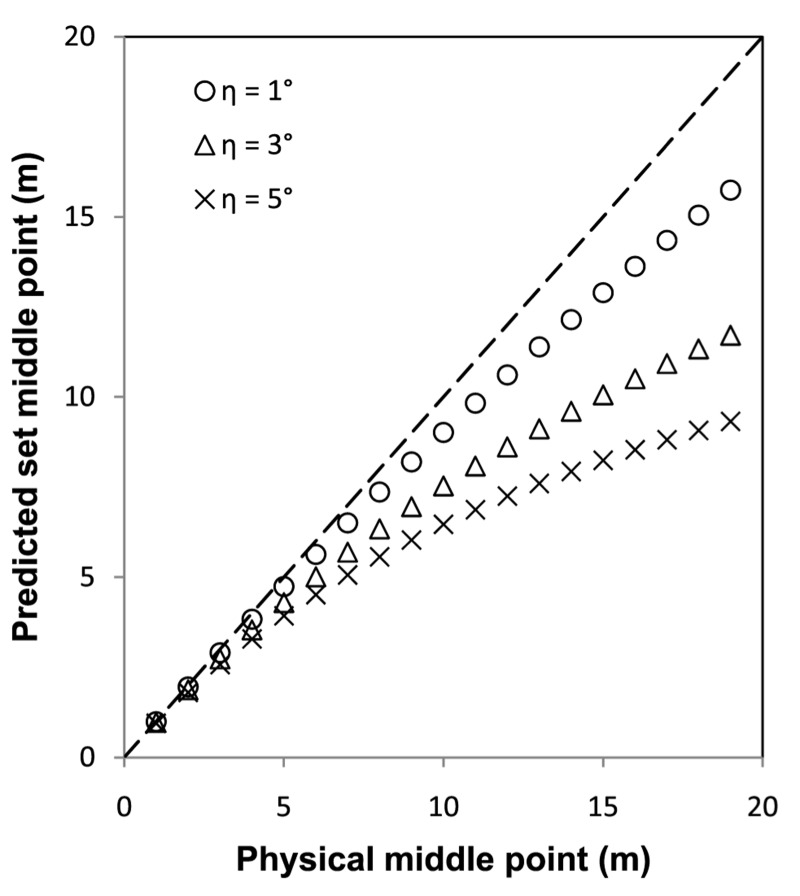
Figure 6 shows the predicted (by Equation 3) set middle point as a function of the physical middle point in the distance bisection task. It is clear the predicted set middle point is too close to the observer, which is inconsistent with the empirical observations (ie, Lappin et al 2006; Purdy and Gibson 1955).

Figure 6.

Predicted set middle point as a function of physical middle point in the distance bisection task, based on the intrinsic bias hypothesis. η is the assumed bias in the perceived geographical slant of the ground plane.

The reason that the intrinsic bias hypothesis cannot explain the distance fractionation results is because the intrinsic bias hypothesis predicts that the perceived distance should always be a non-linear function of physical distance (ie, the perceived distance is increasingly compressed), as shown in Figures 2, 4, and 6. In fact, the intrinsic bias hypothesis does not distinguish between the perceived egocentric and exocentric distance. However, there is substantial evidence suggesting that perceived egocentric distance is a linear function of the physical distance while the perceived exocentric distance is not (Li et al 2011; Loomis et al 1992; see also Loomis and Philbeck 2008 for a recent review).

4. Evidence and predictions of the angular expansion hypothesis

As shown in Figure 1, right, the angular expansion hypothesis is based on the assumption of exaggerations in two perceptual angular variables—the perceived optical slant and the perceived gaze declination. There is convergent evidence that perceived optical slant is exaggerated. For example, Durgin et al (2010) showed that, for small slants within reach, a 34° slant from horizontal was judged to be 45° from horizontal. Moreover, the effect is spatial, not verbal: a 56° slant from vertical was judged to be 45° from vertical, and when the task was to indicate the bisection point between horizontal and vertical, a surface about 34° was indicated using standard psychophysical staircase procedure.

There is also convergent evidence showing that perceived gaze declination is exaggerated as well. For example, Li and Durgin (2009) asked participants to indicate gaze declination to distant targets (viewed from upper story windows) using both verbal estimation and 2D orientation matches. They found systematic exaggeration in perceived gaze with both measures. Durgin and Li (2011) asked participants to verbally estimate their gaze declinations to targets on the ground (with about 6° geographical slant) and found systematical exaggerations with a linear gain of about 1.5. They also asked different participants to indicate the bisection point of gaze declination between horizontal and vertical and found that a gaze declination of about 31° was indicated. Li et al (2011) showed that exaggeration in perceived gaze angle (with a linear gain of about 1.5) can perfectly explain the egocentric distance foreshortening relative to the horizontal and vertical distances (Higashiyama and Ueyama 1988).

A direct effect of the angular expansion hypothesis is the egocentric distance foreshortening (Figure 1, right). The perceived egocentric distance can be expressed either in terms of the perceived gaze declination γ′, ie, D′ = H/tan(γ′), or in terms of the perceived optical slant β′, ie, D′ = H/tan(β′). The perceived gaze angle is a linear function of actual gaze angle from 0° to about 50° (Durgin and Li 2011; Li and Durgin 2009; Li et al 2011), ie

$${\displaystyle {\gamma }^{\prime }=1.5\gamma }$$ (4)

In contrast, the perceived optical slant β′ has been found to be not only a function of actual optical slant β but also a function of viewing distance D (Li and Durgin 2010), ie

$${\displaystyle {\beta }^{\prime }=k_1\beta +k_2\ln (D)+C}$$

Because the slant gain k₁ is close to 1.5, if we fix k₁ to 1.5 and force C to 0, the perceived optical slant function can be simplified as

$${\displaystyle {\beta }^{\prime }=1.5\beta +k\ln (D)}$$ (5)

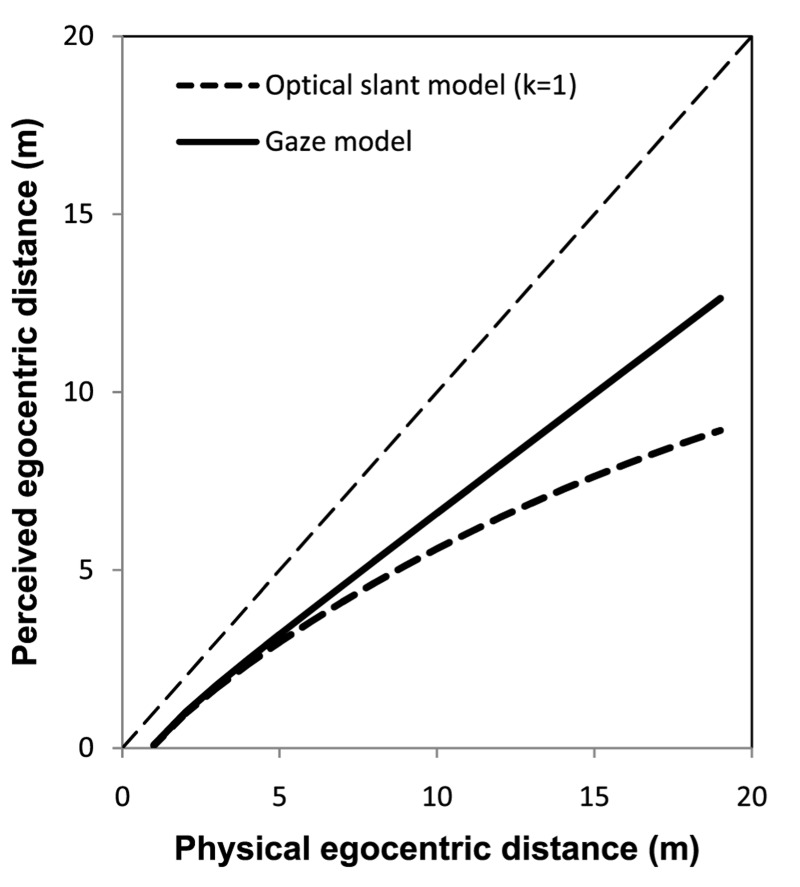
Equation 4 and 5 suggest that, when looking at a flat ground plane, the perceived optical slant and the perceived gaze angle would be similar for near distances, but they would be divergent at far distances (ie, the ground plane may look tilted up at far distance). Therefore, the perceived distance function would be different depending on which angular variable (gaze angle or optical slant) is used to determine the perceived distance. For example, the perceived egocentric distance would be linearly compressed if it is determined by perceived gaze angle alone (Figure 7, solid line)—but perceived egocentric distance would be increasingly compressed if it is determined primarily by perceived optical slant (Figure 7, dashed line).

Figure 7.

Predicted perceived egocentric distance functions based on the angular expansion hypothesis when the perceived distance is determined by perceived gaze angle alone (solid line) or by perceived optical slant alone (dash line).

This dual feature of the angular expansion hypothesis allows it to account for differences observed between the perceived egocentric distance function and the perceived exocentric distance function (Loomis et al 1992), which could not be explained by the intrinsic bias hypothesis. To account for an observed perceived distance function using the angular expansion hypothesis, we need to figure out which visual information (ie, optical slant or gaze angle) is used primarily by the visual system to determine the perceived distance. For example, in most egocentric distance perception studies, the perceived gaze angle is more reliable than the perceived optical slant (especially when distance is far). This is because when the distance is far, the visual information for perceiving optical slant (eg, the texture gradients and the disparity gradient) becomes less reliable. In contrast, the reliability of perceived gaze declination seems largely unaffected by distance. Thus, in order to model perceived egocentric distance, the gaze model (Equation 4) would be appropriate. As shown in Figure 7, the gaze model predicts a nearly linear relationship between the perceived egocentric distance and physical egocentric distance, which is consistent with most direct measures of egocentric distance (Foley et al 2004; Loomis et al 1992; see also Loomis and Philbeck 2008 for review).

For the distance fractionation tasks (ie, distance bisection or trisection), because the visual angles subtended by the two sagittal extents are relatively large, the gaze model would still be appropriate to model the perceived distances. Because the gaze model predicts a linear relationship between the perceived and physical distance (Figure 7), it predicts nearly accurate performance in the distance fractionation task (as shown by Purdy and Gibson 1955). The reason that Lappin et al (2006) found the middle point set was too close to the observer (especially in the lobby and hall way conditions) may be because the indoor environment shifts the perceived horizon downward (Messing and Durgin 2005), which in turn changes the perceived gaze declination and perceived distances (Ooi et al 2001).

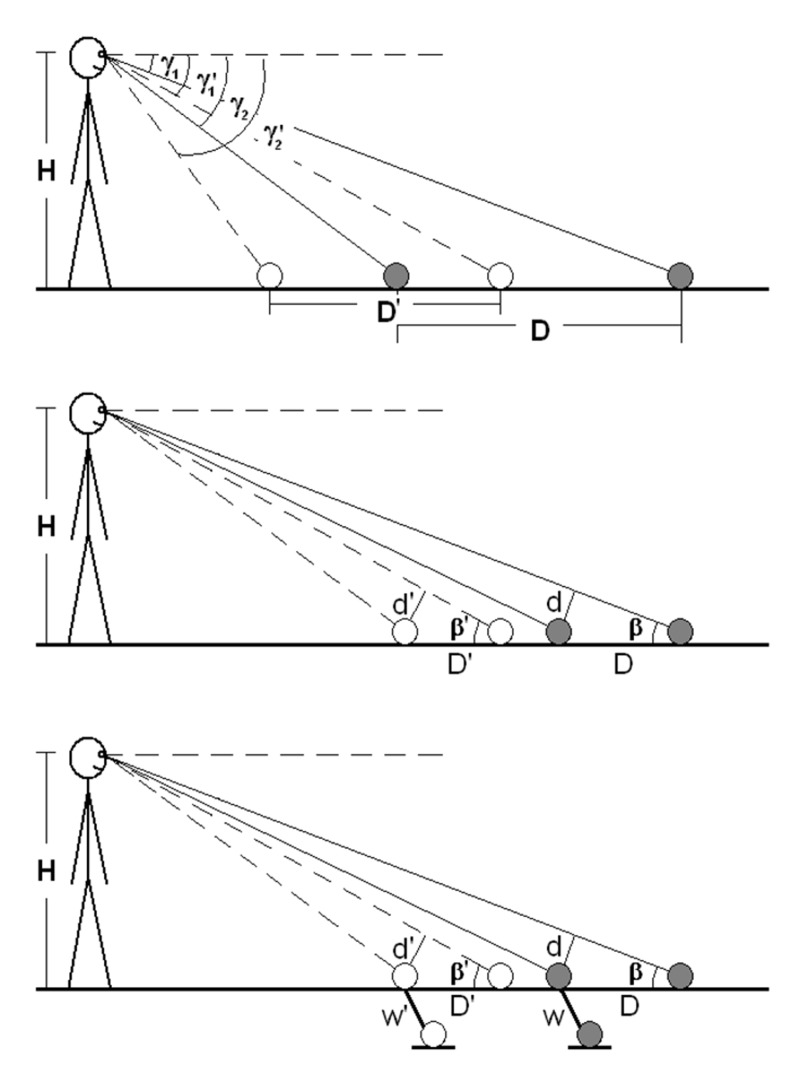
To model the perceived exocentric distance is more complicated because in different tasks the relative reliability of perceived gaze angle and of perceived optical slant could be different. To model the perceived exocentric sagittal distance D′ using the perceived gaze declination alone we can use Equation 6 (Figure 8, top),

$${\displaystyle D^{\prime }=H·\frac{\sin [1.5({\gamma }_2-{\gamma }_1)]}{\sin (1.5{\gamma }_1)·\cos (1.5{\gamma }_2)}}$$ (6)

Figure 8.

Diagrams depicting the exocentric sagittal distance foreshortening based on the angular expansion hypothesis. Top, the gaze model. Middle, the optical slant model with isolated exocentric extent. Bottom, the optical slant model of the aspect ratio task. The gray circles represent the physical targets. The white circles represent the perceived targets.

where H is the observer's eye height; γ₁ and γ₂ are the physical gaze declination to the far and near targets, respectively; and γ₂-γ₁ is the physical visual angle subtended by the exocentric sagittal distance extent.

According to Equation 6, the reliability of the perceived exocentric sagittal distance D′ would depend not only on the reliability of the perceived gaze declinations to the far and near targets (ie, 1.5γ₁ and 1.5γ₂) but also on the reliability of the perceived visual angle subtended by the distance extent (ie, 1.5(γ₂-γ₁)). If the physical visual angle of the sagittal extent is small, its perceived value may not be reliable. This suggests the gaze model may not be appropriate to model perceived exocentric sagittal extent if the physical visual angle of the sagittal extent is small.

When the visual angle of the sagittal distance is small and the gaze model is not appropriate to model the perceived exocentric distance, we can use the optical slant model (Equation 5). But we need assumptions. If the task involves only an isolated exocentric sagittal extent (Figure 8, middle), we may need to assume the observer can approximately accurately perceive the frontal projected distance, d, of the sagittal extent, D (ie, d′ ≈ d). This assumption is based on the size constancy. We then have

$${\displaystyle D^{\prime }=D·\frac{\sin (\beta )}{\sin ({\beta }^{\prime })}}$$ (7)

Substituting β′ with Equation 5 we have

$${\displaystyle D^{\prime }=D·\frac{\sin (\beta )}{\sin [1.5\beta +k\ln (D)]}}$$ (8)

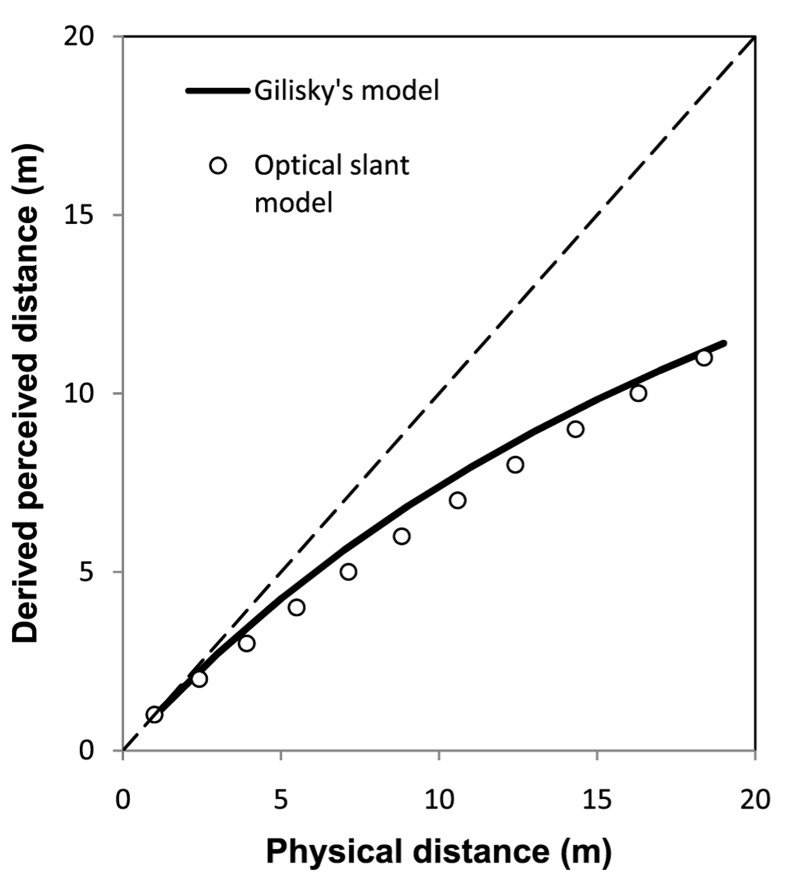
This model can be used to explain Gilinsky's (1951) finding. Gilinsky asked her participants to successively produce a standard length (1 meter or 1 foot) along the ground starting from their feet. Although she conceptualized her study as one of perceived egocentric distance, her task clearly involved perception of isolated exocentric sagittal distance, which can be modeled by Equation 7. Figure 9 shows the (angular expansion) model-predicted result of Gilinsky's study (using Equation 7, with k = 1), which is fairly similar to her observation⁽¹⁾

Figure 9.

The egocentric distance function derived by applying the optical slant model of the angular expansion hypothesis (ie, Equation 7) to Gilinsky's (1951) successive equal apparent interval procedure (circles) compared to Gilinsky's hyperbolic-space model (thick line) of her data.

5. Similarity between the two hypotheses

Loomis and colleagues have employed an aspect ratio task to study perceived exocentric sagittal ground distance (eg, Loomis et al 1992; Loomis and Philbeck 1999), which involves comparison between the sagittal ground extent D and a frontal extent W next to it (Figure 8, bottom). To model the aspect ratio task we only need to assume the perceived ratio between the frontal projection of the sagittal distance and the frontal extent approximates its physical ratio (ie, d′/w′ ≈ d/w). With this assumption, we can model the perceived aspect ratio R′ (ie, D′/w′), ie

$${\displaystyle R^{\prime }=R·\frac{\sin (\beta )}{\sin [1.5\beta +k\ln (D)]}}$$ (9)

Li and Durgin (2010) have shown that the optical slant model can well explain the observed results of the aspect ratio experiments (ie, Kudoh 2005; Loomis et al 1992; Loomis and Philbeck 1999). In fact, the intrinsic bias hypothesis could also well explain the aspect ratio data (Ooi et al 2006). Essentially, both models attribute the foreshortening in perceived exocentric sagittal distance to the exaggeration in perceived slant. Whereas the intrinsic bias hypothesis assumes a constant exaggeration (ie, β′ = β + η) due to the intrinsic bias, the angular expansion hypothesis assumes a nonlinear function of the perceived optical slant (ie, β′ = 1.5β + ·ln(D)).

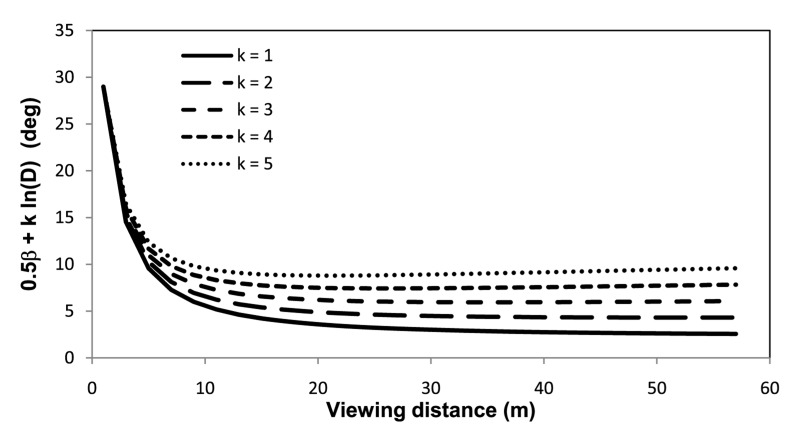
Mathematically, η in the intrinsic bias model corresponds to 0.5β + ·ln(D) in the optical slant model. Figure 10 shows the 0.5β + ·ln(D) as a function of viewing distance D and of k. It is clear that when the distance is long (ie, > 10 m), 0.5β + ·ln(D) approaches a nearly constant value. This helps explain why the intrinsic bias model (by assuming a constant slant error) is similar to the optical slant model in explaining the results of aspect ratio tasks.

Figure 10.

The component, 0.5β + ·ln(D), as a function of viewing distance D and of k. This component in the optical slant model corresponds to the slant error η in the intrinsic bias hypothesis.

6. Dissimilarity between the two hypotheses

There are many differences between the intrinsic bias hypothesis and the angular expansion hypothesis, but one important difference is that the angular expansion hypothesis assumes the gaze declination is perceptually exaggerated while the intrinsic bias hypothesis assumes it is accurately perceived. Both assumptions have supporting evidence.

Ooi et al (2001, 2006) found that when participants performed the blind walking and gesturing task to a previewed target light in an otherwise dark environment, their walked distance and their gestured height often deviated from the physical distance and height of the target, but the implied gaze declination remained approximately accurate. How does the angular expansion hypothesis account for this result?

There is evidence that action (performance) is calibrated to visual experience (Harris 1963; Li and Durgin 2012). That is, accurate performance does not necessarily depend on accurate visual perception but may depend on correct expectation of the outcomes of motor actions. If action performance is well calibrated to visual experience, then action will be accurate even when there is perceptual bias in visual experience. A good example of the calibrated action idea is prism adaptation (Helmholtz 1867; Held and Freedman 1965; Ooi et al 2001). When visual perception is distorted by the prism in front of the eyes, the action system can quickly adapt to the changed perceptual consequences of actions by modifying the expected effects of actions (learned/calibrated through feedback). For example, to reach (apparently) forward to a target while wearing displacement prisms requires a different motor action than the one required when the prisms are off. Upon removal of the prisms, an error in the opposite direction of the action can be observed due to recalibrated expectation of the action. Because such adaptation does not always transfer to an unadapted effector, such as the other hand, Harris (1963) noted that the adaptation is proprioceptive.

In locomotion, there is evidence that the perceived self-motion speed is calibrated to optical flow speed. After being adapted to walking on a treadmill towed behind a tractor (in which optical flow speed is inconsistent with biomechanical speed), participants showed substantial errors in blind walking to a previewed target (Rieser et al 1995). When the biomechanically perceived self-motion speed was faster, participants walked too long (because they perceived the self motion speed being too slow)—but when optical flow speed was faster, they walked too short (because they perceived the self motion speed being too fast). If perceived gaze declination is exaggerated, as proposed in the angular expansion hypothesis, perceived optical flow (created by relative motion of the ground plane) would be slower than the physical optical flow. After adaptation, people might walk longer (than the perceived distance) to a previewed target. Thus, their walked distance would be about right (as the physical target distance) because, although the perceived distance is foreshortened, the perceived self motion speed is also underestimated. Like prism adaptation, these effects on locomotion are also effector specific (Durgin et al 2003).

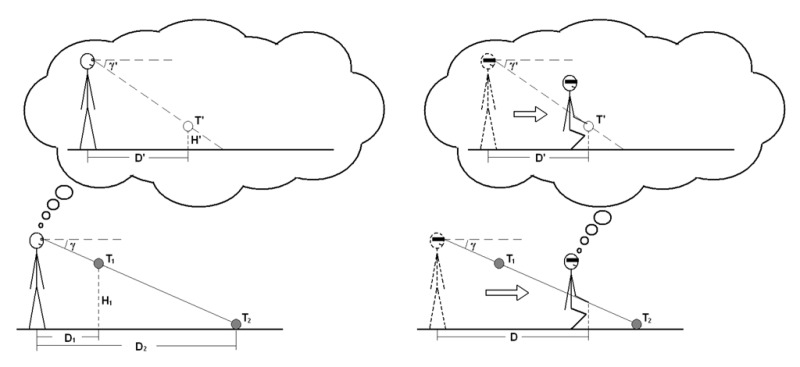
Figure 11 shows a possible explanation of the nearly accurate indication of perceived gaze declination in the blind walking and gesturing performance (ie, Ooi et al 2001, 2006). In a dark environment, participants may perceive two targets, T₁ and T₂, as being in the same location T′ (with perceived distance D′ and perceived height H′; Figure 11, left). The perceived gaze declination is exaggerated according to the angular expansion hypothesis, as illustrated in the thought bubbles for each case. However, during blind walking, the participants also underestimate their self motion speed (due to calibration to the angular expansion) so that their physically walked distance D is longer than their perceived walked distance D′. Thus, although the perceived gaze declination of the target is greater than it is, the indicated gaze declination (by the gesture) still falls along the line of their true gaze declination simply because their actions are already calibrated (Figure 11, right).

Figure 11.

Diagrams of explanation of the nearly accurate indication of the perceived gaze declination in the blind-walking and gesturing tasks. The lower plots are the physical situations while the upper plots (inside the bubbles) are the perceived situations according to the angular expansion hypothesis.

7. Advantages of the angular expansion hypothesis

As we have discussed, there are many situations in which the intrinsic bias hypothesis makes predictions that are similar to those of the optical slant model of the angular expansion hypothesis. Thus, most of the empirical data that could be explained by the intrinsic bias model can also be well accounted for by the optical slant model of the angular expansion hypothesis. However, the angular expansion hypothesis, because it incorporates biases in perceived gaze declination as well, can also explain empirical findings in distance perception that the intrinsic bias hypothesis cannot explain (eg, evidence that perceived egocentric distance is nearly a linear function of actual egocentric distance).

Because the intrinsic bias hypothesis is constructed on the assumption of a bias in perceived geographical slant of the ground plane, it is constrained primarily to explaining biases in perceived distance on the ground plane. In contrast, the angular expansion hypothesis is built on assumptions of misperception in angular variables, which allows it not only to explain the biases in perceived distance but also to account for the biases in perceived uphill and downhill slant⁽²⁾ (eg, Li and Durgin 2009, 2010; Durgin et al 2010) and to account for the biases in perceived height (eg, Li et al 2011). For example, the angular expansion model of hill perception based on the optical slant model provides an excellent fit to published slant data (Li and Durgin 2010). Moreover, the fact that downhill surfaces look steeper than they are is also difficult to understand based on the intrinsic bias hypothesis, but it can be quantitatively understood by the angular expansion theory (Li and Durgin 2009).

8. A note on reports of non-Euclidean properties of visual space

Studies of the geometry of visual space often conclude that visual space possesses non-Euclidean properties (eg, Battro et al 1976; Blank 1953; Doumen et al 2005; Foley 1964; Foley et al 2004; Indow 1991; Kelly et al 2004; Koenderink et al 2000; Koenderink et al 2008; Luneburg 1947, 1950; Norman et al 2005; Wagner 1985). Some of these studies have involved ground-based extents, but many have not. The angular expansion theory supposes that, locally, certain angular variables are misperceived and that this results in distortions of visual space that are locally consistent with Euclidean analyses.

There are a variety of findings and theories that are lumped together as evidence for non-Euclidean space, but some of these, we believe, can be interpreted as locally Euclidean but non-veridical estimation of local spatial (angular) variables. For example, Foley et al (2004) concluded that visual space was non-Euclidean, despite using a model of perceived size that was locally Euclidean once the angles and egocentric distances in the underlying equations were assumed to be distorted. That is, Foley et al's model suggests that perceived spatial variables are locally consistent with Euclidean axioms. However, Foley et al treated the angular distortions as convenient fictions in their model. In contrast, the angular expansion theory has measured some of them directly and found that perceived angles appear to be explicitly distorted in perceptual experience (Durgin and Li 2011; Li and Durgin 2009).

While visual space may be locally distorted in a manner that is consistent with Euclidean analyses, these distortions will certainly lead to global inconsistencies with Euclidean principles. For example, Koenderink et al (2000) examined the global Euclidean properties of large-scale space perception using an exocentric pointing task in a field of tall grass that minimized the availability of ground-based information. They showed that perceived orientations across views implied a global space that was non-Euclidean. These findings could be understood as resulting from local errors in recovering angular variables, such as optical slant of the surface of the pointer (Li and Durgin 2010) and/or egocentric direction to the pointer and target (Philbeck et al 2008, Experiment 3). It is only when comparing judgments across views (ie, over wide angular separations) that it becomes clear that these particular tasks produce implied contradictions to Euclidean principles, which may be resolved by assuming either that (1) global perceived space is non-Euclidean or (2) that the visual system is not designed to represent (or provide conscious access to) global space in this way. Either of these conclusions is theoretically important, but neither contradicts the angular expansion theory.

We therefore emphasize here that the theories being contrasted in the present article concern local (rather than global) estimation of spatial structure and that these theories assume the availability of ground information. Of course, even these criteria are insufficient to exclude all cases that have been described as non-Euclidean. For example, Norman et al (2005) used a ground-based spatial task in which 8 participants tried to position poles (moved by experimenters) into equilateral ground shapes. The researchers found between-participant variability in performance of this task and also found alternative results when a slightly different task was used and concluded that there was no unique geometric representation that fit all observers. Using much larger N, however, Li et al (2011) reported mean trends in similar large-scale shape matching tasks that seem to reflect highly stable geometrical relationships consistent with locally Euclidean models (consistent with angular expansion). Importantly, these data patterns closely replicated those reported in studies by Higashiyama and Ueyama (1988). Although there may be strategic variability in performance between individual observers in a single study (eg, Durgin et al 2012), and there may be task effects related to the kinds of information available for various tasks, we would emphasize that there also appear to be stable patterns of perceptual bias across observers that have been replicated on different continents, in different centuries.

In conclusion, although the two theories considered here assume that a Euclidean analysis is locally possible, this assumption has not been made lightly. That is, the specific data that has been amassed in support of these ideas is consistent and stable across many laboratories. Neither does the use of Euclidean geometry in these models contradict the alternative claim that local judgments of size and orientation are often non-veridical in ways that necessarily imply global inconsistencies with Euclidean assumptions. We do not wish even to claim that local geometry is always consistent with Euclidean assumptions, but only that the present models, which utilize Euclidean axioms, can provide a coherent account of a great deal of data concerning the perception of ground extents in locomotor space.

9. Conclusions

In the present paper, we reviewed and compared two theories regarding the perception of ground extents in locomotor space. The intrinsic bias hypothesis and the angular expansion hypothesis are based on very different geometrical assumptions, but they make similar predictions about exocentric ground distance tasks. Although both hypotheses attribute perceived exocentric ground distance foreshortening to perceived slant exaggeration, the angular expansion hypothesis also accounts for egocentric distance foreshortening with exaggeration in perceived gaze declination. This allows the angular expansion hypothesis to distinguish two types of ground distance foreshortening—linear compression (mainly caused by exaggeration in perceived gaze declination) and non-linear compression (mainly contributed by exaggeration in perceived optical slant). Whereas both hypotheses account for exocentric sagittal ground distance compression equally well, the angular expansion hypothesis can explain a broader range of empirical findings concerning spatial biases, including linear compression in perceived egocentric ground distance, exaggeration in uphill and downhill slant perception, and anisotropy between perceived egocentric ground distance and frontal height.

Biography

Zhi Li completed a PhD in neurobiology at Shanghai Institutes for Biological Sciences in the Chinese Academy of Sciences. He has been a postdoctoral fellow at Swarthmore College working on a new theory of space perception since the fall of 2008. He is interested in how distortions of perceived space may reflect efficient angular coding strategies.

Frank Durgin studied classics and philosophy at St. John's College, Annapolis, where he became interested in perception and cognition. After a year at MIT, and two at the University of Pennsylvania, he moved to the University of Virginia where he completed a PhD studying aftereffects of texture density. He has been teaching at Swarthmore College for nearly twenty years and published on a variety of topics including metaphor processing, numerosity perception, perceptuomotor adaptation, cognitive interference, self-motion perception and spatial perception.