Protein-coat dynamics and cluster phases in intracellular trafficking

Abstract

Clustering of membrane proteins is a hallmark of biological membranes' lateral organization and crucial to their function, however the physical properties of these protein aggregates remain poorly understood. Ensembles of coat proteins, the example considered here, are necessary for intracellular transport in eukaryotic cells. Assembly and disassembly rates for coat proteins involved in intracellular vesicular trafficking must be carefully controlled: their assembly deforms the membrane patch and drives vesicle formation, yet the protein coat must rapidly disassemble after vesiculation. Motivated by recent experimental findings for protein-coat dynamics, we study a dynamical Ising-type model for coat assembly and disassembly, and demonstrate how simple dynamical rules generate a robust, steady-state distribution of protein clusters (corresponding to intermediate budded shapes) and how cluster sizes are controlled by the kinetics. We interpret the results in terms of both vesiculation and the coupling to cargo proteins.

1. Introduction

Cell function is controlled through molecule ensembles, such as receptor and signaling complexes, adhesion complexes, trafficking intermediates, and proteo-lipid domains such as lipid rafts [1]. It is a challenge to correctly describe these highly-dynamic, non-stoichiometric complexes. Are there general physical concepts important for the correct understanding and modeling of such constantly-changing ensembles? Any theoretical or computational model should respect the salient features of these assemblies, which include heterogeneous size and composition, frequent turnover of individual components, as well as geometric constraints [2]. Recent theoretical and experimental work in equilibrium thermodynamics has precipitated the concept of a “cluster phase” – an equilibrium phase of clusters or assemblies with a well-defined size distribution that results from the competition between short-range attraction and longer-range repulsion [7, 3, 4, 5, 9, 10]. Most biological systems, however, are nonequilibrium dissipative systems. In the context of protein-coat dynamics in intracellular vesicular transport, we present here a simple nonequilibrium model that exhibits a dynamic cluster phase even in the absence of longer-range interactions, and provides a robust mechanism for cells to achieve self-organized spatial structures.

Aggregation of specialized membrane-bound proteins into a coat plays a central role in intracellular transport of cargo molecules in eukaryotic cells [1]. Cells use vesicles to transport proteins between intracellular organelles or between the plasma membrane and an organelle. Vesicle formation usually involves membrane-recruitment of cytosolic coat proteins and their aggregation into semi-rigid coats that bend the membrane and recruit cargo molecules; when the coat grows sufficiently large (around 50-100 nm) the coated membrane forms a nearly spherical vesicle that is eventually released from the membrane [11]. The assembly and disassembly of the protein coats poses a problem for the cell; on the one hand, if disassembly of the proteins from the coat is too rapid, the coat will not grow large enough to deform the membrane and drive vesicle fission. On the other hand, the coat proteins must disassociate quickly once the vesicle has pinched off, so that fusion of the vesicle with its target membrane is not inhibited. We concentrate here on COPI and COPII (shorthand for “coat protein one” and “coat protein two”) – proteins which mediate both interorganelle (between the endoplasmic reticulum and the Golgi apparatus) and intraorganelle (between the Golgi and itself) vesicular transport. For the COP system, the assembly and disassembly of the coat components on the membrane is coupled to the GTP/GDP cycle of a GTPase protein: Sar1 for COPII and Arf1 for COPI [11, 12, 13]. In its active GTP-bound state, the GTPases bind to the membrane and recruit coat proteins to form coat units that later aggregate to form coats. Disassembly is driven by hydrolysis of the bound GTP. Experiments reveal that the exchange kinetics of the coat components is much faster than the rate of vesicle secretion and that the stochastic assembly and disassembly of coat protein clusters continue even in the absence of vesiculation [14]. Due to the resemblance to microtubule dynamics, it has been suggested that the competition between growth and unbinding may produce stable coats of fixed area [15]. A recent theoretical study of coat assembly and disassembly by Foret and Sens [16] has suggested a switching mechanism between a quiescent membrane and a vesicle-producing membrane as a function of the exchange kinetics. The quiescent state is characterized by protein clusters which do not grow large enough to drive vesiculation. What limits the size of protein clusters in the quiescent state and how is the size determined by exchange kinetics? In order to get a better understanding of the emergence of a cluster-size distribution and its dependence on coat kinetics, we study a simple statistical model of coat kinetics that exhibits a cluster phase with an effectively unimodal cluster-size distribution and hence a well-defined characteristic cluster size.

In our model, the membrane is represented by a two-dimensional hexagonal lattice of size N, and the coat units are represented by particles which perform random walks on the lattice (representing the 2D diffusion of protein coat units). Previous studies have employed 1D and 2D lattices in various ways to model the clustering of membrane proteins with short-range interactions [17, 18]. Here, we choose a hexagonal lattice to make the model compatible with the 2D close-packing of protein coat units in a cluster, and to reduce the effect of lattice artifacts. We associate with each lattice site a variable σ_i, with σ_i = 1 if the i-th site is occupied and σ_i = 0 otherwise. In the absence of exchange kinetics, the total energy of the system is

$$E=-J\sum _{<i,j>}{\sigma }_i{\sigma }_j$$ (1)

where the sum is over nearest neighbors and J is the interaction strength measured in units of k_BT, with k_B being the Boltzmann constant and T the temperature of the system. The thermodynamic system described by the energy function in Eq. 1 can be mapped to a 2D Ising model on a triangular lattice, which exhibits a phase transition at the critical strength J_c = ln(3) ≃ 1.1 [19]. For J < J_c, the system is in a homogeneous state, while for J > J_c, the system phase separates into regions of high and low density. The exchange kinetics is modeled by particle association and dissociation at rates characterized by the parameters k_on and k_off, respectively. In our model, we do not account for the effects of curvature on line tension and membrane surface tension, which would lead to more complex energy dependence of a cluster on its size. In the work by Foret and Sens [16], this nontrivial energy landscape plays an important role in stabilizing clusters of finite size and governing the switch to a state of vesicle secretion. Here we will demonstrate how even a simple, local energy function can lead to clusters of finite size arising from the kinetics. In this sense, our model constitutes a minimal model for generating cluster phases in a non-equilibrium context.

Coat proteins are being continuously recycled between the membrane and the cytosol. In our lattice model, particles are uniformly deposited and removed from the lattice with characteristic rates k_on (the association rate) and k_off (the dissociation rate) to account for the formation of membrane coat units, and their release from the membrane shortly after GTP hydrolysis. We have studied two systems: one with a constant off rate k_off, and one where the probability for a particle to be removed from the lattice (p^off) depends on its local environment. The latter is motivated by recent experiments suggesting a strong dependence of GTP-hydrolysis of the GTPase Arf1 (and subsequent coat disassembly) on local membrane curvature for COPI [15, 20, 21]. These rates can increase by over two orders of magnitude making it far more likely for a coat unit to dissociate from the membrane in regions of high particle concentration (that is, from the interior of clusters). To implement this, we choose the dissociation probability for a protein from a lattice site i to be proportional to ${\gamma }_i^n$, where γ_i is the fraction of occupied nearest-neighbor sites of particle i, and where we set n = 2, a value that ensures particles typically disassociate from the interior of the cluster. (The results do not depend sensitively on the value of n.) We note that for both constant and locally-variable off-rate systems, we have a nonequilibrium model. In an equilibrium model, the off rate would be lower for particles in clusters, as determined by the Boltzmann weights, since it energetically favorable for particles to cluster. The steady-state cluster phases that we find here do not represent equilibrium states, and they do not obey detailed balance [23]. Results from the two systems, one with neighborhood-independent off rate and the other where p^off depends on its local environment, were found to be qualitatively similar. Therefore, due to its biological significance and relative simplicity, we concentrate in this paper on the second system (with neighborhood-dependent off rate).

We use a Metropolis Monte-Carlo algorithm to simulate the system. A randomly-selected particle is moved to one of its unoccupied neighboring sites with an acceptance probability p = min(1,e^−ΔE) where ΔE is the energy change due to the proposed displacement of the particle. One Monte-Carlo time step corresponds to one attempted move for each particle present. Periodic boundary conditions are used in both x and y directions. We choose the interaction strength to be J > J_c, so that the particles spontaneously form clusters, in accordance with experimental observations of membrane-bound coat units. Moreover, to account for protein recycling from the membrane, at each time step, a new particle can be inserted at an empty lattice site with probability p^on = k_on, and a particle can be removed from an occupied lattice site i with probability $p_i^{\text{off}}=k_{\text{off}}{\gamma }_i^2$.

We chose a system size of N = 1000 × 1000 and first let the simulations run for t_eq = 100000 Monte-Carlo steps (for the system to reach steady state) before data was collected over 10000 Monte-Carlo steps. We explored a range of values for k_on, k_off, and the interaction strength J. We note that the estimated off rate is 0.1-10 s⁻¹ based on FRAP experiments [16]. For a diffusion constant of 0.1 μm²/s and lattice unit a ∼ 5 nm, this corresponds to an estimated off rate ∼ 10⁻⁵-10⁻³ in our lattice simulations. Moreover a complete vesicle is expected to have a couple of hundred protein coat units [16], thus in the quiescent membrane we expect clusters typically of size one hundred or smaller. For the results shown in this paper, unless otherwise indicated, the interaction strength, J, was chosen to be 4.0, a value greater than the critical strength J_c. The resulting system exhibits a cluster phase with a characteristic distribution of cluster sizes at steady state (Figs. 1, 2, and 3). The highly-peaked distribution observed here is in sharp contrast to the broad distribution of cluster sizes obtained in a different (though somewhat related) kinetic model [22], that was introduced in the context of lipid rafts. In that model, particle disassociation from the membrane occurred primarily via removal of clusters or domains, corresponding to lipid recycling, whereas in our model individual particles disassociate from cluster interiors. We also note that the steady states observed in our simulations are stable and robust in the sense that a state with the same statistics is achieved for different initial conditions; e.g., whether the system is initially in the homogeneous phase, or in a state where all the particles are in one cluster. Protein clusters in steady state have been observed experimentally in protein-coat systems [24].

Figure 1.

A snapshot of the system showing clusters formed by particle aggregation. Particles representing coat units diffuse on an underlying hexagonal lattice; they associate and dissociate at rates given by k_on and k_off, respectively.

Figure 2.

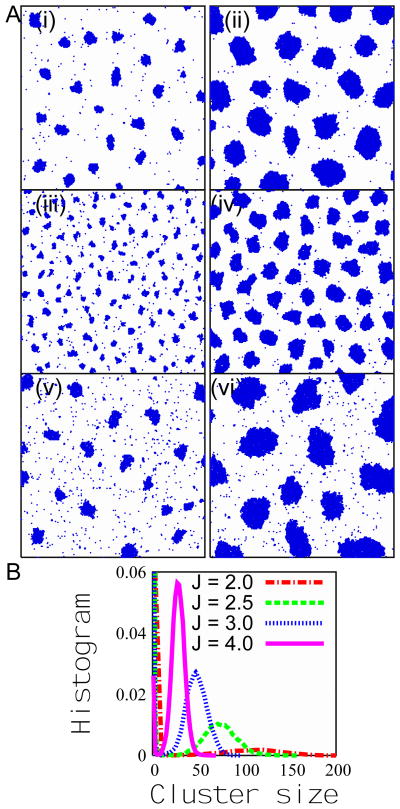
(A) Snapshots of a portion of the system at different values of k_on, k_off. The interaction strength is J = 4.0 in Figs. (i)-(iv), and J = 1.6 in Figs. (v) and (vi). The parameters are (i) k_on = 3 × 10⁻⁶, k_off = 5 × 10⁻⁵, (ii) k_on = 3 × 10⁻⁶, k_off = 1×10⁻⁶, (iii) k_on = 3×10⁻⁵, k_off = 5×10⁻⁴, (iv) k_on = 3×10⁻⁵, k_off = 1×10⁻⁴, (v) k_on = 3 × 10⁻⁶, k_off = 5 × 10⁻⁵, and (vi) k_on = 3 × 10⁻⁶, k_off = 1 × 10⁻⁵. We note that all snapshots shown here correspond to J > J_c, and that lower values of J (provided J > J_c) lead to larger (though fewer) clusters and to a larger fraction of particles existing as monomers. (B) The distribution of cluster size at different values of the interaction strength J, with k_on = 3×10⁻⁶ and k_off = 5×10⁻⁵. We find that the peak cluster size increases as J decreases (provided J > J_c), even though the height of the peak goes down, consistent with the previous observation that a larger fraction of particles exist as monomers at lower values of J.

Figure 3.

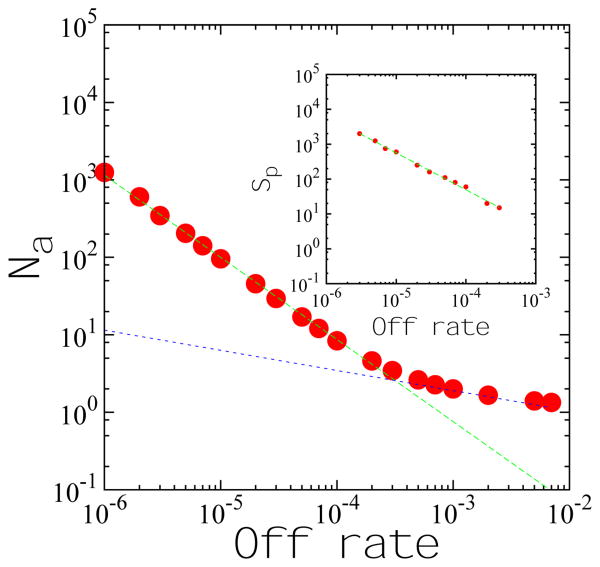
The aggregation number as a function of the dissociation rate. The association rate is 3 × 10⁻⁶. For dissociation rates less 3 × 10⁻⁴, the data are well described by a power law (dotted line) with exponent −1.06. For dissociation rates larger than this (association-rate dependent) crossover, the aggregation number asymptotes to 1. Inset: Peak size as a function of the dissociation rate. The association rate is 3 × 10⁻⁶. The points are fitted to a power law (dotted line), with exponent −1.00.

In Figure 2B, we plot the histograms of the cluster sizes at different values of J for fixed association and dissociation rates in the steady state. A typical cluster-size distribution is effectively unimodal, with a robust, Gaussian-like peak at a finite cluster size. (We say “effectively unimodal” because of the complication of whether to class the numerous and ever-present monomers as “clusters of size one”. If the monomers are included as the very smallest clusters, then there is, located at size one, an additional peak which will not much concern us in this paper.) This distribution is remarkably different from that expected in equilibrium for a system with local interactions. We note that both the position and the height of the distribution peak vary with parameters in the model, such as the interaction strength J, the association rate and the dissociation rate. With other parameters fixed, the position of the peak cluster size increases with an increase of the value of the association rate, or a decrease of the dissociation rate, or of the interaction strength J. Thus by controlling the protein deposition rate, the GTP hydrolysis rate, and the protein-protein affinity, the cell can tune the cluster sizes.

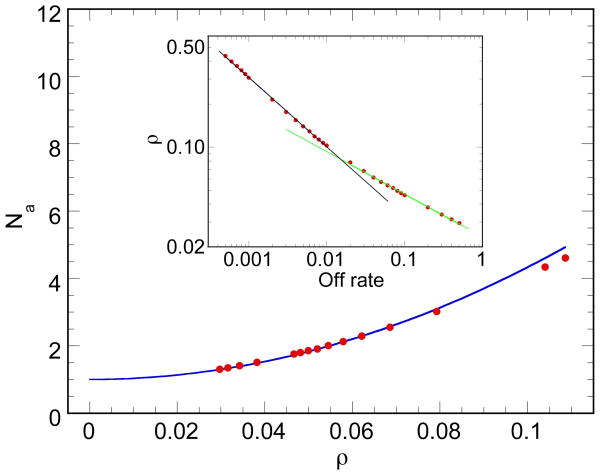
We use two measures to characterize cluster sizes in the cluster phase: aggregation number and the cluster size corresponding to the peak of the size distribution. The aggregation number which is given as N_a = N_m/N_c, where N_m is the total number of particles and N_c is the number of clusters (including clusters of size one) on the lattice. The aggregration number, N_a, is plotted against the dissociation rate k_off on a log-log scale in Fig. 3. At low values of k_off, N_a scales with an exponent ∼−1.06; for k_off above a critical value (≈ 8⁻³ in Fig. 3) N_a as a function of k_off deviates strongly from this power law regime and asymptotes to one for sufficiently large k_off. The peak cluster size (S_p) of the distribution curve (Fig. 2B), which is another measure of the characteristic size of the clusters, also follows a power law with respect to k_off, with an exponent ∼−1.0 (Fig. 3 inset). These results are crucial to understanding how the disassociation rate can control cluster size. We also plot the dependence of average particle density on k_on, and the dependence of aggregation number on ρ. While the dependence of cluster size looks approximately linear at intermediate values of ρ in Fig. 4 (as is observed in the cluster phases of colloidal systems [3]), we find a better fit to a parabolic function that goes to 1 as ρ goes to zero.

Figure 4.

The aggregation number as a function of density. At low densities, the aggregation number approaches 1 and a quadratic fit of the form 1 + ½(ρ/c)² is shown. Inset: The average density of the system as a function of the dissociation rate. The association rate is 3 × 10⁻⁴. A crossover at dissociation rate 1.5 × 10⁻² separates high-density from low-density scaling, with associated exponents of −0.49 and −0.30, respectively. Since at low dissociation rates, the density is expected to asymptote to 1, the domain of validity of that scaling behavior is correspondingly circumscribed.

The characteristic cluster size arises from a balance between cluster growth and shrinkage. Cluster growth occurs through the attachment of diffusing membrane-bound coat units at the cluster boundary while shrinkage occurs primarily by particle dissociation from the cluster interior. Ignoring boundary corrections, the shrinkage rate is proportional to the number of particles in the cluster times the off rate k_off. Growth of a cluster will depend on the competition for particles with nearby clusters. For a sufficiently large value of the interaction strength, we can assume clusters act as sinks for freely-diffusing particles lying within their domain of attraction; a rough measure of the domain of attraction is the Voronoi cell corresponding to points closer to that cluster than to any other cluster. The average dimension of the Voronoi cell is approximately given by the average distance from the cluster to its neighboring clusters, R_ave. The growth rate depends primarily on the area of the basin of attraction $\left({\mathit{\text{R}}}_{\text{ave}}^2\right)$ times the on-rate k_on; R_ave in turn depends primarily on k_on and on the interaction strength J. Thus, in a mean sense, we can take the growth rate to be independent of cluster size (assuming a cluster size larger than the critical nucleus size) and k_off. For clusters of the characteristic size, on average the growth rate balances the shrinkage rate. Since growth rate is independent of cluster size and k_off, k_off N_a = C, where C is independent of k_off and N_a. Thus, we expect N_a ∝ 1/k_off, as observed in Fig. 3 for one range of k_off. This argument breaks down at higher values of k_off since the clusters are smaller on average, boundary effects begin dominating and clusters are less stable. Our physical picture can also qualitatively explain the dependence of cluster size on J. At higher values of J, it is easier to nucleate new clusters, thus leading to a decrease in R_ave and, correspondingly, a decrease in the growth rate. Since the shrinkage rate does not directly depend on J and the value of aggregation number is determined by the balance of growth and shrinkage rates, higher values of J correspond to smaller aggregation number; i.e., smaller clusters on average. The dependence of aggregation number on k_on arises via control of growth rate; however, dependence of growth rate on k_on is more complex since R_ave is not independent of k_on. A more quantitative analysis of this dependence remains for a future study.

In conclusion, we present a simple, local, statistical-mechanical model that leads to a cluster phase with cluster sizes controlled by the off rate. The cluster phase arises purely due to the kinetics of the system; the free energy minimum for the corresponding thermodynamic system occurs either for the homogeneous state or the fully phase-separated state corresponding to one giant cluster. In intracellular trafficking, the off rate depends on binding to cargo molecules [25], so that in the absence of cargo, the off rate is high and clusters do not grow large enough for vesiculation. Thus this dependence of cluster size on the off rate provides a mechanism for coupling of vesiculation to cargo. We leave a more complete model of the stochastic dynamics of the coat system coupled to membrane curvature for future work.