On Consideration of Radiated Power in RF Field Simulations for MRI

Abstract

In numerical analyses of RF fields for MRI, RF power is often permitted to radiate out of the problem region. In reality, RF power will be confined by the magnet bore and RF screen enclosing the magnet room. We present numerical calculations at different frequencies for various surface and volume coils, with samples from simple spheres to the human body in environments from free space to a shielded RF room. Results for calculations within a limited problem region show radiated power increases with frequency. When the magnet room RF screen is included, nearly all the power is dissipated in the human subject. For limited problem regions, inclusion of a term for radiation loss results in an underestimation of transmit efficiency compared to results including the complete bore and RF screen. If the term for radiated power is not included, calculated coil efficiencies are slightly overestimated compared to the complete case.

INTRODUCTION

The expectation that the percentage of input power that is radiated will increase dramatically with excitation frequency is cited as a challenge to RF coil design in high field MRI (1–7). Applying the concepts of radiation efficiency as developed for antenna theory (where typically the antenna is far from lossy media and at least partially exposed tovast regions offree space) to MRI (where the RF coil is typically adjacent lossy dielectric material and surrounded by conductive surfaces), however, is not straightforward. Certainly, at higher frequencies the mechanism for energy transfer from any given coil to the sample becomes more radiative in nature, also allowing for the RF fields to propagate far from the coil and a nearby region of interest (ROI). While radiated energy may be associated with less effective containment of the RF energy to a nearby ROI at higher frequencies (8–10), designs based intentionally on principles for radiative antennas have recently been used in high field MRI with some potential advantages over more traditional approaches (11, 12).

In field calculations, where typically only a small portion of a shielded magnet room is considered, it is often possible to calculate the portion of the input power dissipated in matter as well as that radiated out of the “problem region” considered in the calculation. While this has been done a number of times for shielded and unshielded coils in free space (i.e., without magnet bore or magnet room RF screen present) with or without a lossy sample present (1, 3, 13–17), it is important to recognize that from the early days of this type of calculation, it was assumed that any amount of RF power radiated out of the problem region in the calculations would in reality be contained within the magnet bore andshielded magnet room, and thus be dissipated in lossy dielectric materials in the magnet room (primarily the human subject). Indeed, it was this logic that was used to justify treating a term for radiated power like that for power dissipated in the biological samplein early calculations (13).

Numerical methods of calculation are used increasingly in design and analysis of coils for MRI. While it is possible to perform calculations with full representation of the magnet bore and shielded magnet room (18), due to time and memory requirements it is more common to perform a simulation of a limited region allowing RF energy to radiate beyond associated boundaries. In this work we first calculate the percent of input power that is radiated out of the problem region over a range of frequencies for comparison to some prior calculations. We then compare different approaches of accounting for energy radiated out of the problem region to a case where the entire shielded magnet room is included in the simulation. The studies are designed to characterize inaccuracies that arise when simulations of an MR system are limited to a relatively small region surrounded by infinite free space.

METHODS

Numerical calculations were performed using the Finite Difference Time Domain (FDTD) method of calculation for electromagnetics (19) considering different volume and surface coils loaded with samples from simple spheres to the human body while within environments from free space to a closed magnet room. Calculations could be separated into three groups.

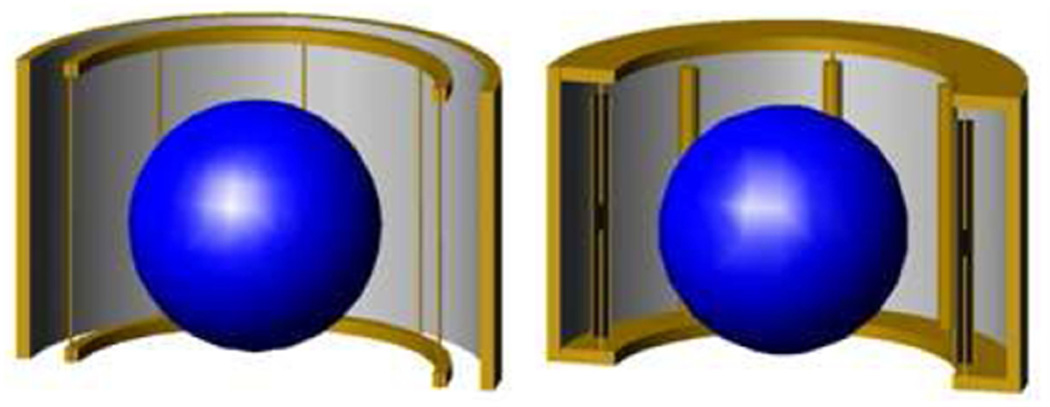
A first group of calculations compared percent of the power radiated across a range of frequencies for different coil geometries in free space when loaded with a spherical sample having dimensions (18 cm diameter) and electrical properties similar to brain. Coils included a square surface coil (11cm per side, placed with its center 1.25 cm from the surface of the sphere), a shielded high-pass birdcage coil (8 elements, 27 cm coil diameter, 34 cm shield diameter, and 22 cm length), and a TEM-type volume resonator (similar geometry to the birdcage coil). Calculations for the birdcage coil were performed at frequencies of 125, 175, and 300 MHz, those for the TEM-type coil at 300, 345, and 400 MHz, and those for the surface coil were performed at all these frequencies. Coil models were tuned (20, 21) with lumped-element (for the surface coil and birdcage coil) or distributed (TEM-type coil) capacitors to the desired frequency and then excited with sinusoidal waveforms with sources placed as they would be in experiment. To simulate infinite free space, the sample and coil were placed at the center of a 5m cubic problem region with a Liao absorbing outer boundary condition (22). Figure 1 shows the geometry of the birdcage and TEM-type resonators loaded with the cylindrical sample.

Figure 1.

Geometry of the birdcage coil (left) and TEM-type resonator (right) loaded with the spherical sample for the first group of calculations.

In a second group of calculations, percent power radiated and transmit efficiency for a surface coil were compared across cases with different levels of completeness in models of the sample and environment. Sample models included a sphere (as in the first group of calculations, but with the coil center 1.0 cm from the surface of the sphere), a human head and shoulders (with the coil center 1 cm from the back of the head), and a complete human body (with the coil again placed adjacent the occipital lobe). Environment models included free space (no magnet bore or magnet room RF screen present), a magnet bore (represented as a 2.45m-long stainless steel annulus with outer radius 1.075m and inner radius 0.4475m), and both the magnet bore and RF screen (bordering magnet room 5.8m long, 3.85m wide, and 3m high) at 300 MHz. For these calculations the coil was excited with voltage sources across four gaps in the coil spaced equidistantly. The problem region was 6.2m long, 4.225m wide, and 3.4m high and had a 7-cell perfectly-matched layer absorbing outer boundary condition (23).

In a third group of calculations, percent power radiated and transmit efficiency for a patch antenna placed 100 cm superior to the head of a human body model were compared across cases with different levels of completeness in the model of the environment. Calculations were performed for the coil and body located in free space, in a magnet bore, and within both the magnet bore and magnet room RF screen. The models for the problem region, magnet bore, and RF screen were the same as in the second group of calculations. The patch antenna was tuned to 300MHz and driven in quadrature with voltage sources between the ground plate and radiating plate at two locations 14 cm from the center and 90° apart. The radiating plate (closer to the subject) was 50 cm in diameter and placed 4.5 cm from the 80 cm-diameter ground plate with free space between.

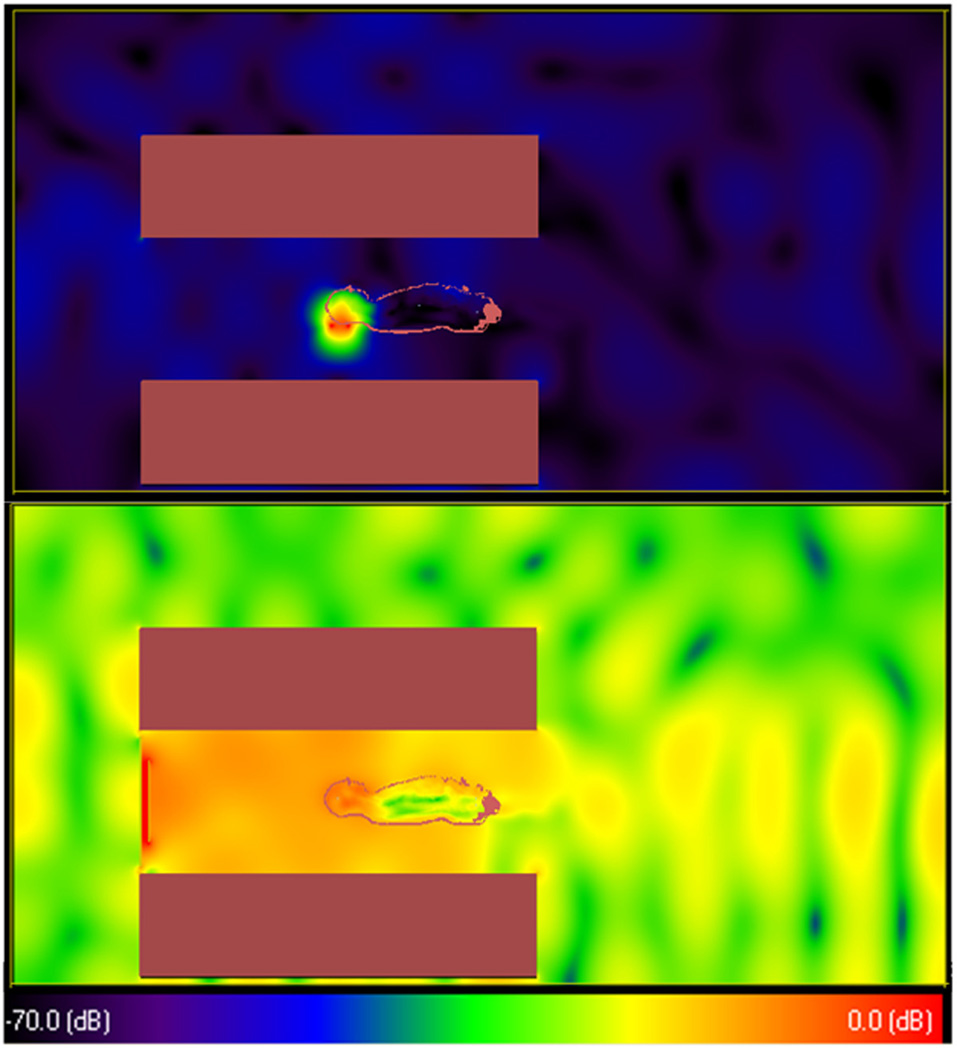
For the frequencies 125, 175, 300, 345, 400, and 600 MHz the electrical conductivities of the sphere were chosen to be 0.54, 0.59, 0.66, 0.68, 0.7, and 0.76 S/m, respectively, and relative electrical permittivities to be 66.9, 59, 50.6, 49, 47.7, and 45, respectively. The electrical properties of human tissues were acquired from published results (24). The coils, shields, and magnet room RF screen were assigned conductivity of copper (σ=5.8×10⁷S/m). The problem region extended beyond the location of the copper RF screen by 20cm in all directions. The magnet casing was assigned conductivity of stainless steel (σ=1.7×10⁶ S/m). All simulations were performed using commercially-available software (xFDTD, Remcom, Inc.) on a Dell Precision workstation with 3.0 GHz Intel Xeon X5450 processors and over 8GB RAM. To accommodate the large volumes considered in the second and third groups of calculations, grid resolution varied from 5mm in the human body model to 25mm at locations far from the coil using a variable mesh density feature available in modern commercial FDTD software packages. To run the largest simulations here in four parallel streams, the simulation required 2.2GB of memory and 8.2 hours. For the complete case that includes the body model, magnet bore, and RF screen, Figure 2 shows the distribution of the RF magnetic (B₁) field produced by the surface coil and patch antenna.

Figure 2.

Geometry and B₁ field distribution on mid-sagittal plane for the most complete case in calculations involving a surface coil (second group of calculations) and patch antenna (third group of calculations) at 300 MHz. Fields are scaled to have a ||B₁|| of 2µT at the center of the brain, and the maximum value of the logarithmic color scale (0dB) is 10µT.

In all cases, the average amplitude of the pertinent circularly-polarized component of the B₁ field (B₁⁺) in the sphere or brain was calculated. B₁⁺ at any one location is calculated as

$${{\mathrm{B}}_1}^{+}=|({\mathrm{B}}_{\mathrm{x}}+{\text{iB}}_{\mathrm{y}})|÷2$$ Eq 1

where B_x and B_y are the complex amplitudes of the orthogonal transverse components of the B₁ field, i is the imaginary unit, and imaginary components are 90° out of phase with respect to the real components.

The amount of power dissipated in the sample (P_diss) was determined as

$${\mathrm{P}}_{\text{diss}}=\frac{1}{2}{\displaystyle \underset{\text{sample}}{\int }{\mathrm{\sigma }}_{\mathrm{x}}{|{\mathrm{E}}_{\mathrm{x}}|}^2+{\mathrm{\sigma }}_{\mathrm{y}}{|{\mathrm{E}}_{\mathrm{y}}|}^2+{\mathrm{\sigma }}_{\mathrm{z}}{|{\mathrm{E}}_{\mathrm{z}}|}^2\text{dV}}$$ Eq 2

throughout the sample where E is electric field amplitude, σ is electrical conductivity, and subscripts x, y, and z indicate orthogonal components. The power radiated out of the problem region (P_rad) was determined by integrating the normal component of the time-average Poynting vector on the surface of a large box enclosing the coil, sample, and bore (when present). Mathematically, this can be expressed

$${\mathrm{P}}_{\text{rad}}=\frac{1}{2}{\displaystyle \underset{\text{box}}{∯}\text{Re}({\mathbf{E}\times \mathbf{H}}^{*})}•\mathrm{d}\overrightarrow{\mathrm{s}}$$ Eq 3

where E and H are the vector electric and magnetic field intensities (having complex components in each direction) and the asterisk indicates complex conjugate. In the first group of calculations, the box was a cube 2.5m on each side. In the second and third groups, the box was 5.9m long, 3.95m wide, and 3.1m high.

The percent of the power radiated was calculated as

$$\frac{{\mathrm{P}}_{\text{rad}}}{{\mathrm{P}}_{\text{rad}}+{\mathrm{P}}_{\text{diss}}}100\%$$ Eq 4

and transmit efficiency was calculated as

$$\frac{{\overline{\mathrm{B}}}_1^{+}}{\sqrt{{\mathrm{P}}_{\text{diss}}+{\mathrm{P}}_{\text{rad}}}}$$ Eq 5

where ${\overline{\mathrm{B}}}_1^{+}$ is the average value of B₁⁺ over the sphere or brain, as relevant for the specific calculation. To compare different methods of considering P_rad, transmit efficiency was calculated both by including it and by ignoring it. For cases that included the magnet room RF screen, P_rad is zero as calculated with Eq. 3 on a closed surface outside the RF screen.

RESULTS

Table 1 shows the percent of the input power radiated out of the problem region for the first group of calculations that considers different coils in free space loaded with a spherical sample. As expected, for each coil the percent of the power radiated increases with frequency. No results are shown for the birdcage coil at very high frequencies or the TEM coil at very low frequencies due to challenges in tuning these models in those ranges using reasonable material properties and capacitor values.

Table 1.

Percent of the input power radiated out of the problem region for the first group of calculations, where a surface coil, birdcage coil, and TEM coil are loaded with a sphere having properties similar to brain and surrounded by free space.

	125 MHz	175 MHz	300 MHz	345 MHz	400 MHz	600 MHz
Surface coil	2.9	3.7	6.6	8.7	11	26
Birdcage coil	3.8	6.8	8.4
TEM			2.8	18	27

Table 2 presents the percent of the input power radiated out of the problem region and the transmit efficiency for the second group of calculations, considering a surface coil positioned adjacent to different samples and contained in different environments at 300 MHz. Transmit efficiency data are normalized to the most complete case, which includes the body, bore and screen. When P_rad is included in calculations of transmit efficiency, the resulting values are slightly lower than when the magnet and magnet room RF screen are included. When P_rad is omitted from calculations of efficiency, the resulting values are slightly higher than when the magnet and magnet room RF screen are included. The power radiated for the case of the sphere in Table 2 (5.1%) is slightly less than that reported for a similar case in Table 1 (6.6%). The cross-sectional geometry of the coil conductor was like a thin copper tape in the second group of calculations (Table 2), but more like a 5mm diameter wire in the first group (Table 1). With 5mm grid resolution in the region of the coil and sample, this results in the coil center being effectively 2.5 mm closer to the sample in the second group, so that the ratio of radiated power to dissipated power will be slightly lower.

Table 2.

Percent of the input power radiated out of the problem region and transmit efficiency (normalized to the most complete case) for the second group of calculations, considering a surface coil adjacent different samples and in different environments at 300 MHz. The actual efficiency for the most complete case was 0.306 µT/√W. For cases where P_rad is nonzero, the efficiency calculated without including P_rad is given in parentheses.

		No bore, no screen	Bore, No screen	Bore and Screen
% of power radiated	Sphere	5.1	3.2	0
	Head	8.3	5.8	0
	Head & Body	6.3	2.5	0
Efficiency	Sphere	0.89(0.91)	8.9(0.90)	0.90
	Head	0.96(1.0)	0.98(1.0)	0.99
	Head & Body	0.97(1.0)	1.0(1.0)	1

The results for the third group of calculations, for a patch antenna at 300MHz, are presented in Table 3. Because the patch antenna is some distance from the subject, it radiates most of its power when neither the magnet bore nor the magnet room RF screen are present in the simulation. As in the second group of calculations, calculated efficiency is underestimated when P_rad is included and is slightly overestimated when P_rad is omitted.

Table 3.

Percent of the input power radiated out of the problem region and transmit efficiency (normalized to the most complete case) for the third group of calculations, which considers a patch antenna at 300 MHz in different environments. The actual transmit efficiency for the most complete case was 0.121µT/√W. For cases where P_rad is nonzero, the efficiency calculated by omitting P_rad is given in parentheses.

	No bore, no screen	Bore, no screen	Bore and Screen
% of power radiated	91	24	0
Efficiency	0.40(1.4)	0.89(1.0)	1

DISCUSSION

Today, numerical simulations rarely include the entire magnet room and its RF screen. This raises questions about how to consider the RF power that is radiated out of the problem region, P_rad. Here we have performed some basic examinations of P_rad in free space as a function of frequency and as it contributes to transmit efficiency in different environments relative to cases when it is rendered effectively zero by the shielding of the magnet bore or RF screen‥

It can be seen that in the absence of magnet bore and RF screen, radiated power increases with frequency. This is in agreement with expectations and findings of a number of prior studies (1–7, 13–17). For the birdcage coil, the values seen here are notably less than those reported previously using numerical (14) and analytical (1) calculations. Using numerical calculations, Ibrahim et al. (14) reported 7% of the power to be radiated at 64MHz and 39% to be radiated at 200MHz and using analytically-based calculations, Harpen (1) predicted more than 50% of the power to be radiated at frequencies above 150MHz. Both of these works, however, considered unshielded coils, and in Harpen’s work (1) the amount of radiated power was calculated without the load present and the amount of power dissipated in the sample was calculated without considering the effects of electric permittivity in the sample. All of these factors would result in higher estimates of radiated power than for the case considered here. One previous study showed that use of realistic permittivity values increases the amount of power dissipated in the sample relative to that radiated (15). Using analytical methods, Keltner et al. calculated 15% of the power to be radiated at 400MHz for a surface coil positioned near a spherical phantom. This is in reasonably good agreement with the value of 11% reported here. The relatively minor disagreement could be caused by slight differences in coil size and geometry (rectangular vs. circular), sample electric properties and size, and distance between the coil and sample.

It was found that inclusion of P_rad results in an underestimate of transmit efficiency compared to the complete case, and omission of this term results in an overestimate. By including the P_rad term from simulation in Eq5, one pessimistically assumes that none of the energy radiated from the problem region would contribute constructively to B₁ in the ROI when contained by the magnet bore and RF screen in realty. In cases where a surface coil was placed near the sample the differences were relatively small (less than 10% variance in efficiency as a function of environment only), but for the patch antenna placed far from the sample the difference was much more significant. Omission of the P_rad term results in an overestimate of transmit efficiency. Interestingly, in each case considered here the overestimate found by ignoring P_rad is smaller than the underestimate seen when including it, so that the result of ignoring P_rad is more accurate.

It is important to note that in these simulations, the power dissipated in good conductors was less than 0.1% of that dissipated in the sample. At 300 MHz, roughly 99.995% of power from a plane wave is reflected from a copper sheet (25), so in reality negligible power should be dissipated in the shield, magnet casing, and RF room screen, but it is possible that calculated coil losses are unrealistically low due to challenges in getting accurate representation of small skin depths in good conductors using the FDTD method. While a variety of other approaches can provide better representation of coil losses, the FDTD method models very well the RF fields in complex lossy dielectric structures such as the human body. Thus, while we are confident in the values reported here for the relative proportions of power radiated from the problem region versus dissipated in the sample, the real values for overall efficiency may be a bit lower owing to coil losses. For the coils simulated here, however, coil losses are expected to be small compared to both sample losses (26) and radiative losses (3). Also, details of structures next to the magnet casing, such as gradient coils and metal in the patient table (18) that may affect the distribution of fields were not considered here, but this should have little effect on the relative amounts of dissipated and radiated power.

Modeling of the entire magnet room is often not practical. In simulations for MRI today, it is common to consider a problem region much smaller than the magnet room and having an absorbing orradiating outer boundary condition. Often, this provides a reasonably accurate result while requiring fewer resources and less time than simulating the entire magnet room. In one prior study for body transmit coils (17), it was found that changing the boundary condition of a limited problem region from a radiating type to a perfectly-conducting type provided more realistic estimates of coil efficiency. Here we found that when radiating boundary conditions are used in simulations with a reduced problem region, better estimates of coil efficiency are calculated by ignoring the radiated power than by including it. This demonstrates the need for careful evaluation of methods for considering radiated power in simulations for MRI.