Abstract
The order in which participants choose to recall words from a studied list of randomly selected words provides insights into how memories of the words are represented, organized, and retrieved. One pervasive finding is that when a pair of semantically related words (e.g. “cat” and “dog”) is embedded in the studied list, the related words are often recalled successively. This tendency to successively recall semantically related words is termed semantic clustering (Bousfield and Sedgewick, 1944; Bousfield, 1953; Cofer et al., 1966). Measuring semantic clustering effects requires making assumptions about which words participants consider to be similar in meaning. However, it is often difficult to gain insights into individual participants’ internal semantic models, and for this reason researchers typically rely on standardized semantic similarity metrics. Here we use simulations to gain insights into the expected magnitudes of semantic clustering effects given systematic differences between participants’ internal similarity models and the similarity metric used to quantify the degree of semantic clustering. Our results provide a number of useful insights into the interpretation of semantic clustering effects in free recall.
Introduction
The free recall paradigm has participants study lists of items – typically words – and subsequently recall the studied items in the order they come to mind. Because the participants are instructed to recall the items in the order they come to mind, the recall sequence reflects how the items are stored and retrieved from memory. By analyzing recall sequences during free recall, researchers have uncovered a number of trends that many participants exhibit. For example, the recency and primacy effects refer to the well-established tendency of participants to show superior recall of items from the ends, and to a lesser extent, from the beginnings of the studied lists (Deese and Kaufman, 1957; Murdock, 1962). Another well-studied phenomenon, termed temporal clustering, refers to participants’ tendencies to successively recall items that occupied neighboring positions in the studied lists (Kahana, 1996). In addition to ordering recalls by the study positions of the items, participants also exhibit striking effects of semantic clustering (Bousfield and Sedgewick, 1944; Jenkins and Russell, 1952; Bousfield, 1953; Cofer et al., 1966; Romney et al., 1993), whereby recall of a given item is more likely to be followed by recall of a similar or related item than a dissimilar or unrelated one.
The primacy, recency, and temporal clustering effects may be measured objectively by examining the relative probabilities of recalling or transitioning between items that appeared at each serial position on a studied list. By contrast, measuring semantic clustering requires making assumptions about what each word means to each participant. For example, by one metric, successively recalling the words “dog” and “collar” might serve as evidence of semantic clustering, since the two words might be expected to appear in similar contexts: the two words might be described as falling under the general category of “things related to common household pets.” However, by another metric, successively recalling “dog” and “collar” might serve as evidence against semantic clustering, because dogs should fall under the category of “mammals” whereas collars should fall under the category of “inanimate objects.” These issues are further complicated if one considers that the associations an individual forms between words, and the meanings ascribed to the words, likely depend on that individual’s subjective experiences.
Over the past decade, a number of techniques have been developed for systematically quantifying the relative meanings of words. Latent semantic analysis (LSA; Landauer and Dumais, 1997) derives a set of pairwise similarity values by examining the co-occurrences of words in a large text corpus. Another measure of semantic similarity, termed the Google similarity distance (Calibrasi and Vitanyi, 2005), uses the Google search engine to compute the number of web pages containing both word x and y, relative to the total number of pages containing each word individually; a similar metric relies on Wikipedia links to measure the similarities between topics (Milne and Witten, 2008). A fourth technique, Word association spaces (WAS; Nelson et al., 2004; Styvers et al., 2004) derives its similarity values from a series of free association experiments in which participants were given a cue item and responded with the first word that came to mind. The goal of each of these techniques is to compute a set of pairwise similarities between the words that bears some resemblance to the similarities ascribed by a “typical” person.
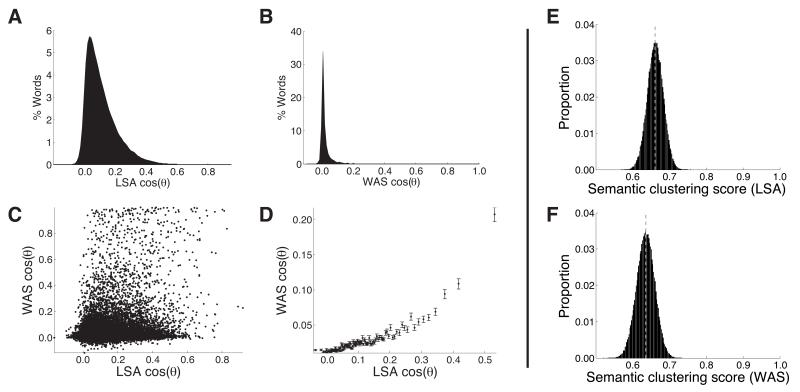
Although the similarity values produced by each of these myriad similarity metrics are somewhat related, the pairwise correlations between the measures tend to be surprisingly low. For example, for the set of 308 highly imageable nouns listed in Table 1, the Pearson’s correlation between the LSA- and WAS-derived pairwise semantic similarity values is r = 0.23 (Spearman’s ρ = 0.18). The full distributions of similarity values derived from the two metrics are shown in Figure 1, Panels A and B. The relation between LSA and WAS similarity is illustrated in Panels C and D. If these seemingly objective semantic similarity metrics based on huge text corpora and experimental datasets fail to agreeon a set of pairwise semantic similarities, how could one possibly expect to study effects of semantic organization in individual participants? In particular, how should the magnitudes of semantic clustering effects be interpreted? In the present manuscript we use simulations to study these questions.
Table 1. Simulation word pool.
| ANT | CAR | EGG | HORSE | PALM | SEED | STREET |
| APE | CARD | ELF | HOSE | PANTS | SHARK | STRING |
| ARK | CART | FACE | HOUSE | PARK | SHEEP | SUIT |
| ARM | CASH | FAN | ICE | PASTE | SHEET | SUN |
| AXE | CAT | FARM | INK | PEA | SHELL | SWAMP |
| BADGE | CAVE | FENCE | JAIL | PEACH | SHIELD | SWORD |
| BAG | CHAIR | FILM | JAR | PEAR | SHIP | TAIL |
| BALL | CHALK | FISH | JEEP | PEARL | SHIRT | TANK |
| BAND | CHEEK | FLAG | JET | PEN | SHOE | TAPE |
| BANK | CHIEF | FLAME | JUDGE | PET | SHRIMP | TEA |
| BARN | CHIN | FLEA | JUICE | PHONE | SIGN | TEETH |
| BAT | CLAY | FLOOR | KEY | PIE | SINK | TENT |
| BATH | CLIFF | FLUTE | KING | PIG | SKI | THREAD |
| BEACH | CLOCK | FOAM | KITE | PIN | SKUNK | THUMB |
| BEAK | CLOTH | FOG | LAKE | PIPE | SKY | TIE |
| BEAN | CLOUD | FOOD | LAMB | PIT | SLEEVE | TOAD |
| BEAR | CLOWN | FOOT | LAMP | PLANE | SLIME | TOAST |
| BED | COAT | FORK | LAND | PLANT | SLUSH | TOE |
| BEE | COIN | FORT | LAWN | PLATE | SMILE | TOOL |
| BELL | CONE | FOX | LEAF | POLE | SMOKE | TOOTH |
| BENCH | CORD | FROG | LEG | POND | SNAIL | TOY |
| BIRD | CORN | FRUIT | LIP | POOL | SNAKE | TRAIN |
| BLOOM | COUCH | FUDGE | LOCK | PRINCE | SNOW | TRASH |
| BLUSH | COW | FUR | PURSE | SOAP | TRAY | |
| BOARD | CRANE | GATE | MAP | QUEEN | SOCK | TREE |
| BOAT | CROW | GEESE | MAT | RAIN | SOUP | TRUCK |
| BOMB | CROWN | GIRL | MAZE | RAKE | SPARK | VAN |
| BOOK | CUBE | GLASS | MILK | RAT | SPEAR | VASE |
| BOOT | CUP | GLOVE | MOLE | RIB | SPONGE | VEST |
| BOWL | DAD | GOAT | MOON | RICE | SPOON | VINE |
| BOX | DART | GOLD | MOOSE | ROAD | SPRING | WALL |
| BOY | DEER | GRAPE | MOTH | ROCK | SQUARE | WAND |
| BRANCH | DESK | GRASS | MOUSE | ROOF | STAIR | WAVE |
| BREAD | DIME | GUARD | MOUTH | ROOM | STAR | WEB |
| BRICK | DITCH | HAND | MUD | ROOT | STEAK | WEED |
| BRIDGE | DOCK | HAT | MUG | ROPE | STEAM | WHALE |
| BROOM | DOG | HAWK | MULE | ROSE | STEM | WHEEL |
| BRUSH | DOLL | HEART | NAIL | RUG | STICK | WING |
| BUSH | DOOR | HEN | NEST | SAIL | STONE | WOLF |
| CAGE | DRESS | HILL | NET | SALT | STOOL | WOOD |
| CAKE | DRUM | HOLE | NOSE | SCHOOL | STORE | WORLD |
| CALF | DUCK | HOOF | OAK | SEA | STORM | WORM |
| CANE | EAR | HOOK | OAR | SEAL | STOVE | YARD |
| CAPE | EEL | HORN | OWL | SEAT | STRAW | ZOO |
We used the set of pairwise similarities for this set of 308 highly imageable nouns in our simulations. This word pool has been used in several published free recall studies (Sederberg et al., 2003, 2007a,b; Manning et al., 2011).
Figure 1. A. -D. Two measures of semantic similarity.
A. Distribution of the pairwise LSA-derived semantic similarity values for the words shown in Table 1. B. Distribution of the pairwise WAS-derived semantic similarity values for the same words. C. The panel shows a scatterplot comparing the LSA- and WAS-derived similarity values. Each dot corresponds to a single comparison between two words. Pearson’s correlation: r = 0.255, p < 10−3; Spearman’s correlation: ρ = 0.184, p < 10−3. D. This panel shows a binned variant of the scatterplot in panel C. We first divided the distributions of LSA-derived pairwise similarity values into 100 equally sized bins (the centers of the bins are plotted along the x-coordinate). The heights of each dot reflect the mean WAS-derived similarity values for the same pairs of words (error bars denote ± SEM). The binning reveals an approximately monotonic relation between the two similarity measures. Binned Pearson’s correlation: r = 0.875, p < 10−3; Spearman’s correlation: ρ = 0.954, p < 10−3. E., F. Semantic clustering simulations. E. We generated 5-item recall sequences that maximized the WAS-derived semantic clustering score for 100,000 simulated participants presented with 50 15-item lists each (see text for details). The panel shows the proportion of simulated participants that yielded the mean LSA-derived semantic clustering scores shown along the x-axis. F. This panel is identical to panel E, but here we generated recall sequences that maximized the LSA-derived semantic clustering scores, and plot the distribution of observed mean WAS-derived clustering scores. The same 5,000,000 randomly chosen 15-item lists were used in both panels. The dotted gray lines indicate the means of each distribution.
Analysis
Our simulations are intended to estimate the maximum expected magnitude of semantic clustering effects in free recall. Our approach is motivated by the notion that, although we may measure the degree of semantic clustering using semantic similarity metric f(), the semantic similarity metric that would have best described a given participant’s “true” internal semantic similarity model is a different metric, gp().1 Assuming that the participant exhibits perfect semantic clustering according to metric gp(), should we expect that the participant would also exhibit reliable semantic clustering effects according to metric f()?
In most free recall studies, gp() is unknown. In theory, one could estimate gp() for a given participant by having the participant make judgements about the semantic similarities between each pair of studied words. Then one could use gp() to quantify semantic clustering in that participant’s recall sequences. However, this method becomes impractical as the number of study item grows, since the number of pairwise comparisons grows with the square of the number of study items.
Rather than derive each participant’s gp() empirically, we instead construct a pool of 100,000 simulated participants, whose gp()’s are known. Each simulated participant encounters many word lists, and we simulate a sequence of recalls after each studied list. As described below, the recall sequences are constructed to maximize semantic clustering (according to gp()) for each participant. We then measure the degree of semantic clustering according to a different similarity metric, f(). We quantify the degree of semantic clustering using the semantic clustering score (Polyn et al., 2009), described in the next section. The distribution of semantic clustering scores according to f() tell us about the range of semantic clustering scores we should expect to observe in real participants, given that we use the “wrong” semantic similarity model to measure semantic clustering.
Semantic clustering score
The semantic clustering score, developed by Polyn et al. (2009), is intended to quantify the extent to which a given recall sequence shows evidence for semantic clustering (according to metric f()), taking into account the set of words that appeared on the studied list. For each recall transition we create a distribution of semantic similarity values (using f()) between the just-recalled word and the set of studied words that have not yet been recalled. We next generate a percentile score by comparing the semantic similarity value corresponding to the next item in the recall sequence with the rest of the distribution. Specifically, we calculate the proportion of the possible similarity values that the observed value is greater than, since strong semantic clustering will cause the observed similarity values to be larger than average. When there is a tie, we score this as the percentile falling halfway between the two items. In this way, if a participant always chose the closest semantic associate, then their semantic clustering score would be 1. A semantic clustering score of 0.5 indicates no effect of semantic clustering. The semantic clustering score must be computed independently for each studied list. Weobtain a single semantic clustering score for each simulated participant by averaging the semantic clustering scores across all lists that the participant encountered.
Generating recall sequences that maximize the semantic clustering score
As defined above, the semantic clustering score according to metric gp() is maximized (i.e., equal to 1) if the participant always chooses to next recall the closest semantic associate to the just-recalled word. Suppose the simulated participant has just studied a list of n words. We would now like to generate a k-item recall sequence (where k ≤ n) that maximizes the semantic clustering score according to gp().2
We begin by selecting the first recalled word, i1, at random from the set of n studied words. We then create a pool of the n - 1 remaining words from the studied list. We order the words in the pool by their semantic similarity (according to gp()) to i1. We select the word with the highest semantic similarity as the next recall, i2, and remove i2 from the pool. We then re-order the n - 2 remaining words in the pool by their semantic similarities to i2 and select the word most similar to i2 to be recalled next. This process continues until the kth word is recalled. Because this procedure ensures that each recall will be followed by the most similar word that is yet to be recalled, by definition it will maximize the semantic clustering score according to gp().
Results
We ran two batches of simulations. In the first batch, we constructed gp()’s for each of 100,000 simulated participants according to the LSA-derived similarities between each pair of words in Table 1. We computed each word’s LSA vector by applying the LSA algorithm (Landauer and Dumais, 1997) to the Touchstone Applied Science Associates, Inc. (TASA) corpus. We then computed the similarity between each pair of words by measuring the cosine of the angle between the corresponding LSA vectors. In our simulations, all of the gp()’s were identical, and gp(x,y) corresponded to the cosine of the angle between the LSA vectors for x and y. For each participant we also constructed 50 lists of 15 unique items each, drawn from the word pool. We then generated 5-item recall sequences after each list that maximized each participant’s semantic clustering scores according to LSA (see Analysis). Finally, we computed each participant’s mean semantic clustering score using WAS similarity (Nelson et al., 2004; Steyvers et al., 2004). The distribution of simulated WAS-derived semantic clustering scores is shown in Figure 1E. We found that the mean semantic clustering score was 0.636. The analysis yields the distribution of maximum expected semantic clustering scores (computed using WAS similarity), given that participants’ “true” internal models of semantic similarity are perfectly described by LSA.
The second batch of simulations used the identical set of 15-item lists, presented to the same simulated participants. However, for the second batch of simulations, we generated recall sequences that maximized the semantic clustering scores according to WAS-derived similarity. We then measured each participant’s mean semantic clustering score using LSA-derived similarity. The distribution of simulated LSA-derived semantic clustering scores is shown in Figure 1F. We found that the mean semantic clustering score was 0.662. This second batch of simulations yields the distribution of maximum expected semantic clustering scores (computed using LSA similarity), given that participants’ “true” internal models of semantic similarity are perfectly described by WAS.
We also found that the semantic clustering scores computed using LSA were slightly (but reliably) higher than those computed using WAS (paired t-test: t(99,999) = 270.65, p < 10−6; mean difference: 0.026). This indicates that different semantic similarity metrics used in analyses of semantic clustering may introduce slight biases. We expect that these biases are related to the form of the semantic similarity distributions derived from each measure (see Fig. 1) and to the particulars of how each measure is derived. Given that the clustering scores obtained using any given model of semantic similarity are likely to be only noisy reflections of any true patterns in the data, one should use multiple models of semantic similarity whenever possible. If one observes (or fails to observe) a similar pattern of clustering scores across experimental conditions when using multiple semantic similarity models (e.g. LSA and WAS), then it is less likely that the observed patterns simply reflect the mismatches between participants’ internal similarity models and the similarities assumed by the scoring model. Note that our analysis makes no attempt to distinguish whether the LSA- or WAS-derived similarities more accurately reflect participants’ internal similarity models.
Across the 200,000 simulated recall sequences, and combining across the two semantic similarity measures, the observed semantic clustering scores ranged from 0.522 to 0.757. These scores reflect the range of maximum clustering scores one would expect, given that participants’ internal semantic similarity models differed systematically from the similarity measure used to quantify the degree of semantic clustering. This shows that even participants who exhibit strong semantic clustering may still show clustering scores near 0.5. Similarly, it is exceedingly unlikely that one would observe semantic clustering scores near 1 when aggregating over many lists, as this would suggest a near-perfect match between the participant’s internal similarity model and the (arbitrarily chosen) scoring model.
Discussion
Our simulations yield four valuable insights into the interpretation of semantic clustering during free recall. First, it is important to use multiple measures of semantic similarity if one is to obtain an accurate estimate of whether participants are semantically clustering their recalls. Second, an observed near-chance clustering score does not necessarily indicate a true lack of semantic clustering, but may instead indicate a mismatch between a participant’s internal similarity model and the scoring model. For this reason the precise clustering score one observes is difficult to interpret, and one would be better served by instead comparing distributions of clustering scores obtained across conditions in an experiment or across participants. Third, an observed near-ceiling clustering score (> 0.757 by our simulations) must be interpreted with caution, as it is unlikely for the scoring model to precisely match participants’ internal model of semantic similarity. Rather, a near-ceiling clustering score may reflect the specific sequence of words presented to the participant, or the specific structure of the experiment. In such cases, one might use simulations analogous to those we present here to gain insights into the range of clustering scores one might expect under various models (e.g. high semantic clustering vs. low semantic clustering). Fourth, when fitting computational models that aim to predict semantic clustering, it is important to take the potential mismatch between participants’ internal similarity models and the scoring model into account. One might accomplish this by using, for example, an LSA-derived scoring model while using a WAS-derived internal similarity model in their simulation (or vice versa) as we have done here.
We have focused on a single semantic clustering metric, the semantic clustering score (Polyn et al., 2009), and two semantic similarity metrics, LSA (Landauer and Dumais, 1997) and WAS (Nelson et al., 2004; Steyvers et al., 2004). Our use of these metrics is not intended to imply that they are the only, or even necessarily the best, such measures. Rather, we simply found the semantic clustering score toprovide a convenient means of quantifying semantic clustering. We chose the two semantic similarity metrics as representative examples from the broader range of metrics discussed in the introduction. LSA represents one technique for deriving similarity values via automated text processing. By contrast, WAS derives similarity values using experimental data from psychological experiments. The specific choice of clustering and similarity metrics used in analyses of experimental data should reflect the goals of the experiment and/or analyses.
In addition to measuring participants’ tendencies to semantically cluster their recalls, a number of recent studies have begun to examine how individual words are represented by measuring the patterns of neural activity evoked when a word or image is viewed (e.g. Shinkareva et al., 2008; Mitchell et al., 2008; Just et al., 2010). There is some evidence that similarities in the neural patterns evoked by thinking about a given pair of words predict the tendencies of participants to successively recall the words, given that both appeared on the studied lists (Manning, 2011). In this way, one might objectively infer each participant’s internal semantic similarity model by measuring their neural activity as they studied and recalled list items.
Studying semantic clustering effects requires making assumptions about participants’ internal semantic similarity models. In the absence of pairwise judgements or neural data, researchers must rely on measures that attempt to capture the semantic relations between words without knowing the specifics of participants’ subjective experiences, or about the way their brains represent the words. Our simulations demonstrate the degree of semantic clustering that can be expected, given that the semantic model used to measure the clustering effects is not a perfect match for participants’ internal models.
Acknowledgements
We acknowledge useful discussions with Lynn Lohnas, Sean Polyn, and Per Sederberg. This research was funded by NIMH grants MH55687 and F31MH088118. The content is solely the responsibility of the authors and does not necessarily represent the official views of our supporting organizations.
Footnotes
Here the functions f() and gp() are mappings from two words, a and b, onto scalar similarity values. Note that f() and gp() need not produce the same mapping. The subscript p serves as a reminder that participants’ true internal similarity models may differ across individuals.
For all of the simulations reported in this manuscript, we used n = 15 and k = 5. However, the techniques developed here are equally applicable to arbitrary choices of n and k.
References
- Bousfield WA. The occurrence of clustering in the recall of randomly arranged associates. Journal of General Psychology. 1953;49:229–240. [Google Scholar]
- Bousfield WA, Sedgewick CHW. An analysis of sequences of restricted associative responses. Journal of General Psychology. 1944;30:149–165. [Google Scholar]
- Calibrasi RL, Vitanyi PMB. The Google similarity distance. IEEE Transactions on Knowledge and Data Engineering. 2005;19(3):370–383. [Google Scholar]
- Cofer CN, Bruce DR, Reicher GM. Clustering in free recall as a function of certain methodological variations. Journal of Experimental Psychology. 1966;71:858–866. doi: 10.1037/h0023217. [DOI] [PubMed] [Google Scholar]
- Deese J, Kaufman RA. Serial effects in recall of unorganized and sequentially organized verbal material. Journal of Experimental Psychology. 1957;54:180–187. doi: 10.1037/h0040536. [DOI] [PubMed] [Google Scholar]
- Jenkins JJ, Russell WA. Associative clustering during recall. Journal of Abnormal and Social Psychology. 1952;47:818–821. doi: 10.1037/h0063149. [DOI] [PubMed] [Google Scholar]
- Just MA, Cherkassky VL, Aryal S, Mitchell TM. A neurosemantic theory of concrete noun representation based on underlying brain codes. PLoS One. 2010;5(1):e8622. doi: 10.1371/journal.pone.0008622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahana MJ. Associative retrieval processes in free recall. Memory & Cognition. 1996;24:103–109. doi: 10.3758/bf03197276. [DOI] [PubMed] [Google Scholar]
- Landauer TK, Dumais ST. Solution to Plato’s problem: The latent semantic analysis theory of acquisition, induction, and representation of knowledge. Psychological Review. 1997;104:211–240. [Google Scholar]
- Manning JR. PhD Dissertation in Neuroscience. University of Pennsylvania; Philadelphia, PA: 2011. Acquisition, storage, and retrieval in digital and biological brains. [Google Scholar]
- Manning JR, Polyn SM, Baltuch G, Litt B, Kahana MJ. Oscillatory patterns in temporal lobe reveal context reinstatement during memory search. Proc Natl Acad Sci USA. 2011;108(31):12893–12897. doi: 10.1073/pnas.1015174108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milne D, Witten IH. An effective, low-cost measure of semantic relatedness obtained from Wikipedia links; Proceedings of the AAAI 2008 Workshop on Wikipedia and Artificial Intelligence; 2008. [Google Scholar]
- Mitchell T, Shinkareva S, Carlson A, Chang K, Malave V, Mason R, Just M. Predicting human brain activity associated with the meanings of nouns. Science. 2008;320(5880):1191. doi: 10.1126/science.1152876. [DOI] [PubMed] [Google Scholar]
- Murdock BB. The serial position effect of free recall. Journal of Experimental Psychology. 1962;64:482–488. [Google Scholar]
- Nelson DL, McEvoy CL, Schreiber TA. The University of South Florida free association, rhyme, and word fragment norms. Behavior Research Methods, Instruments and Computers. 2004;36(3):402–407. doi: 10.3758/bf03195588. [DOI] [PubMed] [Google Scholar]
- Polyn SM, Norman KA, Kahana MJ. A context maintenance and retrieval model of organizational processes in free recall. Psychological Review. 2009;116(1):129–156. doi: 10.1037/a0014420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romney AK, Brewer DD, Batchelder WH. Predicting clustering from semantic structure. Psychological Science. 1993;4:28–34. [Google Scholar]
- Sederberg PB, Kahana MJ, Howard MW, Donner EJ, Madsen JR. Theta and gamma oscillations during encoding predict subsequent recall. Journal of Neuroscience. 2003;23(34):10809–10814. doi: 10.1523/JNEUROSCI.23-34-10809.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sederberg PB, Schulze-Bonhage A, Madsen JR, Bromfield EB, Litt B, Brandt A, Kahana MJ. Gamma oscillations distinguish true from false memories. Psychological Science. 2007a;18(11):927–932. doi: 10.1111/j.1467-9280.2007.02003.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sederberg PB, Schulze-Bonhage A, Madsen JR, Bromfield EB, McCarthy DC, Brandt A, Tully MS, Kahana MJ. Hippocampal and neocortical gamma oscillations predict memory formation in humans. Cerebral Cortex. 2007b;17(5):1190–1196. doi: 10.1093/cercor/bhl030. [DOI] [PubMed] [Google Scholar]
- Shinkareva SV, Mason RA, Malave VL, Wang W, Mitchell TM, Just MA. Using fMRI brain activation to identify cognitive states associated with perception of tools and dwellings. PLoS One. 2008;e1394:1–9. doi: 10.1371/journal.pone.0001394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steyvers M, Shiffrin RM, Nelson DL. Word association spaces for predicting semantic similarity effects in episodic memory. In: Healy AF, editor. Cognitive Psychology and its Applications: Festschrift in Honor of Lyle Bourne, Walter Kintsch, and Thomas Landauer. American Psychological Association; Washington, DC: 2004. [Google Scholar]