Abstract
Acquiring both anatomical and functional images during one scan, PET/CT systems improve the ability to detect and localize abnormal uptakes. In addition, CT images provide anatomical boundary information that can be used to regularize PET images. Here we propose a new approach to maximum a posteriori (MAP) reconstruction of PET images with a level set prior guided by anatomical edges. The image prior models both the smoothness of PET images and the similarity between functional boundaries in PET and anatomical boundaries in CT. Level set functions are used to represent smooth and closed functional boundaries. The proposed method does not assume an exact match between PET and CT boundaries. Instead, it encourages similarity between the two boundaries, while allowing different region definition in PET images to accommodate possible signal and position mismatch between functional and anatomical images. While the functional boundaries are guaranteed to be closed by the level set functions, the proposed method does not require closed anatomical boundaries and can utilize incomplete edges obtained from an automatic edge detection algorithm. We conducted computer simulations to evaluate the performance of the proposed method. Two digital phantoms were constructed based on the Digimouse data and a human CT image, respectively. Anatomical edges were extracted automatically from the CT images. Tumors were simulated in the PET phantoms with different mismatched anatomical boundaries. Compared with existing methods, the new method achieved better bias-variance performance. The proposed method was also applied to real mouse data and achieved higher contrast than other methods.
1. Introduction
Positron emission tomography (PET) is widely used for diagnosis and staging of cancer, image-guided therapy planning, and monitoring of treatment response. With the introduction of combined PET/CT scanners [Townsend et al., 2004, Townsend, 2008], people can use co-registered anatomical information from CT to assist the interpretation of functional images for more accurate diagnosis [Schalder et al., 2004, Goerres et al., 2004, Czernin et al., 2007] and also to improve the quality of PET images.
While the most common use of CT images in PET reconstruction is for attenuation correction [Kinahan et al., 1998, Pan et al., 2005], researchers have investigated utilizing anatomical boundary information in CT and MRI to regularize PET image reconstruction [Leahy and Yan, 1991, Fessler et al., 1992, Comtat et al., 2002, Bowsher et al., 1996, Sastry and Carson, 1997, Hero et al., 1999, Rangarajan et al., 2000, Baete et al., 2004b, Somayajula et al., 2007, Bataille et al., 2006, Ouyang et al., 1994, Lipinski et al., 1997, Pramuthu and Hero, 1998, See, 2005, Ardekani et al., 1996, Alessio and Kinahan, 2006, Hsu and Leahy, 1997, Cao and Peter, 2010, Dewaraja et al., 2010, Tang and Rahmim, 2009a,b]. This is because CT and MR images have higher resolution than PET images and the PET tracer distribution tends to be smooth within each organ. Using the anatomical boundary information, one can encourage spatial smoothness inside each organ in PET images without blurring organ boundaries. However, because of the differences in scan time and contrast-generation mechanisms, there are often position and signal mismatches between the anatomical and functional data [Comtat et al., 2002]. Thus, care must be taken to handle the possible mismatches to avoid reconstruction artifacts.
Fessler et al. [1991, 1992] used blurred weighting factors to deal with the imperfectness of the anatomical information. Comtat et al. [2002] and Bataille et al. [2006] used blurred anatomical labels to control the Bayesian quadratic prior for the whole body and brain PET images, respectively. These methods reduce the strength of all anatomical information including those of the correct boundaries. Instead of suppressing anatomical information, several groups used weighted line site methods where anatomical edge information is only used to determine the likelihood of forming a functional boundary, but does not create a functional boundary by itself [Gindi et al., 1993, Ouyang et al., 1994]. Zhang et al. [1995] estimated region labels in a PET image using both the MR labels and the projection data, and then applied smoothing only between pixels with the same label. Ardekani et al. [1996] applied an edge-preserving smoothing filter derived from the corresponding MR image to the PET image reconstruction so that it can preserve the edges matched with the MR. However, it cannot preserve any functional edge that does not co-localize with an anatomical edge. The Bayesian joint mixture model approach [Rangarajan et al., 2000] reconstructs emission tomography images with the anatomical image intensity and anatomical label information. Tang and Rahmim proposed one-step-late MAP algorithms with the joint entropy prior between intensities of the anatomical and functional images in [Tang and Rahmim, 2009a] and the spatial feature images generated using wavelets in [Tang and Rahmim, 2009b]. However, the resulting images may not be spatially smooth because these methods ignored the spatial relationship among neighboring pixels [Rangarajan et al., 2000, Tang and Rahmim, 2009a]. Somayajula et al. [2007] used the mutual information between the anatomical and functional images. They used different features including intensity, local mean, and directional gradients to generate spatially smooth PET images with the aid of anatomical intensity and boundary information. The joint estimation methods can reduce the effect of incorrect anatomical boundaries while using correct ones to improve PET image quality. However, most of these methods do not explicitly model the continuity and smoothness of functional boundaries. Other approaches that have been proposed to solve the mismatch issues include the multi-resolution mesh modeling [Brankov et al., 2002], minimax approaches [Chiao et al., 1994, Piramuthu and Hero, 1998, Hero et al., 1999], tissue composition models [Sastry and Carson, 1997, Baete et al., 2004a,b], and segmented thin-plated regression model [Hsu and Leahy, 1997].
Here we propose a novel approach to maximum a posteriori (MAP) reconstruction of PET images with a level set prior guided by anatomical edges. The image prior models both the smoothness of PET images and the similarity between functional boundaries in PET and anatomical boundaries in CT. Level set functions (LSFs) are used to describe functional boundaries in PET images. Level set method (LSM) does not define a boundary explicitly, but represents it as the zero-level curve of an LSF. As a result, LSM guarantees closed boundaries and can easily represent complex topologies. It can also handle topology changes, which reduces the requirement for initialization. We use the multi-phase level set method proposed by Vese and Chan [2002], in which regions are determined by the combination of the signs (positive or negative) of multiple LSFs, so that L LSFs can define up to 2L regions. This substantially reduces the number of LSFs required in image reconstruction, as we do not need to assign one LSF to each region. We refer to the proposed method as the anatomically guided level set method (ALSM). One feature of the ALSM is that it does not assume that functional boundaries match with anatomical boundaries exactly, rather it allows different boundary definition in PET images. The possibility of a functional boundary to appear at a certain location is assigned based on an anatomical edge map. This approach does not require the anatomical boundaries to be closed and is able to utilize incomplete anatomical edges extracted from a smoothed CT image. Some preliminary results of this work were presented at conferences [Liao and Qi, 2007, Cheng-Liao and Qi, 2009].
Compared with weighted line site methods [Gindi et al., 1993, Ouyang et al., 1994], which also use anatomical edge information to influence the formation of functional boundaries at each pixel, the proposed method o ers several advantages by using level set functions. The functional boundaries in the proposed method are guaranteed to be closed contours, whereas it is difficult to enforce continuity of the functional boundaries in line site methods. The proposed method can also regularize the smoothness of the functional boundaries by minimizing the length of the contours. Although line site methods usually minimize the total number of positive line sites, such regularization is less effective because it does not always result in smooth contours without a continuity constraint.
This paper is organized as follows. Section 2 describes the image reconstruction method with the anatomical prior. Section 3 describes the computer simulation and evaluation methods. Section 4 describes the real mouse data experiment. Reconstruction results and comparisons with other methods are presented in Section 5. Discussions are given in Section 6. Finally, we draw conclusions in Section 7.
2. Methods
2.1. MAP image reconstruction
PET measurements can be modeled as a collection of independent Poisson random variables with the expectation
| (1) |
where is the unknown PET tracer distribution, is the system matrix with the (i, j)th element being the probability of an event originated in voxel j being detected by detector pair i, and is the expectation of scattered and random events. The appropriate log-likelihood function, after dropping constant terms, is
| (2) |
Maximizing the log-likelihood function often results in noisy images. Therefore, we estimate PET images by maximizing the log posterior density function:
| (3) |
where p(x, ϕ; ICT) is an image prior that incorporates anatomical information from CT image ICT into PET image reconstruction. are the LSFs used to describe functional regions and the corresponding boundaries. The image prior can be written as
| (4) |
where Z is a normalization constant. The prior energy contains two parts: an image smoothness energy U(x; ϕ) defined on x and a shape energy V(ϕ; ICT) defined on ϕ.
The image smoothness energy U(x; ϕ) is given by
| (5) |
The first term is a global smoothing term, which minimizes the sum of the squared di erence between the estimated pixel intensity and the mean intensity of the region in which it resides. It is included to accelerate the convergence of the LSFs. Cp is the mean intensity of region p, χpj is the value of the pth region characteristic function at pixel j, β1 is the hyperparameter of the global smoothing terms, and L is the number of LSFs. The characteristic function of each region, χp, is defined by the combination of the signs of the LSFs. For two LSFs, the characteristic functions are defined as
| (6) |
| (7) |
| (8) |
| (9) |
where H(x) is the Heaviside function that equals 1 for x > 0 and 0 otherwise. In our implementation, we used the modified Heaviside function proposed by Chan and L.Vese [2001]:
| (10) |
where ε is a parameter that controls the width of the transition band area. The modified Heaviside function extends the LSF update to all level curves and allows automatic detection of interior contours.
The second term in (5) is a local smoothing term, which minimizes the weighted squared differences between neighboring pixels (j and k), where djk is the distance between pixels j and k, and β2 is the hyperparameter. b(ϕj, ϕk) is a weighting factor to prevent smoothing across functional boundaries and is given by
| (11) |
When pixels j and k belong to the same region, b(φj, φk) is close to one; otherwise, b(φj, φk) is close to zero.
The shape prior V(ϕ; ICT) is used to regularize functional boundaries and to incorporate anatomical information. It is given by
| (12) |
where μ1 and μ2 are the weighting factors, ∇ is the gradient operator, and f is an edge potential map calculated from the CT image by
| (13) |
where Gσ is a Gaussian kernel with variance σ2, “*” denotes the convolution operator, and Edge(ICT) is an edge map obtained from the CT image. We use the Canny edge detector [Canny, 1986] to extract edges. The width of the Gaussian kernel controls the effective area of the anatomical edge. It is chosen based on the possible extent of position mismatch between anatomical and functional boundaries and PET spatial resolution. The function Norm{·} is to scale the smoothed edge map such that the range of f is from 0 to 1, regardless of the width of the Gaussian kernel. Consequently, f is equal to 1 at pixels far away from anatomical boundaries, and close to 0 near an anatomical edge.
The effect of the first term in (12) is to attract functional boundaries to an anatomical boundary that is close-by, and to minimize the length of the functional boundaries elsewhere. The second term in (12) is used to keep the slope of the LSFs close to unity. This regularization term can prevent level set functions from developing shocks, very sharp and/or flat shape during the evolution, which makes further computation inaccurate [Li et al., 2005].
2.2. Optimization procedure and parameter selections
We use an alternating optimization algorithm to find the maximizer of the posterior density function. The algorithm updates the image x and LSFs ϕ alternately. The update formula for the image and LSFs are derived in the Appendix and are given in (22) and (28), respectively.
All reconstructions start from a uniform image. We first run 20 iterations of image update (22) with β1 = 0, a suitable β2 value, and a set of LSFs initialized from the unsmoothed anatomical edge map Edge(ICT). A unique LSF sign combination (see the examples of the characteristic function given in equations (6)-(9)) is assigned to each region with a closed anatomical boundary. All edge pixels (Edge(ICT) > 0) that do not belong to a closed boundary are also given a unique LSF sign combination. The parameter ε in the Heaviside function is set to zero here so that b(ϕj, ϕk) takes values of either zero or one. This procedure prevents any smoothing across anatomical boundaries. We refer to this method hereinafter as the anatomical MAP (AMAP). The suitable β2 value (SBV) is determined based on our experience with the conventional MAP reconstruction (without anatomical prior). The value is chosen to produce a reasonable contrast recovery coefficient (between 0.85 to 0.9) for a hot region that is about twice of the PET resolution. It can be determined either experimentally or by theoretical calculation [Qi and Leahy, 1999]. If an ROI in an image is very small, such as the blood pool in an FDG mouse scan, the initial image updates are performed using the ML-EM algorithm without the prior to preserve functional edges.
After the initial image updates, we initialize the LSFs as the signed distance functions to the initial region boundaries and run (28) for 400 steps. Initial regions are defined manually either by drawing simple shapes for known organs or by thresholding the initial reconstruction. Since LSFs can handle topology changes, initial regions do not need to include every tissue type. Then we start the alternating update procedure. At each iteration, we first fix the LSFs and update the image by running (22) for 5 iterations and then evolve the LSFs with the current image estimate for 200 steps. During the alternating updates, a reasonable choice of the image smoothness parameters is β1 = SBV and β2 = SBV/2. The shape prior is active only in this part with positive μ1 and μ2. The boundary smoothness parameter is set to where cmin is a rough estimate of the lowest contrast between regions of interest in the final image. We use the lowest contrast to avoid over-smoothing of functional boundaries. The second shape parameter μ2 is set to μ2 = μ1/2 and we found that the reconstruction is quite insensitive to this value.
Once the LSFs become stable, we perform the final image updates for 300 iterations with β1 = 0 to avoid potential bias caused by the global smoothing term.
The step size dt in (28) affects the convergence speed of the algorithm. Large dt can speed up the evolution of LSFs, but it does not guarantee an ascent in the object function. To solve this problem, we use a step bound [Mitchell, 2008] to control the LSFs evolution speed. The step bound in our experiments was chosen such that the maximum absolute change of φ is 0.3.
3. Computer Simulations
We evaluated the performance of the proposed method using computer simulation studies. Two digital phantoms, a mouse-size phantom and a human-size phantom, were used to study how the proposed method accommodates different signal and position mismatches between functional and anatomical images.
3.1. The mouse phantom
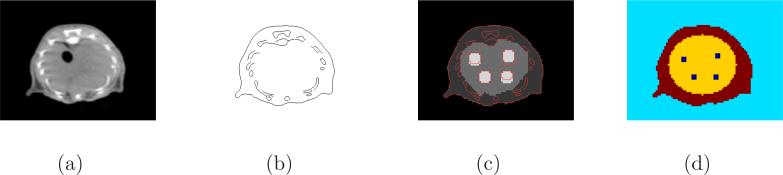
The mouse phantom (Figure 1) was derived by segmenting an abdomen CT slice and the corresponding cryosection image in the Digimouse dataset [Dogdas et al., 2007, Stout et al., 2002]. The pixel size of the CT image was 0.1 × 0.1 mm2 and the pixel size of the PET phantom was 0.4 × 0.4 mm2. The anatomical edges were extracted from the CT slice by using the Canny edge detector implemented in MATLAB (function “edge” with method “canny”). The standard deviation of the Gaussian kernel Gσ in (13) was set to one CT pixel. We added four hot tumors in the liver region with different anatomical boundaries: matched, enlarged, reduced, and shifted boundaries (see Figure 1(c)). Each pixel in the PET phantom contains one type of tissue. The activities of the tumors, liver, and other soft tissue are 4, 2, and 1, respectively. The digital PET phantom was forward projected using a precomputed system model corresponding to the microPET II scanner [Tai et al., 2003]. The system model included the solid angle effect and radially variant blurring effect caused by crystal penetration. The attenuation of the object was computed analytically by assigning a uniform attenuation coefficient of 0.095 cm−1 to soft tissues and 0.15 cm−1 to bones. The resulting attenuation factors were included in the system matrix for both data generation and image reconstruction. Randoms and scatter events were modeled as a uniform sinogram with 10% of the true coincidence counts. Poisson noise was introduced to the noise-free sinogram resulting in a total of 0.1 million events. One hundred independent realizations were generated. Figure 1(d) shows the initial regions of LSFs, including 4 regions: the mouse body, liver, tumors, and air. The mouse body outline was taken from the CT boundary, while the liver and tumor regions were simple geometries drawn manually.
Figure 1.
Images of the mouse phantom: (a) CT image, (b) edges extracted from the CT image, (c) PET activity image with CT edges overlaid, and (d) initial regions for the level set functions.
3.2. The human phantom
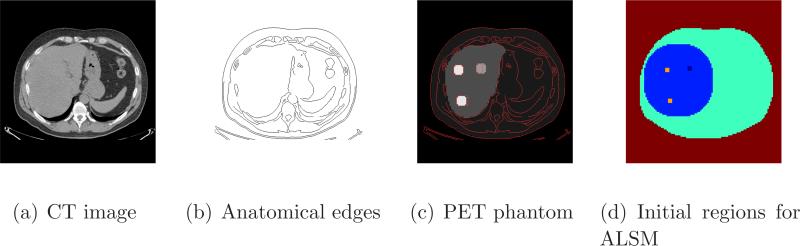
The human phantom was generated from the CT image shown in Figure 2(a). The pixel size of the CT image is 0.15 × 0.15 mm2. The anatomical edges extracted from the CT image are shown in Figure 2(b). We generated a PET phantom from the CT image and added three tumors with different contrast level as shown in Figure 2(c). The pixel size of the PET image is 0.6 × 0.6 mm2. The contrast is 2:1 for the low-contrast tumor and 3:1 for the two high-contrast tumors. One tumor has a matched anatomical boundary and the other two have an enlarged and reduce anatomical boundary, respectively. Similar to the mouse phantom, we assigned the attenuation coefficient of 0.095 cm−1 to soft tissues and 0.15 cm−1 to bones. The calculated attenuation factors were included in the system matrix for both data generation and image reconstruction. We forward projected the PET phantom image and added a uniform sinogram with 20% of the true events to model randoms and scatters. Poisson noise was then introduced resulting in a total of 0.4 million events. One hundred independent realizations were generated. The initial five regions in the human phantom are shown in Figure 2(d): the two high contrast tumors, the low contrast tumor, the liver, the human body, and air. Again, the body outline was obtained from the CT image, and the liver and tumor regions were drawn manually.
Figure 2.
Images of the human phantom: (a) CT image, (b) edges extracted from the CT image, (c) PET activity image with CT edges overlaid, and (d) initial regions for the level set functions.
3.3. Parameter settings
Because there are four regions in the mouse phantom and five regions in the human phantom, we used two (log2(4)) LSFs for the mouse phantom data and three (ceil(log2(5))) LSFs for the human phantom data. Parameters, β1, β2, μ1, and μ2, were chosen according to Section 2.2. For the mouse phantom data, the initial SBV value for β2 is 0.4. At the final image update stage, we used a range of β2 values (β2 = [0, 0.03, 0.1, 0.3, 1, 3, 10]) to obtain reconstructed images with different resolution versus noise properties for quantitative comparisons. For the human phantom data, the initial SBV value for β2 was 0.01. The value is smaller than that for the mouse phantom because the system matrices were different. At the final image update stage, we also reconstructed the images with a range of β2 values (β2 = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1]) to study the resolution versus noise tradeo.
3.4. Methods to compare
We compared the proposed method with the maximum likelihood expectation maximization (ML-EM) method, conventional MAP (CMAP) with a uniform log-quadratic prior, anatomical MAP (AMAP) which does not smooth PET images across anatomical edges, and a level set method (LSM) that does not use any anatomical information by setting fj = 1 in the shape energy for all pixels. The ML-EM algorithm was regularized by the number of iterations and the other methods were regularized by the local smoothing term with the same β2 values as those used in the ALSM. The number of iterations was 300 for all MAP methods.
3.5. Quantitative comparisons
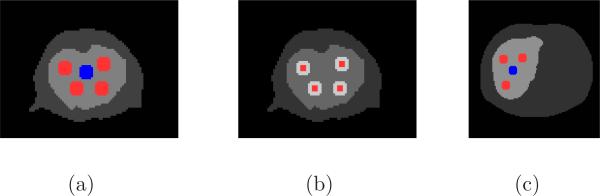
We compared the performance of different methods for region of interest (ROI) quantification. The ROIs were the tumor regions shown in red in Figure 3 (a) for the mouse phantom and (c) for the human phantom (45 pixels each). We also defined a background region (shown in blue) in each phantom to calculate the contrast recovery coefficient (CRC).
Figure 3.
The selected ROIs in the simulation studies. (a) The full size tumor ROIs in red and the background region in black for the mouse phantom. (b) The central ROIs (9 pixels) for the tumors in the mouse phantom. (c) The full size tumor ROIs in red and the background region in blue for the human phantom.
First we calculated the bias and standard deviation images as
| (14) |
| (15) |
where is the rth reconstructed image, xtrue is the true image, and R is the number of realizations.
Then, the relative bias and standard deviation in each ROI were calculated as
| (16) |
| (17) |
where tROI is the indicator function of the ROI, i.e., if pixel j is inside the ROI, and tROI,j = 0 otherwise. We plot the bias versus standard deviation curve to compare the performance of different methods.
We also calculated the CRC of each tumor region for each realization as
| (18) |
where tbg is the indicator function of the background ROI. Then, we calculated the mean and standard deviation of the CRC of each tumor region from 100 noisy realizations and plot the mean CRC versus standard deviation curves. To evaluate the effect of ROI delineation, we also performed the same analysis using only the 9 central pixels in each tumor as the ROI (figure 3(b)).
4. Real mouse data
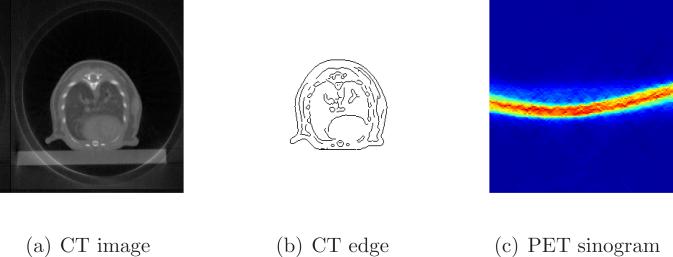
We applied the proposed method to a set of mouse [18F]-FDG data acquired on the microPET II/microCT scanner ([Liang et al., 2007]). The voxel size of the CT image was 0.15 mm, and the voxel size of the PET image was 0.6 mm. We chose an image slice containing the myocardium, blood pool, and lung regions. Figure 4(a) shows the CT image and Figure 4(b) shows the extracted anatomical edges. The PET sinogram is shown in Figure 4(c). The random fraction was estimated to be 15% and the random sinogram was assumed to be uniform in the reconstruction. No attenuation correction was applied, which is a standard practice in mouse imaging.
Figure 4.
Images of the real mouse data: (a) the CT image, (b) extracted CT edges, and (c) the PET sinogram.
The initial reconstruction in the ALSM was performed by 20 iterations of the ML-EM algorithm to preserve the functional edges. The suitable smoothing parameter for this system matrix is 0.05. Therefore, the parameters [ β1, β2, μ1, μ2, σ] were set to [ 0.05, 0.02, 0.1, 0.05, 2] for the ALSM. We compared the proposed method with the CMAP and AMAP with a matched local smoothing parameter of 0.02.
5. Results
5.1. Results of the mouse phantom
5.1.1. Sample images
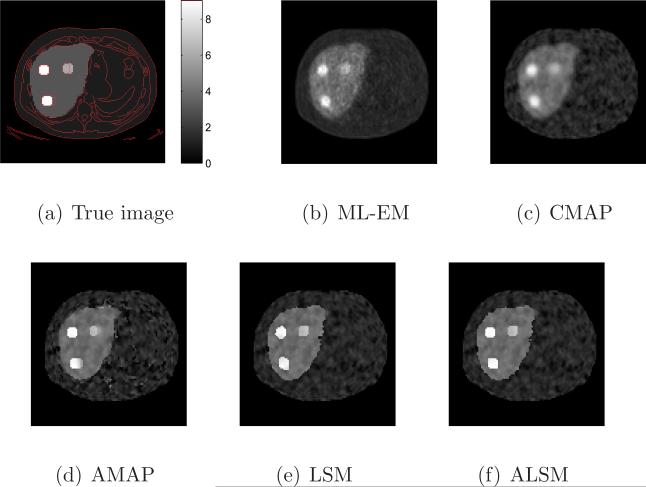
Sample reconstructed images of all methods with a similar resolution (ML-EM with 10 iterations, and all regularized methods with local smoothing β2 = 0.3) are shown in Figure 5. The tumors in the images reconstructed by the ML-EM and CMAP are blurred, while the tumors in the AMAP image have different shapes caused by the mismatched boundaries. The tumors in the ALSM and LSM images are less affected by the mismatched anatomical boundaries. The ALSM reconstruction is closer to the true image than the LSM reconstruction, especially at the locations with a matched anatomical edge.
Figure 5.
Sample reconstructed images from different methods for the mouse phantom.
5.1.2. Bias and standard deviation images
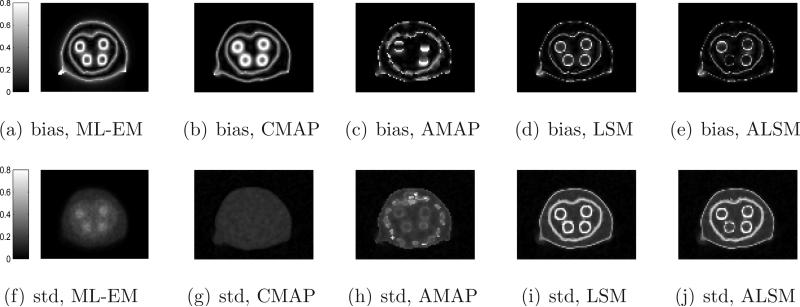
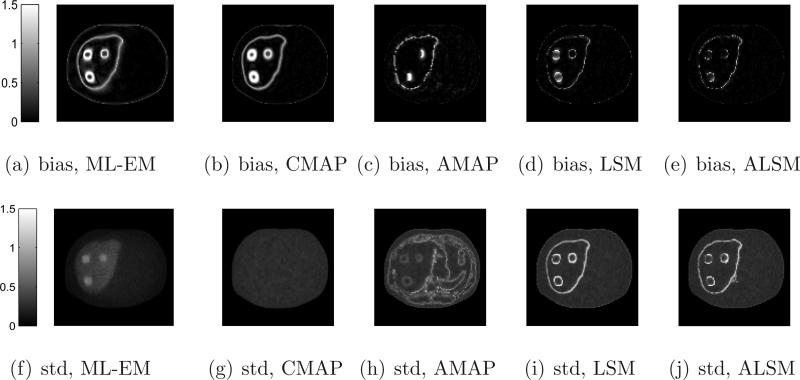
We calculated the absolute bias and standard deviation images of different methods from 100 independent reconstructions and the results are shown in Figure 6. In general, we can see that the ML-EM and CMAP produce larger bias at region boundaries, but relatively uniform standard deviation, due to their spatial-invariant regularizations, while edge preserving methods (AMAP, LSM, and ALSM) result in less bias but higher standard deviation at region boundaries.
Figure 6.
Absolute bias and standard deviation images of different methods for the mouse phantom.
5.1.3. ROI quantifications
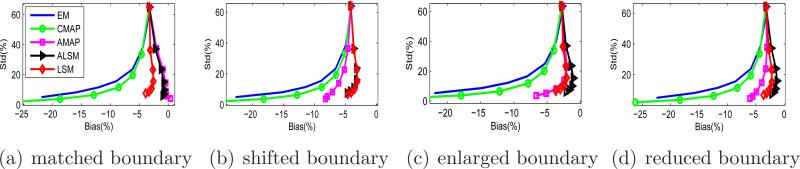
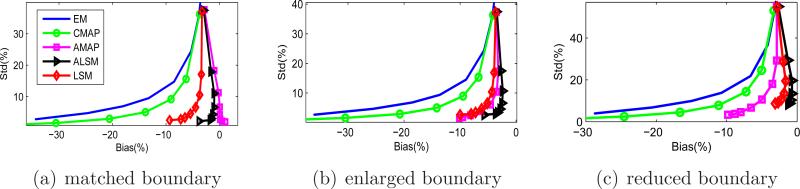
From the bias and standard deviation images, we computed the average bias versus average standard deviation inside each tumor ROI. The results are shown in Figure 7. For the tumor with a matched anatomical boundary, the performance of the ALSM is the same as that of the AMAP, which is expected to be the best under this condition. For tumors with a mismatched anatomical boundary, the ALSM has better performance (less bias at a given standard deviation) than the AMAP and other methods.
Figure 7.
Bias versus standard deviation curves of the tumor ROIs in the mouse phantom.
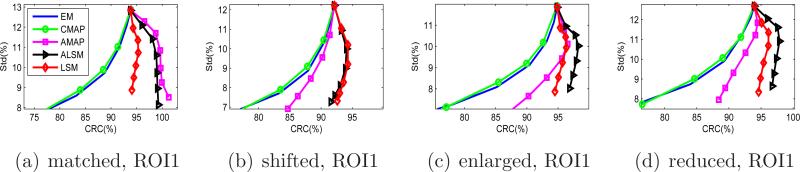
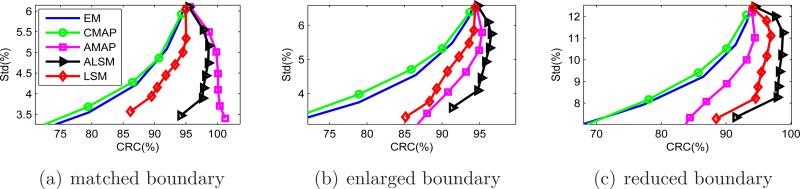
Figure 8 shows the CRC versus standard deviation curves for the full size tumor ROIs. Again, the ALSM has the best performance for all ROIs. For the tumor with a matched anatomical boundary, the ALSM achieves nearly 100% CRC with 8% standard deviation, while the ML-EM and CMAP achieve only 80% CRC at the same standard deviation level. For tumors with a mismatched anatomical boundary, the CRC of the ALSM is slightly less than 100%, but is still much higher than those achieved by other methods.
Figure 8.
CRC versus standard deviation curves of the full-size tumor ROIs in the mouse phantom.
The results of the central ROIs (9 pixels) are shown in Figure 9. The ALSM and LSM consistently achieve close to 100% CRC under different smoothing parameters for all ROIs, while the CMAP and ML-EM exhibit over-shoot and under-shoot depending on the smoothing parameter values. The results show that the proposed method is more robust to ROI delineation than the other approaches.
Figure 9.
CRC versus standard deviation curves of the central tumor ROIs in the mouse phantom.
5.2. Results of the human phantom
5.2.1. Sample images
Sample reconstructed images of all methods with a similar resolution (ML-EM at 15 iterations, and all penalized methods with local smoothing β2 = 0.01) are shown in Figure 10. Similar to the mouse phantom results, the ML-EM and CMAP result in blurred tumor boundaries and the AMAP reconstructs tumors with different shapes caused by the mismatched boundaries. Visually, the image reconstructed by the ALSM is closest to the true image. The shapes of the reconstructed tumors by the ALSM match with the true tumor shape better than those by the LSM especially at the locations with a matched edge.
Figure 10.
Sample reconstructed images from different methods for the human phantom.
5.2.2. Bias and standard deviation images
We calculated the absolute bias and standard deviation images of different methods from 100 independent reconstructions and the results are shown in Figure 11. Similar to the mouse phantom results, the ML-EM and CMAP result in a larger bias at region boundaries, but relatively uniform standard deviation, due to their spatial-invariant regularizations. The edge preserving methods (AMAP, LSM, and ALSM) resulted in less bias but higher standard deviation at region boundaries than the ML-EM and CMAP. Unlike the AMAP, false anatomical edges from bones do not introduce high noise in ALSM reconstructions.
Figure 11.
Absolute bias and standard deviation images of different methods for the human phantom.
5.2.3. ROI quantifications
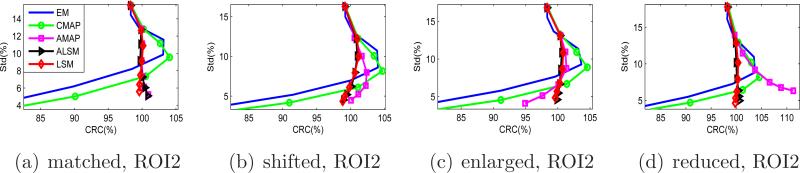
Figure 12 compares the average bias versus average standard deviation curves for the three tumor ROIs. For the tumor with a matched boundary, the ALSM result is slightly worse than that of the AMAP, but better than those of the other methods. For tumors with either an enlarged or reduced anatomical boundary, the ALSM has the best performance among all methods. Overall, the ALSM can reduce pixel standard deviation from about 40% (no regularization) down to less than 10% without any noticeable increase in the bias.
Figure 12.
Bias versus standard deviation curves for the ROIs of the human phantom.
Figure 13 shows the CRC versus standard deviation curves. Similar to the bias versus standard deviation comparison, the ALSM achieves the best performance for the tumors with mismatched boundaries and close to the best performance for the tumor with a matched boundary. Overall, the ALSM can reduce the standard deviation by about 40% compared to the unregularized reconstruction while keeping the contrast recovery coefficient above 95%. In comparison, the CMAP reduces CRC to less than 80% for the same amount of variance reduction.
Figure 13.
CRC versus standard deviation curves for the human phantom.
5.3. Results of the real data
Figure 14 shows the reconstructed images of the real mouse FDG data using the (a) CMAP, (b) AMAP, (c) LSM, and (d) ALSM, each overlaid with the CT boundaries. The ALSM and LSM images are visually similar, and show the highest contrast between the myocardium and the blood pool. We thresholded each reconstructed image independently to define two ROIs: one for the myocardium and one for the left ventricle. The calculated contrasts between the two regions are shown in Table 1. The contrasts in the ALSM and LSM images were twice of those obtained by the other two methods.
Figure 14.
Reconstructed real mouse images overlaid with the CT edges.
Table 1.
Reconstructed contrast between the myocardium and blood pool.
| CMAP | AMAP | LSM | ALSM | |
|---|---|---|---|---|
| Contrast | 1.49 | 1.52 | 3.03 | 3.05 |
6. Discussion
Past studies in PET reconstruction using blurred weights or blurred labels showed little [Fessler et al., 1992] or moderate improvement [Comtat et al., 2002]. Both phantom studies here showed that the proposed method was clearly superior than the MLEM, CMAP, LSM, and AMAP with imperfect boundaries. While all methods su er some degree of bias-variance tradeo , the proposed ALSM achieves less bias and higher CRC than other methods at a given noise level and the performance is less affected by mismatched anatomical boundary than that of the AMAP. For a tumor with a perfectly matched anatomical boundary, the ALSM achieves similar performance as the AMAP, which is expected to be the best. For tumors with a mismatched anatomical boundary, the ALSM is clearly better than the AMAP and non-edge preserving methods (ML-EM and CMAP). The advantage of using anatomical edge information is demonstrated by the improvement of the ALSM over the LSM, i.e. less bias at a fixed standard deviation for the ROIs with a matched or partially matched anatomical boundary. Overall, the proposed ALSM can substantially reduce the standard deviation without increasing the bias or reducing the CRC for the tumor ROIs. We see that there is a small negative bias for all tumor ROIs in the unregularized reconstruction images. This is because the noise is high in unregularized images and the nonnegativity constraint used in the reconstruction causes a positive bias in low activity regions (background), which in turn reduces the estimated activity in the tumors in order to satisfy the imaging equation in (1). This negative bias reduces as we increase the count level of the sinograms.
In the real mouse experiment, both the ALSM and LSM obtained higher contrast than the other two methods. We saw little di erence between the ALSM and LSM results, because there is no anatomical boundary between the myocardium and the blood pool. To confirm this, we performed an additional simulation study using the reconstructed image in Figure 14(d) as the ground truth and the same CT prior. Multiple realizations were generated by introducing Poisson noise to the noise-free sinogram. The results from the simulation study showed similar contrast recovery between the ALSM and LSM reconstructions, which is consistent with the real data results.
The proposed method requires tuning a number of regularization parameters. To address this issue, we have developed a procedure for choosing proper parameter values (see Section 2.2). Among these parameters, the local smoothing parameter β2 plays a major role in controlling the image roughness within each region. It works in the same way as the smoothing parameter in the conventional MAP reconstruction, except it does not smooth across functional boundaries. The level set functions are mostly controlled by β1, μ1, and μ2, which were borrowed directly from level set segmentation literature. In general, the global smoothing parameter β1 controls the strength of the intensity matching term in LSF segmentation. A large value of β1 can also accelerate the initial convergence of level set functions. The parameter μ1 controls the smoothness of the functional boundaries and the strength of the anatomical prior. A large μ1 will push the functional boundaries closer to the anatomical edges and make functional boundaries that are away from an anatomical edge smoother. The second shape prior parameter μ2 is used to regularize the slope of LSFs to reduce the frequency of redistance procedure, so it has little effect on the resulting regions. We performed sensitivity study on these three parameters by varying them from 1/10th to 10 times of their suggested values and obtained similar results for the phantom studies. The last parameter is σ in (13) which controls the strength of the anatomical prior. A larger σ produces smoother edge potential map f so that the anatomical prior has less effect on the resulting regions and the ALSM results become closer to the LSM results. We recommend σ to be less than half of the potential mismatch between the anatomical edge and functional edge convolved with the PET intrinsic resolution.
Initial region definition may also affect the resulting functional regions, because the level set method can only converge to a local optimum. A good LSF initializaton will also reduce the number of iterations required to reach the final solution. In addition, the interaction between the image update and LSF update may cause artifacts if a functional boundary is trapped at an erroneous location. To reduce the influence of initial regions on reconstructed images, we start an image reconstruction with 20 iterations of AMAP (or ML-EM) algorithm before updating LSFs, as described in Section 2.2. Furthermore, in the first pass of the LSF update, we run (28) for 400 steps so that the resulting functional boundaries are close to their correct locations. In our simulation studies, we include an initial region for each tumor, which can be identified from an initial reconstruction. We also tried initializing the LSFs with all the regions in Figure 2(d) except one of the three tumors in the human phantom simulation. The reconstructed images were similar, but the convergence of the LSFs was slower. This demonstrates that it is not necessary to include all regions in the LSF initialization. However, an initialization that is closer to the truth is always preferred.
Because of the LSF update, the proposed method takes longer computation time than the CMAP. For the mouse phantom with two LSFs, one step of the LSF update took 0.03 second, about 26% of the computation time of one image update. The total computational time of the ALSM for reconstructing one image was 90 seconds, about 3 times of the cost of the CMAP. For the human phantom with three LSFs, one step of the LSF update took 0.17 second, about 50% of the computation time of one image update. The reconstruction time of one image was 415 seconds for the ALSM and 190 seconds for the CMAP, respectively. The timing results were obtained from reconstruction codes implemented in MATLAB. Substantial speed up can be achieved for both codes by implementing them in C/C++.
7. Conclusion
We have developed a novel approach to MAP reconstruction of PET images with a CT-guided level set prior. The image prior models both the smoothness of PET images and the similarity between functional boundaries in PET and anatomical boundaries in CT. Our approach allows different boundaries in the PET images to accommodate possible signal and position mismatch between PET and CT images. Computer simulation experiments showed that the proposed method improved quantitative accuracy of PET images compared to other existing methods. Application of the proposed method to a real mouse PET scan also showed promising results.
Acknowledgments
The authors would like to thank anonymous reviewers for their comments and suggestions that substantially improved the quality of the manuscript.
This work was supported by Award Numbers R01EB000194 and RC4EB012836 from the National Institute Of Biomedical Imaging And Bioengineering. The content is solely the responsibility of the authors and does not necessarily represent the o cial views of the National Institute Of Biomedical Imaging And Bioengineering or the National Institutes of Health.
Appendix
Derivation of the update equations
The optimization algorithm updates the image and LSFs alternatingly to maximize the objective function. At each iteration, image x is updated using an optimization transfer method and LSFs ϕ are updated using a steepest descent algorithm.
Image update
We use the surrogate function in the ML-EM algorithm [Lange, 1984] for the log-likelihood function, which is
| (19) |
For the image smoothness energy, we use the De Pierro's surrogate function to decouple the local smoothness term [Pierro, 1995],
| (20) |
Combining (19) and (20), x(n+1) is obtained by finding the positive root of
| (21) |
which is given by
| (22) |
where
| (23) |
| (24) |
| (25) |
LSF Update
With a fixed image x, we alternatively update the LSFs ϕ and the region means Cp. We first fix ϕ and obtain Cp by solving
| (26) |
which results in
| (27) |
We then fix the region means Cp and update the LSFs in series using a steepest descent algorithm
| (28) |
where dt is an update step size.
The gradient of the image smoothness energy can be written as
| (29) |
where denotes the gradient of the global smoothing term and the gradient of the local smoothing term. When two LSFs are used, we have
| (30) |
| (31) |
where δε(·) is the derivative of Hε(·) [Vese and Chan, 2002] that controls the effective update area of the LSFs. The gradient of the local smoothing term is
| (32) |
for the LSF with the maximum |Hε(φlj) − Hε(φlk)| at pixel j, and is zero for all other LSFs.
The gradient of the shape energy function is given by
| (33) |
where div(·) is the divergence operator and Δ is the Laplacian operator. The first two terms are obtained by following the derivation in [Kichenassamy et al., 1996] and the last term is from [Li et al., 2005]. The effect of ∇f · ∇ϕ is to attract the functional boundaries to the nearby anatomical edges, and the effect of is to smooth all the boundaries but preserving the shape of the portion that is very close to the anatomical edges. Because the resolution of CT is higher than PET, f and ∇f are down-sampled to the PET resolution at this step.
References
- Alessio AM, Kinahan PE. Improved quantitation for PET/CT image reconstruction with system modeling and anatomical priors. Medical Physics. 2006;33(11):4095–4103. doi: 10.1118/1.2358198. [DOI] [PubMed] [Google Scholar]
- Ardekani BA, Braun M, Hutton BF, Kanno I, Iida H. Minimum cross-entropy reconstruction of PET images using prior anatomical information. Physics in Medicine and Biology. 1996;41(11):2497–2517. doi: 10.1088/0031-9155/41/11/018. [DOI] [PubMed] [Google Scholar]
- Baete K, Nuyts J, Laere KV, Van Paesschen W, Ceyssens S, De Ceuninck L, Gheysens O, Kelles A, Van den Eynden J, Suetens P, Dupont P. Evaluation of anatomy based reconstruction for partial volume correction in brain FDG-PET. NeuroImage. 2004a;23(1):305–317. doi: 10.1016/j.neuroimage.2004.04.041. [DOI] [PubMed] [Google Scholar]
- Baete K, Nuyts J, Van Paesschen W, Suetens P, Dupont P. Anatomical-based FDG-PET reconstruction for the detection of hypo-metabolic regions in epilepsy. IEEE Transactions on Medical Imaging. 2004b;23(4):510–519. doi: 10.1109/TMI.2004.825623. [DOI] [PubMed] [Google Scholar]
- Bataille F, Comtat C, Jan S, Sureau FC, Trebossen R. Brain PET partial-volume compensation using blurred anatomical labels. Nuclear Science Symposium Conference Record. 2006;3:1817–1824. [Google Scholar]
- Bowsher JE, Johnson VE, Turkington TG, Jaszczak RJ, Floyd Jr. C. E., Coleman RE. Bayesian reconstruction and use of anatomical a priori information for emission tomography. IEEE Transactions on Medical Imaging. 1996;15(5):673–686. doi: 10.1109/42.538945. [DOI] [PubMed] [Google Scholar]
- Brankov JG, Yang Y, Leahy RM, Wernick MN. Multi-modality tomographic image reconstruction using mesh modeling. Proceedings IEEE International Symposium on Biomedical Imaging. 2002:405–408. [Google Scholar]
- Canny J. A computational approach to edge detection. IEEE Trans. Pattern Analysis and Machine Intelligence. 1986;8(6):679–698. [PubMed] [Google Scholar]
- Cao L, Peter J. Bayesian reconstruction strategy of fluorescence-mediated tomography using an integrated SPECT-CT-OT system. Physics in Medicine and Biology. 2010;55(9):2693–2708. doi: 10.1088/0031-9155/55/9/018. [DOI] [PubMed] [Google Scholar]
- Chan T, Vese L. Active contours without edges. IEEE Transaction on Image Processing. 2001;10:266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- Cheng-Liao J, Qi J. PET image reconstruction with incomplete anatomical edge information using level set method (abstract). IEEE on Nuclear Science Symposium and Medical Imaging Conference. 2009 [Google Scholar]
- Chiao P, Rogers WL, Fessler JA, Clinthorne NH, Hero AO. Model-based estimation with boundary side information or boundary regularization cardiac emission CT. IEEE Transactions on Medical Imaging. 1994;13(2):227–234. doi: 10.1109/42.293915. [DOI] [PubMed] [Google Scholar]
- Comtat C, Kinahan PE, Fessler JA, Beyer T, Townsend DW, Defrise M, Michel C. Clinically feasible reconstruction of 3D whole-body PET/CT data using blurred anatomical labels. Physics in Medicine and Biology. 2002;47:1–20. doi: 10.1088/0031-9155/47/1/301. [DOI] [PubMed] [Google Scholar]
- Czernin J, Allen-Auerbach M, Schelbert HR. Improvements in Cancer Staging with PET/CT: Literature-Based Evidence as of September 2006. Journal of Nuclear Medicine. 2007;48(1 suppl):78S–88S. [PubMed] [Google Scholar]
- Dewaraja YK, Koral KF, Fessler JA. Regularized reconstruction in quantitative spect using ct side information from hybrid imaging. Physics in Medicine and Biology. 2010;55(9):2523–2539. doi: 10.1088/0031-9155/55/9/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dogdas B, Stout D, Chatziioannou A, Leahy RM. Digimouse: A 3d whole body mouse atlas from ct and cryosection data. Physics in Medicine and Biology. 2007;52(3):577–587. doi: 10.1088/0031-9155/52/3/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fessler JA, Clinthorne NH, Rogers WL. Regularized emission image reconstruction using imperfect side information. IEEE on Nuclear Science Symposium and Medical Imaging Conference. 1991;3:1991–1995. [Google Scholar]
- Fessler JA, Clinthorne NH, Rogers WL. Regularized emission image reconstruction using imperfect side information. IEEE Transactions on Nuclear Science. 1992;39(5):1464–1471. [Google Scholar]
- Gindi G, Lee M, Rangarajan A, Zubal IG. Bayesian reconstruction of functional images using anatomical information as priors. IEEE Transactions on Medical Imaging. 1993;12(4):670–680. doi: 10.1109/42.251117. [DOI] [PubMed] [Google Scholar]
- Goerres GW, von Schulthess GK, Steinert HC. Why Most PET of Lung and Head-and-Neck Cancer Will Be PET/CT. Journal of Nuclear Medicine. 2004;45(1 suppl):66S–71S. [PubMed] [Google Scholar]
- Hero AO, Piramuthu R, Fessler JA, Titus SR. Minimax emission computed tomography using high-resolution anatomical side information and B-spline models. IEEE Transactions on Information Theory. 1999;45(3):920–938. [Google Scholar]
- Hsu CL, Leahy RM. Medical Imaging 1997: Image Processing. Vol. 3034. SPIE; 1997. PET image reconstruction incorporating anatomical information using segmented regression. pp. 381–392. [Google Scholar]
- Kichenassamy S, Kumar A, Olver P, Tannenbaum A, Yezzi A. Conformal curvature flows: From phase transitions to active vision. Archive for Rational Mechanics and Analysis. 1996;134(3):275–301. [Google Scholar]
- Kinahan PE, Townsend DW, Beyer T, Sashin D. Attenuation correction for a combined 3D PET/CT scanner. Medical Physics. 1998;25(10):2046–2053. doi: 10.1118/1.598392. [DOI] [PubMed] [Google Scholar]
- Lange K. EM reconstruction algorithms for emission and transmission tomography. Journal of computer assisted tomography. 1984;8(2):306–316. [PubMed] [Google Scholar]
- Leahy R, Yan X. Lecture notes in computer science, Information Processing in Medical Imaging. Springer; 1991. Incorporation of anatomical MR data for improved functional imaging with pet. [Google Scholar]
- Li C, Xu C, Gui C, Fox MD. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE Computer Society; 2005. Level set evolution without re-initialization: A new variational formulation. pp. 430–436. [Google Scholar]
- Liang H, Yang Y, Yang K, Wu Y, Boone JM, Cherry SR. A microPET/CT system for in vivo small animal imaging. Physics in Medicine and Biology. 2007;52(13):3881–3894. doi: 10.1088/0031-9155/52/13/015. [DOI] [PubMed] [Google Scholar]
- Liao J, Qi J. PET image reconstruction with anatomical prior using multiphase level set method. Nuclear Science Symposium Conference Record, 2007. IEEE. 2007;6:4163–4168. Oct. Nov. [Google Scholar]
- Lipinski B, Herzog H, Rota Kops E, Oberschelp W, Muller-Gartner HW. Expectation maximization reconstruction of positron emission tomography images using anatomical magnetic resonance information. IEEE Transactions on Medical Imaging. 1997;16(2):129–136. doi: 10.1109/42.563658. [DOI] [PubMed] [Google Scholar]
- Mitchell IM. The flexible, extensible and e cient toolbox of level set methods. Journal of Scientific Computing. 2008;35(2):300–329. [Google Scholar]
- Ouyang X, Wong WH, Johnson VE, Xiaoping H, Chen C. Incorporation of correlated structural images in PET image reconstruction. IEEE Transactions on Medical Imaging. 1994;13(4):627–640. doi: 10.1109/42.363105. [DOI] [PubMed] [Google Scholar]
- Pan T, Mawlawi O, Nehmeh SA, Erdi YE, Luo D, Liu HH, Castillo R, Mohan R, Liao Z, Macapinlac HA. Attenuation Correction of PET Images with Respiration-Averaged CT Images in PET/CT. Journal of Nuclear Medicine. 2005;46(9):1481–1487. [PubMed] [Google Scholar]
- De Pierro AR. A modified expectation maximization algorithm for penalized likelihood estimation in emission tomography. IEEE Transactions on Medical Imaging. 1995;14(1):132–137. doi: 10.1109/42.370409. [DOI] [PubMed] [Google Scholar]
- Piramuthu R, Hero AO. Side information averaging method for PML emission tomography. International Conference on Image Processing. 1998;2:671–675. [Google Scholar]
- Pramuthu R, Hero AO. Penalized maximum likelihood image reconstruction with min-max incorporation of noisy side information. IEEE International Conference on Acoustics, Speech, and Signal Processing. 1998;5:2865–2868. [Google Scholar]
- Qi J, Leahy RM. A theoretical study of the contrast recovery and variance of MAP reconstructions from PET data. IEEE Transactions on Medical Imaging. 1999;18(4):293–305. doi: 10.1109/42.768839. [DOI] [PubMed] [Google Scholar]
- Rangarajan A, Hsiao I, Gindi G. A bayesian joint mixture framework for the integration of anatomical information in functional image reconstruction. Journal of Mathematical Imaging and Vision. 2000;12(3):199–217. [Google Scholar]
- Sastry S, Carson RE. Multimodality bayesian algorithm for image reconstruction in positron emission tomography: a tissue composition model. IEEE Transactions on Medical Imaging. 1997;16(6):750–761. doi: 10.1109/42.650872. [DOI] [PubMed] [Google Scholar]
- Schalder H, Yeung HWD, Gonen M, Kraus D, Larson SM. Head and Neck Cancer: Clinical Usefulness and Accuracy of PET/CT Image Fusion. Radiology. 2004;231(1):65–72. doi: 10.1148/radiol.2311030271. [DOI] [PubMed] [Google Scholar]
- See ESK. A new novel PET/CT reconstruction algorithm by using prior image model with simulated annealing process. Proceedings of 2005 International Symposium on Intelligent Signal Processing and Communication Systems. 2005:661–664. [Google Scholar]
- Somayajula S, Rangarajan A, Leahy RM. PET image reconstruction using anatomical information through mutual information based priors: A scale space approach. 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, ISBI 2007. 2007:165–168. [Google Scholar]
- Stout D, Chow P, Silverman R, Leahy RM, Lewis X, Gambhir S, Chatziioannou A. Creating a whole body digital mouse atlas with PET, CT and cryosection images. Molecular Imaging and Biology. 2002;4(4):S27. [Google Scholar]
- Tai Y, F Chatziioannou A, Yang Y, W Silverman R, Meadors K, Siegel S, Newport DF, Stickel JR, Cherry SR. MicroPET II: design, development and initial performance of an improved microPET scanner for small-animal imaging. Physics in Medicine and Biology. 2003;48(11):1519–1537. doi: 10.1088/0031-9155/48/11/303. [DOI] [PubMed] [Google Scholar]
- Tang J, Rahmim A. Bayesian PET image reconstruction incorporating anato-functional joint entropy. Physics in Medicine and Biology. 2009a;54(23):7063–7075. doi: 10.1088/0031-9155/54/23/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J, Rahmim A. Anatomy assisted MAP-EM PET image reconstruction incorporating joint entropies of wavelet subband image pairs. Nuclear Science Symposium Conference Record (NSS/MIC), 2009 IEEE. 2009b:3741–3745. [Google Scholar]
- Townsend D, Carney J, Yap JT, Hall NC. PET/CT today and tomorrow. Journal of Nuclear Medicine. 2004;45:4s–14s. [PubMed] [Google Scholar]
- Townsend DW. Dual-Modality Imaging: Combining Anatomy and Function. Journal of Nuclear Medicine. 2008;49(6):938–955. doi: 10.2967/jnumed.108.051276. [DOI] [PubMed] [Google Scholar]
- Vese L, Chan T. Multiphase level set framework for image segmentation using the mumford and shah model. International Journal of Computer Vision. 2002;50(3):271–293. [Google Scholar]
- Zhang Y, Fessler JA, Clinthorne NH, Rogers WL. Incorporating MRI region information into SPECT reconstruction using joint estimation. ICASSP-95. International Conference on Acoustics, Speech, and Signal Processing, 1995. 1995;4:2307–2310. [Google Scholar]