Abstract
Quantum.Ligand.Dock (protein–ligand docking with graphic processing unit (GPU) quantum entanglement refinement on a GPU system) is an original modern method for in silico prediction of protein–ligand interactions via high-performance docking code. The main flavour of our approach is a combination of fast search with a special account for overlooked physical interactions. On the one hand, we take care of self-consistency and proton equilibria mutual effects of docking partners. On the other hand, Quantum.Ligand.Dock is the the only docking server offering such a subtle supplement to protein docking algorithms as quantum entanglement contributions. The motivation for development and proposition of the method to the community hinges upon two arguments—the fundamental importance of quantum entanglement contribution in molecular interaction and the realistic possibility to implement it by the availability of supercomputing power. The implementation of sophisticated quantum methods is made possible by parallelization at several bottlenecks on a GPU supercomputer. The high-performance implementation will be of use for large-scale virtual screening projects, structural bioinformatics, systems biology and fundamental research in understanding protein–ligand recognition. The design of the interface is focused on feasibility and ease of use. Protein and ligand molecule structures are supposed to be submitted as atomic coordinate files in PDB format. A customization section is offered for addition of user-specified charges, extra ionogenic groups with intrinsic pKa values or fixed ions. Final predicted complexes are ranked according to obtained scores and provided in PDB format as well as interactive visualization in a molecular viewer. Quantum.Ligand.Dock server can be accessed at http://87.116.85.141/LigandDock.html.
INTRODUCTION
Understanding protein–ligand interactions is a major focus for modern molecular biophysics and structural bioinformatics research. On the practical side, application of drug design techniques requires the availability of fast and reliable docking methods that can account for all major aspects of molecule interaction physics. Despite the progress in prediction via in silico methods, intricacies in protein–ligand interactions are still beyond our reach (1–3). The introduction of Fourier correlation methods (4) brought reasonable speed of algorithms for rigid-body docking. Graphic processing unit (GPU) supercomputer systems provided additional breakthrough in this class of molecular modeling techniques (5). Thus, the crucial next step is to focus on the precise description of the physics of protein–ligand interactions. The most reliable description is via ab initio quantum mechanical methods, and the recent possibilities to access adequate computing power obliges the community to address the problem in the context of practical protein–ligand analysis tools. Another issue is the treatment of long-range electrostatics and protonation states (6–10). Modern docking algorithms are expected to treat self-consistency of long-range interactions and the mutual effect of the protein and ligand molecules on each other protonation state. In this respect, we have already contributed in the case of protein–protein docking and now apply this concept in protein–small molecule interaction case though with a novel advanced high-performance implementation.
Prediction of protein–protein and protein–ligand interactions via docking methods is at the focus of intense research (11–22). An essential step of any docking workflow is to find a list of ranked mutual orientations based on a scoring measure for shape complementarity and long-range interactions (electrostatics). The methods implementing rigid-body dock borrow ideas from protein–protein docking approaches such as the popular ZDOCK (11), Hex (12), PIPER (13) and GRAMM-X (14). The first rigid body docking program based on fast Fourier transformation is the pioneering DOT application (15).
A subsequent step is aimed at refinement of rigid docking results by taking into account short-range interactions. A precise treatment requires account for backbone and side chain flexibility (16)—e.g. RosettaDock (17) and HadDock (18). Specific popular applications for protein–ligand docking that dominate the field are AutoDock (20) and SwissDock (21). An alternative idea for docking is the search for analogy in known protein–ligand interfaces reminiscent of the protein–protein docking as implemented in PRISM (22).
However, all these methods do not face two issues—quantum effects and the self-consistency of electrostatic interactions (including the mutual influence of docking partners on their protonation states through interdependent perturbation of pKa values).
Our contribution is the implementation of this essential but missing link in the context of protein–ligand interactions and its realization on a massively parallel GPU supercomputer via C/C++/OpenCL programming environment. Thus, we have developed ultrafast docking code with a strong potential for large-scale systems biology projects. Concurrently, we have put on a sound theoretical basis the interdependency of protein–ligand electric fields, the mutual influence on pKa values (ionization states) upon molecule encounter and the fundamentally important quantum entanglement effect.
On the docking algorithmic side, we make use of the significant speedup of the fast Fourier transform (FFT) parallelized effectively under OpenCL environment. However, the Fourier transform is not used in the spirit of the traditional grid-based Katchalski-Katzir algorithm (4). We implement a version of 6D correlation search which makes use of spherical polar functions (22). It is a gridless method implemented via spherical polar Fourier representation of docking partners and several 1D FFT.
On the electrostatics side, we apply an improvement of our own self-consistent and rigorous method, GPU.proton.DOCK/PHEPS/PHEMTO (23–25). Our approach to electrostatics is characterized by implementation of fast algorithms and methods with reasonable, sound physics background that is reliably proven by numerous benchmarks—unequivocal validation by comparison with experimental studies (NMR and IR data) as shown in a number of peer-reviewed publications over the years (26–30). The estimation of protein electrostatic potential distribution is based on the GPU parallelization via CUDA kernels—our previous implementation (23)—and an implementation of a hierarchical fast multipole method (FMM) in OpenCL environment for additional speedup. Thus, our intrinsic fast electrostatics becomes ultrafast—an essential breakthrough since each sampling step of the 6D translation–rotation space (5 rotational and 1 translational degree of freedom) requires estimation of electrostatic energies, update of pKa values and reassignment of protonation charges.
Along with these improvements we implement reasonable and practical approach for estimation of a fundamental quantum mechanism (quantum entanglement) which is emerging as a major topic in modern molecule science but still ignored in current docking approaches. Quantum entanglement contribution to the protein–ligand interaction is estimated via calculation of entangled states of the composite protein–ligand Hilbert space. Technically speaking, it is the tensor product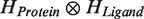 
of the Hilbert spaces of the protein molecule (
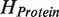) and the ligand molecule (
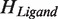). For example, by using basis vectors 
, 
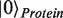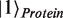for the Hilbert space 
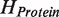and basis vectors 
, 
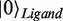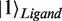for the Hilbert space 
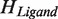, we can define the following entangled Bell state:
 |
(1) |
However, we are not going to theorize in this publication (details are given at the Quantum.Ligand.Dock Server—the Supplement and Benchmark pages). We aim to provide a practical tool including this effect, and this article describes the major steps of the implementation without delving deep in the theory. The motivation for this development and the proposal of the method to the community hinges upon two arguments—the importance of quantum entanglement contribution in overall protein–ligand interaction and the realistic possibility nowadays to implement it by the availability of supercomputing power. In this way, we provide for the community a modern docking method with practical interface and at the same time one that transcends some limitations of other docking tools. Note that using this measure does not interfere or overlap with the classical continuum electrostatics (pKa evaluations, including mutual interactions) or steric overlap measure.
MATERIALS AND METHODS
Molecular recognition factors - The Art of Quantum Fugue
A fascinating dimension of the protein–ligand recognition is the inclusion of the quantum entanglement contribution. Entanglement is often referred to as a profound and important concept in molecule science, but our server provides concrete implementation to practical protein–ligand docking problems. This issue is timely since quantum entanglement is proved to be ubiquitous in molecular interactions and there is considerable evidence of its robustness in biological systems.
In molecule physics, there is a relation linking binding energy with entanglement measure, and we implement this notion in the scoring function. It has been our purpose to provide this essential feature for the practicing structural bioinformatician and expert computational biophysicist. Estimation of binding energy contribution is just one side of quantum entanglement evaluation. Of fundamental interest is the explanation of the correlation that is responsible for the energy change upon protein–ligand docking. Thus, application of quantum entanglement to the molecule recognition problem seems compelling in itself. These calculations have motivic kinship to other issues such as the widely discussed and exciting quantum non-locality in molecular systems including biological macromolecules. For example, besides the overall measure (witness) characterizing entanglement between the protein and the ligand molecule, one can also report the so-called connectivity which informs us about the quantum correlation range. There is still more cunning in this concept but we will restrict our discussion of it in terms of the practical application docking service. We are not going to delve into details of implementation but just a feeling of the accessibility of this measure for practical protein–ligand interactions and a notion for the methods used to calculate it. The task is to estimate the amount of entanglement between two subsystems—the protein molecule and the ligand molecule—and measure for estimation of the amount of quantum entanglement is the so-called logarithmic negativity, a quantity derived from the eigenvalues of corresponding density matrices as well as the Schmidt rank (details are given at the Quantum.Ligand.Dock Server—the Supplement and Benchmark pages).
Implementation of major concepts
In devising our docking scheme, we were supposed to think contrapuntally but design the workflow sequentially. Four major threads of thought emerge as essential: rigid-body fit by shape complementarity, long-range electrostatics treatment, mutual impact of docking partners’ ionization states and quantum entanglement contribution. We consider our method intrinsically satisfying—reflection of a full picture of protein–ligand interaction, merging new tendencies with high-performance realization of earlier concepts and forging a unique workflow. Although we shifted the overall weight to quantum contributions, let us have a look at the first step rigid-body dock with shape complementarity based on FFT.
Spherical FFT sampling of translation–rotation space
Whatever level of treatment, a reasonable first step is to search for shape complementarity between the protein and the ligand molecule. It is a common theme of modern docking algorithms to implement Fourier transform-based search for rigid-body docking. Briefly, the molecules are mapped on grids and then a correlation of the maps is calculated via the FFT algorithm. The theoretical arguments lie in the convolution theorem. The method turned out to be a breakthrough but still poses several inconveniences. For example, each sampling step in rotation space requires pre-calculation of grids. Recently, we have implemented grid-free algorithms based on the spherical harmonic functions in C/CUDA (23). Gridless (grid-free) representation of the protein molecule and the ligand is based on 3D polynomial expansion of spherical polar basis functions (spherical harmonic functions) (14). Then, sampling docking correlations is reduced to estimation of coefficient vectors of the docking partners.
The major result, i.e. complementarity, is calculated conveniently via a series of 1D FFT which are efficiently handled for GPU systems:
 |
(2) |
where the vectors of expansion coefficients for ‘receptor’ is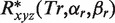 
and for ‘ligand’ molecule is 
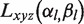. Rotation is via matrix elements of the real Wigner rotation matrices. Translation is performed in Gauss-Laguerre basis functions (31).
Just as a reminder the FFT algorithm reduces algorithmic complexity to N log N. More details on this issue is given in our previous publication (23) describing this procedure in the context of protein–protein docking and its supplement section, including benchmark results. In fact, any interaction potential describing physics of molecule recognition can be represented via spherical polar functions, and in the next section, we describe how to cope with situation of long-range electrostatics.
Although a rigid docking algorithm, Quantum.Ligand.Dock gives some flexibility by inclusion of a softer scoring function. Hence, some structures seem to penetrate each other in visualization mode.
In resume, a combination of modern day approaches solves the problem of the computational complexity in sampling protein–ligand search space. Thus, after a careful implementation of the above algorithms, we have to focus on accuracy of the interactions treatment itself.
Long-range electrostatics
Adequate treatment of electrostatics interactions is the central issue in molecular simulations. This is due to their long-range and pairwise nature (quadratic computational complexity). An additional problem to solve in concurrence with electrostatic interactions is the self-consistent treatment of the ionization states of the ligand and the protein and the interdependency of the pKa values evaluation (see next section). We have long-term experience with protein electrostatics and its algorithmic implementation, so we avidly look for new ways to improve both accuracy and computational efficiency. In this work, we offer several improvements based on the fast multipole formalism and its efficient parallelization within the C++/OpenCL environment. A natural extension is to follow the Fourier representation of the previous section, i.e. utilization of a polynomial expansion to encode the electrostatic potential field and charge distribution of the protein macromolecule and the ligand small molecule. Note that this case requires pre-computed electrostatic field and charge distribution (which is still a good approximation relevant to standard formal treatment of electrostatics). Then, the pH-dependent electrostatic energy of a protein complex can be expressed as a multiple integral of converged electrostatic potential distribution of the protein molecule and the charge distribution of the ligand molecule. The electrostatic potential computation is performed via multipole expansion (N log N computational complexity).
 |
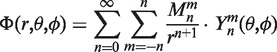(3) |
where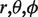 
define the point to calculate electrostatic potential, 
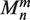are the moments of expansion and 
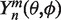is the spherical harmonic of degree n and order m.
To apply grid-free correlation, the electrostatic potential is represented as an expansion of spherical polar function basis functions. Again, the orthogonality property gives the overlap of spherical polar functions as a scalar product of the expansion coefficients. This convenient formalism gives us the tool to express electrostatic energy as a scalar product of transformed expansion coefficients for converged electrostatic potential distribution after a converged self-consistent procedure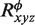 
of protein and the charge distribution of the ligand molecule 
:
 |
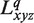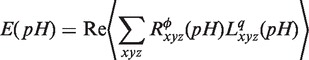(4) |
However, if we want to go beyond pre-computed electrostatics, we have to correlate protein electrostatic fields after a self-consistent iterative procedure, which can be applied at every sampling step. Due to the availability of modern GPU supercomputing resources, this branch of the docking workflow can be performed in real time. In this case, we implemented FMM, which accelerates the multipole method via clever techniques to shift multipole expansions and get local representations. The improvements lead to linear O(N) computational complexity. Our implementation is in C++/OpenCL, which is a novel feature that we would like to provide for practically inclined bioinformaticians who need real-time results. So, we reached the point where exposition of the next theme is naturally required.
Interdependency of electrostatic fields and pKa estimation for docking partners
The interdependency of protonation equilibria should be held in perfect balance as is the case for mutually interlocking parenthetical structure. A major point is the mutual influence of the docking partners. Such a calculation requires a separate self-consistent electrostatics run which includes mutual effect of docking partners on each other ionization sites and hence proton equilibria. In this case, we implement an additional kernel to achieve performance adequate for real-time simulation.
The model accepts experimentally measured pKa of model compounds (e.g. N-acetyl amides of each ith ionogenic amino acids) (pKmod,i) and evaluates Born term—a linear response approximation. Partial charges assume values from molecular mechanics parameterization sets—AMBER (CHARMM is supported too).
The pairwise interaction between any ith and jth ionic groups can be simulated by an empirical three-term function: Wij (r, ak) = ∑k (ak/rijk), k = 3. The ak values are estimated by a non-linear procedure for best fit to experimental data reflecting electrostatic interactions in proteins.
At a stage before accounting for ionization, the procedure calculates intrinsic constants: pKint,i = pKmod,i + ΔpKBorn,i + ΔpKpar,i, where pKmod,i is the pKa of the ith site according to model compounds, ΔpKBorn,i is the Born self-energy of the ith and ΔpKpar,i is the contribution of the ith site interacting with the set of partial (permanent, fixed) atomic charges. For each protonation group and at each step of the iterative self-consistent method, we estimate the pKa shift of the ith site caused by interactions with all other proton-binding groups. Here, the focus is on the interpretation of the Tanford-Roxby pKa value as an average measure to describe the energy required to protonate individual site at a given pH:
 |
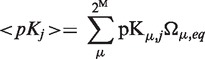(5) |
where Ω(p) is the distribution function of the protonation states and the form of Ω(p) that minimizes G is the equilibrium distribution function of the system, and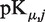 
is the pK value of group j in microscopic state μ.
This Tanford-Roxby style procedure is a well-controlled approximation of the strict statistical mechanics treatment. We would like to write down the exact expression (derivation can be found at the Supplementary section of the Quantum.Ligand.Dock Server):
 |
(6) |
Here, p is the protonation vector, G is the free energy of the corresponding ionization state, M is the number of proton-binding groups and E is the site–site electrostatic interaction energy. This relation can be derived in reverse order starting from the canonical Tanford-Roxby equation by trivial substitutions.
When the self-consistent iterative procedure meets convergence criteria, the new charge distribution is applied for calculation of the electrostatic potential grid. It is at this point that we have accelerated the code by applying C++/OpenCL implementation of the FMM. A multilevel summation technique was also tested but fast multipole algorithms achieved higher performance. A brief exposition of fast multipole application can be found in the Implementation section.
The Ways of Quantum.Ligand.Dock
Quantum.Ligand.Dock server workflow allows access to several approaches of increasing detail and sophistication in exploring protein–ligand docking mechanism—in analogy to our protein–protein workflow (23). All of them take into account at different levels subtle issues in accounting for ionization states—appropriate treatment of pH dependence and protonation states self-consistence.
Upon coming at a stage to evaluate electrostatic interactions of the charge system and face the contribution of protonation-dependent electrostatics to correlation functions, Quantum.Ligand.Dock server provides three alternatives to cope with the diverse needs and specific requirements for electrostatic docking calculation by the protein scientist:
A standard, straightforward method that relies on simple Coloumb electrostatics and immutable fields. This is the fastest approach. Each sampling step uses a pre-computed electrostatic field.
A step towards improvement—still immutable field at each step but a preliminary computation is performed via self-consistent iterative electrostatics. Thus, we have a converged protonation charge distribution after the iterative procedure for a given pH value but no update at each sampling step.
Mutual electrostatic influence of the docking partners. We consider this step an essential and crucial contribution to the docking algorithms field—both for the protein–protein docking (23) and the current application to the protein–ligand case. Each sampling step in the 6D docking space requires reevaluation of electrostatic potential and reassignment of protonation charges.
Whatever mode for calculation is chosen, the user can define a range of pH values to ‘titrate’ docking results. The user is provided with interactive Jmol Java applet to view docked structures. The results are also available as PDB-formatted complexes enlisted according to the docking score. The user can download all predictions in NMR/MODEL PDB format as well as archives of differently numbered sets of single PDB files. Such type of output can be readily used for visualization using convenient molecular modelling software for rendering protein 3D structure—Chimera (32), VMD (33), etc. The final pages of the Quantum.Ligand.Dock workflows provide interactive visualization for each of the predicted complexes.
IMPLEMENTATION
The first note related to implementation is our wish to mention and accent the novel features related to our previous protein–protein docking realization. These are the efficient FMM for estimation of electrostatics (OpenCL), more stringent summation algorithm for ionization states (OpenCL) and the quantum entanglement contribution (OpenCL). In general, algorithms implementing docking methods (FFT correlation), electrostatics modeling, quantum effects estimation and protein structure handling are written in C/C++/CUDA (some improvements in the parallel code are realized in OpenCL), Perl and Haskell by the author. C/C++/CUDA/OpenCL environment is used to code computationally demanding algorithms, which are the bottleneck in computing time. The heart of the acceleration is composed of GPU kernels. GPU supercomputers are based on massively parallel and multithreaded hardware architecture and thus achieve their limit with fine-grained parallel decompositions. As mentioned but still worth noting, our application of GPU parallelization is at the stages of long-range pairwise electrostatic calculation, the evaluation of the complementarity correlations by Fourier Transforms—FFT algorithm and the quantum entanglement contribution. The direct approach for electrostatics grid estimation is of quadratic time complexity O(mn) for n charge sites and m grid points. Our GPU kernel gave several tens fold speedup over a single core Central Processing Unit (CPU). Kernel development for electrostatic potential distribution via direct summation is straightforwardly parallelized (actually the outer loop of the serial implementation). It is worth to note significant improvements based on the fast multipole formalism and its efficient parallelization within the C++/OpenCL environment. FMMs are amenable for efficient parallel implementation and their computational complexity is linear O(N). Nowadays, they are proved to be the most efficient methods in the class of hierarchical N-body approaches. The FMM idea works as follows: A region of the system transmits its far field expansion to other regions. There are several steps. At first particle-to-multipole (P2M) expansion is performed. Then follow multipole-to-multipole (M2M) expansion, multipole-to-local (M2L), local-to-local expansion (L2L), local-to-particle expansion (L2P) and particle-to-particle (P2P) expansion. Technical details of the implementation and the benchmark of the performance can be found in the Benchmark and Supplement sections of the Quantum.Ligand.Dock server.
For the bottleneck of the docking run—the Fourier Transform—we make use of the FFT algorithm provided by CUFFT library (a CUDA implementation). Our method relies on multiple 1D FFTs instead of a 3D FFT.
‘Perl’ excels at efficient and elegant protein structure parsing, parsing parametrization sets and convenient data structure manipulation. The web implementation itself is driven by ‘CGI/PERL’ routines with ‘Java’ employed to run molecular viewer for interactive visualization of dipole/electric moments relative to 3D protein structure. The Java applet is part of Jmol applet molecular viewer distribution (http://jmol.sourceforge.net). Quantum.Ligand.Dock server expects as an input two coordinate files in PDB format—both protein structure and ligand are supposed to be PDB formatted. Protein structure files containing HETATM records are given special attention—an option is present to account for additional user-defined parametrization of charge properties explicitly in the electrostatic interaction calculation. As an additional asset, the user is given relevant information about the protein molecule and warned about certain inconsistencies in protein structure that might impact adversely ensuing calculation, e.g. interruption in residue numbering, which influences electrostatics through the appearance of terminal amino positive and carboxy negative charge sites with intrinsic pKs. The user is given the possibility to edit initial setup of ionogenic groups (attention to cysteine residues in disulfide bonds and excluding covalently modified groups). This is accomplished by user-friendly panel selection of ionizable groups that are going to be accounted for in the consequent self-consistent electrostatic calculation, alleviating the efforts of the user to customize input protein structure. Direct edit of PDB file allows for a range of options aimed at the advanced user: adding missing terminal charges, fixed (non-titratable) integer or partial charges and titratable groups with user-defined pKa intrinsic. We consider such rich electrostatic setup a significant practical boost for our Quantum.Ligand.Dock server. Reasonably acquainted users could address a number of subtle issues, e.g. effects of ligands, cofactors, inhibitors and ions. All other parameters used as input are predefined or automatically calculated. These steps complete the initial setup. Calculation proceeds through aforementioned stages—evaluation of solvent access—ibilities and the linear response Born term ΔpKBorn,i, perturbation of pKa by partial charges ΔpKpar,i and finally the iterative procedure for self-consistent evaluation of titratable ΔpKtit,i.
In accord with our previous implementation, we sample rotation–translation space with the following default values. First, we sample a 6D space—1 translational and 5 rotational degrees of freedom. The traditional sampling is also 6D but consists of 3 rotational and 3 translational degrees of freedom. The sampling step for translation is 0.9 Å; rotational steps = 6 angular degrees. Default polynomial expansion order is 20. The total number of mutual orientations of docking partners in sampling is in the order of billions—109.
Just for reminder to estimate and compare electrostatic energies and potentials, the following energy conversion units were used: 1 kcal = 4.186 kJ = 1.68 RT units (at 298 K) = 0.735 pKa units. The units of φi(pH) in kcal/mol·e is equal to 43.176 mV or 30.24 mC/m2.
Quantum entanglement calculations are described in detail at the Benchmark and Supplement pages at the Quantum.Ligand.Dock Server.
BENCHMARKS AND EXTENSIVE TESTS
In resume, computational bottlenecks appear at FFT-based algorithms, protein electrostatics treatment with FMMs, proton equilibria summation algorithms and quantum entanglement contribution to the docking score. However, emergence of extremely powerful GPU parallel architectures gives the possibility to present the service to the wide protein community—from the accomplished protein docking experts and adept structural bioinformaticians to the novice systems biology practitioners. Approaches outlined above were applied to a benchmark collection of protein–ligand interactions (see corresponding table uploaded at Quantum.Ligand.Dock server site Supplement page). Extensive tests for reliability and accuracy on standard benchmarks were performed as well as comparative analysis in relation to other docking algorithms. However, direct comparison with other docking algorithms should be careful. It is not trivial to compare objectively different docking methods. Besides search problems of equal complexity, the algorithms must be compared under the conditions of equal running times to produce docking solutions. Thus, it is not straightforward to draw conclusions of general applicability. One should take into account the difference in scoring functions, the strategy for sampling search space, the step parameter for the search, etc. Our approach is comparable with Hex at the level of representation and sampling the search space (spherical polar Fourier representation). The core of the acceleration is the sampling of the mutual orientation space and the Supplement section contains a table with Quantum.Ligand.Dock (millions of orientations per second) speeds of sampling compared with one of our previous GPU.proton.DOCK realizations and at same time against Hex performance for different polynomial expansion orders. However, inclusion of sophisticated treatment of electrostatics and protonation equilibria makes direct comparisons in speed inconsistent.
On the other hand, the reliability (accuracy) of prediction can be described in terms of root mean square deviation (RMSD) score. We have extensively tested the predictive performance of our method on several popular standard benchmark test sets. Comparison with the predictive ability of other methods is also presented. Here, we report (Table 1) the predictive performance of Quantum.Ligand.Dock against the modern ‘Astex diverse set’ (34), which consists of 85 protein–ligand complexes. The predictive performance within 2 Å RMSD from the experimentally defined structures is 78% of the test cases. Upon dropping the quantum contribution, the predictive performance also drops to 65%. Tests with this benchmark using AutoDock gives predictive performance 81.7% (35).
Table 1.
| Docking method | For RMSD < 2 Å (%) | For RMSD < 1 Å (%) |
|---|---|---|
| Quantum.Ligand.Dock | 78 | 59 |
| AutoDock (35) | 81.7 | NA |
| ChemPLPa (34,36) | 81 | 59 |
| GoldScorea (34,36) | 69 | 50 |
| ChemScorea (34,36) | 76 | 48 |
| ASPa (36) | 72 | 44 |
| LigDockCSA (35) | 84.7 | NA |
| MolGroVirtual Docker (37) | 74 | NA |
ahttp://www.ccdc.cam.ac.uk/case_studies/life_science/workcase_posepred.pdf (Cambridge crystallographic data centre).
Another popular test benchmark set is the ‘Ligand Protein DataBase’ (37). Our tests showed prediction within 2 Å RMSD for 72% (Quantum.Ligand.Dock) and 67% (without quantum corrections). The same benchmark is used to test SwissDock predictive accuracy—70% (21).
It seems that treatment of subtle aspects of protein–ligand interaction physics contributes to the reliability of docking methods. Although computationally demanding, the method still falls in the category ‘ultrafast’, and our intentions are to apply it in large-scale systems biology/structural bioinformatics projects. For the contemporary status of docking accuracy, Quantum.Ligand.Dock is adequate and consistent.
CONCLUSION AND FUTURE DEVELOPMENT
We have the confidence that Quantum.Ligand.Dock server will be of high interest and practical utility for a wide range of scientists—molecular biophysics and bioinformatics experts. Concurrently, it is exciting that the unique account of novel features will reveal as yet uncharted possibilities for prediction, analysis and explanation of protein–ligand interactions. However, our development effort continues towards novel functionality and methodological improvements.
Sophistication of quantum effects treatment (38)
Eliciting interplay of dipole/electric moments in protein–ligand recognition
Explicit modelling of water molecules effect on docking
Applications in virtual screening context
Striving for development of novel high-performance treatment of electrostatics
FUNDING
National Fund ‘Scientific Research’, Sofia, Bulgaria [D-002-126]. Funding for open access charge: Waived by Oxford University Press.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
We thank Prof. Barry Honig, Columbia University, New York and Prof. Emil Alexov for kind donation of a computer cluster which boosted our development effort and led to our achievements in scientific in high-performance parallel programming. Inspiritment and invigoration by my devoted grandma baba Nadka Pertcheva-Kantardjieva is gratefully appreciated. I strongly believe that Creativity and its stringent analytically weaved counterpoint voice imprinted in this publication is impacted by the music of the immeasurable and inexhaustible The Art of Fugue by JS Bach, being not just the music atmosphere throughout my work but a profound relation in my mentality.
REFERENCES
- 1.Halperin I, Ma B, Wolfson H, Nussinov R. Principles of docking: an overview of search algorithms and a guide to scoring functions. Proteins. 2002;47:409–443. doi: 10.1002/prot.10115. [DOI] [PubMed] [Google Scholar]
- 2.Smith GR, Sternberg MJE. Prediction of protein-protein interactions by docking methods. Curr. Opin. Struct. Biol. 2002;12:28–35. doi: 10.1016/s0959-440x(02)00285-3. [DOI] [PubMed] [Google Scholar]
- 3.Ritchie D. Recent progress and future directions in protein-protein docking. Curr. Protein. Pept. Sci. 2008;9:1–15. doi: 10.2174/138920308783565741. [DOI] [PubMed] [Google Scholar]
- 4.Katchalski-Katzir E, Shariv I, Eisenstein M, Friesem AA, Aflalo C, Vakser IA. Molecular surface recognition: determination of geometric fit between proteins and their ligands by correlation techniques. Proc. Natl Acad. Sci. USA. 1992;89:2195–2199. doi: 10.1073/pnas.89.6.2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stone J, Hardy D, Ufimtsev I, Schulten K. GPU-accelerated molecular modeling coming of age. J. Mol. Graph. Model. 2010;29:116–125. doi: 10.1016/j.jmgm.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Warshel A. Electrostatic basis of structure-function correlation in proteins. Acc. Chem. Res. 1981;14:284–290. [Google Scholar]
- 7.Honig B, Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 8.Antosiewicz J, McCammon J, Gilson M. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 1994;238:415–436. doi: 10.1006/jmbi.1994.1301. [DOI] [PubMed] [Google Scholar]
- 9.Bashford D, Karplus M. pKas of ionization groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 1990;29:10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 10.Warshel A, Papazyan A. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Curr. Opin. Struct. Biol. 1998;8:211–217. doi: 10.1016/s0959-440x(98)80041-9. [DOI] [PubMed] [Google Scholar]
- 11.Chen R, Li L, Weng Z. ZDOCK: an initial-stage protein-docking algorithm. Proteins. 2003;52:80–87. doi: 10.1002/prot.10389. [DOI] [PubMed] [Google Scholar]
- 12.Macindoe G, Mavridis L, Venkatraman V, Devignes M, Ritchie D. HexServer: an FFT-based protein docking server powered by graphics processors. Nucleic Acids Res. 2010;38:W445–W449. doi: 10.1093/nar/gkq311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kozakov D, Brenke R, Comeau S, Vajda S. PIPER: an FFT-based protein docking program with pairwise potentials. Proteins. 2006;65:392–406. doi: 10.1002/prot.21117. [DOI] [PubMed] [Google Scholar]
- 14.Tovchigrechko A, Vakser IA. GRAMM-X public web server for protein-protein docking. Nucleic Acids Res. 2006;34:W310–W314. doi: 10.1093/nar/gkl206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mandell JG, Roberts VA, Pique ME, Kotlovyi V, Mitchell JC, Nelson E, Tsigelny I, Ten Eyck LF. Protein docking using continuum electrostatics and geometric fit. Protein Eng. 2001;14:105–113. doi: 10.1093/protein/14.2.105. [DOI] [PubMed] [Google Scholar]
- 16.Andrusier N, Mashiach E, Nussinov R, Wolfson HJ. Principles of flexible protein-protein docking. Proteins. 2008;73:271–289. doi: 10.1002/prot.22170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lyskov S, Gray JJ. The RosettaDock server for local protein-protein docking. Nucleic Acids Res. 2008;36:W233–W238. doi: 10.1093/nar/gkn216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dominguez C, Boelens R, Bonvin AMJJ. HADDOCK: a protein-protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc. 2003;125:1731–1737. doi: 10.1021/ja026939x. [DOI] [PubMed] [Google Scholar]
- 19.Ogmen U, Keskin O, Aytunas S, Nussinov R, Gursoy A. PRISM: protein interactions by structural matching. Nucleic Acids Res. 2005;134:W331–W336. doi: 10.1093/nar/gki585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Morris GM, Goodsell DS, Halliday RS, Huey R, Hart WE, Belew RK, Olson AJ. Automated docking using a Lamarckian Genetic Algorithm and an empirical binding free energy function. J. Comput. Chem. 1998;19:1639–1669. [Google Scholar]
- 21.Grosdidier A, Zoete V, Michielin O. SwissDock, a protein-small molecule docking web service based on EADock DSS. Nucleic Acids Res. 2011;39:W270–W277. doi: 10.1093/nar/gkr366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ritchie D, Kozakov D, Vajda S. Accelerating and focusing protein-protein docking correlations using multi-dimensional rotational FFT generating functions. Bioinformatics. 2008;24:1865–1873. doi: 10.1093/bioinformatics/btn334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kantardjiev AA. GPU.proton.DOCK: genuine protein ultrafast proton equilibria consistent DOCKing. Nucleic Acids Res. 2011;139:W223–W228. doi: 10.1093/nar/gkr412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kantardjiev AA, Atanasov BP. PHEPS: web-based pH-dependent protein electrostatics server. Nucleic Acids Res. 2006;134:W43–W47. doi: 10.1093/nar/gkl165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kantardjiev AA, Atanasov BP. PHEMTO: protein pH-dependent electric moment tools. Nucleic Acids Res. 2009;137:W422–W427. doi: 10.1093/nar/gkp336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Atanasov B, Mustafi D, Makinen MW. Protonation of the β-lactam nitrogen is the trigger event in the catalytic action of class A β-lactamases. Proc. Natl Acad. Sci. USA. 2000;97:3160–3165. doi: 10.1073/pnas.060027897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Karshikov AD, Engh R, Bode W, Atanasov BP. Electrostatic interactions in proteins: calculations of the electrostatic term of free energy and the electrostatic potential field. Eur. Biophys. J. 1989;17:287–297. [Google Scholar]
- 28.Spassov VZ, Karshikov AD, Atanasov BP. Electrostatic interactions in proteins: a theoretical analysis of lysozyme ionization. Biochim. Biophys. Acta. 1989;999:1–6. [Google Scholar]
- 29.Roumenina LT, Kantardjiev AA, Atanasov BP, Waters P, Gadjeva M, Reid KBM, Mantovani A, Kishore U, Kojouharova MS. Role of Ca2+ in the electrostatic stability and the functional activity of the globular domain of the human C1q. Biochemistry. 2005;44:14097–14109. doi: 10.1021/bi051186n. [DOI] [PubMed] [Google Scholar]
- 30.Roumenina LT, Bureeva S, Kantardjiev AA, Karlinsky D, Andia-Pravdivy JE, Sim R, Kaplun A, Popov M, Kishore U, Atanasov BP. Complement C1q-targetproteins recognition is inhibited by electric moment effectors. J. Mol. Recognit. 2007;20:405–415. doi: 10.1002/jmr.853. [DOI] [PubMed] [Google Scholar]
- 31.Biedenharn LC, Louck JC. Angular Momentum in Quantum Physics. Reading, MA: Addison-Wesley; 1981. [Google Scholar]
- 32.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera—a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 33.William Humphrey W, Dalke A, Schulten K. VMD—visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 34.Hartshorn MJ, Marcel L, Verdonk ML, Chessari G, Brewerton SC, Mooij W, Mortenson PN, Murray CF. Diverse, high-quality test set for the validation of protein-ligand docking performance. J. Med. Chem. 2007;50:726–741. doi: 10.1021/jm061277y. [DOI] [PubMed] [Google Scholar]
- 35.Shin WH, Heo L, Lee J, Ko J, Seok C, Lee J. LigDockCSA: protein-ligand docking using conformational space annealing. J. Comput. Chem. 2011;32:3226–3232. doi: 10.1002/jcc.21905. [DOI] [PubMed] [Google Scholar]
- 36.Verdonk ML, Cole JC, Hartshorn MJ, Murray CW, Taylor RD. Improved protein-ligand docking using GOLD. Proteins. 2003;52:609–623. doi: 10.1002/prot.10465. [DOI] [PubMed] [Google Scholar]
- 37.Roche O, Kiyama R, Brooks CL., III Ligand-protein database: linking protein-ligand complex structures to binding data. J. Med. Chem. 2001;44:3592–3598. doi: 10.1021/jm000467k. [DOI] [PubMed] [Google Scholar]
- 38.Kantardjiev AA, Atanasov BP. Australia: iConcept Press Ltd; 2011. Sequence and Genome Analysis: Methods and Applications (Chapter 10) [Google Scholar]