KOSMOS: a universal morph server for nucleic acids, proteins and their complexes

Abstract

KOSMOS is the first online morph server to be able to address the structural dynamics of DNA/RNA, proteins and even their complexes, such as ribosomes. The key functions of KOSMOS are the harmonic and anharmonic analyses of macromolecules. In the harmonic analysis, normal mode analysis (NMA) based on an elastic network model (ENM) is performed, yielding vibrational modes and B-factor calculations, which provide insight into the potential biological functions of macromolecules based on their structural features. Anharmonic analysis involving elastic network interpolation (ENI) is used to generate plausible transition pathways between two given conformations by optimizing a topology-oriented cost function that guarantees a smooth transition without steric clashes. The quality of the computed pathways is evaluated based on their various facets, including topology, energy cost and compatibility with the NMA results. There are also two unique features of KOSMOS that distinguish it from other morph servers: (i) the versatility in the coarse-graining methods and (ii) the various connection rules in the ENM. The models enable us to analyze macromolecular dynamics with the maximum degrees of freedom by combining a variety of ENMs from full-atom to coarse-grained, backbone and hybrid models with one connection rule, such as distance-cutoff, number-cutoff or chemical-cutoff. KOSMOS is available at http://bioengineering.skku.ac.kr/kosmos.

INTRODUCTION

A great deal of effort has been devoted to studying macromolecular dynamics to elucidate the relationship between structure and function. An earlier attempt with all-atom normal mode analysis (NMA) using empirical potential showed that only a few of the lowest normal modes of a protein are needed to adequately capture the protein’s collective motions, which are believed to be strongly correlated with that protein’s biological functions (1,2). Although this all-atom-based approach is a rigorous method for analyzing molecular vibrations, its computational cost is high for large proteins. Alternatively, the coarse-grained elastic network model (ENM), which employs a single parameter force field, was introduced as a well-balanced approach for understanding the intrinsic vibration features of proteins, with consideration given to the modeling accuracy and computation time (3–7). In particular, this simplified NMA has successfully revealed that large-amplitude domain motions play critical roles in ligand binding, signal transduction and allosteric responses in proteins (8–11).

There are already several web services that provide an easy-to-use interface for the calculation of the normal modes of proteins. ANM (12), oGNM (13) and WEBnm@ (14) similarly adopt point-mass-based models, such as a Cα coarse-grained model and an all-atom model, whereas NOMAD-Ref (15) and ElNémo (16) utilize the building block approach to reduce the computational burden by grouping several consecutive amino acids along the backbone of proteins (17). Obviously, these coarse-graining methods are computationally efficient and easy to implement, but such an automatic approach without any consideration of the intrinsic rigidity (and/or flexibility) of proteins is not suitable for capturing large-scale domain motions effectively (18,19). To overcome this drawback, rigid-cluster-based ENMs have been proposed. Domain-NMA assigns a much higher spring constant to the intra-domain contacts (18). Cluster-NMA (19) and a hybrid elastic network model (HENM) (20) fully utilize mathematical details on the translation and rotation motions of rigid domains.

In addition to the coarse-graining levels, the network connectivity is also one of the most important key factors in determining the quality of ENM-based analysis. Currently, the distance-cutoff method is widely used for the ENM because of its simplicity. However, a small cutoff value reduced the stability of the ENM, whereas a large cutoff value makes the system too stiff so that we cannot observe functional hinge motions, especially from closed to open conformations, in some cases. Alternatively, the chemical-cutoff method has been proposed (21). In this method, different spring constants are assigned to each pair of representative atoms, depending on the types of chemical interactions involved.

KOSMOS (Korea Skku Morph Server) was recently launched, emphasizing its versatility regarding target systems, coarse-graining levels and connection rules. First, KOSMOS accepts any macromolecular structure, including DNA/RNA, proteins and even their complexes. Second, it provides a variety of choices for ENMs, ranging from all-atom to a hybrid model. Information of the rigidity of the macromolecules can be incorporated through the HENM technique. Third, a connection rule can be selected for the ENM, from simple distance-cutoff rule to the more sophisticated chemical-cutoff rule. In addition, KOSMOS can also generate transition pathways between two known conformations using elastic network interpolation (ENI) (22).

WEB SERVER ACCESS

Figure 1 demonstrates the entire procedure of KOSMOS. The server is implemented using HTML, Java Script and PHP for the input and output web environments. KOSMOS accepts only standard PDB files. Users can either upload their own file in PDB format or type a PDB ID. When a PDB ID is entered, to prevent duplication, KOSMOS automatically searches the database and then lists all previous results. There are two different query options in KOSMOS, basic and advanced. A basic query requires only a PDB ID as an input. The calculations will be performed automatically using the default parameters and options. An advanced query consists of several consecutive steps to determine more detailed analysis conditions. The user is asked to choose the coarse-graining level, the connection rule, the cutoff value, etc. When a query is completed, a new window is automatically opened, in which the user can check the status of the computation and access to the results page directly.

Figure 1.

Flow of the web interface for KOSMOS. The user can access the query and database page through the main menu on the left. (A) At the first step of the query, the user should provide an input structure by either entering a PDB ID or uploading a PDB file. KOSMOS provides an advanced query, as well as a simple query. (B) At the last step of the query, the status of the computation and the link to the results page are displayed. (C) The user can access the results page through the database and can search the previous results in many different categories. (D) The result page displays the information for the macromolecules, the computation conditions, a downloadable data set and a 3D interactive animation. Both vector and cartoon representations are available.

KOSMOS runs in the MATLAB environment. When the inquiry is accepted, MATLAB starts to run the preprogrammed codes and passes the results to a MySQL database. The user can not only sort the database by individual parameters, but also search the entire database based on various categories provided. The result page provides a 3D visualization tool using a JMOL plug-in so that one can interactively animate the NMA or ENI results. Analysis conditions and downloadable results files are also available on this page.

MATERIALS AND METHODS

Linking method and potential function

As a default, KOSMOS performs the macromolecular dynamics analysis based on coarse-grained ENMs. Only the atomic coordinates of Cαs and phosphates are sampled from an input file to represent amino acids and nucleotides, respectively. For ENI computations, KOSMOS automatically aligns the two given PDB files by only taking common residues available in both structures. All of the representative atoms are then networked with virtual linear springs. Depending on the user’s choice of coarse-graining levels and connection rules, the connectivity and spring constants should be determined separately. For example, if the basic query is selected with the distance-cutoff method as a default, a uniform spring constant is assigned to each pair of representative atoms within the cutoff distance of 12 or 24 Å for proteins and DNA/RNA, respectively. These default values are carefully determined by considering the system stability of the ENMs (21). In contrast to the distance-cutoff method, the chemical-cutoff method assigns different spring constants that depend on the type of chemical interaction (e.g. covalent bonds, disulfide bonds, hydrogen bonds, salt bridges and Van der Waals interactions). Once the construction of the ENM is complete, KOSMOS develops a simple Hookean potential energy function:

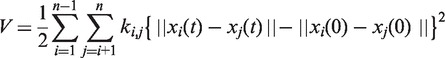(1)

where k_i,j is a spring constant between the ith and jth atom, x_i(0) is the initial position of the ith atom and 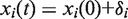. Here, we assume that δ_i is small fluctuation of x_i(0). Because the standard NMA procedure has been widely reported on in the literature, we will not describe it in detail here. A full description can be obtained from Ref. (22).

Pathway generation (ENI)

ENI is a topology-oriented optimization method to generate transition pathways between two known conformations of the same macromolecule (23,24). ENI starts from standardized coordinates by adjusting the center of mass and principal axis between two conformations because these conformations may have different initial positions and orientations. One can iteratively generate intermediate conformations by solving the following potential-like cost function, in which the initial conformation is systematically deformed toward the target conformation to reduce the root mean square deviation (RMSD) between these conformations:

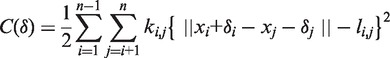(2)

where l_i,j is the desired length at a certain intermediate state determined by distance interpolation. The quality of the generated pathways is quantitatively evaluated by assessing the overlap with the NMA results and the changes in the minimum distance and cost during the transition.

Hybrid elastic network model

Unlike the point mass-based models, hybrid models are necessary to decompose the structure into rigid clusters and point masses. One can use various web servers, such as FlexWeb, KINAR-Web, RigidFinder and PiSQRD, to determine rigid clusters in proteins (25–28). Once the rigid cluster information is loaded into KOSMOS, the position vector of residue i within rigid cluster b at time t is defined as:

(3)

where 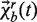is a translation vector of rigid cluster b and 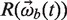is a rotation matrix formed by:

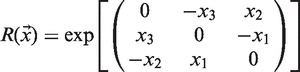(4)

Using Equation (2), one can derive the total potential energy for HENM (20), consisting of the following three partial terms:

(5)

where the superscripts of p, r and h represent point–point, rigid–rigid and point–rigid interactions, respectively. Each potential energy term is as follows:

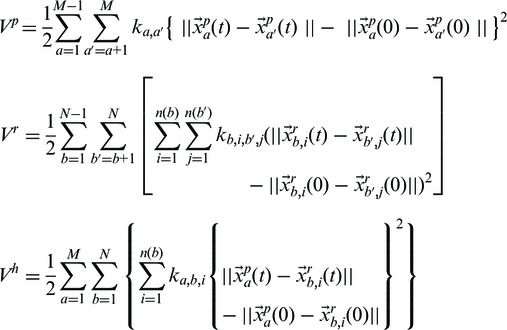(6)

where N is the number of point masses, which do not belong to any rigid cluster, and M is the number of clusters.

RESULTS AND DISCUSSION

Case study I: lactoferrin

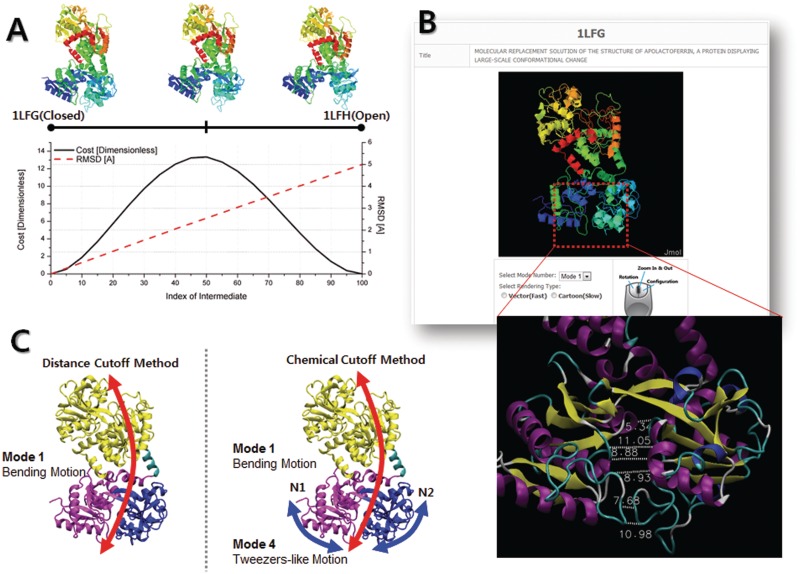
Lactoferrin is a transferrin protein that is responsible for iron ion transport. Ligand binding induces a conformational change in lactoferrin that involves a rigid-body rotation of the N2 domain relative to the N1 domain (29). To observe such a ‘tweezers-like’ motion, we performed the ENI from the holo form (PDB ID: 1LFG) to the Apo form (PDB ID: 1LFH). We evaluated intermediate conformations with cost and RMSD values to verify the plausibility of the computed pathway, which primarily consists of vertical bending and tweezers-like motion (Figure 2A). Both the distance-cutoff NMA and the chemical-cutoff NMA of the closed forms of lactoferrin were tested. As shown in Figure 2B, the conventional distance-cutoff method causes over-constraints between two close lobes, whereas the chemical-cutoff method properly rules out such inter-domain interactions. As a result, Figure 2C demonstrates that the chemical-cutoff NMA captures both the bending motion and the tweezers-like motion at Mode 1 and Mode 4, respectively. The distance-cutoff NMA shows only a bending motion in the low-frequency modes. This result shows the superior performance of the chemical-cutoff method over the simpler distance-cutoff method in terms of the reality of the ENM, especially for the closed forms of macromolecules.

Figure 2.

NMA and ENI results for lactoferrin. (A) The ENI pathway from the closed form to the open form is illustrated with the smooth changes in the RMSD and cost, which is considered to be semi-evidence of the energy barrier between the two states. (B) The result page of the NMA. The gap between two lobes in this closed form is <12 Å in most places, which causes over-constraints in the conventional distance-cutoff method. However, most of the inter-domain interactions (displayed as dotted lines here) are excluded in the chemical-cutoff method. (C) In the low-frequency modes, the distance-cutoff method reveals only bending motions because the over-constrained N1 and N2 domains move together like a single rigid body, whereas the chemical-cutoff method captures both the bending and tweezers-like motions very well.

Case study II: ribosome

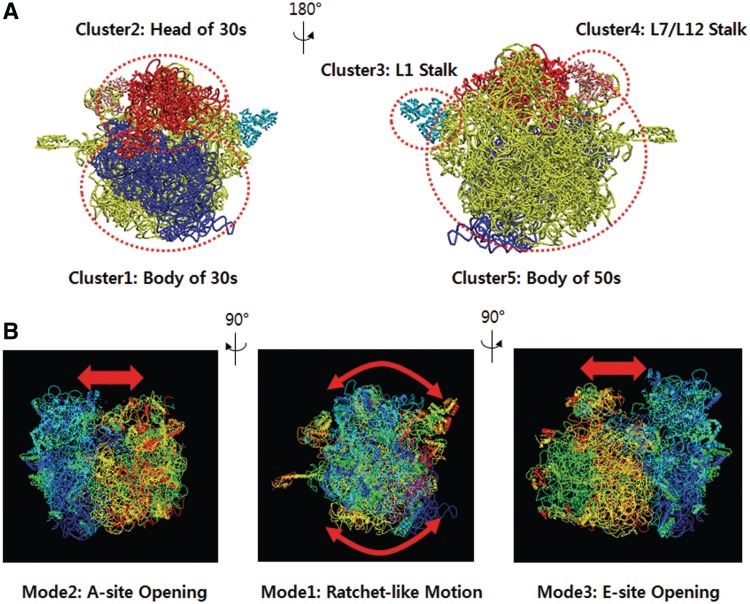
The ribosome is responsible for the protein synthesis process, called translation, which decodes the genetic information of mRNA to synthesize proteins. The 70S ribosome consists of a small 30S subunit containing the 16S rRNA and 21 proteins and a large 50S subunit composed of the 23S rRNA, the 5S rRNA and 34 proteins. Frank and Agrawal (30) have experimentally observed that elongation factor G induces a ratchet-like rotation in the 30S subunit relative to the 50S subunit during ribosomal translocation. There have been several computational efforts to determine the large conformational transition of the ribosome in atomic detail. Specifically, Wang and Tama have individually reproduced the ratchet-like motion by NMA based on a coarse-grained representation of the ribosome (31,32). The 70S ribosome structure was built by fitting the 30S and 50S subunits (PDB ID: 1GIX and 1GIY) and was tested on various NMA web servers. Most servers failed to analyze this protein–RNA complex. Although WEBnm@ and ElNémo returned NMA results, WEBnm@ missed all of the RNA information during computation and ElNémo showed a limitation in capturing the collective motion evidenced by small collectivity values <0.02. Figure 3A illustrates the HENM of the ribosome constructed by a mixture of five rigid clusters and coarse-grained point masses representing tRNA, rRNA and proteins near the flexible interface between the two subunits. As shown in Figure 3B, the predicted motions on KOSMOS demonstrated good agreement with the current hypothesis (30). In addition, unlike the previous NMA results, KOSMOS returned the main ratchet-like motion as the lowest mode of the ribosome, which was found at the third lowest mode elsewhere (31,32). This result implies that the proposed HENM can capture the intrinsic dynamics of the ribosome more precisely than other modeling tools.

Figure 3.

HENM-based NMA results for the ribosome (PDB IDs: 1GIX and 1GIY). (A) The assembly of the 30S and 50S subunits is represented by the mixture of five rigid clusters and point masses that lie near the interface between the two subunits. (B) The first three lowest modes apparently illustrate the intrinsic dynamics of the ribosome, such as ratchet-like movement and A/E site opening.

CONCLUSION

A fully automated ENM-based morph server, called KOSMOS, was recently launched to provide both harmonic and anharmonic analyses represented by NMA and ENI, respectively. Although several webs services already exist that deal with either NMA or transition pathway generation in proteins, KOSMOS is the first automated web server handling analyses for both DNA/RNA and proteins, with an extensive choice of various coarse-graining types and connection rules. In particular, the HENM is a computationally efficient method for studying supramolecular dynamics. The chemical-cutoff method provides more realistic NMA results for macromolecules in closed forms. Regarding visualization, KOSMOS adopts a user-oriented JMol plug-in, which gives us another degree of freedom in 3D interactive visualization. Consequently, the versatility and reliability of KOSMOS will have a significant impact on the area of computational structural biology and bioinformatics by making open access to analysis results, which is optional in KOSMOS, and source codes available to the public.

FUNDING

National Research Foundation of Korea funded by the Ministry of Education, Science and Technology [R33-10079, 2011-0014584]; Faculty Research Funds from Sungkyunkwan University. Funding for open access charge: National Research Foundation of Korea funded by the Ministry of Education, Science and Technology [R33-10079].

Conflict of interest statement. None declared.