Lunisolar tidal force and the growth of plant roots, and some other of its effects on plant movements

Abstract

Background

Correlative evidence has often suggested that the lunisolar tidal force, to which the Sun contributes 30 % and the Moon 60 % of the combined gravitational acceleration, regulates a number of features of plant growth upon Earth. The time scales of the effects studied have ranged from the lunar day, with a period of approx. 24·8 h, to longer, monthly or seasonal variations.

Scope

We review evidence for a lunar involvement with plant growth. In particular, we describe experimental observations which indicate a putative lunar-based relationship with the rate of elongation of roots of Arabidopsis thaliana maintained in constant light. The evidence suggests that there may be continuous modulation of root elongation growth by the lunisolar tidal force. In order to provide further supportive evidence for a more general hypothesis of a lunisolar regulation of growth, we highlight similarly suggestive evidence from the time courses of (a) bean leaf movements obtained from kymographic observations; (b) dilatation cycles of tree stems obtained from dendrograms; and (c) the diurnal changes of wood–water relationships in a living tree obtained by reflectometry.

Conclusions

At present, the evidence for a lunar or a lunisolar influence on root growth or, indeed, on any other plant system, is correlative, and therefore circumstantial. Although it is not possible to alter the lunisolar gravitational force experienced by living organisms on Earth, it is possible to predict how this putative lunisolar influence will vary at times in the near future. This may offer ways of testing predictions about possible Moon–plant relationships. As for a hypothesis about how the three-body system of Earth–Sun–Moon could interact with biological systems to produce a specific growth response, this remains a challenge for the future. Plant growth responses are mainly brought about by differential movement of water across protoplasmic membranes in conjunction with water movement in the super-symplasm. It may be in this realm of water movements, or even in the physical forms which water adopts within cells, that the lunisolar tidal force has an impact upon living growth systems.

Nature – the source of all knowledge – rarely replies to questions unless they are put to her in the form of experiments to which she can say ‘yes’ or ‘no’. She is not loquacious; she merely nods in the affirmative or in the negative …. She will silently show us a picture. But she never explains. You have to work things out yourself first'

Hans Selye (1976)

INTRODUCTION

The question of which factors govern rhythmic aspects of plant growth (Sweeney, 1969), where the rhythmic periods range from minutes and hours (as in nutations) to days and months, is, in most cases, still something of a mystery (Gardner et al., 2006). Circadian rhythm research has become immensely sophisticated, especially since the identification of clock genes (McClung, 2006; Hanano et al., 2008). Nevertheless, aside from the possibility that such clocks and their metabolic loops work differently in shoots and roots (James et al., 2008), it is possible that not all factors which affect these rhythms, especially as they apply to organ growth, have been considered. In any case, it is possible for two distinct rhythms affecting different life processes to be contained within one and the same cell (Roenneberg and Morse, 1993) and for each to be regulated by a different timekeeper.

Many experiments designed to unravel the clock which regulates rhythmic growth use methods of entrainment, such as the employment of light conditions that depart from the usual diurnal regime of light/dark (LD) of 16 h:8 h, but in which apparently constant environmental conditions are otherwise maintained. Entrainments can undoubtedly set up new growth rhythms (Salomé and McClung, 2005); but the question is whether any new rhythm can persist when the entraining influence is subsequently withdrawn and, if so, what period is adopted (Nozue et al., 2007). Furthermore, the very sophistication of present-day circadian rhythm research has caused its departure from relevance to plant growth regulation in real time. Features which are studied nowadays often relate to temporal patterns of gene promoter activity and gene expression in the context of subjective time, in accordance with schedules of light/dark regimes in growth cabinets [though an exception is found in the work of Connor and Gracey (2011) who used marine tidal levels as the time base]. Thus, what is being witnessed (see McClung and Gutiérrez, 2010) is the uncovering of a huge concatenation of metabolic cycles comprised of both anabolic and catabolic events, each being governed by their own intrinsic rate constants and involving molecules of determinate half-life, some of whose steps, not surprisingly, show sensitivity to the entraining light regime. Such cycles of events have led to detailed simulations of circadian rhythms (e.g. Forger and Peskin, 2003).

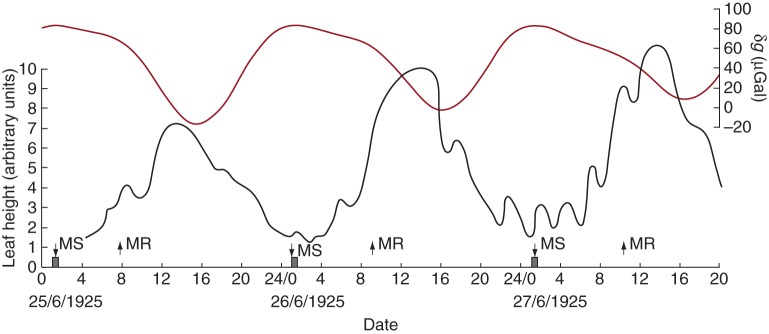
In experiments which make use of the constant environment of growth chambers, and even of sealed sub-terranean bunkers in the case of experiments with human subjects (Globig, 2007), organisms are isolated from disturbing factors prevalent in the outside environment. Nevertheless, it is possible that not every potentially disturbing factor [e.g. the lunisolar-regulated changes in atmospheric pressure (Zurbenko and Potrzeba, 2010), or the effects of solar weather and electromagnetic fluxes of natural origin (Markson, 1971; Khabarova and Dimitrova, 2009)] has been, or can be, entirely eliminated, a circumstance which, if it were achieved, could allow the rhythm under study to be freely expressed. In fact, the effect of extraneous influences on biological systems was an acute problem in the early days of rhythm research, as noted by Stoppel (1940) and others of her era; and they deflected attention from the internal regulators which were considered to be the bases of the various rhythms exhibited by plant organs. After studying the rhythms of flower petal movements, Stoppel (1926) turned her attention to the ‘sleep’ movements of bean leaves. She made a remarkable observation on the leaves of a seedling of Phaseolus multiflorus during the prolonged Icelandic mid-summer days of 1926, in which the day/night lengths were about LD 23 h:1 h (Fig. 1). The leaf movements of her plant, grown in natural light conditions, were apparently autonomous and did not relate to the night and day periods. Similarly, when Stoppel (1926) examined leaf movements in a blacked-out cellar in Iceland at much the same time of year, their period was also unrelated to the durations of night and day. Nevertheless, in this and in other work by Stoppel, and also in the work of Gerrit Brouwer in 1924 at Delft, The Netherlands, certain puzzling features of the leaf movements were encountered by these authors – so puzzling, in fact, that a mysterious ‘Factor X’ had to be invoked in order to explain certain unexpected aspects of the movements. In view of the unweakened continuous nature of the leaf movements within what were apparently constant growth conditions, Brouwer (1926, p. 85) wrote in relation to ‘Factor X’ that, ‘by its periodic changes [it] brings about sleep movements when ‘all’ (Brouwer's parenthetical emphasis) external conditions are apparently kept constant’. Thus, it is evident that some influence which regulated leaf movements could not be entirely eliminated from the experimental procedures. Nor could ‘Factor X’ be conclusively identified; it was itself rhythmic, and it interfered with the rhythms of leaf movements which had been entrained by night/dark environmental stimuli.

Fig. 1.

Leaf movements of Phaseolus multiflorus in relation to the lunisolar gravity profile. Leaf height (black line) was traced by a kymograph. An increasing height on the trace, and on the left-hand axis, indicates the descent of the leaf to its ‘sleep’ position, whereas a decreasing height indicates leaf ascent. The units on the vertical scale for leaf height are arbitrary. The plant was grown in natural daylight at Akureyri, Iceland, during June 1925. The light/dark period was approx. LD 1 h:23 h. Dark bars on the horizontal axis indicate the night period at this location, when the centre of the Sun's disc had descended below 0 ° of the horizon. However, the Sun did not descend below –6 °, the limit of civil twilight. Times of moonrise (MR) and moonset (MS) are indicated by vertical arrows on the horizontal time axis. Deviation of the lunisolar gravimetric tide (gravity profile), δg, is shown (dark red line) for the dates, times and place of the leaf movement observations. The leaf begins each ascent when δg is minimal, at a ‘turning point’; leaf descent commences during the maximal portion of the δg profile. Leaf movement data have been redrawn from fig. 1 in Stoppel (1926).

It is interesting to read Brouwer's conclusions about ‘Factor X’, and then to keep them in mind whilst reading the present article. ‘Not only is it as yet unknown what X is, but we know even less why it changes periodicity every day. Now, it seems to me not unlikely that it is the alternation of day and night which causes the periodicity … When X is one or another factor in the atmosphere, it is to be understood that its daily change must be felt also interiorly, in dark chambers, so that in continued light or darkness, with all conditions constant, the periodic changes of this unknown make sleep movements of the leaves continue.’ (p. 98) … ‘In summary, we can say, not as an explanation but as a working hypothesis, that there is an unknown factor X in the atmosphere which undergoes changes in a daily period … Different plants have specially arranged organs, the nodes, which are extremely sensitive to the mentioned changes of X, causing turgor differences in the nodes which bring a leaf or a leaf stalk or leaflet into a desired position … What is X? I can be brief, since there is no single datum to be found’ (p. 99) (Brouwer, 1926).

We contend that one ever-present, but diurnally varying, environmental factor has been overlooked in leaf rhythm research, and perhaps in rhythm research in general, and that this factor fits with the properties of the mentioned ‘Factor X’: it is the diurnal variation of the combined gravitational force which the Sun and Moon exert upon the Earth. These three bodies and their respective orbits are responsible for the lunisolar tidal (or gravitational) variation with reference to the Earth; and it is a persistent accompaniment to life on Earth. About 30 % of the tidal force is due to the mass of the Sun and about 60 % is due to that of the Moon. One overt consequence of the lunisolar tide is the rhythm of the marine and oceanic tides, a factor which has been invoked as an entraining influence on behaviour, especially of animal life dwelling in the sea or intertidal zones (Palmer, 1976, 1995). However, these biological effects may, a priori, be due to the lunisolar tidal variation itself; in fact, Brown et al. (1955) suggested this as an alternative to a behaviour pattern based on memorization of the timing of the marine tide. The coupling of the biological events with the high and low marine tides could be a coincidence since these tides, even though they are visible and measurable events, are nevertheless proxy markers of the lunisolar tidal force.

One major subject of the present communication concerns the possible influence of variations of the lunisolar tidal force on root elongation growth. A rhythmic pattern of elongation was noted by Yazdanbakhsh and Fisahn (2011) for roots of Arabidopsis thaliana growing in conditions of constant light and temperature. The results summarized here (a more detailed account is in preparation) describe the correlation between the naturally occurring oscillations of the root elongation rate and the changing profile of the lunisolar tidal force. These results also go some way towards validating the earlier findings of Kolisoko and Kolisko (1939) who, from carefully conducted experiments, established a connection between plant growth and lunar phases.

It has often been stated that ‘correlation does not necessarily imply causation’, and this creed has tended to handicap the investigation of many interesting possible links between intractable environmental parameters and biological phenomena (e.g. Hoffmann et al., 1991). Nevertheless, correlations, if supported by sufficient replicates and statistically significant P-values, do hint at relationships between variables which might be worthy of further consideration (for an excellent example of this, see Juckett and Rosenberg, 1993). A cautionary note concerning correlation is all the more acute when one of the variables, such as the tidal force, can never be modified or neutralized [by use of a klinostat, as attempted by Kleinhoonte (1932), for example]. However, the lunisolar tidal force is continually variable in a predictable way, and so experiments could be set up in advance of an anticipated variation of the lunisolar tide. Moreover, this approach might usefully be carried out simultaneously at a number of different locations. Aspects of the biological system could then be analysed for their conformity or otherwise to a hypothesis that posits the lunisolar profile as an entraining influence and thus a possible proximate causative agent. Such pro-active research is for the future, however.

Another approach to validating a lunisolar influence is to multiply the number of examples in which the changing lunisolar gravitational force correlates with significant inconstancies in the time course of a biological process. This is best done by considering a range of distinct biological systems. Then, by virtue of the sheer number of replicates, a certain critical mass of evidence accumulates; and this, in turn, could be persuasive enough to lead to the belief that there is an unknown influence (an unseen geophysical influence maybe, analogous to ‘Factor X’, mentioned earlier) which should be examined more closely for its effect on apparently susceptible biological processes.

In line with this last-mentioned approach, suggestive examples from a variety of biological systems will be briefly summarized before the putative effects of lunar gravity on roots are presented. However, before this is undertaken, it is necessary to describe how the lunisolar tidal force is evaluated.

LUNISOLAR GRAVITY PROFILE

Standing proxy for a direct measurement of the lunisolar tidal force is an estimate of the gravimetric tide provided by the program ‘Etide’. The program is based upon the 50 parameters which compute the vertical component of the lunisolar tidal force (the horizontal component of which is negligible; Longman, 1959) and is coupled with an elasticity factor of 1·16 for the body of the Earth. The input to Etide consists of the latitude, longitude and altitude of the location in question, together with the calendar dates for which local gravimetric tidal estimates are required. The output is a time course of δg (a gravity profile), the increase and decrease of the Earth's gravitational acceleration at any particular location brought about by the combined gravitational forces of the Sun and Moon. Numerically, it consists of gravimetric values in units of μGals (the gravitational acceleration at the Earth's surface, 1 g = 9·81 × 10⁸ μGals; 1 Gal = 1 cm s⁻²; 1 g = 9·81 m s⁻²) estimated at 15 min intervals over the required period. The δg time courses are prepared with reference to Coordinated Universal Time (UTC) and therefore need to be matched to the local times at which the biological data were recorded. When required, times of sunrise, sunset, moonrise and moonset, for any date at a given location were obtained from: http://aa.usno.navy.mil/data/docs/RS_OneYear.php.

With the aid of the Etide program, biological data can be analysed retrospectively for putative lunisolar relationships. The only requirement is that the numerical biological data be linked to a particular location and, crucially, to a particular calendar date. In the published literature of an earlier era, many highly interesting observations (of leaf movements, for example) from which relevant data can be extracted and digitized are, fortunately, in this carefully notated form. This attention to time and date seems to have been the usual practice in the 1920s and even earlier [see Semon (1905) for example]. However, such detail tends not to be mentioned in publications of later years. Because of this, it is impossible, with some exceptions, to re-analyse much relevant data from the late 1930s onwards. As a consequence, many influential ideas cannot now be re-assessed from any viewpoint other than the one set forth by their authors. [Fortunately, however, the data of Bünning (1931), which led to the concept of the endogenous physiological clock, can be re-assessed: he does place times and dates upon his published figures.]

BIOLOGICAL SYSTEMS AND THE PUTATIVE INFLUENCE OF LUNISOLAR GRAVITATIONAL FORCE

Four different plant biological systems are briefly surveyed upon which the lunisolar gravitional force is suspected to operate. They are: (1) nyctinastic leaf movements; (ii) tree stem diameter variation; (iii) fluctuations of tree wood water volume fraction; and (iv) Arabidopsis primary root elongation. These movements are mediated, respectively, by the following tissues: (a) leaf pulvini; (b) an elastic tissue within the cambium and secondary phloem which girdles the tree stem; (c) the tracheids of secondary xylem; and the mediating tissue in (d), the roots, probably involves the cells of the elongation zone. The relationship of lunisolar gravity to a fifth system, that of plant bioelectrical rhythms, has already been covered in detail (Barlow, 2012).

Leaf movements

The idea that the unforced leaf movements of bean plants might be regulated by the lunisolar tidal force was already introduced via Fig. 1. This proposal traces back to observations on leaf movements of P. multiflorus by Klein (2007) whose data were re-worked and his conclusion confirmed by one of us (Barlow et al., 2008). Further examples of the proposed relationship between these two variables, one biological, the other geophysical, can be established for bean plants of another species, Canavalia ensiformis, which were subject to two different sets of natural conditions (summer and winter months in Delft, The Netherlands) (Figs 2–4), both of which contrast with the conditions in Iceland (cf. Fig. 1) that were made use of by Stoppel (1926). The results presented in Fig. 2 can be re-plotted as a ‘tracking diagram’ (Fig. 3A). The important feature in the tracking diagrams of Fig. 3A, and also of Fig. 3B, is the highlighting of the presumed critical points in each of the two time courses – the biological and the geophysical. In the case of the biological time course (see Fig. 2), the critical points occur at those times when a given leaf commences either to descend from its daytime position, or to ascend from its night-time ‘sleep’ position. In the case of the geophysical δg time course, the critical points occur when the δg lunisolar tidal profile either shows a descent from a maximal value (a peak in the δg profile graph), or shows an ascent from a minimal δg value (a trough). In both leaf and δg profiles, the times when ascent or descent commence are called ‘turning points’.

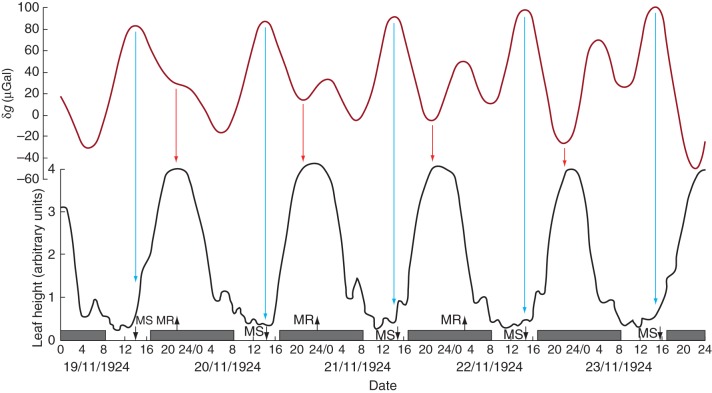
Fig. 2.

Leaf movements of Canavalia ensiformis in relation to the lunisolar gravity profile. The leaf trace was from a plant grown in natural light in a greenhouse at Delft, The Netherlands, during November 1924. The light/dark period was approx. LD 8 h:16 h. Details pertaining to leaf height (black line) and to the lunisolar gravity profile, δg (dark red line), are as described in the legend of Fig. 1. Civil twilight is of approx. 45 min duration before sunrise and after sunset. δg turning points coincident with leaf turning points are marked by arrows: red arrows for near coincidence with the commencement of leaf ascent, blue arrows for the commencement of leaf descent. Conventions used on the horizontal time axis are as described in the legend for Fig. 1. Leaf movement data have been redrawn from fig. 4 in Brouwer (1926).

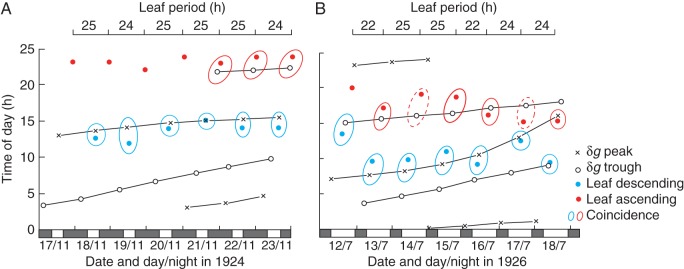
Fig. 3.

Diagrammatic representations of the alterations of leaf positions of Canavalia ensiformis in relation to the lunisolar gravity profile. (A) Summary of the data shown in Fig. 2. Turning points of leaf movement appear to track the turning points in the profile of δg; these turning points are indicated by arrows in Fig. 2. (B) Tracking diagram similar to that shown in (A). Here, it is for leaves of a plant grown in natural light in a greenhouse, also at Delft, but during July 1926, when the LD period was approx. 16 h:8 h, the converse of the LD period shown in Fig. 2 and in (A). Data for these leaf movements in (B) have been redrawn from fig. 1 in Kleinhoonte (1929). In both (A) and (B), the type of turning point is indicated in the code on the right-hand side. Red and blue ovals indicate the closeness of coincidence (within ≤2 h) of the leaf/δg turning points, whose times of occurrence are indicated on both the horizontal and vertical axes. Ovals with broken lines indicate that the range of coincidence of the two turning points is >2 h but <4 h. Filled and unfilled bars on the lower horizontal time axes indicate the night and day periods, respectively. The upper horizontal axes show the period of leaf movement, from one ‘sleep’ position to the next.

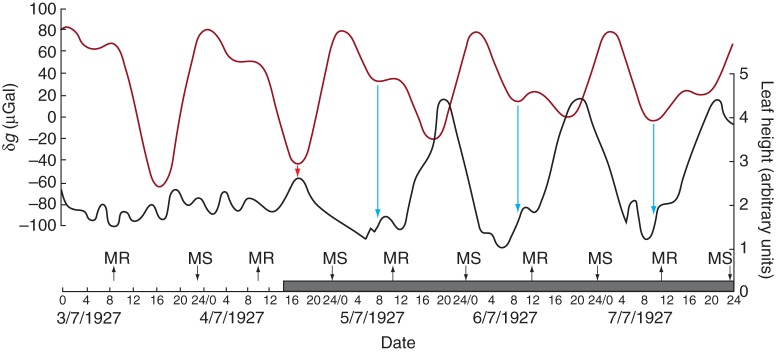
Fig. 4.

A plant of C. ensiformis was placed in continuous light on 21 June 1927 at Delft, The Netherlands. Nine days later, all major leaf movements had ceased, and for three further days (1–3 July) the leaf showed only minor movements. At 1500 h on 4 July, the plant was returned to continuous darkness. Nearly immediately, a small downward movement commenced at a time coincident with a turning point of δg (arrowed). Thereafter, other major leaf movements followed at approx. 24 h intervals, all of them coinciding with δg turning points (dark red line). Conventions used on the horizontal time axis are as described in the legend for Fig. 1. Data for leaf movements of plant P92 have been redrawn from fig. 37 of Kleinhoonte (1929).

In conditions of natural light, it is not possible to say unequivocally that a leaf movement turning point is not associated with a change from day to night, and is perhaps influenced in this respect by the light spectrum of the twilight period, even though the leaf movements may coincide with turning points in the gravity profile. However, in each of these sets of observation, leaf descent occurs during daytime rather than at any precise time with respect to sunset, this being especially evident during the natural day/night regime, LD approx. 16 h:8 h, of summer (see Fig. 3B). Moreover, the tracking diagrams of Fig. 3A and B indicate that the gravimetric tidal turning points are more closely associated with leaf descents than they are with leaf ascents.

Many ingenious and varied experiments were performed by both Brouwer (1926) and Kleinhoonte (1929, 1932) in an attempt to regulate the period of the leaf movement rhythms, and thereby to discover the mechanisms of the putative interaction between the plant and its light environment. Both workers used a growth chamber where they could experimentally alter the duration of the light and dark periods while keeping constant the temperature and humidity. Unusual light/dark regimes, such as LD 18 h:6 h, LD 16 h:16 h, LD 12 h:12 h, and so on, certainly altered the period of leaf movements. However, because the turning points in the profile of δg themselves occur about 6–8 h apart, the new leaf turning points entrained by the new light/dark periods often continued to coincide with the δg turning points because the new LD periods were themselves multiples of 6 or 8 h. However, some of the experimental lighting regimes are helpful in isolating leaf movement turning points that did not coincide with a light/dark switching time but did coincide with a lunisolar tidal turning point. For example, the 48 h light/dark regime, LD 24 h:24 h, resulted in two cycles of leaf movement within the 24 h light period (Kleinhoonte, 1929, fig. 25) rather than the usual single movement cycle found during a regime of LD 16 h:8 h. The extra daily cycle in the light period of the LD 24 h:24 h subjective ‘day’ is under the guidance of the gravimetric tide and is clearly not entirely regulated by the light/dark cycle.

A further observation made by Kleinhoonte (1929, fig. 37) supports this view of an apparently autonomous, but lunisolar regulated, leaf movement cycle. The normal movement cycle of leaves of four replicate Canavalia plants was abolished by 12 d of continuous light, during which time the leaves remained ‘frozen’ in the ‘up’ (daytime) position. Then, within 24 h of placing the experimental plants in continuous darkness, their leaves descended in synchrony and continued to display their usual 24 h movement rhythm until the experiment concluded 4–5 d later (Fig. 4). Although the transition from light to dark could have been sufficient to signal the first of the new movements, there was no other obvious cue from the growing conditions which would determine when the remaining new movements should commence – unless, of course, a memory of some former rhythm had been retained throughout the light period. In answer to this possibility, it should be noticed that the first and subsequent leaf movements during the dark recovery period coincide with the turning points in the δg profile. Hence, it is probable that it was the geophysical signal which initiated the leaf movement. Similarly, after four solar days in LD 8 h:8 h, during which time the period of leaf movements had shifted to about 16 h, the plants were then placed in continuous light for a further 4·5 d (Kleinhoonte, 1932). In the prolonged light period, the movements became progressively weaker but, nevertheless, the ascents and descents of the leaf, now with a period of approx. 23 h, always coincided with a gravimetric tidal turning point (Fig. 5).

Fig. 5.

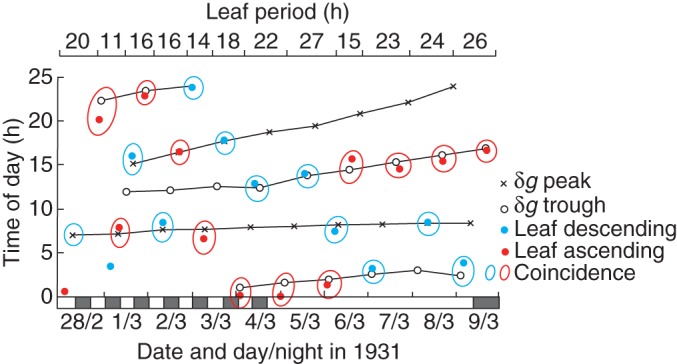
Tracking diagram of turning points of both leaf movements and δg, during observations on a plant grown for 5 d in LD 8 h: 8 h during February–March 1931 at Delft, The Netherlands. Although the leaf turning points are scattered throughout the 24 h day owing to the shortened period of the leaf movements (see upper horizontal axis), they nevertheless coincide with δg turning points. Then, at 1600 h on 4 March, the plant was placed in continuous light. Although the leaf movements then became weaker and more erratic, and their periods longer, the smaller but still discernible descents and ascents continued and coincided with δg turning points. During the last 2 d of the experiment, the plant was returned to continuous darkness. The strong leaf movement on 9 March also coincides with a δg turning point. The conventions used in the tracking diagram are explained in the legend to Fig. 3. Data for leaf movements have been redrawn from fig. 19 in Kleinhoonte (1932).

Leaf movement traces were prepared by Brouwer (1926) during the times when the first pair of leaves of his bean seedlings (C. ensiformis) commenced their movement cycles. In Brouwer's experiment the seedlings were raised in continuous light. The newly initiated leaf movements coincided with the turning points in the gravity profile. The results of Brouwer's experiments have been presented in fig. 15·12 of Barlow (2012). Kleinhoonte (1929) performed a conceptually similar experiment, but used a reversal of the protocol shown in Fig. 4. Here, the plants were placed in continuous light after having spent a long spell in darkness, during which leaf movements had ceased and the leaves remained fixed in the ‘sleep’ position. Leaf movements recovered during the subsequent light period, and their ascents and descents were coincident with δg turning points (data not shown, but the leaf movement profile is shown in fig. 8 of Kleinhoonte's publication). A similar persistence of Xanthium leaf movement rhythms in continuous light was recorded by Hoshizaki et al. (1969) following prior exposure of plants to prolonged darkness, or to a range of different light/dark treatments. Even though no δg profiles can be fitted to these particular rhythms (because the graphs are undated), the results are entirely consistent with a factor, such as the lunisolar tidal variation, being the guiding principle since, in this experiment, light/dark periods are clearly irrelevant to the rhythms of leaf movement. The temperature invariance of the period of bean (P. multiflorus) leaf movements, even when the plants are exposed to a wide range of growing temperatures (Bünning and Tazawa, 1957), is also consistent with a movement-regulating factor (such as the δg variation) lying outside the realm of the growth environment: the turning points of δg would not be affected by temperature and, hence, neither should the turning points of leaf movement (which define the period of leaf movement), even though the amplitude of movement may be affected. Similarly, although amplitude of movement may vary with leaf age, the period remains constant (Alford and Tibbitts, 1970). Furthermore, as shown by both Hoshizaki and Hamner (1964) and Alford and Tibbitts (1970), leaf movements are not necessarily synchronous among the different plants in a single experimental group of newly germinated seedlings. This phenomenon was also observed by Klein (2007), and explained by him as being due to the response by the leaves to different turning points of δg during their emergence. Successive δg turning points are 6–8 h apart, and this is exactly the time by which the leaves were out of phase in all three mentioned sets of observations.

Fig. 8.

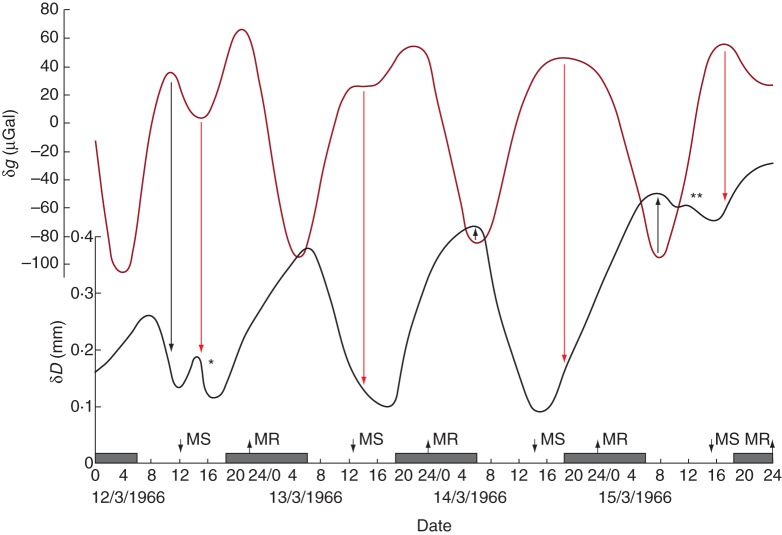
Rhythmic variation of stem diameter δD (black line) recorded from a tree of Pinus canariensis at Adelaide, Australia, during March 1966, together with the estimated contemporaneous variation of δg (dark red line). On two of the days shown, the δD values were affected by weather conditions (asterisks): * indicates the effect of a cold front with mist and 96 % humidity at noon on 12 March, ** indicates a period of continuous rain (10 mm in 12 h) on 15 March. Conventions used on the horizontal time axis are as described in the legend for Fig. 1. Data for δD have been estimated and redrawn from fig. 4 in Holmes and Shim (1968).

The conclusion drawn from these and other observations on bean leaves of various species is that it is the turning points in the δg gravity profile which are influential upon leaf movements. The direction of turn – whether from a peak or a trough – is not necessarily important. Both types of δg turning point mark a zero rate of change of the lunisolar tidal force. This feature may be a key element in many examples of the presently proposed inter-relationship of these two biological and geophysical systems.

Target cells in the leaf

The target cells for the proposed ‘signal’ from the lunisolar tidal acceleration, which initiates leaf movement in C. ensiformis, were discovered by Brouwer (1926) to reside in two ‘articulations’ (pulvini), at the distal and proximal ends of the leaf stalk (petiole). These zones contain groups of extensor and flexor cells on their abaxial and adaxial sides, respectively (for anatomical details, see Mayer et al., 1985). They are concerned with raising or lowering the leaf. According to the results of Brouwer's surgical experiments on these articulations, the descending and ascending movements of the leaf due to the proximal pulvinus are much smaller in magnitude than those movements due to the distal pulvinus. Moreover, the timing of movements in the two zones is different: actually, they work in opposite directions, one zone raising the leaf and the other promoting a descent. Despite this, the turning points recorded by Brouwer (1926) from each articulation coincide with turning points of δg (data not shown).

The bean leaf movement system has been likened to the ‘Rosetta Stone’ by Satter and Galston (1973) on account of the many phenomena that can be ‘read’ from the pulvinar tissues in relation to the movements. These include ionic redistributions, electrical signals, influence of light and phytochrome effects, and now, apparently, perception of lunisolar gravity and its transduction into a behavioural response.

The leaves, like roots, are foraging systems that search for sources of energy. In this respect, the behaviour of the leaves is similar to that of animals – for example, the iguanas (Amblyrhynchus cristatus) of the Galapagos Islands, or the crabs (Carcinus maenas) of the Isle of Man, which forage for food in intertidal zones during periods of activity regulated by lunar signals [relevant data of Wikelski and Hau (1995) and of Naylor (1958) have been re-interpreted, respectively, by J. Fisahn and P. W. Barlow, and P. W. Barlow (both unpubl. res.)].

Tree stem diameter variation

In 1998, Professor Ernst Zürcher drew attention to an apparent concordance between the daily variation in tree stem diameter, δD, and the variation in the gravimetric tide, δg (Zürcher et al., 1998) – as shown in Fig. 6.

Fig. 6.

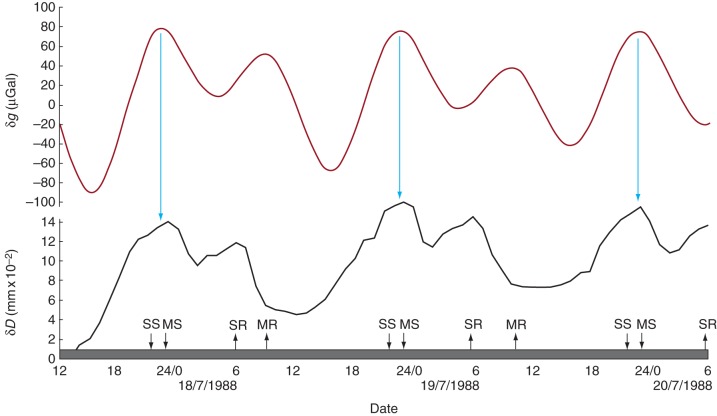
Rhythmic variation of stem diameter δD (black line) recorded from a young tree of Picea abies at Firenze, Italy, during July 1988. The tree was placed in a constant environment chamber, in continuous darkness (filled bar on the horizontal axis) during which time transpiration remained constant at 0·6 g H₂O h⁻¹. This rate was 5·5 times less than the transpiration rate in continuous light. The profile of δg (dark red line) on these same days runs approximately in parallel with the profile of δD. Coincident turning points along the δg and δD profiles are marked by blue arrows. During the 3 d prior to these observations, the tree had been placed in continuous light, so there was no entrainment before its placement in the dark. Moreover, the period of δD was similar during the earlier 3 d in light. The times of sunrise, sunset, moonrise and moonset (SR, SS, MR and MS) in the world outside the growth chamber are indicated on the horizontal time axis. Values of δD have been redrawn from fig. II-6 in Cantiani and Sorbetti Guerri (1989), who also provided data for transpiration and δD values during the preceding light period.

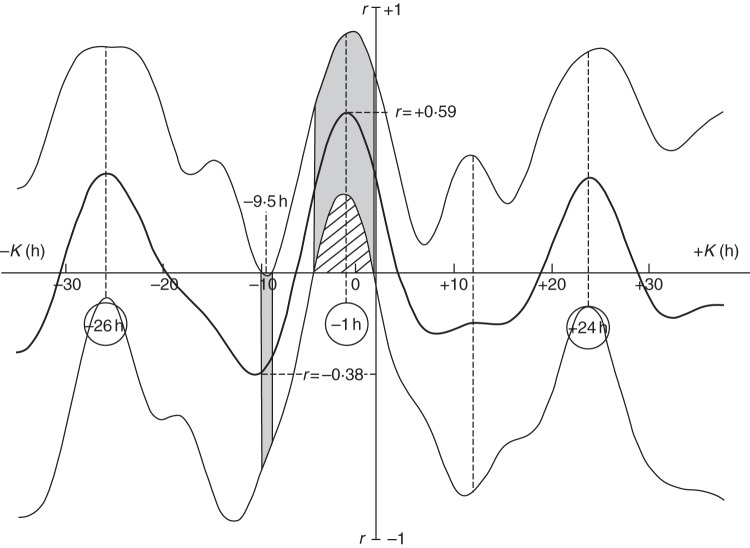
Two evergreen softwood trees of Norway spruce (Picea abies) were placed in darkness within a constant environment chamber. Transpiration of the trees was much diminished and showed no fluctuation which, had it occurred, might have accounted for the diurnal variation of δD. Apart from a concurrent variation in geomagnetic flux, as measured by the Polar Cap Index (Barlow et al., 2010a), the only other known variable which might have significantly affected δD was δg, the variation in the gravimetric tide. Unlike the already described leaf movements, which oscillate sharply between two defined limiting positions, ‘down’ and ‘up’, the variations of δD show a sinusoidal waveform. This being so, it is quite straightforward to perform cosinor cross-correlation analysis, by which means it can be established that, over the 3 d of observation, a significant relationship existed with a delay, K, of about 1 h between the two relevant time courses (Fig. 7).

Fig. 7.

Cross-correlation between the time courses of δD and δg shown in Fig. 6. The correlation coefficient was greatest (r = +0·59) and most significant (hatched and shaded portions of the graph beyond the error boundaries) when the time delay between the two curves was K = –1 h (i.e. the profile of δg was 1 h in anticipation of the profile of δD). The period of the oscillation is approx. 25 h. The value of the correlation coefficient is traced by the bold black line. Thinner lines mark the 95 % error boundary.

Additional analyses of original data concerning δD, summarized by Cantiani et al. (1994), confirmed a relationship between δD and δg. Besides P. abies, the tree species studied included two other evergreen gymnosperms, Abies alba and Psuedotsuga menziesii, and four deciduous hardwood species, Juglans regia, Liriodendron tulipifera, Mespilus germanica and Tilia cordata (Barlow et al., 2010a, b). While one should be cautious that quantifiable environmental variations, such as relative humidity, atmospheric pressure and temperature, might influence the range of the variation δD, or interfere with the accuracy of its measurement (see Innamorati et al., 1980), the correspondence between the turning points in the graphical representation of δD and δg for the mentioned species is remarkable (Barlow et al., 2010a, b). Likewise, additional data from a tree of Pinus canariensis growing in the Southern hemisphere (Holmes and Shim, 1968) indicate that, although the amplitude of the variation δD is influenced by meteorological conditions (Fig. 8), there is, nevertheless, a correspondence, and maybe a coherence (both functionally and statistically), between the periods of δD and δg.

It was noted that on days when the δg profile showed double peaks (as occurs at times of New Moon and Full Moon, when the amplitude of δg is greatest), portions of stems at different heights from the ground, or branches in different regions of the canopy, showed turning points of δD which coincided with one or other of the pair of δg turning points (Barlow et al., 2010a). Indeed, this is similar to the different activity patterns exhibited by two mice studied by Terrracini and Brown (1962, see their fig. 1): each mouse responded independently to one or other of the pair of peaks in the corresponding lunisolar δg profile (P. W. Barlow, unpubl. res.).

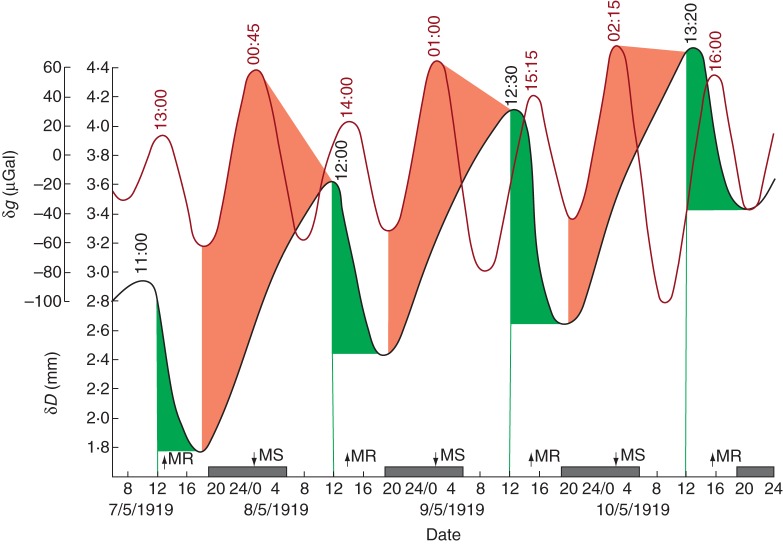
Shown in Fig. 6 is an example where δD and δg are ‘in phase’, i.e. there is a coincidence of peaks and troughs in their respective profiles; but this need not necessarily be so – see Fig. 8 where the two profiles are in ‘anti-phase’. As already mentioned, it may be that it is the δg turning point itself which is influential upon a biological variable, bringing about an alteration in that system's time course. However, even when there is coincidence between the δg and δD turning points, there could still be a substantial time delay (K ≈ 12 h) between the ascending limbs of the δg and of the δD profiles. This is shown in Fig. 9 where the data for δD were obtained from an Arizona ash tree (Fraxinus arizonica) growing under arid conditions by MacDougal (1921). It should also be noted that the peaks and troughs of δD advance by about 45 min on each successive day, similar to the rate of advancement of the peaks and troughs in the δg profile. The latter advancement is a characteristic of the slight prolongation of the lunar day relative to the solar day. Sometimes, δD begins to rise during daytime [e.g. on 6–8 May 1919, as shown in the original figure of MacDougal (1921)]; a few days later (e.g. on 10–11 May 1919), the rise of δD commences early in the night-time period (Fig. 9), even though the time of sunset has not changed perceptibly during this observation period. [Not all the dates and data from these observations of MacDougal (1921) are shown in Fig. 9 of the present paper; for these, fig. 13 of MacDougal's publication should be consulted.]

Fig. 9.

Relationship between stem diameter variation δD (black line) recorded from a tree of Fraxinus arizonica at Tucson, AZ, USA, during May 1919, together with the estimated contemporaneous variation of δg (dark red line). As in the example shown in Fig. 8, the turning points at the δD and δg minima (troughs) coincide, although the subsequent ascending limbs of each graph do not. This suggests a mechanism by which δg affects δD through the internal movement and evaporative loss of water, as described in the text. The pink shaded areas mark periods during the night, commencing at the turning point of δg, when water is moved into the stem at the point where δD was recorded under the putative influence of δg and, hence, δD increases, perhaps assisted by a pre-noon period of transpiration. The green shaded areas indicate periods during the daytime (starting at noon) when water loss by transpiration brings about a decrease in the value of δD. The peaks (and troughs) of δD advance in time on successive days, as indicated (black numerals). This is in keeping with the expected advances of the peaks of δg (dark red numerals), due to the longer period of the lunar day with respect to that of the solar day. Conventions used on the horizontal time axis are as described in the legend for Fig. 1. Data for δD have been redrawn, with modification to the numerals on the vertical axis, from fig. 13 in MacDougal (1921).

Fig. 13.

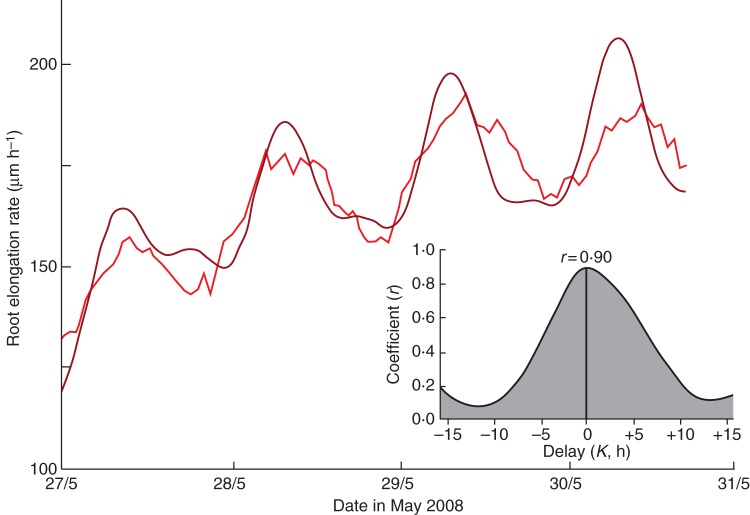
Results similar to those shown in Fig. 12, but in this case they illustrate the relationship between the δg profile (dark red line) and the mean elongation rate (green line) of a further set of roots (n = 6). These roots had been placed in continuous darkness (LD 0 h:24 h) for 4 d before being placed in continuous light (LD 24 h:0 h). Prior to the dark period, the roots had been grown in an LD regime of 16 h:8 h for 20 d. The inset shows the cross-correlation coefficients, r, when various time delays, K, are used.

It should be remarked, however, that Vesala et al. (2000) were unable to substantiate the relationship between δD and δg. These authors recorded variations (δD) in stem and xylem width of Scots pine (Pinus sylvestris) grown (we presume) out of doors. Fourier analysis of the δD variation failed to detect any convincing lunar-related periodicity (though in their paper there is some confusion as to the period that should be searched for). Unfortunately, no meteorological data are given and, as the authors suggest, it may be that water available to the measured stem locations as a result of transpiration simply overwhelmed any water-related variation of δD due to a putative lunar effect.

Target cells in the stem

Let us accept the proposition that the stem diameter variation δD is a marker of water movement into or out of the bark, the latter being occupied by an elastic tissue consisting of cambium and young secondary phloem (Zweifel et al., 2000). With the aid of Fig. 9, a working hypothesis which might accommodate these results can be proposed: we suggest that, since one of the pair of troughs of δg coincides with the single daily trough of δD, which occurs in the late afternoon, the two variables may be co-ordinated in such a way that δD tracks the time course of δg. This coupling, together with an increasing value of δg, could lead to the filling of the elastic tissue with water and, hence, may account for the increase in δD. At around noon on the following day, δD begins to decline. This may be because, at this time, water is withdrawn from tissues that had been filled by water during the previous night. When δg begins to rise at the end of the day, water in the elastic tissues is once again replenished; and so a new cycle of δg–δD interactions re-commences. The degree to which transpiration participates in the decline of δD is uncertain because, as shown by Cantiani and Sorbetti Guerri (1989), this decline can be largely independent of transpiration, a fact which led Zürcher et al. (1998) to propose that some type of lunisolar-modulated water exchange occurred within the bark itself, which accounted for the variation δD.

Stem water volume fraction

H. S. Burr, Professor of Anatomy at Yale University School of Medicine from 1929 until 1958, formed the opinion that it is ‘not at all impossible that the lunar cycle produces, in some as yet undiscovered way, tides in the tree’, and, further, ‘since growth in trees is in part a matter of hydration, it may eventually turn out that the effect of the lunar cycle on the growth of the tree is as direct as on the tide level’ (Burr, 1945). Besides his studies of lunar effects on bioelectricity in trees, Burr also studied the stem diameter variation, δD, mentioned previously (see Barlow, 2012). In accordance with the observations of MacDougal (1921) and the tentative interpretation of his results (see above), a store of water within the wood of a tree should be available both for the process of radial growth and for modulating the diurnal diameter variation, δD. Also, as Burr speculated, water might be brought into the trunk of the tree by a process independent of transpiration.

An interesting observation in this connection is the water volume fraction (or volumetric water content, m³ m⁻³) of tree woody tissue, which has been measured in Pinus contorta by Sparks et al. (2001) using continuous time domain reflectometry. As Canny et al. (2007) note in connection with these measurements: ‘After the morning minimum, the water content rises quickly towards noon … this rise strongly suggests that some air-filled tracheids are being refilled with water’. However, the means by which the water content of the wood is increased is not known. The authors mention theoretical physiological causes for this increase; but these range from the improbable (due to stomatal closure at mid-day) through to the hypothetical. One untested (though not untestable) possibility, suggested by Canny et al. (2007), is the ‘exsolution’ of air from water already present in the tracheids.

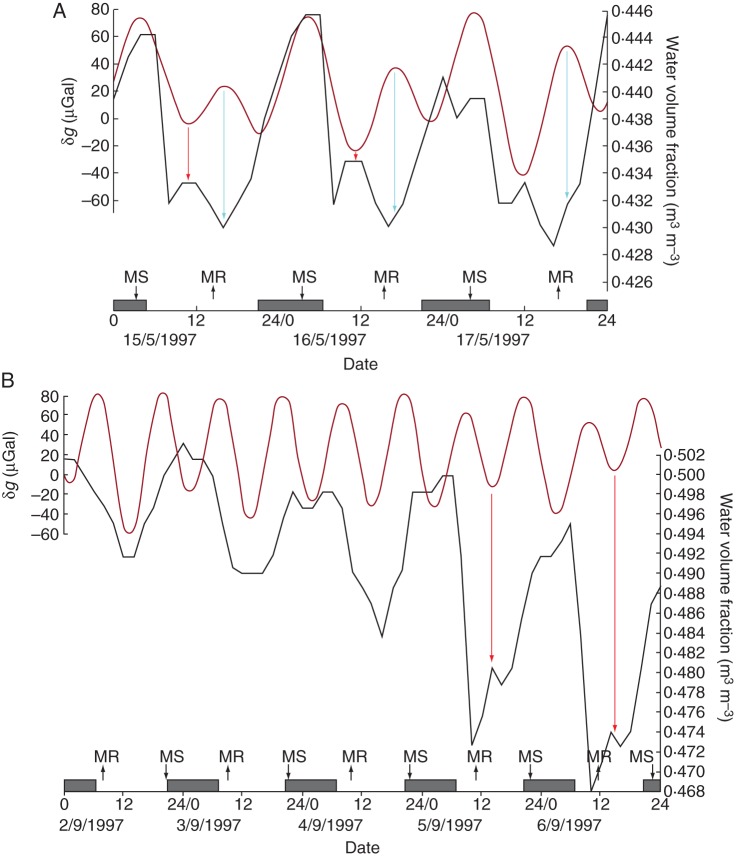
However, a glance at the lunisolar gravity profile at the times (May–September 1997) and place (Potlatch, ID, USA) where Sparks et al. (2001) made their measurements of water volume fraction (Wvf) suggests a further possibility (Fig. 10A, B); namely, that the lunisolar tidal force regulates the water content of the xylem. A survey of the complete data set (part of which is shown in figs 7 and 8 of Canny et al., 2007) consistently shows small mid-day peaks of Wvf which are coincident with turning points in the δg profiles. Although exact correspondences between the two variables would not be expected on every occasion because of variations in the tree's physiology due to meteorological conditions (periods of rainfall, for example), the correspondences, such as shown in Fig. 10A and B, are nevertheless indicative of a Wvf/δg inter-relationship. Again, it seems that the δg turning points are influential on the Wvf turning points: and especially interesting are their relationships with the so far unexplained noon-day peaks of Wvf. The lunisolar tidal force might, therefore, provide a guidance system that modulates the water relations system of the tree. This idea of a guidance, or back-up, system will be followed up in the next section on root elongation growth.

Fig. 10.

Water volume fraction (Wvf) measured at 2-hourly intervals (black line), in the xylem portion of a stem of Pinus contorta at two different stages of the growing season at Potlatch, ID, USA: during (A) mid-May 1997, and (B) early September 1997. Wvf is inherently greater in early September (possibly because of prevailing meteorological conditions) than it is in May. Nevertheless, when Wvf decreases on 5 September, a small, mid-day peak becomes evident, as it was throughout May. The mid-day Wvf peak, as well as the more major peaks, correspond to turning points in the profile of δg (dark red line and red arrows). Troughs in the Wvf profile correspond to troughs in the δg profile (three troughs are linked by blue arrows in A). Conventions used on the horizontal time axis are as described in the legend for Fig. 1.

Root elongation growth

Using high resolution images of Arabidopsis thaliana roots captured on video film at a rate of 1 frame per 30 min, Yazdanbakhsh and Fisahn (2011) prepared detailed profiles of root elongation rate. Seedlings were raised in a growth chamber in which environmental variables – humidity, temperature and light – were held constant. The roots were positioned on nutrient agar so that they grew vertically downward (for details, see Yazdanbakhsh and Fisahn, 2010).

In an experiment to study the effect of LD periods on the subsequent elongation rates of roots, two experimental groups of seedlings were raised during May 2008. The first group was exposed to a photoperiod of LD 12 h:12 h for 4 d, and the second group to a photoperiod of LD 16 h:8 h. During the entraining LD regime, both groups of roots showed a periodic increase and decrease in the elongation rate (left-hand portion of Fig. 11). When the dark period was discontinued and the two groups of seedlings were thereafter exposed to continuous dim light (LD 24 h:0 h) of flux density 100 µmol m⁻² s⁻¹, the roots of each group continued to display an oscillating elongation rate (right-hand portion of Fig. 11). The period of the free-running oscillation for each group of roots altered from 24·0 h (as had been displayed during each of the two entraining LD regimes) to a common period of 24·8 h during the LD 24 h:0 h regime (Fig. 11). This new period was established by spectral analysis of the root elongation rate data. The overall growth rate of the roots also tended to accelerate during the first 4 d following transfer to continuous illumination. This upward trend in rates eventually ceased after about 6 d in the light, although the oscillations of rate continued. The rates now centred upon a constant mean rate of approx. 280 µm h⁻¹ for the first group of roots, and approx. 200 µm h⁻¹ for the second group.

Fig. 11.

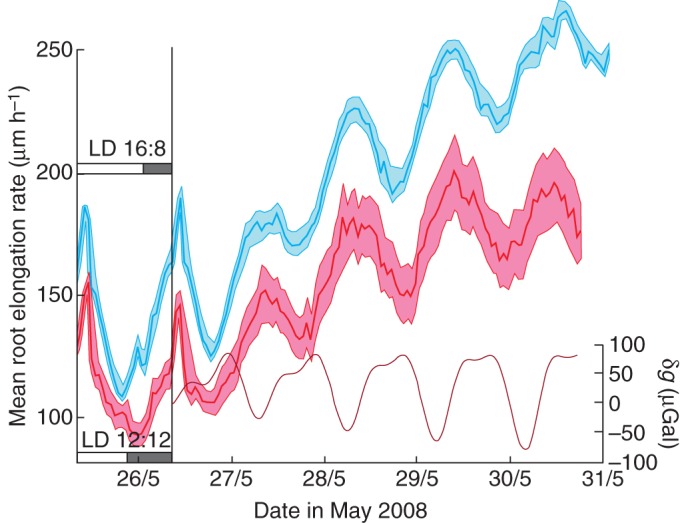
Mean elongation rates of two groups of Arabidopsis thaliana (Col-0) roots, estimated at hourly intervals. Both groups were entrained in alternating light–dark conditions for 4 d: LD 16 h:8 h in the case of roots whose growth is depicted by the blue line (n = 23), and LD 12 h:12 h for roots denoted by the red line (n = 9). Elongation rates on the last day of the entrainment period are shown on the left-hand side. The roots were then placed in continuous light for the remaining time. Shaded bands around the oscillating red and blue lines indicate the limits of the standard error of the respective mean elongation rates. The graph in the lower portion of the right-hand panel shows the δg profile for the period when the roots were in continuous light for the dates indicated. The location of the observations was at Potsdam, Germany.

The fact that, in continuous light, a new, common period of 24·8 h was developed by both groups of roots suggests that a common timekeeping mechanism was at work in each case. An internal memory of the periodicities imposed by the preceding 24·0-h entrainments, produced in accordance with the growth chamber LD environment, seems unlikely since the new period is not precisely 24·0 h. Therefore, a factor exogenous to the roots, and perhaps outside the growth chamber, seems a more probable influence on the free-running elongation rates. That the newly acquired 24·8-h period of each group of roots coincides with the mean period of the lunar day suggests that a lunar (or lunisolar) factor should be considered as the entraining agent during the free-running stage of root growth. Accordingly, the time course of the lunisolar tidal acceleration δg prevailing at the time of the observations of the elongation rate was examined. The profile of δg for the first few days of the free-running growth period is also included in Fig. 11.

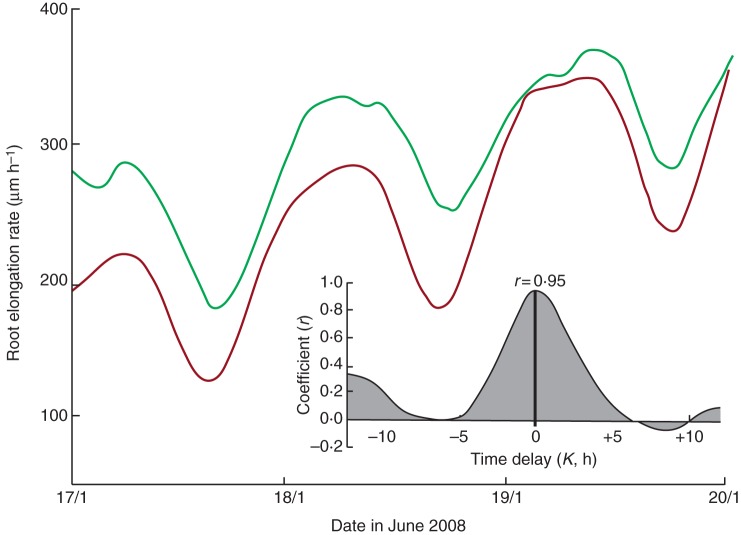
The kinetics of each of the two groups of roots were analysed in order to establish the rhythm of elongation growth. Visual comparisons of the pair of time courses (elongation rate and δg) were enhanced by applying an exponential trend to the δg profile so that it ran with much the same trajectory (Fig. 12) as the accelerating growth rate of the first group of roots (those which had been entrained in LD 12 h:12 h). The δg profile was inverted so that the troughs and peaks in each profile – δg and elongation rate – could be visually matched more readily. In this example (Fig. 12), higher mean elongation rates coincide with lower (negative) δg values. The cross-correlation coefficient between the two data sets is r = 0·90 (Fig. 12, inset). Furthermore, the time delay, K, estimated to the nearest hour, between the pair of time courses is 0 h. This indicates an exact tracking by the roots of the gravimetric tide, with respect to their elongation rate.

Fig. 12.

An exponential trend has been applied to the profile of δg (dark red line) shown in Fig. 11 so that it runs approximately parallel to the root elongation rate (light red line), as was shown in Fig. 11. This transformation emphasizes the concordance between the two time courses and their respective turning points. The inset shows the cross-correlation coefficients (r) between the data from the two time courses when varying time delays (K) are used in the cross-correlation. In this case, maximal r = 0·90 occurs when K = 0 h.

A similar approach, again applying a trend to the δg profile so that it paralleled the trend of increasing root elongation rate, was used for another set of roots. These roots had been subject to LD 16 h:8 h for 20 d during May–June 2008 and then exposed to continuous darkness (LD 0 h:24 h) for 4 d before being continuously illuminated. The two profiles, δg and elongation rate, are shown in Fig. 13. The resulting coefficient of cross-correlation was r = 0·95, and the delay between the two time courses was K = 0 h (Fig. 13, inset). An earlier experiment during the winter of 2007, when the roots on this occasion were entrained by LD 12 h:12 h and then grown in darkness, also produced perfect correspondence between the profiles of elongation rate and δg (r = 0·96; K = 0 h) (data not shown). Seasonal differences (summer vs. winter) therefore did not influence the rhythm of root elongation which, in both experiments, tracked the rhythm of the δg profile.

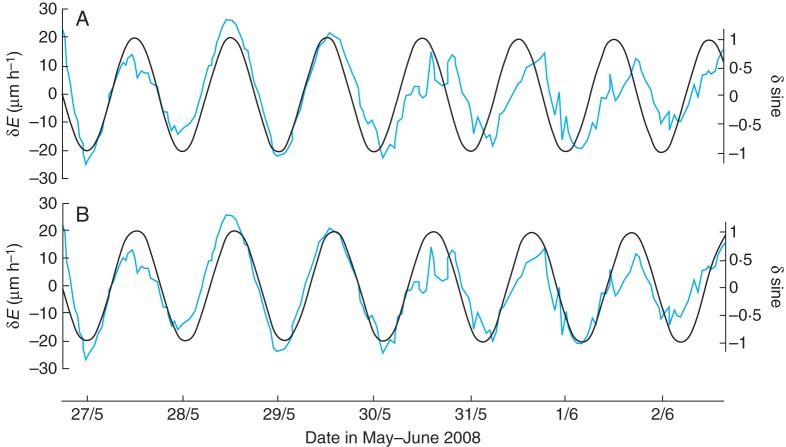
A further test can be applied, which also describes the rhythm of root elongation in the post-entrainment, free-running conditions of continuous light. The roots were those whose details are shown in the upper curve in Fig. 11 (blue line). Elimination of the trend of increasing elongation rate produced an oscillating wave of rates centred upon a notional mean deviation of zero rate. This deviation is shown as ±δE in Fig. 14. Mathematically generated sine waves, of deviation ±δsine, having periods of either λ = 24·0 h or λ = 24·8 h, were superimposed upon the normalized δE (Fig. 14A, B). Congruence between the oscillations δE and δsine was improved when the sine wave of λ = 24·8 h was used (Fig. 14B) – this being the period of the lunar day. In the case of the 24·8-h sine wave, cross-correlation between the complete data sets gave a maximal coefficient of r = 0·85 and a delay of K = 0 h, whereas fitting the sine wave of λ = 24·0 h to the elongation rate data gave a lesser coefficient of r = 0·78. The mean delay, using the whole data set, was K = +4·0 h (i.e. the oscillation of the root elongation rate was in advance of the λ = 24·0 h sine wave).

Fig. 14.

Roots were initially entrained in LD 16 h:8 h, and are the group whose mean rates of elongation are shown in Fig. 11 (blue line). The increasing trend in the elongation rate (blue line) was eliminated by means of a third-order polynomial, which brought the variation in rates, ±δE, to a constant amplitude but did not affect the period. (A) A sine wave of period λ = 24·0 h (black line), with amplitude variation ±δsine, was superimposed upon the δE profile. As time progressed, the period of the root elongation rate becomes more and more out of phase with the δsine profile. (B) A sine wave of period λ = 24·8 h (black line) was superimposed upon the same δE profile. The profiles of the two waves now remain in register.

Also tested was the statistical method of local time series tracking correlation of the two time courses, in the manner suggested by Papadimitriou et al. (2006). Many segments of the time courses gave local correlation coefficients of r = 1·0 (data not shown).

In another experiment, replicated samples of roots of three different genotypes (Col-0, sex and dpe-1) were grown with or without sucrose in the medium. The roots of each group of seedlings had been entrained by 4 d in LD 12 h:12 h before placing them in continuous light. The time courses of the mean root elongation rates of the different genotypes fell into two classes (with slower or faster rates). Nevertheless, despite the difference in rates, each group of roots closely followed the profile of δg (data not shown).

In a final set of observations from Arabidopsis roots, a group of seedlings was raised in continuous light, i.e. the roots were never exposed to darkness, and hence there could not have been any light/dark entrainment. Over 45 d of recording, the root elongation rate did not accelerate. As found previously (cf. Fig. 14), after superimposing either a 24·0-h or a 24·8-h period sine wave to the elongation rate data, it was the latter sine wave (λ = 24·8 h) which gave a better fit and yielded a higher cross-correlation coefficient (r = 0·88; K = 0 h) with the time course of root elongation rates. Using the 24·0-h sine wave, the coefficient was r = 0·81, and the delay K = +1·0 h. A good visual correspondence was also found when the δg profile was used in place of the sine wave. Interestingly, in this latter superimposition of the two time courses, the maximal root growth rate corresponded to the second of the two daily maxima of δg. Because of the presence of two daily peaks in the δg profile, the cross-correlation coefficient was reduced to r = 0·71. In such a case, the mentioned local time series tracking correlation may be a statistical test superior to cross-correlation.

In all the experiments during which the roots were in conditions of continuous light, the period of the free-running elongation rate conformed to the 24·8-h period of the lunisolar tidal force profile. No evidence was found that would give preference to a strictly diurnal 24·0-h period, which might have been attributed to a purely solar influence, or which would support the notion that a preceding light/dark entrainment regime (i.e. the subjective day of the growth cabinet environment) was the source of the period displayed in free-running conditions. Therefore, we conclude that roots perceive the tidal acceleration generated by the orbital motions of the Moon and the Earth, and that this perception is expressed in the rate of root elongation. The fact that time delays, K, between the time courses of the two variables are non-existent (K = 0 h) suggests that perception of the tidal force and its variation is immediate and continuous.

Target cells in the root

All cells at the apex of a root elongate, even though the different cell types vary with respect to their volumetric ratios of ground-cytoplasm and solute-filled vacuole (Barlow et al., 1982). The fastest rates of cell elongation occur in the zone just proximal to the meristem whose cells, especially those of the cortex, develop a prominent vacuole relative to the remainder of the cytoplasm. This zone is also where growth is responsive to tropic stimuli, such as occurs when a root is displaced with respect to the gravity vector, for example. Tropic growth is due to differential growth of the flanks of the root and is expressed in two dimensions. However, the differential elongation growth, whose periodicity has been described above, is a feature of variation of rectilinear growth in a single dimension.

One-dimensional differential growth could be brought about in a number of ways, but all require departure from a steady-state mode of growth. It could, for example, be a consequence of a periodic regulation of meristem size. This would lead to alternating increases and decreases of the number of cells entering the elongation zone during a given time. Alternatively, if meristem size should remain constant, one-dimensional differential growth could be produced by temporal variations in the cellular elongation rate; in a simple case, the elongation zone might expand or contract during a given time span. We tend to favour this second mode of growth regulation in order to account for the varying elongation rates of the Arabidopsis roots. If this mode of growth operates, then a survey of cell lengths along a continuous cell file in, say, the root cortex should reveal an oscillation of lengths over distances corresponding to the number of cells passing through the rapid elongation zone in a 24–25-h period. Periodic cell length variations have occasionally been recorded (Luxová, 1981) but may be due to differential growth in two or three dimensions. The Arabidopsis roots of the present observations did not show nutation, however. The long cell–short cell periodicity in the cortical cell files of sea grasses (see fig. 4 in Barlow and Lück, 2008) may be an example of one-dimensional differential growth which in turn traces to a rhythm of stem cell proliferation.

Details of a circadian rhythm of rice root elongation were reported by Iijima and Matsushita (2011), who also reviewed other published cases of root growth periodicity. The rhythms of these rice roots tended to have periods of ≤24 h, depending on the growth conditions. Similarly, periodic elongation has been recorded for shoots. Normann et al. (2007), for example, describe the shoot extension rhythms of Chenopodium rubrum and C. murale. Their periods may vary between 23 and 27 h.

Interestingly, evidence has been adduced that circumnutation of stems might be modulated by a lunar influence (Charzewska et al., 2010); and it is intriguing that Spurný (1966) observed a nutational period, for pea roots, of 8 h – the interval which separates δg turning points.

Elongation of both roots and shoots depends on the delivery of water to the growing points at the apices. The periodicity of shoot growth may, for instance, depend on the periodicity of root pressure, measured in terms of the rate of water flow through the xylem. The periodicity of this flow may, in turn, be regulated by the permeability of the cellular plasma membranes of the root which is governed by both a passive diffusion mechanism and a more metabolically active gating mechanism dependent upon aquaporin water transporter proteins. Aquaporins have been linked to circadian rhythms (Uehlein and Kaldenhoff, 2006), and roots have featured strongly in such studies, with experimental work being conducted on, for example, roots of Lotus japonicus (Henzler et al., 1999) and A. thaliana (Takase et al., 2011) using artificial light/dark regimes as methods of rhythm entrainment. Particularly intriguing are the reports that root pressure (presumably a response to aquaporin activity) is an autonomous rhythmic process in free-running conditions of constant light (see Hagan, 1949). Thus, it would be of great interest to examine aquaporin gene expression patterns and protein quantities, together with water dynamics, in a system such as that described by Yazdanbahksh and Fisahn (2011), where the time base was in accordance with the solar clock time and not one related to a subjective time base such as time since germination or one constructed with reference to the light/dark cycles of a growth cabinet. Using an objective time base such as UTC, lunisolar gravitational force variation could be included in the interpretation of root growth results.

No mention has been made of target processes through which lunisolar gravitational forces could be perceived and transduced as a growth response. So far, and probably because of conceptual limitations, biologists have hardly given this a thought. The lack of a recognized theoretical perspective is therefore a handicap which perhaps accounts for the omission, within the area of plant biology, of any mention of lunar influences upon growth and development (except for a few early references to the effects of moonlight, e.g. Semmens, 1947). The Discussion which follows will attempt to broach this difficult problem.

DISCUSSION

It has been said that ‘the best theory is that which necessitates the minimum amount of assumptions to unite a maximum number of facts’, and that such a theory should ‘possess the power of assimilating new facts from the unknown without damaging its own structure’ (Selye, 1976, p. 285). Whether our proposal that lunisolar tidal force is in some way responsible for, rather than being merely correlated with, any or all of the movements described herein can be considered a ‘best’ theory is difficult to evaluate, mostly because the proposition cannot easily be put to experimental test. However, as has been indicated, a lunar period of approx. 24·8 h, together with exact knowledge of the timing of critical variations, or turning points, in the gravimetric tidal profile, δg, as well as the coincident critical turning points in the biological time course, seem to provide three elements which support a lunar-based relationship explanatory of the biological observations. Moreover, a 24·8-h lunar rhythm provides the relationship with a basis which is superior to one based on a solar-driven 24·0-h rhythm. All the more telling is that, in some of the biological systems we have described, there was no intrusion of entraining influences which could have simulated information normally provided by a solar day. Therefore, there is no reason to interpret any of our results in the light of a constitutive, endogenous timekeeper developed in response to a prior entrainment regime. Rather, the timekeeper in our biological systems appears to originate outside the immediate environment in which the plants were raised. The Moon and its motion around the Earth, in conjunction with the motion of Earth around the Sun – from both of which the lunisolar tidal variation δg is estimated – seem, therefore, to supply inputs to, and might even be said to be an integral part of, the biological system, the expression of this integration being a biological rhythm.

The quotation above from Selye (1976) mentions that a minimum amount of assumptions should frame a sound theory. One assumption that is crucial in the present context is that Arabidopsis roots, as well as the other plant organs referred to, should, as we indicated above, be integrated with the lunisolar gravitational force. So far, apart from correlative evidence, no direct experimental evidence has been sought for the usual type of stimulus–response relationship. Thus, on the face of it, it looks as though the lunisolar acceleration hypothesis might be a sterile hypothesis, unable to produce any experimental offspring. A sufficient theory could be developed if a link were to be made between the biological observation of rhythmic growth movements, their underlying physical and physiological determinants, and reasonable theoretical conjectures stimulated by the physical events implicit in the time courses of δg, their turning points, and possibly also the amplitudes of δg.

One interesting and attractive theory which allows the development of a cosmic–biological relationship is due to G. Dorda (2004, 2010). In brief, this theory proposes that the three-body unit of Moon, Earth and Sun should be considered from the perspective of a quantum Universe, where gravity and time are both quantum entities. It follows that there should be a quantum unit of time duration. From physical principles, Dorda estimated this quantum duration to correspond to approx. 30 ms, which happens to correspond to the temporal threshold for the perception of touch, sight and sound in animals. Then, there is also an integration time of about 3 s by means of which stimuli can be placed in a temporal order. The 3-s integration period was shown theoretically to be due to the effect of solar gravity acting upon the Earth. Interestingly, for plant roots, the time duration for the susception of a 1 g gravitational accelerative stimulus is about 1 s, and the integration time (or presentation time) is of the order of 8–10 s (Volkmann and Tewinkel, 1996; Hejnowicz et al., 1998; Perbal, 2009). Technical limitations of working with plants and their visible tropic movements may account for the disparity of these estimates from plants in comparison with those gained from animals.

It is also interesting to consider the extent to which the lunisolar tidal force might interact with the Earthly gravitational force in the shaping of the processes of plant development. For example, the form of Arabidopsis seedlings, and the density and orientation of their root system, is altered under conditions of ‘microgravity’ (which, in actuality, is about 10⁻³ g) found within Space Shuttle laboratories. Here, plants are held to express a ‘default’ type of morphology (Millar et al., 2011), i.e. a morphology which is putatively inherent and self-generating, and which has been freed from constraints imposed by Earthly 1 g. Nevertheless, under such circumstances, plants would still be subject to the influence of both solar and lunar gravity and orbital motions, although these would now take modified forms compared with those experienced on Earth. Moreover, if Dorda's theoretical analysis is correct, organisms in a space environment may develop and function within an altered time frame (Dorda, 2004, 2010).

Within the integration time mentioned above, there is a predicted change in the collective state of mass. Water was taken by Dorda (2004) as an example of a material which displays quantized units of mass. He estimated that the mean aggregated mass of water, conserved as a homogeneous and coherent whole, is equivalent to 1·013 × 10⁸ molecules. Within the Earth–Sun gravitational field, the passage of quantal time – the integration time – affects the total coherent mass aggregation (that mass which comprises the total aqueous component of each cell), causing it either to increase or to decrease its mass. The transformation of the water aggregate in terms of its molecular mass, as a result of the action of the varying solar gravitational force, also contributes to the bio-rhythmic clock and hence to a sense of the passing of time (at least in the sense of biological time).

It is proposed that the Moon, due to the entry of its gravity and orbital motion into the Earth–Sun gravity field, has a further influence on the coherent mass transformation of water. At each quantum leap, it was calculated that aggregates of 10⁸ water molecules, of approx. 0·18 µm diameter, are added to or subtracted from the total aggregate of intracellular water (Dorda, 2010, pp. 88–89). [This number of molecules is considerably greater than the number of water clusters that Watterson (1997) claimed to constitute one unit (or pixel, in his terminology, with a dimension of approx. 3 nm) of measurable water pressure.] Therefore, during each lunar half-day, approx. 2 × 10¹¹ water molecules are either added to or subtracted from the total coherent water aggregate. The increase or decrease of water aggregation also varies according to the lunar phase within the lunar month, meaning that there can be either a net gain or a net loss of water molecules with the passing of each day of the lunar month. Hence, there is a corresponding cyclical change of the molecular number associated with the coherent aggregation state. The total cellular water aggregate consists of 1 × 10¹³ molecules, and there is roughly a 2 % net change of water mass per lunar half-day. Now, 1 × 10¹³ water molecules occupy a spherical volume of roughly 8 µm diameter, which is about the dimension of an Arabidopsis root meristem cell, and also of the non-vacuolate portion of an elongating cells. A 2 % change in volume per cell amplified along a file of, say, ten cells, could amount to a measurable increase or decrease in root elongation rate. This variation would be a response to the effect of lunisolar tidal force upon cellular water content. The actual increment or decrement of water molecules per cell, and hence of cell volume, could presumably occur by water exchange between protoplast and cell wall and symplasm, as was suggested by Zürcher et al. (1998), and by Dorda (2004, 2010). In detail, we conjecture that this exchange may involve exo- or endocytotic vesicles containing small coherent water domains, as suggested by the physical observations of Del Giudice and Preparata (1994). Furthermore, and consistent with cytoplasmic microvesicle dimensions, a minimal coherent aggregate of 0·1 µm diameter was proposed by Arani et al. (1995), a value close to the 0·18 µm diameter aggregate estimated by Dorda (2004, 2010).

Dorda (2004) developed his theory in a practical direction with estimates of the cellular volume change in relation to the tree stem diameter variation, δD, for the period during which Zürcher, Cantiani and others had presented data for the gravimetric tide (Zürcher et al., 1998; and see Fig. 6 of the present paper). Taking into account the geographical co-ordinates of the observation site and the contemporaneous phase of the Moon which, as mentioned, also influences the daily volumetric change affecting the total water aggregation state, a close fit was obtained between δD and the predicted change of cell volume. It may be concluded, therefore, that each δg profile is an indicator of the quantal changes affecting the mass of the coherent water aggregate, which in turn translate into losses or gains of water molecules from cells and tissues. These then lead to decreases or increases of cell volume and, hence, to variations of growth rate. Although all cells are theoretically susceptible to lunisolar gravitational force, only certain cells – the target cells – have the capability to manifest, through the rhythmical movements they promote, the quantized water exchange events driven by the lunisolar tidal force.

Given that water can exist in complex domains both naturally (Zheng et al., 2006; Del Giudice et al., 2009a) and within cells (Wiggins, 1996; Shepherd, 2008), and that cellular water domains are distributed between free and bound water complexes, the latter state being a product of an interaction with cytoskeletal and associated proteins, as well as with the hydrophilic components of the cell walls and underlying plasma membrane, it is possible to envisage that some regions of the cell–membrane–wall association give up or accept water more readily than others under the influence of lunisolar gravity. Moreover, Brizhik et al. (2011) found that lunar properties or signals (a lunar eclipse is the example offered by these authors) somehow affect the physical properties of water. These authors go on to suggest that water may be ultrasensitive to external stimuli that apparently ‘impart no purposeful energy to a system’. However, such a system, if it were a living system, could be regarded as being truly an integral element within the Earth–Sun–Moon complex through which quantum field effects are admitted into biology (see Auletta, 2005; Del Giudice et al., 2009b). In this frame of reference, then, it might be possible to interpret the impact of the lunisolar tide upon the molecular cytology of cells, in particular its effect upon water–cytoskeletal coherences and microvesicle distribution and behaviour. In connection with a possible exchange of water between the cytoplasm and cell wall via the protoplast membrane, it is possible that such exchange sites are marked by the contact points between the cytoplasm and wall, i.e. the Hechtian strands revealed by plasmolysis (Lang et al., 2004). These strands may occur at positions between the solute-free exclusion zones composed of structured water complexes which were noted by Zheng et al. (2006) to occur along biological surfaces, such as membranes. Interestingly, the Hechtian strands disintegrate into microvesicles of 0·1–0·25 µm diameter (Lang et al., 2004), which are of the same dimensions as mentioned above for the minimal coherent water domains (Arani et al., 1995).

Certainly, theoretical and experimental studies, particularly in the realm of water biophysics, need to be pursued in order to begin to comprehend possible lunar influences upon water in living material and its behaviour within responsive cells and tissues. However, it may not be unreasonable, in the face of the results presented herein, to tackle the question posed by Del Giudice et al. (2009b) of how it is possible to understand the emergence of novelties in the conceptual framework of contemporary physics and chemistry – and, we may add, in contemporary biology, too. Quantum field theory might indicate a new point of view for biology, providing an understanding of dynamics which mechanistic simulations cannot achieve.