Nonadaptive Algorithms for Threshold Group Testing with Inhibitors and Error-Tolerance

Abstract

A group test gives a positive (negative) outcome if it contains at least u (at most l) positive items, and an arbitrary outcome if the number of positive items is between thresholds l and u. This problem introduced by Damaschke is called threshold group testing. It is a generalization of classical group testing. Chen and Fu extended this problem to the error-tolerant version and first proposed efficient nonadaptive algorithms. In this article, we extend threshold group testing to the k-inhibitors model in which a test has a positive outcome if it contains at least u positives and at most k−1 inhibitors. By using (d + k − l, u; 2e + 1]-disjunct matrix we provide nonadaptive algorithms for the threshold group testing model with k-inhibitors and at most e-erroneous outcomes. The decoding complexity is O(n^u+k log n) for fixed parameters (d, u, l, k, e).

1. Introduction

The nonadaptive group testing (called pooling design in computational molecular biology) is a mathematical tool to significantly reduce the number of tests in DNA library screening, blood testing, multiple access communication and others (Du and Hwang, 2000, 2006; Gao et al., 2006; Hwang and Chang, 2007). In the classical group testing problem, we consider a set S of n items consisting of at most d positive items with the other being negative. A group test is an arbitrary subset of items, also called a pool. A test yields a positive outcome if and only if the test subset of items contains at least one positive item. The task is to identify all positive items in S with group tests as few as possible. However, in practice, the decoding algorithms become even more difficult due to the experimental errors (Thai et al., 2007). With the experimental errors, the test outcomes may consist of false positive or false negative. In the former, a test yields a positive outcome when a test does not contain any positive item. Likewise, in the later, a test yields a negative outcome when a test contains at least one positive item.

In some applications, some special negative items are called inhibitor whose effect is to cancel the effect of positive items. Different models can be formulated by considering different canceled effect. Farach et al. (1997) first proposed 1-inhibitor model in which the presence of a single inhibitor dictates the outcome to be negative regardless of how many positive items are in the test. D'yachkov et al. (2001) have proposed nonadaptive group testing for the 1-inhibitor model. Hwang and Liu (2003) have extended 1-inhibitor model to the error-tolerant version. A generalization of above model is the k-inhibitors model, which was proposed by De Bonis and Vaccaro (2003). In the k-inhibitors model, a test has a positive outcome if and only if it contains one positive item and at most k − 1 inhibitors. Subsequently, Hwang and Chang (2007) have given a pooling design which fits all inhibitor models and obtained a nonadaptive algorithm for the k-inhibitors model.

In 2006, Damaschke first proposed the threshold group testing which is a generalization of classical group testing problem. In threshold group testing, a test is positive (negative) if it contains at least u (at most l) positives and if the number of positives in test is between l and u, the outcome is arbitrary, where l and u are nonnegative integers with 0 ≤ l < u, called the lower and upper threshold, respectively. Obviously, the classical case of group testing is a special with l = 0 and u = 1. Moreover, threshold group testing is also related to guessing secrets (Chung et al., 2001), which is the special case l = 0 and u = p.

Recently, Chen and Fu (2009) have extended threshold group testing to the error-tolerant version where at most e erroneous outcomes are allowed, and proposed an efficient nonadaptive algorithm for the threshold group testing with error-tolerance. In this article, we extend threshold group testing to the k-inhibitors model in which a test has a positive outcome if it contains at least u positives and at most k − 1 inhibitors, and proposed efficient decoding algorithm for the new threshold model with inhibitors and error-tolerance in which complexity is O(n^u+k log n) for fixed parameters (d, u, l, k, e).

The rest of the article is organized as follows. Section 2 introduces some lemmas, notations and defines on which our results depend. Afterwards, we proposed a new threshold model with k-inhibitors and at most e-erroneous outcomes in Section 3. In Section 4, we propose efficient nonadaptive algorithms for the new threshold model with error-free, and its correctness proof and complexity analysis are given simultaneously. Afterwards, we advance efficient nonadaptive algorithms for the new model with error-tolerance, and give correctness proof and complexity analysis similarly.

2. Preliminaries

A group testing is usually represented by an incidence matrix M where the columns are the set of items, the rows are the set of tests, and cell (i, j) has a 1-entry if and only if item j is in the test i. For convenience, we view each column as the set of row indices where the column has 1-entry. Thus, we can talk about the union and the intersection of columns. We say that a set X of columns appears (or is contained in) a row if all columns in X have a 1-entry in the row. A test with a positive (negative) outcome is called a positive (negative) test, respectively.

Definition 2.1

(Du and Hwang, 2000). A binary matrix M is said to be (d, r]-disjunct if for any d + r columns

Definition 2.2

(Stinson and Wei, 2004; Du and Hwang, 2006). A binary matrix M is said to be (d, r; z]-disjunct if for any d + r columns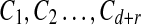

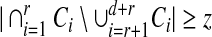This means for any d + r columns there exist at least z rows where each of the r designated columns has 1-entry and each of the other d columns has 0-entry. It is obvious that a (d, r]-disjunct matrix is (d, r; 1]-disjunct.

Lemma 2.1

(Chen et al.,2008). For any positive integers d, r, z and n, with d + r ≤ n, let t(n, d, r; z] denote the minimum number of rows among all (d, r; z]-disjunct matrices with n columns, then t(n, d, r; z] < z(w/r)^r(w/d)^d[1 + w(1 + log(n / w + 1))], where w = d + r.

Definition 2.3

Let X be a subset of columns, i.e. X ⊆ S, and R be any k-subset of columns (i.e. R ⊆ S) with R ∩ X = ∅. We use t(X) to denote the number of negative tests in which all columns in X appear, and t_k(X, R) to denote the number of negative tests in which all columns in X appear and each test contains at least k columns of R. Then, we define function t*(X) = min_R⊆S\Xt(X, R),where t(X, R) = t(X) −t_k(X, R).

Denote by P the set of positive items, and its cardinality is d. Let g = u − l − 1. For the threshold group testing, Damaschke (2006) proved the following two conclusions.

Lemma 2.2

(Damaschke, 2006). If d ≥ u + g, the seeker can identify a set P′ with |P\P′| ≤ g and |P′\P| ≤ g. For d < u + g, we still have the error bound u − 1 rather than g.

Lemma 2.3

(Damaschke, 2006). For any fixed set P′ with |P\P′| ≤ g and |P′\P| ≤ g, the adversary can answer as if P′ were the set of all positives.

3. Description of the Threshold Model with k-Inhibitors

In the section, we extend threshold group testing model with error-tolerance to the k-inhibitors version i.e. threshold model with k-inhibitors and at most e-erroneous outcomes. Now, we first give the definition of the threshold model with k-inhibitors as following.

Consider a set S of n items consisting of at most d positive items and at most q inhibitors with the other being negative items, where d + q < n and u + g ≤ d ≪ n. Suppose l and u are two integers that called the lower and upper threshold respectively, and g ≡ u − l − 1 denotes the gap between the lower and upper thresholds. Let E be a group test for a subset of S, and k be a integer with 1 ≤ k ≤ q. The group test E is positive if it contains at least u positive items and at most k − 1 inhibitors, and E is negative if it contains at most l positive items or at least k inhibitors. When the number of positives in E is between l and u, and the number of inhibitors is at most k − 1 inhibitors, the outcome of E is arbitrary.

Set 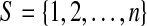which contains subset P of positives and subset I of inhibitors. Let E ⊆ S be a test and the function Outcome(E) be the outcome of test E. Then, the formulated description of the threshold model with k-inhibitors is the following.

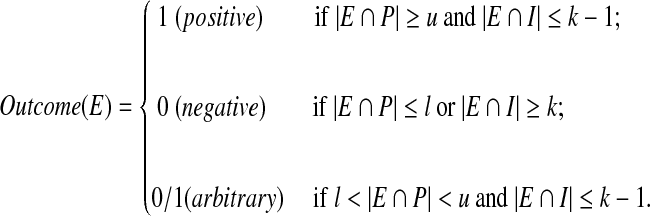Furthermore, if there are at most e erroneous outcomes in the threshold model with k-inhibitor, we can obtain the threshold model with k-inhibitors and at most e-erroneous outcomes. For convenience, we attach parameters (n, d, u, l, k) to the threshold model with k-inhibitors and error-free, and attach parameters (n, d, u, l, k, e) to the threshold model with k-inhibitors and at most e-erroneous outcomes.

4. The Nonadaptive Algorithms for the (n, d, u, l, k) Threshold Model

4.1. Nonadaptive algorithm for the case without gap

For threshold model with k-inhibitors and error-free, we first deal with the case when the gap g = 0, that is, a test is positive if and only if it contains at least u positive items and at most k − 1 inhibitors. For the particular case, we propose an efficient nonadaptive algorithm to identify all positives by using a (d + k −u + 1, u]-disjunct matrix.

Theorem 4.1

Let M be a (d + k − u + 1, u]-disjunct matrix of n columns. For the (n, d, u, l, k) threshold model, when g = 0 we have

• (1) t*(X⁺) ≤ 0, for every u-subset X⁺ ⊆ P;

• (2) t*(X) ≥ 1, for every u-subset X ⊆ S with |X\P| ≥ 1.

Proof

(1) For any u-subset X⁺ ⊆ P, the outcome of test containing X⁺ is either negative or positive. Obviously, the positive test is ineffective to compute t*(X⁺). Therefore, we only consider negative test which contains X⁺. By Definition 2.3, for any k-subset R ⊆ I, it is clear that t(X⁺) = t_k(X⁺, R) since every negative test containing X⁺ must contain at least k inhibitors. It implies that t*(X⁺) = 0. Hence, we have t*(X⁺) ≤ 0 for every u-subset X⁺ ⊆ P.

(2) For each u-subset X ⊆ S and |X\P| ≥ 1, X contains at least one item not in P. Note that |X| = u and g = 0. Thus |X ∩ P| ≤ u − 1 = l. First, we can choose any k-subset R ⊆ S\X. For such X and R, we can choose a (d − l)-subset Y ⊆ S as following: If |P\(X ∪ R)| ≥ d − l, then we choose Y such that Y ⊆ P\(X ∪ R). Otherwise, we can choose Y such that P\(X ∪ R) ⊆ Y ⊆ S\(X ∪ R). By the (d + k − u + 1, u]-disjunctness property, there must exist at least a row containing X but none of Y ∪ R, and the number of positives in the row is at most l. In fact, when P\(X ∪ R) ⊆ Y, it is clearly that this row contains no more than l positive items since |X ∩ P| ≤ l. On the other hand, when |P\(X ∪ R)| ≥ d − l and Y ⊆ P\(X ∪ R), we have |P\(Y ∪ R)| ≤ |P\Y | ≤ l. So the number of positives in this row is at most l too. The test corresponding to the row should be negative since it contains at most l positive items. It implies that t(X) ≥ 1 and t_k(X, R) = 0. Hence t(X, R) = t(X) −t_k(X, R) ≥ 1. By the arbitrary property of R, we have t*(X) ≥ 1 for every u-subset X ⊆ S and |X\P| ≥ 1.   ▪

The following decoding algorithm is the immediate consequence of Theorem 4.1:

Because t*(X) is only dependent on the negative test, so let t₀ be the number of negative tests. To compute the set P, it suffice to verify the condition t*(X) ≤ 0 for each u-subset X separately. So the decoding complexity is . Moreover, note that t₀ ≤ t(n, d + k − u + 1, u;1]. By Lemma 2.1, the decoding complexity is O(n^u+k log n) for fixed parameters (d, u, k).

Theorem 4.2

The decoding complexity of Algorithm 1 is O(n^u+k log n) for fixed parameters (d, u, k).

Algorithm 1.

Identified all positive items under (n, d, u, l, k) threshold model without gap

1.	Use a (d + k − u + 1, u]-disjunct matrix of n columns.
2.	P ← φ
3.	for each u-subset X ⊆ S and k-subset R ⊆ S\Xdo
4.	compute t*(X)
5.	ift*(X) ≤ 0 thenP ← P ∪ X
6.	end for
7.	returnP

Proof

The theorem is obtained by applying Lemma 2.1 and the above discussion.   ▪

4.2. Nonadaptive algorithm for the general case

Now, we consider the general case for the k-inhibitors and error-free, i.e., gap g > 0. Things will become more complicate in the case. This is much different from what happens in the case without gap for which the positive set P can be identified exactly. By Lemmas 2.2 and 2.3, for the threshold model, there exist some set P′ with |P\P′| ≤ g and |P′\P| ≤ g, and this is the best possible result. In view of this, for the (n, d, u, l, k) threshold model with gap g > 0, we give an efficient nonadaptive algorithm to find some P′ with the properties above by using (d + k − l, u]-disjunct matrix, instead of identifying the set P exactly.

Theorem 4.3

Let M be a (d + k − l, u]-disjunct matrix of n columns. Then for threshold model with k-inhibitors and error-free, when g > 0 we have

• (1) t*(X⁺) ≤ 0, for every u-subset X⁺ ⊆ P;

• (2) t*(X) ≥ 1, for every u-subset X ⊆ S with |X\P| ≥ g + 1.

Proof

(1) Similar to the proof of Theorem 4.1, we still have t*(X⁺) ≤ 0 for every u-subset X⁺ ⊆ P.

(2) For each u-subset X ⊆ S with |X\P| ≥ g + 1, X contains more than g items not in P. Note that |X| = u and g = u − l − 1 > 0. We have |X ∩ P| ≤ u − (g + 1) = l. The rest of the proof is same as Theorem 4.1. Therefore, we have t*(X) ≥ 1 for every u-subset X ⊆ S with |X\P| ≥ g + 1.   ▪

By Theorem 4.3 and Damaschke's method (Damaschke, 2006), we can obtain the decoding algorithm for (n, d, u, l, k) threshold model with gap g > 0 as follow:

In Algorithm 2, the predicate that there exist (g + 1)-subset A ⊆ S\P′ and g-subset B ⊆ P′ such that for any u-subset Y ⊆ (P′ ∪ A)\B satisfies 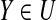is called expandable condition of P′. It is clear that Algorithm 2 terminates when P′ is not extended (i.e., the expandable condition of P′ should not satisfied) or |P′| ≥ d.

Algorithm 2.

Identified all positive items under the general (n, d, u, l, k) threshold model

1.	Use a (d + k + l, u]-disjunct matrix of n columns.
2.	U ← φ
3.	for each u-subset X ⊆ S and k-subset R ⊆ S\Xdo
4.	compute t*(X)
5.	ift*(X) ≤ 0 thenU ← U ∪ {X}
6.	end for
7.	Arbitrarily choose an element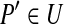
8.	while |P′| < ddo
9.	Flag ← 0
10.	for each (g + 1)-subset A ⊂ S\P′ and g-subset B ⊆ P′ do
11.	if any u-subset Y ⊆ (P′ ∪ A)\B satisfies thenFlag ← 1 and go to 13
12.	end for
13.	ifFlag = 1 thenP′ ← (P′ ∪ A)\B and |P′| ← |P′| + 1
14.	else returnP′
15.	end while
16.	returnP′

Now, we prove the correctness of Algorithm 2 and analysis its complexity.

Theorem 4.4

The set P′ that gives output of Algorithm 2 satisfies |P\P′| ≤ g and |P′\P| ≤ g.

Proof

By Theorem 4.3, it is easy to see that every u-subset X⁺ ⊆ P is in U and every u-subset 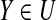satisfies |Y\P| ≤ g after Step 1-6. Hence, let P₁ denote the P′ in Step 7, then P₁ contains no more than g items not in P, i.e. |P₁\P| ≤ g. Suppose that Algorithm 2 obtains m − 1 sets P_i(2 ≤ i ≤ m) by executing the sentence in Step 9–13. According to the construction of P_i(2 ≤ i ≤ m), each P_j(1 ≤ j ≤ m − 1) must satisfy the expandable condition. It implies that |P_i\P| ≤ g(2 ≤ i ≤ m). Otherwise, for the certain P_i(2 ≤ i ≤ m), there exist a u-subset X ⊆ P_i and P_i = (P_i-1 ∪ A)\B such that |X\P| ≥ g + 1, a contradiction to that P_i–1 is extensible. Therefore, the set P′ that gives output of Algorithm 2 satisfies |P′\P| =|P_m\P| ≤ g.

On the other hand, note that Algorithm 2 terminates when P′ is not extended or |P′| ≥ d, we can discuss the following two cases:

• (1) The case that |P′| ≥ d causes the Algorithm 2 terminates. Because of |P′\P| ≤ g and |P| ≤ d, consequently |P ∩ P′| = |P′| − |P′\P| ≥ d − g. Hence, |P\P′| ≤ |P| − |P ∩ P′| ≤ g.

• (2) The case the Algorithm 2 terminates when P_m is not extended. Note that P′ = P_m in this moment. If |P\P′| = |P\P_m| ≥ g + 1 then there exists a set A such that A ⊆ P\P′ ⊆ S\P′ and |A| = g + 1. Since |P′| = |P_m| ≥ |P₁| = u > g and |P′\P| ≤ g, there exits a g-subset B such that P′\P ⊆ B ⊆ P′. Hence, any u-subset Y ⊆ (P′ ∪ A)\B satisfies 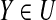since (P′ ∪ A)\B ⊆ P. Contradict to that P_m is not extended. Therefore, |P\P′| ≤ g.   ▪

Theorem 4.5

The complexity of Algorithm 2 is O(n^u+k log n) for fixed parameters (d, u, l, k).

Proof

It suffice to verify the condition t*(X) ≤ 0 for each u-subset X ⊆ S and each k-subset R ⊆ S\X, separately. It need execute 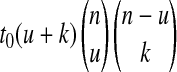times. By Lemma 2.1, for fixed parameters (d, u, l, k), the complexity of Steps 1–6 in Algorithm 2 is O(n^u+k log n) since t₀ ≤ t(n, d + k − l, u;1]. On the other hand, note that the iteration of while-sentence in step 8–15 is at most d − u since it starts with |P′| = u and terminates with |P′| ≤ d. So the complexity of Step 8–15 is at most . Therefore, the complexity of Algorithm 2 is O(n^u+k log n) for fixed parameters (d, u, l, k).   ▪

5. Nonadaptive Algorithms for the (n, d, u, l, k, e) Threshold Model

5.1. The case without gap under (n, d, u, l, k, e) threshold model

Similar to the threshold model with k-inhibitors and error-free, we first deal with the case that gap g = 0 under (n, d, u, l, k, e) threshold model in which there exist at most e erroneous outcome. For the particular case, we advance an efficient nonadaptive algorithm to identify all positives by using a (d + k − u + 1, u;2e + 1]-disjunct matrix.

Theorem 5.1

Let M be a (d + k − u + 1, u;2e + 1]-disjunct matrix of n columns. For the (n, d, u, l, k, e) threshold model, when g = 0 we have

• (1) t*(X⁺) ≤ e, for every u-subset X⁺ ⊆ P;

• (2) t*(X) ≥ e + 1, for every u-subset X ⊆ S with |X\P| ≥ 1.

Proof

(1) Similar to the proof of Theorem 4.1, for any u-subset X⁺ ⊆ P, we have t*(X⁺) ≤ 0 when none erroneous outcome occur. Hence, even for the worst case that e tests are erroneous, we still have t*(X⁺) ≤ e for every u-subset X⁺ ⊆ P.

(2) Similar to the proof of Theorem 4.1, we have t*(X) ≥ 2e + 1 for each u-subset X ⊆ S and |X\P| ≥ 1 when no erroneous outcomes occur. Therefore, even for the worst case that e tests are erroneous, we still have t(X, R) ≥ e + 1. By the arbitrary property of R, it is clear that t*(X) ≥ e + 1 for every u-subset X ⊆ S and |X\P| ≥ 1.   ▪

By Theorem 5.1, we can give a decoding algorithm as follows:

Theorem 5.2

The complexity of Algorithm 3 is O(n^u+k log n) for fixed parameters (d, u, k, e).

Algorithm 3.

Identified all positive items under the (n, d, u, l, k, e) threshold model without gap

1.	Use a (d + k − u + 1, u; 2e + 1]-disjunct matrix of n columns.
2.	P ← φ
3.	for each u-subset X ⊆ S and k-subset R ⊆ S\Xdo
4.	compute t*(X)
5.	ift*(X) ≤ ethenP ← P ∪ X
6.	end for
7.	returnP

Proof

Similar to the proof of Theorem 4.2, we omit it.   ▪

Theorem 5.3

For the (n, d, u, l, k, e) threshold model without gap, there exist an efficient nonadaptive algorithm that successfully identifies up to d positives, using no more than tests. Moreover, the decoding complexity is O(n^u+k log n) for the fixed parameters (d, u, k, e).

Proof

The theorem is obtained by applying Lemma 2.1 and by the above discussion.   ▪

5.2. The general case under (n, d, u, l, k, e) threshold model

For the general case of the (n, d, u, l, k, e) threshold model, that is g = u − l − 1 > 0, we give an efficient nonadaptive algorithm to find some P′ with the properties that there exist some set P′ with |P\P′| ≤ g and |P′\P| ≤ g by using (d + k − l, u; 2e + 1]-disjunct matrix since we cannot identify the set P exactly. Now, we first prove an important conclusion, then state our nonadaptive algorithm for the (n, d, u, l, k, e) threshold model with g > 0 and prove its correctness.

Theorem 5.4

Let M be a (d + k − l, u; 2e + 1]-disjunct matrix of n columns. Then, for the (n, d, u, l, k, e) threshold model, when g > 0 we have

• (1) t*(X⁺) ≤ e, for every u-subset X⁺ ⊆ P;

• (2) t*(X) ≥ e + 1, for every u-subset X ⊆ S and |X\P| ≥ g + 1.

Proof

Similar to the proof of Theorem 4.3, we omit it.   ▪

By Theorem 5.4 and similar to Algorithm 2, we can give the decoding algorithm for (n, d, u, l, k, e) threshold model with gap g > 0 as follows:

Theorem 5.5

The set P′ that gives output of Algorithm 4 satisfies |P\P′| ≤ g and |P′\P| ≤ g, and the complexity of Algorithm 4 is O(n^u+k log n) for fixed parameters (d, u, l, k, e).

Algorithm 4.

Identified all positive items under the general (n, d, u, l, k, e) threshold model

1.	Use a (d + k − l, u; 2e + 1]-disjunct matrix of n columns.
2.	U ← φ
3.	for each u-subset X ⊆ S and k-subset R ⊆ S\Xdo
4.	compute t*(X)
5.	ift*(X) ≤ ethenU ← U ∪ {X}
6.	end for
7.	Arbitrarily choose an element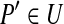
8.	while |P′| < ddo
9.	Flag ← 0
10.	for each (g + 1)-subset A ⊆ S\P′ and g-subset B ⊆ P′ do
11.	if any u-subset Y ⊆ (P′ ∪ A)\B satisfies 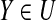thenFlag ← 1 and go to 13
12.	end for
13.	ifFlag = 1 thenP′ ← (P′ ∪ A)\B and |P′| ← |P′| + 1
14.	else returnP′
15.	end while
16.	returnP′

Proof

Similar to the proof of Theorems 4.4 and 4.5, we omit it.   ▪

The following result is immediate consequence of above discussion and Lemma 2.1.

Theorem 5.6

For the general (n, d, u, l, k, e) threshold model, there exist efficient nonadaptive algorithm that successfully identifies some set P′ with |P\P′| ≤ g and |P′\P| ≤ g, using no more than 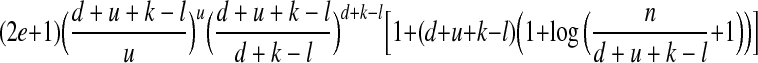tests. Moreover, the decoding complexity is O(n^u+k log n) for fixed parameters (d, u, l, k, e).

Obviously, the results of Chen and Fu (2009) is the particular case when k = 0 for the (n, d, u, l, k, e) threshold model. Furthermore, the decoding algorithm of the threshold model with k-inhibitors and at most e-erroneous outcomes and its decoding complexity O(n^u+k log n) are unrelated to the parameter q that is the most number of inhibitors.

Acknowledgments

This work was supported by the NSF of China (grant10971052).

Disclosure Statement

No competing financial interests exist.