Simultaneous Analysis of Multiple Data Types in Pharmacogenomic Studies Using Weighted Sparse Canonical Correlation Analysis

Abstract

Variation in drug response results from a combination of factors that include differences in gender, ethnicity, and environment, as well as genetic variation that may result in differences in mRNA and protein expression. This article presents two integrative analytic approaches that make use of both genome-wide SNP and mRNA expression data available on the same set of subjects: a step-wise integrative approach and a comprehensive analysis using sparse canonical correlation analysis (SCCA). In addition to applying standard SCCA, we present a novel modification of SCCA which allows different weighting for the various pair-wise relationships in the SCCA. These integrative approaches are illustrated with both simulated data and data from a pharmacogenomic study of the drug gemcitabine. Results from these analyses found little overlap in terms of genes detected, possibly detecting different biological mechanisms. In addition, we found the proposed weighted SCCA to outperform its unweighted counterpart in detecting associations between the genomic features and phenotype. Further research is needed to develop and assess new integrative methods for pharmacogenomic studies, as these types of analyses may uncover novel insights into the relationship between genomic variation and drug response.

Introduction

Variation in response to drug therapies is the result of a combination of many factors, including gene sequence variation, ultimately resulting in differences in mRNA and protein expression. Most of the current methods for analyzing high-dimensional genomic data have focused on analyzing a single data type, or experiment, at a time in a naive fashion. This naive one-at-a-time analysis approach ignores known biological information and the interaction between genes, proteins, and biochemical reactions, which may give rise to complex drug-related phenotypes. With the wealth of data being produced by new technologies, the collection of multiple types of genomic data on a set of samples is becoming commonplace.

Recently, multifactor approaches combining different types of genomic data have been used, in which a multistep procedure is employed to identify potential key drivers of complex traits integrating DNA variation and mRNA expression data (Hauser et al., 2003; Huang et al., 2008; Li et al., 2008; Schadt et al., 2005). Niu and associates (2010) used a step-wise integrative approach to find genes related to the response to radiation therapy. Another set of “integrative genomics” methods analyze the complete set of data in one comprehensive analysis, as opposed to a multistep procedure. One such approach is canonical correlation analysis (CCA; Hotelling, 1936). CCA focuses on maximizing the correlation between linear combinations of different sets of variables. However, when the number of variables far exceeds the number of subjects, as is the case for large-scale genomic studies, traditional CCA methods are no longer appropriate. To overcome this limitation, sparse canonical correlation analysis (SCCA) has recently been proposed for the analysis of two or three data sets (Parkhomenko et al., 2009; Waaijenborg et al., 2008; Witten and Tibshirani, 2009).

In this article, we compare these integrative analysis approaches, including the novel weighted SCCA, using data from a pharmacogenomics study of the cancer agent gemcitabine, in which genome-wide single-nucleotide polymorphisms (SNP) and mRNA expression have been collected on the same set of cell lines (Li et al., 2008, 2009). These methods are also applied to simulated data in which the “truth” is known. In this article, we focus on analysis methods that integrate multiple types of data into one comprehensive analysis, and propose a novel weighted SCCA method for analyzing high-dimensional data in pharmacogenomics studies.

Materials and Methods

Pharmacogenomic study of gemcitabine

To understand the pharmacogenomics of gemcitabine drug therapy, the Coriell Human Variation Panel (HVP) lymphoblastic cell lines were utilized, as previously described (Li et al., 2008, 2009). The HVP contains Epstein-Barr virus (EBV)-transformed B lymphoblastic cells from 100 Caucasians, 100 African-Americans, and 100 Han Chinese Americans. Cytotoxicity assays were performed at various drug doses, followed by estimation of the phenotype IC₅₀ (the effective dose that kills 50% of the cells), using a four-parameter logistic model (Gallant, 1987). The phenotypic variable IC₅₀ was used in the univariate and step-wise integrative methods, while the cytotoxicity values at the eight drug dose levels was used in the SCCA, which is designed for multiple variables. The cell lines have been genotyped using the Illumina HumanHap 550K. Following quality control, a total of 515,039 SNPs remained for integrative statistical analyses. SNPs were quantified as 0, 1, or 2, based on an additive genetic model in terms of the number of minor alleles. Genome-wide mRNA expression data were measured for the cell lines with the Affymetrix U133 Plus 2.0 expression array chip, with 54,613 probe sets available for analysis. In total, 172 cell lines (60 Caucasian, 53 African-American, and 59 Han Chinese American) had all three data types: gemcitabine cytotoxicity measurements, genome-wide mRNA expression data, and genome-wide SNP data.

Statistical analyses of the cell-line gemcitabine pharmacogenomic study

Univariate analyses

The expression array data were normalized on the log scale using guanine cytosine robust multi-array analysis (GCRMA; Bolstad et al., 2003; Wu et al., 2004). The normalized expression data on a log scale were then regressed on gender and race. Residuals from this regression were then standardized to arrive at a standardized adjusted expression value. IC₅₀ values were log transformed and adjusted in a fashion similar to that described for the basal gene expression data. Pearson correlation coefficients were then calculated for the adjusted standardized IC₅₀ and expression levels, followed by a Wald test of the association (p<0.0001).

For all analyses involving SNPs, adjustment for population stratification was completed as outlined in the works by Li and colleagues (2009) and Niu and associates (2010). Briefly, we used a principal component analysis (PCA) approach using genome-wide SNPs to adjust for population stratification (Price et al., 2006), in which PCA was completed by race, with the top five principal components saved. Using these components, the individual genotypes were adjusted. In a similar manner, the IC₅₀ values were log transformed and adjusted for gender and race using the five principal components. The resulting race-adjusted genotypes and IC₅₀ were then used in the genotype-phenotype correlation analysis. The SNP-IC₅₀, and the SNP-expression analyses, were completed in a similar manner.

Step-wise integrative analysis

Based on the univariate analysis results, SNPs associated with IC₅₀ were identified (p<0.0001). Since SNPs may control mRNA expression in either a cis- or a trans-manner, associations between these identified SNPs and genome-wide expression were completed, with SNP-expression associations identified (p<0.0001). Next, we determined if the expression probe sets identified to be associated with an SNP (with the SNP found to be associated with IC₅₀), were also associated with IC₅₀ (p<0.0001). This resulted in a set of candidate genes that could then be assessed for possible biological relevance with the drug. This approach is the same as the one followed by Niu and colleagues (2010).

SCCA integrative methods

CCA is a multivariate statistical method designed to explore the correlation between two sets of quantitative variables (Hotelling, 1936), and has been extended for the analysis of three or more data sets (Via et al., 2007). Suppose that three data sets X, Y, and Z, are of dimensions n×p, n×q, and n×r, with p≤n, q≤n, and r≤n measured on the same set of n subjects. Suppose that the columns of X, Y, and Z are standardized to have mean 0 and standard deviation 1. Let u, v, and w be p×1, q×1, and r×1 vectors of weights, and let ξ=Xu, η=Yv, and θ=Zw be the linear combinations of the variables in data sets X, Y, and Z, respectively, where ξ, η, and θ are n×1 vectors. The first canonical correlation (ρ) is then computed by maximizing the following equation:

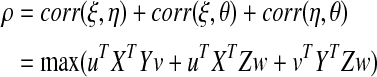[Eq. 1]

subject to u^T X^T Xu=v^T Y^T Yv=w^T Z^T Zw=1.

A limitation of CCA is that when the number of variables far exceeds the number of subjects, as is the case for large-scale genomic studies, the method is not applicable. To overcome this issue, a few important variables are selected using standard model selection criteria, and the canonical correlation is computed using the selected variables (Parkhomenko et al., 2009; Witten and Tibshirani, 2009), referred to as sparse canonical correlation analysis (SCCA). Mathematically, SCCA is performed by maximizing the penalized version of the expression in [Eq. 1] with penalties P₁(u), P₂(v), and P₃(w), placed on u, v, and w, respectively. In this article, maximization of [Eq. 1] and calculation of the loadings were carried out using the method described in Witten and Tibshirani (2009).

However, a disadvantage of the SCCA method is that it does not directly control the sparsity of solution, and as a result it is difficult to achieve effective dimension reduction (Lykou and Whittaker, 2010). Zhou and He (2008) proposed a two-step procedure that uses a BIC criterion, balancing the loss in the correlation and gain in the sparsity of variables. The procedure is carried out iteratively which is given as follows. The pair-wise canonical correlation coefficients (r_ij, r_jk, and r_ik) for the linear combination of the variables selected from SCCA are computed, with ρ_d defined as 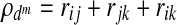, where ρ_d ranges from −3 to +3. Then the BIC value is estimated using

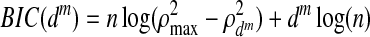[Eq. 2]

where d^m=p^m+q^m+r^m is the total number of parameters at the m^th iteration, n is the sample size, 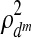is the square of the sum of the pair-wise correlation coefficients with d^m parameters, and 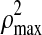is the square of the sum of maximum possible correlation coefficients (e.g., 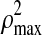=9 for the case involving three pair-wise correlations). Next, the variable with the smallest loading in absolute value is dropped and a new correlation and corresponding BIC value are computed. Thus, the variable filtering is carried out by dropping the variable with the smallest loading at each iteration, followed by the re-computation of the first canonical correlation and the BIC value. The variables corresponding to the minimum BIC value are then selected.

Another limitation of the current definition of SCCA for more than two data sets deals with the fact that the maximization involves the sum of pair-wise correlations of the linear combination of variables among the three data sets. That is, all pairs of correlations are given equal weights, which may not be appropriate in pharmacogenomic studies. In particular, the component representing the correlation between the SNP and expression data can dominate the analysis, with SNP and expression variables being selected that have no relationship with the phenotypes. Therefore, we propose a novel weighted SCCA for analysis of three data sets that allows for weighting of the different pair-wise correlation within the objective function with

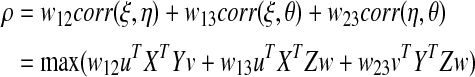[Eq. 3]

subject to u^T X^T Xu=v^T Y^TYv=w^T Z^T Zw=1. For example, in the SCCA of cytotoxicity, expression, and SNP data, one could select variables that maximize the sum of the correlation between the cytotoxicity – expression and cytotoxicity – SNP, with w₁₂=w₁₃=1, thus removing the component representing the correlation between SNP and expression (w₂₃=0). The BIC function is then adjusted accordingly for weighted SCCA using

[Eq. 4]

where 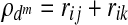, ranging from −2 to +2, and therefore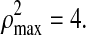

Finally, since applying SCCA to genome-wide SNP data is still computationally intensive, the following dimension reduction steps were completed prior to SCCA. SNPs were partitioned into bins based on their correlation using hierarchical clustering with a liberal threshold of 0.05 (Rinaldo et al., 2005), followed by PCA for the SNPs within the bin. The first principal component for each bin of SNPs was used in the model as the “genetic” variable, as opposed to the individual SNP genotypes. A similar PCA approach has often been carried out for SNPs in a candidate gene to capture the variation of those SNPs within the locus (Gauderman et al., 2007). This approach resulted in 3135 “genetic” factors to be included in the analysis. Adjustment of population stratification and covariates was completed in a similar manner as that outlined for the univariate analysis, with SCCA based on the residuals.

Results

Gemcitabine pharmacogenomic study

Univariate analysis

Five SNPs (Table 1A) were detected with p<10⁻⁵ (6.14×10⁻⁷ to 8.53×10⁻⁶), and nine loci (regions with more than one SNP with p<0.0001) found to be associated with IC₅₀. These regions corresponded to genes PIK3R1, TGFBI, HLA-DRA, MCPH1/ANGPT2, CLDN23, NIPSNAP3A/B, LOC100128586, RAB27A/PIGB, and NPM1P3. Results for these loci are also presented in Table 1B. Analysis of mRNA expression and IC₅₀ detected a total of 261 probe sets associated with IC₅₀ with p<0.0001. The probe sets with p<10⁻⁶ are listed in Table 2. Multiple probe sets in the genes FKBP5, VARS, and VAV3 were found to be associated with gemcitabine IC₅₀.

Table 1.

(A) Univariate SNP-IC₅₀ Associations with p<10⁻⁵ from Univariate Analysis of the Gemcitabine Study. (B) Nine loci (Regions with More Than One SNP with p<0.0001) associated with IC₅₀

	SNP	Chromosome	Position	Nearest gene	MAF	Correlation	p
(A)	rs4272382	8	8470898	CLDN23	0.132	−0.39	6.1E-07
	rs3775182	4	87198607	MAPK10	0.109	0.38	9.6E-07
	rs2290344	15	53407088	PIGB	0.254	0.36	3.6E-06
	rs10761082	9	106555990	NIPSNAP3A	0.36	0.36	4.9E-06
	rs2472476	9	106571777	NIPSNAP3B	0.389	0.35	8.5E-06
(B)	rs7713001	5	67999371	PIK3R1	0.459	−0.32	4.5E-05
	rs12188464	5	67999705	PIK3R1	0.459	−0.32	4.5E-05
	rs13171512	5	68000787	PIK3R1	0.462	−0.32	3.9E-05
	rs2107331	5	135405248	TGFBI	0.456	−0.34	1.5E-05
	rs2282791	5	135405629	TGFBI	0.477	0.32	4.3E-05
	rs7192	6	32519624	HLA-DRA	0.374	0.31	5.7E-05
	rs3129890	6	32522251	HLA-DRA	0.342	0.34	1.0E-05
	rs2922876	8	6384104	MCPH1; ANGPT2	0.164	−0.31	7.2E-05
	rs1375668	8	6384278	MCPH1; ANGPT2	0.363	−0.31	9.1E-05
	rs4272382	8	8470898	CLDN23	0.132	−0.39	6.1E-07
	rs4595128	8	8471286	CLDN23	0.202	−0.32	3.2E-05
	rs10761082	9	106555990	NIPSNAP3A	0.36	0.36	4.9E-06
	rs2472476	9	106571777	NIPSNAP3B	0.389	0.35	8.5E-06
	rs12244977	10	58762688	LOC100128586	0.19	−0.31	9.4E-05
	rs12256364	10	58765694	LOC100128586	0.19	−0.31	9.4E-05
	rs12050885	15	53345916	RAB27A	0.379	0.33	2.2E-05
	rs11636687	15	53392444	PIGB	0.42	0.32	5.3E-05
	rs2290344	15	53407088	PIGB	0.254	0.36	3.6E-06
	rs12050587	15	53414820	PIGB	0.45	0.32	5.0E-05
	rs8024695	15	53426597	PIGB	0.287	0.34	1.4E-05
	rs11639680	16	5500905	NPM1P3	0.193	0.33	2.8E-05
	rs4511535	16	5506393	NPM1P3	0.199	0.31	6.0E-05

MAF, minor allele frequency; SNP, single-nucleotide polymorphism; IC₅₀, effective dose that kills 50% of cells.

Table 2.

Expression Probe Set-IC₅₀ Associations with p<10⁻⁶ from Univariate Analysis of the Gemcitabine Study

Probe set	Chromosome	Gene	Correlation	p
202092_s_at	16	ARL2BP	−0.38	2.6E-07
212437_at	20	CENPB	−0.39	8.3E-08
226017_at	3	CMTM7	−0.36	8.9E-07
211118_x_at	14	ERS2	0.39	6.7E-08
224856_at	6	FKBP5	−0.41	2.1E-08
204560_at	6	FKBP5	−0.39	9.6E-08
224840_at	6	FKBP5	−0.37	5.6E-07
205164_at	22	GCAT	−0.39	9.9E-08
230362_at	10	INPP5F	−0.39	5.9E-08
210644_s_at	19	LAIR1	−0.38	1.7E-07
203726_s_at	18	LAMA3	−0.44	1.2E-09
212715_s_at	22	LOC731210; MICAL3	−0.38	2.3E-07
225391_at	4	LOC93622	−0.36	9.0E-07
206571_s_at	2	MAP4K4	−0.37	5.1E-07
204880_at	10	MGMT	0.40	5.4E-08
209853_s_at	17	PSME3	−0.37	5.5E-07
209815_at	9	PTCH1	0.36	8.8E-07
204759_at	13	RCBTB2	0.37	5.9E-07
205645_at	23	REPS2	−0.36	8.1E-07
224338_s_at	11	RNF26	−0.39	1.2E-07
201796_s_at	6	VARS	−0.40	2.5E-08
201797_s_at	6	VARS	−0.37	3.4E-07
218807_at	1	VAV3	−0.38	1.4E-07
218806_s_at	1	VAV3	−0.37	5.7E-07

IC₅₀, effective dose that kills 50% of cells.

Step-wise integration approach

For the step-wise integration analysis approach, 58 SNPs were found to be associated with IC₅₀ (p<0.0001). For these 58 SNPs, cis- and trans-associations with gene expression were determined. We found associations with 468 unique expression probe sets (538 associations with p<0.0001). In particular, SNP rs922369 (chromosome 10, bp 71020137, 5′ upstream of the gene NEUROG3), was associated with 60 unique expression probe sets, and rs2472476 (chromosome 9, bp 106571777, intronic to NIPSNAP3B and 3′ downstream of NIPSNAP3A) was associated with 41 probe sets. The SNP rs2472476 was also in a locus associated with IC₅₀ containing SNP rs10761082.

Subsequently, the association of these 468 probe sets with IC₅₀ determined 21 probe sets associated with IC₅₀ (p<0.0001). These results are displayed in Table 3. In addition to the gene PIGB detected by the SNP-IC₅₀ analyses, and FKBP5 detected by the expression-IC₅₀ analyses, these two genes were also detected via the three-way step-wise analysis. The four SNPs in PIGB associated with IC₅₀ (p<0.0001) were also found to regulate the expression of PIGB, with the most significant association found between the four SNPs and mRNA expression (242760_x_at) observed for rs2290344 (p=2.55×10⁻¹⁰). This probe set was also found to be associated with IC₅₀ (p=8.98×10⁻⁵), indicating that the SNPs may be indirectly affecting gemcitabine IC₅₀ through the expression of PIGB. In addition, Table 3 presents 15 novel candidate genes detected through a trans mechanism. In particular, SNP rs922369 (chromosome 10; minor allele frequency [MAF]=0.25) in NEUROGF3 was associated with IC₅₀ (p=4.88×10⁻⁵) and mRNA expression for genes TMEM142B, MTRF1, and a cDNA, with the probe sets for these genes also associated with IC₅₀ through a trans mechanism (Table 4).

Table 3.

Twenty-One Probe Sets Found to Be Associated with Gemcitabine IC₅₀ Based on a Step-Wise Integrative Approach

Probe set	Chromosome	Gene	Correlation	p
218812_s_at	7	TMEM142B	−0.29	6.7E-05
219798_s_at	7	BCDIN3	−0.32	1.6E-05
219822_at	13	MTRF1	0.30	5.8E-05
231406_at	7	—	−0.34	3.6E-06
1569396_at	16	RAB40C	0.30	5.4E-05
1570537_a_at	8	—	0.32	1.1E-05
225086_at	15	FAM98B	−0.35	2.1E-06
204560_at	6	FKBP5	−0.39	9.6E-08
242760_x_at	15	PIGB	−0.29	8.9E-05
228832_at	4	FLJ20021	0.29	8.1E-05
203099_s_at	6	CDYL	−0.32	1.0E-05
219338_s_at	15	LRRC49	−0.30	6.1E-05
244276_at	4	KLB	0.30	3.8E-05
231851_at	1	RAVER2	−0.29	6.6E-05
236170_x_at	7	HERPUD2	−0.29	6.7E-05
225391_at	4	LOC93622	−0.36	9.0E-07
203706_s_at	2	FZD7	−0.30	4.7E-05
213056_at	3	FRMD4B	−0.30	6.3E-05
219098_at	17	MYBBP1A	−0.33	8.3E-06
230908_at	2	—	−0.35	1.8E-06
200988_s_at	17	PSME3	−0.35	2.6E-06

IC₅₀, effective dose that kills 50% of cells.

Table 4.

Results for rs922369 (NEUROGF3) Observed to be Associated with Gemcitabine Trans-Acting Manner Through Expression

mRNA expression			rs922369 Expression analysis		Expression IC50 analysis
Probe set	Gene	Chromosome	Correlation	p	Correlation	p
218812_s_at	TMEM142B	7	−0.28	2.0E-06	−0.29	6.7E-05
219798_s_at	BCDIN3	7	−0.25	2.2E-05	−0.32	1.6E-05
219822_at	MTRF1	13	0.29	1.0E-06	0.30	5.8E-05
231406_at	cDNA	7	−0.26	1.1E-05	−0.34	3.6E-06

IC₅₀, effective dose that kills 50% of cells.

SCCA approach

Using the standard (unweighted) SCCA applied to the SNP, mRNA expression, and cytotoxicity data sets, resulted in the selection of 182 genetic variables (defined as the first principal component for the linkage disequilibrium [LD]-based binned SNPs), 2581 expression probe sets, and 2 cytotoxicity variables (doses of 10 μM and 1000 μM) with a SCCA coefficient of 1.0299. The pair-wise SCCA coefficients were: correlation(genotype, expression)=0.734, correlation(genotype, cytotoxicity)=0.153, and correlation(expression, cytotoxicity)=0.143. Applying the BIC-type variable filtering method resulted in a more sparse solution, with only five genetic variables, one expression probe set (215301_at), and one cytotoxicity variable (10 μM) selected. The selected probe set 215301_at corresponds to genes SYCE1L and LOC400547, located at chromosome 16 and position 75804375–75809512. This probe set was not significantly associated with IC₅₀ in univariate analysis (p=0.30). The five selected genetic variables correspond to bins consisting of 106, 220, 7, 9, and 10 SNPs, respectively (a total of 352 SNPs). Three of these SNPs, rs4074037, rs3811259, and rs2930629, were among the SNPs obtained from the univariate SNP IC₅₀ analyses (p=0.0098, 0.0053, and 0.0044, respectively). There were no common SNPs detected from the unweighted SCCA and step-wise approach. Out of 352 total SNPs, the 25 most “important” SNPs with largest first principal component loadings, together with their positions and associated genes, are listed in Table 5A.

Table 5.

SCCA Results, Following BIC Filtering, for the Gemcitabine Pharmacogenomic Study

	SNP	Chromosome	Position	Gene
(A)
	rs3766117a	1	167794480	F5
	rs1894701a	1	167797210	F5
	rs7545236a	1	167796694	F5
	rs6022a	1	167796450	F5
	rs6128a	1	167829528	SELP; F5
	rs6678795	1	167799890	F5
	rs1335532	1	116902480	CD58
	rs6427202	1	167795454	F5
	rs10924103	1	116838074	LOC148766
	rs800292	1	194908856	CFH
	rs505102	1	194886125	CFH
	rs10802189	1	116858253	CD58
	rs10145908	14	62823082	RHOJ
	rs4457900	14	60759645	TMEM30B
	rs3783814	14	60869673	PRKCH
	rs1139130a	14	21037756	TOX4; METTL3
	rs2297093a	14	21025196	TOX4
	rs933192a	14	21033649	TOX4; METTL3
	rs4417466a	14	21042491	TOX4; METTL3
	rs6571850a	14	21020676	TOX4; RAB2B
	rs719785	14	21048133	METTL3
	rs7179423a	15	23471534	ATP10A
	rs2930629a	15	23469059	ATP10A
	rs7181116a	15	23471769	ATP10A
	rs2066711a	15	23474311	ATP10A
(B)
	rs12345642	9	137870884	CAMSAP1
	rs7852055	9	137835056	CAMSAP1, LOC100131786
	rs10116440	9	137896193	CAMSAP1
	rs10858179	9	137945755	UBAC1
	rs12972385	19	5842052	NDUFA11
	rs1678868	19	5843954	NDUFA11
	rs8108064	19	5854807	NDUFA11,VMAC
	rs1015048	21	32871177	TCP10L,C21orf77
	rs1015047	21	32871294	TCP10L,C21orf77
	rs2833890	21	32849757	C21orf77
	rs2833902	21	32862329	C21orf77,TCP10L

^aDetected in both unweighted and weighted SCCA.

SNPs with the highest loadings in the first principal component from selected bins are presented: (A) unweighted SCCA, and (B) weighted SCCA.

SNP, single-nucleotide polymorphism; SCCA, sparse canonical correlation analysis.

When the weighted SCCA was applied to the gemcitabine pharmacogenomic study, 57 genetic variables, 874 expression probe sets, and 2 cytotoxicity variables were selected. The sparse canonical correlation was 0.3611 (correlations between genotype and cytotoxicity equal to 0.1902, and expression and cytotoxicity equal to 0.1709). After applying the BIC filter, only 13 genetic variables, 7 expression probe sets, and 1 cytotoxicity (dose 10 μM) variable were selected. However, these probe sets (1556404_a_at, 1557921_s_at, 1559336_at, 1565742_at, 1566970_at, 215301_at, and 239006_at) were not significantly associated with IC₅₀ in expression-IC₅₀ analyses. The selected genetic variables correspond to bins consisting of 106, 45, 16, 127, 220, 7, 9, 37, 108, 18, 56, 44, and 10 (total of 803 SNPs). Out of these 803 SNPs, rs9651539, rs778972, rs739236, and rs1107514, were also detected in the univariate SNP-IC₅₀ analyses (p=0.0005, 0.0009, 0.0009, and 0.0009, respectively). The 25 most important SNPs with the largest principal component loadings are listed in Table 5A and B, together with their position and associated genes.

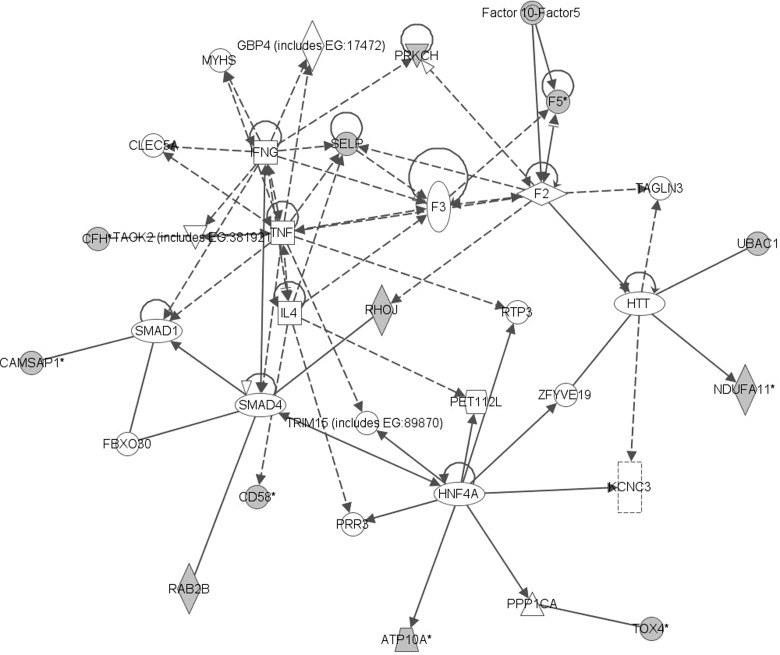
These novel genes detected from SCCA might represent additional mechanisms that could contribute to gemcitabine sensitivity. Therefore, we completed a pathway analysis of these genes using Ingenuity Pathway Analysis (IPA; Ingenuity Systems, Redwood City, CA, USA). This software consists of a curated database and several analysis tools to obtain pathways and networks associated with a set of genes. Networks are constructed in IPA with a set of genes by first identifying other molecules in the IPA database that have evidence of interacting with these genes, and then maximizing the connectivity of these components. The scores of the constructed networks indicate how well the network is “fit” to the set of genes input, and is the log-transformed value of a right-tailed Fisher's exact test result. The top network identified was the TNF pathway (score of 32), and involved 13 of the 16 genes input (Fig. 1). This pathway is extremely important in the inflammatory response and cancer development. Therefore, future functional and mechanistic studies would help to validate this finding.

FIG. 1.

Network showing the top network (TNF pathway) detected with Ingenuity Pathway Analysis.

Comparison of the approaches

The standard SCCA method selected 5 SNP bins, 1 mRNA expression probe set, and 1 cytotoxicity variable, while the weighted SCCA method selected 13 bins of SNPs, 7 mRNA expression probe sets, and 1 cytotoxicity variable. All the variables selected by unweighted SCCA were also selected by weighted SCCA. Comparing the SCCA results with the univariate approach, 4 SNPs (rs9651539, rs778972, rs739236, and rs1107514) from the weighted SCCA method were found to have a significant association with IC₅₀ (p values range from 0.0005−0.0009). However, the SNPs selected from the unweighted SCCA method were not found to have a significant association with IC₅₀ (at p<0.001 level). Also, the mRNA variables selected by both the unweighted and weighted SCCA methods were not detected by either the univariate (p>0.05) or the step-wise analyses. The univariate and step-wise analyses identified several genes in common. The gene PIGB was both detected by the step-wise model and univariate SNP-IC₅₀ analyses. Similarly, gene FKBP5 was detected by both the step-wise and univariate expression-IC₅₀ analyses. In addition, the step-wise method detected 15 novel candidate genes not detected by either the univariate SNP-IC₅₀ or expression-IC₅₀ analysis.

Description of simulated data

Simulation of the genotype data was based on the SNPs within the gemcitabine pathway for the Caucasian HVP cell lines. SNPs mapped to the gemcitabine pathway, which passed quality control, were identified resulting in 749 SNPs in 19 genes. The 19 genes within the pathway were mapped to chromosomes, and haplotypes were phased using the program fastPHASE (Scheet and Stephens, 2006). These haplotype frequencies were used as the “true” haplotype frequencies for the underlying population, with haplotypes simulated using the hapsim library in R (http://cran.r-project.org/web/packages/hapsim/index.html). These haplotypes were then assigned in a sequential fashion to the 200 individuals, producing simulated genotypes for SNPs that mimic realistic LD for the regions in which they lie.

Following the simulation of the genotype data for n=200 subjects, mRNA gene expression data were simulated, such that a few SNPs in the pathway were correlated with mRNA expression levels. The expression data for each individual were simulated using a multivariate normal distribution X∼MVN(μ_i, Σ_X), for which the mean vector for subject i, μ_i=G_i×B, is based on the effect matrix B and subject i's vector of genotypes G_i. Next, SNPs were selected to be associated with gene expression, with an effect size k for those SNP-expression pairs, the effect matrix B is defined as

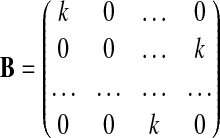[Eq. 5]

with the number of rows equal to the number of SNPs and the number of columns equal to the number of expression variables. Using the mean vector μ_i, and a covariance matrix (Σ_X) based on the observed correlation structure between the mRNA expression values within the gemcitabine pathway, expression data for individual i were simulated. Three SNPs, rs2840075, rs3781281, and rs7776847, were chosen to be associated with three expression variables 203302_at, 209155_s_at, and 223298_s_at, respectively. The effect size was varied, with either a small effect (k=0.3), or a large effect (k=0.6).

Finally, the cytotoxicity values for each individual were generated from a multivariate normal distribution 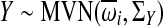. The mean of the distribution was based on the four-parameter logistic function

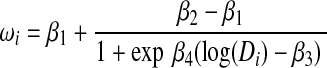[Eq. 6]

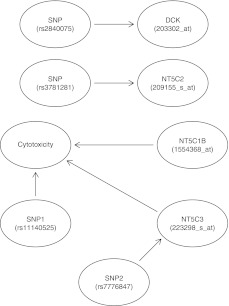
where the responses at infinite and zero concentration are represented by β₁ and β₂, respectively. The parameter β₃ represents log(IC₅₀), β₄ represents the slope of the dose-response curve, and D_i is one of the eight gemcitabine drug concentrations. The parameters β₁, β₂, and β₄ in the four-parameter logistic model were set to 10, 95, and 1.5, respectively. The covariance matrix Σ_Y was estimated from the gemcitabine cytotoxicity data. For simulations with a genetic effect on the phenotype IC₅₀, β₃ was based on the direct effects of two expression probe sets: direct effect of one SNP, and indirect effect of an additional SNP. The genes with mRNA expression affecting the cytotoxicity were NT5C3 and NT5C1B. The SNPs impacting cytotoxicity were rs11140525 and rs7776847. The simulation scenario is depicted in Figure 2. For each effect size (k=0.3 or 0.6), 100 simulations were run with the aforementioned settings.

FIG. 2.

Simulation scenario in which the genotype and expression variables have direct and indirect effects on cytotoxicity. Two genes, NT5C3 and NT5C1B, with probe sets 223298_s_at and 1554368_at, have direct effects on cytotoxicity. SNP rs11140525 has a direct effect and SNP rs7776847 has an indirect effect on cytotoxicity.

Simulation study results

Univariate results

Pearson correlation coefficients were calculated for all possible pairs of variables, followed by a test of association using a Wald test with Fisher's transformation and Bonferroni correction for multiple testing. To compare the methods, the proportion of times the true variables were selected (PTTS), and the average number of false-discovery (AvgFD) were computed. AvgFD was computed by adding all the false-positive variables across all simulations divided by the number of simulations. Therefore, a good analysis method is one with high PTTS and low AvgFD. To adjust for multiple testing, a Bonferroni correction was applied for which the significance threshold was set to 0.001 for the mRNA-IC₅₀ comparisons, 10⁻⁴ for the SNP-IC₅₀ comparisons, and 10⁻⁵ for the SNP-mRNA comparisons due to differing number of tests in these categories. The results are displayed in Table 6A.

Table 6.

Results from Univariate (A), and Unweighted and Weighted SCCA (B) Integrative Analyses of Simulated Data

Analysis approach	Variable/associations	PTTS % (k=0.6)	PTTS % (k=0.3)
(A) Univariate analysis	rs2840075-203302_at	61	25
	rs3781281-209155_s_at	86	37
	rs7776847-223298_s_at	59	31
	rs11140525-IC50	87	58
	rs7776847-IC50	66	18
	223298_s_at-IC50	100	86
	1554368_at-IC50	91	79
(B) Unweighted SCCA	rs11140525	61	53
	rs7776847	72	41
	223298_s_at	66	57
	1554368_at	33	30
Weighted SCCA	rs11140525	63	51
	rs7776847	77	40
	223298_s__at	86	64
	1554368_at	77	43

PTTS, proportion of times the true variables were selected; SCCA, sparse canonical correlation analysis.

For the larger effect size (k=0.6) simulations, all three pairs of the univariate analysis selected the simulated effects with good power. In particular, when the number of tests was smaller (e.g., expression-IC₅₀ analysis), the true variables were selected by almost every simulation (100% and 91% of simulations for 223298_s_at and 1554368_at, respectively). However, when the effect size was decreased to 0.3, the PTTS values were reduced for all three univariate analyses. This reduction in PTTS was larger for the SNP-expression analyses, with the maximum reduction being 49% for the association between rs3781281 and 209155_s_at. The reduction in the PTTS value was also evident for the SNP rs7776847 in the SNP-IC₅₀ analysis, which was simulated to have an indirect effect on IC₅₀ via NT5C3 (probe set 223298_s_at). In addition to the impact on PTTS, as the effect size decreased the avgFD also decreased, with changes in avgFD of: (1) 0.05 and 0.12 for detecting false expression effects from the associations with SNP and IC₅₀, respectively; and (2) 2.68 and 0.81 for detecting false SNP effects from associations with expression and IC₅₀, respectively. For all simulation pairs, the false-positives were scattered among the remaining pairs, with no pair being detected in more than 8% of simulations.

Step-wise integration approach

For the step-wise integrative approach, SNPs associated with cytotoxicity variables were selected with p<10⁻⁴. Then for these selected SNPs, the associations with genome-wide mRNA expression variables was assessed, with mRNA probe sets selected with p<10⁻⁵. Finally, the association of these expression variables with cytotoxicity was determined with mRNA expression probe sets selected to be associated with IC₅₀ at the 0.001 significance level. The focus of the step-wise approach lies in determining the expression variables associated with IC₅₀, given that an SNP was associated with IC₅₀ and expression of the gene; therefore we focused on the proportion of times the NT5C3 gene was selected. The gene NT5C3 (probe set 223298_s_at) was detected in 46% of simulations when the effect size was k=0.6, and 18% of the time when the effect size was k=0.3. The AvgFD was 0.23 and 0.12 when k was 0.6 or 0.3, respectively.

SCCA Approach

Weighted and unweighted SCCA, with an additional BIC step, were applied to the simulated data, with results presented in Table 6B. PTTS values were smaller for the smaller effect size (k=0.3), with similar results for detecting SNP effects between the weighted and unweighted SCCA. However, a larger difference was observed for detection of expression effects between the two SCCA approaches, with higher PTTS rates observed for the weighted SCCA, compared to the unweighted SCCA. The AvgFD values for SNP and mRNA expression analyses were 0.68 (2.24) and 0.26 (0.77), when k=0.6 (k=0.30) for the unweighted SCCA. Similarly, for weighted SCCA, the false-detection rate increased when the effect size decreased. The AvgFD for SNP and expression were 1.57 (1.69) and 0.55 (0.63), when k=0.6 (k=0.30). The selected false variables appeared to be random, and none of the variables were selected in more than 7% of simulations.

Comparison of approaches

The simulation study showed that when the variables are strongly associated with a large effect size (k=0.6), and if the number of tests conducted was relatively small (e.g., expression-IC₅₀ pairs), the univariate approach was able to detect almost all simulated true variables (223298_s_at 100% and 1554368_at 91%). There were fewer true variables selected when the number of comparisons was increased. The SNP-IC₅₀ correlation had the second largest number of tests, and the SNP rs11140525 was selected in 87% of simulations, and SNP rs7776847 was selected in 66%. The SNP expression pair had the largest number of tests, and the true pairs rs2840075-203302_at, rs3781281-209155_s_at, and rs7776847-223298_s_at, were detected in 61%, 86%, and 59% of simulations, respectively. However, when the variables are moderately or even weakly associated (k=0.3), and if the number of tests being conducted is large (e.g., SNP-expression pairs), there was a substantial decrease in the number of true associations detected (the pairs rs2840075-203302_at from 61 to 25%, rs3781281-209155_s_at from 86 to 37%, and rs7776847-223298_s_at from 59 to 31%). However, the fall in the PTTS was smaller when the number of comparisons was smaller in expression-IC₅₀ (14% fall in PTTS for 223298_s_at, and 12% fall in PTTS for 1554368_at). In particular, the PTTS for SNP rs7776847, which was simulated to have an indirect effect with IC₅₀, dropped by 48%, even though the number of tests was moderate.

In contrast, as the effect size decreased, there was less of a drop in the PTTS for the weighted and unweighted SCCA (compared to the univariate approach). In particular, the SCCA methods were able to detect the smaller indirect effect (k=0.3) better than the univariate method (e.g., rs7776847 PTTS of 40–41% versus 18%). Comparing unweighted and weighted SCCA methods, the simulation studies show that the weighted SCCA method is generally better able to detect the true associations between the genotypic and phenotypic variables. Since the focus in pharmacogenomics studies is to determine genomic variables (e.g., SNP and mRNA) associated with drug response, the novel weighted SCCA method may reveal more relevant associations.

Discussion and Conclusions

In this article, we have described several integrative analysis methods that could be applied to pharmacogenomic studies involving multiple types of genome-wide genomic data collected on the same set of subjects. Each of these methods has its benefits and limitations. Univariate analysis approaches, in which each data type is analyzed individually for the association with the phenotype, has been widely used in genome-scale studies. This method allows application of computationally efficient, standard statistical methods. However, the interpretation of the results after millions of tests have been performed for each data type is challenging. In addition, the univariate analysis approach only considers one pair of variables at a time, ignoring other variables which might influence them (i.e., expression quantitative trait loci [eQTL]). As a result, it is difficult to assess complex relationships between the multiple types of genomic data and the drug-response phenotype of interest.

The second method described involves a step-wise approach to integrate SNP and expression data for the selection of candidate genes associated with drug response. In this approach, the relationships between genetic variants (e.g., SNPs) and the phenotype are assessed individually. Variants detected from the pair-wise analysis are then carried forward to determine their association with mRNA expression, followed by the assessment of the significant mRNA probe sets identified with the phenotype. Therefore, this approach for the selection of candidate genes integrates both genetic and mRNA variations. However, the mRNA expression of genes associated with the phenotype could be missed if an SNP was not selected in the step-wise procedure to be associated with the gene's mRNA expression levels. SCCA overcomes this limitation of the step-wise approach, in which a comprehensive integrative analysis is completed to identify candidate genes associated with the drug-response phenotypes. Currently, however, application of existing SCCA methods to high-dimensional data is computationally intensive.

In terms of choice of the phenotype used for the univariate and step-wise analyses, we chose the commonly used summary measure of the dose-response curve, the IC₅₀ (Huang et al., 2008; Li et al., 2008, 2009; Niu et al., 2010). In their research, Fridley's group developed a Bayesian hierarchical nonlinear model to model the genomic effects within a pathway on the entire dose-response curve (Fridley et al., 2009). However, this approach is computationally intensive and cannot be scaled up to genome-scale data. In contrast to the univariate analyses, SCCA is designed to be applied to a set of variables. Therefore, we chose to use all cytotoxicity values, as opposed to the summary measures of IC₅₀, for application of SCCA to the gemcitabine study. However, the SCCA method did not explicitly model the dose-response relationship between the cytotoxicity values and the drug dose. Future work is needed to extend the weighted SCCA to incorporate this dose-response relationship, possibly using an approach similar to that proposed by Leurgans and colleagues (1993).

The application of these analytical approaches to the pharmacogenomic study of the anti-cancer agent gemcitabine, along with their application to simulated data, demonstrated the utility of each of these approaches. These results show that for studies with the goal of finding a large to moderate effect between genomic and phenotypic variables, the simple univariate analysis may be adequate. However, for studies with a large number of variables, if the association between the genomic variables and the phenotype is small to moderate, the univariate analysis method may be unable to detect the association, after adjusting for multiple testing. In contrast, if the true underlying relationship is more complex, a more comprehensive integrative analysis approach, such as SCCA, may be more suitable. For such comprehensive studies, we found that our novel weighted SCCA method outperformed the standard (non-weighted) SCCA method. However, the results from the weighted or unweighted SCCA method do not fully agree with univariate and step-wise methods. It should be noted that a limitation of our implementation of SCCA here is that we have used PCA to reduce the dimensionality of the SNPs, creating bins of SNPs. This was done since there was no feasible way, computationally, to complete SCCA on individual SNP data from large arrays. This may result in loss of information, and therefore could contribute to the differences seen between the results of other methods. Further research is required to improve the performance of the weighted SCCA method, such as enabling it to handle large numbers of variables, and determining the optimal values of weights for the maximization function. In addition, we suggest a sensitivity analysis (i.e., run analyses with a variety of thresholds and determine the impact of differing cut-points on the results).

In conclusion, applying integrative analysis methods to studies involving multiple types of genomic data may lead to novel hypotheses to be tested in future studies. For example, applying SCCA to the pharmacogenomic study of gemcitabine detected a large number of genes involved in the TNF pathway, which may contribute to gemcitabine drug response, as this pathway is extremely important in the inflammatory response and cancer development. Future functional and mechanistic studies would help to validate this finding. In addition to following-up novel hypotheses developed from integrative analysis, further research is needed to develop powerful integrative methods that are able to detect complex relationships in pharmacogenomic studies. Application of such integrative methods may uncover additional insights into the relationship between genomic variation and drug response.

Acknowledgments

This research was supported by the National Institutes of Health (grants CA140879, CA130828, CA138461, CA102701, GM61388, and GM86689), the Minnesota Partnership for Biotechnology and Medical Genomics, and the Mayo Foundation. The funders had no role in study design, data collection and analysis, the decision to publish, or preparation of the manuscript.

Author Disclosure Statement

No competing financial interests exist.