Abstract
In this paper, a simple theoretical model is developed to describe the transmission of force from interstitial fluid flow to the surface of a cell covered by a proteoglycan / glycoprotein layer (glycocalyx) and embedded in an extracellular matrix. Brinkman equations are used to describe flow through the extracellular matrix and glycocalyx layers and the solid mechanical stress developed in the glycocalyx by the fluid flow loading is determined. Using reasonable values for the Darcy permeability of extracellular matrix and glycocalyx layers and interstitial flow velocity, we are able to estimate the fluid and solid shear stresses imposed on the surface of embedded vascular, cartilage and tumor cells in vivo and in vitro. The principal finding is that the surface solid stress is typically one to two orders of magnitude larger than the surface fluid stress. This indicates that interstitial flow shear stress can be sensed by the cell surface glycocalyx, supporting numerous recent observations that interstitial flow can induce mechanotransduction in embedded cells. This study may contribute to understanding of interstitial flow-related mechanobiology in embryogenesis, tumorigenesis, tissue physiology and diseases and has implications in tissue engineering.
Keywords: Mechanotransduction, Flow sensing, Smooth muscle cell, Cancer cell, Collagen gel, 3-dimensional
1 Introduction
Endothelial cells that line blood vessel walls are covered with a glycocalyx layer of proteoglycans and glycoproteins that are in contact with blood (in vivo) or culture media (in vitro). The glycocalyx layer has been described as a mechanosensor and transducer of fluid shear stress on endothelial cells (Florian et al. 2003; Pahakis et al. 2007; Tarbell and Ebong 2008; Tarbell and Pahakis 2006; Thi et al. 2004; Weinbaum et al. 2007; Yao et al. 2007). The Brinkman equation has often been used to describe flow through the porous glycocalyx layer (see Weinbaum et al. 2007 for a review). Using reasonable values for the Darcy permeability of the porous layer and thickness of the glycocalyx, it has been estimated that the fluid shear stress on the endothelial plasma membrane is negligibly small compared to the fluid shear stress imposed at the outer edge of the glycocalyx layer. Instead, most of the imposed shear at the outer edge is transmitted to the solid fibers of the glycocalyx and then distributed to the plasma membrane as a solid mechanical force. Various models have been developed to describe this solid force transmission process (reviewed in Weinbaum et al. 2007), including the simple model presented in Secomb et al. (2001) that we will apply in the present work. This approach employs the Brinkman model to describe fluid flow through the porous glycocalyx layer and mechanical equilibrium of forces in the flow direction to calculate the solid force in the glycocalyx matrix.
Smooth muscle cells and fibroblasts within the artery wall are exposed to interstitial flow driven by the transmural pressure differential across the wall, and this interstitial flow is transduced by the suspended cells into alterations of their gene and protein expression, migration and contraction (Shi et al. 2009, 2010a,b, 2011; Wang and Tarbell 2000), reviewed in Shi and Tarbell (2011). Wang and Tarbell (1995) used the Brinkman model to describe fluid flow around such suspended cells by assuming they were embedded in a uniform extracellular matrix (Darcy media) and were able to calculate the fluid shear stress on the cell surface associated with interstitial flow for various cell packing configurations. Other cell types suspended in matrix are also exposed to interstitial flow shear stresses and associated convective forces. Cancer cells in solid tumors have been studied recently in this regard (Qazi et al. 2011; Shieh and Swartz 2011; Shieh 2011). It has been suggested that since the predicted fluid shear stresses on cell surfaces are so low (order 0.1 dyn/cm2), they are unlikely to drive mechanotransduction and that mass transport mechanisms are more likely responsible for observed interstitial flow effects.
Most recently, however, it has been observed that vascular smooth muscle cells suspended in type I collagen gels and exposed to physiological interstitial flows have an extra-cellular glycocalyx layer that serves as a mechanotransducer (Shi et al. 2010a, 2011; Shi and Tarbell 2011). However, how the embedded cells sense interstitial flows through the glycocalyx layer remains unknown. A glycocalyx layer covers the surface of all eukaryotic cells including tumor cells and stem cells (Krahling et al. 2009; Nairn et al. 2007; Harfouche et al. 2009; Toh and Voldman 2011). If we take this glycocalyx layer into account, we now have a model wherein a cell with a glycocalyx layer on its surface is suspended in an extracellular matrix and these two layers accommodate interstitial flow.
In this paper, we develop a simple theory that will allow us to estimate both the fluid and solid stresses on the surface of a cell exposed to interstitial flow when the glycocalyx layer is taken into account. We will use Brinkman's equation for each Darcy media layer and the development of Secomb et al. (2001) for the solid force transmission. As we shall see, using reasonable estimates of glycocalyx and suspending matrix properties and interstitial flow velocities, solid stresses on suspended cell surfaces can easily be one to two orders of magnitude larger than fluid shear stresses. These solid stresses should be great enough to induce cellular mechanotransduction.
2 Methods
2.1 Preliminaries and simplified theory
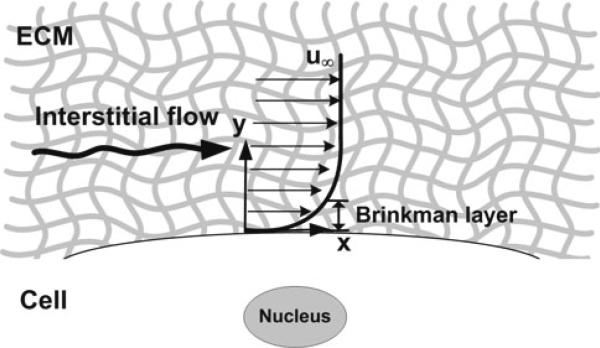
First, we will consider the simplified scenario depicted in Fig. 1. Let x be the flow direction and y be the direction perpendicular to the cell surface. Far from the surface (y → ∞, the velocity (u) approaches the superficial velocity (u∞) and there is a no-slip condition at the surface: u (0) = 0. Using these two boundary conditions and the steady-state Brinkman equation
| (1) |
where P is the pressure, u is the interstitial flow velocity, μ is the fluid viscosity and KP is the Darcy permeability of the porous media, the velocity profile in the Darcy media is given by
| (2) |
The fluid shear stress at the cell surface can then be calculated as
| (3) |
The velocity profile is sketched in Fig. 1 where it is emphasized that there is a boundary layer of characteristic length , the Brinkman layer, within which the velocity changes from u∞ to zero at the cell surface. The flow follows Darcy's law outside the Brinkman layer.
Fig. 1.
Simple schematic of a suspended cell in an infinite Darcy media exposed to interstitial flow. Velocity profile near a cell surface embedded in an infinite extracellular matrix (Darcy media). The Brinkman layer is the surface boundary layer where the flow transitions from an external Darcy flow at velocity u∞ to a no-slip condition at the surface of the cell
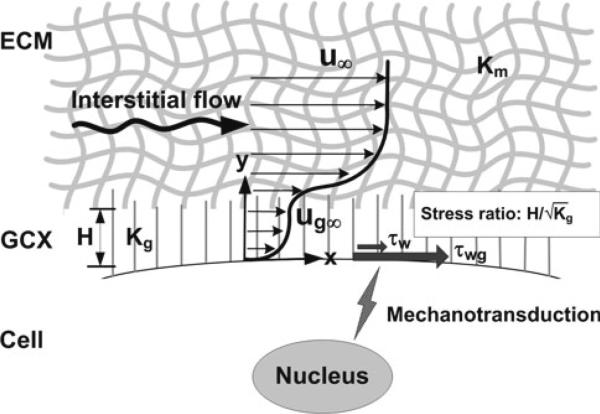
Now, we analyze the suspended cell with a glycocalyx layer depicted in Fig. 2. The glycocalyx layer has thickness H, and its properties are denoted by a subscript, g. The external matrix layer has properties denoted by a subscript, m, and the velocity far from the surface approaches the superficial velocity (u∞). Both layers are described by the Brinkman equation and have the same viscosity but different Darcy permeability values (Kg and Km). A particularly simple analysis is possible when the Brinkman layer in the glycocalyx (thickness of order ) is much thinner than the glycocalyx layer, i.e., when
| (4) |
In this case, the velocity profile in the glycocalyx is given by Eq. 2 with u∞ replaced by ug∞, the external or Darcy flow velocity in the glycocalyx.
| (5) |
Fig. 2.
Glycocalyx senses interstitial flow. Summary figure showing the velocity profile in the ECM (extracellular matrix) and the GCX (glycocalyx) surrounding a cell. Interstitial flow shear stress can be sensed by the glycocalyx layer. The ratio of the surface solid stress (τwg) to the surface fluid stress (τw) is . The solid stress can be 10–100-fold higher than fluid stress at the plasma membrane. Glycocalyx-mediated interstitial flow mechanotransduction may depend on ECM-integrin-cytoskeletal linkage. For simplicity, integrins and the cytoskeleton are not shown in the figure. H-glycocalyx thickness, Kg-Darcy permeability of the glycocalyx, Km-Darcy permeability of the surrounding media, u-the superficial velocity far from the surface, ug-the velocity in the glycocalyx layer far from the cell surface (beyond the Brinkman layer)
There is another boundary layer near the interface between the glycocalyx and the surrounding matrix with thickness of order on the glycocalyx side and of order on the matrix side. Outside these boundary layers, the velocities are ug∞ in the glycocalyx layer and u∞ in the matrix layer. Assuming that the Brinkman layer thickness in the matrix (order ) and the glycocalyx thickness (H) are small compared to cell spacing in the matrix, we will consider u∞ to be the local superficial velocity in the matrix. The fluid shear stress at the surface of the cell follows from Eq. 5 and the analysis leading to Eq. 3.
| (6) |
Assuming there is no flow normal to the cell surface (y direction), it follows that the pressure gradient, dP/dx, is the same in both layers. Furthermore, Darcy's law applies in both layers away from the cell surface and the interface between the layers where the velocity profiles are flat (Fig. 2). Under these circumstances,
| (7) |
Substituting Eq. 7 for ug∞ into Eq. 6, we arrive at the final approximate formula for the fluid wall shear stress
| (8) |
To calculate the solid stress in the glycocalyx (τg) following Secomb et al. (2001), we recognize that the mechanical equilibrium of forces in the x direction requires that the y derivative of τg must equal the loading resulting from fluid flow through the layer, i.e.,
| (9) |
There are two simple and relevant boundary conditions that can be applied to Eq. 9. First, we consider the case in which the glycocalyx is not tethered or connected to the external matrix and invoke the simple condition τg (H) = 0. Substituting for ug from Eq. 5, integrating Eq. 9 and applying the simple boundary condition, we obtain
| (10) |
Invoking the assumption of Eq. 4, we arrive at the following prediction for the solid stress at the cell surface (y=0)
| (11) |
where τw is the fluid shear stress at the wall and is the ratio of solid stress over fluid stress at the cell plasma membrane. If we finally substitute Eq. 8 for τw into Eq. 11, we arrive at the interesting result
| (12) |
Equation 12, which uses the observable superficial velocity u∞ instead of ug∞, predicts that the solid stress at the cell surface is independent of the Darcy permeability of the glycocalyx layer.
The second simple boundary condition that can be applied to calculate the solid stress in the glycocalyx is associated with the case where the glycocalyx is firmly tethered or connected to the external matrix. In this case, we assume that the small × displacement of matrix strands forming the glycocalyx is zero at the interface. Deformation of the glycocalyx results in the generation of a shear stress
| (13) |
where t0 is the tension in the glycocalyx matrix per unit area and U is the displacement. If this shear stress relationship is substituted into Eq. 9, a second-order equation in U is obtained. Applying the two boundary conditions, U=0 at y=0 and y=H, to solve for U leads to a solution for τg(not shown). When τg is evaluated at the cell surface and the assumption in Eq. 4 is invoked, the result is
| (14) |
Note that the value given by Eq. 14 for the zero displacement boundary condition is exactly 1/2 the value given by Eq. 12 for the zero stress boundary condition. This might have been anticipated from the symmetry of the displacement boundary conditions requiring that the stress be shared equally by the surfaces at y=0 and y=H.
2.2 Detailed theory
When the simplified assumptions of the preceding section (thin Brinkman layers near all interfaces) do not apply, the full problem for fluid and solid stresses associated with flow over a cell embedded in an extracellular matrix with a glycocalyx surface layer (Fig. 2) must be solved. The solution is outlined in this section. The Brinkman equation for each layer is given in Eqs. 15 and 16.
| (15) |
| (16) |
The boundary conditions are given below:
y = H, velocity match and stress match
The detailed solutions for ug and um are given in Eqs. 17 and 18.
| (17) |
| (18) |
where
The fluid shear stress in the glycocalyx layer is given by Eq. 19a,
| (19a) |
The fluid shear stress at the cell surface (y=0) is given by Eq. 19b,
| (19b) |
The solid stress in the glycocalyx for the case when the glycocalyx is untethered from the external matrix is computed by applying Eq. 9 to the glycocalyx velocity profile (Eq. 17) with the zero stress boundary condition at y=H. The result is
| (20a) |
where
The solid glycocalyx stress at the cell surface (y=0) is then given by
| (20b) |
The glycocalyx stress for the case when there is firm tethering of the glycocalyx to the external matrix follows from Eq. 13 applied to Eqs. 9 and 17 with zero displacement boundary conditions at y=0, H. The result is
| (21) |
where
The glycocalyx stress at the cell surface (y=0) is given by
| (22) |
The ratios of solid stress over fluid stress at the cell plasma membrane for both untethered and tethered conditions are (C − A)/A and (D − A)/A, respectively.
3 Results
3.1 Review of parameters required to evaluate fluid and solid stresses on the cell surface
To evaluate the fluid and solid stresses, it is necessary to specify the Darcy permeability of the matrix (Km) and the glycocalyx (Kg), the thickness of the glycocalyx (H) and the superficial velocity (u∞). We will assume a plasma viscosity of 1.2cp at 37°C (Kesmarky et al. 2008) for all estimations. Table 1 provides estimates of Km and u∞ for different tissues including arteries, tumors, cartilage and collagen gels in vitro. Kg has been estimated for endothelial cells, but not for suspended cells. Fortunately, we can estimate the solid stress at the cell surface without knowledge of Kg (recall Eqs. 12 and 14). The glycocalyx thickness (H) has been estimated in several studies in endothelial cells, but limited estimates of H are available for suspended cells (Table 2).
Table 1.
Darcy permeability and interstitial flow velocity
| Matrix or tissue | Darcy permeability(K, cm2) | Interstitial fluid flow velocity (u∞,μm/s) | References |
|---|---|---|---|
| Aorta | 10–14 | 0.01–0.1 | (Wang and Tarbell 1995; Tedgui and Lever 1984; Shi et al. 2009; Levick 1987) |
| Glioma tumors | 10–12 | 0.1–2 | (Qazi et al. 2011; Swartz and Fleury 2007; Jain 1999) |
| Hepatoma | 10–13 | Unknown | (Levick 1987) |
| Subcutaneous layer | 10–11 | 0.1–1 | (Levick 1987) |
| Cartilage | 10–12–10–13 | 0.01 | (Mansour 2004) |
| Collagen I (2–45mg/ml) | 10–12 – 10–8 | 0.5–3a | (Shi et al. 2009; Ng and Swartz 2003; Ramanujan et al. 2002; Wang and Tarbell 2000; Qazi et al. 2011) |
| Endothelial glycocalyx | 10–10 – 10–13 | Not applicable | (Secomb et al. 2001; Weinbaum et al. 2007) |
Flow velocity depends on pressure differential across the gel layers
Table 2.
The thickness of glycocalyx in different types of cells
| Cell type | Thickness of glycocalyx (μm) | References |
|---|---|---|
| Hamster cremaster muscle capillaries | 0.2–0.5 | (Weinbaum et al. 2007) |
| Large retinal vessels (diameter ≥ 90 μm) | 8.9 | (Broekhuizen et al. 2010) |
| Mouse carotid arteries | 2.5 | (Reitsma et al. 2011) |
| Bovine aortic ECs | 11 (in vitro) | (Ebong et al. 2011) |
| Rat fat pad ECs | 5 (in vitro) | (Ebong et al. 2011) |
| SMCs | 1–2 (in collagen) | (Qazi, personal communication) |
| Fibroblasts | Not measured | (Mangakis and Von Mickwitz 1975) |
| Rat chondrocytes | 3–8 (in vitro) | (Boehm et al. 2009) |
| Human breast adenocarcinoma | 2 (in vitro) | (Rilla et al. 2008) |
| Rat intestinal tumor | 0.02–0.2 (in vivo) by ruthenium red/EM | (Jacobs 1981) |
| Embryonic stem cells | Not measured | (Nikmanesh et al. 2012) |
3.2 Predictions of the stress environment of an embedded cell
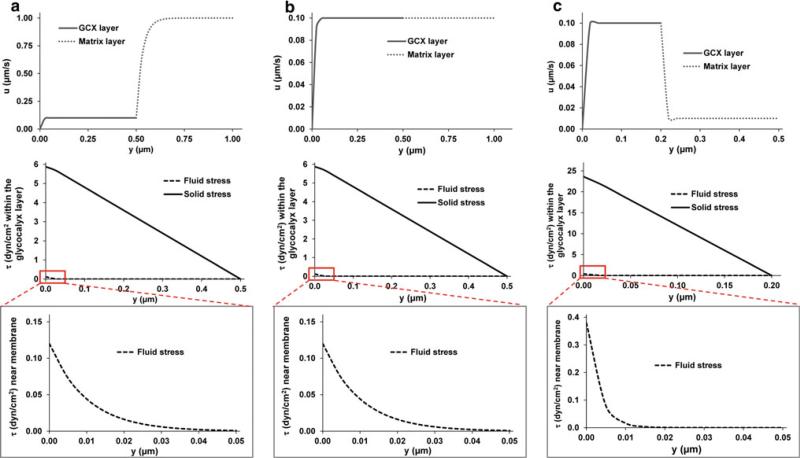
In this section, we present detailed velocity and stress profiles as well as surface stresses for several cases representing physiologically relevant scenarios (Table 3 and Fig. 3). In Fig. 3, we only show the plots of velocity and stress profiles for the untethered cases. We also present the approximate values of the surface stresses given by Eqs. 8, 12, and 14 for comparison (Table 3). Since the thickness and permeability of the glycocalyx layer for each specific embedded cell type are not available, a range of thicknesses (0.05, 0.2, 0.5 and 2 μm) was chosen and permeability was varied from 10−11 to 10−13 cm2. These values were observed in vascular ECs, which may be physiologically reasonable for fibroblasts, smooth muscle cells, chondrocytes, tumor cells, stem cells and other interstitial cells. Recall, however, that for the simplified model (Eq. 12) that is quite accurate for the representative cases in Table 3 as indicated by the ratio of untethered to tethered wall stress (2.0 in the simplified theory), τwg does not depend on the glycocalyx permeability, but depends on the thickness of the glycocalyx layer (Eq. 12).
Table 3.
Representative surface stresses for embedded cells in collagen gels, tumors or tissues
| Representative tissue/matrix | Representative cell type | Tissue/matrix permeability (Km, cm2) | Interstitial flow velocity (u∞, μm/s) | Glycocalyx permeability (Kg, cm2) | Glycocalyx thickness (H, μm) | Surface stresses from the detailed model (y=0) (dyn/cm2) |
Surface stresses from the simplified model (y=0) (dyn/cm2) |
Plots | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fluid (τw) | Solid (τwg) |
Fluid (τw) | Solid (τwg) |
||||||||||
| Untethered | Tethered | Ratio | Untethered | Tethered | |||||||||
| Collagen gels (in vitro) | Fibroblasts | 10–10 | 10 | 10–11 | 0.5 | 0.379 | 6.441 | 2.696 | 2.39 | 0.379 | 6 | 3 | NS |
| SMCs | 10–10 | 1 | 10–11 | 0.5 | 0.038 | 0.644 | 0.270 | 2.39 | 0.038 | 0.6 | 0.3 | NS | |
| Bone cells | 10–11 | 1 | 10–11 | 0.5 | 0.379 | 5.621 | 2.645 | 2.13 | 0.379 | 6 | 3 | NS | |
| Stem cells | 10–11 | 1 | 10–12 | 0.5 | 0.120 | 5.880 | 2.882 | 2.04 | 0.12 | 6 | 3 | Fig. 3a | |
| Tumor cells | 10–11 | 1 | 10–13 | 0.5 | 0.038 | 5.962 | 2.962 | 2.01 | 0.038 | 6 | 3 | NS | |
| etc | 10–11 | 1 | 10–11 | 2 | 0.379 | 23.621 | 11.627 | 2.03 | 0.379 | 24 | 12 | NS | |
| 10–12 | 0.1 | 10–12 | 2 | 0.120 | 23.880 | 11.881 | 2.01 | 0.12 | 24 | 12 | NS | ||
| Tumor (in vivo) | Tumor cells | 10–12 | 1 | 10–12 | 0.5 | 1.200 | 58.800 | 28.824 | 2.04 | 1.2 | 60 | 30 | NS |
| 10–12 | 1 | 10–12 | 0.5 | 0.120 | 5.880 | 2.882 | 2.04 | 0.12 | 6 | 3 | Fig. 3b | ||
| 10–13 | 0.1 | 10–12 | 0.2 | 1.200 | 21.985 | 10.819 | 2.03 | 1.2 | 24 | 12 | NS | ||
| 10–13 | 0.1 | 10–12 | 0.05 | 1.189 | 4.003 | 1.886 | 2.12 | 1.2 | 6 | 3 | NS | ||
| Cartilage (in vivo) | Chondrocytes | 10–13 | 0.01 | 10–12 | 0.5 | 0.120 | 5.880 | 2.882 | 2.04 | 0.12 | 6 | 3 | NS |
| Aorta (in vivo) | SMCs | 10–14 | 0.01 | 10–13 | 0.2 | 0.379 | 23.621 | 11.627 | 2.03 | 0.379 | 24 | 12 | Fig. 3c |
| 10–14 | 0.01 | 10–12 | 0.1 | 1.2 | 9.720 | 4.812 | 2.02 | 1.2 | 12 | 6 | NS | ||
| 10–14 | 0.01 | 10–13 | 0.05 | 0.379 | 5.361 | 2.628 | 2.04 | 0.379 | 6 | 3 | NS | ||
The calculations were performed using a Maple 14 program. The ratios of solid stresses between untethered and tethered cases calculated from the detailed model are shown in the table, while this ratio is always 2 when using the simplified model
NS Plots not shown
Fig. 3.
Three representative cases of velocity and stress profiles to mimic cells suspended in collagen gels, tumor cells in vivo and SMCs in the arterial wall, respectively. Km and Kg were chosen as follows: Km > Kg (a), Km = Kg (b), and Km < Kg (c). The detailed parameters for each case are listed in Table 3. The velocity profiles extend into the ECM space (top figures). The profiles for fluid and solid stresses are only shown for the glycocalyx layer that is untethered (middle figures). The fluid stress profiles near the cell membrane (0–50nm) are highlighted (bottom figures)
From the detailed theory calculations, we can see that fluid shear stresses at both the outer edge of the glycocalyx and the cell plasma membrane are rather small, while solid shear stresses are zero at the outer edge of the glycocalyx but increased to one to two orders of magnitude greater than the fluid shear stresses at the plasma membrane (Fig. 3). The large solid shear stresses at the cell surface are required to balance the imposed pressure gradient in the glycocalyx.
From the simplified theory, we know that without the glycocalyx layer, the fluid shear stress on the surface is given by as in the original model of Wang and Tarbell (1995). With the glycocalyx layer, the solid shear stress at the surface is given by μu∞H/Km. The ratio of the solid stress with a glycocalyx layer to the fluid stress without a glycocalyx layer is . Values in Table 3 can be used to estimate that this ratio is of order 5 in a collagen gel and 500 in an aorta.
3.3 Generalization of the predictions of the surface stress environment
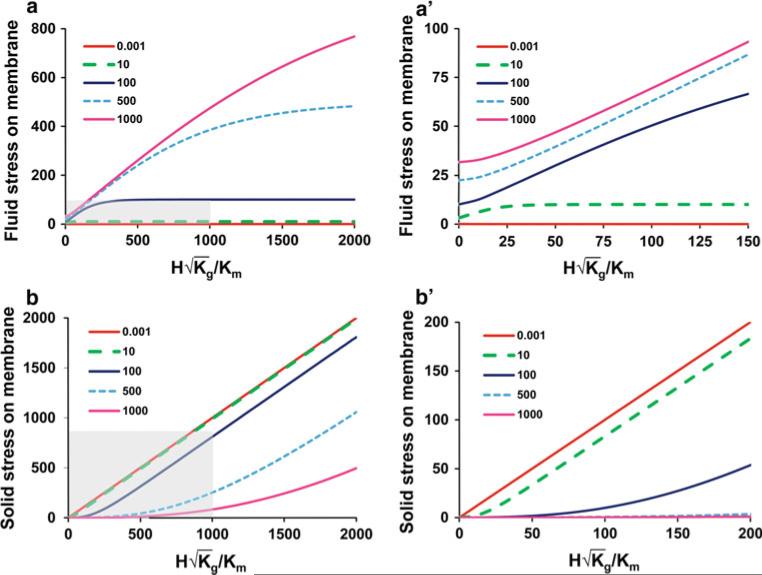
Examination of Eqs. 17–22 reveals that there are 3 independent dimensionless parameters that describe the surface stresses on the cell: , Kg/Km, and . Thus, we have , and . It is useful for exploring more general trends in the model predictions to plot the normalized fluid and solid cell surface stresses ( and ) as a function of Kg/Km and . This is presented in Fig. 4. For the physiological cases in Table 3, Kg/Km lies in the range 0.01–100 and lies in the range 1–1,000. The physiological dimensionless fluid stress () and solid stress () at the cell surface (membrane) are in the ranges of (0.01–100) and (1–800) for the untethered cases, respectively. These ranges are shaded in Fig. 4 and extended to reveal more general trends. Several useful asymptotic functions and limits for fluid and solid surface stresses are given below.
Fig. 4.
Plots of the normalized fluid and solid cell surface stresses ( and ) as functions of Kg/Km and . According to Table 3, physiological Kg/Km ranges from 0.01 to 100 and ranges from 1 to 1,000. Fluid (a) and solid (b) surface stresses (dimensionless) are plotted versus with Kg/Km varying from 0.001 to 1,000. Plots are for untethered conditions. The physiological dimensionless fluid and solid stresses at the cell surface (membrane) obtained from Table 3 are in the ranges of (0.01–100) and (1–800) for the untethered cases, respectively. The physiological ranges of fluid and solid stresses and are indicated in the shaded areas on (a) and (b). The close-up plots of fluid and solid stresses as are shown in (a') and (b'), respectively
When and . When and . When and . The first and third set of asymptotes describe (approximately) the data in Table 3 and are identical to the simplified theory's Eq. (8) for the fluid stress when Kg/Km → 0, and Eq. (12) for the solid stress when . The second set of asymptotes describes cases of unknown physiological significance.
4 Discussion
In this paper, we presented the first theory to describe the solid mechanical forces transmitted to a cell's surface as a result of interstitial flow through a suspending matrix and a surface glycocalyx layer. A simplified theory was developed initially leading to approximate formulas for the surface fluid and solid shear stresses in terms of measurable parameters (Eqs. 8, 12 and 14). The predictions of these simple equations are in good agreement with the more detailed model predictions (Table 3). The theory presented here was based on planar geometry as an approximation to the more complex shapes of suspended cells. It should be noted, however, that simple planar models provide proper order of magnitude predictions for the fluid wall shear stress on cylindrical cells arranged in various packing configurations in an extracellular matrix (Wang and Tarbell 1995).
The predictions of the theory for several physiologically relevant sets of parameters describing artery walls, cartilage, solid tumors and in vitro gels suggest that the fluid shear stresses on the cell surface are one to two orders of magnitude smaller than the solid stresses, which dominate the transmittal of interstitial flow force to the cell body. The theory also draws attention to the paucity of data on glycocalyx thickness and permeability for suspended cells in tissues and suggests important future research needs. For cancer cells, smooth muscle cells and other embedded cell types, the actual glycocalyx lengths may be much greater than the ones measured by ruthenium red staining and electron microscopy (Jacobs 1981) due to dehydration artifacts as discussed by Ebong et al. (2011). However, the model in the present paper only considers the flow and stress profiles between the cell membrane and the ECM where the glycocalyx should be able to move freely in response to flow. The gap between the cell membrane and the ECM in a tissue is expected to be on the order of 20–50nm (length of the integrin binding complex) in the vicinity of an integrin-based cell-matrix adhesion site (Hynes 1992; Shi et al. 2011). But it is reasonable to expect that this gap increases substantially in regions removed from the focal adhesion site. This gap has been observed to be 50–100nm in osteocytes (Fritton and Weinbaum 2009). So for both the untethered and tethered glycocalyx cases, the effective spaces for stress sensing are the gap between the cell membrane and the ECM. This is what we considered as the length of the glycocalyx in the modeling, although it may be much shorter than the actual length of the glycocalyx that may extend into the ECM. In contrast, for in vitro cases, the pore sizes of the ECM are much larger (order 1 μm for collagen gels) (Wang and Tarbell 2000; Shi et al. 2009); the ECM is much more permeable than in real tissue (recall Table 1); and the effective length of the glycocalyx may be much longer than in vivo. Therefore, in the Table 3, the longest glycocalyx we used for tissues was 0.5 μm, rather than 2 μm for in vitro collagen gels. We also modeled the velocity and stress profiles when the glycocalyx is 50nm long to mimic sites where the glycocalyx is co-localized with integrin-mediated cell-matrix adhesions.
In addition to solute transport effects (Levick 1987; Swartz and Fleury 2007), the mechanical effects of interstitial flow on cells have received considerable attention recently. For example, we have shown that the heparan sulfate proteoglycan (HSPG) components of the glycocalyx can sense inter-stitial fluid flow and transduce this mechanical stimulus into biochemical signals that regulate matrix metalloproteinase (MMP) expression through activation of the focal adhesion kinase (FAK), extracellular signal-regulated kinase 1/2 mitogen-activated protein kinase (ERK1/2 MAPK) and the c-Jun signaling axis (Shi et al. 2011). The increased MMP expression up-regulates vascular SMC and fibroblast motility in 3D collagen gels (Shi et al. 2009, 2010b, 2011). Glycocalyx-mediated ERK1/2 activation may also modulate vascular SMC and myofibroblast phenotype (Shi et al. 2010a). Other studies have shown that interstitial flow can also regulate tumor cell migration in a 3D matrix by stimulating FAK activation and chemokine and cytokine release (Polacheck et al. 2011; Shields et al. 2007; Qazi et al. 2011; Shieh et al. 2011). That such subtle interstitial flows (~ 0.5μm/s) and fluid shear stresses (~ 0.1dyn/cm2, predicted when the glycocalyx layer is omitted) can induce impressive biochemical responses is intriguing (Shi et al. 2009; Shi and Tarbell 2011). Through the present modeling study, we have shown that the interstitial flow-induced solid shear stress on the glycocalyx is one to two orders of magnitude higher than fluid shear stress at the plasma membrane. For most of the physiologically relevant parameter cases in Table 3, the solid shear stresses at the surface are predicted to lie between 5 and 60dyn/cm2. This range of shear stress (calculated from fluid mechanical measurements and models and implicitly imposed on the outer edge of the glycocalyx) is well known to activate endothelial cells (Malek et al. 1999). But other modeling studies have indicated that endothelial cell surface shear stress is transmitted to the cell primarily through the solid matrix of the glycocalyx and not the fluid, as suggested here for the embedded cells (Secomb et al. 2001; Weinbaum et al. 1994). Thus, we interpret shear stresses on endothelial cells reported in the literature as solid shear stresses. In addition, this range of shear stress has been predicted for osteocytes (Weinbaum et al. 1994) and has been used in 2D studies of many other cell types including vascular SMCs and fibroblasts (Shi and Tarbell 2011), chondrocytes (Yokota et al. 2003), stem cells (Stolberg and McCloskey 2009) and tumor cells (Chang et al. 2008), suggesting that interstitial flow-mediated mechanotransduction is plausible.
The effects of disease states on the glycocalyx of suspended cells have not, to our knowledge, been investigated. We do know that the glycocalyx of endothelial cells is degraded in many diseases including atherosclerosis (Vink et al. 2000), diabetes (Nieuwdorp et al. 2006) and hypertension (Oberleithner et al. 2011). If this occurs for suspended cells, we would expect Kg to increase and H to decrease. Assuming that Km is not affected, u∞ should similarly be unaffected. In these circumstances, perusal of Eqs. 8 and 12 of the simplified theory indicates that the fluid stress on the cell surface (τw) would increase and the solid stress (τwg1) would decrease. If the extracellular matrix is also degraded, Km and u∞ would increase and the trends for τw and τwg1 would be difficult to predict without detailed knowledge of the parameters u∞, Kg and Km. On the other hand, during the formation of integrin-mediated cell-matrix adhesions, it is possible that there is a local compression of the pre-existing glycocalyx near the sites that may lead to a decrease in glycocalyx length and a decrease in glycocalyx permeability (Paszek et al. 2009). In this case, it is also difficult to predict the effect on stresses without detailed knowledge of the parameters of H and Kg and a more complex model.
It should also be noted that glycocalyx-mediated inter-stitial flow mechanotransduction depends on integrin-mediated cell-matrix adhesions and cell cytoskeletal rigidity (Shi et al. 2011). The ECM-integrin-cytoskeletal linkage plays an essential role in mechanotransduction (Hoffman et al. 2011; Schwartz 2010). However, glycocalyx core proteins (e.g., syndecan-1 and syndecan-4) can co-localize with integrins and support integrin-mediated cell-matrix adhesions (Vuoriluoto et al. 2008; Couchman et al. 2001). Glycocalyx core protein-mediated mechanotransduction can be a parallel signaling pathway to that of integrins (Denhez et al. 2002; Shi et al. 2011). Furthermore, the glycocalyx itself can bind to ECM fibers and form cell-matrix adhesions, which may be able to transmit mechanical forces to the cell body (Bellin et al. 2009). In our previous conceptual model, we proposed that interstitial fluid flow is sensed mainly by the cell surface glycocalyx and then converted to biochemical signals through the cell cytoskeleton and integrin-mediated adhesions (Shi et al. 2011). In the current theoretical model, integrin-mediated cell-matrix adhesions are not shown in the schematic figures, and the effects of restraining forces on integrins induced by fluid flow are not considered. However, the transmission of fluid and solid stresses from the glycocalyx to the cell body may still depend on integrin-mediated cell-matrix adhesions as we discussed previously (Shi and Tarbell 2011; Shi et al. 2011).
While recognizing the very interesting phenomenon of stress sensing through the cell surface glycocalyx described by the present theoretical model, we should note that glycocalyx components may also serve as co-receptors for many biochemical signaling processes (Bernfield et al. 1999) and/or regulate solute transport in the tissue interstitium to the cells (Levick 1987), which modulate cell function and behavior. Therefore, to precisely evaluate the effects of tissue fluid flow on cell physiology and pathology in vivo, both chemical and mechanical effects through the glycocalyx should be considered.
5 Conclusion
The current theoretical model shows, for the first time, that the surface glycocalyx layer on embedded cells experiences interstitial fluid flow-induced solid stress that is one to two orders of magnitude higher than fluid shear stress at the cell membrane. This force may be high enough to induce mechanotransduction regulating cell function. The solid/fluid stress ratio at the plasma membrane depends on the ratio of the effective glycocalyx thickness to the square root of its permeability. The theory can be summarized with a simplified schematic as shown in Fig. 2. The fluid and solid shear stresses induced by interstitial flow are sensed by the glycocalyx layer and transmitted to the cell body where mechanotransduction leads to responses that regulate cell function. This provides an explanation for several recent experimental observations of cellular mechanotransduction induced by interstitial flow (Qazi et al. 2011; Shi and Tarbell 2011; Shi et al. 2011). This study may be of interest in understanding interstitial flow-induced mechanobiology in stem cell differentiation, tumor metastasis, tissue physiology and diseases and has implications in tissue engineering.
Acknowledgments
This work was supported by National Institutes of Health (NIH) National Heart, Lung, and Blood Institute (NHLBI) grant RO1 HL094889 (to JMT). The authors thank Dr. Peng Guo for help with Maple programming.
References
- Bellin RM, Kubicek JD, Frigault MJ, Kamien AJ, Steward RL, Jr, Barnes HM, Digiacomo MB, Duncan LJ, Edgerly CK, Morse EM, Park CY, Fredberg JJ, Cheng CM, LeDuc PR. Defining the role of syndecan-4 in mechanotransduction using surface-modification approaches. Proc Natl Acad Sci USA. 2009;106(52):22102–22107. doi: 10.1073/pnas.0902639106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernfield M, Gotte M, Park PW, Reizes O, Fitzgerald ML, Lincecum J, Zako M. Functions of cell surface heparan sulfate proteoglycans. Annu Rev Biochem. 1999;68:729–777. doi: 10.1146/annurev.biochem.68.1.729. [DOI] [PubMed] [Google Scholar]
- Boehm H, Mundinger TA, Boehm CHJ, Hagel V, Rauch U, Spatz JP, Curtis JE. Mapping the mechanics and macromolecular organization of hyaluronan-rich cell coats. Soft Matter. 2009;5(21):4331–4337. [Google Scholar]
- Broekhuizen LN, Lemkes BA, Mooij HL, Meuwese MC, Verberne H, Holleman F, Schlingemann RO, Nieuwdorp M, Stroes ES, Vink H. Effect of sulodexide on endothelial glycocalyx and vascular permeability in patients with type 2 diabetes mellitus. Diabetologia. 2010;53(12):2646–2655. doi: 10.1007/s00125-010-1910-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang SF, Chang CA, Lee DY, Lee PL, Yeh YM, Yeh CR, Cheng CK, Chien S, Chiu JJ. Tumor cell cycle arrest induced by shear stress: roles of integrins and Smad. Proc Natl Acad Sci USA. 2008;105(10):3927–3932. doi: 10.1073/pnas.0712353105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couchman JR, Chen L, Woods A. Syndecans and cell adhesion. Int Rev Cytol. 2001;207:113–150. doi: 10.1016/s0074-7696(01)07004-8. [DOI] [PubMed] [Google Scholar]
- Denhez F, Wilcox-Adelman SA, Baciu PC, Saoncella S, Lee S, French B, Neveu W, Goetinck PF. Syndesmos, a syndecan-4 cytoplasmic domain interactor, binds to the focal adhesion adaptor proteins paxillin and Hic-5. J Biol Chem. 2002;277(14):12270–12274. doi: 10.1074/jbc.M110291200. [DOI] [PubMed] [Google Scholar]
- Ebong EE, Macaluso FP, Spray DC, Tarbell JM. Imaging the endothelial glycocalyx in vitro by rapid freezing/freeze substitution transmission electron microscopy. Arterioscler Thromb Vasc Biol. 2011;31(8):1908–1915. doi: 10.1161/ATVBAHA.111.225268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Florian JA, Kosky JR, Ainslie K, Pang Z, Dull RO, Tarbell JM. Heparan sulfate proteoglycan is a mechanosensor on endothelial cells. Circ Res. 2003;93(10):e136–e142. doi: 10.1161/01.RES.0000101744.47866.D5. [DOI] [PubMed] [Google Scholar]
- Fritton SP, Weinbaum S. Fluid and solute transport in bone: flow-induced mechanotransduction. Annu Rev Fluid Mech. 2009;41:347–374. doi: 10.1146/annurev.fluid.010908.165136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harfouche R, Hentschel DM, Piecewicz S, Basu S, Print C, Eavarone D, Kiziltepe T, Sasisekharan R, Sengupta S. Glycome and transcriptome regulation of vasculogenesis. Circulation. 2009;120(19):1883–1892. doi: 10.1161/CIRCULATIONAHA.108.837724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman BD, Grashoff C, Schwartz MA. Dynamic molecular processes mediate cellular mechanotransduction. Nature. 2011;475(7356):316–323. doi: 10.1038/nature10316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hynes RO. Integrins: versatility, modulation, and signaling in cell adhesion. Cell. 1992;69(1):11–25. doi: 10.1016/0092-8674(92)90115-s. [DOI] [PubMed] [Google Scholar]
- Jacobs LR. Alterations in surface ultrastructure and anionic sites of rat dimethylhydrazine-induced intestinal tumors. Virchows Arch B Cell Pathol. 1981;37(2):207–216. doi: 10.1007/BF02892569. [DOI] [PubMed] [Google Scholar]
- Jain RK. Transport of molecules, particles, and cells in solid tumors. Annu Rev Biomed Eng. 1999;1:241–263. doi: 10.1146/annurev.bioeng.1.1.241. [DOI] [PubMed] [Google Scholar]
- Kesmarky G, Kenyeres P, Rabai M, Toth K. Plasma viscosity: a forgotten variable. Clin Hemorheol Microcirc. 2008;39(1–4):243–246. [PubMed] [Google Scholar]
- Krahling H, Mally S, Eble JA, Noel J, Schwab A, Stock C. The glycocalyx maintains a cell surface pH nanoenvironment crucial for integrin-mediated migration of human melanoma cells. Pflugers Arch. 2009;458(6):1069–1083. doi: 10.1007/s00424-009-0694-7. [DOI] [PubMed] [Google Scholar]
- Levick JR. Flow through interstitium and other fibrous matrices. Q J Exp Physiol. 1987;72(4):409–437. doi: 10.1113/expphysiol.1987.sp003085. [DOI] [PubMed] [Google Scholar]
- Malek AM, Alper SL, Izumo S. Hemodynamic shear stress and its role in atherosclerosis. JAMA. 1999;282(21):2035–2042. doi: 10.1001/jama.282.21.2035. [DOI] [PubMed] [Google Scholar]
- Mangakis N, Von Mickwitz CU. Electron microscopical investigations on the glycocalyx of cultivated cells after incubation with extracts from rapidly growing normal and tumour tissues. Pathol Eur. 1975;10(2):105–114. [PubMed] [Google Scholar]
- Mansour JM. Biomechanics of cartilage. In: Oatis CA, editor. Kinesiology: the mechanics and pathomechanics of human movement. Lippincott Williams and Wilkins; Philadelphia: 2004. pp. 66–79. [Google Scholar]
- Nairn AV, Kinoshita-Toyoda A, Toyoda H, Xie J, Harris K, Dalton S, Kulik M, Pierce JM, Toida T, Moremen KW, Linhardt RJ. Glycomics of proteoglycan biosynthesis in murine embryonic stem cell differentiation. J Proteome Res. 2007;6(11):4374–4387. doi: 10.1021/pr070446f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng CP, Swartz MA. Fibroblast alignment under interstitial fluid flow using a novel 3-D tissue culture model. Am J Physiol Heart Circ Physiol. 2003;284(5):H1771–H1777. doi: 10.1152/ajpheart.01008.2002. [DOI] [PubMed] [Google Scholar]
- Nieuwdorp M, van Haeften TW, Gouverneur MC, Mooij HL, van Lieshout MH, Levi M, Meijers JC, Holleman F, Hoekstra JB, Vink H, Kastelein JJ, Stroes ES. Loss of endothelial glycocalyx during acute hyperglycemia coincides with endothelial dysfunction and coagulation activation in vivo. Diabetes. 2006;55(2):480–486. doi: 10.2337/diabetes.55.02.06.db05-1103. [DOI] [PubMed] [Google Scholar]
- Nikmanesh M, Shi ZD, Tarbell JM. Heparan sulfate proteoglycan mediates shear stress-induced endothelial gene expression in mouse embryonic stem cell-derived endothelial cells. Biotechnol Bioeng. 2012;109(2):583–594. doi: 10.1002/bit.23302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oberleithner H, Peters W, Kusche-Vihrog K, Korte S, Schillers H, Kliche K, Oberleithner K. Salt overload damages the glycocalyx sodium barrier of vascular endothelium. Pflugers Arch. 2011;462(4):519–528. doi: 10.1007/s00424-011-0999-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pahakis MY, Kosky JR, Dull RO, Tarbell JM. The role of endothelial glycocalyx components in mechanotransduction of fluid shear stress. Biochem Biophys Res Commun. 2007;355(1):228–233. doi: 10.1016/j.bbrc.2007.01.137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paszek MJ, Boettiger D, Weaver VM, Hammer DA. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. PLoS Comput Biol. 2009;5(12):e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polacheck WJ, Charest JL, Kamm RD. Interstitial flow influences direction of tumor cell migration through competing mechanisms. Proc Natl Acad Sci USA. 2011;108(27):11115–11120. doi: 10.1073/pnas.1103581108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qazi H, Shi ZD, Tarbell JM. Fluid shear stress regulates the invasive potential of glioma cells via modulation of migratory activity and matrix metalloproteinase expression. PLoS One. 2011;6(5):e20348. doi: 10.1371/journal.pone.0020348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramanujan S, Pluen A, McKee TD, Brown EB, Boucher Y, Jain RK. Diffusion and convection in collagen gels: implications for transport in the tumor interstitium. Biophys J. 2002;83(3):1650–1660. doi: 10.1016/S0006-3495(02)73933-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reitsma S, Oude Egbrink MG, Vink H, van den Berg BM, Lima Passos V, Engels W, Slaaf DW, van Zandvoort MA. Endothelial glycocalyx structure in the intact carotid artery: a two-photon laser scanning microscopy study. J Vasc Res. 2011;48(4):297–306. doi: 10.1159/000322176. [DOI] [PubMed] [Google Scholar]
- Rilla K, Tiihonen R, Kultti A, Tammi M, Tammi R. Pericellular hyaluronan coat visualized in live cells with a fluorescent probe is scaffolded by plasma membrane protrusions. J Histochem Cytochem. 2008;56(10):901–910. doi: 10.1369/jhc.2008.951665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz MA. Integrins and extracellular matrix in mechanotransduction. Cold Spring Harb Perspect Biol. 2010;2(12):a005066. doi: 10.1101/cshperspect.a005066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Secomb TW, Hsu R, Pries AR. Effect of the endothelial surface layer on transmission of fluid shear stress to endothelial cells. Biorheology. 2001;38(2–3):143–150. [PubMed] [Google Scholar]
- Shieh AC. Biomechanical forces shape the tumor microenvironment. Ann Biomed Eng. 2011;39(5):1379–1389. doi: 10.1007/s10439-011-0252-2. [DOI] [PubMed] [Google Scholar]
- Shi ZD, Tarbell JM. Fluid flow mechanotransduction in vascular smooth muscle cells and fibroblasts. Ann Biomed Eng. 2011;39(6):1608–1619. doi: 10.1007/s10439-011-0309-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi ZD, Ji XY, Qazi H, Tarbell JM. Interstitial flow promotes vascular fibroblast, myofibroblast, and smooth muscle cell motility in 3-D collagen I via upregulation of MMP-1. Am J Physiol Heart Circ Physiol. 2009;297(4):H1225–H1234. doi: 10.1152/ajpheart.00369.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi ZD, Abraham G, Tarbell JM. Shear stress modulation of smooth muscle cell marker genes in 2-D and 3-D depends on mechanotransduction by heparan sulfate proteoglycans and ERK1/2. PLoS One. 2010;5(8):e12196. doi: 10.1371/journal.pone.0012196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi ZD, Ji XY, Berardi DE, Qazi H, Tarbell JM. Interstitial flow induces MMP-1 expression and vascular SMC migration in collagen I gels via an ERK1/2-dependent and c-Jun-mediated mechanism. Am J Physiol Heart Circ Physiol. 2010;298(1):H127–H135. doi: 10.1152/ajpheart.00732.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi ZD, Wang H, Tarbell JM. Heparan sulfate proteoglycans mediate interstitial flow mechanotransduction regulating MMP-13 expression and cell motility via FAK-ERK in 3D collagen. PLoS One. 2011;6(1):e15956. doi: 10.1371/journal.pone.0015956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shieh AC, Swartz MA. Regulation of tumor invasion by interstitial fluid flow. Phys Biol. 2011;8(1):015012. doi: 10.1088/1478-3975/8/1/015012. [DOI] [PubMed] [Google Scholar]
- Shieh AC, Rozansky HA, Hinz B, Swartz MA. Tumor cell invasion is promoted by interstitial flow-induced matrix priming by stromal fibroblasts. Cancer Res. 2011;71(3):790–800. doi: 10.1158/0008-5472.CAN-10-1513. [DOI] [PubMed] [Google Scholar]
- Shields JD, Fleury ME, Yong C, Tomei AA, Randolph GJ, Swartz MA. Autologous chemotaxis as a mechanism of tumor cell homing to lymphatics via interstitial flow and autocrine CCR7 signaling. Cancer Cell. 2007;11(6):526–538. doi: 10.1016/j.ccr.2007.04.020. [DOI] [PubMed] [Google Scholar]
- Stolberg S, McCloskey KE. Can shear stress direct stem cell fate. Biotechnol Prog. 2009;25(1):10–19. doi: 10.1002/btpr.124. [DOI] [PubMed] [Google Scholar]
- Swartz MA, Fleury ME. Interstitial flow and its effects in soft tissues. Annu Rev Biomed Eng. 2007;9:229–256. doi: 10.1146/annurev.bioeng.9.060906.151850. [DOI] [PubMed] [Google Scholar]
- Tarbell JM, Ebong EE. The endothelial glycocalyx: a mechano-sensor and -transducer. Sci Signal. 2008;1(40):pt8. doi: 10.1126/scisignal.140pt8. [DOI] [PubMed] [Google Scholar]
- Tarbell JM, Pahakis MY. Mechanotransduction and the glycocalyx. J Intern Med. 2006;259(4):339–350. doi: 10.1111/j.1365-2796.2006.01620.x. [DOI] [PubMed] [Google Scholar]
- Tedgui A, Lever MJ. Filtration through damaged and undamaged rabbit thoracic aorta. Am J Physiol. 1984;247(5 Pt 2):H784–H791. doi: 10.1152/ajpheart.1984.247.5.H784. [DOI] [PubMed] [Google Scholar]
- Thi MM, Tarbell JM, Weinbaum S, Spray DC. The role of the glycocalyx in reorganization of the actin cytoskeleton under fluid shear stress: a “bumper-car” model. Proc Natl Acad Sci USA. 2004;101(47):16483–16488. doi: 10.1073/pnas.0407474101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toh YC, Voldman J. Fluid shear stress primes mouse embryonic stem cells for differentiation in a self-renewing environment via heparan sulfate proteoglycans transduction. Faseb J. 2011;25(4):1208–1217. doi: 10.1096/fj.10-168971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vink H, Constantinescu AA, Spaan JA. Oxidized lipoproteins degrade the endothelial surface layer: implications for platelet-endothelial cell adhesion. Circulation. 2000;101(13):1500–1502. doi: 10.1161/01.cir.101.13.1500. [DOI] [PubMed] [Google Scholar]
- Vuoriluoto K, Jokinen J, Kallio K, Salmivirta M, Heino J, Ivaska J. Syndecan-1 supports integrin alpha2beta1-mediated adhesion to collagen. Exp Cell Res. 2008;314(18):3369–3381. doi: 10.1016/j.yexcr.2008.07.005. [DOI] [PubMed] [Google Scholar]
- Wang DM, Tarbell JM. Modeling interstitial flow in an artery wall allows estimation of wall shear stress on smooth muscle cells. J Biomech Eng. 1995;117(3):358–363. doi: 10.1115/1.2794192. [DOI] [PubMed] [Google Scholar]
- Wang S, Tarbell JM. Effect of fluid flow on smooth muscle cells in a 3-dimensional collagen gel model. Arterioscler Thromb Vasc Biol. 2000;20(10):2220–2225. doi: 10.1161/01.atv.20.10.2220. [DOI] [PubMed] [Google Scholar]
- Weinbaum S, Cowin SC, Zeng Y. A model for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. J Biomech. 1994;27(3):339–360. doi: 10.1016/0021-9290(94)90010-8. [DOI] [PubMed] [Google Scholar]
- Weinbaum S, Tarbell JM, Damiano ER. The structure and function of the endothelial glycocalyx layer. Annu Rev Biomed Eng. 2007;9:121–167. doi: 10.1146/annurev.bioeng.9.060906.151959. [DOI] [PubMed] [Google Scholar]
- Yao Y, Rabodzey A, Dewey CF., Jr Glycocalyx modulates the motility and proliferative response of vascular endothelium to fluid shear stress. Am J Physiol Heart Circ Physiol. 2007;293(2):H1023–H1030. doi: 10.1152/ajpheart.00162.2007. [DOI] [PubMed] [Google Scholar]
- Yokota H, Goldring MB, Sun HB. CITED2-mediated regulation of MMP-1 and MMP-13 in human chondrocytes under flow shear. J Biol Chem. 2003;278(47):47275–47280. doi: 10.1074/jbc.M304652200. [DOI] [PubMed] [Google Scholar]