Variations in photoreceptor directionality across the central retina

Abstract

Cones show a differential sensitivity to light coming from different portions of the pupil, typically being most sensitive to light from the center of the pupil. We measured the directional properties of the cones across the central 6 deg of the retina, using an optical imaging technique. We find that the cones in the center of the fovea have the broadest tuning. The width of the angular tuning changes rapidly from 0 deg to 1 deg retinal eccentricity, with cones at 1 deg being much more narrowly tuned than the cones in the center of the fovea. Directional tuning of the cones remains relatively constant from 1 deg to 3 deg retinal eccentricity. Receptoral disarray contributes minimally to the measured directional properties of the foveal cones, and there is no evidence of asymmetry between horizontal and vertical retinal locations. There are only small differences among the five subjects in the change in angular tuning of the cones with retinal location. We find that at the foveal center the directional tuning of the cones is limited by the diameter of the cone apertures.

1. INTRODUCTION

The cone photoreceptors of the human retina are directionally selective, typically being more sensitive to light coming from the center of the pupil than to light coming from the edge of the pupil.¹ A number of advantages to the visual system arise from this directional sensitivity, including a decreased total volume of photopigment being needed for the same effective optical density,² a decreased sensitivity of the cones to stray light that would decrease the contrast of images, and decreased effects of optical aberrations that are more common near the edges of the pupil and would likewise blur images. The directional selectivity of the cones is a result of their physical properties: their diameter, shape,³ and index of refraction make them act as small fiber optics,^4,5 preferentially collecting light that enters the inner segments from the direction of the center of the pupil and guiding the light along the outer segments. The physical orientation of the cones toward the center of the pupil⁶ makes the cones most sensitive to light that originates from that direction, and thus measurement of the directionality of the cones is a powerful tool for probing the physical properties of the cones in vivo.

Typically, researchers have used psychophysical techniques to measure the directional sensitivity of the cones^1,7–9 (see Applegate and Lakshminaryanan¹⁰ for a review). However, it is also possible to use optical techniques to measure photoreceptor directionality.^11–15 The optical techniques are based on the principle that light entering the inner segments of the cones is guided along the outer segment and is absorbed by the photopigment, multiply scattered into the deeper retinal layers, or singly scattered or reflected back along the outer segments, thereby retracing its path.^13,16 This light is then radiated from the inner segments back toward the pupil. Thus, by examining the pupillary distribution of light returning from the retina, it is possible to measure the directionality of the cone photoreceptors. The results of these optical measurements are modeled with two components: (1) a diffuse component of the light that represents the multiply scattered light and is modeled as a uniform background light filling the pupil and (2) the directed component of the light that represents the light that has been guided by the cones back toward the pupil. The directed component produces a spatial distribution of light in the plane of the pupil. This distribution is typically modeled with five parameters: the sum of a four-parameter Gaussian distribution and a dc term (see Gorrand and Delori¹⁷). The four parameters of the Gaussian are the location of the maximum reflectance in the plane of the pupil (x and y), the amplitude of the directed component at its peak, and the spatial localization or tuning of the distribution. We express the last parameter, the narrowness of the light distribution, as ρ (in units of inverse millimeter squared) to allow direct comparison with the results of psychophysical studies that use this same parameter. In general, the optical measures give a narrower estimate of the angular tuning of the cones than do psychophysical techniques,^12–14 though this is in part due to the fact that for peripheral pupil entry psychophysical techniques are sensitive to light that escapes from one cone and is absorbed by neighboring cones.¹⁸

In the current paper we examine the normal directional properties of the cones near and in the fovea. The cones of the human retina vary widely in their properties across the retina. The cones in the central retina are tightly packed,¹⁹ smaller in diameter,^19–21 and longer²⁰ than the cones just a short distance away. As a result, the photopigments of the cones in the center of the fovea have higher effective optical densities.^22–25 The cones also vary in their directionality across the fovea. Although in the normal eye all cones in the retina point to roughly the same location,⁶ the angular extent over which they accept light varies. Cones in the center of the fovea have broader acceptance angles than cones further from the center.^3,7,17

It has been suggested that the overall directional sensitivity of the cones represents both the directionality of individual cones and a variability in the location of optimal stimulation from cone to cone^26,27 or from region to region. MacLeod⁸ has estimated that in the central fovea the effect of this variability is small. The cones in the central fovea must be aligned to the same point in the pupil with a standard deviation of 1 deg or less (0.32 mm in the plane of the pupil). At 6 deg retinal eccentricity he found evidence of more disarray. Psychophysical measurements of these properties have been limited by the long measurement times and the requirement for highly accurate fixation over these long measurement times. The use of an optical technique allows the rapid, independent estimate of the changes in cone directionality across the central fovea as well as the ability to tie the results directly to the physical properties of the cones. In the current study we use an optical technique to measure the change in ρ with retinal location and to test whether changes in ρ with retinal location are due to changes in the variability of the alignment of the cones.

2. METHODS

A. Apparatus

We used an imaging reflectometer to measure the spatial distribution of light remitted from the retina in the plane of the eye’s pupil. The apparatus has been described in detail by Burns et al.¹⁴ Briefly, a portion of the retina is illuminated with a Maxwellian view system. The position of the entrance pupil can be changed under computer control. Light returning from the retina passes through a 2-deg aperture in a retinal conjugate plane. The image of the pupil is then formed on a cooled, 16-bit CCD camera (Princeton Instruments). Fixation is controlled by a separate optical channel. The location of the fixation point is also variable and under experimental control. The measurement light was 543 nm, and field stops were either 1 deg or 0.5 deg in the current experiments. The measurement beam pupil was formed by using a pinhole and a spatial filter and was 18 µm in diameter, imaged in the plane of the eye’s pupil.

B. Subjects

Six normal subjects participated in this research, two females and four males. Ages were between 26 and 46 years. One of the males had deuteranomalous color vision; the other subjects were all color normal. No reliable differences in the measurements were noted between the deuteranomalous subject and the others. All subjects were dilated with 0.5% Mydriacyl after informed consent was obtained. Three of the subjects participated in all of the experiments; the other three, owing to time constraints, participated only in the main experimental conditions.

C. Experimental Conditions

The retinal illuminance of the measurement beam was varied by using a series of computer-controlled neutral density filters. The measurement beam was approximately 5.4 log trolands. To improve the signal-to-noise ratio, we summed 3 × 3 pixel regions on the CCD chip, providing a usable pixel size of 0.08 mm in the plane of the pupil. Typically an integration time of 1 s was used both to increase sensitivity and to decrease the effect of speckle on the image.

1. Determination of Optimal Pupil Entry Location

At the start of each experimental session on a new subject, we made a series of measurements of the distribution of light in the pupil for a wide range of pupil entry locations. First, we located the point in the pupil for which a fixed amount of light entering the pupil produced the largest amount of light exiting the pupil, by making a series of measurements while varying the input pupil position. This location was used as the optimal location. These initial images were saved and used in the analysis procedures.

2. Variations in Cone Directionality with Retinal Location

Cone photoreceptor directionality was measured with use of a 1-deg measurement light at retinal locations of 3, 2, 1, and 0.5 deg (temporal, nasal, superior, and inferior) eccentricity, as well as at the fovea. We also made measurements using a 0.5-deg measurement light at 1, 0.5, and 0.25 degrees (temporal and nasal) as well as at the fovea. Fixation was varied by moving a fixation target. The fixation target was first aligned to the same position as the measurement beam when the measurement beam entered the eye at the optimal pupil entry position. All motions of the fixation target were then made relative to this position. This preliminary adjustment of the fixation target was necessary to control for the aberration-induced changes in the retinal position of the measurement beam with pupil entry position.

We typically performed multiple, repeated measurements at 0 and 3 deg temporal to the fovea, to be used in the analysis of photoreceptor disarray. These repeated measurements involved both multiple measurements at the optimal pupil entry position and measurements with a series of pupil entry positions. For other retinal positions we concentrated on obtaining measurements with the optimal pupil entry locations.

D. Data Selection

In each session, between 40 and 100 measurements were made of the light exiting the pupil. Of these measurements a small percentage could not be used for further analysis because of unnoticed blinks, unwanted reflections off optical surfaces of the eye, or other similar events. In most cases we were able to acquire data for the condition of interest. We have encoded as missing data missing images and images that were not of sufficient quality rather than incorporating the results into the analysis. In addition, we include only conditions for which the parameter-fitting routine was able to adequately converge on an estimate of directionality that accounted for more than 70% of the variance in the 1-deg test conditions and 60% of the variance in the 0.5-deg measurement conditions (see below).

E. Data Processing

A MATLAB program (MathWorks, Inc., Natick, Mass.) was used to process the measured intensity distributions. First, we subtracted the black level of the camera for each image. This was computed as the response of the camera in a portion of the image that was outside the aperture of the lenses and therefore received no light. Next, we located the center of the dilated pupil^28,29 by interactively selecting points on the perimeter of the pupil and computing the best-fitting circle to the pupil margin. All spatial computations, including the location of the reflectometric peak and the location of the entry pupil, were corrected for the small changes in eye position that occur during a measurement session. Following alignment of the images, the locations of the major Purkinje reflexes were located interactively, and a mask was computed to omit regions of the image influenced by the Purkinje images. Finally, we fitted the resulting intensity distributions by using a 5-parameter model.

$$L_{\text{pupil}}=B+A*{10}^{-r*d^2}$$ (1)

where B is the intensity of the diffuse component, A is the intensity of the directed component, ρ (in inverse millimeters squared) is the space constant of the Gaussian fit to the directed component, and d is [(x₀ − x)² + (y₀ − y)²]^1/2, the distance from the peak of the intensity distribution (x₀, y₀). The diffuse component for our optical configuration consists of both light that is widely scattered in the retina and light originating from the foveal reflex, which is spread across the pupil.¹⁴ For comparison with psychophysical studies of the Stiles–Crawford effect, we express the space constant as ρ, in units of mm−2. However, the interpretation of ρ with this method is slightly different from that of the psychophysically measured ρ, which is typically broader than the optically determined value.^12–14,30

3. RESULTS

A. Directional Tuning

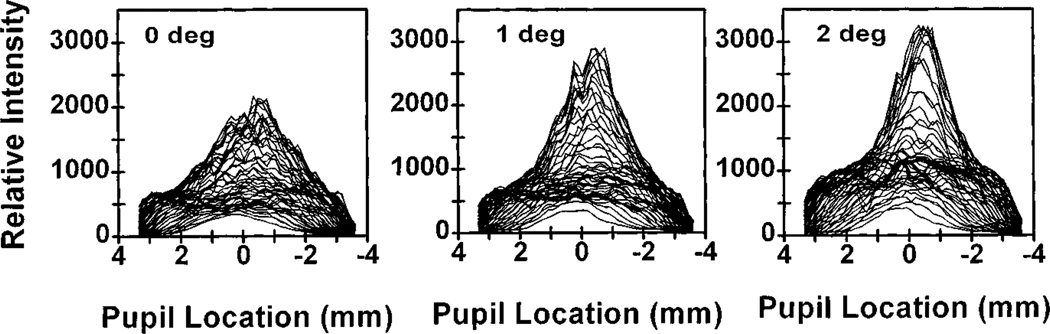
The distribution of light exiting the eye in the plane of the pupil varies with retinal position. Figure 1 shows profiles of the pupil intensity at three retinal positions measured with use of a 1-deg field size. In all cases there is a pedestal of light that fills the pupil, visible in Fig. 1 as a sharp edge at roughly ±3.5 mm. In addition to this diffuse component, there is a peaked component in the intensity distribution that is the directed portion of the retinal reflection. For all subjects this directed component is broadest when the measurement field is centered at fixation and narrows progressively from 0 to 2 deg.

Fig. 1.

Profiles of the distribution of light measured in the plane of the pupil when different retinal locations are illuminated. Each line in a profile represents the intensity distribution along a single column of pixels. Thus the overall distribution is oriented vertically with the upper half of the pupil plotted as positive numbers and the lower half plotted as negative numbers. Left, illumination of the central fovea with a 1-deg-diameter illumination spot; center, illumination of a region of retina 1 deg nasal to the fovea with a 1-deg illumination spot; right, illumination of a region of retina 2 deg nasal to the fovea with a 1-deg illumination spot.

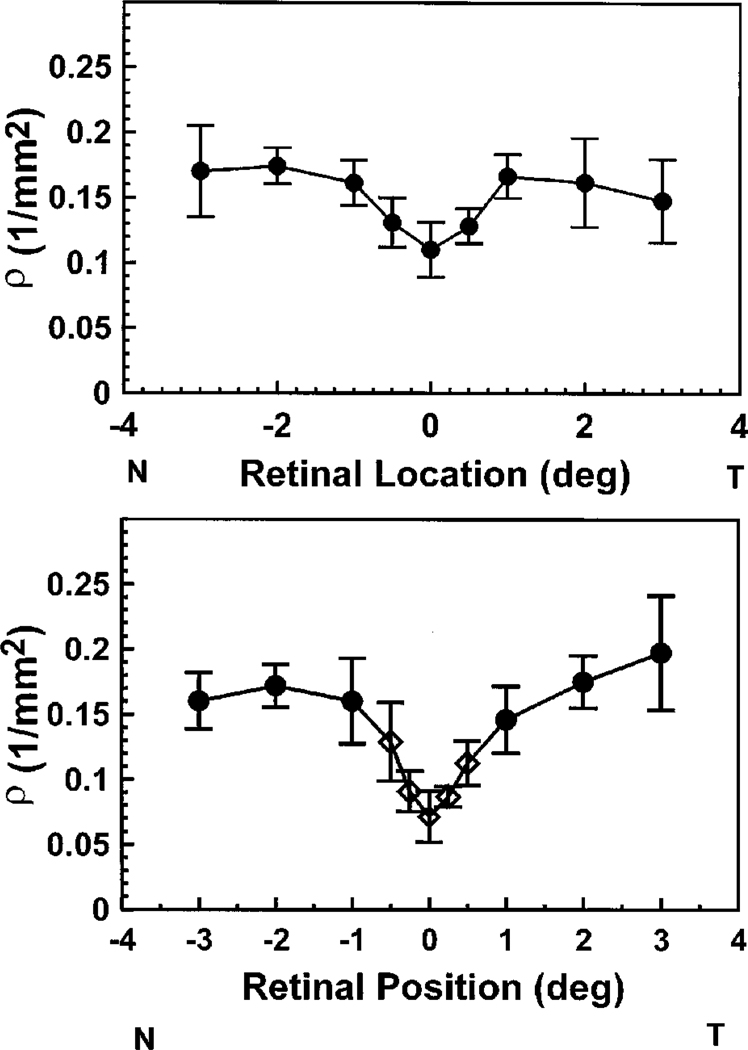
For all subjects the cones in the center of the retina were more broadly tuned than cones measured at a fraction of a degree away. This decrease in the angular tuning is expressed by a decrease in the ρ parameter (decreased tuning or broadest light distribution) in moving from the fovea to 2 deg retinal eccentricity. The top panel in Fig. 2 is a summary plot of ρ as a function of retinal eccentricity for one subject with the 1-deg illumination. The data are the average for four measurement sessions obtained over a period of four months (error bars are ±2 standard errors of the mean). For this subject, ρ was smallest in the fovea, increased to ~1 deg retinal eccentricity, and then remained constant beyond 1 deg. This constancy of ρ from 1 deg to 3 deg was not found in all of our subjects; some increased slightly, some decreased, but on average ρ was constant. The bottom panel shows mean data for the five subjects who participated in the main portion of this experiment. This change of ρ with retinal location presumably arises from the difference in the diameter of the cones across the central fovea (see Section 4). For these subjects, with a 0.5-deg measurement field ρ changed by more than a factor of 2, from 0.070 to 0.152, in just 1 deg. This corresponds to a change in the width of the light distribution measured in the plane of the pupil from 4.2 mm to 2.6 mm (full width at half-height).

Fig. 2.

Best fitting ρ values as a function of retinal location. The measurement field size was 1 deg in diameter. Top, mean ±2 standard errors of the mean for a single subject. Data were collected in four separate measurement sessions over four months. Bottom, average results for five subjects. Error bars represent ±2 standard errors of the mean. Circles, values collected with a 1-deg-diameter illumination spot; diamonds, measurements made with a 0.5-deg spot.

The standard deviation of the measurements was largest at 3 deg in the temporal retina, in part because for some subjects the images contained an additional light reflex imaged in the pupil. When this reflex was visible, we did not include it in the data analysis, but undetected contributions could have increased the variability of the fits. The presence of this reflex does not affect the conclusions of the paper, which concern the contribution of cone diameter and photoreceptor disarray to the directed component.

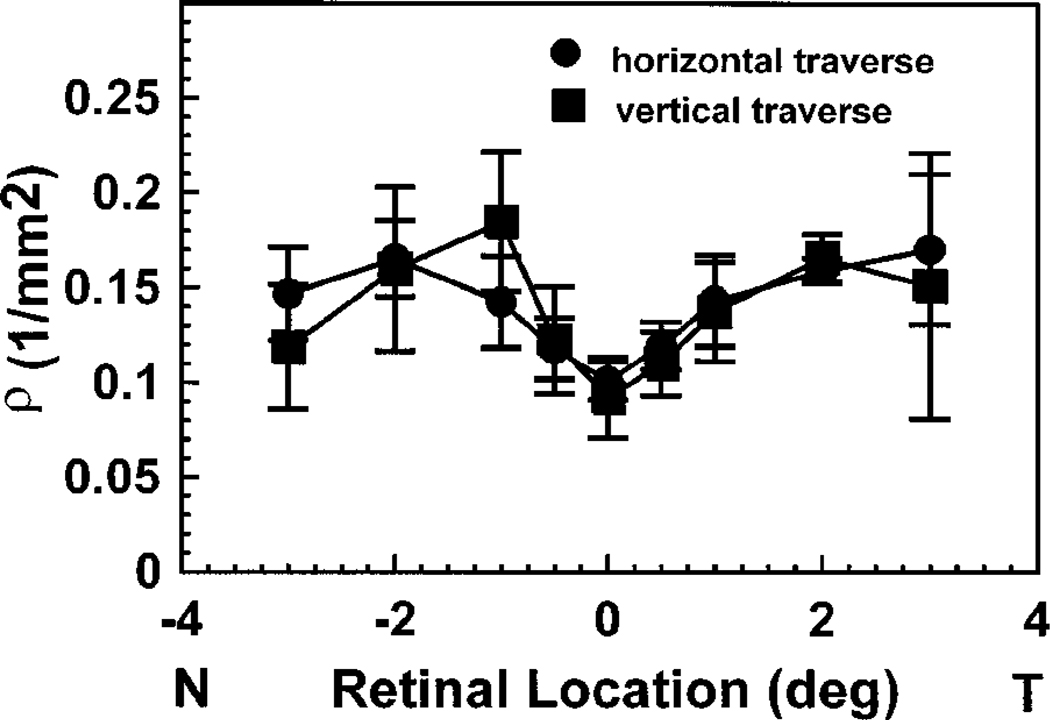
There is no apparent difference in the directionality of the cones between the horizontal and the vertical traverses for our conditions. We measured positions displaced vertically on the retina in three of the subjects. The ρ measured for the vertical traverses is plotted as a function of retinal location in Fig. 3, and for comparison the horizontal measurements made on the same days in the same subjects are also plotted.

Fig. 3.

Comparison of the average of the best-fitting ρ values for horizontal and vertical traverses of the central retina for three subjects. All data for each subject were collected on the same date with use of a 1-deg-diameter illumination spot.

B. Location within the Pupil of the Peak Directionality

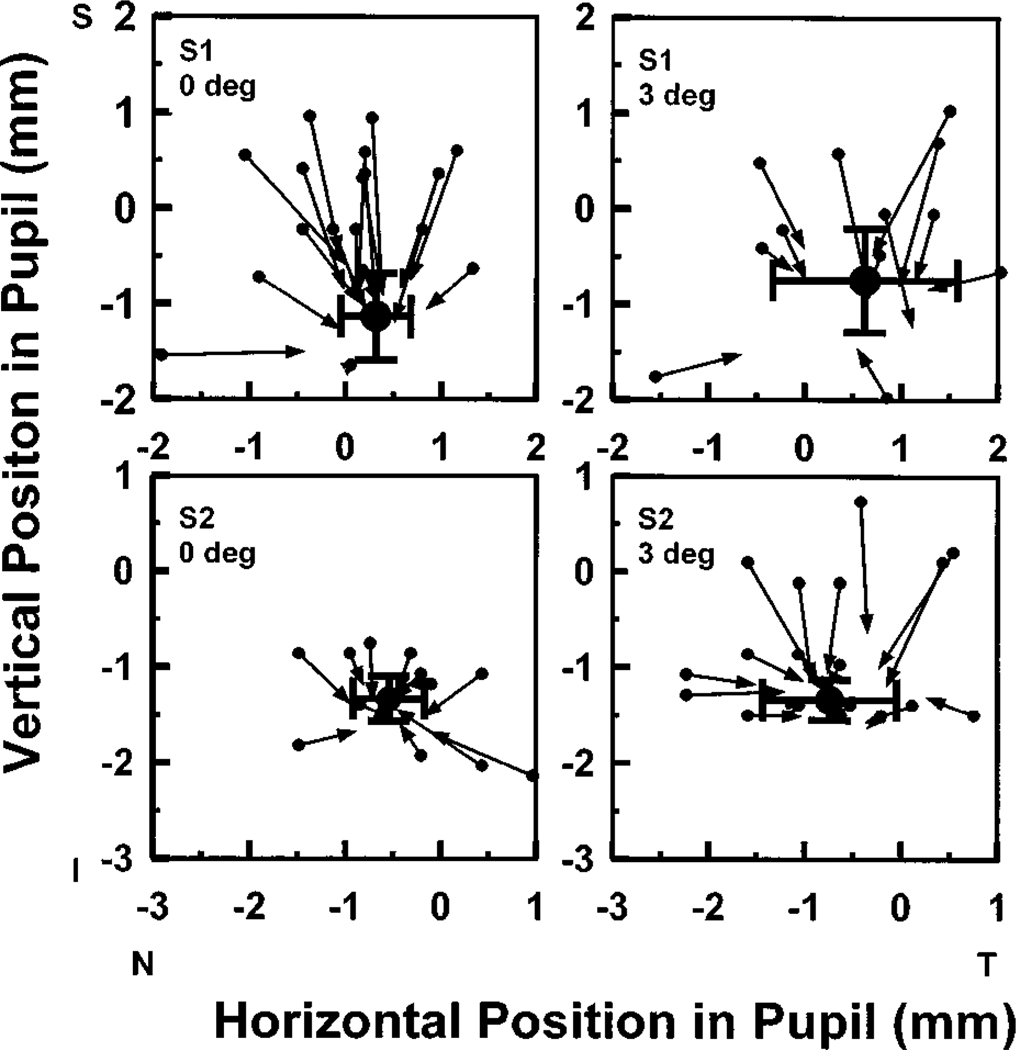
The location of the entrance pupil played a small role in determining the location of the estimated peak of the directed portion of the light returning from the retina. Figure 4 compares the location of the light exiting the pupil for near-optimal entry pupil locations (symbols and error bars) with the exit location for entry positions some distance away from the optimal location. Each panel of Fig. 4 displays the results of multiple measurements at a single retinal location obtained in a single experimental session. For each entry pupil position we plotted an arrow: the tail of the arrow indicates the location in the pupil of the illuminating light, and the head points to the location of the center of the corresponding exit distribution as determined from the parameter-fitting procedure. The large solid circles and the error bars represent the mean ±2 standard deviations in the position of the peak reflectance for at least four measurements obtained within a single experimental session. In general, small movements between measurements make it impossible to repeat measurement positions exactly. Thus the estimate of the peak location is decreased by both errors in determining the fit that are due to noise and trial-to-trial variation in the entry pupil position resulting from head movements. Similar results were obtained for three other subjects. The exit pupil location for the more distant pupil entry positions is less reliably determined because of the decreased amplitude of the directed component for these locations (as expressed by the variance accounted for by the fits; see below).

Fig. 4.

Variation in the location of the maximum in light exiting the eye with changes in the entry pupil location. Each panel represents multiple measurements made for a single subject on one day. A single measurement is represented by a single arrow. The solid symbol at the base of each arrow is the location of the entry pupil for a single measurement. The point of each arrow is located at the peak in the distribution of light exiting the eye for that entry pupil position. The large solid circles represent the average peak in light returning out of the pupil when the entry pupil position is near its optimal location. The error bars show ±2 standard deviations of the estimate of the location of the peak. Each row represents a different subject. The left-most plots are for foveally fixated measurement lights; the right-most plots are locations 3 deg in the nasal retina. Similar results (not shown) were obtained for two other subjects.

4. DISCUSSION

A. Variation in Directional Tuning with Retinal Position

Westheimer³ pointed out that the diameter and shape of the foveal cones should affect their directional tuning. He confirmed this prediction psychophysically, and since then it has been well established that ρ varies with retinal eccentricity.^3,7,15 Enoch and Hope⁷ measured ρ from 0 to 10 deg in the temporal retina. They found that ρ was minimum at the center of the fovea, increased rapidly out to 2–5 deg eccentricity, and then decreased very slowly. Starr et al.,³¹ using a 2-min test target and careful control of the optical correction of the eye, found that for the very center of the retina the cones’ directional sensitivity was flat across the pupil. Recently Delint et al.¹⁵ used an optical method based on a scanning laser ophthalmoscope to measure ρ as a function of retinal position. In agreement with Enoch and Hope⁷ and Gorrand and Delori,¹³ de Lint et al.¹⁵ found that ρ was small in the center of the fovea and increased to either side. However, they observed that beyond 2 deg, ρ decreased very rapidly: at 3–4 deg retinal eccentricity ρ reached a value similar to that measured in the center of the fovea. This differs from the finding of a broad peak by Enoch and Hope⁷ and from the results of the current study. Delint et al. suggest that the difference between their results and the results of Enoch and Hope arises from a mixture of rod and cone measurements in the perifoveal retina, since the rods have broad acceptance angles.³² Such an intrusion might be seen by means of a vertical–horizontal asymmetry, since the proportion of rods rises more steeply along the vertical than along the horizontal axis.¹⁹ We did not find such an asymmetry. Our technique, which fixes the entry pupil and measures all the light exiting the pupil, avoids the potential problem of changing the relative contributions of rods and cones within a measurement, since the entire directionality function can be obtained with a single input pupil position. In addition, if the rods are contributing to our measurement, they are so broadly tuned that they will essentially add a constant to the diffuse component of the fits and will not distort our estimate of ρ.

For two reasons, unrecognized foveal reflexes are unlikely to cause our data to be artificially narrow. First, specular reflections from the retina are expected to fill the exit pupil of the eye and thus should appear as an additional contribution to the diffuse component of the fits. Second, if the shape of the retinal crest were irregular, producing a focused reflection in the plane of the pupil, then the position of such an image would move systematically with changes in the position of the entrance pupil. Although we have observed such an effect in the presence of small foveal scars, we did not observe this in any of the subjects from the current study. Thus, while it is evident that ρ does decrease in the far periphery,^33,34 the reason for the difference in results at 3 deg between the two different optical methods is unclear.

B. Is There Photoreceptor Disarray in the Central Retina?

The measured directionality of the cones is made up of both the directionality of individual photoreceptors and the variability of the directionality among the measured photoreceptors. Safir and Hyams²⁷ proposed that the acceptance angle of individual photoreceptors was quite narrow but that there was considerable splaying of orientation between cones. This disarray in the orientation of the photoreceptors could be the source of phenomena such as the transient Stiles–Crawford effect³⁵ and the inability to invisibly interchange lights that have been equated for the Stiles–Crawford effect.³⁶ However, MacLeod,⁸ using directionally selective adaptation, was unable to detect significant receptor disarray in the fovea. He was able to measure variability in the alignment of the photoreceptors at a retinal eccentricity of 6 deg, as were Birch and Sandberg.³⁷ If there is variation among receptors or groups of receptors in alignment, then changing the entrance pupil should produce predictable changes in the measured directionality.

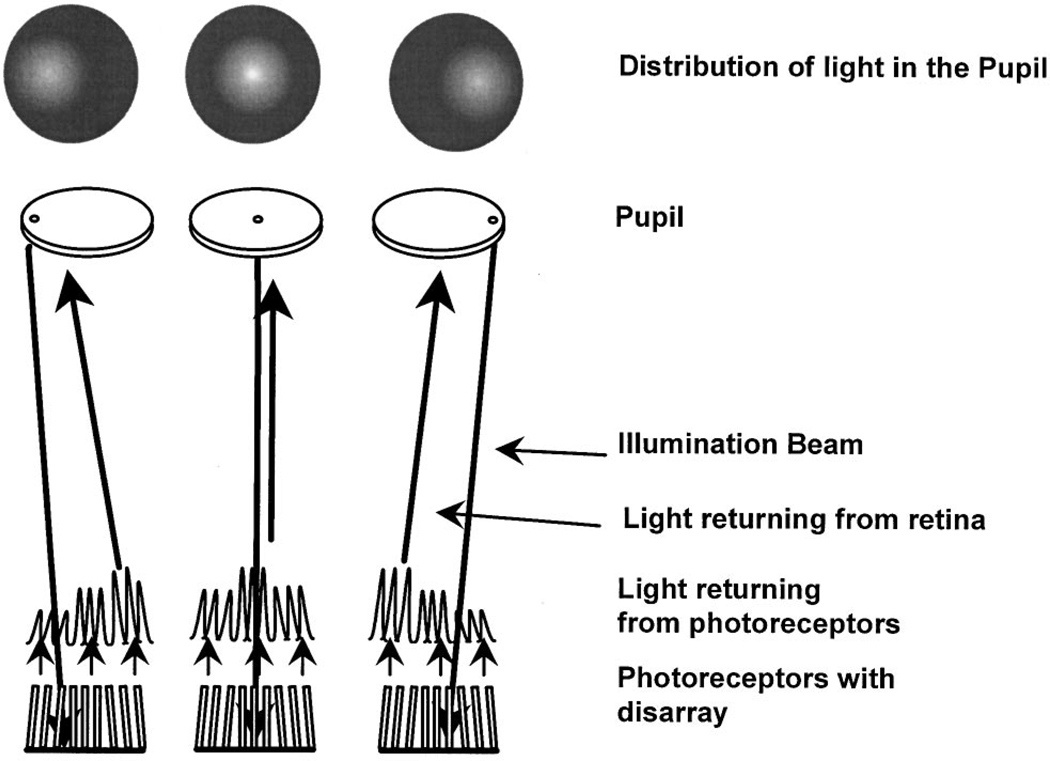
Figure 5 is a schematic diagram of what should be measured if receptors point to different locations in the pupil. If we measure the distribution of the light returning from the retina when the entry pupil is placed at the left edge of the pupil (Fig. 5, left side), photoreceptors oriented more toward the left should capture more light and should reemit some of the light back along their axis, toward the left side of the pupil. If the entry pupil position were moved to the right (Fig. 5, right side), the receptors pointing to the right would capture and return relatively more light. The result would be that the measured peak in directionality would move toward the entry pupil position (shown in the simulated results in the top row of Fig. 5).

Fig. 5.

Schematic diagram of the logic of the tests for photoreceptor disarray. The left column shows what should happen if we illuminate a group of photoreceptors from the left side of the pupil. If there were disarray, then the illumination light would be maximally coupled into the photoreceptors that point more to the left side of the pupil. These would return more light than photoreceptors that are pointing toward the right edge of the pupil. The resulting distribution of light in the plane of the pupil (top row) would therefore be skewed toward the left edge of the pupil. The center and right columns show the same logic for entry pupil positions near the center and right edges of the pupil, respectively. Thus, if there were significant photoreceptor disarray, the measured peak of the retinal light distribution in the would move toward the location of the illumination light in the pupil. If there were no photoreceptor disarray, then the directed portion of the exit distribution would be invariant in shape but would vary in amplitude in proportion to the coupling between the illumination and the photoreceptors.

The results in Fig. 4 showed that illuminating the retina from a position in the pupil away from the optimal entry pupil location does move the exit pupil position but only by ~1 mm. This 1 mm represents a maximum value for the foveal cones, since refraction of light at the sides of the foveal pit can move the measured location of the Stiles–Crawford peak slightly.³⁸ This curvature could account for ~0.5 mm of movement in the pupil, even if there were no misalignment in the cones.³⁸

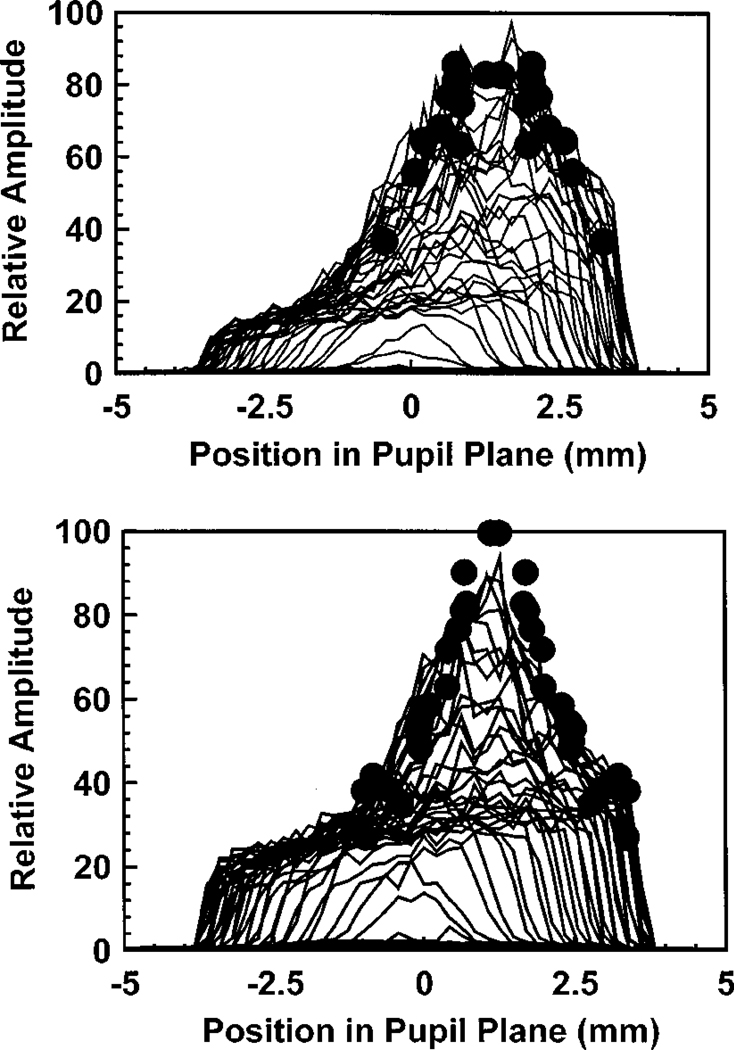
What is not clear from Fig. 4 is that the amplitudes of the directed component for the more distant entry pupil positions are low and that as a result the reliability of the estimate of the peak location is reduced. If there are cones pointing at an angle to the group mean, they must be relatively rare. To test for a small contribution from photoreceptors directed away from the group mean, we analyzed the data for the nonoptimal pupil entry positions in another way. If there is significant receptoral disarray, then the amplitudes of the directed components for nonoptimal pupil entry positions should be larger than predicted on the basis of the measurements made with an optimal pupil entry position. This is because they would be closer to the optimum entry location for the receptors oriented at an angle to the group mean and would return more light than they did in the optimum alignment condition. Thus the amplitude for the nonoptimal entry pupil positions should decrease with increasing distance more slowly than the pupil intensity measured when the retina is illuminated from the optimal pupil entry position. Figure 6 shows this comparison for one subject at two retinal positions. Similar results were obtained for two other subjects. The profile of the intensity distribution in the pupil when the pupil was illuminated from the optimal position is plotted as solid lines. We computed the distance between the entry pupil positions and the optimal exit pupil positions for each of the nonoptimal pupil entry positions. The fitted estimates of the total amplitude (diffuse plus directed) are plotted as solid circles, displaced from the peak according to the distance. For all three subjects we found that the distribution of the peak amplitudes was not wider than the intensity distribution taken for a single entry pupil position. This supports the conclusion that if there is receptor disarray for normal subjects, it involves at most a small percentage of the photoreceptors.

Fig. 6.

Profile of the intensity distribution of light in the pupil (solid lines) for an optimal pupil entry location is compared with the estimates of the peak amplitude (the sum of the directed and the diffuse components of the light) obtained for different pupil entry positions. The distance between each entry pupil location and the optimum entry pupil location was measured. We then plotted the amplitude for each measurement at the proper distance from the peak of the optimum distribution (solid circles). Results are shown for one subject at 0 (top) and 3 deg retinal eccentricity (bottom). Similar results were obtained for two other subjects.

There is another line of evidence that can be used to estimate the amount of disarray in the foveal cones. This evidence comes from the breadth of the directionality function that is measured at the center of the fovea. At a given wavelength the angular sensitivity of single cones is determined by the waveguide properties, which in turn depend on two main factors: the relative index of refraction of the intracellular and extracellular spaces and the physical diameter of the cones.^3,39 Thus the angular tuning of a region of retina will depend on these two factors plus the variance in the orientation of the group of cones being measured. In general, neither the exact values of the appropriate indices of refraction nor the proper shape and size of the cone aperture are known (see Rowe and Pugh⁴⁰). However, it is possible to compute the smallest possible angle into which a cone can radiate. This computation is performed by simply treating the cone as a small aperture illuminated by a plane wave. We can then compute the diameter of the Airy disk that would appear in the pupil for an aperture of this diameter. We made these calculations for different retinal positions by using the cone aperture data of Curcio.²¹ These predictions depend only on the wavelength of the light, the diameter of the cone aperture, and the optical length of the eye, and thus the predictions are independent of the measurements. In fact, the calculated values may overestimate the size of the cone aperture, since the work of Rowe et al.⁴⁰ and the estimates of MacLeod et al.⁴¹ suggest that the effective aperture is smaller than the diameter of the inner segment. If there is an overestimation of the cone aperture, its effect is conservative. A smaller cone aperture predicts a broader tuning function.

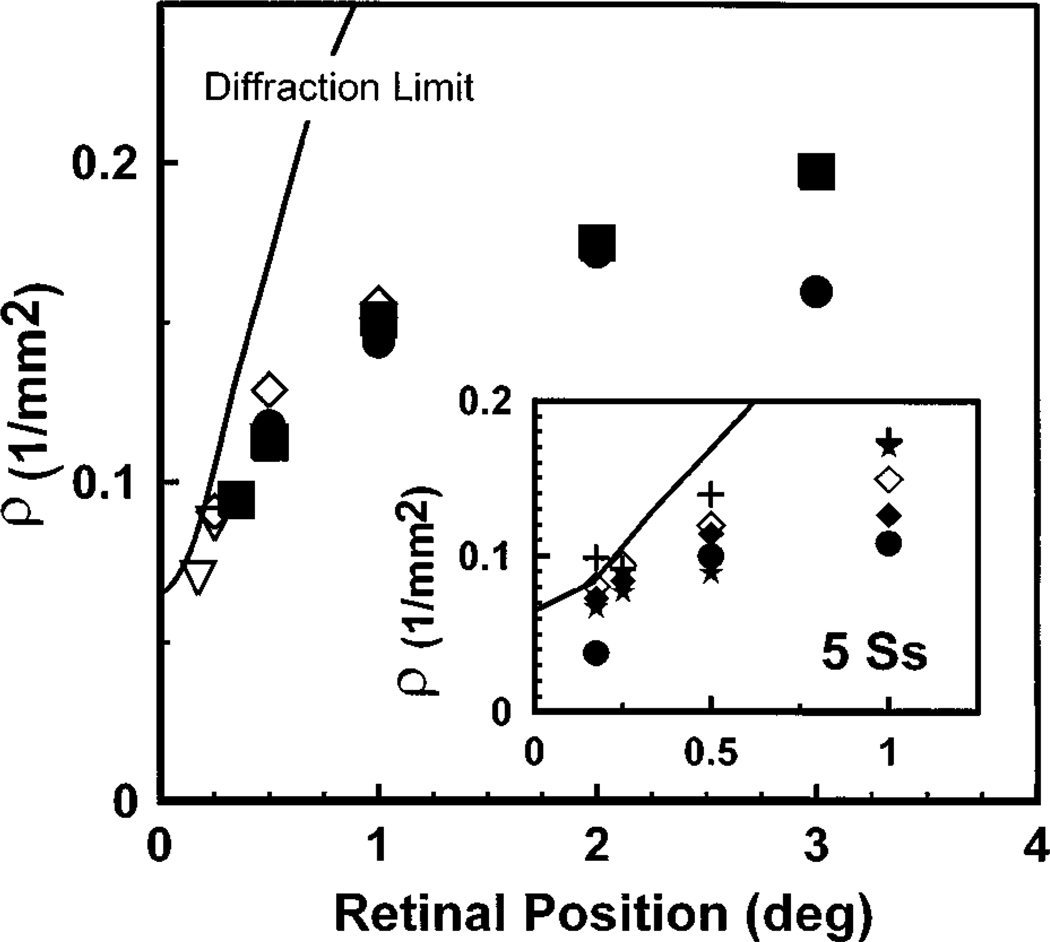
Figure 7 compares these predictions based on diffraction by the cone apertures (solid line) with the data from our subjects. At the center of the fovea the directional tuning measured in the plane of the pupil seems to be determined by the physical size of individual cones, with no need to invoke waveguide properties. In addition, since receptoral disarray should broaden the measured light distribution, the close match between the predictions for simple diffraction and the measured distributions is further evidence that receptoral disarray is minimal in the center of the fovea. Away from the center of the fovea, the photoreceptors’ inner segments increase in diameter, and thus the physical prediction for the emission angle for a coherent source of the same diameter as a photoreceptor narrows rapidly. This places a theoretical upper limit on ρ, the measured ρ increases much more slowly than the physical prediction, and the measured distributions are never narrower than the diffraction predictions. Therefore, although the diameter of the cone inner segment seems to control ρ in the center of the fovea, the directional tuning is controlled by other factors, such as the waveguide properties of the cones, away from the center of the fovea.

Fig. 7.

Comparison of the predicted ρ and the measured ρ’s (symbols) for diffraction-limited cones (solid line). The diffraction limit represents the narrowest possible directional tuning for cones with aperture sizes obtained from Curcio.²¹ We assumed that the cones were simple apertures illuminated from behind with a plane wave. This represents the limiting case, and for the center of the fovea the measured values of ρ approach this limit. Large plot: plot of the measured ρ for 1-deg (solid symbols) and 0.5-deg (open symbols) measurements averaged across five observers. Temporal and nasal retinal measurements are portrayed on the same axis. The retinal position for the centrally fixated stimuli were corrected for the size of the measurement fields by computing the average retinal position of the fields. Inset: measured ρ for the five subjects with use of a 0.5-deg measurement field compared with the diffraction limit. The retinal position was corrected for the average position of the measurement spot.

It is also of note that the variability in the estimates of directional tuning for our subjects is relatively small. The inset panel of Fig. 7 shows ρ for the 0.5-deg test size measurements at retinal locations between 0 and 1 deg. The intersubject variability is small, and for all subjects the measured ρ values approach the diffraction limit closely.

5. CONCLUSIONS

From these measurements of cone directionality we conclude the following:

1. The directional tuning of the cones varies rapidly across the central 6 deg of the retina.

2. Cones at the center of the fovea have the broadest tuning.

3. The width of the directional tuning function for the cones in the central fovea is limited by diffraction. This result could provide the basis for a sensitive measure of early damage or loss of photoreceptors.

4. The change in directional tuning between 0 and 3 deg represents changes in the properties of the photoreceptors themselves and cannot be attributed to changes in the amount of photoreceptor disarray. We find little evidence for receptor disarray in normal eyes for the central 6 deg of the retina. If there is disarray, it must affect only a small percentage of the cones.