Non-Iterative, Regression-Based Estimation of Haplotype Associations with Censored Survival Outcomes

Abstract

The general availability of reliable and affordable genotyping technology has enabled genetic association studies to move beyond small case-control studies to large prospective studies. For prospective studies, genetic information can be integrated into the analysis via haplotypes, with focus on their association with a censored survival outcome. We develop non-iterative, regression-based methods to estimate associations between common haplotypes and a censored survival outcome in large cohort studies. Our non-iterative methods—weighted estimation and weighted haplotype combination—are both based on the Cox regression model, but differ in how the imputed haplotypes are integrated into the model. Our approaches enable haplotype imputation to be performed once as a simple data-processing step, and thus avoid implementation based on sophisticated algorithms that iterate between haplotype imputation and risk estimation. We show that non-iterative weighted estimation and weighted haplotype combination provide valid tests for genetic associations and reliable estimates of moderate associations between common haplotypes and a censored survival outcome, and are straightforward to implement in standard statistical software. We apply the methods to an analysis of HSPB7-CLCNKA haplotypes and risk of adverse outcomes in a prospective cohort study of outpatients with chronic heart failure.

1 Introduction

Genetic association studies often focus on estimating the association between haplotypes—combinations of alleles at adjacent loci on a chromosome—and a disease trait. A haplotype-based analysis may offer an attractive data reduction and efficiency gain compared to an analysis based on individual single-nucleotide polymorphisms (SNPs). However, linkage phase is typically unknown, so that there may be more than one pair of haplotypes that is consistent with the observed genotype for each individual. Thus, haplotype risk estimation is frequently based on sophisticated iterative algorithms that iterate between haplotype imputation and risk estimation. Currently, there exist reliable haplotype-based estimation methods for a binary trait in case-control studies and for continuous or discrete traits in cohort studies (e.g., Schaid et al., 2002; Schaid, 2004; Venkatraman et al., 2004). We focus on large, population-based prospective cohort studies with a censored survival outcome, for which the development of estimation methods is ongoing and their application to clinical research is increasing.

Several iterative estimation methods exist for population-based cohort studies in which primary interest lies in a censored survival outcome. Lin (2004) and Tregouet and Tiret (2004) introduced an expectation-maximization (EM) algorithm for estimation based on a proportional hazards regression model. Tan et al. (2005) developed estimation procedures for longevity studies based on a proportional hazards regression model, and estimated haplotype hazard ratios from population survival information. Lin and Zeng (2006) established semi-parametric maximum likelihood estimation for cohort studies. Chen et al. (2004) developed a haplotype-based score test for detecting the association of a disease with a genomic region of interest using prospective information and unphased genotype data collected from cohort studies with a censored survival outcome. Subsequently, Chen and Chatterjee (2006) examined the statistical properties of alternative EM-based procedures for haplotype risk estimation in cohort studies. Souverein et al. (2008) extended EM-based approaches to rare haplotypes using a penalized proportional hazards regression model. Recently, Scheike et al. (2010) introduced estimation for haplotype effects in survival data based on estimating equations.

We develop non-iterative, regression-based methods to estimate associations between common haplotypes and a censored survival outcome in large cohort studies. Our approaches enable haplotype imputation to be performed once as a simple data-processing step, and thus avoid implementation based on complex algorithms that iterate between haplotype imputation and risk estimation. We focus on moderate associations of common haplotypes inferred from tag SNPs in small numbers of genes in large prospective studies. Our goal is to allow haplotypes to be integrated into the analysis of a censored survival outcome, so that analyses combining genetic and environmental information can be conducted in standard software by researchers expert in the relevant subject matter, rather than by statisticians using specialized software.

Our non-iterative methods—weighted estimation and weighted haplotype combination—are both based on the Cox regression model, but differ in how the imputed haplotypes are integrated into the model. French et al. (2006) introduced non-iterative weighted estimation in the context of case-control data. The method is based on creating multi-record data, in which the data for each individual consist of multiple records, one for each diplotype consistent with the unphased genotype. Weighted logistic regression is used to relate the haplotypes to the binary disease outcome, in which the weights are set to the conditional probability of each diplotype given the observed genotype. A robust or ‘sandwich’ variance estimator is used for standard error estimation. For a case-control outcome, weighted estimation provides valid tests for genetic associations and reliable estimates of moderate effects of common haplotypes. For analyses of case-control data, weighted estimation is implemented in the R package haplo.ccs (French and Lumley, 2007). Recently, Neuhausen et al. (2009) applied non-iterative weighted estimation to an analysis of insulin-like growth factor variants and incidence of breast cancer.

Weighted haplotype combination is based on creating single-record data from the set of diplotypes consistent with the observed genotype. For each individual, a weighted combination of the set of diplotypes consistent with the observed genotype is determined, in which the weights are determined by the conditional probability of the diplotypes given the observed genotype. We have applied weighted haplotype combination to collaborative research projects regarding haplotypes of BRCA1- and BRCA2-interacting genes and incidence of ovarian and breast cancer (Rebbeck et al., 2009; Rebbeck et al., 2011). The approach is similar to that of Zaykin et al. (2002) in that diplotype probabilities are used as predictors. However, Zaykin creates a multi-record dataset with unaveraged diplotype probabilities.

In Section 2, we detail non-iterative weighted estimation and weighted haplotype combination in the context of a censored survival outcome. In Section 3, we use a simulation study to evaluate their statistical properties. In Section 4, we apply the methods to investigate associations between HSPB7-CLCNKA haplotypes (Cappola et al., 2010; Stark et al., 2010) and risk of adverse outcomes in a prospective study of chronic heart failure patients. We provide concluding discussion in Section 5. In the Appendix, we provide instructions for implementation in Stata (StataCorp, College Station, Texas).

2 Statistical Methods

2.1 Notation and model

Let T_i and C_i denote the event time and censoring time, respectively, for individual i = 1, … , n such that Y_i = min(T_i, C_i) denotes the possibly censored event time. Let δ_i denote the event indicator such that δ_i = 1 if Y_i = T_i and δ_i = 0 if Y_i = C_i. Let G_i denote the unphased genotype and Z_i denote a set of environmental exposures. Thus, {Y_i, δ_i, G_i, Z_i} compose the observed data for individual i.

The survival model is specified as a function of Z_i and D_i, the unobserved diplotype (or pair of haplotypes). We assume that if the diplotypes were known, then we would fit a Cox regression model (Cox, 1972) to estimate the association between {D_i, Z_i} and {Y_i, δ_i}. Recall that the Cox regression model employs a log function to relate the hazard function to a linear combination of the diplotypes and environmental exposures:

$$\text{log }{\lambda }_i(t)=\text{log }{\lambda }_0(t)+D_i{\beta }^D+Z_i{\beta }^Z,$$ (1)

where: λi(t) is defined as the instantaneous rate at which failures occur for individuals that are surviving at time t:

$${\lambda }_i(t)=\underset{\mathrm{\Delta }t\to 0}{\text{lim}}\mathrm{P}[t\le T_i<t+\mathrm{\Delta }t|T_i\ge t]/\mathrm{\Delta }t;$$ (2)

λ₀(t) is an unspecified baseline hazard function, possibly stratified by an exposure of interest; β^D are regression parameters that correspond to diplotypes D_i, and β^Z are regression parameters that correspond to environmental exposures Z_i. In the context of an association study, β = {β^D, β^Z} represents the target of inference. Note that in our case study, diplotypes and exposures are only measured at baseline and are hence constant over time. In the situation of time-independent exposures, λ_i(t) is often referred to as a ‘proportional hazards’ regression model.

2.2 Haplotype imputation

Because linkage phase may be unknown, there may be more than one pair of haplotypes that is consistent with the observed genotype. In this case, a set of diplotypes may be imputed and corresponding posterior probabilities may be estimated for each individual. Let d(G_i) denote the set of all possible diplotypes consistent with the unphased genotype G_i and p_id denote the population haplotype frequencies that correspond to each diplotype d in d(G_i). Let π_id ≡ π_id(p_id, β) denote the conditional probability of diplotype d given d(G_i).

We impute haplotypes and estimate population haplotype frequencies using haplo.em, an implementation of an EM algorithm (Dempster, 1977) included in the R package haplo.stats (Sinnwell and Schaid, 2009), which computes maximum likelihood estimates of haplotype probabilities from unphased genotypes measured on unrelated individuals. Unlike the standard EM algorithm that attempts to enumerate all possible pairs of haplotypes before iterating over the EM steps, the implementation in haplo.em is based on a ‘progressive insertion’ algorithm that progressively inserts batches of loci into haplotypes of growing lengths, runs the EM steps, trims off pairs of haplotypes per individual when the posterior probability of the pair is below a specified threshold, and then continues the insertion, EM, and trimming steps until all loci are inserted into the haplotype. Haplotype imputation and estimation of population haplotype frequencies can also be performed using Bayesian methods implemented in software such as PHASE (Stephens and Donnelly, 2003).

2.3 Non-iterative weighted estimation

Weighted estimation is based on creating multi-record data, in which each individual contributes multiple records to the analysis, one for each diplotype consistent with the unphased genotype. Let X_id denote the multi-record design matrix (or set of covariates) that includes both diplotype information and environmental exposures. Diplotype information is integrated into X_id as a vector of haplotype counts for all imputed haplotypes except the referent. For example, consider the following imputed haplotypes and corresponding conditional probabilities for four hypothetical individuals (i = 1, 2, 3, 4) based on our simulation study (Table 1):

i	A	B	C	D	E	F*	G	H	I	πid
1	0	0	0	1	0	1	0	0	0	0.8
1	0	0	1	0	0	0	1	0	0	0.2
2	0	0	0	0	0	1	0	0	1	0.6
2	0	0	0	0	0	0	1	1	0	0.4
3	0	1	0	1	0	0	0	0	0	1.0
4	0	0	0	0	0	2	0	0	0	1.0

^*Referent

Two individuals (i = 3, 4) have one possible diplotype; two individuals (i = 1, 2) have two possible diplotypes. Therefore, the latter two individuals would each contribute two rows to X_id. The column indicating the reference haplotype (here, haplotype F) would be excluded.

Table 1.

Common haplotypes and estimated population frequencies for AGTR1.

Label	Haplotype	Frequency
A	ATTATGCATCTC	0.029
B	ATTATGTGATCC	0.051
C	TCCACGCATCTC	0.027
D	TCCACGCATCTT	0.090
E	TCTGTGCAACTT	0.029
F*	TCTGTGCATCTC	0.223
G	TCTGTGCATCTT	0.188
H	TTTACACATCTC	0.038
I	TTTACACATCTT	0.032

^*Referent

Non-iterative weighted estimation is straightforward to implement in the context of a censored survival outcome:

1. Impute haplotypes and estimate population haplotype frequencies p assuming Hardy-Weinberg Equilibrium (HWE);

2. Create multi-record data for each individual:

   1. Form a design matrix X_id containing the set of diplotypes d consistent with the observed genotype d(G_i);
   2. Set π_id to the conditional probability of diplotype d given the observed genotype d(G_i), and;

3. Estimate β using a weighted Cox regression model.

Appendix A provides instructions on implementing weighted estimation in Stata. Note that β̂ is obtained as the solution to an estimating equation based on the weighted Cox partial likelihood:

$$𝒰(\beta )={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{d\in d(G_i)}}\frac{\partial l_{\mathit{\text{id}}}(\beta )}{\partial \beta }=0,$$

in which:

$$l_{\mathit{\text{id}}}(\beta )={\delta }_{\mathit{\text{id}}}{\pi }_{\mathit{\text{id}}}(p_{\mathit{\text{id}}},\beta )[X_{\mathit{\text{id}}}\beta -\text{log}{\displaystyle \sum _{i\prime \in R(t_i)}}\text{exp }{X}_{i\prime d}\beta ],$$ (4)

and R(t_i) denotes the set of individuals at risk at time t_i. Standard error estimates for confidence intervals and hypothesis tests must be based on a robust variance estimator. By estimating robust standard errors from multirecord data, weighted estimation accounts for the uncertainty in phase, in addition to the sampling variability of the data. Inference for one or more elements of β are based on univariable or multivariable Wald tests. Under the null hypothesis, the estimator is valid and efficient, because the estimating function is the expectation of the known-phase score function given all the available data.

2.4 Weighted haplotype combination

Weighted haplotype combination is based on creating single-record data from the set of diplotypes consistent with the observed genotype for each individual. Let X_i denote the single-record design matrix that includes both diplotype information and environmental exposures. For each individual, diplotype information is integrated into X_i as a weighted combination of the set of diplotypes consistent with the observed genotype, in which the weights are determined by the conditional probability of the diplotypes given the observed genotype. For example, the four sets of imputed haplotypes given in Section 2.3 would each be averaged according to the conditional probability for each diplotype:

i	A	B	C	D	E	F*	G	H	I
1	0	0	0.2	0.8	0	0.8	0.2	0	0
2	0	0	0	0	0	0.6	0.4	0.4	0.6
3	0	1.0	0	1.0	0	0	0	0	0
4	0	0	0	0	0	2.0	0	0	0

^*Referent

Therefore, each individual would contribute one record to the analysis. Note that the column indicating the reference haplotype (F) would be excluded.

It is also straightforward to implement weighted haplotype combination in the context of a censored survival outcome:

1. Impute haplotypes and estimate population haplotype frequencies p assuming HWE;

2. Create single-record data for each individual:

   1. Form a design matrix $X_i={\pi }_{\mathit{\text{id}}}^T{X}_{\mathit{\text{id}}}$ as a weighted combination of the set of diplotypes d consistent with the observed genotype d(G_i), in which the weights are determined by π_id, and;

3. Estimate β using an unweighted Cox regression model.

Appendix B provides instructions on implementing weighted haplotype combination approach in Stata. Note that β̂ is obtained as the solution to an estimating equation based on the unweighted Cox partial likelihood:

$$𝒰(\beta )={\displaystyle \sum _{i=1}^n}\frac{\partial l_i(\beta )}{\partial \beta }=0,$$ (5)

in which:

$$l_i(\beta )={\delta }_i[X_i\beta -\text{log}{\displaystyle \sum _{i\prime \in R(t_i)}}\text{exp }{X}_{i\prime }\beta ].$$ (6)

Model-based standard error estimates may be used for confidence intervals and hypothesis tests, because the data consist of one record for each individual. Because the set of possible diplotypes for each individual are averaged using weights determined by their conditional probability given the observed genotype, weighted haplotype combination also accounts for the uncertainty in phase, in addition to the sampling variability of the data. Inference for one or more elements of β are based on univariable or multivariable Wald tests. The estimator is exactly valid under the null hypothesis.

3 Simulation Study

We designed a simulation study to evaluate the statistical properties of non-iterative methods to estimate associations between common haplotypes and a censored survival outcome. Simulated genotypes were based on haplotype frequencies for angiotensin II receptor, type 1 (AGTR1), a gene in the renin-angiotensin system, which regulates blood pressure (French et al., 2006; Merciante et al., 2007). Table 1 provides common AGTR1 haplotypes and their corresponding estimated population frequencies. Simulated AGTR1 diplotypes had moderate phase ambiguity: approximately 60% of individuals had an unambiguous diplotype; and approximately 90% had a highest posterior probability of having a particular diplotype greater than 0.75.

3.1 Parameters

At each of 1000 iterations, we generated event times for a sample of either n = 200, 500, or 1000 individuals from an Exponential distribution, in which the log-rate was determined by a linear combination of the haplotypes according to an assumed genetic risk model with additive inheritance: no genetic effects, moderate effects, strong effects characterized by a single SNP, and strong effects not characterized by a single SNP. For effects characterized by a single SNP, a haplotype was related to risk if and only if it had the minor allele at a particular locus (here, the 12th locus). We defined moderate genetic effects as hazard ratios between 1.0 and 2.0 (or between 1.0 and 1/2.0) relative to the reference haplotype (here, haplotype F), and strong effects as hazard ratios equal to 4.0. We generated an independent censoring process from an Exponential distribution and selected the rate such that either 10% or 25% of individuals were censored before their event time.

We used four metrics to compare weighted estimation and weighted haplotype combination. First, to evaluate the performance of standard error estimation, we compared the average of the estimated standard errors to the empirical standard deviation of the estimated log-hazard ratios for each haplotype. Second, for each haplotype we created error intervals by calculating the difference between the estimated and true log-hazard ratios at every iteration and calculating the 5th, 50th, and 95th percentile. These error intervals approximate the bias in the estimated log-hazard ratios. Third, we calculated percent coverage of estimated 95% confidence intervals. Fourth, at every iteration we conducted a two-sided hypothesis test (α = 0.05) for each haplotype effect based on its estimated log-hazard ratio and standard error. Across all iterations, the rejection rate quantified the type-I error rate for null effects and statistical power for non-null effects. We present results obtained assuming known phase to illustrate that, due to sampling variability, there is error inherent in the log-hazard ratio estimates obtained from the Cox regression model even when the haplotypes are known.

3.2 Results

Simulations with 10% and 25% censoring yielded similar results. Therefore, we only present results assuming 25% censoring. For brevity, we only present results with n = 200 and 1000.

Table 2 provides average standard error estimates and the empirical standard deviation of estimated log-hazard ratios under no genetic effects, i.e., all log-hazard ratios equal to 0 relative to the reference haplotype. When the sample size is small (n = 200), every estimation method under-estimates the standard error; the average standard error estimate for every haplotype is systematically smaller than the corresponding empirical standard deviation. However, when the sample size is large (n = 1000), every estimation method properly estimates the standard error; the average standard error estimate for every haplotype is approximately equal to the corresponding empirical standard deviation.

Table 2.

Average standard error estimates (‘Estimated’) and empirical standard deviation of estimated log-hazard ratios (‘Empirical’) under no genetic effects, 25% censoring.

		Weighted estimation		Weighted combination		Known phase
n	Haplotype	Estimated	Empirical	Estimated	Empirical	Estimated	Empirical
200	A	0.307	0.365	0.333	0.395	0.324	0.366
	B	0.242	0.265	0.252	0.272	0.249	0.266
	C	0.264	0.300	0.419	0.450	0.334	0.364
	D	0.193	0.215	0.207	0.226	0.200	0.220
	E	0.305	0.357	0.355	0.408	0.321	0.358
	G	0.147	0.157	0.171	0.183	0.158	0.167
	H	0.249	0.265	0.339	0.361	0.285	0.300
	I	0.265	0.298	0.351	0.387	0.307	0.320
1000	A	0.135	0.136	0.138	0.138	0.137	0.137
	B	0.106	0.107	0.108	0.109	0.108	0.107
	C	0.119	0.124	0.172	0.177	0.142	0.145
	D	0.085	0.085	0.089	0.089	0.086	0.088
	E	0.135	0.136	0.141	0.142	0.137	0.137
	G	0.064	0.064	0.074	0.075	0.068	0.067
	H	0.109	0.110	0.140	0.140	0.121	0.121
	I	0.120	0.125	0.145	0.151	0.131	0.133

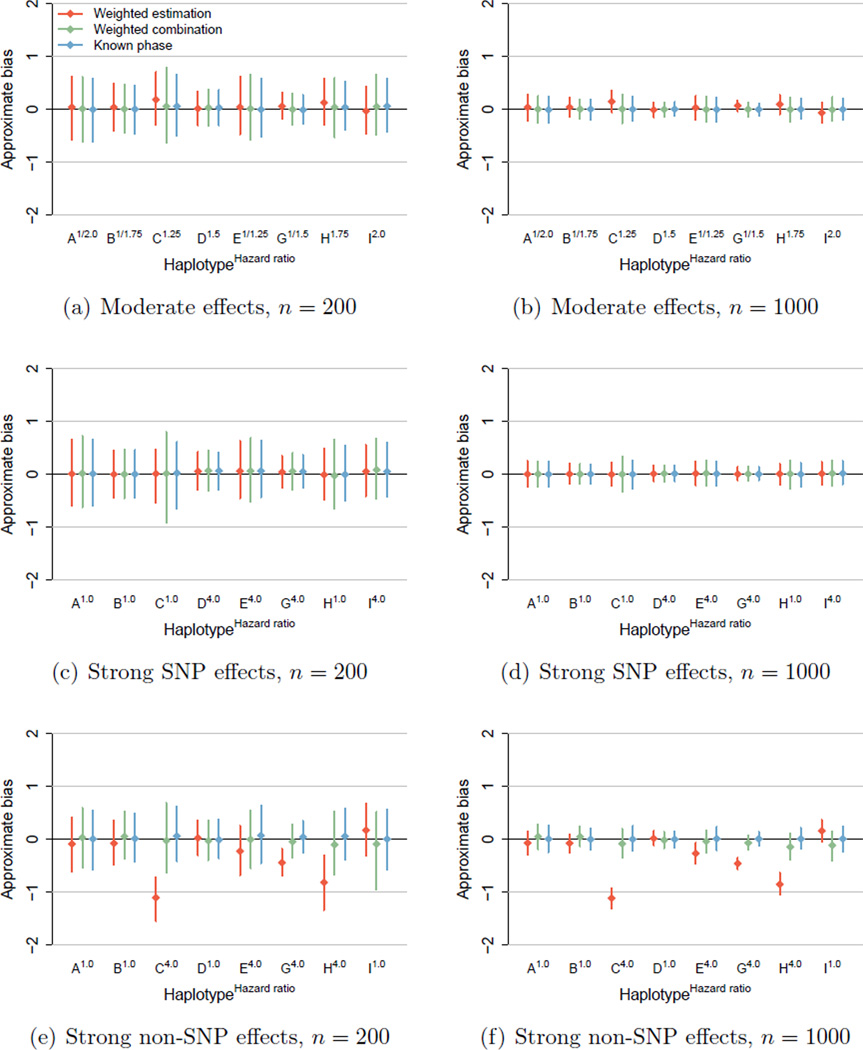
Figure 1 presents error intervals, Table 3 provides estimated coverage of 95% confidence intervals, and Table 4 provides the estimated rejection rate of two-sided hypothesis tests (α = 0.05) for AGTR1 haplotype effects with n = 200 and 1000. In every scenario, estimation based on the known phase provides approximately unbiased parameter estimates with proper confidence interval coverage and the nominal type-I error rate. Under no genetic effects (results not shown), every estimation method provides approximately unbiased parameter estimates with proper coverage and the nominal type-I error rate. Under moderate genetic effects, weighted haplotype combination provides approximately unbiased parameter estimates, as shown by the green error intervals in Figures 1(a) and 1(b) centered at zero, with proper coverage. However, weighted estimation may provide slightly biased parameter estimates, as shown by the red error intervals in Figures 1(a) and 1(b) centered away from, yet covering zero. Coverage is reduced due to the small amount of bias in the parameter estimates, especially when the sample size is small due to under-estimation of standard errors. Power is modest for all methods when the sample size is small.

Figure 1.

Error intervals for AGTR1 haplotype effects, 25% censoring.

Table 3.

Estimated coverage (%) of 95% confidence intervals for AGTR1 haplotype effects, 25% censoring.

			Weighted estimation		Weighted combination		Known phase
Risk model	Haplotype	Hazard ratio	n = 200	n = 1000	n = 200	n = 1000	n = 200	n = 1000
Moderate effets	A	1/2.0	91	94	94	95	94	95
	B	1/1.75	93	93	94	96	95	95
	C	1.25	81	76	94	95	94	94
	D	1.5	94	94	95	95	94	95
	E	1/1.25	92	93	95	95	94	95
	G	1/1.5	92	82	95	96	95	96
	H	1.75	87	84	93	94	94	95
	I	2.0	94	91	94	95	94	96
Strong SNP effects	A	1.0	90	95	92	95	92	95
	B	1.0	94	95	94	96	96	95
	C	1.0	92	94	95	95	94	95
	D	4.0	93	96	94	96	94	96
	E	4.0	90	92	94	94	94	94
	G	4.0	92	94	94	95	95	96
	H	1.0	92	95	95	94	94	95
	I	4.0	92	94	95	95	94	94
Strong non-SNP effects	A	1.0	94	90	96	94	95	95
	B	1.0	93	87	93	92	94	94
	C	4.0	2	0	96	95	94	95
	D	1.0	92	94	94	96	93	95
	E	4.0	84	39	96	95	94	95
	G	4.0	19	0	95	86	94	94
	H	4.0	18	0	93	82	94	94
	I	1.0	86	69	91	88	95	94

Table 4.

Estimated rejection rate (%) of two-sided hypothesis tests (α = 0.05) for AGTR1 haplotype effects, 25% censoring. Type-I error rate presented in italic type; statistical power presented in standard type.

			Weighted estimation		Weighted combination		Known phase
Risk model	Haplotype	Hazard ratio	n = 200	n = 1000	n = 200	n = 1000	n = 200	n = 1000
Moderate effects	A	1/2.0	48	100	49	100	51	100
	B	1/1.75	53	100	55	100	57	100
	C	1.25	40	84	14	27	17	38
	D	1.5	62	100	58	100	62	100
	E	1/1.25	9	30	7	34	7	36
	G	1/1.5	64	100	63	100	74	100
	H	1.75	81	100	48	98	60	100
	I	2.0	71	100	63	100	74	100
Strong SNP effects	A	1.0	10	5	8	5	8	5
	B	1.0	6	5	6	4	4	5
	C	1.0	8	6	5	5	6	5
	D	4.0	100	100	100	100	100	100
	E	4.0	99	100	97	100	99	100
	G	4.0	100	100	100	100	100	100
	H	1.0	8	5	5	6	6	5
	I	4.0	100	100	97	100	100	100
Strong non-SNP effects	A	1.0	6	10	4	6	5	5
	B	1.0	7	13	7	8	6	6
	C	4.0	16	62	91	100	99	100
	D	1.0	8	6	6	4	7	5
	E	4.0	98	100	97	100	99	100
	G	4.0	100	100	100	100	100	100
	H	4.0	52	99	95	100	100	100
	I	1.0	14	31	8	12	5	6

Under strong effects characterized by a single SNP, every estimation method provides approximately unbiased parameter estimates with proper confidence interval coverage. In addition, the type-I error rate is near the nominal 5% level for null effects (haplotypes A, B, C, H), and power is high for non-null effects (haplotypes D, E, G, I). However, under strong effects not characterized by a single SNP, weighted estimation may provide heavily biased parameter estimates, as shown by the red error intervals in Figures 1(e) and 1(f) that do not cover zero. In this case, the approximate bias is negative, so that the bias is toward the null. Due to the large bias in the parameter estimates, coverage is substantially reduced. The type-I error rate is above the nominal 5% level for null effects (haplotypes A, B, D, I), particularly when the sample size is large. Power is reduced for non-null effects (haplotypes C, H), particularly when the sample size is small. Under strong effects not characterized by a single SNP, weighted haplotype combination may provide slightly biased (toward the null) parameter estimates, as shown by the green error intervals in Figures 1(e) and 1(f) centered away from, yet covering zero. Coverage is reduced due to the small amount of bias in the parameter estimates. Compared to weighted estimation, the type-I error rate is lower and the power level is higher for weighted haplotype combination.

Non-iterative, regression-based methods provide valid tests for genetic associations and reliable estimates of moderate associations between common haplotypes and a censored survival outcome. Weighted estimation and weighted haplotype combination provided estimates with reasonable bias under moderate SNP effects. In addition, weighted haplotype combination provided estimates with reasonable bias under large non-SNP effects.

4 Case Study

4.1 Background

The Penn Heart Failure Study is a prospective cohort study of outpatients with chronic heart failure recruited from referral centers at the University of Pennsylvania (Philadelphia, Pennsylvania), Case Western Reserve University (Cleveland, Ohio), and the University of Wisconsin (Madison, Wisconsin). The primary inclusion criterion was a clinical diagnosis of heart failure. Participants were excluded if they had a non-cardiac condition resulting in an expected mortality of less than six months as judged by the treating physician, or if they were unable to provide consent. At time of study entry, detailed clinical data were obtained using standardized questionnaires administered to the participant and physician, with verification via medical records, as previously described (Ky et al., 2009). Subsequent adverse events, including all-cause mortality, cardiac transplantation, and placement of a ventricular assist device were prospectively ascertained every six months via direct patient contact and verified through death certificates, medical records, and contact with family members by research personnel. All participants provided written, informed consent; the study protocol was approved by participating Institutional Review Boards.

The goal of this analysis was to estimate associations between HSPB7-CLCNKA haplotypes at 1p36 and risk of adverse outcomes. SNPs at 1p36 have been shown to be associated with heart failure and dilated cardiomyopathy in case-control studies (Cappola et al., 2010; Stark et al., 2010).

4.2 Materials and Methods

We limited our analysis to the combined outcome of all-cause mortality, cardiac transplantation, or placement of a ventricular assist device to focus on the most serious adverse outcomes associated with heart failure. Genotyping was performed using the IBC cardiovascular SNP array (Keating et al., 2008), which includes 14 SNPs across the 1p36 locus. To account for potential population stratification, we used multi-dimensional scaling of ~30,000 SNP genotypes to identify a homogenous subgroup of 1149 genetically inferred Caucasians, as previously described (Cappola et al., 2011).

Cox regression models were used to estimate associations between common HSPB7-CLCNKA haplotypes and the combined outcome. The EM algorithm was used to impute the set of all haplotypes consistent with the observed unphased genotype for each participant. Corresponding posterior probability estimates were either used as weights (weighted estimation) or to obtain a weighted average of the imputed haplotypes for each participant (weighted haplotype combination). Haplotypes with an estimated population frequency less than 0.02 were defined as rare and recoded into one category. Because participants entered the cohort at different stages of their disease progression, the baseline hazard function was stratified by New York Heart Association (NYHA) functional classification (class I, II, III, or IV), a standard system to classify severity of heart failure symptoms. Additional adjustment was made for gender, age, heart failure etiology (ischemic or non-ischemic), and clinical site. Age exhibited non-proportional hazards and was adjusted for using a time-varying covariate, which was obtained by multiplying age by a linear term for the natural log of time.

4.3 Results

HSPB7-CLCNKA genotypes were available for 1149 genetically inferred Caucasians; 803 (70%) were male and the median age at study entry was 58.4 years (inter-quartile range, 49.7 to 66.4 years). Ischemic heart failure etiology was reported by 409 participants (36%). Approximately 18%, 44%, 30%, and 9% of participants were classified as a NYHA class I, II, III, and IV, respectively. Approximately 65% of participants had an unambiguous diplotype; 90% had a highest posterior probability of having a particular diplotype greater than 0.765. The median follow-up time was 2.9 years (maximum, 5 years), during which 251 participants (22%) experienced an adverse event: 152 deaths, 75 cardiac transplantations, and 25 ventricular assist device placements.

In individual Cox regression analyses of 14 pre-selected SNPs in the HSPB7-CLCNKA gene, adjusted for gender, age (time-varying), etiology, and site and stratified by NYHA class, we found that only one SNP, SNP 5 (rs12083572), was associated with adverse outcomes at the α = 0.05 level. Using the EM algorithm, we inferred 10 haplotypes with an estimated population frequency > 0.02 from all 14 HSPB7-CLCNKA SNPs (Table 5). In global tests of association, both analysis methods found marginally significant haplotype associations with adverse outcomes (weighted estimation: p = 0.015; weighted combination: p = 0.026). Using the most common haplotype (haplotype W, estimated frequency 0.299) as the reference haplotype, we observed a decreased risk of adverse outcomes with carriage of haplotype T (which differs from the referent at SNPs 1, 3, 4, 5, 6, 7, 8) and haplotype V (which differs from the referent at SNPs 7, 8, 10, 14). However, neither of these associations would be considered statistically significant after adjustment for multiple comparisons. Of note, both analysis methods yielded very similar point estimates, 95% confidence intervals, and p values.

Table 5.

Common HSPB7-CLCNKA haplotypes, estimated population frequencies, and estimated associations with risk of all-cause mortality, cardiac transplantation, or ventricular assist device placement: Hazard ratio (HR) and 95% confidence interval (CI). Individual p values obtained from univariable Wald test to evaluate whether the hazard ratio is equal to 1; overall p value obtained from multivariable Wald test to evaluate whether all hazard ratios are equal to 1.

			Weighted estimation		Weighted combination
Label	Haplotype	Frequency	HR (95% CI)	p	HR (95% CI)	p
Q	AGAGCGAGACGAGG	0.036	1.19 (0.80, 1.77)	0.39	1.19 (0.76, 1.87)	0.44
R	AGAGCGAGGGAAGG	0.160	1.04 (0.80, 1.35)	0.79	1.05 (0.81, 1.37)	0.73
S	AGAGCGGAGCAAGA	0.036	1.20 (0.80, 1.77)	0.38	1.20 (0.74, 1.94)	0.47
T	AGCGAGAGGCAAGA	0.066	0.55 (0.34, 0.88)	0.014	0.53 (0.32, 0.90)	0.019
U	GACGCGGAGCGCGG	0.063	0.80 (0.53, 1.20)	0.28	0.80 (0.52, 1.21)	0.29
V	GGAACAAGGGAAGG	0.037	0.49 (0.26, 0.92)	0.025	0.43 (0.21, 0.88)	0.021
W	GGAACAGAGCAAGA	0.299	Referent		Referent
X	GGAACAGAGCAAGG	0.048	1.36 (0.95, 1.95)	0.089	1.44 (0.95, 2.19)	0.090
Y	GGAGCAAGGCAAGG	0.050	1.15 (0.78, 1.69)	0.49	1.15 (0.77, 1.72)	0.49
Z	GGCGCGGAGCAAGG	0.031	1.09 (0.62, 1.92)	0.76	1.10 (0.64, 1.87)	0.73
Overall				0.015		0.026

5 Discussion

In this paper, we developed non-iterative, regression-based methods to estimate associations between common haplotypes and a censored survival outcome in large cohort studies, such that haplotype imputation is done once as a data-processing step. We focused on moderate associations of common haplotypes inferred from tag SNPs in small numbers of genes in large prospective studies. In our simulation study, we showed that non-iterative weighted estimation and weighted haplotype combination provide valid tests for genetic associations and reliable estimates of moderate associations between common haplotypes and a censored survival outcome. Our case study provided an example in which the estimation methods provided very similar results because there was modest phase ambiguity.

Our simulation study focused on effects of common haplotypes. Thus, our results do not extend to estimating effects of rare haplotypes, nor to small cohort studies, in which common haplotypes may appear to be rare. In our case study, we grouped together all imputed haplotypes with an estimated population frequency < 0.02. In addition, our simulation study focused on cohort studies of unrelated individuals. Thus, we did not consider situations in which individuals are related. However, our methodology may be applicable to studies of related individuals, and may in fact perform better, because phase can be estimated much more accurately from related individuals. There are options for estimating haplotype associations in family-based studies using FBAT/PBAT (Laird et al., 2000).

An advantage of non-iterative estimation methods is their relative ease of implementation in standard statistical software. For weighted haplotype combination, implementation only requires the standard Cox regression model. For non-iterative weighted estimation, implementation requires that the Cox regression model accommodate probability weights, and depends on the availability of a robust variance estimator. Both options are typically available in standard software. In addition, because implementation of both methods depends on the Cox regression model, it is straightforward to adjust for or specify interaction with environmental exposures, construct confidence intervals for haplotype associations, and generate inference via Wald tests. It is also straightforward to extend the Cox model to include any requisite time-varying covariates and/or stratify the baseline hazard function by a key factor. For example, in our case study, we included a time-varying covariate for age and stratified the baseline hazard function by NYHA functional classification. Given the reliability of non-iterative methods to estimate moderate associations of common haplotypes, and their ease of implementation in standard software, we continue to recommend them to applied researchers as a viable option for haplotype risk estimation. In the Appendix, we provide instructions for implementing non-iterative weighted estimation and weighted haplotype combination in Stata.

Appendix

Stata Implementation

In this Appendix, we provide Stata commands for implementing non-iterative methods to estimate haplotype associations with a censored survival outcome. We assume that a program such as PHASE is used to impute the haplotypes and estimate population haplotype frequencies. The commands below use the following notation: event time time; event indicator event; exposure x; imputed haplotypes h1, h2, … , hk, with the referent haplotype removed; estimated diplotype probability prob; subject identifier id.

A Non-iterative weighted estimation

Create a multi-record dataset by merging the imputed haplotypes with the outcome and exposure data. Declare the data to be survival data with probability weights:

stset time [pweight=prob], failure(event)

Fit the Cox regression model with a robust variance estimator:

stcox h1-hk x, vce(cluster id)

See help stcox for additional options, including those for specifying stratification factors and including time-varying covariates.

B Weighted haplotype combination

Collapse the set of imputed haplotypes for each individual according to the estimated diplotype probabilities:

foreach var of varlist h1-hk {
  quietly replace ‘var’ = ‘var’*prob
}
drop prob
collapse (sum) h1-h10, by(id)

Create a single-record dataset by merging the resultant haplotype data with the outcome and exposure data. Declare the data to be survival data and fit the Cox regression model:

stset time, failure(event)
stcox h1-hk x