Image formation by linear and nonlinear digital scanned light-sheet fluorescence microscopy with Gaussian and Bessel beam profiles

Abstract

We present the implementation of a combined digital scanned light-sheet microscope (DSLM) able to work in the linear and nonlinear regimes under either Gaussian or Bessel beam excitation schemes. A complete characterization of the setup is performed and a comparison of the performance of each DSLM imaging modality is presented using in vivo Caenorhabditis elegans samples. We found that the use of Bessel beam nonlinear excitation results in better image contrast over a wider field of view.

1. Introduction

Traditional wide-field optical fluorescence microscopes are proven invaluable tools that accomplish the most diverse imaging tasks at the cellular and sub-cellular level. Nevertheless, when the systems (organisms or tissues) containing the fluorescent structures grow in size and complexity, traditional microscopy methods become limited or unusable. The main reason for this is that wide-field microscopes detect both the desired in-focus and undesired out-of-focus light. In a thick sample the high-resolution information from the focal plane can become “buried” in the blurred light from the surrounding tissue. The problem is more evident when the task involves following fast dynamical processes over time, with a limited amount of photons. That is why having an alternative technique that would allow the observation of fast events with high spatial resolutions over a large field of view (FOV) is extremely important. To overcome the problem of out-of-focus light, techniques referred as laser point scanning microscopy (LSM), such as confocal and multi-photon microscopies, have been introduced [1]. LSM techniques generate images only from in-focus light providing intrinsic optical sectioning. Then, by digitally combining a stack of these images a three dimensional representation of the fluorescent sample can be obtained. In addition to out-of-focus light, another important issue to take into consideration when imaging biological samples is the photodamage (photobleaching and phototoxicity). In LSM techniques, as excitation and collection occurs along the same axis, the entire sample is repeatedly irradiated when taking an image stack. As a consequence, cumulative photodamage is induced within the sample [2].

To overcome such problems, selective plane illumination microscopy (SPIM) was proposed [3]. In SPIM, a static sheet of excitation light is produced onto the sample plane using a cylindrical lens. Then, the fluorescence light emerging from this plane is collected through a microscope objective (MO) placed along the axis orthogonal to the excitation sheet. This uncoupling between the excitation and collection branches provides SPIM with: i) 2D optical sectioning capability in large fields of view that does not require point-scanning, and ii) decoupled resolution in the transversal and axial directions, determined by the collection numerical aperture (NA) and light-sheet thickness, respectively [3]. Perhaps the most valuable benefit of this technique is the reduction of the photodamage to the sample, due to the restriction of the irradiation to the plane under observation [4]. Since it also can provide rapid acquisition speed, SPIM has emerged as a powerful tool for in vivo time lapse studies, from single cells to whole organisms and tissues [5]. Even though SPIM has proven to be a good alternative to conventional fluorescence microscopy methods, it still holds some drawbacks: i) a broadening of the light sheet deep inside the sample caused by scattering and aberrations, ii) the formation of stripe artifacts induced by absorption and scattering along the illumination axis, and iii) inhomogeneity of the sheet due to diffraction generated by the limiting diaphragm. Moreover, for having large FOVs, the depth of field in the cylindrical lens should be increased. This is achieved by using low NA lenses. However, this also reduces the optical sectioning capability of SPIM as the thickness (waist) of the generated cylindrical beam is increased. The balancing between both parameters has to be chosen carefully for the specimen of interest.

Recently two-photon excited fluorescence single plane illumination microscopy (2p-SPIM) was demonstrated for imaging the pharynx of cameleon labeled Caenorhabditis elegans [6]. The use of two-photon excitation allows better out-of-focus light rejection, improving the quality of the optical sections and reducing the photodamage. These improvements rely on: i) the use of NIR excitation wavelength matching the optical window of biological samples and therefore allowing less sensitivity to scattering, better penetration depth, and reduced linear absorption; and ii) the nonlinear nature of the absorption in TPEF virtually eliminates the conversion of the scattered excitation into fluorescence [7]. However, compared to two-photon LSM, in 2p-SPIM the total intensity of the nonlinear excitation beam is reduced as the beam is distributed over a plane as opposed to a single point. This drastically reduces the efficiency of fluorescence excitation.

Another interesting alternative implementation of SPIM (in which the beam is static) relies on the generation of the light sheet by scanning in one direction a focused Gaussian beam. This is termed digital scanned (laser) light sheet microscopy (DSLM) [8,9]. There are several advantages to this implementation over widefield SPIM: i) The full power of the excitation light is concentrated into the single scanned line providing better illumination efficiency and lower exposure times, ii) each line in the specimen is illuminated with the same intensity generating a homogenous light-sheet, where the height can be easily controlled with the amplitude of the scanning. Nevertheless the degrading effects of excitation scattering present in SPIM are inherited by DSLM. Further improvements were reported (Keller et al.) by combining DLSM (and SPIM) with structured illumination (SI), with the aim to mitigate the blurring effects of the out-of-focus scattered light [10]. In this approach the sheet is modulated to create sinusoidal patterns over the sample. Digital post-processing of the obtained images allows for the rejection of fluorescence generated by scattered excitation light, resulting in an enhanced optical sectioning and increased contrast. Multidirectional selective plane illumination microscopy (mSPIM) [11] has also been proposed to reduce absorption and scattering artifacts. In mSPIM the light sheet is i) rapidly tilted about the detection axes, and ii) sequentially directed onto the sample from two opposing directions, providing an evenly illuminated focal plane. The two images obtained are further combined by digital image fusion techniques [12]. Notwithstanding, for large and highly scattering samples, and due to the short excitation wavelength, some of the aforementioned problems remain: undesired intensity modulations, loss of resolution and limited penetration depth.

Recently, Truong et al. [13] reported on the use of a scanned light sheet microscope using TPEF (2p-DSLM) for live imaging of fruit fly and zebra fish embryos. They show the advantages of using 2p-DSLM for imaging large highly scattering samples over the conventional 2p-LSM and 1p-DSLM. Basically, the use of TPEF increases the penetration depth, improves background rejection and reduces phototoxic effects. In addition, the line scanning configuration improves the excitation efficiency and increase the tolerance to aberrations. These advantages allow deep, fast, non-phototoxic imaging of living organisms. Another improvement that has been implemented in order to alleviate the deleterious effect of scattering on scanned sheet microscopy is the use of Bessel beams (BB) [14]. Self-healing properties of these beams allowed imaging 50% deeper inside human skin when compared with Gaussian beams. However, as side lobes of the BB normally introduce a certain amount of background signal to the images acquired, the use of confocal-line detection should be implemented. Another alternative is the use of high NA objective lenses to combine BB with both TPEF and SI. This technique was reported in terms of achieving enhanced isotropic 3D resolutions and was compared to other super-resolution techniques for imaging intracellular features in single cells in a small field of view [15].

In this paper we will show how 2p-DSLM combined with advanced spatial shaping of the beam, by using BB, can be used to improve the optical sectioning, the resolution and the intensity distribution uniformity of the light sheet in large fields of view and for moderately large specimens. This is compared with Gaussian beams in the nonlinear regime and with both Gaussian and BB in the linear regime. We present results on the system characterization and on imaging living C. elegans. To the best of our knowledge, this is the first time that 2p-DSLM has been combined with BB excitation to image multi-cellular organisms. The results are put in to context (and for reference purposes only), by producing an image stack using a well demonstrated and optimized SPIM imaging system [16] (in this case working at the excitation wavelength of 488 nm and having a standard GFP band-pass filter (GFP: 526/39) in the collection path).

2. Experimental setup

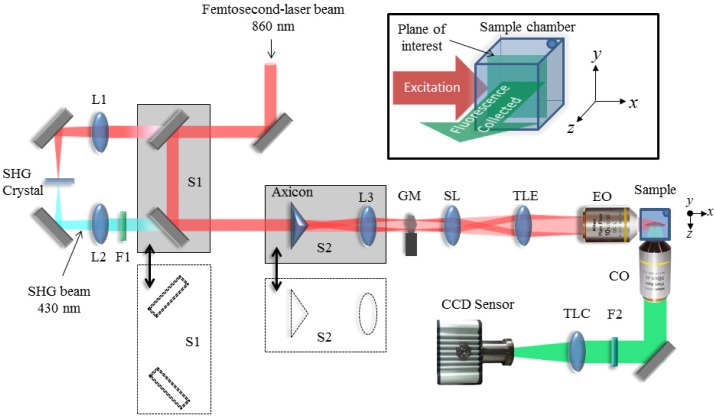
The optical setup we have implemented is shown in Fig. 1 . The xy plane is defined as the image plane (plane of interest) of the collection lens, and the z axis as the direction orthogonal to that plane along the direction where the fluorescence is collected (see the inset of Fig. 1). In our DSLM system, the excitation beam propagates along the x axis and the light sheet is generated in the xy sample plane by scanning the beam along the y direction using a galvo mirror GM. A telescopic system, composed of a scanning lens SL as well as a tube lens TLE, placed after the GM is such that i) the EO back focal plane and the GM axis plane are conjugates and ii) the effective numerical aperture of the lens EO (10×, NA= 0.3, WD = 16 mm, Nikon, Japan) is reduced to half its value, i.e., NA=0.15. This last condition is set to adapt the size of the Gaussian excitation beams to that given by the BB spectral ring. The collection objective lens CO (10×, NA= 0.45, WD = 4 mm) is placed with its axis orthogonal to the sample plane, along the z direction. A regular tube lens TLC, providing the objective “design” magnification is used to form an image of the fluorescent structures onto the CCD sensor (Orca R2, 6.45 μm pixel size, 1344x1024 pixels, Hamamatsu). The system can be configured to work in one of the following four modalities: i) linear DSLM with Gaussian beams (DSLM-Gauss), ii) nonlinear DLSM with Gaussian beams (2p-DSLM-Gauss), iii) linear DSLM with BB (DSLM-Bessel), and iv) nonlinear DLSM with BB (2p-DSLM-Bessel). The main excitation source for our DSLM system is a Kerr lens mode-locked Ti:sapphire laser (MIRA 900f, Coherent, France), emitting pulses of 160 fs duration, 76 MHz repetition rate and working at the central wavelength of 860nm.

Figure 1.

Schematic diagram of our DLSM setup. The translation stage S1 allows switching between linear DSLM, where the beam pass through the SHG crystal and lenses L1 and L2, and 2p-DLSM where the femtosecond-laser beam pass unmodified. Gaussian or Bessel beams are selected by moving the translation stage S2 that contains an axicon and the Fourier transforming lens L3. A galvo mirror GM, a scan lens (SL), a tube lens (TLE) and an excitation objective lens (EO) are used to create the light sheet with the desired properties at the sample plane. The fluorescence generated in the sample is collected at 90 degrees by a collection objective lens (CO) and a regular tube lens (TLC) that forms image onto the CCD sensor with the designed magnification. Filters F1 and F2 are used to cut off the excitation light from the fluorescence images collected. The inset (top-right) shows the excitation-collection geometry that defines the notation of the axes used in this work.

For the nonlinear modalities the femtosecond laser beam is directly used for excitation. In these cases, the laser light is injected into the system through a couple of mirrors mounted on a translation stage S1. For the linear modalities S1 is set aside allowing the femtosecond-laser beam to enter an alternative optical path where a lens L1 focus the beam on a BBO Second Harmonic Generation (SHG) crystal (cut at 29.2º, 800 nm). A lens L2 is used to collimate the frequency doubled light (at 430nm) emerging from the crystal. For the modalities employing Gaussian beams, both the linear and nonlinear excitation beams reach the DSLM system without any further modification. Otherwise, for the modalities employing BB, an axicon (UVFS glass, apex angle 176º) and a lens L3 are inserted into the optical path by moving the translation stage S2. This combination is such that it produces the Fourier transform of the BB at the GM. This ensures that the BB is formed at the sample plane. To remove the interference of the lower spatial frequency components generated by the round-tip defect of the axicon prism, a circular (opaque) stop is used [17,18]. This is placed at the back focal plane of the EO and coinciding with the BB Fourier plane given by L3. Filter F1 (BG-39) is used to cut the fundamental beam form the generated SHG light from the BBO crystal and F2 is a band-pass filter (CFP: 479/40) used to cut the excitation light from the fluorescence images. The specimen under observation is mounted on a holder with six degrees of freedom that allows for a fine adjustment of position and tilt with respect to the excitation sheet. The holder is mounted upon a computer-controlled linear translational stage (M-505.6DG, Physik Instrumente GmbH & Co. KG, Karlsruhe, Germany) that scans the sample along z direction.

3. Sample preparation

3.1. Coumarin/fluorescent beads

For characterization of the system two different samples were employed: i) A quartz cuvette filled with a solution of Coumarin 540 dissolved in methanol to a concentration of 0.5 mmol and ii) a solid agar sample containing 0.5 μm diameter green fluorescent beads (G500, solution 1% solids Duke Scientific Corp., USA). For the latter, a 1:10 bead-water solution was created. This was then mixed 1:100 with melted 2% agarose. Then, a 200μl drop of the bead-agar solution was cooled to room temperature on a glass slide for 10 minutes. Once the agar was solidified, a 90° corner was cut. The coverslip with the cut agar was mounted on the holder with one of its face pointing towards the excitation lens and the other towards the collection lens. This configuration allows that all excitation and imaging to be performed using air objectives.

3.2. Worm samples

To test the system for biological applications, samples containing one or more C. elegans nematodes were prepared. At the beginning, adult hermaphrodite worms were immobilized into a 5μl drop of sodium azide (NaN₃, 25 mM) for 10 minutes. The worms were then picked and mounted on top of a 5mm thick agar (at 2%) bench to preserve them properly hydrated. As in the case of the fluorescent beads, this configuration allowed us to image the worms using air objectives. We employed a genetically modified strain of C. elegans expressing the fluorescent protein “cameleon” in the pharynx. This protein is normally used as calcium indicator for imaging calcium transients in intact C. elegans [19]. It is composed of four domains, cyan fluorescent protein (CFP), calmodulin, M13 (a calmodulin binding domain), and yellow fluorescent protein (YFP). In our experiment, only CFP fluorescence was excited as this is convenient to visualize the whole pharynx. Furthermore, since the worms were anesthetized no calcium transients were expected.

4. Results

4.1. System characterization

We performed two sets of experiments to characterize the four modalities available in our system i) measurement of the dimensions of the fluorescent line excited by the light beam and ii) determining the resolution of our system by measuring the transversal and axial dimensions of the point spread function (PSF) of each modality of the system. For this work, we use the full-width-at-half-maximum (FWHM) of the normalized intensity profiles along the axis of interest and centered at the point of maximum intensity to characterize the dimensions of the different intensity distributions.

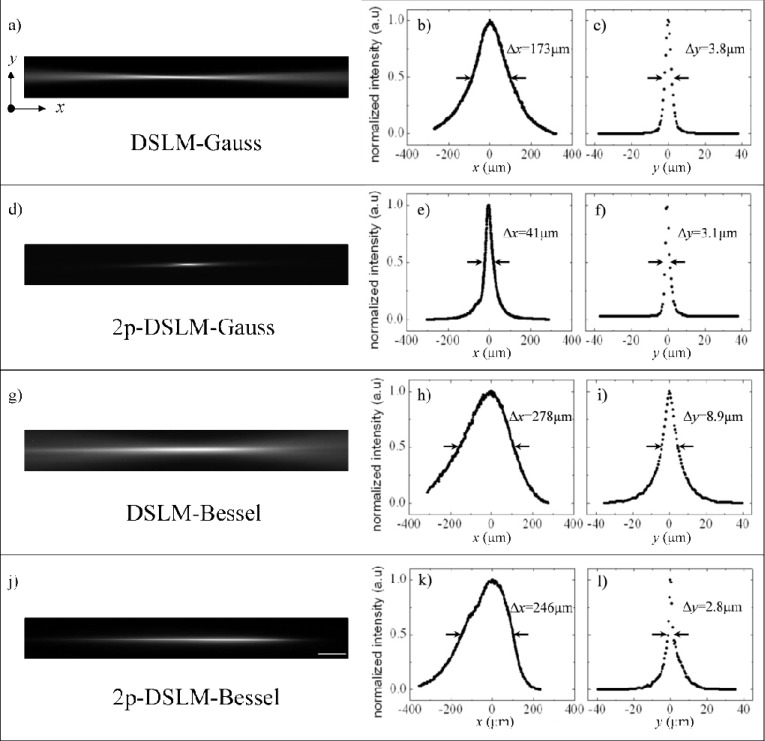
The first set of experiments was performed by using a Coumarin solution sample as described in section 3.1. For this, the GM was set to be static and the fluorescent line generated into the sample was imaged on the CCD camera. The images of the excitation lines and the extracted profiles along x and y axes are presented in the Fig. 2 for each modality: a-c) DSLM-Gauss, d-f) 2p-DSLM-Gauss, g-i) DSLM-Bessel and j-l) 2p-DSLM-Bessel. The FWHM widths Δx and Δy obtained from the profiles are shown over each plot and are summarized in Table 1 . From Fig. 2 it is possible to see that when using Gaussian beams in the nonlinear regime (2p-DSLM), an important decrease of the length of the usable FOV occur (down to 0.25× compared with linear DSLM). Nonetheless, for the linear case a considerable amount of background is added from the fluorescence excited outside the Rayleigh range of the beam (see Fig. 2(a)). Then, a hard aperture is required to exclude the “tails” by either matching the Rayleigh range of the beam to the CCD sensor or by direct clipping of the usable FOV with a custom made limiting pupil.

Figure 2.

Normalized fluorescence images and intensity profiles along x and y for the different excitation beams: a-c) DSLM with Gaussian beams, d-f) 2p-DSLM with Gaussian beams, g-i) DSLM with BB and j-l) 2p-DSLM with BB. The FWHM widths are indicated between arrows for each modality and their corresponding values Δx and Δy are included. These values are also summarized in Table 1. Profiles were taken along x and y directions with the point of maximum intensity located at the origin of coordinates, see the reference axes in Fig. 1(a). Scale bar: 50 μm, a pixel of the image corresponds to 0.44 μm in the sample.

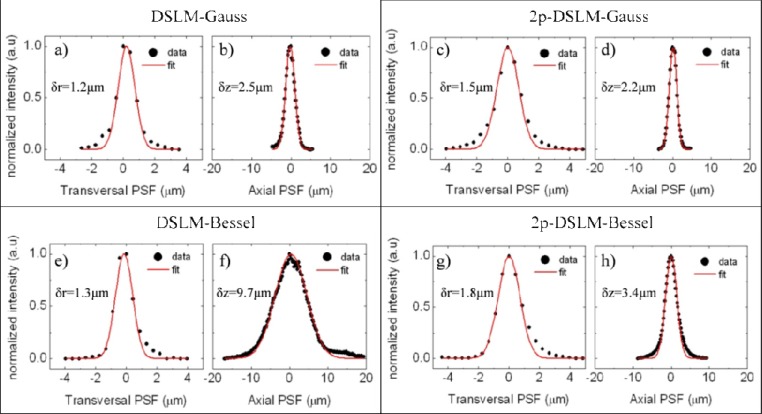
Table 1. Summary of the FWHM widths measured for the light lines (Fig. 2) and for the PSFs of the system (Fig. 3). An error of one pixel was assumed on the light lines. The mean value and statistical error in the PSFs was obtained over 30 measurements.

	Dimensions of the fluorescent light line		PSF from fluorescent beads
Modality	Δx (μm)	Δy (μm)	Δr (μm)	Δz (μm)
DSLM-Gauss	173	3.8±0.4	1.2±0.2	2.6±0.5
2p-DLSM-Gauss	41	3.1±0.4	1.5±0.2	2.3±0.1
DSLM-Bessel	278	8.9±0.4	1.3±0.1	10.7±0.9
2p-DSLM-Bessel	246	2.8±0.4	1.4±0.2	3.2±0.3

On other hand, the modalities using BB show an increased FOV evidenced by the increment of the width along x dimension (see Figs. 2(h) and 2(k)). Interestingly, the line width Δy shows little variation among all modalities, except for the case of linear excitation with BB where it becomes more than twice as thick as compared with the case using Gaussian beams, as shown in Fig. 2(i). In addition, Fig. 2(g) shows that for the linear case the blurring of the tails outside the usable FOV worsens when using BB. This would be solved by the use of a hard clipping procedure as described before for the case of Gaussian beams. This is in contrast with the two photon based modalities, Figs. 2(d) and 2(j), where the tails are naturally non existing by the confined nature of the nonlinear excitation. Also, it is worth noting that by using BB the intensity profile along the x direction is asymmetric for both linear and nonlinear modalities as can be appreciated in Figs. 2(h) and 2(k). This effect has been observed before for ideal refractive axicons where a slower decay rate is expected for the points farther from the axicon tip (see for example Akturk et al. [18]). In addition to this, the 2p-DSLM-Bessel image shows some irregularities within the FWHM. Such imperfections in the axial profile are attributed to the mask to remove the low spatial frequency components generated by the imperfect tip at the Fourier spectrum of the BB [17,18]. This mask was chosen in order to give the best trade-off between optical transmission and beam homogeneity in the 2p-DSLM-Bessel configuration. Therefore the small defect observed in Fig. 2(k) can be attributed to undesired angular frequencies that remain after filtering. This defect was not observed in the DSLM-Bessel image (Fig. 2(i)) due to: i) small differences of the spatial frequency spectra at the filtering plane, that make the BB generated with the SHG and femtosecond-laser beams to be slightly different, and ii) the background generated by the BB side lobes that masks any perturbation induced in its axial intensity profile.

A second set of experiments was performed in order to measure the size of the transversal (δr) and axial (δz) PSFs of the four DSLM modalities. For this, we employed a sample of beads immersed in agar as described in section 3.1. For each modality, a stack of images was recorded by moving the sample in steps of 0.2 μm along the z direction, capturing one image per step. For each image stack, several (~30) beads in the center of the FOV were selected and cropped to isolate their individual volumetric intensity distributions. In all cases, the brightest voxels of the intensity distributions were found and the intensity profiles were selected along the three reference axes of maximum intensity. The intensity distributions were fit to a Gaussian function and the FWHM values were calculated. Some examples of the intensity profiles and the Gaussian fits obtained for each modality are shown in Fig. 3 . The results are summarized in the Table 1. To obtain the transversal PSF width δr, we used both x and y measurements as δr= 0.5(δx+ δy).

Figure 3.

Example of the PSFs obtained for the system using a sample of fluorescent beads in agar. The experimental intensity profiles (black dots) and Gaussian fits (red lines) for both transversal (δr) and axial (δz) dimensions are shown for the different modalities: a, b) DSLM with Gaussian beams, c, d) 2p-DSLM with Gaussian beams, e, f) DSLM with BB and g, h) 2p-DSLM with Bessel beams. The FWHM widths calculated from the Gaussian fit are shown over each graph. The average values of the PSF widths for 5 beads are reported in the Table 1

It has been shown that the transversal resolution of a SPIM system depends exclusively on the optical properties of the collection lens, whereas the axial resolution is determined by both detection lens and the light-sheet thickness [20]. Therefore, we expect to have a similar transversal resolution for all the modalities and a diversity of axial resolutions dependent on the thickness as well on quality of the light-sheet for each modality. This is precisely what we have found in our experiments: as can be seen from the Table 1, although the transversal resolution is slightly better in both linear DSLM modalities, they are all very similar. This is not the case for the axial resolution, which is found to be different for each of the modalities and smaller in the nonlinear regimes. Also, as expected, there is a clear correlation between the light-sheet thickening and the axial resolution degradation, as is revealed by comparing Figs. 2(c), 2(f), 2(i), and 2(l) with Figs. 3(b), 3(d), 3(f), and 3(h), Table 1 columns Δy and δz. All these indicate that when imaging we should expect better axial resolution when DSLM in the nonlinear regime is performed. This should also be the case when imaging biological samples, a hypothesis that we verify in a series of experiments using fluorescently labeled C. elegans pharynxes.

4.2. C. elegans imaging

We started by imaging the pharyngeal muscle of C. elegans expressing the Cameleon fluorescence protein in a conventional SPIM setup, where the light sheet is formed via a cylindrical lens. This conventional SPIM technique [16] has proven to be useful for a number of samples including chick and mouse tissue and organs, Drosophila embryos and for imaging zebrafish development [21] and C. elegans. The results obtained with C. elegans are used as a reference for our different DSLM images obtained using Gaussian beams (DSLM-Gauss and 2p-DSLM-Gauss). The different experimental conditions are listed in the following Table 2 and Fig. 4 shows the results of such comparison.

Table 2. Summary of the experimental parameters employed to collect the data supporting Fig. 4.

Modality	Parameters
	Objectives		Wavelength (nm)	Avg. power (mW)	Integration Time (ms)	z step (μm)
	Excitation	Collection
SPIM	Air, Leica 5×/0.12 NA Plan Epi	Water, Leica 10×/0.3 HCX APO	488	<1	500	2
DSLM-Gauss	Air, Nikon 10×/0.15NA, Plan Fluor (nominal NA=0.3)	Air, Nikon 10×/0.45NA, Plan Apo	430	2	180	2
2p-DLSM-Gauss			860	58	220	2

Figure 4.

Images of a CFP-fluorescent pharynx of a C. elegans. Figures (a-c) are maximum intensity projections (MIP) of z stacks taken with a) the reference state-of-the-art SPIM system (Media 1 ^{(170.5KB, AVI)} ), b) DSLM-Gauss (Media 2 ^{(179.9KB, AVI)} ) and c) 2p-DSLM-Gauss (Media 3 ^{(188.1KB, AVI)} ). Figures d) to f) show some individual sections of the z stacks obtained with SPIM (Media 4 ^{(162.2KB, AVI)} ), DSLM (Media 5 ^{(256.9KB, AVI)} ) and 2p-DSLM (Media 6 ^{(365.4KB, AVI)} ) modalities using Gaussian beams, respectively. All z-stacks are composed of 54 images taken in steps of 2 μm. Scale bars: 20 μm.

Figures 4(a)-(c) show the maximum intensity projection (MIP) and optical sections obtained from the pharynx region of the nematode using the standard SPIM, DSLM-Gauss and 2p-DSLM-Gauss techniques, respectively (see also Media 1 ^{(170.5KB, AVI)} , Media 2 ^{(179.9KB, AVI)} and Media 3 ^{(188.1KB, AVI)} ). By comparing these figures it is possible to see that similar results are obtained for both SPIM and DSLM techniques. However, by directly comparing Figs. 4(d)-(f), it is appreciated that in the two-photon images the pharynx appears less blurry and some details are better discriminated.

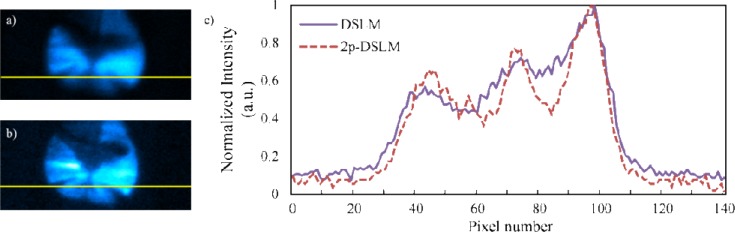
To quantify the results obtained with our DSLM system, we provide a plot of the intensity profiles along a line on the fluorescent structures. This has been done for the same worm (and therefore, the same pharynx) as well as for the same optical sections for both modalities, see yellow marked ROIs in Figs. 4(e) and 4(f) that correspond to Figs. 5(a) and 5(b), respectively. In this way, a proper quantification of the local intensity and the background signal is obtained. The results can be seen in Fig. 5. By looking at Fig. 5(c), it is possible to see that the 2p-DSLM presents a reduced background. In addition, some structures show higher modulations, indicating higher contrasts.

Figure 5.

Example of the contrast enhancement obtained by using 2p-DSLM. Regions of interest (ROI) taken from single optical sections (yellow squares on Fig. 4) for a) DSLM and b) 2p-DSLM. c) Plot of the intensity profiles along the selected lines for both modalities. Intensity values of the plots have been normalized to the maximum of each distribution.

We then proceed to test the use of BB to explore their impact on the length of the FOV. For this we prepared a sample of several worms, all in the same plane and aligned in a row along the direction of incidence (x) of the excitation beam (Fig. 6(a) ). For the four cases the beam was scanned to the amplitude that generates a light sheet that fills the entire FOV in the y direction. The experimental parameters employed to obtain the images of the Fig. 6 are outlined in Table 3 . It shows that the longest CCD integration time, and the highest excitation power levels correspond to 2p-DSLM with BB, whereas the same signal level can be obtained with 1p-DSLM using Gaussian beams with lower integration time and using very low (<1mW) excitation power.

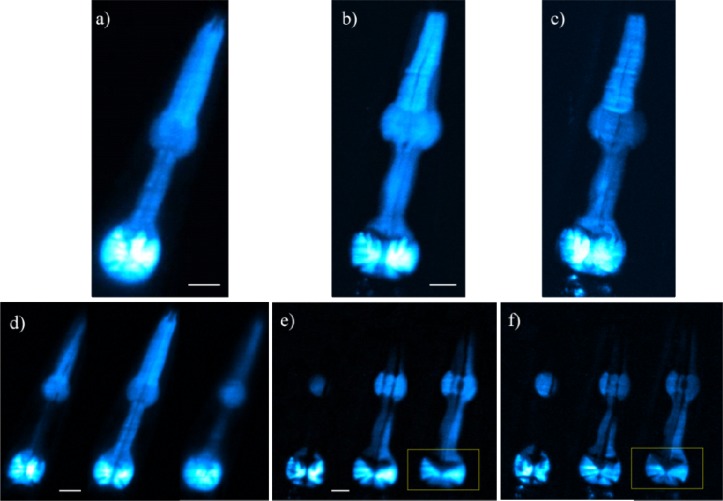
Figure 6.

Fluorescent images of a row of C. elegans aligned along the x direction. Figure a) shows the sample configuration as a reference (image taken using oblique illumination). Figures (b-e) are maximum intensity projections of z stacks taken with the four modalities available in our setup: b) DSLM-Gauss, c) 2p-DSLM-Gauss, d) DSLM-Bessel and e) 2p-DSLM-Bessel. The insets below each image indicate the position and extension of the excitation focal lines of Fig. 2. All z-stacks are composed of 50 images taken in steps of 2 μm. Scale bars: 50 μm.

Table 3. Summary of the experimental parameters employed to collect the data supporting Fig. 6.

	Parameters
Modality	Wavelength (nm)	Avg. power (mW)	Int. time (ms)	z step (μm)
DSLM-Gauss	430	<1	2000	2
DSLM-Bessel	430	<1	2000	2
2p-DLSM-Gauss	860	72	2000	2
2p-DLSM-Bessel	860	290	3000	2

The results are shown in Figs. 6(b)-(e), where MIPs of the z stacks are shown for all of our DSLM configurations. Also, the previously obtained excitation focal lines (see Fig. 2) were included below each figure as an indication of the expected effective FOV. From Fig. 6 it is possible to see the increase of the FOV in the x direction by using BB, in both linear and nonlinear modalities. Note that this is remarkably extended in the nonlinear regime (compare Figs. 6(c) and 6(e)). Now, in terms of image homogeneity the DSLM-Bessel gives better results when compared to any other modality, as seen in Fig. 6(d). However, the generated image is more blurry due to the side lobes characteristic of the BB. This is in agreement with our characterization results presented in Fig. 2(i) and 3(f). Finally, both DSLM-Gauss and DSLM-Bessel images require hard clipping in the collection path to eliminate the signal from the extremes of the generated beams. This can be clearly seen in the first and last worms in Figs. 6(b) and 6(d). This is not the case for the nonlinear techniques in which the image at the effective FOV is in focus showing sharper details (Figs. 6(c) and 6(e)).

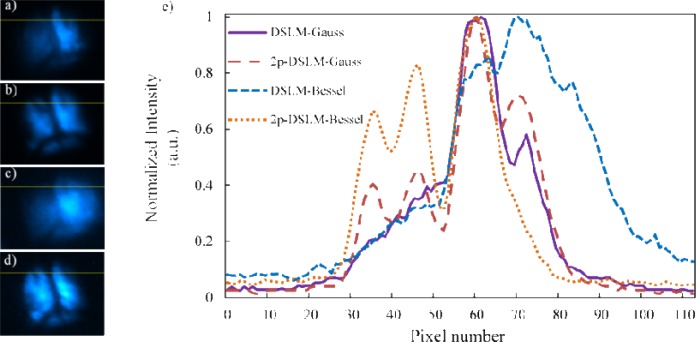
To quantify these results, optical sections were selected from the stack of images for each image modality at the ROIs marked in Fig. 6, as it is shown in Figs. 7(a)-(d) . A plot of the intensity profiles along the lines drawn in the optical sections is provided in Fig. 7(e). From this figure it is possible to see that the DSLM-Bessel case produces the largest generated fluorescence intensity. However, the optical sectioning is badly affected by the side lobes of the BB, causing a complete blurring of the details. In addition (and similarly to Fig. 5), we also found that both 2p-DSLM modalities allows for better contrast of the different sample structure, as well as a reduced background.

Figure 7.

Normalized profiles along a selected line taken from approximately the same optical section for all the DSLM modalities. Optical sections showing the same ROI and the selected line in yellow for a) DSLM with Gaussian beams, b) 2p-DSLM with Gaussian beams, c) DSLM with Bessel beams, and d) 2p-DSLM with Bessel beams. Plots of the intensity profiles along the selected lines are shown in e). Intensity of each plot has been normalized to its respective maximum value.

5. Discussion

We have built a very versatile DSLM system that allows changing between different modalities without affecting significantly the light-sheet’s properties (position and tilt). Thanks to this, a fair comparison between the different modalities can be done up to the level of a single optical section.

To start off with our comparative analysis, we can see, from Fig. 4, that 2p-DSLM offers better image quality than DSLM in terms of a higher contrast and a reduced background noise. However, its reduced FOV can become a limiting factor in applications requiring visualizations of large samples. To ameliorate this, bidirectional illumination can be used [11]. This could effectively double the usable FOV in 2p-DLSM [15]. Furthermore, thanks to the localized nature of two photon excitation it would allow for the superposition of the two counter-propagating excitation beams with minimal mutually induced background. Nevertheless, for highly refracting samples, or even for asymmetric preparations, the light path coming from the opposite sides can be severely degraded and tilted. This would lead to a poor overlap of the beams, affecting the axial resolution and the contrast. In such case, the 2p-DSLM-Bessel would play an important role in preserving image quality. This would also give an imaging system with enhanced penetration depths as well as with high axial resolution across the FOV. This indicates that BB are good alternative if a nonlinear technique is to be used and large FOV is required. Also, it is interesting to note that the FOV is increased in size up to four-fold as compared with the case using Gaussian beams, without compromising the axial resolution (see also Table 1). Figure 6(e) shows this fact clearly: the image quality is equivalent to the 2p-DSLM image using Gaussian beams (Fig. 6(c)) but more pharynxes are now evident in the extended FOV. Again, the localized nature of two-photon excitation seems to be the key to the good performance.

This is not the same for the linear case (DSLM-Bessel), as the image resolution is degraded due to the side lobes that generate fluorescence that broadens the axial PSF by a factor of almost 3 (see Table 1). As a consequence, its imaging capabilities are severely degraded in terms of contrast and background reduction as can be seen in figures 6(d) and 7(e). This calls for the use of more advanced detection methods such as line confocal approaches that enable the filtering of the undesired fluorescence and help to recover the contrast of the images acquired [22]. However, if for a given application resolution is not important, the use of DSLM-Bessel will give larger FOV and will produce, in a very efficient way (i.e. with small excitation powers producing high fluorescent signals), very homogenous images.

In terms of fluorescence yield, the modalities using linear excitation seem to be much more efficient, as can be seen in Tables 2 and 3. The excitation powers needed to obtain the same fluorescence signal are less than 1mW in the linear cases compared to tens or hundreds of mW for the nonlinear cases. In particular, the DSLM-Gauss modality shows a good trade-off between fluorescence generation, resolution and FOV coverage. This could be very useful for imaging applications of samples that do not tolerate large excitation powers or when dealing with faint or moderate fluorescing samples.

Finally, regarding the laser power levels employed for our experiments as reported in Tables 2 and 3, it is important to stress that for the maximum power level employed, which corresponds to 2p-DSLM-Bessel modality, the peak intensity at the sample plane was about 100 GW/ cm². This is below the 200 GW/cm² threshold for avoiding phototoxicity in long term imaging experiments [23]. In fact, for all the experiments reported here, all the worms recovered approximately 30 minutes after being anesthetized, and all of them showed again good activity on the agar bench.

6. Conclusions

We have demonstrated a DSLM system with four different modalities using a single ultrashort-pulsed laser. Switching between linear and non-linear, or between Gaussian and BB can be done in a reliable way. This has enabled us to perform a complete characterization and comparison of the performance for imaging of the different modalities using the same living sample. For practical purposes having available several DSLM modalities allows us to adapt the system to the particular requirements of each experiment. In fact, DSLM with Gaussian beams can be used when dealing with dim fluorescence samples and where there is more value in gathering many photons than having superior performance in terms of optical sectioning and contrast. 2p-DSLM with Gaussian beams will be appropriate to image localized structures inside highly scattering samples with high resolution and high fluorescence yield. The use of BB together with DSLM, although giving a large and homogeneous field of view, it can impose some restrictions in the axial resolution and the overall contrast of the images due to the fluorescence excited by the side lobes. This indicates that, to effectively use it for real microscopy applications a light rejection strategy, such as line confocal detection, has to be implemented. Finally, the use of BB combined with 2p-DSLM results in a system with a larger FOV and improved image contrast, providing an ideal technique for deep, high resolution imaging over moderately large FOVs, but using two orders of magnitude higher average powers. Finally, all the methods proposed here are fully compatible with in vivo long-term imaging experiments since we have shown that even in case of two photon modalities that require high powers, the intensities created at the sample plane are half the known value for avoiding phototoxicity.