Global hypothesis testing for high-dimensional repeated measures outcomes

Abstract

High-throughput technology in metabolomics, genomics, and proteomics gives rise to high dimension, low sample size data when the number of metabolites, genes, or proteins exceeds the sample size. For a limited class of designs, the classic ‘univariate approach’ for Gaussian repeated measures can provide a reasonable global hypothesis test. We derive new tests that not only accurately allow more variables than subjects, but also give valid analyses for data with complex between-subject and within-subject designs. Our derivations capitalize on the dual of the error covariance matrix, which is nonsingular when the number of variables exceeds the sample size, to ensure correct statistical inference and enhance computational efficiency. Simulation studies demonstrate that the new tests accurately control Type I error rate and have reasonable power even with a handful of subjects and a thousand outcome variables. We apply the new methods to the study of metabolic consequences of vitamin B6 deficiency. Free software implementing the new methods applies to a wide range of designs, including one group pre-intervention and post-intervention comparisons, multiple parallel group comparisons with one-way or factorial designs, and the adjustment and evaluation of covariate effects.

1. Introduction

1.1. Overview

High-throughput technology in metabolomics, genomics, and proteomics enables studying the abundance of hundreds or thousands of metabolites, mRNA molecules, and proteins (biomarkers) across a range of experimental conditions (e.g., disease states or treatments). Concentrations of each biomarker can be compared individually with a univariate method for local hypothesis testing. The tests collectively lead to multiple comparison problems and require an adjustment for the inflation of the false positive (Type I) rate. Many developments have focused on correcting local hypothesis testing on individual variables [1]. Our objective for the new method was to provide valid and powerful statistical tests for the global difference on all variables collected in general designs (i.e., allowing for complex between-subject and within-subject designs). A global test typically has better sensitivity to a collection of small differences than do local individual tests. When comparing gene expressions between a treatment group and a control group, a global hypothesis test declares significance if any subset of genes are differentially expressed between the two groups.

The explosion of the number of variables (biomarkers) gives rise to high dimension, low sample size (HDLSS) data when the number of variables (e.g., number of metabolites, mRNA molecules, or proteins) exceeds the sample size. More precisely, we assume throughout that HDLSS refers to have a finite number of response variables (b) larger in number than the error degrees of freedom (ν_e) in a linear model, namely 0 < ν_e < b < ∞, with ν_e and b in any ratio.

Many sets of HDLSS data for metabolomic, genomic, and proteomic variables have been measured in the same scale and units. Such data may be described as commensurate. A special case of commensurate data arises when the data consist of repeated measurements taken on a single variable for an ordered set of several points in time or space. In most important ways, a common theory applies to the analysis of commensurate and repeated measures.

Although originally developed in the context of a sample size greater than the number of variables, the ‘univariate approach’ to repeated measures (UNIREP) remains well defined for HDLSS global hypothesis testing. The UNIREP statistic is proportional to the ratio of the traces of the hypothesis and error sums of squares matrices [2, Chapter 3] and hence remains well defined when the sample covariance matrix becomes singular due to HDLSS. In this paper, we use analytic and simulation methods to generalize and investigate the performance of the classic UNIREP methods with HDLSS. We provide valid and accurate extensions of the UNIREP theory and practice to HDLSS inferences.

1.2. Unbiased tests and invariance

A test is said to be unbiased if the probability of rejecting the null hypothesis is less than or equal to the target Type I error rate (α) when the null hypothesis is true, and if the probability of rejection is greater or equal to α when the alternative hypothesis is true. In the history of the development for hypothesis testing, the property of unbiasedness under the null hypothesis is typically first sought before the search for good statistical power. For data with more than one outcome variable, a test must account for the error covariance structure to control Type I error rate accurately. Study design plays a major role in determining the structure, as does the choice of contrast matrix defining within-subject comparisons.

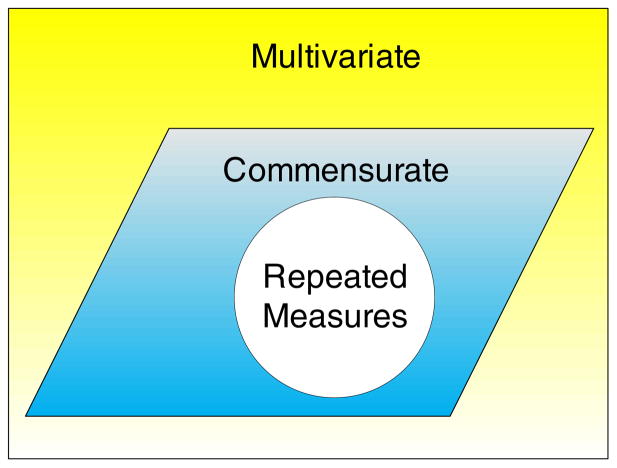
Designs for collecting more than one outcome variable can lead to one of the three types of data: pure multivariate, commensurate data, or repeated measures. Figure 1 depicts the categorization of the type of multivariate data. Multivariate outcomes encompass both pure multivariate and commensurate measures. The latter are distinguished by having all variables measured on the same measurement scale and units. Repeated measures give a special case for commensurate observations. We aim to provide unbiased tests for HDLSS repeated measures and commensurate observations that are useful in metabolomic, genomic, and proteomic studies.

Figure 1.

Categorization of the type of multivariate data.

The appeal of invariance properties has led to their playing a central role in the development of statistical tests for linear models. HDLSS data greatly complicate the consideration of invariance. For classic multivariate analysis with more subjects than variables, the multivariate analysis of variance (MANOVA) methods not only provide unbiased tests across different error covariance structures, but also are invariant to full-rank linear transformation (excluding location shifts) of original variables. With HDLSS, all MANOVA statistics become undefined because of the singularity of the error covariance matrix. Furthermore, no nontrivial size-α test with affine invariance is possible [3]. Srivastava and Du [3] and Srivastava [4] considered tests possessing local scale invariance for the analysis of pure multivariate data.

Our results take advantage of a different form of invariance, namely invariance to orthonormal transformations. Analytically, the property simplifies derivations by simplifying covariance structures. Simplified expressions improve computational efficiency and accuracy, which can be invaluable as the number of variables grow to thousands and beyond.

1.3. Review of existing high dimension, low sample size methods

Most of the existing methods for HDLSS global hypothesis testing focus on analysis of multivariate outcomes. Exceptions were the papers of Ahmad et al. [5] for one-sample designs and Brunner [6] for two-sample designs for modified UNIREP-type statistics in the analysis of high-dimensional repeated measures. Many other suggestions have been made to overcome the nonexistence (due to HDLSS) of the error covariance matrix inverse needed in classical multivariate test statistics. Srivastava [7] proposed an HDLSS multivariate test based on the Moore–Penrose generalized inverse of the error covariance matrix, and derived asymptotic null distributions by assuming that both the sample size and the number of variables go to infinity. Warton [8] used a ridge-regularization approach to shrink eigenvalues of correlation matrices to create full-rank matrices in computing a Hotelling–Lawley analog statistic and applied a permutation technique to establish a null distribution. Dempster [9] and Bai and Saranadasa [10] proposed modified statistics by removing the inverse sample covariance matrix (nonexistent due to HDLSS) from the Hotelling’s one-sample and two-sample T² statistics and derived large sample Gaussian approximations. Subsequently, Chen and Qin [11] developed a two-sample test that does not require explicit conditions in the relationship between the sample size and the number of variables. Srivastava and Du [3] inverted the diagonal matrix of sample variances to compute a form like the Hotelling–Lawley statistic and assumed that both large sample size and large number of variables derive an approximate Gaussian distribution. Srivastava and Fujikoshi [12] proposed a statistic defined as a function of the traces of hypothesis and error sums of squares matrices and derived a large sample approximation for testing a linear hypothesis in a multivariate linear model.

Table I summarizes the characteristics (type of HDLSS data and study design) driving the development and invariance properties of the existing tests. Most of the multivariate methods are limited to one-sample or two-sample designs. Exceptions are the k-sample methods by Srivastava [7] and Srivastava and Fujikoshi [12] and the evaluation of covariate effects by Srivastava and Fujikoshi [12]. Although the multivariate methods may in theory apply to repeated measures, contrasts of interest for repeated measures designs were rarely evaluated in terms of the control of the Type I error rate. Ahmad et al. [5] and Brunner [6] tailored a solution for one-sample and two-sample HDLSS repeated measures designs. In addition to the lack of global hypothesis testing methods for general repeated measures designs, the large sample approximations that some methods rely on may not be accurate in HDLSS designs.

Table I.

Developing characteristics and invariance properties of the existing high dimension, low sample size global hypothesis testing methods in a chronological order.

	Multivariate			Repeated measures		Invariance
	One sample	Two sample	Predictor/covariate	One sample	Two sample	Orthonormal	Local scale
Dempster [9]	√	√				√
Bai and Saranadasa [10]	√	√				√
Srivastava and Fujikoshi [12]	√	√	√			√
Srivastava [7]	√	√				√
Srivastava and Du [3]	√	√					√
Warton [8]		√					√
Ahmad et al. [5]				√		√
Brunner [6]				√	√	√
Chen and Qin [11]	√	√				√

With HDLSS, none of the existing global hypothesis tests are invariant to nonsingular linear transformations of the original variables. Some methods are invariant to orthonormal transformations (as listed in Table I), whereas methods proposed by Srivastava and Du [3] and Warton [8] are invariant to local scale transformations to accommodate multivariate outcomes measured in different scales and measurement units. All tests are invariant to a global scale transformation.

1.4. New univariate approach to repeated measures extension

Unlike the classic UNIREP methods, new methods are developed from the perspective of having data with more variables than subjects. The dual of the error sum of square matrix (i.e., the outer not inner product) lies in the heart of our derivations. When the number of variables exceeds the sample size, the dual matrix becomes a better means for deriving analytically stable estimates and for facilitating computational efficiency due to its smaller size and full-rank nature. Computation time for any covariance matrix increases quadratically with the number of variables. Ahn et al. [13] and Jung and Marron [14] took advantage of the dual matrix in evaluating asymptotic properties in HDLSS. Our results use the dual matrix in a different way to derive parameter estimators in finite samples. The new methods, as extensions of the UNIREP approach to the general linear multivariate model, account for the correlation of any structure among the outcomes and support a wide range of study designs, including k-sample (k ≥ 1) comparisons with one-way or factorial designs, as well as the adjustment and evaluation of covariate effects. One of the proposed tests coincides with the corrected Huynh–Feldt test (defined in Section 2.1) for simple designs but outperforms the Huynh–Feldt test in the simulations when a covariate is considered.

The proposed tests are invariant to global scale and orthonormal transformations. The property allows considering only diagonal error covariance matrices in analytic and numerical evaluations. As with all UNIREP methods, the new methods do not have local scale invariance, a feature not relevant for repeated measures or commensurate data.

The rest of the paper is organized as follows. In Section 2, we review the existing UNIREP methods in the context of HDLSS. In Section 3, we formally define the dual matrix and derive the new tests. Section 4 includes simulations evaluating and comparing the new methods to existing competitors with respect to the control of the Type I error rate and power attained. In Section 5, we apply the new methods to variables from a study of metabolic consequence of vitamin B6 deficiency. In Section 6, we discuss future research directions.

2. The univariate approach to repeated measures methods

2.1. The multivariate model and univariate approach to repeated measures tests

Following Muller and Barton [15], we state classic UNIREP tests in terms of the general linear multivariate model. The approach ensures that all results explicitly cover a wide variety of useful models, and defines simple expressions for estimates and tests. Table II summarizes the notation for parameters and constants, adopted from studies of Muller and Stewart [2] and Muller et al. [16] for the usual case when the sample size is greater than the number of variables.

Table II.

Parameters and constants for general linear multivariate model Y = XB +E and associated general linear hypothesis H₀: Θ = Θ₀.

Symbol	Size	Definition and properties
N	1 × 1	Sample size
p	1 × 1	Number of outcome variables
q	1 × 1	Number of predictors
X	N × q	Fixed, known design matrix
B	q × p	Primary (mean) parameters
νe = N − rank (X)	1 × 1	Error degrees of freedom
a	1 × 1	Number of between-subject contrasts
b	1 × 1	Number of within-subject contrasts
C	a × q	Between-subject contrast matrix
U	p × b	Within-subject contrast matrix
Θ = CBU	a × b	Secondary parameters
Θ0	a × b	Null values of secondary parameters
M = C(X′X)−C′	a × a	Middle matrix
Δ = (Θ − Θ0)′M−1(Θ − Θ0)	b × b	Nonstandardized noncentrality
Σ	p × p	Error covariance of [rowi (E)]′
Σ* = U′ΣU	b × b	Hypothesis error covariance of [rowi (EU)]′
λ	b × 1	Vector of eigenvalues of Σ*
$\begin{array}{l}∊={\text{tr}}^2({\mathbf{\sum }}_{\ast })/\left[b\text{tr}({\mathbf{\sum }}_{\ast }^2)\right]\\ ={\left({\sum }_{k=1}^b{\lambda }_k\right)}^2/\left(b{\sum }_{k=1}^b{\lambda }_k\right)\end{array}$	1 × 1	Sphericity parameter

The general linear multivariate model Y = XB + E has rows of Y (N × p) and E (N × p), corresponding to subjects (independent sampling units), and columns of Y and E, corresponding to repeated measures or multivariate outcomes. Classic assumptions specify a homogeneous covariance structure (i.e., 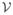[row_i (Y)|X] = Σ, i ∈ {1, …, N}) and finite Σ. Least squares estimation gives B̃= (X′X)⁻X′Y and Σ̂ = (Y − XB̃)′(Y − XB̃)/ν_e. The Gaussian assumption leads to independently and identically distributed row _i(E)′ ~ 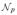(0, Σ), equivalently E ~ 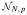(0, I_N, Σ) for a matrix Gaussian distribution, as defined by Muller and Stewart [2, Chapter 8]. The three parameters give the expected value matrix, the covariance among rows, and the covariance among columns. In turn, B̃ ~ 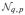[(X′X)⁻X′XB, (X′X)⁻, Σ], and ν_eΣ̂ ~ 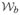(ν_e, Σ) for a central Wishart distribution with degrees of freedom ν_e and scale parameter Σ [2, Chapter 10].

The multivariate general linear hypothesis covers many tests, including Hotelling’s T² for one or two samples, repeated measures and MANOVA, multivariate regression, discriminant analysis with two or more groups, and canonical correlation. The hypothesis regarding the secondary parameters may be stated as H₀: Θ = CBU = Θ₀. A set of regularity conditions is required to define estimable and testable Θ: rank(C) = a ≤ q, C = C(X′X)⁻(X′X) and rank(U) = b ≤ p. Both least squares and maximum likelihood estimation methods give Θ̂ = CB̃U.

The UNIREP test statistic is proportional to the ratio of the trace (diagonal sum) of the hypothesis sum of square matrix S_h = (Θ̂ − Θ₀)′M⁻¹(Θ̂ − Θ₀) = Δ̂ to the trace of error sum of square matrix S_e = ν_eU′Σ̂U = ν_eΣ̂_*, that is, t_u = [tr(S_h)/a]/[tr(S_e)/ν_e]. Box [17, 18] and Greenhouse and Geisser [19] gave an F distribution to approximate the distribution of t_u in terms of the sphericity parameter ∊:

$$Pr\{t_u\le f_0\}\approx Pr\{F(ab∊,{\nu }_{e}b∊)\le f_0\}.$$ (1)

The parameter ∊ (1/b ≤ ∊ ≤ 1) quantifies the spread of population eigenvalues. Perfect sphericity requires ∊ = 1, which occurs with all eigenvalues equal. Minimal sphericity has ∊ = 1/b, which occurs with one nonzero eigenvalue.

The four classic UNIREP tests all use the Box F approximation but differ in the value chosen for ∊, which discounts the degrees of freedom. A conservative test uses the fixed ∊_l = 1/b, the lower bound of ∊, whereas the original test uses the fixed ∊_u = 1, the upper bound of ∊. With sphericity, the ∊_u-adjusted test is size α and uniformly most powerful (among similarly invariant tests). The other two widely used tests use the observed data to estimate ∊. The ∊̂-adjusted test reduces degrees of freedom by the maximum likelihood estimator of ∊, namely $\widehat{∊}=b^{-1}{\text{tr}}^2({\widehat{\mathbf{\sum }}}_{\ast })/\text{tr}({\widehat{\mathbf{\sum }}}_{\ast }^2)$. In seeking an approximately unbiased estimator, Huynh and Feldt [20] and Huynh [21] used a ratio of unbiased estimators, namely ∊̃₀ =(Nb∊̂ − 2)/[b(N − G − b∊̂)], for G-sample comparisons. Lecoutre [22] corrected an error in ∊̃₀ with ∊̃ = [(N − G + 1) b∊̂ − 2]/[b(N − G − b∊̂)] for the case with G ≥ 2. The fact that ∊̃ may exceed the upper bound of ∊ leads to using ∊̃_r = min (∊̃, 1) and the ∊̃_r -adjusted test for designs with one between-subject factor. Gribbin [23] generalized the results to cover general designs with any number of between-subject factors and covariates. The order of the degrees of freedom multipliers, ∊_l ≤ ∊̂ ≤ ∊̃_r ≤ ∊_u, leads to the Type I error rate and power following the same order and p-values in data analysis having the reverse order.

2.2. Univariate approach to repeated measures properties with high dimension, low sample size

The classic UNIREP theory was developed in the context of a sample size greater than the number of variables. Allowing more outcomes than subjects (HDLSS) implies more contrasts within subject than error degrees of freedom: b > ν_e. As a result, the density of the hypothesis error covariance matrix estimate Σ̂_* = S_e/ν_e does not exist, and a direct likelihood approach becomes unavailable. Throughout the paper, we assume that the rank of the design matrix X does not exceed the sample size, leading to fewer contrasts between subjects than error degrees of freedom: a < ν_e.

The distributional properties and performance of the classic UNIREP methods with HDLSS outcomes have not been examined in detail. Therefore, we present new HDLSS analytic results and their proofs in the Appendix. Theorem 1 gives the invariant distributional forms for the hypothesis sum of square matrix S_h = Δ̂ and error sum of square matrix S_e = ν_e Σ̂_*. Both b × b matrices follow a Wishart distribution but become singular with HDLSS (a < ν_e < b), that is, rank (S_h) = a and rank(S_e ) = ν_e. The singularity, however, has no impact on the distributional form for the UNIREP test statistic t_u but does affect the estimation of the sphericity parameter, ∊. Theorem 2 provides the exact distributional form for t_u and its invariant properties for HDLSS. The subsequent corollary validates the use of the Box approximation (in Equation (1)) with HDLSS.

The generalization of the Box approximation to HDLSS leads to considering a variety of classic UNIREP degrees of freedom multipliers. The ∊̂-adjusted and ∊̃_r -adjusted tests were developed to achieve a middle ground between the overly conservative ∊_l -adjusted test and the overly liberal ν_u-adjusted test. Maxwell and Arvey [24] conducted HDLSS two-sample comparisons with N = {10, 12} and p = 13. In their simulations, the ∊̂-adjusted test was very conservative especially when the population eigenvalue pattern was nearly spherical (∊ = 1). In contrast, the original Huynh–Feldt test (without Lecoutre’s correction) was liberal especially when the population eigenvalue pattern was far from sphericity. Our HDLSS simulations in Section 4.2 involve a more complex design with a three-sample comparison and a covariate.

3. New methods for high-dimensional global testing

3.1. The dual matrix

The result that the Box F approximation in Equation (1) remains valid with HDLSS leads to an opportunity for improving estimation of ∊. By the definition of ∊ in Table II, the parameter ∊ is a nonlinear function of the eigenvalues of the hypothesis error covariance matrix Σ_*. We have tailored our estimation approach to the HDLSS setting by considering a full-rank dual matrix for estimating functions of eigenvalues of Σ_*, and thus ∊.

With HDLSS (b > ν_e), the error sum of square matrix S_e = ν_eΣ̂_* becomes singular and in turn gives poor estimates of eigenvalues of Σ_*, the traditional path to estimating ∊. In contrast, the dual of the error sum of square matrix, S_d as defined in Equation (2), shares the nonzero eigenvalues of S_e, is full rank with HDLSS, and provides a better path to estimating ∊. Ahn et al. [13] used the dual matrix to study the geometric presentation of HDLSS data, whereas Jung and Marron [14] took advantage of the dual matrix to investigate the asymptotic behavior of the principal component directions when the variable dimension is large.

The error sum of square matrix can be expressed as the inner product of hypothesis variables Y_u = YU projected into the complement of the covariate space, namely ${\mathit{S}}_e={\nu }_e{\mathit{U}}^{\prime }\widehat{\mathbf{\sum }}\mathit{U}={\mathit{Y}}_u^{\prime }[{\mathit{I}}_N-\mathit{X}{({\mathit{X}}^{\prime }\mathit{X})}^{-}{\mathit{X}}^{\prime }]{\mathit{Y}}_u=({\mathit{Y}}_u^{\prime }{\mathit{L}}_0)({\mathit{L}}_0^{\prime }{\mathit{Y}}_u)={\mathit{Y}}_0^{\prime }{\mathit{Y}}_0$. Here, L₀ (N × ν_e) is orthonormal of rank ν_e, ${\mathit{L}}_0{\mathit{L}}_0^{\prime }=[{\mathit{I}}_N-\mathit{X}{({\mathit{X}}^{\prime }\mathit{X})}^{-}{\mathit{X}}^{\prime }]$, and ${\mathit{Y}}_0={\mathit{L}}_0^{\prime }{\mathit{Y}}_u$ is ν_e × b. The dual matrix is the ν_e × ν_e outer product of Y₀, defined as

$${\mathit{S}}_d={\mathit{Y}}_0{\mathit{Y}}_0^{\prime }.$$ (2)

Through the singular value decomposition of Y₀, it can be shown that the two matrices S_e and S_d have the same nonzero eigenvalues. Hence, either can be used to estimate functions of eigenvalues of Σ_*, including the parameter ∊.

Using S_d with HDLSS data has two advantages. First, the full-rank nature of S_d with b > ν_e allows deriving analytically stable estimates of ∊ and improving the F approximation for the null distribution of the UNIREP statistic. For Gaussian data, properties of the elements of S_d can be expressed in terms of summary functions of the eigenvalues of Σ_*. The summary functions are directly estimable and in turn provide all of the building blocks needed to estimate ∊. Properties of the elements of S_e, in contrast, are expressed in terms of complex functions of the eigenvalues of Σ_*, which are not directly estimable given that the eigenvalues themselves are not estimable with HDLSS.

The second advantage of using S_d with HDLSS data is computational efficiency. When the number of variables grows considerably greater than the sample size, computing S_d is much more computationally efficient than computing S_e. For example, with ν_e = 20 and b = 1000, computing S_e (with 500,500 unique values) requires about 2400 times the time needed for computing S_d (with 210 unique values). In the simulation examining the performance of classic UNIREP tests, it took about 9.5 h to complete the 90 HDLSS conditions (b ∈ {64, 256, 1024}, ν_e ∈ {4, 8, 16}, α ∈ {0:01, 0:05}, and five eigenvalues patterns) for calculations based on the dual matrix and more than 600 h for calculations based on the high-dimensional error sum of square matrix.

3.2. New tests for high dimension, low sample size

The analytic results in the Appendix provide the exact distribution of the UNIREP test statistic with HDLSS. The exact distribution depends only on the dimensions of the problem and λ = {λ_k}, the b eigenvalues of Σ_*. The unknown nature of λ disallows computing the exact distribution in data analysis.

The Box F approximation has great appeal in that it accounts for differences in covariance pattern by directly using ∊ = f(λ) and does not require knowing individual values of λ_k. As can be seen from consideration of the characteristic function and results in the Appendix, the approximation provides second-order accuracy for approximating the distribution function. In the practice of data analysis, ∊ remains unknown and must be estimated.

For ∊ = b⁻¹τ₁/τ₂, obtaining unbiased estimators for the numerator ${\tau }_1={\left({\sum }_{k=1}^b{\lambda }_k\right)}^2$ and the denominator ${\tau }_2={\sum }_{k=1}^b{\lambda }_k^2$ leads to an estimator of ∊, namely b⁻¹τ̂₁/τ̂₂ with E(τ̂₁) = τ₁ and E(τ̂₂) = τ₂. Matching moments of the dual matrix S_d provides a means to derive estimators that are valid with HDLSS. For Gaussian data, S_d is a weighted sum of identically and independently distributed Wishart matrices. Each Wishart has one degree of freedom and identity scale matrix, while the weights equal the eigenvalues of Σ_*. Theorem 3 contains explicit expressions and the first two moments of elements of S_d. Matching the common variance of diagonal elements $\left(2{\sum }_{k=1}^b{\lambda }_k^2\right)$ and the common variance of off-diagonal elements $\left({\sum }_{k=1}^b{\lambda }_k^2\right)$ allows deriving the unbiased estimator ${\widehat{\tau }}_2=[{\nu }_e\text{tr}({\mathit{S}}_d^2)-{\text{tr}}^2({\mathit{S}}_d)]/[{\nu }_e({\nu }_e^2+{\nu }_e-2)]$. In turn, ${\widehat{\tau }}_1=[({\nu }_e+1){\text{tr}}^2({\mathit{S}}_d)-2\text{tr}({\mathit{S}}_d^2)]/{\nu }_e({\nu }_e^2+{\nu }_e-2)$ is an unbiased estimator of τ₁. As a result, a new estimator of ∊ is based on ∊̃_D0 = b⁻¹ τ̂₁/τ̂₂. With some algebra, it can be shown that ∊̃_D0 = [(ν_e + 1) b∊̂ − 2]/[b(ν_e − b∊̂)] and reduces to ∊̃ in the special case for designs considered by Lecoutre [22]. The fact that ∊̃_D0 may exceed 1.0 leads to using ∊̃_D1 = min (∊̃_D0, 1).

An improvement over ∊̃_D1 may be achieved by adjusting for the inversion of τ̂₂ in ∊̃_D1. For ν_a = (ν_e − 1) + ν_e (ν_e − 1)/2, the approximation (τ̂₂ · ν_a/τ₂)^1/2 ~ χ²(ν_a) gives $\text{E}\left[{({\widehat{\tau }}_2/{\tau }_2)}^{-1}\right]\approx {\nu }_a^2/[({\nu }_a-2)({\nu }_a-4)]$ (on the basis of the second moment of a reciprocal chi-square random variable; [25, Equation 18.8]). Clearly, $({\nu }_a-2)({\nu }_a-4)/{\nu }_a^2<1$. The adjustment gives a second estimator defined as ${\stackrel{\sim }{∊}}_{D2}=max\{min[{\stackrel{\sim }{∊}}_{D0}({\nu }_a-2)({\nu }_a-4)/{\nu }_a^2,1],1/b\}$ to incorporate truncation, with∊̃_D2 ≤ ∊̃_D1.

We define test T₁ by using ∊̃_D1 and test T₂ by using ∊̃_D2 to estimate ∊ in the Box F approximation with ab∊ numerator and ν_e b∊ denominator degrees of freedom for the distribution of the UNIREP statistic. Test T₁ coincides with the ∊̃_r -adjusted test (the corrected Huynh–Feldt test) when there is only one between-subject factor and no covariate. The order of the new degrees of freedom multipliers, ∊̃_D2 ≤ ∊̃_D1, leads to the Type I error rate and power following the same order, T₂ ≤ T₁, and p-values in data analysis in the reverse order.

The two new tests T₁ and T₂ are invariant to global scale and orthonormal transformations. The properties allow diagonalizing the hypothesis error covariance for analytic and numerical explorations. As extensions of classic UNIREP methods, they do not have local scale invariance, a feature not needed for repeated measures or commensurate data. Simulation results in Section 4 support the conclusion that the new methods give robust control of the Type I error rate for HDLSS three-sample comparisons with a covariate, non-HDLSS two-sample comparisons, and HDLSS one-sample and two-sample comparisons. Furthermore, the control of the Type I error rate was consistent across patterns of the hypothesis error covariance structure Σ_*. The classic UNIREP tests failed to control the Type I error rate, except at boundary conditions, for samples as small as 9 when a covariate was present.

4. Simulations

4.1. Simulation methods and design

A series of simulations helps evaluate the performance of T₁ and T₂ and also compare them to existing UNIREP and HDLSS specific tests. We conducted all computations in SAS/IML® (SAS Institute, Inc: Cary, NC)[26]. We used the SAS Normal function to generate an N×b matrix of pseudorandom Gaussian data. The property of orthonormal invariance as stated in Theorem 2 allows assuming, without loss of generality, Σ_* = Dg (λ) and λ = [λ₁, …, λ_b]′. For k ∈ {b, b − 1, …, 1}, λ_k = (b − k + 1)^π, with subsequent normalization to achieve λ = 1. The parameter π dictated the spread of λ_k values, with π = 0 corresponding to λ_k ≡ 1/b (giving ∊ = 1, sphericity) and larger values of π giving more deviation from sphericity (∊ ↓ 1/b). A three-way complete factorial design was adopted with π varied to specify a wide range for ∊. Other factor levels were error degrees of freedom ν_e and the number of hypothesis variables b. For HDLSS three-sample comparisons with a covariate 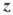~ N(0, 1), ν_e ∈ {6, 27}, and b ∈ {64, 256, 1024}, with b > ν_e. For non-HDLSS two-sample comparisons, ν_e ∈ {32, 64, 128}, and b ∈ {4, 8, 16}, with b < ν_e. Lastly, for HDLSS one-sample and two-sample comparisons, ν_e ∈ {4, 8, 16}, and b ∈ {64, 256, 1024}. The simulation design for ∊ estimation expanded the simulation design by Ahmad et al. [5]. Targeted Type I error rate was α = 0.05 or α = 0.01. For each condition, empirical Type I error rate was tabulated for 100,000 replications that provide a 95% confidence interval half-width of $0.0014(1.96\sqrt{0.95·0.05/100,000})$ around α̂ = 0.05.

4.2. High dimension, low sample size three-sample comparisons with a covariate

We conducted simulations to compare the proposed tests with the four classic UNIREP tests: the ∊_u-adjusted test for using the upper bound of ∊; the ∊̂-adjusted test for using the maximum likelihood estimator of ∊; the ∊̃_r -adjusted for using a ratio of unbiased estimators ∊̃_r ; and the ∊_l -adjusted test for using the lower bound of ∊. The simulation design involved a continuous covariate for three-sample problems, a condition in which the proposed test T₁ is analytically different from the ∊̃_r -adjusted test. Table III lists empirical Type I error rates × 100 for targeted Type I error rates of α = 0.05. When the sphericity parameter ∊ is known, the F approximation provided excellent, although not perfect, control of the Type I error rate across the combinations of sample size, number of variables, and covariance structure. The ∊_l -adjusted and ∊̂-adjusted tests were very conservative except when the population eigenvalue pattern was far away from sphericity with ∊ near the lower bound (∊ = 1/b). The conservatism increased as the ratio of sample size to the number of variables became smaller and as ∊ increased. The ∊̃_r -adjusted test also gave a conservative Type I error rate except when ∊ was very small or when the sample size was sufficiently large (i.e., ν_e = 27 for N = 30, and b ∈ {64, 256}). In contrast, the ∊_u-adjusted test greatly inflated the Type I error rate except with sphericity. The ∊_u-adjusted test is exactly of size α when ∊ = 1 because the Box F approximation becomes exact with sphericity.

Table III.

High dimension, low sample size three-sample comparison with a covariate: empirical Type I error rates × 100 for 100,000 replications and α = 0.05.

b	νe	∊	Type I error rates × 100
			∊ known	T1	T2	∊̃u-adjusted	∊̃r -adjusted	∊̂-adjusted	∊̃l-adjusted
64	6	0.016	4.99	4.99	4.99	35.9	4.99	4.99	4.99
		0.268	4.99	6.70	3.29	18.8	2.85	0.05	0.00
		0.560	5.08	6.12	3.05	10.6	1.17	0.00	0.00
		0.756	5.04	5.38	2.84	7.51	0.65	0.00	0.00
		1.000	4.99	4.18	2.43	4.99	0.30	0.00	0.00
	27	0.016	5.06	5.06	5.06	31.1	5.06	5.06	5.06
		0.268	5.10	5.35	5.21	18.0	5.15	2.07	0.00
		0.560	5.18	5.29	5.14	10.6	4.90	0.74	0.00
		0.756	5.11	5.17	5.04	7.55	4.66	0.36	0.00
		1.000	5.00	4.77	4.71	5.00	4.35	0.13	0.00
256	6	0.004	5.03	5.03	5.03	39.2	5.03	5.03	5.03
		0.266	5.07	6.43	3.00	19.3	0.28	0.00	0.00
		0.557	5.06	6.08	2.91	10.9	0.01	0.00	0.00
		0.752	5.08	5.36	2.76	7.72	0.00	0.00	0.00
		1.000	5.02	4.21	2.47	5.02	0.00	0.00	0.00
	27	0.004	5.05	5.05	5.05	34.8	5.05	5.05	5.05
		0.266	5.04	5.18	5.05	19.0	4.47	0.15	0.00
		0.557	5.05	5.14	5.00	10.9	3.81	0.00	0.00
		0.752	5.18	5.20	5.06	7.80	3.45	0.00	0.00
		1.000	5.17	4.95	4.87	5.17	2.98	0.00	0.00
1024	6	0.001	5.05	5.05	5.05	41.4	5.05	5.05	5.05
		0.265	5.02	6.37	2.97	19.6	0.00	0.00	0.00
		0.556	5.04	5.95	2.73	11.0	0.00	0.00	0.00
		0.750	5.12	5.36	2.69	7.78	0.00	0.00	0.00
		1.000	5.07	4.25	2.42	5.07	0.00	0.00	0.00
	27	0.001	4.95	4.95	4.95	36.2	4.95	4.95	4.95
		0.265	5.24	5.30	5.16	19.7	2.91	0.00	0.00
		0.556	5.08	5.13	5.00	11.0	1.52	0.00	0.00
		0.750	5.03	5.13	4.98	7.71	0.99	0.00	0.00
		1.000	5.02	4.78	4.72	5.02	0.57	0.00	0.00

The new test T₁ kept the Type I error rates at or above the target except when ∊ = 1 (homogeneous eigenvalues for the hypothesis error covariance Σ_*), whereas the new test T₂ in general kept the Type I error rates at or below the target. The test-size accuracy of both T₁ and T₂ improved as sample size increased regardless of the number of variables and the spread of population eigenvalues. Test T₂ will be preferred by data analysts willing to accept some conservatism to reduce any liberality in hypothesis testing.

Table IV lists the empirical means of the sphericity estimates to allow comparing the new and existing estimators of ∊. The two new estimators, ∊̃_D1 and∊̃_D2, used in tests T₁ and T₂, respectively, on average provided estimates much closer to the true values, whereas the classic estimators were very biased except at boundary conditions. The ∊_u-adjusted test has unbiased estimation of the sphericity parameter only when ∊ = 1. The ∊_l -adjusted, ∊̂-adjusted, and ∊̃_r -adjusted tests use unbiased sphericity estimators only when ∊ = 1/b.

Table IV.

High dimension, low sample size three-sample comparison with a covariate: empirical means of sphericity estimates over 100,000 replications.

b	νe	∊	Empirical means
			∊̃D1	∊̃D2	∊̃u	∊̃r	∊̂	∊̃l
64	6	0.016	0.016	0.016	1.000	0.016	0.016	0.016
		0.268	0.319	0.196	1.000	0.187	0.060	0.016
		0.560	0.628	0.400	1.000	0.275	0.068	0.016
		0.756	0.782	0.529	1.000	0.311	0.070	0.016
		1.000	0.902	0.671	1.000	0.343	0.072	0.016
	27	0.016	0.016	0.016	1.000	0.016	0.016	0.016
		0.268	0.272	0.267	1.000	0.265	0.159	0.016
		0.560	0.565	0.555	1.000	0.537	0.233	0.016
		0.756	0.761	0.748	1.000	0.712	0.261	0.016
		1.000	0.973	0.964	1.000	0.919	0.286	0.016
256	6	0.004	0.004	0.004	1.000	0.004	0.004	0.004
		0.266	0.311	0.191	1.000	0.088	0.018	0.004
		0.557	0.622	0.396	1.000	0.105	0.019	0.004
		0.752	0.777	0.525	1.000	0.110	0.019	0.004
		1.000	0.901	0.670	1.000	0.114	0.019	0.004
	27	0.004	0.004	0.004	1.000	0.004	0.004	0.004
		0.266	0.268	0.263	1.000	0.244	0.073	0.004
		0.557	0.560	0.551	1.000	0.467	0.085	0.004
		0.752	0.756	0.743	1.000	0.596	0.089	0.004
		1.000	0.972	0.964	1.000	0.741	0.092	0.004
1024	6	0.001	0.001	0.001	1.000	0.001	0.001	0.001
		0.265	0.309	0.190	1.000	0.029	0.005	0.001
		0.556	0.620	0.394	1.000	0.030	0.005	0.001
		0.750	0.777	0.525	1.000	0.031	0.005	0.001
		1.000	0.902	0.671	1.000	0.031	0.005	0.001
	27	0.001	0.001	0.001	1.000	0.001	0.001	0.001
		0.265	0.267	0.263	1.000	0.194	0.023	0.001
		0.556	0.560	0.550	1.000	0.312	0.024	0.001
		0.750	0.755	0.742	1.000	0.365	0.025	0.001
		1.000	0.972	0.964	1.000	0.415	0.025	0.001

4.3. Non-high dimension, low sample size two-sample comparisons

We also examined the performance of the proposed tests, which was compared with that of the ∊̂-adjusted test with low-dimensional data, that is, when the sample size exceeds the number of variables. Table V lists empirical Type I error rates × 100 for a target Type I error rate of α = 0.05 for ν_e ∈ {32, 128}, and b ∈ {4, 16}. We obtained similar results for ν_e = 64 or b = 8, which were omitted for the sake of brevity. Although derived for more variables than subjects, the new tests T₁ and T₂ outperformed the ∊̂-adjusted test except when ∊ was small. Both T₁ and T₂ slightly inflated the Type I error rates when ∊ = 1 or ∊ = 1/b. Overall, T₂ provides control of the Type I error rate as good as or better than T₁ except when sphericity held. Test T₁ coincides exactly with the ∊̃_r -adjusted test for non-HDLSS two-sample comparisons.

Table V.

Non-high dimension, low sample size two-sample comparison: empirical Type I error rates × 100 for 100,000 replications and α = 0.05.

b	νe	∊	Type I error rates × 100
			T1	T2	∊̂-adjusted
4	32	0.250	4.96	4.96	4.96
		0.345	5.20	5.14	5.02
		0.636	5.20	5.14	4.75
		0.833	5.18	5.11	4.56
		1.000	4.91	4.88	4.30
	128	0.250	5.03	5.03	5.03
		0.345	5.00	5.00	4.97
		0.636	5.03	5.02	4.93
		0.833	5.01	5.01	4.85
		1.000	4.92	4.92	4.76
16	32	0.063	5.05	5.05	5.05
		0.277	5.28	5.23	4.44
		0.574	5.23	5.14	3.56
		0.773	5.16	5.08	3.00
		1.000	4.89	4.86	2.47
	128	0.063	4.80	4.80	4.80
		0.277	5.25	5.24	5.04
		0.574	5.17	5.17	4.65
		0.773	5.19	5.19	4.50
		1.000	4.88	4.88	4.09

4.4. High dimension, low sample size one-sample comparisons

We conducted simulations for one-sample problems to compare the proposed tests with the test of Ahmad et al. [5], denoted as T_AWB. In our notation, Ahmad et al. [5] required a = 1 to define $T_{\text{AWB}}=\text{tr}({\mathit{S}}_h)/[\text{tr}({\mathit{Y}}_u^{\prime }{\mathit{Y}}_u)/N]$. Their chi-square approximation leads to (s₁/s₂)T_AWB ~ χ²(s₁/s₂) as {[N/(N − 1)] s_1/s2 T_AWB ~ χ² {[N/(N − 1)s₁/s₂]} with $s_1/s_2=[{\sum }_{i=1}^{N-1}{\sum }_{k=i+1}^N\left({\mathit{Y}}_{ui}^{\prime }{\mathit{Y}}_{ui}\right)\left({\mathit{Y}}_{uk}^{\prime }{\mathit{Y}}_{uk}\right)]/[{\sum }_{i=1}^{N-1}{\sum }_{k=i+1}^N{\left({\mathit{Y}}_{ui}^{\prime }{\mathit{Y}}_{uk}\right)}^2]$, and Y_ui the ith row of Y_u for i ∈ {1, … N}. Table VI lists empirical Type I error rates × 100 for targeted Type I error rates of α = 0.05 and α = 0.01. In general, T_AWB, which applies only to one-sample problems, had a good control of the Type I error rate except when both the sample size and ∊ are very small. Test T₁, coincided exactly with the ∊̃_r -adjusted tests for one-sample comparisons and kept the Type I error rates at or above the target except when ∊ = 1, whereas T₂ kept the Type I error rates at or below the target. With a very small sample, for example, N = 5 (ν_e = 4), T₂ could be rather conservative. The test-size accuracy of the new test T₁ improved as sample size increased regardless of the number of variables and the spread of population eigenvalues. With N > 9 (ν_e = 8), test T₂ was preferable if slight conservatism was in favor over liberalism in hypothesis testing.

Table VI.

High dimension, low sample size one-sample comparison: empirical Type I error rates × 100 for 100,000 replications.

b	νe	∊	Type I error rates × 100
			100 × α = 5.00			100 × α = 1.00
			T1	T2	TAWB	T1	T2	TAWB
64	4	0.016	5.04	5.04	3.57	1.02	1.02	0.00
		0.268	7.08	2.16	5.01	2.50	0.44	0.07
		0.560	6.29	1.87	5.00	1.91	0.34	0.17
		0.756	5.37	1.75	4.91	1.29	0.25	0.21
		1.000	4.07	1.43	4.82	0.79	0.19	0.20
	8	0.016	5.12	5.12	4.74	0.96	0.96	0.25
		0.268	5.91	4.66	5.21	1.72	1.11	0.86
		0.560	5.58	4.33	5.08	1.46	0.96	0.82
		0.756	5.30	4.14	4.98	1.20	0.81	0.79
		1.000	4.42	3.79	5.01	0.80	0.61	0.77
	16	0.016	4.97	4.97	4.89	1.03	1.03	0.69
		0.268	5.47	5.16	5.18	1.46	1.33	1.14
		0.560	5.43	5.08	5.19	1.26	1.10	1.02
		0.756	5.24	4.88	5.05	1.18	1.03	0.99
		1.000	4.79	4.59	5.08	0.90	0.85	0.95
256	4	0.004	4.98	4.98	3.50	1.03	1.03	0.00
		0.266	6.87	1.95	5.01	2.35	0.39	0.27
		0.557	6.21	1.74	4.99	1.81	0.31	0.31
		0.752	5.31	1.69	4.99	1.31	0.27	0.35
		1.000	4.10	1.49	4.97	0.77	0.20	0.35
	8	0.004	5.00	5.00	4.65	1.06	1.06	0.32
		0.266	5.77	4.43	5.22	1.52	0.96	0.89
		0.557	5.68	4.24	5.11	1.37	0.81	0.83
		0.752	5.20	4.01	4.94	1.27	0.80	0.87
		1.000	4.34	3.60	4.93	0.81	0.61	0.82
	16	0.004	5.02	5.02	4.92	1.02	1.02	0.66
		0.266	5.40	5.06	5.17	1.23	1.09	1.00
		0.557	5.21	4.85	5.02	1.17	1.02	1.00
		0.752	5.21	4.87	5.09	1.12	0.98	0.99
		1.000	4.60	4.41	4.95	0.90	0.82	0.94
1024	4	0.001	5.11	5.11	3.61	1.00	1.00	0.00
		0.265	6.89	1.82	5.05	2.29	0.34	0.36
		0.556	6.18	1.77	5.08	1.70	0.30	0.40
		0.750	5.28	1.57	5.05	1.35	0.28	0.44
		1.000	4.10	1.48	4.91	0.79	0.20	0.45
	8	0.001	5.02	5.02	4.64	1.00	1.00	0.28
		0.265	5.69	4.24	5.18	1.41	0.86	0.92
		0.556	5.52	4.15	5.06	1.35	0.86	0.92
		0.750	5.20	3.95	4.93	1.20	0.76	0.88
		1.000	4.41	3.67	5.03	0.78	0.58	0.86
	16	0.001	5.05	5.05	4.96	1.01	1.01	0.68
		0.265	5.23	4.86	5.10	1.15	1.03	1.02
		0.556	5.26	4.89	5.14	1.13	0.98	1.02
		0.750	5.05	4.69	4.95	1.09	0.96	0.97
		1.000	4.61	4.42	4.98	0.91	0.84	0.97

Test T_AWB was proposed by Ahmad et al. [5].

Table VII lists summary statistics of the ∊ estimators, ∊̃_D1, ∊̃_D2, and ∊̃_AWB, used in test T₁, T₂, and T_AWB, respectively. Ahmad et al. [5] defined ∊̃_AWB = [N/(N − 1)]s₁/(bs₂) to estimate the sphericity of population eigenvalues. The simulation design expanded simulations by Ahmad et al. [5] for compound symmetry (CS) and autoregressive (AR) hypothesis error covariance structure Σ_* with ν_e ∈ {4, 8, 16}, b ∈ {64, 256, 1024}, and ρ = 0.5 for CS, and ρ = 0.6 for AR. Overall, means of all three estimates were above the true ∊ regardless of the covariance structure and data dimensions; however, as sample size increased, biases decreased. In most cases, ∊̃_D2 gave the least biases except for AR covariance and ν_e ∈ {4, 8}. The fact that ∊̃_AWB has no adjustment for truncation for the upper and lower bounds of ∊ led to some improper values of ∊̃_AWB, which in turn might affect the performance of T_AWB.

Table VII.

High dimension, low sample size one-sample comparison: summary statistics of ∊ estimators for 100,000 replications.

b	νe	Σ*	∊	Estimator	Min	Max	Mean	Std
64	4	CS(0.5)	0.060	∊̃D1	0.022	1.000	0.172	0.195
				∊̃D2	0.016	1.000	0.078	0.104
				∊̃AWB	0.027	14.36	0.198	0.269
		AR(0.6)	0.477	∊̃D1	0.093	1.000	0.577	0.237
				∊̃D2	0.040	1.000	0.268	0.151
				∊̃AWB	0.115	11.12	0.762	0.435
	8	CS(0.5)	0.060	∊̃D1	0.022	1.000	0.102	0.083
				∊̃D2	0.019	1.000	0.085	0.070
				∊̃AWB	0.026	1.352	0.109	0.084
		AR(0.6)	0.477	∊̃D1	0.140	1.000	0.516	0.135
				∊̃D2	0.117	1.000	0.431	0.114
				∊̃AWB	0.182	1.770	0.579	0.152
	16	CS(0.5)	0.060	∊̃D1	0.027	0.815	0.077	0.035
				∊̃D2	0.026	0.779	0.073	0.034
				∊̃AWB	0.028	0.807	0.081	0.035
		AR(0.6)	0.477	∊̃D1	0.250	0.921	0.490	0.071
				∊̃D2	0.240	0.880	0.468	0.068
				∊̃AWB	0.261	0.983	0.520	0.075
256	4	CS(0.5)	0.015	∊̃D1	0.006	1.000	0.060	0.115
				∊̃D2	0.004	1.000	0.027	0.058
				∊̃AWB	0.007	6.162	0.063	0.129
		AR(0.6)	0.472	∊̃D1	0.102	1.000	0.564	0.236
				∊̃D2	0.044	1.000	0.261	0.149
				∊̃AWB	0.117	9.736	0.741	0.427
	8	CS(0.5)	0.015	∊̃D1	0.006	0.926	0.028	0.030
				∊̃D2	0.005	0.774	0.023	0.025
				∊̃AWB	0.007	0.997	0.030	0.029
		AR(0.6)	0.472	∊̃D1	0.167	1.000	0.503	0.128
				∊̃D2	0.139	1.000	0.420	0.108
				∊̃AWB	0.197	1.884	0.565	0.143
	16	CS(0.5)	0.015	∊̃D1	0.007	0.245	0.020	0.010
				∊̃D2	0.007	0.235	0.019	0.010
				∊̃AWB	0.008	0.274	0.021	0.010
		AR(0.6)	0.472	∊̃D1	0.269	1.000	0.481	0.062
				∊̃D2	0.257	0.979	0.460	0.060
				∊̃AWB	0.262	1.153	0.510	0.066
1024	4	CS(0.5)	0.004	∊̃D1	0.001	1.000	0.019	0.059
				∊̃D2	0.001	1.000	0.008	0.029
				∊̃AWB	0.002	6.925	0.018	0.059
		AR(0.6)	0.471	∊̃D1	0.081	1.000	0.561	0.236
				∊̃D2	0.035	1.000	0.260	0.150
				∊̃AWB	0.119	14.39	0.736	0.425
	8	CS(0.5)	0.004	∊̃D1	0.002	0.620	0.007	0.010
				∊̃D2	0.001	0.517	0.006	0.009
				∊̃AWB	0.002	0.414	0.008	0.009
		AR(0.6)	0.471	∊̃D1	0.176	1.000	0.500	0.126
				∊̃D2	0.147	1.000	0.418	0.106
				∊̃AWB	0.229	1.796	0.562	0.141
	16	CS(0.5)	0.004	∊̃D1	0.002	0.085	0.005	0.003
				∊̃D2	0.002	0.094	0.005	0.003
				∊̃AWB	0.002	0.089	0.005	0.003
		AR(0.6)	0.471	∊̃D1	0.273	0.851	0.479	0.060
				∊̃D2	0.261	0.813	0.457	0.058
				∊̃AWB	0.315	0.896	0.508	0.064

The estimator∊̃_D1 is used in T₁, ∊̃_D2 in T₂, and ∊̃_AWB in T_AWB.

4.5. High dimension, low sample size two-sample comparisons, Type I error, and power

We also simulated two-sample problems to compare the proposed tests with the tests of Srivastava and Fujikoshi [12] and Srivastava and Du [3]. The simulation assumed two groups of equal size. For t₁ = tr(S_e)/bν_e, $t_2=\left\{\text{tr}\left({\mathit{S}}_e^2\right)-\left[{\text{tr}}^2\left({\mathit{S}}_e\right)\right]/{\nu }_e\right\}/b({\nu }_e-1)({\nu }_e-2)$, and $t_3=t_1^2/t_2$, Srivastava and Fujikoshi [12] defined $T_{\text{SF}}={\left[{bt}_3/2a(1+a{\nu }_e^{-1})\right]}^{1/2}[\text{tr(}{\mathit{S}}_h\text{)}-{\mathit{abt}}_1]/{bt}_1$. If ν_e → ∞ and b → ∞, then T_SF follows a standard Gaussian distribution. Srivastava and Du [3] used the diagonal vector of Σ̂_*, ν = {〈Σ̂_* 〉 _j,j to define R = [Dg (ν)^−1/2 Σ̂_*Dg (ν) ^−1/2 and full rank Σ̂_*ν Dg (ν). If ν_e and b → ∞, then T_SD = t_*n/(2t_*d)^1/2 has an asymptotically standard Gaussian distribution with t_*d = (tr(R²) − b²/ν_e)(1 + tr(R²)/b^3/2, N₁ and N₂ are the sample sizes of the two groups, and $t_{\ast n}=\text{tr}(\widehat{\mathbf{\Theta }}{\widehat{\mathbf{\sum }}}_{\ast v}^{-1}{\widehat{\mathbf{\Theta }}}^{\prime })N_1{N}_2/(N_1+N_2)-b{\nu }_e/({\nu }_e-2)$.

Table VIII lists empirical Type I error rates × 100 for targeted Type I error rates of α = 0.05 and α = 0.01. In most cases, the two new tests T₁ and T₂ had better control of Type I error rate than the existing tests T_SF and T_SD, except for small samples leading to ν_e = 16 when compared with T_SF. Test T_SF consistently inflated the Type I error rates, whereas T_SD largely inflated the Type I error rates except when ν_e = 16 and b ∈ {256, 1024}. In general, the test-size accuracy of T_SF and T_SD improved as either the sample size or the number of variables increased, which reflected the asymptotic properties of the T_SF and T_SD approximations requiring both the sample size and number of variables to be large. Test T₂ always gave smaller Type I error rates than T₁, with the difference in performance diminishing as the sample size increased. When α = 0.01, T₂ gave better control of Type I error rate than T₁ in all cases except when sphericity (∊ = 1) was held. With sphericity, T₁ consistently outperformed T₂.

Table VIII.

High dimension, low sample size two-sample comparison: empirical Type I error rates × 100 for 100,000 replications.

b	νe	∊	Type I error rates × 100
			100 × α = 5.00				100 × α = 1.00
			T1	T2	TSF	TSD	T1	T2	TSF	TSD
64	4	0.016	4.91	4.91	12.49	42.08	0.98	0.98	9.48	28.56
		0.268	7.04	2.18	8.49	42.18	2.52	0.40	4.25	28.63
		0.560	6.23	1.90	8.32	41.96	1.84	0.39	3.62	28.41
		0.756	5.36	1.74	8.26	41.81	1.29	0.26	3.37	28.35
		1.000	4.07	1.49	8.13	42.12	0.73	0.18	3.18	28.63
	8	0.016	5.05	5.05	8.97	11.80	1.00	1.00	6.35	4.87
		0.268	5.99	4.70	6.09	11.81	1.74	1.14	2.80	4.91
		0.560	5.80	4.44	5.85	11.79	1.47	0.95	2.01	4.88
		0.756	5.35	4.20	5.72	11.73	1.26	0.85	1.82	4.80
		1.000	4.38	3.68	5.78	11.91	0.82	0.61	1.67	4.85
	16	0.016	5.07	5.07	7.14	5.81	1.06	1.06	4.73	1.68
		0.268	5.51	5.17	5.03	5.72	1.39	1.27	2.15	1.65
		0.560	5.43	5.06	5.06	5.72	1.24	1.10	1.62	1.70
		0.756	5.29	4.99	5.15	5.71	1.21	1.08	1.54	1.66
		1.000	4.76	4.60	5.25	5.74	0.92	0.85	1.35	1.68
256	4	0.004	5.00	5.00	9.68	36.91	0.99	0.99	6.27	24.28
		0.266	6.94	2.00	8.26	37.06	2.43	0.40	3.39	24.33
		0.557	6.02	1.72	8.11	36.94	1.73	0.31	3.05	24.34
		0.752	5.41	1.63	8.14	37.19	1.23	0.25	2.98	24.49
		1.000	4.08	1.53	8.23	37.18	0.77	0.19	3.09	24.42
	8	0.004	4.99	4.99	7.24	7.23	0.97	0.97	4.32	2.33
		0.266	5.66	4.32	5.82	7.23	1.49	0.95	1.86	2.36
		0.557	5.61	4.32	5.77	7.40	1.35	0.83	1.56	2.43
		0.752	5.43	4.13	5.85	7.35	1.26	0.83	1.63	2.39
		1.000	4.43	3.75	5.79	7.19	0.82	0.61	1.48	2.33
	16	0.004	4.93	4.93	5.94	3.49	0.94	0.94	3.26	0.70
		0.266	5.44	5.05	5.14	3.50	1.22	1.07	1.38	0.65
		0.557	5.19	4.84	5.05	3.49	1.14	1.00	1.21	0.66
		0.752	5.08	4.71	5.09	3.36	1.09	0.94	1.17	0.62
		1.000	4.66	4.46	5.16	3.43	0.89	0.82	1.14	0.63
1024	4	0.001	4.98	4.98	8.51	29.13	1.04	1.04	4.15	17.77
		0.265	6.81	1.81	8.19	28.88	2.31	0.36	3.04	17.62
		0.556	6.27	1.78	8.19	29.00	1.82	0.32	3.03	17.53
		0.750	5.32	1.60	8.18	29.04	1.28	0.26	2.96	17.63
		1.000	4.04	1.43	8.09	28.93	0.73	0.16	2.97	17.54
	8	0.001	4.90	4.90	5.87	2.61	0.92	0.92	2.53	0.55
		0.265	5.49	4.13	5.89	2.63	1.38	0.89	1.55	0.51
		0.556	5.57	4.24	5.96	2.63	1.39	0.85	1.51	0.55
		0.750	5.37	4.14	5.91	2.64	1.23	0.79	1.46	0.56
		1.000	4.37	3.62	5.76	2.54	0.80	0.60	1.43	0.50
	16	0.001	5.00	5.00	5.05	1.10	0.97	0.97	2.06	0.12
		0.265	5.35	5.00	5.18	1.01	1.17	1.02	1.17	0.11
		0.556	5.18	4.83	5.09	1.10	1.09	0.94	1.08	0.10
		0.750	5.23	4.89	5.25	1.15	1.12	1.00	1.17	0.12
		1.000	4.59	4.42	5.11	1.04	0.84	0.78	1.11	0.09

Test T_SF was given by Srivastava and Fujikoshi [12] and T_SD by Srivastava and Du [3].

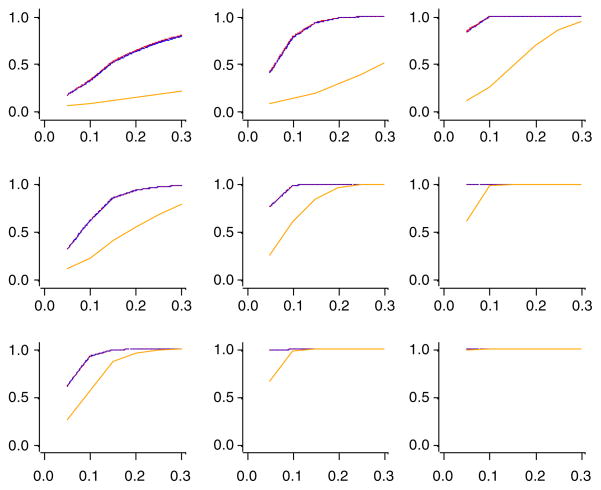
We also simulated data under the alternative hypothesis that a proportion of the variables with the largest variances have means greater than zero. Because statistical power is a function of Type I error rate, fair power comparisons between the new test and the existing test require adjustments for an equal control of the Type I error rate. At an α = 0.05 level, we sorted and computed the 95th percentile of the empirical p-values for each condition and test. Figure 2 summarizes the empirical powers based on controlling the Type I error rates to α. With the adjustments for equal Type I error rate control, the new tests T₁ and T₂ had very similar power patterns as the existing test T_SF, and all three clearly outperformed T_SD. The fact that T₁, T₂, and T_SF were derived from the UNIREP approach may be the key of their success. We note that despite the comparable power of T_SF, the inflation of the Type I error rate (Table VIII) as a result of the asymptotic Gaussian approximation makes T_SF less attractive in practice.

Figure 2.

High dimension, low sample size two-sample comparison. Empirical powers for 100,000 replications. Columns are (left to right) b = 64, b = 256, and b = 1024; rows are (top to bottom) ν_e = 4, ν_e = 8, and ν_e = 16. The vertical axes are empirical powers, and the horizontal axes are the proportions of non-null variables of the greatest variations. Purple denotes the test by Srivastava and Fujikoshi [12]; orange denotes the test by Srivastava and Du [3]; red denotes the proposed T₁ test; blue denotes the proposed T₂ test.

5. The vitamin B6 study

Although low vitamin B6 nutritional status increases risk for cardiovascular disease and stroke, the mechanism remains unknown. A study was conducted to assess the metabolic consequences of marginal deficiency of vitamin B6, a common status in the USA. After testing to verify nutritional adequacy for the major vitamins affecting one-carbon metabolism, 13 healthy participants consumed a diet low in vitamin B6 for 4 weeks to achieve marginal deficiency of vitamin B6. Blood samples and tracer infusion procedures were conducted before and after the vitamin B6 depletion. The data contained static concentrations of 19 amino acids, all measured in units of μmol/L. The goal was to identify metabolic features responsive to marginal deficiency of vitamin B6.

Missing data led to analyzing measurements from 12 subjects. We logarithmically transformed all 19 metabolic measures to meet the assumptions of Gaussian distribution and homogeneity between subjects and then computed pre–post differences. For a test of a zero difference in pre–post profile, test T₁ gave a p-value of p ≈ 2.7 × 10⁻⁸, and T₂ gave p ≈ 7.0 × 10⁻⁷, with both implying significant change in metabolic profile after vitamin B6 depletion at α = 0.05. The tests of Srivastava and Fujikoshi [12] and Srivastava and Du [3] also gave p-values of less than 10⁻⁷ supporting significant change. If univariate paired t -tests were used for each of the 19 measures, a Bonferroni correction requires a significance level of 0.05=19/0.0026 for each test. Only one measure achieves significance with the correction.

In addition to examining changes in metabolic profile after vitamin B6 depletion, scientists were also interested in knowing if metabolic changes as a whole were affected by the change in plasma pyridoxal 5′-phosphate (PLP) concentration, the indicator for vitamin B6 status. Vitamin B6 in the form of PLP acts as coenzyme in many pathways of amino acid metabolism. By incorporating PLP change as a covariate, test T₁ gave a p-value of 0.1393, T₂ gave 0.1492, and the test of Srivastava and Fujikoshi [12] gave 0.2489, all suggesting that changes in static measures after vitamin B6 depletion were not significantly associated with the PLP change.

A free SAS/IML® program LINMOD (visit http://www.health-outcomes-policy.ufl.edu/muller/) implements the new method and was used for the example analysis. The software supports a feature not available elsewhere that is needed for the example analysis, a UNIREP test of the MANOVA hypothesis (U = I_b). The example corresponds to a one-sample Hotelling’s T² test of the overall differences.

6. Discussion

When high-throughput technology generates data with more variables than subjects, the UNIREP approach becomes a natural choice for global hypothesis testing of repeated measures or commensurate data because it does not require inverting the sample covariance matrix. However, classical UNIREP tests fail to control the inflation of false positive inference (Type I error rate) in HDLSS settings except when all variation concentrates on one variable or spreads equally across all variables (sphericity) or when the study design involves only one between-subject factor.

We provided new analytic results. We proved that the invariance properties of UNIREP test remain true when the number of variables exceeds the sample size. We derived the exact distribution of the UNIREP test statistic with HDLSS. We also validated the use of the Box F approximation in calculations about the population. The invariance properties and the dual matrix allowed developing new and accurate test approximations, and greatly improved computational speed and accuracy for HDLSS.

We derived the new tests T₁ and T₂ from second-moment properties of the dual matrix. They outperform all existing tests in one of two ways. First, both tests provide (somewhat differently) control of the Type I error rate in any combination of finite variable dimension and sample size, with or without HDLSS. In contrast, existing methods available for some particular cases can have inflated Type I error rate when sample size is very small. After adjusting for the control of Type I error rate, the new tests have better statistical power than the existing tests, at least for the limited cases considered. Second, the new tests apply to all the special cases covered by the direct competitors. More generally, the new tests apply to any general linear multivariate hypothesis with more outcome variables than subjects, and fewer between-subject contrasts than subjects. Applications include one group pre-intervention and post-intervention comparisons, multiple parallel group comparisons with one-way or factorial designs, and the adjustment and evaluation of covariate effects. All existing tests we know of have sample size or hypothesis generality limits. We prefer test T₂ over test T₁ because it avoids being too liberal in controlling Type I error rate.

The current results open the door to extensions in future research. As described by Muller and Barton [15], random critical values, such as the ones used by T₁ and T₂, require special treatment in developing power and sample size methods. A more extensive simulation will allow in-depth investigation of the power properties of the new and existing tests.

Given an overall significant global test such as T₁ or T₂, step-down tests may be desired to identify individual variables that are important. The Type I error control of the traditional multiple comparison techniques from UNIREP methods, for example, Scheffé and Tukey techniques, should be inherited as long as the adjustments associated with the critical value have been determined by the new tests (T₂ and T₁). It will be interesting to compare step-down power with competitors developed for HDLSS, especially methods related to the false discovery rate [1].

Properties inherited from multivariate linear models ensure that the new tests provide analysis methods for a useful class of linear mixed models [16]. The relationship suggests that extensions to allow for missing data or time-varying covariates may be available with additional research.

Extending the approach to allow accurate inference with non-Gaussian data provides another direction for future work. In some cases, the Box–Cox transformation approach allows eliminating the problem. For example, metabolomic measures of concentration are typically log-normal. More generally, rank or permutation approaches may appeal as described by Bathke et al. [27].

APPENDIX A

Theorem 1

For the general linear multivariate model Y = XB + E, the following are true for b ≤ ν_e and b > ν_e (HDLSS). (i) Maximum likelihood estimation gives Θ̂ = CB̃U ~ 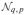(CBU, M, Σ_*) with B̃ = (X′X)⁻X′Y, M = C(X′X)⁻C′, and full rank M if rank(C) = a ≤ q = rank(X). (ii) With Σ̂ = Y′[I_N − X(X′X)⁻X′]Y and $\mathbf{\Omega }={(\mathbf{\Theta }-{\mathbf{\Theta }}_0)}^{\prime }{\mathit{M}}^{-1}(\mathbf{\Theta }-{\mathbf{\Theta }}_0){\mathbf{\sum }}_{\ast }^{-1}$, the hypothesis sum of square matrix S_h = (Θ̂ − Θ₀)′M⁻¹(Θ̂ − Θ₀) ~ ( 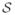) 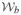(a, Σ_*, Ω) and the error sum of square matrix S_e = ν_eU′Σ̂U ~ ( 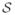) 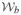(ν_e, Σ_*, 0) are mutually independent and Wishart distributed. (iii) If a ≥ b, then S_h is sample-nonsingular and otherwise sample-singular. If ν_e ≥ b, then S_e is sample-nonsingular and otherwise sample-singular.

Proof

(i) Assuming that E ~ 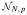(0, I_N, Σ) gives Y ~ 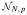(XB, I_N, Σ). For known and fixed X, B̃ = X′X)⁻X′Y implies that B̃ ~ ( 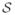) 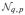[(X′X)⁻X′XB, (X′X)⁻, Σ] or B̂ ~ 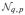[B, (X′X)⁻¹, Σ] for rank(X) = q. For full rank C and U, and C(X′X)⁻X′X = C, Θ̂ = CB̃U ~ 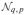(CBU, C(X′X)⁻C′, Σ_*. (ii) Without loss of generality, Θ₀ = 0 [2, Theorem 16.15]. Both S_h and S_e are multivariate Gaussian quadratic forms. For Y_u = YU ~ 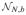(XBU, I_N, Σ_*), A_h = X(X′X)⁻C′M⁻¹C(X′X)⁻X′ and ${\mathit{S}}_h={\mathit{Y}}_u^{\prime }{\mathit{A}}_h{\mathit{Y}}_u$, and A_e = I_N − X(X′X)⁻X′ and ${\mathit{S}}_e={\mathit{Y}}_u^{\prime }{\mathit{A}}_e{\mathit{Y}}_u$. Linear model and quadratic form results guarantee idempotent A_h of rank a, idempotent A_e of rank ν_e, and A_hA_e = 0, which implies independence of multivariate Gaussian quadratic forms, for any rank of A_h and A_e [2, Theorem 10.8]. Idempotence and matrix Gaussian distributions give S_h ~ ( 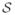) 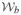(a, Σ_*, Ω₀) and S_e ~ ( 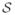) 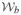( ν_e, Σ_*, 0) with ${\mathbf{\Omega }}_0={\mathbf{\Theta }}^{\prime }{\mathit{M}}^{-1}\mathbf{\Theta }{\mathbf{\sum }}_{\ast }^{-1}$. (iii) For full rank Σ_*, sample singularity occurs when the Wishart dimension exceeds the degrees of freedom.

Theorem 2

(i) The UNIREP test statistic t_u = [tr(S_h)/a]/[tr(S_e)/ν_e ] is invariant to orthonormal transformation of columns of U. (ii) The random components of the numerator and the denominator of t_u are independent weighted sums of independent chi-square random variables. Under the null hypothesis, for independent y_kh ~ χ²(a) and y_ke ~ χ²(ν_e), $\text{tr}({\mathit{S}}_h)={\sum }_{k=1}^b{\lambda }_k{y}_{kh}$, and $\text{tr}({\mathit{S}}_e)={\sum }_{k=1}^b{\lambda }_k{y}_{ke}$. (iii) The distribution function of t_u can be expressed exactly as

$$Pr\{t_u\le f_0\}=Pr\left\{{\sum }_{k=1}^b{\lambda }_k{y}_{kh}-\frac{f_{0}a}{{\nu }_e}{\sum }_{k=1}^b{\lambda }_k{y}_{ke}<0\right\}.$$ (3)

Proof

(i) For WW′ = I_b, replacing U by UW gives the statistic t_u* = [tr(W′S_hW)/a]/[tr(W′S_eW)/ν_e ] = [tr(S_hWW′)/a]/[tr(S_eWW′)/ν_e] = [tr(S_h)/a]/[tr(S_e)/ ν_e] = t_u. (ii) Matrices ${\mathit{S}}_h={\mathit{Y}}_u^{\prime }{\mathit{A}}_h{\mathit{Y}}_u$ and ${\mathit{S}}_e={\mathit{Y}}_u^{\prime }{\mathit{A}}_e{\mathit{Y}}_u$ are multivariate quadratic forms in matrix Gaussian Y_u = YU and follow Wishart distributions [2, Definitions 10.1 and 10.2]. As noted earlier, A_h = X(X′X)⁻C′M⁻¹C(X′X)⁻X′ and A_e =I_N − X(X′X)⁻X′ lead to A_hA_e = 0, which in turn give independence of S_h and S_e and imply independence of tr(S_h) and tr(S_e). For λ, the b × 1 vector of eigenvalues of full rank Σ_*, $\text{tr}({\mathit{S}}_h)={\sum }_{k=1}^b{\lambda }_k{y}_{kh}$ and $\text{tr}({\mathit{S}}_e)={\sum }_{k=1}^b{\lambda }_k{y}_{ke}$ with independent random variables y_kh ~ χ²(a, ω_kh) and y_k ~ χ²(ν_e), for ω_kh the kth diagonal element of $\mathbf{\Omega }={(\mathbf{\Theta }-{\mathbf{\Theta }}_0)}^{\prime }{\mathit{M}}^{-1}(\mathbf{\Theta }-{\mathbf{\Theta }}_0){\mathbf{\sum }}_{\ast }^{-1}$ [28]. Under the null hypothesis, y_kh ~ χ²(a). (iii) As in the study by Coffey and Muller [29],

$$\begin{array}{l}Pr\{t_u\le f_0\}=Pr\{[\text{tr}({\mathit{S}}_h)/a]/[\text{tr}({\mathit{S}}_e)/{\nu }_e]\le f_0\}\\ =Pr\{[\text{tr}({\mathit{S}}_h)-({af}_0/{\nu }_e)[\text{tr}({\mathit{S}}_e)]\le 0\}\\ =Pr\left\{{\sum }_{k=1}^b{\lambda }_k{y}_{kh}-({af}_0/{\nu }_e){\sum }_{k=1}^b{\lambda }_k{y}_{ke}<0\right\}.\end{array}$$ (4)

Corollary

Under the null, Satterthwaite’s approximation gives (i) tr(S_h)/tr(Σ_*) ~χ²(ab∊) and (ii) tr(S_e)/tr(Σ_*) ~ χ²(ν_e b_∊). (iii) In turn, Box [17, 18] approximation in Equation (1) applies, namely Pr {t_u ≤ f₀} ≈ Pr {F(ab∊, ν_e b∊) ≤ f₀}. (iv) The Box approximation exactly matches two moments of the numerator of t_u and two moments of the denominator of t_u [30]. Also, Equation (4) allows concluding that the approximation provides a two moment match to the generalized quadratic form $Q={\sum }_{k=1}^b{\lambda }_k{y}_{kh}-({af}_0/{\nu }_e){\sum }_{k=1}^b{\lambda }_k{y}_{ke}$ with Pr {t_u ≤ f₀} = Pr {Q ≤ 0}. Hence, the Box approximation is a second-order approximation for the corresponding characteristic function (and therefore distribution function).

Theorem 3

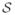
(i) The dual matrix is a weighted sum of identically and independently distributed Wishart random matrices, namely ${\mathit{S}}_d={\sum }_{k=1}^b{\lambda }_k{\mathit{W}}_k$ with mutually independent W_k ~ 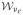(1, I_νe) and {λ_k} eigenvalues of Σ_*. (ii) $\text{E}({\mathit{S}}_d)={\sum }_{k=1}^b{\lambda }_k{\mathit{I}}_{{\nu }_e}$. (iii) The common variance of diagonal elements is $2{\sum }_{k=1}^b{\lambda }_k^2$, and the common variance of off-diagonal elements is ${\sum }_{k=1}^b{\lambda }_k^2$. (iv) An unbiased estimator of ${\tau }_2={\sum }_{k=1}^b{\lambda }_k^2$ gives ${\widehat{\tau }}_2=\left[{\nu }_e\text{tr}({\mathit{S}}_d^2)-{\text{tr}}^2({\mathit{S}}_d)\right]/\left[{\nu }_e({\nu }_e^2+{\nu }_e-2)\right]$. (v) An unbiased estimator of ${\tau }_1={\left({\sum }_{k=1}^b{\lambda }_k\right)}^2$ gives ${\widehat{\tau }}_1=\left[({\nu }_e+1){\text{tr}}^2({\mathit{S}}_d)-2\text{tr}({\mathit{S}}_d^2)\right]/{\nu }_e({\nu }_e^2+{\nu }_e-2)$.

Proof

(i) For spectral decomposition Σ_* = ϒDg (λ) ϒ′ with ϒ′ϒ = I_b, it follows that ${\mathit{L}}_0^{\prime }{\mathit{Y}}_u{\mathbf{\Upsilon }}^{\prime }~{\mathcal{N}}_{{\nu }_e,b}[\mathbf{0},{\mathit{I}}_{{\nu }_e},\text{Dg}(\mathit{\lambda })]$. In turn, Z ~ 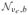(0,I_νe, I_b)has identically and independently distributed columns, 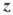_k ~ 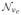(0, I_νe) and independent ${\mathit{W}}_k={\mathit{z}}_k{\mathit{z}}_k^{\prime }~\mathcal{S}{\mathcal{W}}_{{\nu }_e}(1,{\mathit{I}}_{{\nu }_e})$. Also, ${\mathit{S}}_d={\mathit{Y}}_0{\mathit{Y}}_0^{\prime }={\mathit{L}}_0^{\prime }{\mathit{Y}}_u{\mathbf{\Upsilon }}^{\prime }{({\mathit{L}}_0^{\prime }{\mathit{Y}}_u{\mathbf{\Upsilon }}^{\prime })}^{\prime }=\mathit{Z}\text{D}g(\mathit{\lambda }){\mathit{Z}}^{\prime }={\sum }_{k=1}^b{\lambda }_k{\mathit{z}}_k{\mathit{z}}_k^{\prime }={\sum }_{k=1}^b{\lambda }_k{\mathit{W}}_k$, E(W_k) = I_νe, 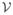(〈W_k〉) _j1j2 = 2 if j₁ = j₂ and 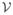(〈W_k〉_j1j2) = 1 if j₁ ≠ j₂. (ii) $\text{E}({\mathit{S}}_d)={\sum }_{k=1}^b{\lambda }_k\text{E}({\mathit{W}}_k)=({\sum }_{k=1}^b{\lambda }_k){\mathit{I}}_{{\nu }_e}$. (iii) $\mathcal{V}({\langle {\mathit{S}}_d\rangle }_{j_1{j}_2})=\left({\sum }_{k=1}^b{\lambda }_k^2\right)\mathcal{V}({\langle {\mathit{W}}_k\rangle }_{j_1{j}_2})$. If j₁ = j₂, then $\mathcal{V}({\langle {\mathit{S}}_d\rangle }_{j_1{j}_2})=2{\sum }_{k=1}^b{\lambda }_k^2$, and j₁ ≠ j₂ gives $\mathcal{V}({\langle {\mathit{S}}_d\rangle }_{j_1{j}_2})={\sum }_{k=1}^b{\lambda }_k^2$. (iv) Matching second moments of S_d allowed deriving τ̂₂ as a weighted sum of two estimators. If τ̂_2a is 1/2 times the estimated variance of the diagonal elements, namely ${\widehat{\tau }}_{2a}=\left\{{\sum }_{j=1}^{{\nu }_e}{({\langle {\mathit{S}}_d\rangle }_{jj})}^2-{\nu }_e{[\text{tr}({\mathit{S}}_d)/{\nu }_e]}^2\right\}/[2({\nu }_e-1)]$, and τ̂_2b is the sample mean of off-diagonal variances, namely ${\widehat{\tau }}_{2b}=\left\{{\sum }_{j=2}^{{\nu }_e}{\sum }_{j^{\prime }=1}^{{\nu }_e-1}{({\langle S_d\rangle }_{{jj}^{\prime }})}^2\right\}/[{\nu }_e({\nu }_e-1)/2]$, then ${\widehat{\tau }}_2=\left[{\nu }_e\text{tr}({\mathit{S}}_d^2)-{\text{tr}}^2({\mathit{S}}_d)\right]/\left[{\nu }_e({\nu }_e^2+{\nu }_e-2)\right]$. It is straightforward to prove that E (τ̂₂) = τ₂ based on results in Appendix A of Muller et al. [16] that $\text{E}\left[\text{tr(}{\mathit{S}}_e^2\text{)}\right]={\nu }_e({\nu }_e+1){\tau }_2+{\nu }_e{\tau }_1=\text{E}\left[\text{tr(}{\mathit{S}}_d^2\text{)}\right]$ and $\text{E}\left[{\text{tr}}^2({\mathit{S}}_e)\right]=2{\nu }_e{\tau }_2+{\nu }_e^2{\tau }_1=\text{E}\left[{\text{tr}}^2({\mathit{S}}_d)\right]$. (v) Given $\text{E}\left[{\text{tr}}^2({\mathit{S}}_d)\right]=2{\nu }_e{\tau }_2+{\nu }_e^2{\tau }_1$ and E(τ̂₂) = τ₂, an unbiased estimator of τ₁ is ${\widehat{\tau }}_1=\left[{\text{tr}}^2({\mathit{S}}_d)-2{\nu }_e{\widehat{\tau }}_2\right]/{\nu }_e^2=\left[({\nu }_e+1){\text{tr}}^2({\mathit{S}}_d)-2\text{tr}({\mathit{S}}_d^2)\right]/{\nu }_e({\nu }_e^2+{\nu }_e-2)$.