Avoiding bias in mixed model inference for fixed effects

Abstract

Analysis of a large longitudinal study of children motivated our work. The results illustrate how accurate inference for fixed effects in a general linear mixed model depends on the covariance model selected for the data. Simulation studies have revealed biased inference for the fixed effects with an underspecified covariance structure, at least in small samples. One underspecification common for longitudinal data assumes a simple random intercept and conditional independence of the within-subject errors (i.e., compound symmetry). We prove that the underspecification creates bias in both small and large samples, indicating that recruiting more participants will not alleviate inflation of the Type I error rate associated with fixed effect inference. Enumerations and simulations help quantify the bias and evaluate strategies for avoiding it. When practical, backwards selection of the covariance model, starting with an unstructured pattern, provides the best protection. Tutorial papers can guide the reader in minimizing the chances of falling into the often spurious software trap of nonconvergence. In some cases, the logic of the study design and the scientific context may support a structured pattern, such as an autoregressive structure. The sandwich estimator provides a valid alternative in sufficiently large samples. Authors reporting mixed-model analyses should note possible biases in fixed effects inference because of the following: (i) the covariance model selection process; (ii) the specific covariance model chosen; or (iii) the test approximation.

1. Introduction

1.1. Motivation

The Context

The general linear mixed model has become a standard tool for modeling correlated continuous data from longitudinal and clustered sampling. The stacked-data structure creates parallels with univariate linear regression. The arrangement allows simple interpretation of mean values, which has helped make it popular with researchers with limited statistical background, as well as statisticians working with them.

The Problem

The flexibility of the general linear mixed model has created a false sense of security about robustness to covariance misspecification and assumption diagnostics, particularly in large samples. We demonstrate that underfitting the covariance structure for the responses can optimistically bias inference about fixed effects. Furthermore, the amount of bias remains unchanged as the number of subjects increases to infinity. Analytic, simulation, and enumeration results quantify the amount of bias in small and large samples.

The Solution

Good statistical practice can avoid or solve the problem. Conscientious application of existing tools gives a dependable strategy for selecting, verifying, and reporting a covariance model giving accurate inference about fixed effects in small and large samples. Analysis of a large longitudinal study of child care highlights the importance of the strategy, even in large samples.

1.2. Asthma in childhood

Asthma affects more than nine million American children 0-17 years old [1]. In a cross-sectional study, Blackman and Gurka [2] found that children with severe asthma were more than four times more likely to have chronic developmental and behavioral problems of various sorts, including depression or anxiety and conduct problems. However, the cross-sectional sampling plan limits the value of the results.

In contrast, a longitudinal design lies at the heart of the Study of Early Child Care and Youth Development (SECCYD) [3]. The SECCYD followed up children from 10 US sites from birth through age 15 years. Families were recruited during hospital visits following the birth of the child in 1991. A total of 1364 families enrolled from the 8986 eligible births. By phase IV (2005-2008; age 14-15 years), 1056 families remained enrolled. The repeated collection of standard psychometric measures throughout childhood provided a unique opportunity to examine the role of chronic asthma in the development of a child. Interest lay solely in fixed effects inference: does the average longitudinal profile for children with asthma differ from the profile for those without? Although selection of the covariance model was secondary, the choice was found to be vital in making correct decisions for the primary aim.

2. Previous research and current views

The linear mixed model is composed of fixed effects, random effects, and a residual error. In medical research, the first component is typically of interest, whereas the latter two components comprise the covariance portion of the model. There are no fully reliable ways to identify the best covariance model, at least in small samples [4]. Verbeke and Molenberghs [5, pp. 125-127] noted that it is common to include random intercepts and additional random effects only for time-varying covariates. They then presented a set of guidelines for the inclusion of additional random effects, noting that they ‘favor the inclusion of too many random effects rather than omitting some’ (p. 127). However, they also noted that inclusion of too many random effects may lead to nonconvergence.

In practice, limitations of current software and user behaviors, magnified in small sample settings or in the presence of missing data, make nonconvergence common. Many analysts interpret a model failing to converge as empowering them to simplify the model, whether it be through the fixed effects or the covariance model. A more parsimonious fixed effect structure may be an effective remedy for nonconvergence, particularly in the presence of a small number of subjects and/or a limited number of repeated measures (in the case of time-varying covariates). In the context of covariance model selection, the press of time and a belief in the robustness of the mixed model with respect to fixed effects inference encourage this approach.

Some authors have considered covariance misspecification for tests about means, that is, fixed effects in mixed models. Liang and Zeger [6] proposed the ‘sandwich’ estimator for $\nu \left(\widehat{\beta }\right)$ in seeking inference about the fixed effects robust to misspecified covariance. Verbeke and Molenberghs [5, p. 62] noted the following: (i) the sandwich estimator is less efficient than the one using the correct covariance model; and (ii) valid inference requires additional assumptions about the missing data. In addition, the sandwich estimator has not been fully evaluated in small samples.

Another approach to covariance misspecification has been to ask whether underfitting can allow valid inference. Jacqmin-Gadda et al. [7] demonstrated an inflated type I error rate with covariance misspecification in simulations in the general linear mixed model with Gaussian errors. For some special cases with complete and balanced Gaussian data, Lange and Laird [8] proved that ‘fitting a parsimonious covariance structure need not give inappropriate variance estimates, even if the parsimonious structure is inadequate.’ They demonstrated in the special cases considered that inclusion of both a random intercept and slope is conservative in that the variance estimates of the fixed intercept and slope will not be biased downward. The theory and simulations in the present paper expand on their discussion, specifically providing evidence against the use of the compound symmetry assumption in general longitudinal settings.

Scientists in a variety of health and social science settings often assume compound symmetry for the covariance model of longitudinal responses. Some do so by fitting a random-intercept-only mixed model and assuming residual error covariance is diagonal with homogeneous variances [9, 10], whereas others use the uncorrected univariate approach to repeated measures (UNIREP) test [11, 12]. The unadjusted UNIREP test assumes compound symmetry. Muller and Stewart [13], among many others, have provided further discussion of the UNIREP approach. In addition, convergence failure leads some data analysts to remove additional random effects and retain only a random intercept (and implicitly assume compoundsymmetry of the responses). Scientists often assume compound symmetry to simplify a power analysis for the design of a longitudinal study. Some free software for planning repeated measures studies use compound symmetry exclusively [14].

Despite the widespread use of a compound symmetric (CS) covariance model for longitudinal responses, little evidence can be marshaled to defend the approach. Equally important, many authors studying the UNIREP approach, dating back to Box [15, 16], have demonstrated inflated type I error when falsely assuming compound symmetry. We present analytic and numerical evidence to demonstrate that underspecification of the covariance model can lead to very inaccurate fixed effect inference in a mixed model because of an inflated type I error rate and suggest ways to ensure accurate inference.

3. Analytic results

3.1. Notation

We use the notation in Chapters 3-5 of Muller and Stewart [13]. Subscripts have been added as needed to distinguish distinct expressions, which play parallel roles in distinct model formulations, with M for multivariate and m for mixed models. All results assume Gaussian errors and testable hypotheses (estimable secondary parameters with full-rank contrast matrices). The linear mixed model, that in the form which Laird and Ware [17] described, may be written in the notation of Muller and Stewart [13, Chapter 5] as follows:

$$y_i=X_i\beta +Z_i{d}_i+e_i.$$ (1)

Here, i ∈ {1,…, N }, for N the number of independent sampling units (usually subjects) y_i is a p_i × 1 vector of observations on person i; X_i is a p_i ×q known design matrix for person i, whereas β is a q×1 vector of unknown population parameters. Also, Z_i is a p_i×m known design matrix for person i corresponding to the m×1 vector of unknown random effects d_i, whereas e_i is a p_i×1 vector of unknown residual errors. The vectors d_i and e_i are Gaussian and independent with mean 0 and covariance matrices Σ_di (τ_d) and Σ_ei (τ_e), respectively. In turn, $\nu \left(y_i\right)={\sum }_i=Z_i{\sum }_{di}\left({\tau }_d\right)Z_i^{\prime }+{\sum }_{ei}\left({\tau }_e\right)$ is characterized by the finite set of parameters in the r×1 vector τ containing the unique parameters in τ_d and τ_e.

A focus on inference about ‘fixed’ effects, the mean response values, has led others to consider the ‘population average’ model,

$$y_i=X_i\beta +e_{+i}$$ (2)

where e_+i = Z_id_i + e_i. Formulation (1) allows conveniently specifying latent random intercepts, slopes, and others, which implies a covariance model for the responses. In contrast, formulation (2) allows directly specifying the response covariance model, which in some cases implies the latent random components. A functional mapping from random effects to a covariance structure always exists. However, the mapping need not be unique.

Clustered data arising from schools, hospitals, and others usually generate CS data. Such observations have a common variance and a common correlation for any pair. Cluster i has p_i observations. The same covariance structure arises by specifying the following: (i) a random intercept as the only random effect, so Z_i=1_pi and d_i is 1×1, a scalar; and (ii) ${\sum }_{ei}\left({\tau }_e\right)={\sigma }_e^2{I}_{pi}$ (a conditional independence assumption for within-subject residual). The responses have

$$\nu \left(y_i\right)={\sum }_i=1_{pi}{\sigma }_d^2{1}_{pi}^{\prime }+{\sigma }_e^2{I}_{pi}.$$ (3)

For intraclass correlation coefficient ρ between observation j and j’, the model implies $\nu \left(y_{ij}\right)={\sigma }_d^2+{\sigma }_e^2={\sigma }^2$ and ${\sigma }_d^2={\sigma }^2\rho$. Having ${\sigma }_d^2\ge 0$ requires ρ ≥ 0, whereas −1/ (p_i – 1) < ρ suffices for compound symmetry. The matrix ν (y_i) has a largest eigenvalue of λ_1iD=σ² [1+(p_i – 1) ρ] with eigenvector p_i^−1/2p_i, whereas all other p_i –1 eigenvalues are λ₂=σ² (1 – ρ). Typically, cluster designs are discussed in terms of {γ²;ρ} [18] rather than the equivalent pair {λ_1i ;λ₂}.

3.2. A useful class of mixed models

We restrict attention to tests of fixed effects in the general linear mixed model with Gaussian errors. In this section and the next, we will prove the following statement:

Proposition 1 Inference for fixed effects in the general linear mixed model is not robust to covariance misspecification

Specifically, we prove that falsely assuming compound symmetry, which ignores heterogeneity within subject, creates biased tests and confidence intervals for data with no missing values (complete and balanced). The result holds in small and also in asymptotically large samples. The often-used assumption of compound symmetry serves as a logical counterexample that allows us to make the previously mentioned claim.

To prove and enumerate the impact of under fitting the covariance model on tests of fixed effects, we focus on a restricted class of models, which allows finding closed-form and small-sample (exact) answers. Hence, our proof centers on the following: (i) mixed models, which can be stated as a multivariate model; and (ii) hypotheses, which can be stated as a general linear multivariate hypothesis. The multivariate model corresponds to the ‘population average’ model formulation in Equation (2), which has no explicitly defined random effects. This multivariate model, as Muller and Stewart [13, Chapter 3] defined, has restrictions that demand a design with complete balance within subjects, with no missing or mistimed data and no repeated covariates. An unstructured covariance matrix will be assumed to be the correct model for the responses.

Muller and Stewart [13, Table 6.5, Table 6.6, Section 12.1, and especially Equation 12.5] described how to state any multivariate model as a general linear mixed model. As traditionally written, the multivariate model Y =X_MB+E describes N rows of independent sampling units (subjects) and p columns of repeated measures. Here, B is a q×p matrix of parameters with rows corresponding to between-subject effects and columns (time indicator) to within-subject (time) effects. By describing only the data for subject i and therefore row i in the multivariate model gives 1×p matrix Y_i = X_{M i} B + E_i, with Y_i = row_i (Y) and X_Mi = row_i (X_M), whereas E_i = row_i (E). The equivalent mixed model form arises as

$$\begin{array}{cc}\hfill \text{vec}\left(Y_i\right)& =\text{vec}\left[{\left(X_{Mi}B\right)}^{\prime }\right]+\text{vec}\left(E_i\right)\hfill \\ \hfill & =(X_{Mi}\otimes I_p)\text{vec}\left(B^{\prime }\right)+\text{vec}\left(E_i\right)\hfill \\ \hfill y_i& =X_{mi}\beta +e_{+i},\hfill \end{array}$$ (4)

which is the population average model with n = N · p observations, and ⊗ is the Kronecker product. The error term can be interpreted as e_{+ i} = Z_id_i + e_i . For example, if Z_i =1_pi and elements of the residual ei are independent and identically distributed (i.i.d.), then ν (y_i) will be CS.

For inference about population means (i.e., fixed effects), the parameter matrix of mean differences for the multivariate model is Θ =C_MBU with hypothesis H₀ : C_MBU = Θ₀. Transforming to the mixed model creates vector θ = C_mβ=vec (Θ)=(C_m ⊗ U’)vec(B’). The multivariate matrix C_M defines contrasts between groups. The multivariate matrix U defines contrasts within an independent sampling unit (such as person) across level of response (such as time). The mixed model contrast matrix C_m does the work of both C_M and U.

3.3. Incorrectly assuming compound symmetry; ignoring heterogeneity within subject

A test of all time trends from linear through p–1 for p repeated measures will illustrate the analytic and simulation results, which actually cover a wider class of situations. Stacking all of the data together as y_s=[y’₁ … y’_i … y’_N]’ and X_s=[X’₁ … X’_i … X’_N]’ allows writing y_s=X_sβ+e_+s and provides a convenient form for the Wald statistic in the mixed model:

$$F_m={(\widehat{\theta }-{\theta }_0)}^{\prime }{\left[C_m{\left(X_s^{\prime }{\widehat{\sum }}_s^{-1}{X}_s\right)}^{-1}{C}_m^{\prime }\right]}^{-1}(\widehat{\theta }-{\theta }_0)∕a_m,$$ (5)

with a_m = rank(C_m) and ${\widehat{\Sigma }}_s=\widehat{\nu }\left(y_s\right)$. A mixed model corresponding to a multivariate model has C_m = (U’ ⊗ C_M and $\widehat{\theta }=\text{vec}\left(\widehat{ϴ}\right)=(U^{\prime }\otimes C_M)\text{vec}\left(\widehat{B}\right)$. Kenward and Roger [16] mentioned that in such models, F_m is a 1−1 function of the Hotelling–Lawley statistic in the multivariate model. The exact distribution of F_m when falsely assuming compound symmetry for a multivariate equivalent model may be derived as outlined in Appendix A. Assuming compound symmetry in the mixed model further reduces the statistic to the original UNIREP statistic. The following theorem and corollary summarize the most important conclusions that can be deduced.

Theorem 1

An interesting class of general linear mixed models have the following: (i) complete and balanced Gaussian data; (ii) a common (finite and full rank) population covariance matrix for each independent sampling unit (e.g., subject); and (iii) no time-varying covariates. Assuming CS covariance of the responses for any such model leads to a simple closed-form expression for the Wald statistic from a test of fixed effects. Algorithms for computing the distribution function of quadratic forms allows exact calculation of test size and power.

Proof

Appendix A contains an explicit derivation of easily computed expressions for the distribution function of the test statistic in small and asymptotic samples.

Corollary 1

Incorrectly assuming compound symmetry among responses inflates type I error rate for Wald tests of fixed effects in a general linear mixed model for small or large samples.

Proof

Finite and infinite large-sample examples in the exact calculations in the following text (Section 3.4) prove the corollary by giving counterexamples to the implicit claim of guaranteed correct test size.

An abundance of results [15, 16, 19, 20] make it clear that the uncorrected UNIREP test can badly inflate type I error rate in small samples. The same test arises in the general linear mixed model whenever compound symmetry has been assumed but does not hold. The between-within approach for mixed models (sas (SAS Institute Inc., Cary, NC, USA) PROC MIXED) [21] provides one direct path. However, all other mixed model test choices (such as containment, residual, Satterthwaite, and Kenward–Roger in sas) will also inflate type I error rate because of the assumption error. The proof contains results that show that type I error inflation remains just as high as N → ∞.

3.4. Exact calculations

Exact calculations illustrate the bias described in the corollary for each combination of N ∈{50, 100, ∞} and p ∈ {5; 10}, based on models that assumed two groups with a mean model including only intercept, time (linear), group, and group time (linear), so X_i had rank 4. The p_i time points were equally spaced from 0 to 1.

Using the same mean model structure, four covariance models were considered true. They may be summarized as covariance model: random effects and within-unit residual error, namely

1. 1,IID: random intercept and i.i.d. within-unit residual (i.e., compound symmetry);

2. 1,AR: random intercept and a first-order AR(1), autoregressive within-subject residual;

3. 2,IID: random intercept and slope, with an i.i.d. within-unit residual; and

4. 2,AR: random intercept and slope (correlated = 0.25) with an AR(1) within-unit residual.

Population variances of the random intercept and slope (when included) were 2 and 1, respectively. The within-unit residual variance was 1 with an AR(1) correlation of 0.25 when included.

Enumerations used the _QPROB module from the free software powerlib [22]. Kim et al. [23] described the _QPROB algorithm (because of Davies [24]). Exact asymptotic calculations used the sas chi-square function. We calculated the type I error rate for testing the fixed effect of group time (linear) interaction (i.e., the group difference in slopes) when assuming compound symmetry.

Correctly assuming compound symmetry (1,IID) gives the correct type I error rate of 5%. When p = 5, incorrectly assuming compound symmetry gives a type I error rate of 9.0% when the true covariance was (1, AR). Type I error rate increases to 9.8% and 13.7% when the true covariance also contains a random slope: (2,IID) and (2,AR), respectively. When p = 10, the type I error rate rises to 14.5% and 19.7% when assuming compound symmetry, and the true covariance is (2,IID) and (2,AR), respectively. The exact Type I error rates for p ∈ {5, 10} were equal (to three digits of accuracy) for N ∈50; 100;∞}. The proof requires no missing data (to take advantage of simplifications in the theory for multivariate models). Obviously, complete and balanced data rarely occur in some applications, such as clinical trials. However, the simulations (Section 4) support the general proposition that with or without missing data, incorrectly assuming compound symmetry inflates type I error rate in the general linear mixed model.

For the sake of brevity, parallel results about ignoring heterogeneity between subjects, as distinct from ignoring heterogeneity within subjects, have been omitted. Key features are well-known from the study of univariate linear models: heterogeneity between subjects strongly interacts with unequal cell sizes to inflate type I error rate for three or more groups in ANOVA [25]. The mixed model inherits the same vulnerability. However, a knowledgeable and conscientious analyst can directly model such heterogeneity in a mixed model formulation.

4. Simulation study

We have proved that incorrectly assuming compound symmetry leads to inflated type I error rates, with complete and balanced data. Simulations extend the results to missing data. All simulations used sas/iml, PROC MIXED, and the DATA step. The normal function generated pseudorandom Gaussian values. The exact conditions presented in Section 3.4 were replicated for the simulations. We generated 10,000 pseudorandom samples for each {N; p_i} ∈ {{50, 5}, {50, 10}, {100, 5}, {100; 10}}, with each subject having p_i time points equally spaced from 0 to 1. With α = 0.05, the 10,000 pseudorandom samples give a confidence region for the estimated type I error rate of $\widehat{\alpha }\in [0.0498,0.0502]$. In practice, the acceptability of a particular type I error rate will vary with the preferences of the reader. A total of 20% of the data were set to missing by pseudorandom deletion within person (uniform sampling without replacement).

We calculated the type I error rate for testing the fixed effect of Group×Time (Linear) interaction (i.e., the group difference in slopes). For each of the four true population covariance structures (listed in Section 3.4), we tabulated type I error rates when fitting the same four distinct covariance models, in addition to fitting an unstructured covariance. We employed restricted maximum likelihood (REML) estimation with the Kenward–Roger approach [26] for all five cases. We also tabulated the type I error rate when assuming compound symmetry with the sandwich estimator, which required the containment method [21] because the Kenward–Roger approach does not apply.

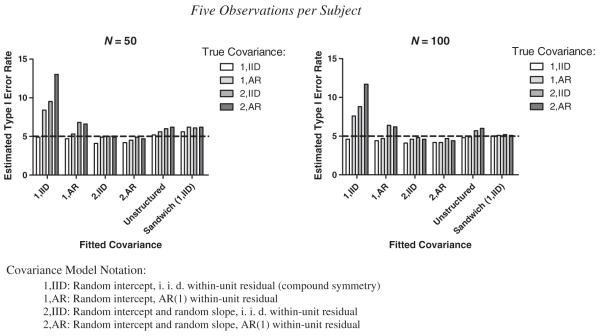
Figure 1 presents empirical type I error rates for the simulations with p_i = 5 observations per subject. Results from the simulations with {N; p_i } ∈ {{50, 10} ; {100, 10}} were similar and are not shown. The results illustrate the generality of the theorem and the substantial bias that can occur. Even with a correctly specified covariance model, observed type I error rate has some modest bias for smaller sample sizes, especially when the true models include, an AR(1) within-unit error covariance. The (true) (1,AR) model has a 5.3% type I error rate when correct, and the (true) (2,AR) model has a 4.7% type I error rate when correct, for N = 50. As expected, moderate to severe bias in type I error rate can occur when incorrectly assuming compound symmetry, with type I error rates no smaller than 7.6% for any of the other examined true covariance models. The bias remains substantial even when the number of subjects increases from 50 to 100.

Figure 1.

Observed type I error rate (×100) of fixed effect interaction for α = 0:05. Four true covariance models, 20% missing completely at random, 10,000 replications per condition*.

*Except in the sandwich cases, we performed inference using the Kenward-Roger approach.

It is important to note what works in the absence of reliable covariance model identification techniques. Not surprisingly, if the covariance model chosen contained the true model as a special case, or differed only modestly from the true model, then type I error rate was roughly correct. For example, the random intercept and slope (i.i.d. error) covariance model that Lange and Laird [8] considered controlled type I error rate for the four simple models considered, with a small conservative bias when the true model is indeed compound symmetry (4.1% and 4.2% when N = 50 and N = 100, respectively). Our results imply that it would be a simple exercise to find other covariance patterns for which the choice fails to control type I error rate. Fitting an unstructured covariance model always gives a safe choice when focused on inference about fixed effects, if one is willing to accept a type I error rate no greater than about 6%. It is clear that the unstructured covariance model is over-fitting data generated from a model with at most two random effects. As many practitioners know, estimating an unstructured covariance can create convergence problems, especially as the number of observations per subject increases or the number of independent observations decreases. For example, with N 100 and p 10 (results not shown), convergence for the unstructured model was achieved only 61% ofDthe time. Among the models that converged, type I error rates were inflated, no matter what the underlying true model was. For the sample sizes considered, using the sandwich estimator improved inference no matter what covariance model was assumed, without the convergence problems. However, bias similar to what was observed for the unstructured model remains, particularly for small samples.

5. Application to the Study of Early Child Care and Youth Development asthma data

Modeling behavioral outcomes over time in the SECCYD data further illustrate the analytical and numerical results. Specifically, assuming CS errors or equivalently including only a random intercept with conditional independence of within-subject error leads to different inferences than for more general covariance models. Both look plausible, although both cannot be correct because they disagree. The analytic and simulation results suggest that the results for the complex covariance model are the correct ones.

Developmental measures collected in the SECCYD allow comparing children with and without various phenotypes of asthma. The primary outcome was the Child Behavior Checklist (CBCL) [27]. The CBCL measures social competence as well as externalizing and internalizing behavior problems. The parent completed age-specific versions of the CBCL, standardized as a ‘T-score’ (mean = 50, SD = 10), at age 36 and 54 months, as well as during grades 1, 3, 4, 5, and 6, and at age 15 years. Higher scores indicate more problematic behavior, with T-scores greater than 70 considered as clinically relevant.

We compared internalizing behavior trends between those who developed asthma early (by age 4 years) and those who never developed asthma. Asthma status could be classified for 795 children: 58 children had asthma, whereas 737 did not. Linear, through cubic orthogonal polynomial trends for time, were initially included as predictors, as well as all corresponding interactions, with the interactions of age with asthma status of particular interest. Covariates included sex, maternal age at birth, the mean maternal depression score during years 0-3, the mean home environment score (higher indicating better) during years 0-3, and the mean child care quality score during years 0-3 (higher indicating better). Initially, compound symmetry was assumed. A backward stepwise selection procedure was performed for the fixed effects by removing the least-significant higher-order interactions one by one until only significant interactions (and/or main effects) remained. Table I displays the estimates and the p-values for the final fixed effects model of internalizing CBCL T-scores when assuming compound symmetry. In addition, estimates were calculated for the final (fixed effect) model using two additional covariance models: (i) unstructured; and (ii) random intercept and slope with an AR(1) within-unit error. The sandwich estimator (with containment) assuming compound symmetry was also applied. With respect to the recommendation of Verbeke and Molenberghs [5, Section 2.3], we fitted additional models not shown here. Given the consistency of these other models, we did not display results from these others, including one with random effects through cubic age. Table I also displays the corresponding fixed effects estimates and the p-values for these other covariance models.

Table I.

Study of Early Child Care and Youth Development final model results of child behavior checklist internalizing T-scores; 795 children (58 with asthma by age 4 years) followed up from 3–15 years old

	Covariance model
	Random intercept (CS)		Unstructured		Random Int C Slope		Sandwich estimator
Fixed predictor*	Estimate	p-value	Estimate	p-value	Estimate	p-value	Estimate	p-value
Intercept	143.6	< 0.01	143.4	< 0.01	143.7	< 0.01	143.6	< 0.01
Years	−1.63	< 0.01	−1.77	< 0.01	−1.72	< 0.01	−1.63	< 0.01
Years2	0.73	0.01	0.84	< 0.01	1.19	< 0.01	0.73	< 0.01
Years3	−2.22	< 0.01	−2.08	< 0.01	−2.31	< 0.01	−2.22	< 0.01
Differences in intercept
Male	−1.02	0.47	−1.29	0.35	−1.19	0.40	n	0.47
Maternal age	−0.37	< 0.01	−0.39	< 0.01	−0.38	< 0.01	−0.37	< 0.01
Maternal depression	1.25	< 0.01	1.29	< 0.01	1.28	< 0.01	1.25	< 0.01
Home environment	0.41	0.02	0.44	0.01	0.42	0.02	0.41	0.02
Asthma	0.39	0.88	−0.28	0.92	0.25	0.93	0.39	0.88
Interaction with years
Male	−1.10	0.02	−1.10	0.08	−1.01	0.12	−1.10	0.09
Home environment	0.18	< 0.01	0.18	0.01	0.18	0.01	0.18	0.02
Asthma	2.10	0.03	2.08	0.11	2.10	0.11	2.10	0.10
Interaction with years2
Home environment	−0.12	0.01	−0.04	< 0.05	−0.15	< 0.01	−0.12	0.08
Interaction with years3
Home environment	0.20	< 0.01	0.15	< 0.01	0.19	< 0.01	0.20	< 0.01

^*We used orthogonal polynomial coefficients for the time variables; we centered maternal age, depression, and home environment scores around their means.

^**p-values in bold indicate significance for a fixed predictor in the compound symmetry model that was not significant in the other models.

Comparisons of the fixed effect estimates and the p-values for the various covariance models reveal agreement for most values (Table I). However, asthma status was found to significantly interact with age (p = 0:03) in a linear fashion when assuming compound symmetry; there was no such significant interaction when fitting any of the other covariance models (p ≥ 0:10 in all cases). If one were to have fit a random-intercept-only model to these data, one would have concluded, apparently erroneously, that those with asthma exhibited higher internalizing behavior scores over time. A similar contrast is also observed in considering gender and behavior over time, with the compound symmetry model giving a significant linear change in behavior scores between boys and girls as they mature. We emphasize that it is safer to select the fixed-effect model based on a sufficiently complex covariance model. We omit the details simply for the sake of brevity and simplicity.

6. Discussion

A common choice for a covariance model of the responses in a general linear mixed model arises from including only a random intercept and assuming homogeneous and independent errors within subject. The choice requires the responses to have CS covariance, an assumption that arises in a variety of ways.

We proved that incorrectly assuming compound symmetry inflates type I error for inference about the fixed effects in a general linear mixed model, in both small and large samples. Numerical results illustrate the magnitude of the problem. Simulations demonstrate that the problem occurs with missing data. Our focus here has been the compound symmetry assumption; the proof does not directly apply to other assumed covariance structures (e.g., random intercept plus slope, etc.). However, our results prove that robustness of fixed effects inference with an underspecified covariance model cannot be guaranteed in small or large samples. The generalization applies not only to mixed models that incorporate random effects but also to any multivariate model, particularly those with repeated measurements.

The results provide some guidance for achieving accurate inference for fixed effects. The first step involves considering general covariance models. Many analysts, including ourselves, would not consider compound symmetry for longitudinal data. Despite that, many recently published studies explicitly or implicitly make the assumption. The false hope that large samples allow ignoring insufficient covariance model complexity may motivate the approach. In contrast to longitudinal data, cluster-based sampling typically provides exchangeability of observations and hence CS correlation within cluster. A careful review of the sampling plan to ensure the validity of the exchangeability assumption seems necessary.

In addition to the use in data analysis, the compound symmetry assumption has been used often for power analysis. Although preferred for cluster samples, realistic correlation patterns for longitudinal data include a linear exponent autoregressive (LEAR) reliable or damped exponential model [28], which generalize AR(1) structure. In parallel to the results on type I error rate, a valid power analysis requires a covariance model aligned with the population. The example power values for repeated measures designs in [29] allow concluding that misspecification of the covariance matrix can lead to computing power either too high or too low because of misalignment.

If the data allow it, one should model an unstructured covariance. Unfortunately, convergence often becomes an issue with mixed models. Cheng et al. [30] provided practical advice on improving the chances for convergent models. The least appreciated strategies center on minimizing collinearity in both fixed and random predictors. The importance of centering and scaling all predictors (especially time) and the use of full-rank coding schemes, preferably orthogonal, cannot be overemphasized.

When a simple covariance model (compound symmetry, unstructured) can not be assumed, the mixed model provides advantages in that one can incorporate random effects to model the covariance structure. Our work extends the results of Lange and Laird [8] by demonstrating that modest expansion of the random effects (covariance structure) helps but cannot be guaranteed to be sufficient. We warn against underspecification of the covariance model, no matter whether it is a general structure or one composed of random effects. Fortunately, conscientious attention to good statistical practices in covariance model fitting can provide confidence in fixed effect inference in a mixed model.

The sandwich estimator appeals simply because it does not require an elaborate covariance model selection process and can simplify convergence. As far as we know, its performance in small-sample settings has been relatively unstudied and should be the focus of future work. Specifically, DOF approximations should be studied with the sandwich estimator. However, in large-sample settings, where we prove that assuming compound symmetry results in substantial bias, the sandwich estimator seems to be a valid alternative.

We have focused on settings with primary interest in inference about fixed effects and little interest in covariance structure itself. Even with a focus on fixed effects, accurate inference requires selecting an adequate approximation for the true covariance structure. Unfortunately, although many model selection criteria have been suggested, none has been found to be clearly superior. Part of the difficulty stems from the interaction between fixed effect and covariance model selection. Overall, one principle seems clear: controlling type I error for tests of fixed effects demands avoiding an underfitted covariance model.

Appendix A. Proof of the theorem

For the sake of brevity, we use the notation and many results in [13, Chapters 1, 3, 5, 12, 14, 16, 18] without specific references. We restrict attention to mixed models that are valid multivariate models. Stacking all of the data sorted by subject gives vec(Y’) = vec[(X_MB)’]+vec(E’) = (X_M ⊗ I_p)vec(B’)+vec(E’), which may be stated as y_s=X_sβ + e_+s, the population average model for all n= N·p observations. Here, y_s=[y’₁ … y’_i 7#x2026; y_N]’ and X_s=[X’₁ … X’_i … X_N]’.

With ν (y_i) = Σ_i for subject i , the multivariate model gives maximum-likelihood estimations noniteratively: $\tilde{B}=\left(X_M^{\prime }{X}_M\right){}^{-1}{X}_M^{\prime }Y$ and $\tilde{\Sigma }={(Y-X_M\tilde{B})}^{\prime }(Y-X_M\tilde{B})∕N$. Here $\tilde{B}$ is functionally independent of ${\tilde{\Sigma }}_i$, so $\tilde{B}$ is invariant to ${\tilde{\Sigma }}_i$, a property not guaranteed in the mixed model. REML estimates are $\widehat{B}=\tilde{B}$ and $\widehat{\Sigma }=\tilde{\Sigma }N∕(N-r_M)$ for r_M = rank(X_M). Mixed model estimates are $\widehat{\beta }=\text{vec}\left(\widehat{B}\right)$, $\widehat{\theta }=\text{vec}\left(\widehat{ϴ}\right)$, ${\widehat{\Sigma }}_i$ for subject i and ${\widehat{\Sigma }}_s=I_N\otimes {\widehat{\Sigma }}_i$. Hence, $X_s^{\prime }{\widehat{\Sigma }}_s^{-1}{X}_s={(X_M\otimes I_P)}^{\prime }{(I_N\otimes {\widehat{\Sigma }}_i)}^{-1}(X_M\otimes I_P)=(X_M^{\prime }\otimes I_p)(I_N\otimes {\widehat{\Sigma }}_i^{-1})(X_M\otimes I_P)=X_M^{\prime }{X}_M\otimes {\widehat{\Sigma }}_i^{-1}$ and $C_m{\left(X_s^{\prime }{\widehat{\Sigma }}_s^{-1}{X}_s{X}_s\right)}^{-1}{C}_m^{\prime }=(C_M\otimes U^{\prime }){[X_M^{\prime }{X}_M\otimes {\widehat{\Sigma }}_i^{-1}]}^{-1}(C_M^{\prime }\otimes U)=\left[C_M{\left(X_M^{\prime }{X}_M\right)}^{-1}{C}_M^{\prime }\right]\otimes \left(U^{\prime }{\widehat{\Sigma }}_{i}U\right)=M_M\otimes {\widehat{\Sigma }}_{\ast }$. The Wald statistic reduces to $F_m={(\widehat{\theta }-{\theta }_0)}^{\prime }{\left[C_m{\left(X_s^{\prime }{\widehat{\Sigma }}_s^{-1}{X}_s\right)}^{-1}{C}_m^{\prime }\right]}^{-1}(\widehat{\theta }-{\theta }_0)∕a_m={\left[\text{vec}(\widehat{ϴ}-{ϴ}_0)\right]}^{\prime }{(M_M\otimes {\widehat{\Sigma }}_{\ast })}^{-1}\left[\text{vec}(\widehat{ϴ}-{ϴ}_0)\right]∕a_m=\left[\text{vec}(\widehat{ϴ}-{ϴ}_0)\right]\prime (M_M^{-1}\otimes {\widehat{\Sigma }}_{\ast }^{-1})\left[\text{vec}(\widehat{ϴ}-{ϴ}_0)\right]∕a_m$. Here, F_m is invariant to full-rank transformation of columns of U and ${ϴ}_0:(M_M^{-1}\otimes {\widehat{\Sigma }}_{\ast }^{-1})\text{vec}(\widehat{ϴ}-{ϴ}_0)=(M_M^{-1}\otimes {\widehat{\Sigma }}_{\ast }^{-1})(T^{-1}\otimes I_a)(T\otimes I_a)\text{vec}(\widehat{ϴ}-{ϴ}^0)=(M_M^{-1}\otimes {\widehat{\Sigma }}_{\ast }^{-1})\text{vec}\left[(C\widehat{B}UT-{ϴ}_{0}T)\right]$. Singular value decomposition gives U =L₊Dg(s)R’ with L₊ and R orthonormal by column. Using T =RDg(s)⁻¹ allows assuming U =L₊, the eigenvectors of UU’ for nonzero eigenvalues.

A p × p CS covariance is ${\sum }_{iCS}={\sigma }^2[1_p{1}_p^{\prime }\rho +I_p(1-\rho )]=V\text{Dg}\left(\lambda \right)V^{\prime }=\left[\begin{array}{cc}\hfill {\nu }_0\hfill & \hfill V_t\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\lambda }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_2{I}_{p-1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\nu }_0^{\prime }\hfill \\ \hfill V_t^{\prime }\hfill \end{array}\right]$. Here, λ₁ = σ² [1+(p – 1) ρ] and λ₂ = σ² (1 – ρ), whereas ν₀=1_p/p^1/2 and V_t may be taken to be any p×(p – 1) orthonormal matrix with $V_t^{\prime }{\nu }_0=0$.

Three distinct classes of hypotheses occur: (i) pure between hypotheses have p×1 U =w·ν₀ for w ≠ 0; (ii) pure within hypotheses have U’ν₀ = 0; and (iii) combinations have U’ν₀ ≠ 0 and rank(U) > 1. For the sake of brevity, we provide an explicit form only for pure within hypotheses. The other cases have the same structure with different weights in the resulting quadratic forms. If U’ν₀ = 0 and p × bU = L₊, then without loss of generality Vt = [L₊L₀] with L0 any p – 1 – b ≥ 0 eigenvectors of UU’ for zero eigenvalues.

Compound symmetric estimates may be computed in terms of the unstructured maximum likelihood $\left({\tilde{\Sigma }}_i\right)$ and unstructured REML $\left({\tilde{\Sigma }}_i\right)$ covariance estimates [31]. Here, ${\widehat{\sigma }}^2=\text{tr}\left({\widehat{\Sigma }}_i\right)∕p={\tilde{\sigma }}^{2}N∕(N-r_M)$ and $\tilde{\rho }=[1_p^{\prime }{\tilde{\Sigma }}_i{1}_p-\text{tr}\left({\tilde{\Sigma }}_i\right)]∕\left[\text{tr}\left({\widehat{\Sigma }}_i\right)(p-1)\right]=1_p^{\prime }{\widehat{\Sigma }}_i{1}_p-\text{tr}\left({\widehat{\Sigma }}_i\right)∕\left[\text{tr}\left({\widehat{\Sigma }}_i\right)(p-1)\right]=\widehat{\rho }$ give ${\widehat{\lambda }}_1=\widehat{\sigma }[1+(p-1)\widehat{\rho }]=\text{tr}\left({\widehat{\Sigma }}_i\right)∕p+(1_p^{\prime }{\widehat{\Sigma }}_i{1}_p-\text{tr}\left({\widehat{\Sigma }}_i\right)∕p)=1_p^{\prime }{\widehat{\Sigma }}_i{1}_p∕p$ and ${\widehat{\lambda }}_2={\widehat{\sigma }}^2(1-\widehat{\rho })=\text{tr}\left({\widehat{\Sigma }}_i\right)∕p-[1_p^{\prime }{\widehat{\Sigma }}_i{1}_p-\text{tr}\left({\widehat{\Sigma }}_i\right)]∕[p-(p-1)]=[p\text{tr}\left({\widehat{\Sigma }}_i\right)-1_p^{\prime }{\widehat{\Sigma }}_i{1}_p]∕\left[p(p-1)\right]$. Hence, the REML estimate for a CS covariance matrix in a general linear mixed model corresponding to a multivariate model may be computed noniteratively as ${\widehat{\Sigma }}_{i\text{CS}}=\left[\begin{array}{cc}\hfill {\nu }_0\hfill & \hfill V_t\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\widehat{\lambda }}_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\widehat{\lambda }}_2\hfill \end{array}{I}_{p-1}\right]\left[\begin{array}{c}\hfill {\nu }_0^{\prime }\hfill \\ \hfill V_t^{\prime }\hfill \end{array}\right]$. Assuming compound symmetry in the mixed model gives ${\widehat{\Sigma }}_i={\widehat{\Sigma }}_{i\text{CS}}\text{and}{\widehat{\Sigma }}_s=(I_N\otimes {\widehat{\Sigma }}_{i\text{CS}})$

For pure within hypotheses (such as a test of the linear trend), $U^{\prime }{\widehat{\Sigma }}_{i\text{CS}}U=L_{+}^{\prime }\left(\left[\begin{array}{ccc}\hfill {\nu }_0\hfill & \hfill L_{+}\hfill & \hfill L_0\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\widehat{\lambda }}_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\widehat{\lambda }}_2{I}_{p-1}\hfill \end{array}\right]{\left[\begin{array}{ccc}\hfill {\nu }_0\hfill & \hfill L_{+}\hfill & \hfill L_0\hfill \end{array}\right]}^{\prime }\right)L_{+}={\widehat{\lambda }}_2{I}_b$. With ${\widehat{\theta }}_k$ indicating column k of $\widehat{ϴ}$,

$$\begin{array}{cc}\hfill a_m{F}_m& ={\left[\text{vec}(\widehat{ϴ}-{ϴ}_0)\right]}^{\prime }\left[{(M_M\otimes {\widehat{\lambda }}_2{I}_b)}^{-1}\right]\left[\text{vec}(\widehat{ϴ}-{ϴ}_0)\right]\hfill \\ \hfill & ={\left[\text{vec}(\widehat{ϴ}-{ϴ}_0)\right]}^{\prime }(M_M^{-1}\otimes I_b){[{({\widehat{\theta }}_1-{\theta }_{0,1})}^{\prime }\cdots ({\widehat{\theta }}_1-{\theta }_{0,1})]}^{\prime }∕{\widehat{\lambda }}_2\hfill \\ \hfill & ={\widehat{\lambda }}_2^{-1}\sum _{k=1}^b{({\widehat{\theta }}_k-{\theta }_{0,k})}^{\prime }{M}_M^{-1}({\widehat{\theta }}_k-{\theta }_{0,k})=tr\left[{(\widehat{ϴ}-{ϴ}_0)}^{\prime }{M}_M^{-1}(\widehat{\theta }-{ϴ}_0)\right]∕{\widehat{\lambda }}_2.\hfill \end{array}$$ (6)

Writing $\Delta ={(ϴ-{ϴ}_0)}^{\prime }{M}_M^{-1}(ϴ-{ϴ}_0)$ implies $a_m{F}_m=\text{tr}\left(\widehat{\Delta }\right)∕{\widehat{\lambda }}_2$ with a_m = a_Mb for Θ a_M ×b. Multivariate model results give $\widehat{\Delta }={(\widehat{ϴ}-{ϴ}_0)}^{\prime }{M}_M^{-1}(\widehat{ϴ}-{ϴ}_0)~{\mathcal{W}}_b(a_M,U^{\prime }{\Sigma }_{i}U,\Delta )$ and $\widehat{\Delta }$ independent of ${\widehat{\Sigma }}_i$, which insures $\widehat{\Delta }$ independent of ${\widehat{\lambda }}_2=\left[p\text{tr}({\widehat{\Sigma }}_i-1_p^{\prime }{\widehat{\Sigma }}_i{1}_p)\right]∕\left[p(p-1)\right]$.

Under H₀, $\mathrm{tr}\left(\widehat{\Delta }\right)={\Sigma }_{k=1}^b{\lambda }_{hk}{X}_{hk}$ for i.i.d. X_hk~χ² (a_M) and λ_hk an eigenvalue of Σ_h=U’Σ_iU. If $\widehat{E}=Y-X_M\widehat{B}$, then $p(p-1){\nu }_e{\widehat{\lambda }}_2=p\mathrm{tr}\left({\widehat{E}}^{\prime }\widehat{E}\right)-\mathrm{tr}\left(1_p^{\prime }{\widehat{E}}^{\prime }\widehat{E}{1}_p\right)=p\mathrm{tr}\left(\widehat{E}{\widehat{E}}^{\prime }\right)-\mathrm{tr}\left(\widehat{E}{1}_p{1}_p^{\prime }{\widehat{E}}^{\prime }\right)$. In turn, ${\nu }_e(p-1){\widehat{\lambda }}_2=\mathrm{tr}\left[\widehat{E}(I_p-1_p{1}_p^{\prime }∕p){\widehat{E}}^{\prime }\right]$. Here, $(I_p-1_p{1}_p^{\prime }∕p)=\left[\begin{array}{cc}\hfill {\nu }_0\hfill & \hfill V_t\hfill \end{array}\right]\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill I_{p-1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\nu }_0^{\prime }\hfill \\ \hfill V_t^{\prime }\hfill \end{array}\right]=V_t{V}_t^{\prime }$ so ${\nu }_e(p-1){\widehat{\lambda }}_2=\mathrm{tr}\left(\widehat{E}{V}_t{V}_t^{\prime }{\widehat{E}}^{\prime }\right)=\mathrm{tr}\left(V_t^{\prime }{\widehat{E}}^{\prime }\widehat{E}{V}_t\right)$ and ${\widehat{\lambda }}_2=\mathrm{tr}\left(V_t^{\prime }{\widehat{\Sigma }}_i{V}_t\right)∕(p-1)$ with ${\nu }_e{V}_t^{\prime }{\widehat{\Sigma }}_i{V}_t~{\mathcal{W}}_{p-1}({\nu }_e,V_t^{\prime }\Sigma V_t,0)$. Hence, ${\nu }_e(p-1){\widehat{\lambda }}_2={\Sigma }_{k=1}^{p-1}{\lambda }_{ek}{X}_{ek}$ for i.i.d. X_ek ~ χ² (ν_e; 0) and λ_ek an eigenvalue of Σ_e =V’_tΣ_Vt . Finally, $\mathrm{Pr}\{F_m\le f\}=\mathrm{Pr}\{\mathrm{tr}\left(\widehat{\Delta }\right)∕\left(a_m{\widehat{\lambda }}_2\right)\le f\}=\mathrm{Pr}\{\mathrm{tr}\left(\widehat{\Delta }\right)-a_{m}f{\widehat{\lambda }}_2\le 0\}=\mathrm{Pr}\{Q\le 0\}$, for $Q={\Sigma }_{k=1}^b{\lambda }_{hk}{X}_{hk}-a_{m}f{\Sigma }_{k=1}^{p-1}{\lambda }_{ek}{X}_{ek}$ a quadratic form with positive and negative weights.

The fact that Pr {F_m≤f } = Pr{Q ≤ 0} allows computing the exact distribution function of the Wald statistic in finite samples with the Kenward–Roger approximation. Results in [12] allows using modules from POWERLIB [28] that implements exact methods described in [29].

In large samples, under H₀, the numerator distribution of F_m does not change as N → ∞ because $\mathrm{tr}\left(\widehat{\Delta }\right)$ does not depend on N for i.i.d. X_hk ~ χ² (a_M). The denominator converges to a constant, ${\widehat{\lambda }}_2=\mathrm{tr}\left(V_t^{\prime }{\widehat{\Sigma }}_i{V}_t\right)∕(p-1)\to \mathrm{tr}\left(V_t^{\prime }{\Sigma }_i{V}_t\right)∕(p-1)$ and thereby becomes known. Hence, under the null $\underset{N\to \infty }{\text{lim}}{F}_m={\Sigma }_{k=1}^b{\lambda }_{hk}{X}_{hk}∕\left[a_M\mathrm{tr}\left(U^{\prime }{\Sigma }_{i}U\right)\right]$, a quadratic form, which allows exact probability calculations. Satterthwaite’s method gives an accurate approximation.

Under H_A, as in [15], U’Σ_iU = γDg(λ_*)γ’ defines noncentrality ${\omega }_{\ast k}={\nu }_k^{\prime }{(ϴ-{ϴ}_0)}^{\prime }{M}_M^{-1}(ϴ-{ϴ}_0){\nu }_k∕{\lambda }_{\ast k}$ a diagonal element of Ω_* = γ’ΔγDg(λ_h)⁻¹. Here, $\mathrm{tr}\left(\widehat{\Delta }\right)={\Sigma }_{k=1}^b{\lambda }_{hk}{X}_{hk}$ for i.i.d. X_hk ~ χ² (a_M, ω_*k) and λ_hk an eigenvalue of Σ_h = U’Σ_iU. Methods in [29] allow exact computation and accurate approximation of the cumulative distribution function of F_m for finite samples. In large samples, as under H₀, ${\widehat{\lambda }}_2\to \mathrm{tr}\left(V_t^{\prime }{\Sigma }_i{V}_t\right)∕(p-1)$. With nonlocal alternatives $\underset{N\to \infty }{\text{lim}}{F}_m\to \infty$ and power → 1. For local alternatives β. N^−1/2 β and ${\omega }_{\ast k}={\nu }_k^{\prime }{(ϴ-{ϴ}_0)}^{\prime }{C}_M{\left[\mathrm{Es}{\left(X_M\right)}^{\prime }\mathrm{Es}\left(X_M\right)\right]}^{-1}{C}_M^{\prime }(ϴ-{ϴ}_0){\nu }_k∕{\lambda }_{\ast k}$. The essence matrix Es(X_M) contains one copy of each unique row of X_M, and M_M = N⁻¹C_MEs (XM)’ Es (X_M)]⁻¹ C’_M.