Local image statistics: maximum-entropy constructions and perceptual salience

Abstract

The space of visual signals is high-dimensional and natural visual images have a highly complex statistical structure. While many studies suggest that only a limited number of image statistics are used for perceptual judgments, a full understanding of visual function requires analysis not only of the impact of individual image statistics, but also, how they interact. In natural images, these statistical elements (luminance distributions, correlations of low and high order, edges, occlusions, etc.) are intermixed, and their effects are difficult to disentangle. Thus, there is a need for construction of stimuli in which one or more statistical elements are introduced in a controlled fashion, so that their individual and joint contributions can be analyzed. With this as motivation, we present algorithms to construct synthetic images in which local image statistics—including luminance distributions, pair-wise correlations, and higher-order correlations—are explicitly specified and all other statistics are determined implicitly by maximum-entropy. We then apply this approach to measure the sensitivity of the human visual system to local image statistics and to sample their interactions.

1. INTRODUCTION

Basic visual judgments, such as detection, discrimination, and segmentation, are fundamentally statistical in nature. Because the space of signals that the visual system encounters is very high-dimensional, there is a very wide variety of image statistics that, a priori, could be used to drive these judgments. On the other hand, there is much evidence that only a very limited number of image statistics are, in fact, actually used. For example, in texture discrimination and segmentation, only certain features of the luminance histogram appear perceptually relevant [1] and, with a limited number of exceptions, only pair-wise spatial correlations are used [2–4]. However, these conclusions are based on stimuli in which a single, mathematically-convenient, image statistic is introduced or manipulated. This is in contrast to natural visual stimuli, whose statistical structure is complex [5,6]: the well-known “1/f” correlation structure [7] coexists with highly non-Gaussian luminance statistics [8], as well as many other kinds of statistical features [9–12].

Thus, to understand visual responses to natural images, it is necessary to analyze not only how image statistics are processed individually, but also how they interact. To pursue such an analysis, it is desirable to have stimulus sets in which multiple image statistics—including luminance statistics and spatial correlations—can be introduced in a controlled and independent fashion. The goal of this paper is to present a procedure for doing this and to illustrate its use in delineating the perceptual saliency of these statistics, alone and in combination.

A related motivation for this work arises out of the analysis of receptive fields at the physiologic level. As a consequence of the high-dimensional nature of visual signals, one cannot characterize input-output relationships exhaustively—so it is necessary to sample the space of inputs in some fashion. Generally, the sampling strategies fall into two categories. One category has a primarily mathematical motivation, and relies on stimuli such as sinusoids and white noise because they are convenient for determining the parameters of simple model classes (such as linear transformations or Taylor expansions and their generalizations). The other category is primarily biologically-motivated and focuses on the inputs under which the visual system functions and evolves, i.e., “natural scenes.”

Either approach alone appears to be insufficient. Mathematical models built from stimuli such as white noise provide only a fair account of responses to natural scenes [13]. The obstacle is that mathematically-convenient stimuli rarely sample the kinds of stimulus features that are common in natural scenes, so substantial errors in model structure may be overlooked. The use of naturalistic stimuli avoids that problem, but makes it difficult to achieve a mechanistic understanding. This is because natural scenes have many different kinds of statistical structure (as mentioned above: luminance histograms, correlations of low and high order, edges, occlusions, etc.). Since these elements are entangled in natural scenes, the role(s) that they play in visual processing can be difficult to sort out. As is the case for understanding visual function at a psychophysical level, there is a need for principled stimulus sets in which multiple statistical elements can be independently controlled.

To meet this need, three related issues need to be addressed. First, because the number of image statistics is so large, one must select a subset to focus on. Second, selecting this subset of statistics and specifying their values stops short of specifying the entire stimulus, because of all the other image statistics whose values are unspecified. Thus, it is also necessary to have a principled procedure for choosing the values of the statistics that are not specified explicitly. Finally, one needs a procedure to create images that exemplify these statistics.

In choosing the statistical elements to focus on, two considerations are immediately relevant: which image statistics are informative about natural images and which ones are salient to the visual system. The notion of “efficient coding” [14] suggests that these considerations are likely to be aligned. A recent analysis of natural images [10] supports this view, not only for luminance statistics and pair-wise correlations, but also for multipoint correlations. The latter analysis used binarized natural images; this made it possible to enumerate the distribution of four-point configurations that are present in natural images. A main conclusion of the analysis [10] was that only some kinds of four-point correlations were informative. Moreover, the dichotomy between informative and uninformative configurations matched the dichotomy between four-point correlations that are visually salient and those that are not [4].

Therefore, we focus on the correlations that this previous study[10] identified as both informative and visually-salient: the statistics of 2 × 2 arrays of binarized pixels. As we show below, the joint probability distribution that describes the ways that these arrays can be colored is specified by 10 parameters, i.e., 10 local image statistics.

Having selected a subset of image statistics and specified their values, the next step is to address the second issue: choosing the values of all of the image statistics outside of the selected subset. Here our strategy is guided by the goal of analyzing the effect of the specified statistics on visual processing. In view of this goal, it makes sense to choose the other statistics in a manner that adds no further structure. We do this implicitly—by maximizing the entropy of the image ensemble, subject to the constraints of the subset of specified image statistics. Maximizing the entropy of the image ensemble solves the problem of choosing values for all other statistics, since the maximum-entropy distribution is unique.

Because the maximum-entropy criterion represents a principled way to create distributions that are as assumption-free (i.e., as random) as possible given specific constraints [15,16], maximum-entropy methods have been applied in numerous domains, including analysis of neural data [17–19] and image analysis [20]. Maximum-entropy distributions are simple and easy to construct when the constraints are few and simple: a Poisson distribution maximizes the entropy when the mean is constrained, a Gaussian distribution maximizes the entropy when the variance is constrained, and a Markov process maximizes the entropy when sequential correlations are constrained.

When the constraints are more complex—as they are for local image statistics—maximum-entropy distributions are less-familiar and explicit construction of them is not necessarily straightforward. The basic problem that arises is that iterative constructions—which are guaranteed to work for one-dimensional processes such as Markov chains—may fail for two-dimensional processes. The reason that iterative constructions do not necessarily extend from one dimension to two dimensions is that the constructions along each dimension may conflict with each other. Below, we use an important result of Pickard [21] to determine when these conflicts occur. In the absence of such conflicts, iterative constructions enable creation of examples of images with the desired statistics (i.e., sampling the maximum-entropy ensemble). In the presence of these conflicts, we develop a set of alternative image-synthesis algorithms, that allow us to achieve our goal. The result is a set of procedures for construction of images that have independently specified values of the 10 local image statistics. Finally, we use these stimulus sets in psychophysical studies, to demonstrate the selective sensitivity of the visual system to the individual statistics and their interactions.

Although we focus on construction of maximum-entropy binary images given a specified set of statistics for 2 × 2 arrays, most of the strategies we develop are not restricted to this particular case. Therefore, to facilitate extensions of this approach, we describe not only the algorithms themselves, but also their interrelationships and the conditions that allow them to succeed.

2. IMAGE CONSTRUCTION

There are two components of this paper: first, algorithms for the construction of visual stimuli that are specified by a set of image statistics and second, psychophysical studies based on selected examples of these constructions. As mentioned in the Introduction, we focus on the image statistics that describe 2 × 2 blocks of pixels in a binary image. In this section, we show that this is a 10-dimensional space and how to navigate in it. That is, we construct stimuli along the coordinate axes, stimuli on or near the coordinate planes, and in other directions, corresponding to arbitrary natural stimuli. Below (Section 4), we use these stimuli in psychophysical experiments: we measure the sensitivity along the axes of the space and in selected coordinate planes, to provide a glimpse of the ways in which the coordinates interact. The results of the psychophysical experiments are also important to support some of the strategic choices made during stimulus construction.

The basic problem that we wish to solve is the following: given a set of local image statistics, construct images that are as random as possible—i.e., maximum entropy—given these constraints. As described below, the local image statistics we consider are those that refer to the contents of a 2 × 2 array of pixels or on a subset of this array.

We begin this section by setting up a notation and defining the key terms. We then use this notation to refine the statement of the problem and to provide a formal characterization of the solution. The formal characterization, though, does not provide a construction, and a constructive solution is necessary to achieve our goal. We then develop constructive solutions, proceeding incrementally from the simplest case (independent pixels) to correlations along one dimension, to correlations along two dimensions that are specified by a single parameter, to correlations along two dimensions that are specified by pairs of parameters, to more complex correlation structures, including those that arise in natural images.

A. Preliminaries: Ensembles, Images, and Block Probabilities

To make the notion of randomness rigorous, we need to consider image ensembles, rather than individual images. An image ensemble is simply a collection of images, with a probability assigned to each. Within the ensemble, individual images are represented as an array of values a_ij, where a_ij is the luminance of the pixel in row i and column j. Arrays are of finite size (so that averages can be simply calculated), but we are only concerned with the limiting behavior as the size of the array grows without bound.

We will only consider binary images: each a_ij is either 0 or 1, with 0 arbitrarily is assigned to represent black and 1 to represent white. We note, though, that many of the constructions below readily generalize to images with multiple gray levels (see for example Appendix A).

A “block probability” is the probability that a set of pixels in particular configuration have a given set of values. As a simple example, p(0) is the probability that a pixel value a_ij is black; $p(\begin{array}{cc}0& 1\end{array})$ is the probability that a 1 × 2 window contains a black pixel on the left and $p\left(\begin{array}{cc}1& \\ 1& 1\end{array}\right)$ is the probability that an L-shaped region contains three white pixels.

To ensure that the formalisms of image ensembles are relevant to laboratory experiments and real world visual behavior, it is essential that the statistics of local patches of images typify the statistics of the ensemble. To meet this criterion, we require that the ensemble of images has two properties: stationarity and ergodicity. Stationarity formalizes the notion that the statistics of the images are the same in all locations and ergodicity formalizes the notion that the statistics of an individual image typify those of the ensemble. Each of these properties can be expressed in terms of different ways of calculating the block probabilities. For example, one can choose a specific location and sample that location across the ensemble. Or, one can choose a specific image within the ensemble and sample that image at all locations. Stationarity asserts that the first calculation does not depend on the location sampled. Ergodicity asserts that the second calculation yields the same result as the first. Together, these properties ensure that the statistics of local patches typify the statistics of the ensemble.

B. A Coordinate System to Simplify the Dependencies among Block Probabilities

While at first it might appear that the individual block probabilities are the most natural way to describe local statistics, they have a significant drawback: the property of stationarity (along with the general rules of probability) implies certain interrelationships among them. So our next step is to introduce a coordinate system for the block probabilities that simplifies the task of specifying sets of block probabilities that conform to these constraints.

To see how these constraints arise, assume that we have specified the block probabilities for all colorings of a 2 × 2 array, as $p\left(\begin{array}{ll}A\hfill & B\hfill \\ C\hfill & D\hfill \end{array}\right)$. These implicitly specify the probabilities of smaller blocks—for example,

$$p\left(\begin{array}{ll}A\hfill & B\hfill \\ C\hfill & \hfill \end{array}\right)=p\left(\begin{array}{ll}A\hfill & B\hfill \\ C\hfill & 0\hfill \end{array}\right)+p\left(\begin{array}{ll}A\hfill & B\hfill \\ C\hfill & 1\hfill \end{array}\right)$$ (1)

and

$$\begin{array}{l}p\left(\begin{array}{cc}A& B\\ & \end{array}\right)=p\left(\begin{array}{cc}A& B\\ 0& \end{array}\right)+p\left(\begin{array}{cc}A& B\\ 1& \end{array}\right)\\ =p\left(\begin{array}{cc}A& B\\ 0& 0\end{array}\right)+p\left(\begin{array}{cc}A& B\\ 0& 1\end{array}\right)+p\left(\begin{array}{cc}A& B\\ 1& 0\end{array}\right)+p\left(\begin{array}{cc}A& B\\ 1& 1\end{array}\right).\end{array}$$ (2)

Similarly, $p\left(\begin{array}{cc}& \\ C& D\end{array}\right)$ can be written in terms of the 2 × 2 block probabilities:

$$\begin{array}{l}P\left(\begin{array}{cc}& \\ C& D\end{array}\right)=p\left(\begin{array}{cc}0& \\ C& D\end{array}\right)+p\left(\begin{array}{cc}1& \\ C& D\end{array}\right)\\ =p\left(\begin{array}{cc}0& 0\\ C& D\end{array}\right)+p\left(\begin{array}{cc}0& 1\\ C& D\end{array}\right)+p\left(\begin{array}{cc}1& 0\\ C& D\end{array}\right)+p\left(\begin{array}{cc}1& 1\\ C& D\end{array}\right).\end{array}$$ (3)

Stationarity requires that $p\left(\begin{array}{c}AB\\ \end{array}\right)=p\left(\begin{array}{c}\\ AB\end{array}\right)$. Thus, for A = C and B = D, the right-hand sides of Eqs. (2) and (3) must be equal. This in turn means that for each of the four ways of assigning binary values to A and B, there is a linear relationship among eight of the 2 × 2 block probabilities:

$$p\left(\begin{array}{cc}A& B\\ 0& 0\end{array}\right)+p\left(\begin{array}{cc}A& B\\ 0& 1\end{array}\right)+p\left(\begin{array}{cc}A& B\\ 1& 0\end{array}\right)+p\left(\begin{array}{cc}A& B\\ 1& 1\end{array}\right)=p\left(\begin{array}{cc}0& 0\\ A& B\end{array}\right)+p\left(\begin{array}{cc}0& 1\\ A& B\end{array}\right)+p\left(\begin{array}{cc}1& 0\\ A& B\end{array}\right)+p\left(\begin{array}{cc}1& 1\\ A& B\end{array}\right).$$ (4)

Similar relationships among subsets of block probabilities follow from stationarity requirements for the probabilities of 2 × 1 blocks, namely,

$$p\left(\begin{array}{cc}A& \\ C& \end{array}\right)=p\left(\begin{array}{cc}& A\\ & C\end{array}\right)$$ (5)

and individual pixels, namely,

$$p\left(\begin{array}{cc}A& \\ & \end{array}\right)=p\left(\begin{array}{cc}& A\\ & \end{array}\right)=p\left(\begin{array}{cc}& \\ A& \end{array}\right)=p\left(\begin{array}{cc}& \\ & A\end{array}\right).$$ (6)

An additional complication is that these relationships are not independent of each other.

As we next show, we can replace the block probabilities with a coordinate system in which these interdependencies are eliminated. The coordinate system is a transformation of the block probabilities:

$$\varphi \left(\begin{array}{cc}{s}_1& s_2\\ s_3& s_4\end{array}\right)=\sum _{A_1,A_2,A_3,A_4}p\left(\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right){\left(-1\right)}^{A_1{s}_1+A_2{s}_2+A_3{s}_3+A_4{s}_4},$$ (7)

where s₁, s₂, s₃, and s₄ are 0 or 1. Note that the original block probabilities can readily be obtained from the transformed quantities ϕ:

$$p\left(\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right)=\frac{1}{16}\sum _{s_1,s_2,s_3,s_4}\varphi \left(\begin{array}{cc}{s}_1& s_2\\ s_3& s_4\end{array}\right){\left(-1\right)}^{A_1{s}_1+A_2{s}_2+A_3{s}_3+A_4{s}_4}.$$ (8)

This is because the new quantities ϕ are, in essence, the Fourier transforms of the block probabilities, along the four intensity axes A₁ through A₄. (For additional details on this construction, its further properties, and how it generalizes to images with multiple gray levels, see Appendix A.)

The reason that the transformed quantities ϕ simplify the relationships among the block probabilities is the following: setting one of the indices s_i to 0 in Eq. (8) removes A_i from the exponent and hence produces transformed quantities that sum over the corresponding location A_i. For example, $\varphi \left(\begin{array}{cc}{s}_1& s_2\\ s_3& 0\end{array}\right)$ depends only on $p\left(\begin{array}{cc}{A}_1& A_2\\ A_3& \end{array}\right)$ and $\varphi \left(\begin{array}{cc}{s}_1& s_2\\ 0& 0\end{array}\right)$ depends only on $p\left(\begin{array}{cc}{A}_1& A_2\\ & \end{array}\right)$. So the stationarity constraints [Eq. (5)] due to 1 × 2 block probabilities, $p\left(\begin{array}{cc}A& B\\ & \end{array}\right)=p\left(\begin{array}{cc}& \\ A& B\end{array}\right)$ , are compactly expressed in the transformed coordinates as

$$\varphi \left(\begin{array}{cc}{s}_1& s_2\\ 0& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& 0\\ s_1& s_2\end{array}\right).$$ (9)

This is a much more compact form than Eq. (4), which entails eight of the original block probabilities.

In like manner, the stationarity constraints related to the 2 × 1 block probabilities [Eq. (5)] are equivalent to

$$\varphi \left(\begin{array}{cc}{s}_1& 0\\ s_3& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& s_1\\ 0& s_3\end{array}\right),$$ (10)

and the stationarity constraints related to individual pixels, [Eq. (6)], becomes

$$\varphi \left(\begin{array}{cc}s& 0\\ 0& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& s\\ 0& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& 0\\ s& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& 0\\ 0& s\end{array}\right).$$ (11)

The 16 2 × 2 block probabilities must of course also sum to 1 and this is equivalent to

$$\varphi \left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)=1.$$ (12)

The constraints (9), (10), (11), and (12) are still not independent, but their relationship to each other is much simpler than that of Eq. (4) and its analogs. Specifically, when expressed in terms of the transformed quantities ϕ, the constraints are nested: setting one of the arguments in Eqs. (9) or 10 to zero leads to Eq. (11), and setting both to zero leads to Eq. (12). This motivates our final step in setting up the coordinate system: ranking the quantities ϕ according to the number of arguments that are nonzero. The result is 10 independent quantities, as follows:

$$\alpha =\varphi \left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right),$$ (13)

$$\begin{array}{l}{\theta }_{⌟}=-\varphi \left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right),{\theta }_{⌞}=-\varphi \left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right),\\ {\theta }_{⌝}=-\varphi \left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right),{\theta }_{⌜}=-\varphi \left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right),\end{array}$$ (14)

$$\begin{array}{l}{\beta }_{-}=\varphi \left(\begin{array}{cc}1& 1\\ 0& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& 0\\ 1& 1\end{array}\right),\\ {\beta }_{\mid }=\varphi \left(\begin{array}{cc}1& 0\\ 1& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& 1\\ 0& 1\end{array}\right),\\ {\beta }_{\backslash }=\varphi \left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),\\ {\beta }_{/}=\varphi \left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),\end{array}$$ (15)

and

$$\gamma =-\varphi \left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right)=-\varphi \left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)=-\varphi \left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)=-\varphi \left(\begin{array}{cc}0& 0\\ 0& 1\end{array}\right).$$ (16)

(We have introduced minus signs in Eqs. (14) and (16) for consistency with previous work [22,23]).

Note that the expressions for γ, β, and θ involve ϕ’s with zero arguments. (Here and below, an unsubscripted β or θ denotes any one of the β’s or θ’s.) Thus, when expressed in terms of block probabilities, γ, β, and θ can be calculated from smaller blocks [as can be seen formally from Eq. (7)]. For example,

$${\theta }_{⌟}=p\left(\begin{array}{cc}& 1\\ 1& 1\end{array}\right)-p\left(\begin{array}{cc}& 0\\ 1& 1\end{array}\right)-p\left(\begin{array}{cc}& 1\\ 0& 1\end{array}\right)+p\left(\begin{array}{cc}& 0\\ 0& 1\end{array}\right)-p\left(\begin{array}{cc}& 1\\ 1& 0\end{array}\right)+p\left(\begin{array}{cc}& 0\\ 1& 0\end{array}\right)+p\left(\begin{array}{cc}& 1\\ 0& 0\end{array}\right)-p\left(\begin{array}{cc}& 0\\ 0& 0\end{array}\right),$$ (17)

$${\beta }_{-}=p(\begin{array}{cc}1& 1\end{array})-p(\begin{array}{cc}0& 1\end{array})-p(\begin{array}{cc}1& 0\end{array})+p(\begin{array}{cc}0& 0\end{array}),$$ (18)

and

$$\gamma =p(1)-p(0).$$ (19)

In sum, the linear transformation (7) replaces the 16 interdependent block probabilities by 10 independent quantities, {γ, β₋, β_|, β_\, β_/, θ_⌟, θ_⌜, θ_⌝, α}, which we denote collectively by ϕ_i (i ∈ {1, …, 10}). (The reverse transformation, from the ϕ_i to the block probabilities according to Eq. (8), is provided in Table 1). Each of these range from −1 to 1 and has a simple interpretation. γ captures the overall luminance bias of the image: γ = 1 means that all pixels are white, γ = −1 means that all pixels are black. The β’s capture the pair-wise statistics: β = 1 means that all pixels match its nearest neighbor (in the direction indicated by the subscript) and β = −1 means that they all mismatch. The θ’s capture the statistics of triplets of pixels arranged in an L: θ = 1 means that all such L-shapes contain either three white pixels or one white pixel and two black ones; θ = −1 means the opposite. α captures the statistics of quadruplets of pixels in a 2 × 2 block: α = 1 means that an even number of them are white and α = −1 means that an odd number are white. For an image in which all pixels are independently assigned to black and white, with equal probability, all of these coordinates are 0.

Table 1.

Conversion between Block Probabilities and Coordinates^a

1 × 1 blocks

$\begin{array}{lll}p(0)=\hfill & \frac{1}{2}(1\hfill & -1\gamma )\hfill \\ p(1)=\hfill & \frac{1}{2}(1\hfill & +1\gamma )\hfill \end{array}$

1 × 2 blocks

$\begin{array}{llll}p(\begin{array}{ll}0\hfill & 0\hfill \end{array})=\hfill & \frac{1}{4}(1\hfill & -2\gamma \hfill & +1\beta )\hfill \\ p(\begin{array}{ll}1\hfill & 0\hfill \end{array})=\hfill & \frac{1}{4}(1\hfill & \hfill & -1\beta )\hfill \\ p(\begin{array}{ll}0\hfill & 1\hfill \end{array})=\hfill & \frac{1}{4}(1\hfill & \hfill & -1\beta )\hfill \\ p(\begin{array}{ll}1\hfill & 1\hfill \end{array})=\hfill & \frac{1}{4}(1\hfill & +2\gamma \hfill & +1\beta )\hfill \end{array}$

2 × 2 blocks

$\begin{array}{llllllllllll}p\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & -4\gamma \hfill & +2{\beta }_{-}\hfill & +2{\beta }_{\mid }\hfill & +1{\beta }_{\backslash }\hfill & +1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & +1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & -2\gamma \hfill & \hfill & \hfill & -1{\beta }_{\backslash }\hfill & +1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & +1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & -2\gamma \hfill & \hfill & \hfill & +1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 1\\ 0& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & \hfill & +2{\beta }_{-}\hfill & -2{\beta }_{\mid }\hfill & -1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & +1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & +1\alpha )\hfill \\ p\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & -2\gamma \hfill & \hfill & \hfill & +1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & +1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 0\\ 1& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & \hfill & -2\beta \hfill & +2{\beta }_{\mid }\hfill & -1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & +1\alpha )\hfill \\ p\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & \hfill & -2\beta \hfill & -2{\beta }_{\mid }\hfill & +1{\beta }_{\backslash }\hfill & +1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & +1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & +1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & +2\gamma \hfill & \hfill & \hfill & -1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}0& 0\\ 0& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & -2\gamma \hfill & \hfill & \hfill & -1{\beta }_{\backslash }\hfill & +1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & +1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & \hfill & -2{\beta }_{-}\hfill & -2{\beta }_{\mid }\hfill & +1{\beta }_{\backslash }\hfill & +1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & +1\alpha )\hfill \\ p\left(\begin{array}{cc}0& 1\\ 0& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & \hfill & -2{\beta }_{-}\hfill & +2{\beta }_{\mid }\hfill & -1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & +1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & +1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & +2\gamma \hfill & \hfill & \hfill & +1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}0& 0\\ 1& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & \hfill & +2{\beta }_{-}\hfill & -2{\beta }_{\mid }\hfill & -1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & +1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & +2\gamma \hfill & \hfill & \hfill & +1{\beta }_{\backslash }\hfill & -1{\beta }_{/}\hfill & -1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & +2\gamma \hfill & \hfill & \hfill & -1{\beta }_{\backslash }\hfill & +1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & -1{\theta }_{⌞}\hfill & -1{\theta }_{⌜}\hfill & -1{\theta }_{⌝}\hfill & -1\alpha )\hfill \\ p\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)=\hfill & \frac{1}{16}(1\hfill & +4\gamma \hfill & +2{\beta }_{-}\hfill & +2{\beta }_{\mid }\hfill & +1{\beta }_{\backslash }\hfill & +1{\beta }_{/}\hfill & +1{\theta }_{⌟}\hfill & +1{\theta }_{⌞}\hfill & +1{\theta }_{⌜}\hfill & +1{\theta }_{⌝}\hfill & +1\alpha )\hfill \end{array}$

^aTabulated coefficients are determined from the inverse transformation [Eq. (8)] and the definitions [Eqs. (13) through (16)].

Each kind of coordinate thus corresponds to a “glider”—for γ, a single pixel; for β, a pair of pixels that share an edge or corner; for θ, a triplet of pixels in an L, and for α, four pixels in a 2 × 2 block. The value of the coordinate compares the fraction of positions in which the glider contains an even number of white pixels to the fraction of positions in which the glider contains an odd number of white pixels. Specifically, for an image R, the value of a coordinate ϕ_i can be expressed as

$${\varphi }_i(R)=\frac{n_{+}(R,i)-n_{-}(R,i)}{n(R,i)},$$ (20)

where n₊(R, i) denotes the number of placements of the glider for ϕ_i that contain an even number of white pixels, n₋(R, i) denotes the number of placements that contain an odd number of white pixels, and n(R, i) = n₊(R, i) + n₋(R, i) denotes the total number of placements. We call n₊(R, i) and n₋(R, i) the “parity counts.” In sum, the gamut of each coordinate ϕ_i is from +1 to −1: a value of +1 indicates that all glider placements contain an even number of white pixels (n₋(R, i) = n(R, i)) and a coordinate value of −1 indicates that all placements contain an odd number of white pixels (n₋(R, i) = n(R, i)).

We mention that there are bounds on certain linear combinations of the coordinates because block probabilities and their sums must be nonnegative. Some examples are: the expressions for $p(\begin{array}{cc}0& 0\end{array})$ and $p(\begin{array}{cc}1& 1\end{array})$ (Table 1) together imply that

$$2\mid \gamma \mid \le 1+{\beta }_{-};$$ (21)

the expressions for $p\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)+p\left(\begin{array}{cc}1& 1\\ 0& 0\end{array}\right)+p\left(\begin{array}{cc}0& 0\\ 0& 1\end{array}\right)+p\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)$ and similar quantities together imply that

$$\mid {\theta }_{⌟}\mid +\mid {\theta }_{⌞}\mid \le 1+{\beta }_{-};$$ (22)

and the expressions for $p\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)+p\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)+p\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)+p\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)$ and similar quantities together imply that

$$\mid {\theta }_{⌟}\mid +\mid {\theta }_{⌜}\mid \le 1+{\beta }_{\backslash }.$$ (23)

C. Formal Solution and Overview of Approach

Our aim is to construct images in which one or more of these coordinates are assigned a value and all other image statistics are chosen so that the ensemble is as random as possible. In principle, this consists of two steps: first, determination of the image ensemble whose entropy is maximum, given the constraints of the coordinates ϕ_i and, second, unbiased sampling of images within this ensemble. The first step has a formal solution that follows readily from general properties of maximum-entropy distributions. However, the formal solution is not a constructive one: that is, while it determines the unique maximum-entropy distribution, it does not show how to create it. The formal solution therefore does not directly address the second step, that of choosing typical images from within this distribution. Therefore, we need to develop special-purpose constructive algorithms to sample the distribution and show that the samples they construct correspond to the distribution specified by the formal solution.

The formal solution is a specification of the probability p(R) of encountering a large block R in an image drawn at random from the ensemble (or, equivalently, in a random location within a single typical image). These probabilities are to be determined so that the entropy

$$H=-\sum _{R}p(R)lnp(R)$$ (24)

is maximized, subject to the block-probability constraints ${\varphi }_i^0$ for one or more of the coordinates ϕ_i. The constraints ${\varphi }_i^0$ refer to the expected value of a coordinate ϕ_i(R), averaged over all regions placements on R:

$${\varphi }_i^0=\langle {\varphi }_i(R)\rangle =\sum _{R}p(R){\varphi }_i(R).$$ (25)

In view of Eq. (20), this can be written as

$${\varphi }_i^0=\sum _{R}p(R)\frac{n_{+}(R,i)-n_{-}(R,i)}{n(R,i)}.$$ (26)

Note that n(R, i), which is the number of ways that the glider corresponding to ϕ_i can be placed on the block R, depends only on the shape of the glider and of R, but is independent of how R is colored. Thus, n(R, i) is constant for all terms in the above sum.

We use a standard approach to maximize the entropy [Eq. (24)] under the constraints of Eq. (26), namely, Lagrange multipliers. To apply the Lagrange multiplier method, we introduce a multiplier λ_i for each constraint [Eq. (26)], as well as a multiplier λ₀ for the normalization Σ_Rp(R) = 1. We then maximize

$$Q=-\sum _{R}p(R)lnp(R)+\sum _i{\lambda }_i\sum _{R}p(R)\frac{n_{+}(R,i)-n_{-}(R,i)}{n(R,i)}+{\lambda }_0\sum _{R}p(R),$$ (27)

by setting ∂Q/∂p(S) = 0 and considering each of the p(S)’s to be independent. This yields equations for the p(R)’s in terms of the Lagrange multipliers λ_i, which then need to be solved to satisfy the constraints of Eq. (26) and the normalization constraint. Importantly, the maximizing distribution p(R) is guaranteed to be unique, since the constraints [Eq. (26)] are linear and entropy is a convex function. That is, there cannot be two separate local maxima—because if there were, then a mixture of them would necessarily yield a solution of even higher entropy.

To carry out the maximization, we calculate ∂Q/∂p(S) from Eq. (27) and set it to 0:

$$\frac{\partial Q}{\partial p(S)}=-1-lnp(S)+\sum _i{\lambda }_i\frac{n_{+}(S,i)-n_{-}(S,i)}{n(S,i)}+{\lambda }_0.$$ (28)

Setting this to 0 yields a formal solution:

$$p(S)=exp\left({\mu }_0+\sum _i{\mu }_i(n_{+}(S,i)-n_{-}(S,i))\right),$$ (29)

where we have used μ₀ = λ₀ − 1 and μ_i = λ_i/n(S, i). (The latter is justified since n(S, i), the number of placements of the glider for ϕ_i, depends only on i and the size of the region S and not on its contents.)

As is typical of maximum-entropy problems, we can eliminate the multiplier μ₀ by enforcing the normalization constraint:

$$p(S)=\frac{Z(S)}{Z},$$ (30)

where

$$Z(S)=exp\left(\sum _i{\mu }_i(n_{+}(S,i)-n_{-}(S,i))\right)$$ (31)

and

$$Z=\sum _{S}Z(S).$$ (32)

Z corresponds to the “partition function” that is central to the maximum-entropy problems that arise in statistical mechanics. As in statistical mechanics, the partition function provides for a concise formal representation of the constraints. Combining Eqs. (32), (31), and (26) yields

$$\frac{\partial lnZ}{\partial {\mu }_i}=\frac{1}{Z}\frac{\partial Z}{\partial {\mu }_i}=n(S,i){\varphi }_i^0.$$ (33)

We note that Eq. (29) [or Eqs. (30) and (31)] have an intuitive interpretation that extends the tie-in to statistical-mechanics. Since n₊(S, i) and n₋(S, i) count the number of occurrences of even- and odd-parity counts of white pixels for each placement of the glider for ϕ_i, we can view the Lagrange multiplier μ_i as an kind of interaction energy within each placement of the glider. We calculate Z(S) by inspecting each glider placement, one by one, and accumulating counts for n₊(S, i) and n₋(S, i). If the number of white pixels in the glider is even, n₊(S, i) is incremented, which in turn changes the probability of the configuration S by a factor of e^μi. If the number of pixels is odd, n₋(S, i) is incremented and the probability is changed by the reciprocal of that factor.

Although Eq. (30) provides an expression for the block probabilities of the unique maximum-entropy ensemble, it is not a constructive solution. The reason is that the Lagrange multipliers μ_i are as yet unknown. Finding them requires solving the constraint equations for the counts n₊(S, i) and n₋(S, i) [Eq. (26) or, equivalently, Eq. (33)], which are nonlinear. If this can be done, then the image ensemble is explicitly specified via Eq. (30) and we can then choose random samples from within it. In some cases (Section 2.4–Section 2.7), the direct approach works; in other cases, another strategy appears necessary (Section 2.8).

D. Ensembles Specified by a Bias on the Number of White and Black Pixels

We consider first the simplest case, in which there is only a single constraint and it is a constraint on λ, the bias between the number of white and black pixels. Since there are no correlations between pixels, the solution to the maximum-entropy problem is well known: an image ensemble in which each pixel is independently colored (an independent, identically-distributed (IID) distribution). The probabilities of white and black pixels are determined by p(1) − p(0) = λ [Eq. (19)] and the normalization constraint p(1) + p(0) = 1. Nevertheless, it is helpful to carry out this simple example in detail, as it illustrates how the above formalism works in a situation in which the constraint equations can be solved. This will also indicate how elements of this IID solution can be generalized.

We begin by calculating the partition function, Eq. (32). Here, there is only one multiplier μ₁. Substituting Eq. (31) into Eq. (32) yields.

$$Z=\sum _{S}Z(S)=\sum _{S}exp\left({\mu }_1(n_{+}(S,1)-n_{-}(S,1))\right).$$ (34)

This is a sum over all possible colorings S. For each coloring S, n₊(S, 1) is the number of black pixels (i.e., a 1-block containing an even number of white pixels) and n₋(S, 1) is the number of white pixels (i.e., a 1-block containing an odd number of white pixels). Since each term of the sum [Eq. (34)] depends only on the number of pixels of each color and not their arrangement, we can evaluate the sum by grouping the configurations S according to the number of black and white pixels (n₊ and n₋, with n₊ + n₋ = n) that it contains. The number of such configurations is given by the binomial coefficient $\left(\begin{array}{c}n\\ n_{+}\end{array}\right)=\frac{n!}{n_{+}!n_{-}!}$. With this regrouping, we find,

$$Z=\sum _{n_{+}+n_{-}=n}\frac{n!}{n_{+}!n_{-}!}exp\left({\mu }_1(n_{+}-n_{-})\right).$$ (35)

Applying the binomial theorem yields a simple expression for the partition function:

$$Z={(e^{{\mu }_1}+e^{-{\mu }_1})}^n.$$ (36)

Equation (33) now yields the relationship between the unknown Lagrange multiplier μ₁ and the constraint, ${\varphi }_1^0=-\gamma$:

$$-\gamma ={\varphi }_1^0=\frac{1}{n}\frac{\partial lnZ}{\partial {\mu }_1}=\frac{e^{{\mu }_1}-e^{-{\mu }_1}}{e^{{\mu }_1}+e^{-{\mu }_1}}=tanh({\mu }_1).$$ (37)

The Lagrange multiplier μ₁ is thus given by

$${\mu }_1=-{tanh}^{-1}(\gamma )=\frac{1}{2}ln\frac{1-\gamma }{1+\gamma }$$ (38)

so the partition function [Eq. (36)] is equal to

$$\begin{array}{l}Z={\left(\sqrt{\frac{1+\gamma }{1-\gamma }}+\sqrt{\frac{1-\gamma }{1+\gamma }}\right)}^n={\left(\sqrt{\frac{1+\gamma }{1-\gamma }}\left(1+\frac{1-\gamma }{1+\gamma }\right)\right)}^n\\ ={\left(\frac{2}{\sqrt{(1+\gamma )(1-\gamma )}}\right)}^n.\end{array}$$ (39)

We can now obtain an expression for the probability of any configuration. We start with Eq. (30), p(S) = Z(S)/Z, and substitute the value of μ₁ determined by Eq. (38) into Eq (31) for Z(S). This yields

$$p(S)=\frac{1}{Z}exp{\mu }_1(n_{+}(S,1)-n_{-}(S,1))=\frac{1}{Z}{\left(\frac{1-\gamma }{1+\gamma }\right)}^{\frac{n_{+}(S,1)-n_{-}(S,1)}{2}}.$$ (40)

We then use Eq. (39) for the partition function Z:

$$p(S)=2^{-n}{((1+\gamma )(1-\gamma ))}^{n/2}{\left(\frac{1-\gamma }{1+\gamma }\right)}^{\frac{n_{+}(S,1)-n_{-}(S,1)}{2}}.$$ (41)

Making use of the relationship n = n₊(S, 1) = n₋(S, 1) leads to the desired result, which has a simple and symmetric form:

$$p(S)={\left(\frac{1-\gamma }{2}\right)}^{n_{+}(s,1)}{\left(\frac{1+\gamma }{2}\right)}^{n\_(s,1)}$$ (42)

Equation (42) thus defines the maximum-entropy ensemble constrained by ${\varphi }_1^0=-\gamma$. The result is not surprising and corresponds to an IID process: if a configuration S has n₊(S, 1) black pixels and n₋(S, 1) white pixels, then its probability is a product of n₊(S, 1) copies of the probability of a black pixel ( $p(0)=\frac{1-\gamma }{2}$) and n₋(S, 1) copies of the probability of a white pixel ( $p(1)=\frac{1+\gamma }{2}$).

There are two important aspects of this analysis that are crucial for the more complex cases that we consider below. First, we note that Eq. (42) does more than just define the probability of a configuration S—it also provides a way of generating samples that have the desired probability distribution. Specifically, it indicates that each pixel’s color can be assigned independently. Each pixel is considered in turn and it is colored white with probability $p(1)=\frac{1+\gamma }{2}$ and black with probability $p(0)=\frac{1-\gamma }{2}$. This construction, rather than the explicit value of p(S), is our goal. For other kinds of textures, we will be able to sample the distribution, but we may not be able to write an explicit expression for the probability of any given configuration. The latter requires explicit summation of the partition function [Eq. (32)], as well as solution of the constraint equations, Eq. (33).

The second point is even though we only specified one coordinate (in this case, ϕ₁ = −γ), the maximum-entropy construction determined the values of the other coordinates, and these values turn out to be nonzero. This is readily seen from Eq. (42): the probability of a two-pixel block S with two white pixels is $\frac{{(1+\gamma )}^2}{4}$; with one white pixel, $\frac{(1+\gamma )(1-\gamma )}{4}$; and with no white pixels, $\frac{{(1-\gamma )}^2}{4}$. From these, it follows [e.g., from Eq. (18)] that β = γ². Similar calculations show that θ = γ³ and α = γ⁴. That is, the trajectories specified by maximum entropy (here, β, θ, α) = (γ², γ³, γ⁴)), are curved with respect to the coordinate axes, a phenomenon that is characteristic of “information geometry” [24]. Near the origin (i.e., near γ = 0), this curvature is small and the maximum-entropy trajectories approximate the coordinate axes. As our psychophysical data will show, this mild curvature does not interfere with measurement of meaningful thresholds along the coordinate axes.

E. Ensembles Specified by One Parameter

The above analysis immediately puts us in a position to construct maximum-entropy ensembles specified by a single-parameter constraint ${\varphi }_i={\varphi }_i^0$, for parameters other than ϕ₁ = − γ. The main point is that we can construct samples S of these ensembles in a pixel-by-pixel fashion. This will lead to expressions for the probability of a sample p(S) that are similar to Eq. (42). As is the case for ϕ₁ = −γ, this is equivalent to an expression of the form [Eq. 29)], which demonstrates that it is indeed maximum-entropy.

To begin, we note that each of the coordinates ϕ_i corresponds to a “glider”, i.e., a configuration of pixels that are relevant to the calculation of n₊(S, i) and n₋(S, i) [see comments following Eq. (33)]. We now assign colors to each pixel in S in sequence: top row to bottom row and left to right. The first pixel, a₁₁, is assigned to white or black with equal probability. As each subsequent pixel is considered, we determine whether it is the last pixel to be assigned within a glider. For example, in the case of the glider for β₋ (a 1 × 2 block), the second pixel completes a glider (at positions a₁₁ and a₁₂), as does each subsequent pixel within each row. In the case of the glider for α (a 2 × 2 block), the entire first row does not complete any gliders, but the second and subsequent pixels in the later rows do so.

The assignment of a color depends on whether the pixel completes a glider. If it does not, it is randomly assigned to white or black, each with probability 0.5. If it does complete a glider, we need to choose whether to give it a color which makes the total number of white pixels within the glider even or odd. We do the former with probability $\frac{1+{\varphi }_i^0}{2}$ and the latter with probability $\frac{1-{\varphi }_i^0}{2}$. The average number of gliders that contribute to n₊(S, i) is thus $n(S,i)\frac{1+{\varphi }_i^0}{2}$ and the average number of gliders that contribute to n₋(S, i) is thus $n(S,i)\frac{1-{\varphi }_i^0}{2}$, where, as above, n(S, i) is the number of times that the glider can be placed entirely within the region S.

We now verify that this construction has the required properties. The first requirement is that the expected value of the coordinate ϕ_i is, in fact, ${\varphi }_i^0$ (i.e., that the construction satisfies the constraint). This is straightforward and follows from the biased assignment of colors that is invoked when a pixel completes a glider:

$$\langle {\varphi }_i\rangle =\frac{\langle n_{+}(S,i)\rangle -\langle n_{-}(S,i)\rangle }{n(S,i)}=\frac{1+{\varphi }_i^0}{2}-\frac{1+{\varphi }_i^0}{2}={\varphi }_i^0.$$ (43)

The other requirement is that p(S) is of the form of Eq. (29), which means that it is maximum-entropy. To show this, we begin by noting that, according to the above construction, the assignments of pixels to colors were made in one of three ways. Some of the pixels were assigned to white or black with equal probability, since these pixels did not complete a glider. For a region S of size n, the number of such pixels is n_init = n − n(S, i), since n(S, i) is the number of pixels at which a glider was completed. After these initial pixels were assigned, the others (the ones that completed gliders) were assigned in a biased fashion. There were n₊(S, i) such assignments, each with probability $\frac{1+{\varphi }_i^0}{2}$, that resulted in an even number of white pixels within a glider and there were n₋(S, i) assignments, each with probability $\frac{1-{\varphi }_i^0}{2}$, that resulted in an odd number of white pixels within a glider. Thus,

$$p(S)={\left(\frac{1}{2}\right)}^{n-n(S,i)}{\left(\frac{1+{\varphi }_i^0}{2}\right)}^{n_{+}(S,i)}{\left(\frac{1-{\varphi }_i^0}{2}\right)}^{n_{-}(S,i)}$$ (44)

analogous to Eq. (42). Using the relationship n(S, i) = n₊(S, i) + n₋(S, i), this is seen to be equivalent to

$$p(S)=2^{-n}{((1+{\varphi }_i^0)(1-{\varphi }_i^0))}^{n(S,i)/2}{\left(\frac{1+{\varphi }_i^0}{1-{\varphi }_i^0}\right)}^{\frac{n_{+}(S,i)-n_{-}(S,i)}{2}}.$$ (45)

Since n(S, i), the number of pixels at which a glider was completed, is independent of the way in which S is colored, Eq. (45) is in the form of Eq. (29). Thus, the construction is indeed maximum-entropy and satisfies the coordinate constraints.

Equation (44) or, equivalently Eq. (45), summarizes how the analysis in the previous section for ϕ₁ extends to each of the other coordinates. For these other coordinates, whose gliders are larger than a single pixel, there is an initial step in which n_init = n − n(S, i) pixels are colored at random. Following this, the colors of the remaining n − n_init = n₊(S, i) + n₋(S, i) pixels are assigned to make the parity of the white pixels within the glider as either even or odd, with a probability ratio of $\frac{1+{\varphi }_i^0}{1-{\varphi }_i^0}$. Note that while this choice (even versus odd) is independent at each pixel, the resulting color (white or black) depends on the previous assignments. Thus, the exponents n₊(S, i) and n₋(S, i) tally the choices of even and odd, not the colors themselves.

For reference, we restate the results of the previous section in a form that applies to all coordinates. The generic form of the partition function [Eq. (35)] is

$$Z=2^{n_{\text{init}}}\sum _{n_{+}+n_{-}=n-n_{\text{init}}}\frac{(n-n_{\text{init}})!}{n_{+}!n_{-}!}exp({\mu }_i(n_{+}-n_{-})),$$ (46)

which, after applying the binomial theorem, becomes

$$Z=2^{n_{\text{init}}}{(e^{{\mu }_i}+e^{-{\mu }_i})}^{n-n_{\text{init}}}.$$ (47)

The generic form of Eq. (38) for the Lagrange multiplier μ_i is

$${\mu }_i={tanh}^{-1}({\varphi }_i^0)=\frac{1}{2}ln\frac{1+{\varphi }_i^0}{1-{\varphi }_i^0},$$ (48)

so the partition function [Eq. (47)] can be rewritten as

$$Z=2^{n_{\text{init}}}{\left(\frac{2}{\sqrt{(1+{\varphi }_i^0)(1-{\varphi }_i^0)}}\right)}^{n-n_{\text{init}}}.$$ (49)

Figure 1 shows examples of images generated according to this construction, for each of the coordinates. As can be seen from these examples, each coordinate ϕ_i leads to a different kind of structure. All are visually salient, but to different degrees—an informal observation that we will quantify below (Section 4).

Fig. 1.

The image-statistic coordinate axes. Each patch is a typical sample of an image ensemble in which the indicated statistic is set to a nonzero value and higher-order statistics are determined by maximum entropy.

Interestingly, these differences in salience are solely due the processing limitations of the visual system: from the point of view of an ideal observer (limited only by the statistics of sampling of images), the alterations in image statistics associated with movement along each of the coordinates is equally salient. This property of the coordinates ϕ_i is demonstrated in Appendix B.

Finally, we mention that specification of a nonzero value for one coordinate can lead to nonzero values for the others, as is the case for ϕ₁ = −γ. This happens for β₋ or β_|: in these cases, α = β². This can be seen by calculating the 2 × 2 block probabilities from Eq. (44) and then calculating $\alpha =\varphi \left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)$ from Eq. (7).

F. Ensembles Specified by Two Parameters, along One Dimension

The next sections consider the construction of maximum-entropy ensembles specified by two parameters, say ϕ_i and ϕ_j. We begin with the simplest case, in which the gliders associated with these parameters lie within a single spatial dimension (i.e., a row, a column, or a diagonal). For definiteness, we focus on γ paired with β₋, but the analysis applies equally well to γ paired with one of the other β’s.

Since the coordinates γ and β₋ only refer to correlations within rows, the rows of the maximum-entropy ensemble must be independent. It therefore suffices to provide an algorithm to generate a row of the image and then to apply this algorithm separately to each row. To create each row, we use a recursive procedure, a Markov process, to define each pixel assignment. We show that probabilities of the resulting image samples are consistent with Eq. (29), which confirms the maximum-entropy property. A Markov process is a natural strategy for a maximum-entropy construction, since each state of a Markov process depends only on the previous one.

The Markov property, along with the 1 × 2 block probabilities, specifies the probabilities of all 1 × k blocks. To see this, we first determine the probabilities of the 1 × 3 blocks:

$$p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})=p(\begin{array}{cc}{A}_1& A_2\end{array})p(A_3\mid A_2)=\frac{p(\begin{array}{cc}{A}_1& A_2\end{array})p(\begin{array}{cc}{A}_2& A_3\end{array})}{P(A_2)}.$$ (50)

Here, the first equality expresses the Markov property (that the assignment of A₃ depends only on the state of A₂ and not on A₁) and the second equality follows from the fact that joint probability p(X, Y) is related to the conditional probability p(YjX) by p(X, Y) = p(X)p(Y|X).

Equation (50), applied recursively, specifies the probabilities of all 1 × k blocks:

$$p(A_1\cdots A_k)=\frac{p(\begin{array}{cc}{A}_1& A_2\end{array})p(\begin{array}{cc}{A}_2& A_3\end{array})•\dots •p(\begin{array}{cc}{A}_{k-1}& A_k\end{array})}{p(A_2)p(A_3)•\dots •p(A_{k-1})}.$$ (51)

The numerator is the product of all 1 × 2 block probabilities contained within the 1 × k block; the denominator is the product of all the singleton probabilities, excluding both ends. We note that the 1 × 2 block and singleton probabilities are known, since they are determined from the constraints ϕ₁ = −γ and ϕ₂ = β₋ via Eq. (8) (also, see Table 1).

To show that the probabilities of image samples generated in this fashion are consistent with Eq. (29), we proceed as follows. The probability of an image S is a product of terms such as Eq. (51), one for each row. For each of the four kinds of 1 × 2 blocks, the corresponding block probability will occur as a factor in the numerator every time that this block appears in S. A similar reasoning applies to the denominator. Thus,

$$p(S)=\frac{p{(\begin{array}{cc}0& 0\end{array})}^{n_{00}}p{(\begin{array}{cc}0& 1\end{array})}^{n_{01}}p{(\begin{array}{cc}1& 0\end{array})}^{n_{10}}p{(\begin{array}{cc}1& 1\end{array})}^{n_{11}}}{p{(0)}^{n_0}p{(1)}^{n_1}},$$ (52)

where n_AB counts the number of $(\begin{array}{cc}A& B\end{array})$ blocks in S and n_A counts the number of A-singletons in the interiors of the rows of S. To show that these probabilities are consistent with Eq. (29), the key step is to relate the block counts n_AB and n_A in the above equation to the parity counts n₊(S, i) and n₋(S, i). These count the occurrences of even- and odd-parity 1 × 2 blocks (n_±(S, 2)) and the black and white singletons (n_±(S, 1)). The relationship between the block counts and the parity counts follows from the transformation between the block probabilities and coordinates [Eq. (7)] and Table 1). For example,

$$n_{00}={np}_{00}(S)=\frac{n}{4}(1-2\gamma (S)+{\beta }_{-}(S)),$$ (53)

where p_X (S) indicates the probability of an X block in S and ϕ(S) indicates the transformed coordinate ϕ evaluated from the block probabilities within S. Note that Eq. (53) neglects “end effects”, but this is justified because in the large-k limit, the interior pixels are far more numerous than the edge pixels and consequently dominate the product [Eq. (52)].

Equation (53) and its analogs for the other blocks, along with Eq. (20), lead to the desired relationships between the block counts and the parity counts n_±(S, i):

$$\begin{array}{l}{n}_{00}=\frac{n}{4}+\frac{n_{+}(S,2)-n_{-}(S,2)}{4}+\frac{n_{+}(S,1)-n_{-}(S,1)}{2}\\ n_{01}=\frac{n}{4}-\frac{n_{+}(S,2)-n_{-}(S,2)}{4}\\ n_{10}=\frac{n}{4}-\frac{n_{+}(S,2)-n_{-}(S,2)}{4}\\ n_{11}=\frac{n}{4}+\frac{n_{+}(S,2)-n_{-}(S,2)}{4}-\frac{n_{+}(S,1)-n_{-}(S,1)}{2}\\ n_0=\frac{n}{2}+\frac{n_{+}(S,1)-n_{-}(S,1)}{2}\\ n_1=\frac{n}{2}-\frac{n_{+}(S,1)-n_{-}(S,1)}{2}.\end{array}$$ (54)

Substitution of Eqs. (54) into Eq. (52) yields an equation of the form Eq. (29), confirming the maximum-entropy property of the construction.

G. Ensembles Specified by Two Parameters, along Two Dimensions: Pickard Case

Next we continue the construction of ensembles specified by a pair of constraints, but now consider the case when these constraints correspond to gliders that involve both spatial dimensions. The natural approach is to attempt to extend the Markov construction to two dimensions. However, it is not clear whether this approach will work, as the correlations in the two dimensions may interact. As we will see, the extension works in most cases (the cases in which the “Pickard conditions” [21] hold), but not in all. We first discuss these cases and then handle each of the “non-Pickard” cases separately.

Extending the Markov construction to two dimensions consists of two stages: creating 2 × k blocks by a Markov process and then assembling these blocks by a second Markov process. The rationale for creating the rows in pairs (i.e., 2 × k blocks rather than 1 × k blocks) is that the second row is needed to allow for correlations in the vertical dimension.

To determine the feasibility of this approach, we begin with the row process and calculate the probability of a 2 × 3 block, as a Markov process on 2 × 2 blocks with one column of overlap:

$$\begin{array}{l}p\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\end{array}\right)=p\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)p\left(\begin{array}{cc}{A}_{12}& A_{13}\\ A_{22}& A_{23}\end{array}|\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)\\ =\frac{p\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)p\left(\begin{array}{cc}{A}_{12}& A_{13}\\ A_{22}& A_{23}\end{array}\right)}{p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)}.\end{array}$$ (55)

That is, the probability of a 2 × 3 block is the product of the probabilities of the 2 × 2 blocks it contains, divided by the probability of the 2 × 1 block at their intersection. Once we have created a 2 × k row by a Markov process, we can consider assembling these rows via a second Markov process. At the very least, we need to assemble two 2 × 3 rows to form a 3 × 3 block:

$$p\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right)=\frac{p\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\end{array}\right)p\left(\begin{array}{ccc}{A}_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right)}{p(\begin{array}{ccc}{A}_{21}& A_{22}& A_{23}\end{array})},$$ (56)

Here, the denominator, the probability of the 1 × 3 block intersection, is determined by “marginalizing” Eq. (55), i.e., summing over the possible states of the pixels A_1k that are in the previously determined row:

$$\begin{array}{l}p(\begin{array}{ccc}{A}_{21}& A_{22}& A_{23}\end{array})=\sum _{A_{11},A_{12},A_{13}}p\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\end{array}\right)\\ =\sum _{A_{11},A_{12},A_{13}}\frac{p\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)p\left(\begin{array}{cc}{A}_{12}& A_{13}\\ A_{22}& A_{23}\end{array}\right)}{p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)}\\ =\sum _{A_{12}}\frac{p\left(\begin{array}{cc}& A_{12}\\ A_{21}& A_{22}\end{array}\right)p\left(\begin{array}{cc}{A}_{12}& \\ A_{22}& A_{23}\end{array}\right)}{\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)}.\end{array}$$ (57)

Equations (56) and (57) reveal an issue that did not arise in the one-dimensional case: we need to verify that the probabilities of the lower-row 2 × 2 subblocks of Eq. (56) are consistent with the probabilities of the upper-row 2 × 2 blocks that we started with. Here, the Markov processes along the two dimensions may interact, via the 1 × 3 block probabilities of Eq. (57). So stability of the 2 × 2 block probabilities across rows is not guaranteed. For the one-dimensional case (Section 2.F.), this issue did not arise, since each row was created independently.

1. Pickard Conditions

Pickard [21] identified conditions on the block probabilities that not only guarantee the above stability, but also something much stronger: that the two-dimensional Markov construction samples a maximum-entropy distribution, constrained by the 2 × 2 block probabilities (see also [25]). We state the Pickard conditions and then discuss how they fulfill the above need.

One set of Pickard conditions is that

$$\begin{array}{l}p\left(\begin{array}{cc}& B\\ C& D\end{array}\right)p(D)=p(\begin{array}{cc}C& D\end{array})p\left(\begin{array}{c}B\\ D\end{array}\right)\text{and}\\ p\left(\begin{array}{cc}A& B\\ C& \end{array}\right)p(A)=p(\begin{array}{cc}A& B\end{array})p\left(\begin{array}{c}A\\ C\end{array}\right).\end{array}$$ (58)

This condition may be mirrored in either the horizontal or vertical axis to obtain an alternative set of conditions [not equivalent to Eq. (58)]:

$$\begin{array}{l}p\left(\begin{array}{cc}A& \\ C& D\end{array}\right)p(C)=p(\begin{array}{cc}C& D\end{array})p\left(\begin{array}{c}A\\ C\end{array}\right)\text{and}\\ p\left(\begin{array}{cc}A& B\\ & D\end{array}\right)p(B)=p(\begin{array}{cc}A& B\end{array})p\left(\begin{array}{c}B\\ D\end{array}\right).\end{array}$$ (59)

As Pickard showed (see also [25]), if a set of block probabilities satisfies both halves of (58), or both halves of (59), then the Markov algorithm will generate maximum-entropy samples. Pickard [21] stated the conditions in terms of conditional probabilities, e.g.

$$\begin{array}{l}p\left(\left(\begin{array}{cc}& B\\ C& D\end{array}\right)|D\right)=p((\begin{array}{cc}C& D\end{array})\mid D)p\left(\left(\begin{array}{c}B\\ D\end{array}\right)|D\right)\text{and}p\left(\left(\begin{array}{cc}A& B\\ C& \end{array}\right)|A\right)\\ =p((\begin{array}{cc}A& B\end{array})\mid A)p\left(\left(\begin{array}{c}A\\ C\end{array}\right)|A\right).\end{array}$$ (60)

This form emphasizes that the Pickard conditions effectively factorize the way that the two dimensions interact; Eq. (60) is readily seen to be equivalent to Eq. (58) above according to the rules of conditional probabilities.

While we do not reproduce Pickard’s proof that either set of conditions guarantees that construction is maximum-entropy, we carry out a simpler calculation that provides an intuition for why this is true: we show how the Pickard conditions are related to the stability of the 2 × 2 block probabilities. Additionally—and this will be useful in situations when the Pickard conditions do not hold—the calculation shows that half of a Pickard condition simplifies the expression for 1 × 3 (or 3 × 1) blocks. In particular, we will show that the first half of either Eq. (58) or Eq. (59) simplifies the expression for 1 × 3 block probabilities, when the Markov process is run from left to right and top to bottom. This, in turn, allows us to show that the 2 × 2 block probabilities are stable for a left-to-right, top-to-bottom process. Consequently, when both halves of a Pickard condition hold, then the 2 × 2 block probabilities are stable when the two-dimensional Markov process is run from left-to-right and then from top-to-bottom OR, from right-to-left and then from bottom-to-top. Intuitively, this stability and reversibility are the reasons that the Markov algorithm is a maximum-entropy construction that satisfies the desired constraints (see [21] and [25] for background).

To show that the first half of the Pickard condition simplifies the expression for the 1 × 3 block probabilities, we calculate as follows:

$$p(\begin{array}{ccc}U& V& W\end{array})=\sum _X\frac{p\left(\begin{array}{cc}& X\\ U& V\end{array}\right)p\left(\begin{array}{cc}X& \\ V& W\end{array}\right)}{p\left(\begin{array}{c}X\\ V\end{array}\right)}=\sum _X\frac{p(\begin{array}{cc}U& V\end{array})p\left(\begin{array}{c}X\\ V\end{array}\right)p\left(\begin{array}{cc}X& \\ V& W\end{array}\right)}{p(V)p\left(\begin{array}{c}X\\ V\end{array}\right)}=\sum _X\frac{p(\begin{array}{cc}U& V\end{array})p\left(\begin{array}{cc}X& \\ V& W\end{array}\right)}{p(V)}=\frac{p(\begin{array}{cc}U& V\end{array})p(\begin{array}{cc}V& W\end{array})}{p(V)},$$ (61)

where the first equality is from Eq. (57), the second equality follows from the first half of the Pickard condition [Eq. (58)], and the final equality follows by marginalizing over X.

This simplified expression for 1 × 3 block probabilities, along with Eqs. (55) and (56), combine to provide an expression for the 3 × 3 block probabilities, which we need to determine whether the 2 × 2 probabilities are stable:

$$\begin{array}{l}p\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right)=\frac{p\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\end{array}\right)p\left(\begin{array}{ccc}{A}_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right)}{p(\begin{array}{ccc}{A}_{21}& A_{22}& A_{23}\end{array})}\\ =\frac{p\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)p\left(\begin{array}{cc}{A}_{12}& A_{13}\\ A_{22}& A_{23}\end{array}\right)}{p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)}\frac{p\left(\begin{array}{cc}{A}_{21}& A_{22}\\ A_{31}& A_{32}\end{array}\right)p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right)}{p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)}\frac{1}{p(\begin{array}{ccc}{A}_{21}& A_{22}& A_{23}\end{array})}\\ =\frac{p\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)p\left(\begin{array}{cc}{A}_{12}& A_{13}\\ A_{22}& A_{23}\end{array}\right)p\left(\begin{array}{cc}{A}_{21}& A_{22}\\ A_{31}& A_{32}\end{array}\right)p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right)p(A_{22})}{p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)p(\begin{array}{cc}{A}_{21}& A_{22}\end{array})p(\begin{array}{cc}{A}_{22}& A_{23}\end{array})}.\end{array}$$ (62)

To show that the 2 × 2 probabilities are stable, we show that the distribution of 2 × 2 blocks in the interior of the image is identical to their distribution in the rows and columns that have already been generated. We carry this out by marginalizing over the states of the pixels in the first row and first column of the left-hand-side of 3 × 3 block probabilities [Eq. (62)] and then use the first half of the Pickard condition (58) to simplify the resulting expression:

$$\begin{array}{l}\sum _{A_{11},A_{12},A_{13},A_{21},A_{31}}p\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right)=\sum _{A_{11},A_{12},A_{13},A_{21},A_{31}}\frac{p\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)p\left(\begin{array}{cc}{A}_{12}& A_{13}\\ A_{22}& A_{23}\end{array}\right)p\left(\begin{array}{cc}{A}_{21}& A_{22}\\ A_{31}& A_{32}\end{array}\right)p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right)p(A_{22})}{p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)p(\begin{array}{cc}{A}_{21}& A_{22}\end{array})p(\begin{array}{cc}{A}_{22}& A_{23}\end{array})}\\ =\sum _{A_{12},A_{21}}p\left(\begin{array}{cc}& A_{12}\\ A_{21}& A_{22}\end{array}\right)\frac{p\left(\begin{array}{cc}{A}_{12}& \\ A_{22}& A_{23}\end{array}\right)p\left(\begin{array}{cc}{A}_{21}& A_{22}\\ & A_{32}\end{array}\right)p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right)p(A_{22})}{p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)p(\begin{array}{cc}{A}_{21}& A_{22}\end{array})p(\begin{array}{cc}{A}_{22}& A_{23}\end{array})}\\ =\sum _{A_{12},A_{21}}\frac{p(\begin{array}{cc}{A}_{21}& A_{22}\end{array})p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)}{p(A_{22})}\frac{pp\left(\begin{array}{cc}{A}_{12}& \\ A_{22}& A_{23}\end{array}\right)p\left(\begin{array}{cc}{A}_{21}& A_{22}\\ & A_{32}\end{array}\right)p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right)p(A_{22})}{p\left(\begin{array}{c}{A}_{12}\\ A_{22}\end{array}\right)p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)p(\begin{array}{cc}{A}_{21}& A_{22}\end{array})p(\begin{array}{cc}{A}_{22}& A_{23}\end{array})}\\ =\sum _{A_{12},A_{21}}\frac{p\left(\begin{array}{cc}{A}_{12}& \\ A_{22}& A_{23}\end{array}\right)p\left(\begin{array}{cc}{A}_{21}& A_{22}\\ & A_{32}\end{array}\right)p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right)}{p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)p(\begin{array}{cc}{A}_{22}& A_{23}\end{array})}=\frac{p(\begin{array}{cc}{A}_{22}& A_{23}\end{array})p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right)}{p\left(\begin{array}{c}{A}_{22}\\ A_{32}\end{array}\right)p(\begin{array}{cc}{A}_{22}& A_{23}\end{array})}\\ =p\left(\begin{array}{cc}{A}_{22}& A_{23}\\ A_{32}& A_{33}\end{array}\right).\end{array}$$ (63)

This analysis applies, by symmetry, to the other halves of the Pickard conditions. For example, if only the second half of the second Pickard condition, Eq. (59), held, then the result (63) would still be valid for left-to-right and top-to-bottom processes, but the expression (Eq. 61) for 1 × 3 blocks would need to be replaced by a similar expression for 3 × 1 blocks.

2. Pickard Conditions in Transformed Coordinates

To see how the Pickard conditions apply to our setting, we transform them into the coordinates ϕ_i. We begin with the first half of the condition [Eq. (58)]. The first step is to transform the block probabilities into the coordinates ϕ_i, via Eq. (8) and Eqs. (14) through (16):

$$\begin{array}{l}p\left(\begin{array}{cc}& B\\ C& D\end{array}\right)=\frac{1}{8}\left(1-\left({(-1)}^B+{(-1)}^C+{(-1)}^D\right)\gamma +{(-1)}^{C+D}{\beta }_{-}+{(-1)}^{B+D}{\beta }_{\mid }+{(-1)}^{B+C}{\beta }_{/}-{(-1)}^{B+C+D}{\theta }_{⌟}\right)\\ p\left(\begin{array}{c}B\\ D\end{array}\right)=\frac{1}{4}(1-\left({(-1)}^B+{(-1)}^D\right)\gamma +{(-1)}^{B+D}{\beta }_{\mid })\\ p(\begin{array}{cc}C& D\end{array})=\frac{1}{4}\left(1-\left({(-1)}^C+{(-1)}^D\right)\gamma +{(-1)}^{C+D}{\beta }_{-}\right)\\ p(D)=\frac{1}{2}\left(1-{(-1)}^D\gamma \right).\end{array}$$ (64)

When the above expressions are substituted into the first half of the Pickard condition [Eq. (58)], most terms cancel. The ones that do not cancel have a common factor (−1)^B+C; removing this leads to

$$-{(-1)}^D{\theta }_{⌟}+{\beta }_{/}-{(-1)}^D\gamma {\beta }_{/}+\gamma {\theta }_{⌟}={\gamma }^2-{(-1)}^D\gamma ({\beta }_{-}+{\beta }_{\mid })+{\beta }_{-}{\beta }_{\mid }.$$ (65)

This equation must hold both for D = 0 and for D = 1. This means that the terms not involving D must be equal, as must the terms that are multiplied by (−1)^D. The terms not involving D yield

$${\beta }_{/}+\gamma {\theta }_{⌟}={\gamma }^2+{\beta }_{-}{\beta }_{\mid },$$ (66)

and the terms multiplied by (−1)^D yield

$${\theta }_{⌟}+\gamma {\beta }_{/}=\gamma ({\beta }_{-}+{\beta }_{\mid }).$$ (67)

Because of symmetry, the transformed version of the second half of the Pickard condition (58) can be obtained from Eqs. (66) and (67) by replacing θ_⌟ with θ_⌜ :

$${\beta }_{/}+\gamma {\theta }_{⌜}={\gamma }^2+{\beta }_{-}{\beta }_{\mid },$$ (68)

$${\theta }_{⌜}+\gamma {\beta }_{/}=\gamma ({\beta }_{-}+{\beta }_{\mid }).$$ (69)

Thus, it follows that if either half of the Pickard condition holds, then the other half is equivalent to θ_⌜ = θ_⌟.

Note that the Pickard conditions are nonlinear in the coordinates. Geometrically, this means that the coordinates that satisfy either or both halves of a Pickard condition lie in a curved subset within the coordinate space.

3. Coordinate Pairs, Case-by-Case

Pickard’s result [21] means that the two-dimensional Markov procedure is valid within the curved subsets specified by the Pickard conditions, Eqs. (66) and (67) or Eqs. (68) and (69). Thus, to determine the coordinate pairs for which we can use this procedure to sample the maximum-entropy ensemble, we need to relate the various coordinate planes (ϕ_i, ϕ_j) to the Pickard conditions. We begin with some general comments and then consider the planes in a case-by-case fashion below. The full analysis is summarized in Table 2 and samples of images are shown in Figure 2.

Table 2.

Specification of Maximum-Entropy Ensembles from Pairs of Coordinates^a,^b

Coordinate Method Pair and {Multiplicity}		Value
		γ	β−	β|	β\	β/	θ⌟	θ⌞	θ⌜	θ⌝	α
(γ, β−){2}	1DM (P2)	γ	β−	γ2	γ2	γ2	γβ−	γβ−	γβ−	γβ−	${\beta }_{-}^2$
(γ, β\){2}	1DM (P1)	γ	γ2	γ2	β\	γ2	γ3	γβ\	γ3	γβ\	γ2β\
(γ, θ⌟){4}	2DM (P1)	γ	γ2	γ2	γ2	γ2	θ⌟	γ3	γ3	γ3	γθ⌜
(γ, α){1}	2DM (P2)	γ	γ2	γ2	γ2	γ2	γ3	γ3	γ3	γ3	α
(β−, β|){1}	2DM (P2)	0	β−	β|	β−β|	β−β|	0	0	0	0	r1(β−, β|)
(β−, β\){4}	2DM (P1)	0	β−	0	β\	0	0	0	0	0	r2(β−, β\)
(β\, β/){1}	2DMO	0	0	0	β\	β/	0	0	0	0	β\β/
(β−, θ⌟){8}	2DM (P1)	0	β−	0	0	0	θ⌟	0	0	0	r3(β−, θ⌟)
(β/, θ⌟){4}	2DM (P1)	0	0	0	0	β/	θ⌟	0	0	0	0
(β\, θ⌟){4}	2DMT-DA	0	0	0	β\*	0	θ⌟*	0	β\θ⌜*	0	0
(β−, α){2}	2DM (P2)	0	β−	0	0	0	0	0	0	0	α
(β\, α){2}	2DM (P1)	0	0	0	β\	0	0	0	0	0	α
(θ⌟, θ⌜){2}	2DM (P1)	0	0	0	0	0	θ⌟	0	θ⌜	0	0
(θ⌟, θ⌞){4}	2DM-DA	0	0	0	0	0	θ⌟	θ⌞	0	0	0
(θ⌟, α){4}	2DM (P1)	0	0	0	0	0	θ⌟	0	0	0	α

^aThe row headed by each pair of coordinates indicates the subspaces in which simple maximum-entropy ensembles may be sampled by specific algorithms. Algorithms designated as follows: 1DM: one-dimensional Markov process; 2DM: two-dimensional Markov process; P1: One set of Pickard conditions [Eq. (58) or Eq. (59)] hold; P2: Both sets of Pickard conditions hold; 2DMO: two-dimensional Markov process on oblique axes; 2DMT: two-dimensional Markov process on a tee-shaped glider. For this algorithm,

^*denotes that the parameter values obtained are highly accurate approximations, but not exact—see Appendix C, Section C2. DA: donut algorithm. r₁(β₋, β_|), r₂(β₋, β_\), and r₃(β₋, θ_⌟) denote the roots of specific cubic polynomials (see Appendix C, Section C3).

^bBecause of symmetry, the 45 pairs that can be drawn from the 10 coordinates {γ, β₋, β_|, β_\, β_/, θ_⌟, θ_⌞, θ_⌝, θ_⌟, α} constitute 15 unique classes; only one member of each class is listed. The number in braces next to each coordinate pair indicates the total number of pairs in that class. For example, (β_\, θ_⌟) indicates the four pairs (β_\, θ_⌟), (β_\, θ_⌜), (β_/, θ_⌞), and (β_/, θ_⌝)

Fig. 2.

The image-statistic coordinate planes. Each patch is a typical sample of an image ensemble in which the indicated pair of statistics is set to a nonzero value and the rest are determined according to Table 2.

In many of the coordinate planes, the Pickard conditions hold. This is because within a coordinate plane, two of the texture coordinates are nonzero, and the remaining 8 coordinates are zero. The Pickard conditions involve subsets of the six coordinates {γ, β₋, β_|, β_/, θ_⌟, θ_⌜} and {γ, β₋, β_|, β_/, θ_⌞, θ_⌝}—so if at least one of these subsets is entirely contained in the eight coordinates that are orthogonal to the plane of interest, the Pickard conditions will hold. For these coordinate pairs, a two-dimensional Markov process creates images that are specified by the coordinate pair of interest and are otherwise maximum-entropy.

Among the coordinate planes that are not strictly within the Pickard subset, many are closely approximated by it, i.e., they are tangent to the Pickard subset at the origin. In these cases, our goal of creating images that probe the effects of a pair of coordinates are, in fact, best served by working within this curved subset. The curved subset is a more natural choice than the coordinate plane itself, because of the natural curvature of the space. The natural curvature can be seen by focusing on single texture coordinates. Specifically, (as mentioned above), the maximum-entropy ensembles specified by the coordinate λ, the IID images, do not lie on the coordinate axis itself, but rather, form a curved trajectory, (β, θ, α) = γ², γ³, γ⁴). A further justification for the use of a curved trajectory is that in these cases, the deviation between the curved set and the planes is well below perceptual threshold (see Section 3.B). After considering the coordinate pairs whose planes are tangent to the Pickard subset, we will handle the remaining few pairs, whose planes are not close to the Pickard subset, via another approach, in Section 2.H.

We now turn to the individual coordinate pairs; Table 2 provides a comprehensive summary. (Since there are 10 coordinates, there are a total of 45 coordinate pairs, but because of symmetries among the β’s and θ’s, only 15 coordinate pairs need to be considered explicitly.)

To begin, the coordinate pairs (γ, β₋) and (γ, β_\) have already been handled as one-dimensional Markov processes, so each of them necessarily satisfies a Pickard condition. Note that even in this simple case, it is natural to work in a curved subset, in which the unspecified coordinates are given nonzero values (e.g., the unspecified β’s are set equal to γ²). These are the unique choices for which the one-dimensional Markov processes are independent of each other—thus guaranteeing maximum entropy—and, for the β’s and θ’s, they are the unique choices for which the Pickard conditions hold.

For (γ, θ) and (γ, α), the second coordinate corresponds to a glider that occupies more than one row or column, so the one-dimensional Markov construction is not applicable. But here, the Pickard conditions hold, with the appropriate choices for the β’s and the unspecified θ’s. These choices also guarantee independence of the pixels within the unspecified gliders. The choice of α is unconstrained by the Pickard conditions, so, for (γ, θ), its value is chosen to achieve maximum entropy within the 2 × 2 block. α = γθ_⌟ achieves this because it means that the pixel not contained in the θ_⌟-glider is independent of the ones constrained by θ_⌟. (The procedure of Appendix C, Section C3, confirms that this choice for α maximizes the entropy.)

(β_|, β₋) and (β_|, β_\) also satisfy the Pickard conditions. A zero value for γ and the θ’s is the maximum-entropy choice by the following symmetry argument, based on contrast-inversion. Since contrast-inversion negates the value of γ and θ, the entropy of an ensemble with nonzero values of these parameters could always be further increased by mixing it with its contrast-inverse. Consequently, when maximum-entropy is achieved, these parameters must have a zero value. The choice of α, however, is less straightforward, since any value is consistent with the Pickard conditions and with the above symmetry argument. Appendix C, Section C3 details how it is chosen as a function of the β’s to maximize entropy.

(β_\, β_/) is the first coordinate pair that does not satisfy either Pickard condition, even for limitingly small values of the coordinates. However, we can handle this case by noting that the gliders corresponding to both coordinates only induce correlations of pixels A_ij for which i + j have the same parity. That is, these gliders only induce correlations within the two diagonal sublattices (corresponding to the “red” and “black” pixels of an ordinary checkerboard) and not between them. Since these sublattices are independent, we can construct the image on each of them separately. The latter construction is straightforward: within each diagonal sublattice, (β_\, β_/) behaves like (β_|, β₋). In sum, the (β_\, β_/) case is equivalent to the (β_|, β₋) case on each of two independent sublattices: the sublattice for which i + j is even and the sublattice for which i + j is odd.

The (β, θ) cases depend on how the gliders relate. For a horizontal or vertical β (e.g., (β₋, θ_⌟)), a Pickard condition holds and α is chosen to maximize entropy (Appendix C, Section C3). For a diagonal β that is contained within the θ glider (e.g., (β_/, θ_⌟)), the Pickard conditions hold as well and the choice of α = 0 corresponds to independence of the fourth pixel in a 2 × 2 block and hence, maximum-entropy. Finally, for a diagonal β that is not contained within the θ glider (e.g., (β_\, θ_⌟)), the Pickard conditions do not hold; this case will be treated in the next section (and in detail in Appendix C, Section C1 and Section C2).

The (β, α) cases are straightforward: they all satisfy at least one Pickard condition and symmetry requires that the maximum-entropy choices of the other parameters are zero.

The (θ, θ) cases differ, depending on how the gliders relate. When they overlap on a diagonal (e.g., (θ_⌟, θ_⌜)), a Pickard condition holds and a symmetry argument (discussed in Appendix C, Section C2, in relation to the (β_\, θ_⌟) case) shows that α = 0 is the maximum-entropy choice. When they overlap along an edge (e.g., (α_⌟, α_⌞)), the Pickard conditions do not hold and we use the method described in the following section.

Finally, the (θ, α) case satisfies both Pickard conditions.

H. Donut Algorithm

We now consider the two coordinate pairs, (β_\, θ_⌟) and (θ_⌟, θ_⌞). Because the Pickard conditions do not hold, it is necessary to depart from the Markov construction. The alternative we describe turns out to be much more useful than just providing a solution for these last cases: it also allows for creation of maximum-entropy image ensembles constrained by the 2 × 2 block probabilities derived from an arbitrary image.

The basic idea is a two-step process. In the first step, we generate an ensemble (or a large example drawn from an ensemble) that satisfies the coordinate constraints, but is not necessarily maximum entropy. That is, we generate an ensemble that satisfies the constraints on 2 × 2 blocks, but may have unnecessary correlations among larger blocks. This step is somewhat ad hoc; we use different constructions for (β_\, θ_⌟) and (θ_⌟, θ_⌞), as described below. In the second step, which is generic, we increase the entropy of this ensemble by mixing it, in a way that preserves the constraints.

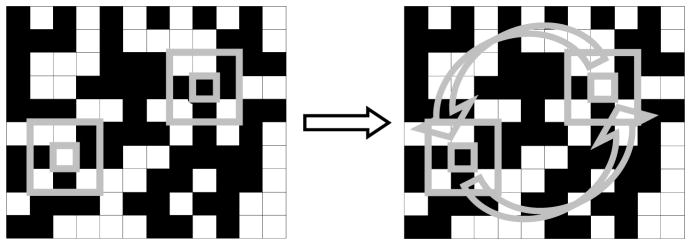
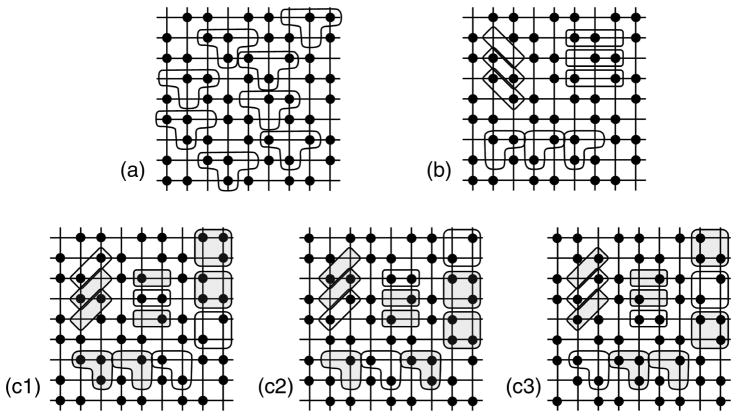
The second step—a procedure for maximizing the entropy by scrambling the pixels in a manner that preserves 2 × 2 block probabilities but not longer-range correlations—is diagrammed in Figure 3. The image is searched to identify two 3 × 3 regions for which the outer 8 pixels match identically. (Since there are 2⁸ possible configurations, many such matches will be present in a typical image of thousands to millions of pixels.) Then, the interior of two such randomly-chosen “do-nuts” are swapped, say, between locations A and B. This swap necessarily preserves the number of 2 × 2 blocks of each configuration, since the 2 × 2 blocks at location A have now been moved to location B and vice-versa. However, longer-range correlations have been reduced, since the pixel at location A now has the longer-range context (e.g., next-nearest neighbors) of B and vice-versa. The procedure is then iterated until the statistical properties of the image have stabilized. Further details and background on this algorithm are provided in Appendix D, including comments on the mathematical justification for the algorithm, its relationship to the classical Metropolis algorithm [26] and how it can be implemented efficiently.

Fig. 3.

Donut construction for maximizing entropy while maintaining 2 × 2 block probabilities. Left: a pair of 3 × 3 regions is identified, for which the outer eight pixels match identically. Right: the interior pixels of the two regions are swapped. This step preserves all 2 × 2 block probabilities. Iterations of this step destroy longer-range correlations.

1. Applying the Donut Algorithm to the Non-Pickard Cases

The simpler of the non-Pickard cases is that in which the coordinates (θ_⌟, θ_⌞) are specified. With γ, the β’s, and the unspecified θ’s (θ_⌝and θ_⌜) set to zero, the second halves of both Pickard conditions [in block probability form, Eqs. (58) and (59)] hold, since all pixels within the θ_⌝ and θ_⌜ gliders are independent. As shown in Appendix C, Section C1, this ensures that when the block probabilities are used to drive a two-dimensional Markov process, the resulting image retains the same block probabilities. However, this does not mean that the construction is maximum-entropy, since neither Pickard condition holds in its entirety, only one half of each. The problem is nonstationarity: the two gliders θ_⌟ and θ_⌞ combine to induce correlations of the end pixels within a 1 × 3 block. The reason for this becomes apparent from considering a block $\left(\begin{array}{ccc}A& B& C\\ D& E& F\end{array}\right)$. Say we choose the first row at random, since we would like the β’s to be zero. θ_⌟ biases the parity of the pixels $\left(\begin{array}{cc}& B\\ D& E\end{array}\right)$ and θ_⌞ biases the parity of the pixels $\left(\begin{array}{cc}B& \\ E& F\end{array}\right)$. Since these two blocks both contain B and E, the parity biases within each induce a correlation among D and F, the end pixels of the second row of the block, $(\begin{array}{ccc}D& E& F\end{array})$. This happens even if no correlation were present between the end pixels of the first row, $(\begin{array}{ccc}A& B& C\end{array})$. It is unclear how to choose the original row to ensure that subsequent rows have similar and maximally-random statistics.

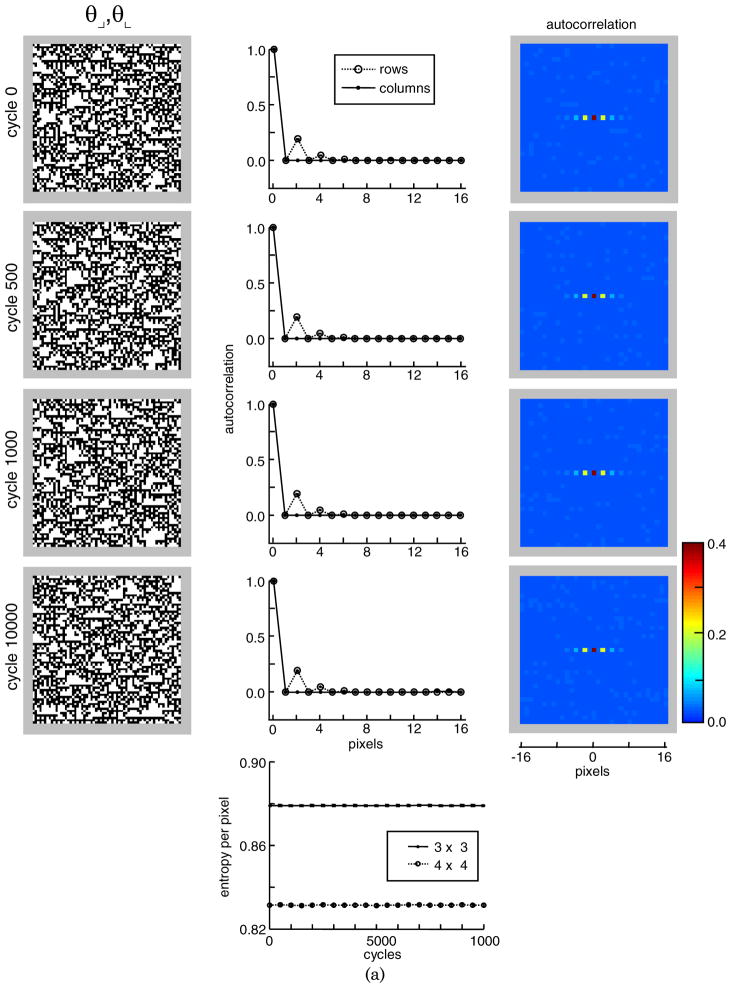
The donut algorithm circumvents this problem. Applying it to the results of the two-dimensional Markov process preserves the 2 × 2 block probabilities and the scrambling process guarantees that a stable, maximum-entropy sample results. In this case—as is seen from Figure 4(a)—there is virtually no change in the entropy that results from the donut procedure or in the visual characteristics of the image samples. So, while the donut procedure is necessary for the construction to be rigorously correct, it appears to have little practical impact.

Fig. 4.

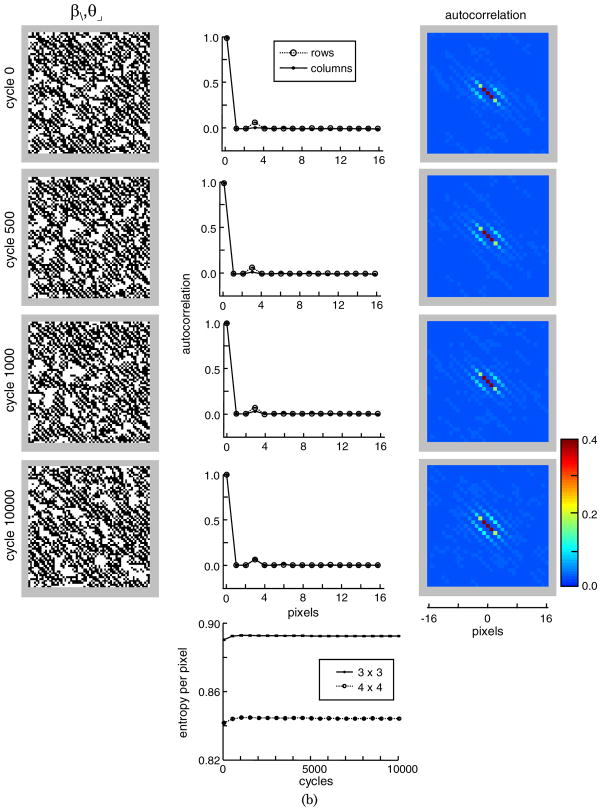
(Color online) Construction of images specified by (θ_⌟, θ_⌞) panel (a) and (β_\, θ_⌟) (b) (see next page). In each case, a starting image is created via an iterative rule [Appendix C, Section C1 for panel (a), Section C2 for panel (b)] and the donut algorithm is applied to ensure maximum entropy. Parameter values are 0.4 in each case. Autocorrelations (along rows, along columns, and in two dimensions) are shown adjacent to each image. The central pixel in the two-dimensional autocorrelogram has a value of 1.0, above the range of the colorbar. Entropy per pixel for 3 × 3 and 4 × 4 blocks is shown in the lower panels. Error bars (most smaller than the symbols) indicate s.e.m across 16 runs. Part (b) is on next page.

For the (β_\, θ_⌟) case, only one half of one Pickard condition holds and the argument of Appendix C, Section C1, does not apply. Thus it is not readily apparent how to create a starting image with the requisite 2 × 2 block probabilities. Appendix C, Section C2 shows one way to do this, via a Markov process based on a “tee” configuration of pixels, $\left(\begin{array}{ccc}A& B& C\\ & D& \end{array}\right)$. A consequence of this construction is that weak correlations are induced at a horizontal spacing of 3 (i.e., between the end-pixels of a 1 × 4 block), but not in a vertical direction. Since the parameters themselves are symmetric with respect to interchange of horizontal and vertical axes, the presence of horizontal but not vertical correlations must be a violation of maximum-entropy.

As shown in Fig. 4(b), the donut algorithm fixes this: as it proceeds, horizontal correlations spread into the vertical direction, until they are equal in strength. Even though vertical correlations are generated, overall entropy increases, because of the effect of the swapping procedure on high-order correlations and larger blocks. As is the case for the θ_⌟ - and θ_⌞-construction [Figure 4(a)], the changes induced by the donut algorithm have only a minor effect (if any) on the visual appearance of typical images.

2. Other Applications of the Donut Algorithm

Above, the donut algorithm was used to fine-tune a procedure that already generated nearly maximum-entropy samples. However, it is much more widely applicable, because it can be applied independent of the way in which the starting image is created. Thus, it can be applied to create classes of ensembles that are not at all close to those that are created by the Markov procedure. We illustrate this with two examples: first, construction of a maximum-entropy image specified by four texture coordinates and second, construction of a maximum-entropy image constrained by the 2 × 2 block probabilities of a binarized natural image.

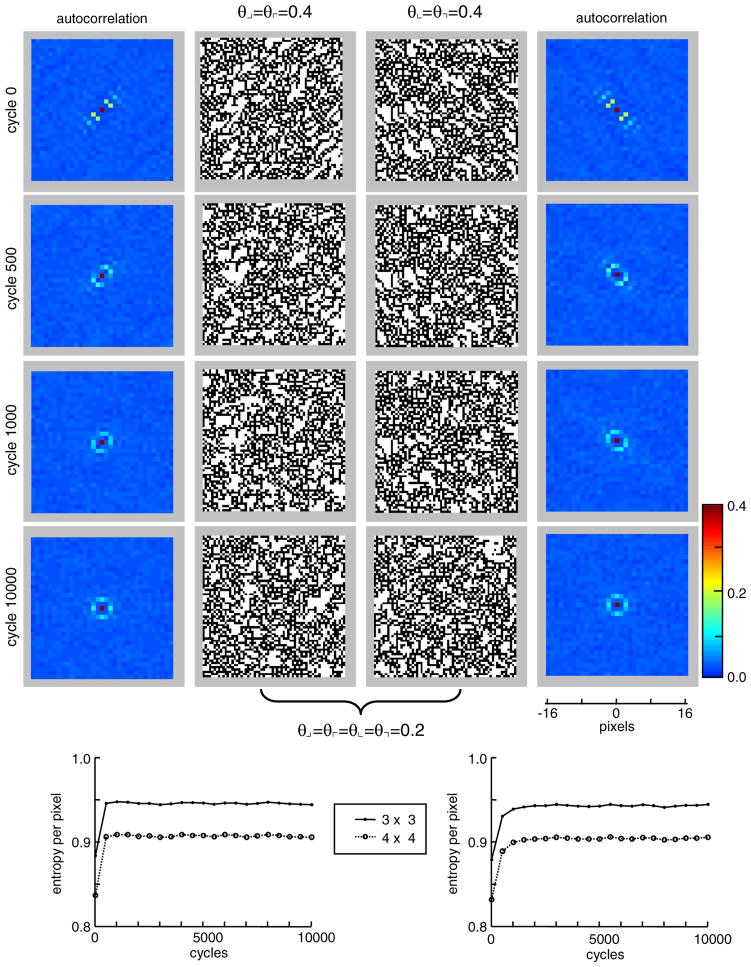
The first example, Fig. 5, is constructed to have a nonzero value of all the θ’s, i.e,. θ_⌟ = θ_⌞ = θ_⌝ = θ_⌜ = 0.2, and all other texture parameters equal to zero. Here, no Pickard conditions hold and the Markov approach also cannot be applied, because it is unclear how it should be initialized. However, this kind of ensemble is readily generated by mixing together a pair of ensembles, each of which satisfies the Pickard conditions: one with θ_⌟ = θ_⌜ = 0.4 and one with θ_⌞ = θ_⌝ =0.4. Swapping of pixels is carried out by the above donut procedure, with pixels free to swap between the ensembles. Since the swaps preserve the combined 2 × 2 counts, the resulting mixture has the desired block probabilities. In contrast to the examples of Fig. 4, the swapping procedure does have a visual effect: the diagonal structure of the starting images is lost. Not surprisingly, this is accompanied by a much larger change in the entropy (approximately 0.1 bit/pixel) compared to Fig. 4 (<0.01 bit/pixel).

Fig. 5.

(Color online) Synthesis of images with multiple specified parameter values by mixing images with specified parameter pairs. Each cycle of the donut algorithm constructs a pair of images, by mixing the pair created on the previous cycle. The starting pair (cycle 0) consists of an image with θ_⌟ = θ_⌜ = 0.4 (left) and an image with θ_⌞ = θ_⌝= 0.4 (right); the final pair consists of images with θ_⌟ = θ_⌞ = θ_⌝ = θ_⌜ = 0.2. All other texture parameters are equal to zero. Autocorrelation functions are shown adjacent to the images. The central pixel in the two-dimensional autocorrelogram has a value of 1.0, above the range of the colorbar. Entropy per pixel for 3 × 3 and 4 × 4 blocks is shown in the lower panels.

Finally, since the donut algorithm does not depend on the structure of the image, it can be applied to natural images as well. We illustrate this in Fig. 6, starting with a texture from the Brodatz [27] library [Fig. 6(a)]. We first binarize it and detrend it, Fig. 6(b), and then apply the donut algorithm. The result is an image in which the general diagonal correlation structure is preserved, but the multiscale detail (of bricks and mortar) is lost [Fig. 6(c), Fig. 6(d)]. This is just as one would expect from a procedure that explicitly preserves only the short-range correlations and the long-range correlations are limited to those that the short-range correlations imply. Put another way, the original image has both a short-range structure (the texture of the bricks and the typical orientation of the brick/mortar interface) and a long-range structure (the regularity of the brickwork lattice). The donut algorithm captures the former, but not the latter, and the resulting image [Fig. 6(d)] shows that the overall slant of the lattice, but not its regularity, is implied by the short-range structure.

Fig. 6.

Application of the donut algorithm to a natural texture. The starting image is a region taken from Brodatz texture 1.4.01 [panel (a)], median-thresholded to create a 64 × 64 binary image (b). (c) and (d): The result of applying the donut algorithm. These images have the same 2 × 2 block probabilities as the starting image [panel (b)]; other statistics are determined by maximum entropy. Even though only short-range correlations are specified, long-range correlations result. Following application of the donut algorithm, the overall oblique slant remains apparent, but the distinction between the two scales (mortar and bricks) is lost.

3. PSYCHOPHYSICAL METHODS

As described above, we established a coordinate system for the local statistics of binary images and developed algorithms that generate visual textures which have specified values of these statistics. Next, we determine visual sensitivity to these statistics, alone and in selected combinations. This section describes the psychophysical methods employed.

Each experiment focuses on one pair of image statistics (i.e., one coordinate pair) and consists of a determination of the salience of each coordinate in isolation and an analysis of how they interact. We use one of two schemes to explore each coordinate pair: a scheme in which we sample five points along each coordinate axis and two points along each of the four diagonals of the coordinate plane or a scheme in which we sample three points in each of 12 directions (including the four coordinate axes). To measure the visual salience of a set of image statistics, we used the texture segmentation paradigm developed by Chubb and coworkers in the study of IID textures [1], described below.

A. Stimuli

The basic stimulus consisted of a 64 × 64 array of pixels, in which a target region (a 16 × 64 rectangle, positioned eight pixels from one of the four edges of the array) is distinguished from the remainder of the array by its statistics. To ensure that the subject responds on the basis of segmentation (rather than, say, a texture gradient), we randomly intermix trials of two types: (a) trials in which the background is random and the target has a nonzero value of one or more image statistics and (b) trials in which the background has the nonzero values and the target is random. The range of values of the image statistics was determined in pilot experiments, to ensure that the experiment included conditions for which performance ranged from near-chance to near-ceiling.

Stimuli were presented on a mean-gray background, followed by a random mask. The display size was 15 × 15 deg (check size, 14 min), contrast was 1.0, and viewing distance was 1 m. Initial studies were carried out on a CRT monitor with a luminance of 57 cd/m², a refresh rate of 75 Hz, and a presentation time of 160 ms driven by a Cambridge Research VSG2/5 system, later studies were carried out on an LCD monitor with a luminance of 23 cd/m², a refresh rate of 100 Hz, and a presentation time of 120 ms, driven by a Cambridge Research ViSaGe system. Results (including one subject, MC, tested under both conditions) were very similar under these two conditions: for γ, sensitivities (see below) were 0.141 for both setups; for θ_⌟, thresholds were 0.730 for the VSG 2/5 system versus 0.735 for the ViSaGe; and for α, 0.495, and 0.523 for the VSG (two measures) versus. 0.536 for the ViSaGe.

B. Subjects

Studies were conducted in 6 normal subjects (two male, four female), ages 25 to 51. Three subjects (AO, CC, RM) were naïve to the purpose of the experiment. Five subjects (all but DT) were practiced psychophysical observers in tasks involving visual textures. DT had no observing experience prior to the current study. All had visual acuities (corrected if necessary) of 20/20 or better.

C. Procedure

The subject’s task was to identify the position of the target (a four-alternative forced choice texture segregation task). Subjects were told that the target was equally likely to appear in any of four locations (top, right, bottom, left), and were instructed to maintain central fixation on a one-pixel dot, rather than to attempt to scan the stimulus. Auditory feedback for incorrect responses was given during training but not during data collection. After performance stabilized (approximately two hours for a new subject), blocks of the 288 trials described above (with trials presented in randomized order) were presented. We collected data from 15 such blocks (4320 trials per subject), grouped into three or four experimental sessions, yielding 120 to 240 responses for each coordinate pair.

D. Analysis

Measured values of the fraction correct (FC) are fit to Weibull functions via maximum likelihood:

$$FC(x)=\frac{1}{4}+\frac{3}{4}(1-2^{-{(x/a_r)}^{b_r}}).$$ (70)

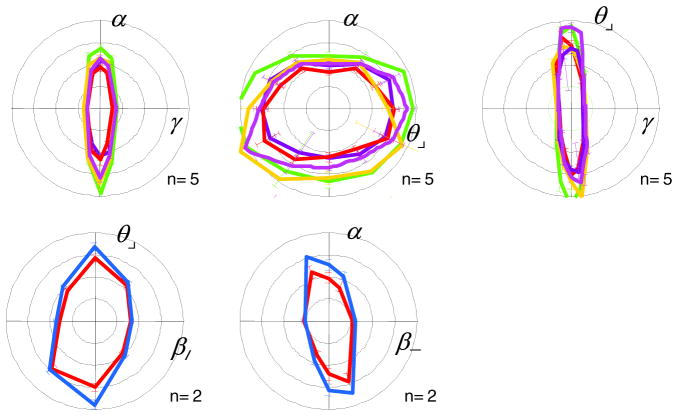
Initially, this is carried out separately along each ray r. For the rays along the coordinate axes, x is the coordinate value; for the rays in the oblique directions, x is the distance from the origin. In most cases, the Weibull shape parameter (the exponent b_r) was in the range 2.2 to 2.6 for each ray or had confidence limits that included this range. Therefore, we then fit the entire dataset in each coordinate plane by a set of Weibull functions, constrained to share a common exponent b, but allowing for different values of the position parameter a_r along each ray. The fitted value of a_r, which is the value of the image statistic that yields performance halfway between floor and ceiling, is taken as a measure of threshold. This measured threshold provides a single point on an isodiscrimination contour (e.g., Fig. 8). Correspondingly, its reciprocal 1/a_r measures perceptual sensitivity to changes in the direction of the ray r. Error bars (95% confidence limits) were determined via 200-sample bootstraps.

Fig. 8.

Isodiscrimination contours (ICs) in five coordinate planes. The distance of the contour from the origin indicates the threshold a_r for individual image statistics (along the axes) and their mixtures (in oblique directions); threshold is defined by the value required to achieve a fraction correct of 0.625, halfway between chance and perfect [Eq. (70)]. The outermost circle corresponds to a coordinate value of 1.0. Error bars, most no larger than the contour line thickness, are 95% confidence limits. Task and subject key as in Fig. 7. ICs are approximately elliptical, and in some planes, they are tilted.

4. PSYCHOPHYSICAL RESULTS

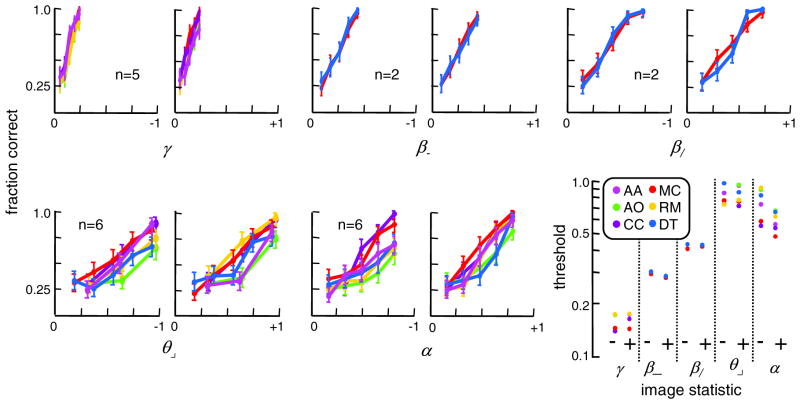
Here, we measure the salience to the human visual system of the image statistics described above to the human visual system, alone and in combination. Following the work of Chubb et al. [1], salience is operationally defined by the ability of a change in a value of the statistic to support texture segmentation. We first consider changes in individual statistics, and then sample their interactions.

A. Discrimination along Coordinate Axes

Figure 7 shows psychometric functions for performance in a four-alternative forced-choice segmentation task (see Methods), driven by variations of each of the kinds of texture coordinates.

Fig. 7.

Line graphs: performance in a brief four-alternative forced choice segmentation task for image statistics γ, β₋, β_/, θ_⌟, and α. Chance performance is a fraction correct of 0.25; error bars are 95% confidence limits. Final panel: summary of thresholds a_r, obtained by Weibull-function fits to the individual psychometric curves [Eq. (70)]. Consistently across subjects, thresholds for negative and positive variations of each statistic are closely matched and sensitivities across the statistics show systematic differences.

As seen from the individual plots, the variation across observers was quite small, for both the shape and position of the psychometric functions. In terms of the thresholds a_r [corresponding to a fraction correct of 0.625, halfway between chance and perfect, Eq. (70)], there was approximately a 10% scatter for γ, β₋, and β_/ and a 20% scatter for θ_⌟ and α.

Within observers, there was little difference in salience for negative versus positive variations of the coordinates: a 20% difference for α (higher sensitivity for positive variations than for negative ones, p < 0.01, two-tailed paired t-test) and less than a 10% difference (p > 0.1) for the others.

Across all observers, the thresholds for a fraction correct of 0.625 are θ_⌟, 0.157 ± 0.006, n = 5; β₋, 0.286 ± 0.003, n = 2; β_/, 0.415 ± 0.009, n = 2; θ_⌟, 0.824 ± 0.047, n = 6; α, 0.648±0.042, n = 6 (mean ± s.e.m, number of subjects). This corresponds to a sensitivity rank-order of γ>β₋>β_/> α >θ_⌟, consistent across all subjects. While sensitivity to lower-order statistics is generally greater than for higher-order statistics, there is only a fivefold difference between the least-salient and the most-salient statistic and sensitivity is not a monotonic function of rank order (i.e., salience is greater for α than for θ_⌟). Thus, the human observer is sensitive to statistics of all orders and the high-order statistics are not simply a sequence of progressively smaller corrections.

The relative sensitivities to the parameters are relevant to the logic of choosing coordinate axes, rather than maximum-entropy loci, when these entities differ. For example (as mentioned above at the end of Section 2.D.), the coordinate axis corresponding to γ (namely, all other parameters set to zero) is not the same as the maximum-entropy locus corresponding to γ [namely, (β, θ, α) = (γ², γ³, γ⁴)]. For measuring the salience of γ, this distinction is moot—even when γ is twice threshold (e.g., γ = 0.3) and performance is at ceiling, the other parameter values are far below their thresholds: (β, θ, α) = (0.09, 0.027, 0.0081). However, when measuring the threshold for α, the distinction is critical: thresholds are at approximately α = 0.5. Had we attempted to measure this along a maximum-entropy trajectory, we would have chosen γ = α^1/4 (rather than γ = 0), which would have been markedly suprathreshold. This generalizes: for measuring the sensitivity to a high-order parameter, low-order parameters must be set to zero so that they don’t contribute to detection, but for measuring the sensitivity to a low-order parameter, this choice (set-to-zero versus maximum-entropy) is moot.

B. Discrimination in Selected Planes

To determine how image statistics interact at the level of perception, we measured segmentation thresholds along oblique directions in coordinate planes. As indicated in Table 2, there are 15 unique kinds of planes, once the symmetries of the coordinates are taken into account. Here we focus on five of these planes ((γ, α), (θ_⌟, α), (γ, θ_⌟), (β_/, θ_⌟), (β₋, α)); this suffices to identify several kinds of behavior and suggest what is likely to be generic. (The unspecified coordinates are set to zero or chosen by maximum entropy as discussed above; see Table 2.)

Results are shown in Fig. 8. Along each ray, the distance to the plotted contour indicates a_r [Eq. (70)], the threshold for a fraction correct of 0.625 in the corresponding direction in the coordinate plane. (For the rays that are along the axes, the plotted values correspond to the thresholds measured in the experiments of Fig. 7). The contours are not circular, because the thresholds depend on the direction in parameter space: the axis of elongation (highest threshold) corresponds to the direction in which changes are least salient. Both on and off the axes, there is close agreement across subjects.

In three of the coordinate planes ((γ, α), (θ_⌟, α), and (β_/, θ_⌟)), the contours are approximately elliptical, with their axes parallel to the coordinate axes. The elliptical shape is consistent with a Euclidean perceptual distance based on two independent mechanisms (of unequal sensitivity) aligned with the two axes. In the other two planes ((γ, θ_⌟) and (β₋, α)), the contours are also elliptical, but are somewhat tilted with respect to the axes: a counterclockwise tilt of 3 to 5 deg for (γ, θ_⌟) and about 20 deg for (β₋, α). Qualitatively, the tilt indicates that the salience of these two parameters varying in the same direction (i.e., both positive or both negative) is greater than when they vary in opposite directions. Tilted elliptical isodiscrimina-tion contours are also consistent with a Euclidean perceptual distance based on two independent perceptual mechanisms, but the tilt requires that the mechanisms do not coincide with the axes. The directions of these mechanisms cannot be determined unambiguously from the shape of the ellipse [28], but the fact that the ellipse is tilted means that the perceptual mechanisms cannot be the same as the coordinate axes: one or more must lie in an oblique direction (and these directions need not even be within the coordinate planes).

5. DISCUSSION

The broad motivation for this work was to combine the benefits of two broad classes of approaches to study vision—those based on stimulus sets that are mathematically simple with components that are easy to manipulate (such as gratings and white noise) and those based on stimulus sets that are biologically relevant (natural scenes). Our strategy was to choose local image statistics that are informative about natural scenes and to use maximum-entropy extension to create stimulus sets that isolated one or more of these statistics. This led to a specific mathematical challenge: how to sample an ensemble of images that is specified by the joint probability distribution of binary pixels and is otherwise maximum entropy. As we showed, this challenge can be met: standard approaches from the maximum-entropy formalism solve part of the problem, results related to two-dimensional Markov processes [21] solve most of the rest, and some new algorithms fill in the remaining gaps. Together, these strategies allow for navigation in a nontrivial space of image statistics. Moreover, they enable projection of an arbitrary natural image into this space, as illustrated in Fig. 6.

It is worthwhile mentioning how this approach contrasts with that of Portilla and Simoncelli [29], which is another way of creating images with multiple specified image statistics. Here, we specify a handful of local image statistics at a single scale and the remaining image statistics are determined implicitly by maximum entropy—and it is guaranteed that the resulting ensembles achieve (or very nearly achieve) the specified statistics. In contrast, in the approach of Portilla and Simoncelli [29], a large number of image statistics, of low and high order and multiple scales, are specified. While the latter approach has the advantage that a much wider variety of image ensembles can be synthesized—including those that are very similar to natural visual textures—it has an important limitation: the image statistics are over-complete. Consequently, they have complex algebraic interrelationships and there is no guarantee that a prespecified set of statistics is self-consistent or can be achieved. Thus, the Portilla and Simoncelli parameters cannot be regarded as “coordinates” for a texture space and there is no way to assure that changing one of them will not change many others. The complementary nature of the approaches reflects, in part, their distinct goals: here, the goal is to analyze the impact of image statistics and their combinations; in [29], the goal is to model natural textures.

Although we focused on one of the simplest cases—only binary textures and only four pixels—the strategies presented are more general. The linear reorganization of block probabilities into a set of transformed coordinates, each of which is identically salient to an ideal observer, applies to any number of gray levels, as described in Appendix A. The donut algorithm, which is the key strategy for completing the construction, also is not restricted to the specific case we consider. However, as the number of gray levels increases, the probability of matching donuts rapidly decreases: if there are G gray levels, there are G⁸ distinct donuts. The number of pixels in the image must be large enough so that such matches are frequent; this requires images containing ~100, 000 pixels for 3 gray levels and ~1, 000, 000 pixels for 4 gray levels. Thus, for the “non-Pickard” cases and more than four gray levels, other approaches are needed. A possible approach is to modify the donut algorithm to allow for inexact matches, but the details remain to be worked out. An important limitation is that our approach focuses on one spatial scale—the chosen pixel size. Natural images have structure across a wide range of spatial scales; inclusion of statistics at multiple spatial scales is not readily accomplished by the techniques described here (see Fig. 6).

One of the advantages of the coordinate system introduced is that in the neighborhood of the origin, changes in all directions are equally detectable to the ideal observer. The human visual system, however, has limited resources and the way that these resources are deployed is likely to be shaped by evolutionary, developmental, and neurophysiological constraints.

As we showed (Fig. 7 and Fig. 8), the human observer is in fact selective: there are substantial and highly consistent differences in the perceptual salience of each image statistic. Some of these differences are not surprising from first principles—for example, that the most salient statistic is the one that indicates overall luminance (γ) and that simple correlations (the β’s) are more salient than the higher-order ones (the θ’s and α). But a priori, it is unexpected that fourth-order correlations are more salient than third-order correlations (Fig. 7) and that there are interactions that are manifest by maximal salience in directions oblique to the coordinate axes (Fig. 8). We speculate that this is a manifestation of the efficient coding hypothesis [14]—that the visual salience of each of the directions in the space of local image statistics corresponds to the informativeness of these statistics about natural scenes. It is interesting to note that if this form of the efficient coding hypothesis holds, then the distribution of local statistics of natural scenes must delineate specific directions in the coordinate space that are maximally informative, and that these directions are, in general, oblique to the coordinate axes.

APPENDIX A: TRANSFORMED COORDINATES

This Appendix provides background for the approach taken to parameterize the space of block probabilities that are consistent with spatial homogeneity. Specifically, we show how the coordinates ϕ defined in the main text [Eq. (7)], can be considered to be Fourier transforms with respect to gray level and, consequently, how the approach applies to images with more than two gray levels. In fact, the mathematical issues are clearer in this more general setting—so we present it first and then note how it reduces to the approach taken in the main text when only two gray levels are present.

We consider images with G gray levels (G ≥ 2), which we denote by the integers from 0 to G - 1. For definiteness, we focus on the statistics that characterize 2 × 2 blocks, but the approach readily extends to blocks of any number of pixels, n. The image intensity at each of the n pixels is thus a separate variable (which we denote A₁, …, A_n), each of which can take a value from 0 to G - 1.

For the purpose of parameterizing the allowed block probabilities, the G gray levels serve as abstract tokens, with no particular relationship to each other. This is because the space of allowed block probabilities has a built-in symmetry: it is preserved under any permutation of the gray levels. That is, if a set of block probabilities is allowed, then so is the set of block probabilities that is obtained from the first by relabeling the gray levels {0, 1, …, G - 1} in a different order. A special case of this symmetry is cyclic permutation of the gray levels: replacing 0 by 1, 1 by 2, …, and G - 1 by 0. In view of this, the block probabilities can be considered to be periodic functions of the gray levels. A coordinate system that takes this into account will have analytical advantages because it makes use of a fundamental symmetry of the problem.

Coordinates that are Fourier transforms with respect to gray level necessarily respect the cyclic permutation symmetry, since they consider block probabilities to be periodic functions of the gray levels {0, 1, …, G - 1}. An immediate benefit of this Fourier approach is that in the transformed coordinates, the constraints of stationarity are simple to express. This is because stationarity is a constraint on the probabilities of smaller blocks, which are obtained by marginalizing the full 2 × 2 block probabilities with respect to several pixels. Each marginalization with respect to a pixel corresponds to evaluating a Fourier component at a frequency of 0, since the DC component of a Fourier transform amounts to an average of the untransformed quantity.

To create the Fourier coordinate system explicitly, we introduce a new set of variables, s₁, …, s_n, one for each pixel. We now transform the original block probabilities (functions whose arguments are the pixel variables A_k) into functions ϕ that depend on the s_k. Carrying this transformation out separately on each pixel leads to:

$$\begin{array}{l}\varphi \left(\begin{array}{cc}{s}_1& s_2\\ s_3& s_4\end{array}\right)=\sum _{A_1=0}^{G-1}\sum _{A_2=0}^{G-1}\sum _{A_3=0}^{G-1}\sum _{A_4=0}^{G-1}p\left(\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right)\times e^{-\frac{2\pi i{A}_1{s}_1}{G}}{e}^{-\frac{2\pi i{A}_2{s}_2}{G}}{e}^{-\frac{2\pi i{A}_3{s}_3}{G}}{e}^{-\frac{2\pi i{A}_4{s}_4}{G}}\\ =\sum _{A_1,A_2,A_3,A_4}p\left(\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right)e^{-(\frac{2\pi i}{G})(A_1{s}_1+A_2{s}_2+A_3{s}_3+A_4{s}_4)}.\end{array}$$ (A1)

This is a discrete Fourier transform in n = 4 variables, each of which can be equal to one of G different values. It reduces to Eq. (7) in the main text for G = 2, since e^πi = −1. Since Eq. (A1) is a discrete Fourier transform, the inverse transformation is immediate:

$$p\left(\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right)=\frac{1}{G^4}\sum _{s_1,s_2,s_3,s_4}\varphi \left(\begin{array}{cc}{s}_1& s_2\\ s_3& s_4\end{array}\right)e^{(\frac{2\pi i}{G})(A_1{s}_1+A_2{s}_2+A_3{s}_3+A_4{s}_4)},$$ (A2)

which reduces to Eq. (8) for G = 2.

As in the G = 2 case considered in the main text, stratifying the transformed coordinates ϕ according to the number of nonzero entries provides a simple way of expressing the normalization and stationarity constraints, as indicated by Eqs. (9)–(12). First-order coordinates have exactly one nonzero argument, second-order coordinates have exactly two nonzero arguments, etc.

With this stratification, stationarity of the 1 × 1 blocks is equivalent to the statement [Eq. (11)] that the first-order co-ordinates, $\varphi \left(\begin{array}{cc}s& 0\\ 0& 0\end{array}\right),\varphi \left(\begin{array}{cc}0& s\\ 0& 0\end{array}\right),\varphi \left(\begin{array}{cc}0& 0\\ s& 0\end{array}\right)$, and $\varphi \left(\begin{array}{cc}0& 0\\ 0& s\end{array}\right)$, all have the same value. That is, the stationarity constraints on the 1 × 1 blocks are encapsulated by the requirement that the first-order transformed coordinates depend only on the value of their sole nonzero argument, not on its position. Note, though, that when G ≥ 3, there is more than one possible value for this nonzero argument. Thus, rather than denote the first-order coordinates by a single quantity γ, the G ≥ 3 case requires a (G - 1)-element set of co-ordinates, {γ₁, …, γ_G−1}. Similarly, in the G ≥ 3 case, each of the four second-order co-ordinates β is a (G - 1)²-element set of two-subscripted quantities, rather than a single scalar. For example, β₋ corresponds to the set of elements $\varphi \left(\begin{array}{cc}{s}_1& s_2\\ 0& 0\end{array}\right)$, where both s₁ and s₂ are nonzero. The stationarity constraints on the 1 × 2 and 2 × 1 block probabilities correspond to the requirement that the second-order transformed coordinates β₋ and β_| have values that depend only on the relative position of their arguments, i.e., that $\varphi \left(\begin{array}{cc}{s}_1& s_2\\ 0& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& 0\\ s_1& s_2\end{array}\right)$ and $\varphi \left(\begin{array}{cc}{s}_1& 0\\ s_3& 0\end{array}\right)=\varphi \left(\begin{array}{cc}0& s_1\\ 0& s_3\end{array}\right)$.

Because the coordinates are Fourier transforms of the block probabilities, they facilitate the description of how image ensembles combine. Specifically, suppose the coordinates ϕ₁ describe the block probabilities of the images in the ensemble U₁ and ϕ₂ describe the block probabilities of the images in the ensemble U₂. A natural way to combine these ensembles is by pixel-wise addition of a random choice of an image in U₁ to a random choice of an image in U₂, and interpretation of the result mod G. The probability distribution of images in the new ensemble U is the convolution of the probability distributions of U₁ and U₂, since an image I in U can arise from any choice of I₁ in U₁ and I₂ = I - I₁ in U₂. Since Fourier transformation converts convolutions into products, it follows that the coordinates ϕ of U are given by ϕ = ϕ₁ϕ₂. This relationship is useful in creating ensembles with specified statistics and also underlies the demonstration of Section C.2.3.

Finally, we mention that for G ≥ 3, there are further symmetries that we have not exploited—for example, a permutation of the labels 1 and 2, which is not a cyclic permutation of the G gray levels. These further symmetries, which result in relationships among the transformed coordinates, can be exploited via generalizations of standard Fourier analysis.

APPENDIX B: ENTROPY AND INTRINSIC DISCRIMINABILITY

Here we calculate the entropy per pixel of samples S drawn from a maximum-entropy ensemble specified by one or more constraints of the form ${\varphi }_i={\varphi }_i^0$, in the limit of a large number of pixels. A main motivation for this calculation is that it determines the ability of an ideal observer to distinguish an image specified by the constraints ${\varphi }_i={\varphi }_i^0$ from a completely random texture (specified by ϕ_i = 0).

1. Setup

The linkage between intrinsic discriminability and entropy is via the Kullback–Leibler divergence, D_KL [16,30]. The Kullback–Leibler divergence D_KL(P||Q) is a measure of the extent to which an ideal observer can determine that samples drawn from a distribution P do not come from some alternative distribution, Q. Specifically, given a set of observations S that are drawn from a distribution P, in which they have probability p(S), the Kullback–Leibler divergence

$$D_{\text{KL}}(P||Q)=\sum _{S}p(S)ln\frac{p(S)}{q(S)}$$ (B1)

is the expected difference between the log likelihood that these observations were in fact drawn from P, and the log likelihood that they were drawn from an alternative distribution Q, in which they have probability q(S). (For background and further details, see [16,30]). Thus, D_KL(P||Q) = 0 only if the distributions are identical, and increasingly positive values of the divergence correspond to greater discriminability. An equivalent statement is that D_KL(P||Q) is the number of bits per observation available to an ideal observer who is asked to determine whether observations that are actually drawn from P were, instead, drawn from Q.

A basic fact about the Kullback–Leibler divergence [which can be deduced from Eq. (B1)] is that when all probabilities in the distribution q(S) are equal (i.e., when Q is “completely random”), the Kullback–Leibler divergence is the difference in entropies between P and Q, i.e., D_KL(P||Q) = H(Q) − H(P). Thus, the entropy of an image is a principled way of quantifying its intrinsic discriminability from randomness.

For the calculation of the entropy, our starting point, from the main text, is

$$p(S)=\frac{Z(S)}{Z}.$$ (B2)

where

$$Z(S)=exp\left(\sum _i{\mu }_{i}n(S,i){\varphi }_i(S)\right)$$ (B3)

and

$$Z=\sum _{S}Z(S).$$ (B4)

[Equation (B2) is text Eq. (30); Eq. (B3) follows from text Eq. (34) via Eq. (20); and Eq. (B4) is text Eq. (32).]

The entropy H = H(P) is defined by

$$H=-\sum _{S}p(S)lnp(S).$$ (B5)

Using Eqs. (B2) and (B4) for p(S), this is equivalent to

$$H=-\sum _{S}p(S)lnZ(S)+lnZ,$$ (B6)

which, via Eq. (B3), is equivalent to

$$H=-\sum _{S}p(S)\sum _i{\mu }_{i}n(S,i){\varphi }_i(S)+lnZ.$$ (B7)

The sum can be simplified, since Σ_Sp(S)ϕ_i(S) is the average value of ϕ_i(S), namely, the constrained value ${\varphi }_i^0$. Thus,

$$H=-\sum _i{\mu }_{i}n(S,i){\varphi }_i^0+lnZ.$$ (B8)

We consider two special cases: ensembles defined by a single constraint (which need not be small) and ensembles defined by multiple constraints, all of which are small. In both cases, we calculate the entropy per pixel and we focus on the limit in which the number of pixels is large. In this limit, we can ignore the distinction between n, the number of pixels in S, and n(S, i), the number of placements of the glider for ϕ_i in S, since they differ only by the number of pixels n_init along some of the edges of S. Consequently, the entropy per pixel, h (in natural-log units) is given by

$$h=\underset{n\to \infty }{lim}\frac{1}{n}{H}_n=-\sum _i{\mu }_i{\varphi }_i^0+\underset{n\to \infty }{lim}\frac{1}{n}ln{Z}_n,$$ (B9)

where Z_n is the partition function for an ensemble of size n.

2. One Constraint

For this case, we use the results from the one-parameter analysis in the main text. The Lagrange multiplier is explicitly given in Eq. (48) by

$${\mu }_i=\frac{1}{2}ln(1+{\varphi }_i^0)-\frac{1}{2}ln(1-{\varphi }_i^0),$$ (B10)

The partition function [Eq. (49)] is

$$Z_n=2^n{\left(\frac{1}{\sqrt{(1+{\varphi }_i^0)(1-{\varphi }_i^0)}}\right)}^{n-n_{\text{init}}},$$ (B11)

so the required limit on the right-hand-side of Eq. (B9) is

$$\underset{n\to \infty }{lim}\frac{1}{n}ln{Z}_n=ln2-\frac{1}{2}ln(1+{\varphi }_i^0)-\frac{1}{2}ln(1-{\varphi }_i^0).$$ (B12)

Substitution of these quantities into Eq. (B9), followed by straightforward algebra, leads to

$$h=-\left(\frac{1+{\varphi }_i^0}{2}ln\frac{1+{\varphi }_i^0}{2}+\frac{1-{\varphi }_i^0}{2}ln\frac{1-{\varphi }_i^0}{2}\right).$$ (B13)

This is the expected result: it is the entropy of a binary choice in ratio $(1+{\varphi }_i^0)/(1-{\varphi }_i^0)$; this is the binary choice that is made when the colors of the interior pixels are chosen.

3. Many Constraints, All Constraint Values Small

In the regime that all of the constraint values ${\varphi }_i^0$ are small, our strategy is to find Lagrange multipliers μ_i that are approximate solutions of the constraint equations [Eq. (33)] and then to use these solutions to approximate both terms of the right-hand-side of Eq. (B9). In the large-n limit, Eq. (33) is equivalent to

$$\frac{1}{n}\frac{\partial ln{Z}_n}{\partial {\mu }_i}={\varphi }_i^0.$$ (B14)

This is a nonlinear system, but it is solved exactly at the origin of the coordinate system (when all ${\varphi }_i^0=0$, corresponding to a completely random image) by μ_i = 0, as indicated above.

Near the origin, we find approximate solutions of Eq. (B14), by using the first term in a Taylor expansion to approximate $\frac{\partial ln{Z}_n}{\partial {\mu }_i}$:

$$\frac{1}{n}\frac{\partial ln{Z}_n}{\partial {\mu }_i}\approx \frac{1}{n}\sum _j{\mu }_j\frac{{\partial }^{2}ln{Z}_n}{\partial {\mu }_j\partial {\mu }_i}.$$ (B15)

The right-hand-side is evaluated via

$$\frac{{\partial }^{2}ln{Z}_n}{\partial {\mu }_j\partial {\mu }_i}=\frac{\partial }{\partial {\mu }_j}\left(\frac{1}{Z_n}\frac{\partial Z_n}{\partial {\mu }_i}\right)=-\left(\frac{1}{Z_n}\frac{\partial Z_n}{\partial {\mu }_j}\right)\left(\frac{1}{Z_n}\frac{\partial Z_n}{\partial {\mu }_i}\right)+\frac{1}{Z_n}\frac{{\partial }^2{Z}_n}{\partial {\mu }_j\partial {\mu }_i}.$$ (B16)

For the first derivative, we use Eq. (B14), which may be restated as

$$\frac{1}{Z_n}\frac{\partial Z_n}{\partial {\mu }_i}=n\langle {\varphi }_i\rangle ,$$ (B17)

since the constraint value, ${\varphi }_i^0$, is equal to the ensemble average 〈ϕ_i〉. For the second derivative [again neglecting edge effects, i.e., setting n = n(S, i) in Eq. (B3)], we calculate

$$\begin{array}{l}\frac{1}{Z_n}\frac{{\partial }^2{Z}_n}{\partial {\mu }_j\partial {\mu }_i}=\frac{1}{Z_n}\frac{{\partial }^2}{\partial {\mu }_j\partial {\mu }_i}\sum _{S}exp\left(n\sum _k{\mu }_k{\varphi }_k(S)\right)\\ =\frac{1}{Z_n}\sum _S{n}^2{\varphi }_j(S){\varphi }_i(S)exp\left(\sum _k{\mu }_{k}n(S,k){\varphi }_k(S)\right)\\ =\sum _S{n}^{2}p(S){\varphi }_j(S){\varphi }_i(S).\end{array}$$ (B18)

That is, the second derivative is proportional to the expected value of the product of ϕ_j(S) and ϕ_i(S), averaged over all samples S. Combining Eqs. (B16), (B17), and Eq. (B18) thus yields

$$\frac{{\partial }^{2}ln{Z}_n}{\partial {\mu }_j\partial {\mu }_i}=n^2(\langle {\varphi }_j{\varphi }_i\rangle -\langle {\varphi }_j\rangle \langle {\varphi }_i\rangle )=n^2\langle ({\varphi }_j-\langle {\varphi }_j\rangle )({\varphi }_i-\langle {\varphi }_i\rangle )\rangle .$$ (B19)

This quantity is the covariance of the coordinate values, as estimated from samples S of size n.

At the origin (μ⃗ = 0), these covariances are simple to calculate. Each placement of the glider for ϕ_i contributes either +1 or −1 to n₊(S,i) − n₋(S, i) and these alternatives occur independently, each with probability 1/2. So the sum of these n contributions, nϕ_i(S) = n₊(S, i) − n₋(S, i), are binomially distributed, with variance n. The off-diagonal terms correspond to the covariance of the counts for different kinds of gliders. This is zero: even if the gliders are overlapping, there must be some pixels that are contained in one glider but not another and since these pixels are randomly assigned, the contributions of the gliders are independent. Thus,

$${\frac{{\partial }^{2}ln{Z}_n}{\partial {\mu }_i\partial {\mu }_j}|}_{{\mu }_i={\mu }_j=0}=n{\delta }_{ij}.$$ (B20)

Substitution of Eq. (B20) into Eq. (B15) yields the desired approximation to the left-hand-side of the constraint equations, Eq. (B14):

$$\frac{1}{n}\frac{\partial ln{Z}_n}{\partial {\mu }_i}\approx \frac{1}{n}\sum _j{\mu }_j\frac{{\partial }^{2}ln{Z}_n}{\partial {\mu }_j\partial {\mu }_i}\approx {\mu }_i.$$ (B21)

That is, near the origin, the constraints [Eq. (B14)] are satisfied when the Lagrange multipliers are approximated by the coordinates themselves:

$${\mu }_i\approx {\varphi }_i^0.$$ (B22)

To complete the estimation of Eq. (B9), we also need to approximate Z_n near the origin.

We do this via a Taylor expansion, again using Eq. (B20) for the second derivatives:

$$\begin{array}{l}ln{Z}_n(\overrightarrow{u})\approx {ln{Z}_n(0)+\frac{1}{2}\sum _{i,j}\frac{{\partial }^{2}ln{Z}_n}{\partial {\mu }_i\partial {\mu }_j}|}_{{\mu }_i={\mu }_j=0}{\mu }_i{\mu }_j\\ =ln{Z}_n(0)+\frac{n}{2}{\mid \overrightarrow{\mu }\mid }^2=nln2+\frac{n}{2}{\mid \overrightarrow{\mu }\mid }^2.\end{array}$$ (B23)

[The first derivative terms are zero because of the constraint equations and we made use of Eq. (B11) for Z_n(0)].

Finally, substituting eqs. (B22) and (B23) into Eq. (B9), we obtain the entropy per pixel near the origin:

$$h=\underset{n\to \infty }{lim}\frac{1}{n}{H}_n=ln2-\frac{1}{2}\sum _i{({\varphi }_i^0)}^2.$$ (B24)

This equation states that near the origin, the intrinsic discriminability, which is determined by the decrease in entropy, is determined by the Euclidean distance in the coordinate space ϕ. In other words, the threshold isodiscrimination contours for an ideal observer are circular.

APPENDIX C: DETAILED ANALYSIS OF SELECTED COORDINATE PAIRS

This appendix provides the calculations and proofs that support several of the constructions of Table 2. The first two sections validate the constructions for images containing the 2 × 2 block probabilities required for the non-Pickard cases (β_\, θ_⌟) and (θ_⌟, θ_⌞); these images are the starting points for the donut algorithm that samples the required image ensembles. Though (θ_⌟, θ_⌞) is of higher order than (β_\, θ_⌟), it is simpler and we consider it first. The third section derives the polynomial equations whose roots (r₁, r₂, and r₃, referred to in Table 2) determine the maximum-entropy choice of α, given specified values of the βs and θs.

1. The non-Pickard (θ_⌟, θ_⌞) Pair

In this section, we demonstrate the construction of an image with specified values of the coordinates θ_⌟ and θ_⌞ and a value of 0 for all other 2 × 2 block probability coordinates, {γ, β₋, β_/, β_\, β_/, θ_⌜, θ_⌝, α}; these images are used as the starting point for the donut algorithm. We construct this image by first creating two columns of pixels, and then extending it column by column.

The first step of the construction is to create an arbitrarily long n × 2 column of pixels, via a Markov process of overlapping 2 × 2 blocks. That is, to extend from a 2 × 2 block to a 3 × 2 block, we use

$$\begin{array}{l}p\left(\begin{array}{cc}A& B\\ D& E\\ G& H\end{array}\right)=p\left(\begin{array}{cc}A& B\\ D& E\end{array}\right)p\left(\begin{array}{cc}D& E\\ G& H\end{array}|\begin{array}{cc}A& B\\ D& E\end{array}\right)\\ =\frac{p\left(\begin{array}{cc}A& B\\ D& E\end{array}\right)p\left(\begin{array}{cc}D& E\\ G& H\end{array}\right)}{p(\begin{array}{cc}D& E\end{array})}.\end{array}$$ (C1)

Consistency of the 2 × 2 probabilities $p\left(\begin{array}{cc}D& E\\ G& H\end{array}\right)$ with those of the original 2 × 2 block follows by marginalizing Eq. (C1) over A and B. By induction, this applies to all of the 2 × 2 blocks that span the first two columns.

We now need to show consistency still holds as we extend this construction to adjacent columns. We extend the 3 × 2 block to a 3 × 3 block, by first appending pixels $\left(\begin{array}{c}C\\ F\end{array}\right)$ to the upper two rows and then a ninth pixel I in the lower right. Both steps are carried out in a Markovian fashion, leading to

$$p\left(\begin{array}{ccc}A& B& C\\ D& E& F\\ G& H& I\end{array}\right)=p\left(\begin{array}{cc}A& B\\ D& E\\ G& H\end{array}\right)\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)}{p\left(\begin{array}{c}B\\ E\end{array}\right)}\frac{p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p\left(\begin{array}{cc}E& F\\ H& \end{array}\right)}.$$ (C2)

We now need to determine whether the block probabilities in the second and third column are identical to those in the first two columns. That is, does marginalizing Eq. (C2) over the first column yield the same result as Eq. (C1)? This in fact turns out to be the case, as we now show.

To calculate the marginalization of Eq. (C2) over the first column, we begin by using Eq. (C1) for the 3 × 2 block in the first two columns:

$$\begin{array}{l}\sum _{A,D,G}p\left(\begin{array}{ccc}A& B& C\\ D& E& F\\ G& H& I\end{array}\right)=\sum _{A,D,G}p\left(\begin{array}{cc}A& B\\ D& E\\ G& H\end{array}\right)\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)}{p\left(\begin{array}{c}B\\ E\end{array}\right)}\frac{p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p\left(\begin{array}{cc}E& F\\ H& \end{array}\right)}=\sum _{A,D,G}\frac{p\left(\begin{array}{cc}A& B\\ D& E\end{array}\right)p\left(\begin{array}{cc}D& E\\ G& H\end{array}\right)}{p(\begin{array}{cc}D& E\end{array})}\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)}{p\left(\begin{array}{c}B\\ E\end{array}\right)}\frac{p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p\left(\begin{array}{cc}E& F\\ H& \end{array}\right)}\\ =\sum _D\frac{p\left(\begin{array}{cc}& B\\ D& E\end{array}\right)p\left(\begin{array}{cc}D& E\\ & H\end{array}\right)}{p(\begin{array}{cc}D& E\end{array})}\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)}{p\left(\begin{array}{c}B\\ E\end{array}\right)}\frac{p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p\left(\begin{array}{cc}E& F\\ H& \end{array}\right)}.\end{array}$$ (C3)

Next, we note that, since β₋ = β_| = θ_⌜ = θ_⌝ = 0, the pixels in the θ_⌜ glider are all uncorrelated, as are the pixels in the θ_⌝ glider. Therefore, the second half of both Pickard conditions, Eqs. (58) and (59), are satisfied. Using the second half of Eq. (58) for the denominator and the second half of Eq. (59) for the numerator yields

$$\begin{array}{l}\sum _{A,D,G}p\left(\begin{array}{ccc}A& B& C\\ D& E& F\\ G& H& I\end{array}\right)=\sum _D\frac{p\left(\begin{array}{cc}& B\\ D& E\end{array}\right)}{p(\begin{array}{cc}D& E\end{array})}\frac{p(\begin{array}{cc}D& E\end{array})p\left(\begin{array}{c}E\\ H\end{array}\right)}{p(E)}\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p\left(\begin{array}{c}B\\ E\end{array}\right)}\frac{p(E)}{p(\begin{array}{cc}E& F\end{array})p\left(\begin{array}{c}E\\ H\end{array}\right)}\\ =\sum _{D}p\left(\begin{array}{cc}& B\\ D& E\end{array}\right)\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p\left(\begin{array}{c}B\\ E\end{array}\right)p(\begin{array}{cc}E& F\end{array})}=p\left(\begin{array}{c}B\\ E\end{array}\right)\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p\left(\begin{array}{c}B\\ E\end{array}\right)p(\begin{array}{cc}E& F\end{array})}=\frac{p\left(\begin{array}{cc}B& C\\ E& F\end{array}\right)p\left(\begin{array}{cc}E& F\\ H& I\end{array}\right)}{p(\begin{array}{cc}E& F\end{array})}.\end{array}$$ (C4)

The last expression is identical in form to Eq. (C1), as required. This shows that when a third column is adjoined to the second column via sequential application of the Markov rule [Eq. (C2)], the resulting second and third columns have the same statistics as the first two columns. Consequently, their 2 × 2 block probabilities are identical to those in the first to columns. Moreover, the probability of a 3 × 2 block that spans the second and third columns corresponds to a Markov process in which the first column is ignored—identical to the process that generates a 3 × 2 block that spans the first two columns. A similar calculation shows that this holds for k × 2 blocks that span the second and third columns, for any k. Inductively, this holds for all subsequent columns. Thus, we conclude that k × 2 block probabilities (and, hence, 2 × 2 block probabilities) remain consistent throughout the entire image.

The above analysis shows that each column has identical statistics, but it is worthwhile noting that this is not true of the rows. The first row can be created in an IID fashion (since β₋ = β_| = θ_⌜ = 0), but in the second row, correlations arise because θ_⌟ and θ_⌞ are both nonzero. Specifically, in the 3 × 3 block considered above, D and F are correlated, because θ_⌟ biases the parity of $\left(\begin{array}{cc}& B\\ D& E\end{array}\right)$, while θ_⌞ biases the parity of $\left(\begin{array}{cc}B& \\ E& F\end{array}\right)$. Since both of these subsets share B and E, the combined effect is that the parity of D and F are correlated by θ_⌟ θ_⌞. This correlation (at a spacing of two along the rows) can be seen in the autocorrelograms of Fig. 4(a).

2. The non-Pickard (β_\, θ_⌟) Pair

Here we detail the construction described in the main text that generates maximum-entropy images specified by a β parameter and a θ parameter that do not satisfy the Pickard conditions. For convenience, we use the coordinates (β_\, θ_⌜) rather than the pair (β_\, θ_⌟) of Table 2, as this will allow us to work from top to bottom of an image (i.e., in order of increasing row number). The construction starts with a row created by a Markov process whose pixels satisfy a particular set of 1 × 3 block probabilities (specified below). Each subsequent row is iteratively determined from the previous row by a “tee” recursion, in which each pixel’s coloring depends on the coloring of the three pixels directly and diagonally above it. We show that (a) the 1 × 3 block probabilities in the second row match those of the starting row and (b) the 2 × 2 block probabilities that span the first two rows have the specified coordinates β_\ and θ_⌜, a non-zero value of θ_⌟ = β_\ θ_⌜, and all other coordinates equal to 0. We note, though, that the iteration step induces a subtle change in the statistical structure of the each newly-created row: while the 1 × 3 block probabilities of the second row match those of the first row, it is no longer Markov. As a result, we cannot prove that subsequent rows have the same coordinates {β_\, θ_⌜, θ_⌟} as the first two rows and thus, the construction is not exact. However, as we show, this deviation small, and is insignificant for practical purposes. Finally, we show (c) that the other coordinates {γ, β₋, β_/, β_/, θ_⌞, θ_⌝, α} remain exactly zero as the process is iterated.

As described in the main text, the donut algorithm can then be applied to an image generated in this fashion, to preserve the 2 × 2 block probabilities while randomizing, as much as possible, all others—resulting in a maximum-entropy texture with controlled values of β_\, θ_⌜, and θ_⌟ = β_\ θ_⌜.

As in the main text, we use transformed coordinates analogous to Eq. (7) to facilitate these calculations. To specify the Markov process for the first row of the construction, we choose

$$p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})=\frac{1}{8}\sum _{s_1,s_2,s_3}\varphi (\begin{array}{ccc}{s}_1& s_2& s_3\end{array}){(-1)}^{A_1{s}_1+A_2{s}_2+A_3{s}_3},$$ (C5)

where all ϕ’s are zero, except for

$$\varphi (\begin{array}{ccc}0& 0& 0\end{array})\mathit{and}\varphi (\begin{array}{ccc}1& 1& 1\end{array})=-g.$$ (C6)

We will choose the nonzero value g = (β_\)²θ_⌜ for a reason that will become evident below. Because this row is generated by a Markov process, probabilities of larger 1 × k blocks are specified by

$$p(\begin{array}{cccc}{A}_1& A_2& A_3& A_4\end{array})=p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})p(\begin{array}{ccc}{A}_2& A_3& A_4\end{array}\mid \begin{array}{cc}{A}_2& A_3\end{array})=\frac{p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})p(\begin{array}{ccc}{A}_2& A_3& A_4\end{array})}{p(\begin{array}{cc}{A}_2& A_3\end{array})}$$ (C7)

[see, for example, Eq. (50)] and

$$p(\begin{array}{ccccc}{A}_1& A_2& A_3& A_4& A_5\end{array})=\frac{p(\begin{array}{cccc}{A}_1& A_2& A_3& A_4\end{array})p(\begin{array}{cccc}{A}_2& A_3& A_4& A_5\end{array})}{p(\begin{array}{ccc}{A}_2& A_3& A_4\end{array})}=\frac{p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})p(\begin{array}{ccc}{A}_2& A_3& A_4\end{array})p(\begin{array}{ccc}{A}_3& A_4& A_5\end{array})}{p(\begin{array}{cc}{A}_2& A_3\end{array})p(\begin{array}{cc}{A}_3& A_4\end{array})}.$$ (C8)

Since the ϕ’s in Eq. (C5) with one or two nonzero entries are zero, the 1 × 2 blocks all have probability 1/4, the 1 × k block probabilities simplify:

$$p(\begin{array}{cccc}{A}_1& A_2& A_3& A_4\end{array})=4p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})p(\begin{array}{ccc}{A}_2& A_3& A_4\end{array})$$ (C9)

and

$$p(\begin{array}{ccccc}{A}_1& A_2& A_3& A_4& A_5\end{array})=16p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})p(\begin{array}{ccc}{A}_2& A_3& A_4\end{array})\times p(\begin{array}{ccc}{A}_3& A_4& A_5\end{array}).$$ (C10)

To specify the recursive process that creates the subsequent row, we choose a set of probabilities on tee-shaped regions, by

$$p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & X& \end{array}\right)=\frac{1}{16}\sum _{s_1,s_2,s_3,s_4}\varphi \left(\begin{array}{ccc}{s}_1& s_2& s_3\\ & s_4& \end{array}\right){(-1)}^{A_1{s}_1+A_2{s}_2+A_3{s}_3+{Xs}_4},$$ (C11)

where all ϕ’s are zero except for

$$\varphi \left(\begin{array}{ccc}1& 0& 0\\ & 1& \end{array}\right)={\beta }_{\backslash },\text{and}\varphi \left(\begin{array}{ccc}0& 1& 1\\ & 1& \end{array}\right)={\theta }_{⌜},\text{and}\varphi \left(\begin{array}{ccc}1& 1& 1\\ & 0& \end{array}\right)=-g.$$ (C12)

That is, given a 1 × 3 block in the first row, the state of the pixel under its middle is assigned according to the rule

$$\begin{array}{l}p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & Z& \end{array}|\begin{array}{ccc}{A}_1& A_2& A_3\end{array}\right)=\frac{p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & Z& \end{array}\right)}{{\displaystyle \sum _X}p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & X& \end{array}\right)}\\ =\frac{p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & Z& \end{array}\right)}{p(\begin{array}{ccc}{A}_1& A_2& A_3\end{array})}.\end{array}$$ (C13)

In the second equality, we used the fact that the block probabilities of Eq. (C11), when marginalized over X, conform to those specified by Eq. (C5). Because of this, it follows that when the recursion (C13) rule is applied to rows specified by Eq. (C5), the resulting tee-shaped block probabilities conform to Eq. (C11).

a. Coordinates of 1 × 3 Block Probabilities in the Second Row

We are now set up to calculate the probabilities of the 1 × 3 blocks in the second row and thus to validate claim (a). First, we combine Eqs. (C10) and (C13) to obtain an expression for the block probabilities of a region that determines a 1 × 3 block $(\begin{array}{ccc}{B}_1& B_2& B_3\end{array})$ in the second row:

$$\begin{array}{l}p\left(\begin{array}{ccccc}U& A_1& A_2& A_3& V\\ & B_1& B_2& B_3& \end{array}\right)=p(\begin{array}{ccccc}U& A_1& A_2& A_3& V\end{array})•p\left(\begin{array}{ccc}U& A_1& A_2\\ & B_1& \end{array}|\begin{array}{ccc}U& A_1& A_2\end{array}\right)p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & B_2& \end{array}|\begin{array}{ccc}{A}_1& A_2& A_3\end{array}\right)\\ \times p\left(\begin{array}{ccc}{A}_2& A_3& V\\ & B_3& \end{array}|\begin{array}{ccc}{A}_2& A_3& V\end{array}\right)=16p\left(\begin{array}{ccc}U& A_1& A_2\\ & B_1& \end{array}\right)p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & B_2& \end{array}\right)p\left(\begin{array}{ccc}{A}_2& A_3& V\\ & B_3& \end{array}\right).\end{array}$$ (C14)

Next, we marginalize this over all values in the first row. The marginalization over U and V, the first and last elements in the top row, are straightforward because these pixels only appear in one term of the product:

$$\begin{array}{l}p\left(\begin{array}{ccc}& & \\ B_1& B_2& B_3\end{array}\right)=\sum _{U,A_1,A_2,A_3,V}p\left(\begin{array}{ccccc}U& A_1& A_2& A_3& V\\ & B_1& B_2& B_3& \end{array}\right)=16\sum _{U,A_1,A_2,A_3,V}p\left(\begin{array}{ccc}U& A_1& A_2\\ & B_1& \end{array}\right)p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & B_2& \end{array}\right)p\left(\begin{array}{ccc}{A}_2& A_3& V\\ & B_3& \end{array}\right)\\ =16\sum _{A_1,A_2,A_3}p\left(\begin{array}{cc}{A}_1& A_2\\ B_1& \end{array}\right)p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & B_2& \end{array}\right)p\left(\begin{array}{cc}{A}_2& A_3\\ & B_3\end{array}\right).\end{array}$$ (C15)

The middle term in the final expression of Eq. (C15) is obtained from Eq. (C11) and the specific values chosen for the coordinates [Eq. (C12)]. The other terms are obtained by marginalization of it. Since most coordinates are zero, only a few terms remain:

$$p\left(\begin{array}{ccc}{A}_1& A_2& A_3\\ & B_3& \end{array}\right)=\frac{1}{16}\left(1+{(-1)}^{A_1+B_2}{\beta }_{\backslash }-{(-1)}^{A_2+A_3+B_2}{\theta }_{⌜}-{(-1)}^{A_1+A_2+A_3}g\right),$$ (C16)

$$\begin{array}{l}p\left(\begin{array}{cc}{A}_1& A_2\\ B_1& \end{array}\right)=\sum _{Z}p\left(\begin{array}{ccc}Z& A_1& A_2\\ & B_1& \end{array}\right)\\ =\frac{1}{8}\left(1-{(-1)}^{A_1+A_2+B_1}{\theta }_{⌜}\right),\end{array}$$ (C17)

$$p\left(\begin{array}{cc}{A}_2& A_3\\ & B_3\end{array}\right)=\sum _{Z}p\left(\begin{array}{ccc}{A}_2& A_3& Z\\ & B_3& \end{array}\right)=\frac{1}{8}\left(1+{(-1)}^{A_2+B_3}{\beta }_{\backslash }\right).$$ (C18)

Combining the above four equations yields

$$p\left(\begin{array}{ccc}& & \\ B_1& B_2& B_3\end{array}\right)=\frac{1}{64}\sum _{A_1,A_2,A_3}(1-{(-1)}^{A_1+A_2+B_1}{\theta }_{⌜})•\left(1+{(-1)}^{A_1+B_2}{\beta }_{\backslash }-{(-1)}^{A_2+A_3+B_2}{\theta }_{⌜}-{(-1)}^{A_1+A_2+A_3}g\right)\left(1+{(-1)}^{A_2+B_3}{\beta }_{\backslash }\right).$$ (C19)

Next, we observe that the only terms that survive the summation are those for which the quantities A₁, A₂, and A₃ occur an even number of times in the exponent of −1. Thus, the only term of the product that survives is the one that corresponds to the θ_⌜ term of the first factor and the β_\ terms of the other two factors:

$$p\left(\begin{array}{ccc}& & \\ B_1& B_2& B_3\end{array}\right)=\frac{1}{8}(1-{(-1)}^{B_1+B_2+B_3}{\beta }_{\backslash }^2{\theta }_{⌜}).$$ (C20)

This demonstrates claim (a), because for g = (β_\)²θ_⌜, Eq. (C20) is identical to Eq. (C5).

b. Coordinates of 2 × 2 Block Probabilities in the First Two Rows

For claim (b), which concerns 2 × 2 block probabilities, the calculation proceeds along the same lines, but is simpler:

$$\begin{array}{l}p\left(\begin{array}{cc}{A}_1& A_2\\ B_1& B_2\end{array}\right)=\sum _{U,V}p\left(\begin{array}{cccc}U& A_1& A_2& V\\ & B_1& B_2& \end{array}\right)=4\sum _{U,V}p\left(\begin{array}{ccc}U& A_1& A_2\\ & B_1& \end{array}\right)p\left(\begin{array}{ccc}{A}_1& A_2& V\\ & B_2& \end{array}\right)=4p\left(\begin{array}{cc}{A}_1& A_2\\ B_1& \end{array}\right)p\left(\begin{array}{cc}{A}_1& A_2\\ & B_2\end{array}\right)\\ =\frac{1}{16}\left(1-{(-1)}^{A_1+A_2+B_1}{\theta }_{⌜}\right)\left(1+{(-1)}^{A_1+B_2}{\beta }_{\backslash }\right)=\frac{1}{16}\left(1+{(-1)}^{A_1+B_2}{\beta }_{\backslash }-{(-1)}^{A_1+A_2+B_1}{\theta }_{⌜}-{(-1)}^{A_2+B_1+B_2}{\theta }_{⌟}\right).\end{array}$$ (C21)

Thus, the β_\ and θ_⌜ coordinates in a 2 × 2 region are the same as the specified values in the original tee-shaped region and θ_⌟, the final coefficient, is given by θ_⌟ = β_\θ_⌜.

c. Coordinates That Are Exactly Zero

The third claim, (c) asserts that the other coordinates, {γ, β₋, β_|, β_/, θ_⌞, θ_⌝, α}, are exactly zero. We show this via a symmetry argument, which is illustrated in Fig. 9. In Fig. 9(a), we select the pixels that lie on two out of every three diagonals. We now consider the consequences of inverting the states of these pixels and we will show that it produces another equally likely example of a process that is generated by the above construction. That is, this inversion does not change the ensemble that is generated—and consequently, it must preserve the values of all the coordinates. The proof will be completed by showing that this inversion can only preserve the values of the coordinates {γ, β₋, β_\, β_/, θ_⌞, θ_⌝, α}if they are in fact exactly zero.

Fig. 9.

A symmetry argument (Subsection C.2.3) that the recursive “tee” construction for (β_\, θ_⌜ produces block probabilities whose coordinates {γ, β₋, β_\, β_/, θ_⌞, θ_⌝, α} are zero. The intersection points represent the centers of individual pixels. The black dots select the pixels lying on two of every three diagonals. (a). Any placement of a “tee” glider contains two or three of the selected pixels. There are only three ways that these selected pixels can be configured within a glider, corresponding to the phase of each glider with respect to the diagonals. (b) All β_\ and θ_⌜ gliders contain an even number of selected pixels. (c1): For gliders in the set {γ, β₋, β_|, β_/, θ_⌞, θ_⌝, α}, two-thirds of their placements contain an odd number of selected pixels (shaded), and one-third contain an even number of selected pixels. (c2,c3): Shifting the selected pixels by one column permutes the placements of the gliders {γ, β₋, β_|, β_/, θ_⌞, θ_⌝, α} that contain an odd number of selected pixels. As shown in Subsection C.2.3, this implies that those image statistics must be exactly zero.

As Fig. 9(a) shows, every placement of a “tee” covers these selected pixels in one of three ways: the three pixels along the midline and the left, the two rightmost pixels on the upper bar, and the three pixels in the arms. We next observe that inversion of any of these sets of pixels leaves the value of the tee probabilities unchanged:

$$\begin{array}{l}p\left(\begin{array}{ccc}A& B& C\\ & D& \end{array}\right)=p\left(\begin{array}{ccc}1-A& 1-B& C\\ & 1-D& \end{array}\right)\\ =p\left(\begin{array}{ccc}A& 1-B& 1-C\\ & D& \end{array}\right)\\ =p\left(\begin{array}{ccc}1-A& B& 1-C\\ & 1-D& \end{array}\right).\end{array}$$ (C22)

This can be seen algebraically from Eqs. (C11) and (C12), but it can also be seen geometrically, in the following way. As shown in Fig. 9(b), the subsets of the tee that determine the block probabilities, i.e., the ones that correspond to nonzero coordinates listed in Eq. (C12), always contain an even number of selected pixels. Thus, their contributions are unaffected when the states of all of the selected pixels are inverted. In other words, these inversions do not change the values of β_\, θ_⌜, or g.

However, inverting these selected pixels (the ones that lie in two of every three diagonals) affects the other coordinates, unless the coordinates have a value of zero. To see why this is true, we begin by noting that the selected subset can be chosen in any of three equivalent ways [Fig. 9(c)]. Consider now the coordinate γ, the luminance bias. If γ is nonzero, it must be nonzero on at least one of the three subsets. [This is because the overall luminance bias is the average of the values calculated separately from each of the three subsets: if γ = (γ₁ +γ₂ + γ₃)/3 is nonzero, then at least one of the γ_k is nonzero.] Inverting the kth subset replaces γ_k by −γ_k and therefore changes the value of γ. Since this transformation must also leave the ensemble unchanged, it follows that all of the γ_k must be zero. Figure 9(c) shows that the same argument holds for the other coordinates in {γ, β₋, β_\, β_/, θ_⌞, θ_⌝, α}: for each of these, each of the three inversions affects a different 233 of the values from which the coordinate is calculated. Since inversion leaves the statistics of the ensemble unchanged, each of these coordinates must therefore be zero.

Thus, the only coordinates that can be nonzero are those for which every glider placement covers an even number of selected pixels in Fig. 9. This includes blocks of size 3m × 3n and pairs of pixels whose centers are offset by multiples of three. The latter accounts for the periodicity seen in the autocorrelograms of Fig. 4(b).

Note also that the symmetry argument applies to the final maximum-entropy ensemble itself and not just to the approximations created by this iterative scheme. Moreover, as mentioned in the main text, this symmetry argument also shows that the maximum-entropy (θ_⌟, θ_⌜) ensemble has zero values for the coordinates {γ, β₋, β_\, β_/, θ_⌞, θ_⌝, α}, since the transformations of Fig. 9 preserve θ_⌟ as well as θ_⌜ and β_\.

d. Comments: Implementation and Deviation from Exactness

We close this analysis with two comments, one on implementation and one on the deviation from exactness. With respect to implementation, Eq. (C20) points the way to a simple strategy: it suffices to initialize the construction procedure with an IID first row (all coordinates 0), rather than the Markov process corresponding to Eq. (C5). This is because the triplet probabilities on the second row, as given by Eq. (C20), do not depend on the value of g.

The second comment concerns the possible deviation of the coordinates from their desired value, as the process is iterated beyond the second row. An analysis similar to that used to derive Eq. (C20) demonstrates that the second row is not Markov. We spare the reader the details and quote the result:

$$p\left(\begin{array}{cccc}& & & \\ B_1& B_2& B_3& B_4\end{array}\right)=\frac{1}{16}\left(1-{(-1)}^{B_1+B_2+B_3}{\beta }_{\backslash }^2{\theta }_{⌜}-{(-1)}^{B_2+B_3+B_4}{\beta }_{\backslash }^2{\theta }_{⌜}-{(-1)}^{B_1+B_4}{\beta }_{\backslash }{\theta }_{⌜}g\right).$$ (C23)

The final term captures the deviation from a Markov process. A Markov process applied to Eq. (C20) would have yielded a coefficient of ${\beta }_{\backslash }^4{\theta }_{⌜}^2$, in contrast to the value of ${\beta }_{\backslash }{\theta }_{⌜}g={\beta }_{\backslash }^3{\theta }_{⌜}^2$ which actually arises. Because the second row is not Markov, this analysis leaves open the possibility that when the tee-shaped recursion rule is applied to the second row, the probabilities in the resulting third row differ from those in the first two rows. Nevertheless, the symmetry argument (Subsection C.2.3) shows that all coordinates other than β_\, θ_⌜, and θ_⌟ are exactly zero, so the resulting image still lies in the desired parameter space.

Moreover, numerical evidence suggests that the desired block probabilities may, in fact, be exactly achieved—even though the above argument does not guarantee that this is the case. For example, a simulation of over 10⁸ pixels (100 examples of a 1024 × 1024 array, beginning with a random first row and β_\ = 0.3, θ_⌜ = 0.4) yields deviations of <0.0005 for all coordinates. Thus we speculate that the Markov property is not necessary for exact equality to hold. Whether or not this speculation proves correct, the analytic observation that the deviation from Markov behavior occurs at very high order [ ${\beta }_{\backslash }^4{\theta }_{⌜}^2$ versus ${\beta }_{\backslash }^3{\theta }_{⌜}^2$, Eq. (C23)] likely underlies the reason that the construction is at least very close to exact.

3. Maximum-Entropy Choices for α

Here, we determine the values of α that maximize the entropy of the images created by the two-dimensional Markov constructions of Table 2, given specifications of pairs of values (β₋, β_|), (β₋, β_\), or (β₋, β_⌟). Since our goal is to maximize the entropy per pixel (in the limit of large areas), rather than of the 2 × 2 blocks themselves, the first step is to determine how these two quantities are related.

This relationship follows from the fact that the images are created first by a Markov process along the rows and then along the columns. Since the rows are created by a Markov process determined by the overlapping 1 × 2 blocks, it follows directly from Eqs. (50) and (51) (or see, for example, Appendix B of [22]), that the entropy of the 1 × k blocks, H_1×k, is given by

$$H_{1\times k}=(k-1)H_{1\times 2}-(k-2)H_{1\times 1}.$$ (C24)

Similarly, since pairs of rows are created via a Markov process that extends overlapping 2 × 2 blocks horizontally, the entropy of the 2 × k blocks, H_2×k, is given by

$$H_{2\times k}=(k-1)H_{2\times 2}-(k-2)H_{2\times 1}.$$ (C25)

Finally, since a j × k block is generated by a Markov process that extends overlapping 2 × k blocks vertically, the entropy of the j × k blocks, H_j×k, is given by

$$\begin{array}{l}{H}_{j\times k}=(j-1)H_{2\times k}-(j-2)H_{1\times k}\\ =(j-1)(k-1)H_{2\times 2}-(j-1)(k-2)H_{2\times 1}-(j-2)(k-1)H_{1\times 2}+(j-2)(k-2)H_{1\times 1},\end{array}$$ (C26)

where the second equality follows via Eqs. (C24) and (C25). Thus, the large-area limit of the entropy per pixel, h, is given by

$$h=\underset{j,k\to \infty }{lim}\frac{1}{jk}{H}_{j\times k}=H_{2\times 2}-H_{2\times 1}-H_{1\times 2}+H_{1\times 1}.$$ (C27)

We now seek to maximize this quantity with respect to α. Since the 1- and 2-pixel blocks do not depend on α, we only need to maximize H_2×2, by setting ∂H_2×2/∂α = 0.

The analysis is straightforward. The first step is to write H_2×2 in terms of the coordinates. Table 1 provides the necessary conversion between block probabilities and coordinates: for any block $\overrightarrow{b}=\left(\begin{array}{ll}{b}_1\hfill & b_2\hfill \\ b_3\hfill & b_4\hfill \end{array}\right)$, the relationship is of the form

$$p(\overrightarrow{b})=\frac{1}{16}\left(1+\sum _{i}c(\overrightarrow{b},i){\varphi }_i\right).$$ (C28)

Thus, for any coordinate ϕ_j,

$$\begin{array}{l}\frac{\partial H_{2\times 2}}{\partial {\varphi }_j}=\frac{\partial }{\partial {\varphi }_j}\sum _{\overrightarrow{b}}-p(\overrightarrow{b})lnp(\overrightarrow{b})=\sum _{\overrightarrow{b}}(-1-lnp(\overrightarrow{b}))\frac{\partial \overrightarrow{b}}{\partial {\varphi }_j}\\ =\frac{1}{16}\sum _{\overrightarrow{b}}(-1-lnp(\overrightarrow{b}))c(\overrightarrow{b},j)=-\frac{1}{16}\sum _{\overrightarrow{b}}c(\overrightarrow{b},j)lnp(\overrightarrow{b}).\end{array}$$ (C29)

The last equality follows from the observation that Σ_b⃗c(b⃗,j) = 0, i.e., that a coordinate ϕ_j does not affect the sum of the block probabilities [see also Eq. (8)]. Thus, ∂H_2×2/∂ ϕ_j = 0 is equivalent to

$$\prod _{\overrightarrow{b}}p{(\overrightarrow{b})}^{c(\overrightarrow{b},j)}=1.$$ (C30)

All of the coefficients c(b⃗, j) are integers, so Eq. (C30) can readily be reformatted into a polynomial equation. Simplification to a cubic generically occurs, as can be seen below for the specific cases required for Table 2.

Case A ((β₋, β_|) and (β₋, β_\)): here, γ = 0 and all θ’s are 0. After simple algebra, Eq. (C30) becomes

$$(1+2{\beta }_{-}+2{\beta }_{\mid }+{\beta }_{\backslash }+{\beta }_{/}+\alpha )(1-2{\beta }_{-}-2{\beta }_{\mid }+{\beta }_{\backslash }+{\beta }_{/}+\alpha )•(1+2{\beta }_{-}-2{\beta }_{\mid }-{\beta }_{\backslash }-{\beta }_{/}+\alpha )(1-2{\beta }_{-}+2{\beta }_{\mid }-{\beta }_{\backslash }-{\beta }_{/}+\alpha )={(1-{\beta }_{\backslash }+{\beta }_{/}-\alpha )}^2{(1+{\beta }_{\backslash }-{\beta }_{/}-\alpha )}^2.$$ (C31)

On both sides of the equation, the highest-order term in α is α⁴, so a cubic results after cancellation. The value r₁(β₋, β_|) of Table 2 is the unique positive root of Eq. (C31) when β_\ = β_/ = β₋β_| and is approximated by ${\beta }_{-}^2+{\beta }_{\mid }^2+O({\beta }^2)$. The value r₂(β₋, β_\) of Table 2 is the unique positive root of Eq. (C31) when β_/ = β_| = 0 and is approximated by ${\beta }_{-}^2+O({\beta }^4)$.

Case B ((β₋, θ_⌟)): here, γ = 0, β₋ and θ_⌟ nonzero, all other β’s and θ’s are zero. Equation (C30) becomes

$$(1+2{\beta }_{-}+{\theta }_{⌟}+\alpha )(1+2{\beta }_{-}-{\theta }_{⌟}+\alpha )(1-2{\beta }_{-}+{\theta }_{⌟}+\alpha )\times (1-2{\beta }_{-}-{\theta }_{⌟}+\alpha )={(1+{\theta }_{⌟}-\alpha )}^2{(1-{\theta }_{⌟}-\alpha )}^2,$$ (C32)

which again reduces to a cubic equation for α. The value r₃(β₋, θ_⌟) of Table 2 is the unique positive root of Eq. (C32) and is approximated by ${\beta }_{-}^2+O({\beta }_{-}^4,{\beta }_{-}^2{\theta }_{⌟}^2)$.

APPENDIX D: DONUT ALGORITHM

This Appendix provides further information on several aspects of the donut algorithm: the mathematical sense in which achieves a maximum-entropy sample, its relationship to the classical Metropolis algorithm [26], and some comments concerning how it can be implemented efficiently.

1. Link between Finite Images and Ensembles

In essence, the donut algorithm is simple: it consists of random swaps that preserve local correlations but destroy others. Here, we link this practical procedure, carried out on single finite images, with the mathematical ideal of a procedure carried out on ensembles, i.e., infinite sets of infinite images. Although the basic intuition behind the donut algorithm is straightforward, this link is not immediate. We consider two issues: first, why does swapping lead to maximum entropy and second, what are the implications of operating on a finite image, rather than on an infinite ensemble? As detailed below, the first issue—the link between swapping and maximum-entropy—is straightforward, provided that infinite ensembles are considered. But to confront the implications of finiteness, we need to formulate a condition that allows finite images to serve as models of infinite ensembles. As described below, this need is fulfilled by asserting that every finite block has a nonzero probability. This condition holds for the cases necessary for Table 2, provided that we stay away from the boundary of the parameter space, i.e., that we avoid any sets of coordinates that would result in a zero probability for a 2 × 2 block.

a. Swapping and Entropy

To make the link between a swapping algorithm and maximum-entropy, we first consider a simpler situation, in which we are able to enumerate all images that satisfy a set of block probabilities. In this case, the desired maximum-entropy distribution is simple to formulate: each image occurs with equal probability—since a maximum-entropy distribution on N objects is one in which each has probability 1/N. This is the approach taken for the one-parameter constructions in the main text: we can calculate the probability of an image and we can construct every possible image, step by step.

However, we don’t need to know N to sample the maximum-entropy distribution; we merely need to ensure that every image is equally likely to be sampled. That is, it suffices to ensure that the ratio of the probabilities of two images is correct. This is the insight behind the classical Metropolis algorithm [26] and it plays a central role here as well.

To see how it works, it is helpful to consider every image as a “macrostate” of a physical system. We then connect these macrostates into a graph—i.e., a network in which each node is a macrostate (i.e., an image), and a connection from node S to node T represents a macrostate transition. In the present context, a “macrostate transition” is a pixel swap as specified by the donut algorithm—that is, macrostates S and T are connected if they are identical, except for swapping a pair of pixels with identical surrounds. We now represent a probability distribution on the ensemble by a probability distribution on the graph of macrostates. A single image thus corresponds to a graph in which one node has a probability of one, and the rest are zero. Our goal is to transform this probability distribution into one in which each node has the same probability. We then sample this probability distribution by simulating a particle’s random diffusion (corresponding to random donut swaps) and choosing the node where it ends.

We therefore need to show that a flat distribution is the equilibrium configuration of a random diffusion process on this graph. This follows from the fact that at equilibrium, the rate at which probability diffuses away from a node must be identical to the rate at which probability diffuses back to the node from its neighbors. The rate at which probability diffuses away from a node, S, is rnp(S), where r is the rate at which any single swap occurs, n is the number of swaps that can occur at node S (i.e,. the number of pairs of 3 × 3 blocks with matching surrounds and distinct centers) and p(S) is the probability currently assigned to S. Similarly, the rate at which probability diffuses towards a node is $r{\sum }_{k=1}^{n}p(T_k)$, where each T_k is a node that can be converted into S by a single swap. The crucial observation is that the number of such nodes is exactly the number of swaps that can be carried out on S—since each such swap leads to a different result. In other words, each macrostate transition is reversible and the graph is symmetric. The consequence of this symmetry is that at equilibrium,

$$np(S)=\sum _{k=1}^{n}p(T_k).$$ (D1)

That is, the equilibrium probability assigned to each node S is the average of the probabilities assigned to its neighbors T_k. As a consequence, the equilibrium probability distribution cannot have local maxima or minima. From this, it follows that the equilibrium probability distribution is constant on all of the nodes that can be accessed from the starting point.

b. Connectedness

The above analysis establishes the link between swapping and maximum-entropy, but only for the nodes that are connected to the node that is initially assigned a probability of one. Thus, to ensure that the equilibrium probability distribution is constant throughout the entire graph, the graph must be connected. Moreover, we need to define “connectedness” in a way that is appropriate both for infinite images and for implementation of the algorithm on finite ones. This is not a trivial point: for sufficiently small images, a naïve notion of connectedness does not hold—there may be multiple images that are consistent with specified 2 × 2 block probability constraints, but which have no matching donuts to allow for swaps.

Therefore, to specify the way in which a finite implementation of the algorithm is a model of an idealized implementation on infinite ensembles, we introduce the following notion of connectedness: that any two finite images, I₁ and I₂, can be incorporated into larger images L₁ and L₂ that can be interconverted by a sequence of swaps. More formally, for any finite size region R and any assignment of its pixels into distinct images I₁ and I₂, our criterion for connectedness is that we can embed the images I₁ and I₂ into larger images L₁ and L₂ for which (a) L_k = I_k on R and (b) L₁ and L₂ are connected by a sequence of swaps.

We now show that a particular technical condition—that every finite block has a nonzero probability—implies that above notion of connectedness holds. To show that this is the case, we construct the connecting path by successively transforming I₁ to I₂, working pixel by pixel within R. At each step of the transformation (say, where we change pixel A_ij from its state in I₁ to its state in I₂), we need to find a 3 × 3 region in L₁ outside of R that matches the surround of A_ij and whose interior matches the state of A_ij in I₂. A swap with this region will thus accomplish the desired change for one pixel in R. Each subsequent transformation of a pixel in R specifies another 3 × 3 region that must be present somewhere in L₁. The condition that all blocks have nonzero probability guarantees that a configuration containing I₁ and all of these 3 × 3 regions exists and thus, that a connecting sequence of swaps can be found.

2. Relationship to the Metropolis Algorithm

The donut algorithm is closely related to the classical Metropolis procedure of thermodynamics [26]. The Metropolis procedure provides a way to sample a maximum-entropy distribution constrained by an average energy. Typically, the energy of a macrostate of a physical system depends on the state assigned to each particle and to energies associated with pair-wise interactions. However, the Metropolis procedure, although it was devised for pair-wise interactions in physical systems, readily extends to higher-order interactions. These interaction energies, after multiplication by 1/kT, correspond to the Lagrange multipliers μ_i in the formal solution given above [Eq. (29)].

The Metropolis procedure consists of a random walk on the graph of all possible macrostates. However, in contrast to the donut procedure, the probability of moving from one state to another depends on the direction of the transition and on the energy difference. Specifically, the probability ratio is e^−ΔE/kT, where ΔE is the energy difference, k is the Boltzmann constant, and T is the temperature. In the donut algorithm, transitions between macrostates are only allowed if they have exactly the same energy (i.e., the same number of 2 × 2 blocks of every kind), but within this stratum, transition probabilities are symmetric. So the donut algorithm is in some sense a low-temperature limit of the Metropolis procedure.

The other contrast between the donut algorithm and the Metropolis procedure is that in a typical application of the latter, the interaction energies [i.e., the Lagrange multipliers in Eq. (29)] are known and the block probabilities are to be determined; here, the block probabilities are known, but the Lagrange multipliers need to be determined. Since determining the Lagrange multipliers from the block probabilities generically requires the solution of a set of nonlinear equations, we cannot simply use the Metropolis procedure. Instead, we determine them implicitly by creating an initial macrostate, as described in Appendix C.

3. Implementation Notes

A literal implementation of the donut algorithm—randomly choosing compatible 3 × 3 blocks at each iteration, and swapping one pair at a time—is quite inefficient and does not make use of vectorized processing available on many computers. Therefore, we adopted the following strategy, in which a single “cycle” encompasses many pair-wise swaps. Each cycle begins by assigning a numerical token (0 to 2⁸ - 1) to each pixel that represents the contents of its eight neighbors, along with a ninth bit that represents the pixel’s state. (This can be done by summing the image array and 8 of its shifts, with each shift multiplied by a different power of 2). Next, we create a histogram of these numerical tokens and randomly choose one token that is shared by many pixels of both colors (tallied in the ninth bit). We then permute these pixels, taking care to change the state of as many of them as possible. If any of these pixels are adjacent, then this permutation step may change the block counts. However, rather than check for adjacency; we conclude each cycle by verifying that the block counts are unchanged. If there is a change in the block counts, the permutation is annulled and the cycle is restarted.