Abstract
Oscillatory phenomenon in electrical activity and cytoplasmic calcium concentration in response to glucose are intimately connected to multiple key aspects of pancreatic β-cell physiology. However, there is no single model for oscillatory mechanisms in these cells. We set out to identify possible pacemaker candidates for burst activity and cytoplasmic Ca2+ oscillations in these cells by analyzing published hypotheses, their corresponding mathematical models, and relevant experimental data. We found that although no single pacemaker can account for the variety of oscillatory phenomena in β-cells, at least several separate mechanisms can underlie specific kinds of oscillations. According to our analysis, slowly activating Ca2+-sensitive K+ channels can be responsible for very fast Ca2+ oscillations; changes in the ATP/ADP ratio and in the endoplasmic reticulum calcium concentration can be pacemakers for both fast bursts and cytoplasmic calcium oscillations, and cyclical cytoplasmic Na+ changes may underlie patterning of slow calcium oscillations. However, these mechanisms still lack direct confirmation, and their potential interactions raises new issues. Further studies supported by improved mathematical models are necessary to understand oscillatory phenomena in β-cell physiology.
Keywords: endoplasmic reticulum, channels, diabetes, mathematical model, metabolism
in pancreatic β-cells, glucose-stimulated insulin secretion is mediated by an elevated cytosolic free calcium concentration ([Ca2+]c). This results from calcium influx through voltage-dependent Ca2+ channels (VDCCs) located in the plasma membrane (PM), which open in response to secretagogues, primarily glucose. Stimulation-secretion coupling in β-cells is different from most other cell types, because instead of being mediated by receptor binding, glucose must be transported into the cytoplasm and metabolized.
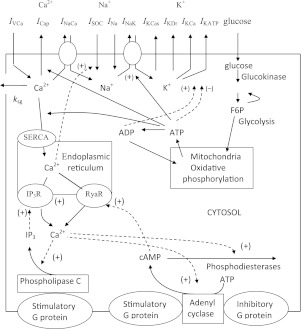
Glucose initiates changes in the PM potential via an increase in the cytoplasmic [ATP]/[ADP] ratio derived from glycolysis and oxidative phosphorylation. This results in closure of ATP-sensitive K+ (KATP) channels. Closure of these channels leads to PM depolarization up to a threshold potential, causing the cell to move from quiescence to initiate electrical activity and VDCC opening. Ca2+ influx through VDCCs leads to increased [Ca2+]c, which is a key signal in the initiation of insulin secretion from the pancreatic β-cells. Consensus mechanisms of glucose-induced PM, cytosolic, and mitochondrial processes are summarized in Fig. 1 (for recent review, see Refs. 71, 74, 76, and 140).
Fig. 1.
General scheme of the main processes involved in bursting and intracellular Ca2+ oscillations in pancreatic β-cells. Plasma membrane currents: voltage-dependent Ca2+ current (IVCa), calcium pump current (ICap), Na+/Ca2+ exchange current (INaCa), Ca2+ release-activated nonselective cation current (ISOC), inward Na+ currents (INa), sodium-potassium pump current (INaK), slow Ca2+-sensitive K+ current (IKCas), delayed rectifying K+ current (IKDr), small conductance Ca2+-activated K+ current (IKCa), ATP-sensitive K+ current (IKATp). ksg is a coefficient of the sequestration rate of Ca2+ by the secretory granules. SERCA is a calcium pump in endoplasmic reticulum (ER), and Ca2+ leaks from ER throw into inositol 1,4,5-triphosphate (IP3) receptor (IP3R) and ryanodine receptor (RyaR). ATP is the free cytosolic form of ATP, and ADPf is free cytosolic ADP. Signals originating from fuel metabolism increase cytosolic calcium. F6P, fructose 6-phosphate. Synthesis and degradation of cAMP are catalyzed by adenylyl cyclase (AC) and phosphodiesterase (PDE), respectively. AC was activated by stimulatory G protein and Ca2+ and deactivated by inhibited G protein, whereas PDE activity was enhanced by Ca2+. Synthesis of IP3 is catalyzed by phospholipase C (PLC). PLC was activated by stimulatory G protein. Solid lines indicate fluxes, and dashed lines indicate inhibitory or stimulatory influences on currents or fluxes.
The β-cell membrane is hyperpolarized to a resting potential of about −60 mV at low glucose levels (∼3–6 mM). Dean and Matthews (32, 33) showed that when glucose rises the PM depolarizes and then generates an electrical activity organized into slow depolarizing waves, called bursting, with a plateau from which action potentials (APs) rapidly fire. Bursts (or active phases) are separated by quiescent (resting) periods at potentials below the AP threshold (Fig. 2). This bursting process results from the metabolic processes and electrical activity of ion channels localized on the β-cell PM and regenerates as long as the glucose concentration is elevated. Rapid depolarization at the beginning of a burst activates VDCCs, whereas the fast repolarization at the end of a burst results in inactivation of VDCCs. This leads to synchronized cyclical spike-burst activity and corresponding cytoplasmic Ca2+ oscillations in response to a rise in extracellular glucose that ultimately determine the oscillatory nature of insulin secretion (71, 76, 140).
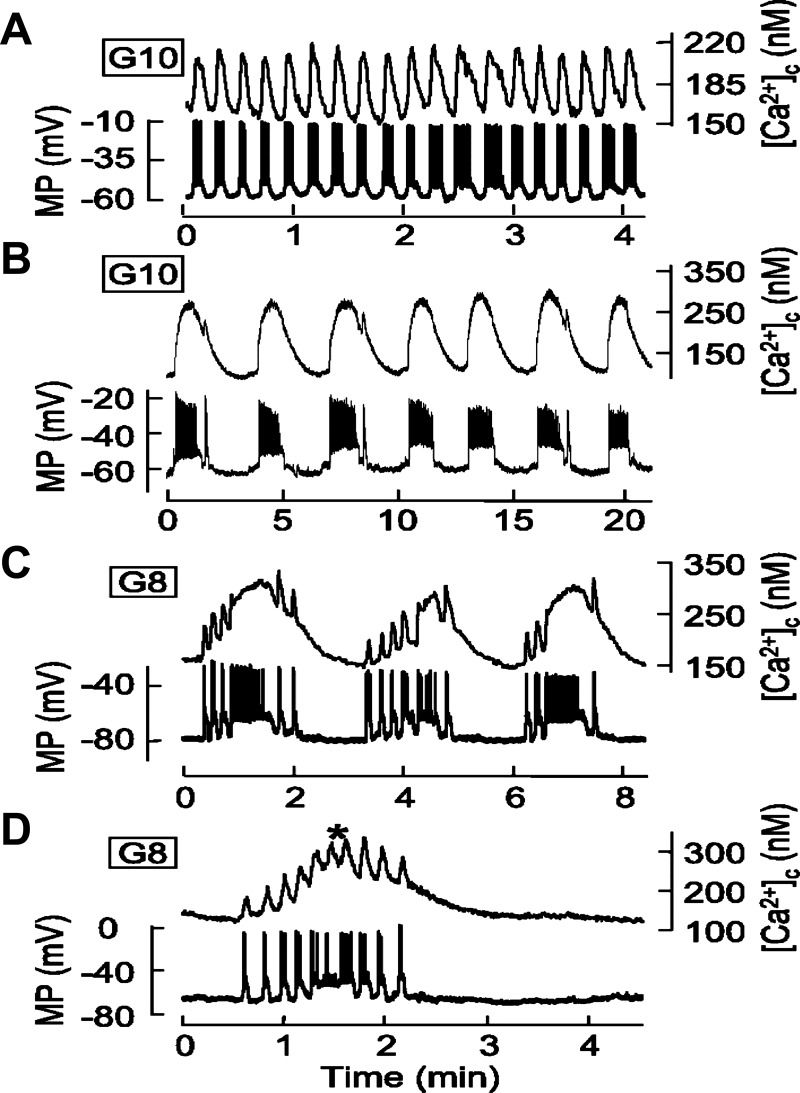
Fig. 2.
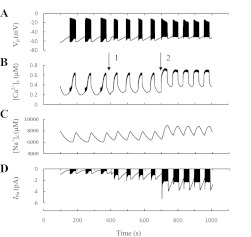
Temporal correlation between membrane potential (MP) and cytosolic free calcium concentration ([Ca2+]c) oscillations (adapted from Ref. 11). Islets from wild mice were perifused with a solution containing 8 (C and D) or 10 mM glucose(A and B) as indicated. The MP was measured in a β-cell within an islet, and [Ca2+]c was measured simultaneously in the same islet.
Increased glucose concentration induces several types of cyclical spike-burst activity and [Ca2+]c oscillations in β-cells with period ranges from several seconds to several minutes (11, 19, 71). We have divided these oscillations into several classes: 1) bursts and [Ca2+]c oscillations with a period of several seconds we term “ultrafast”; 2) oscillations with a period from 10 to 60 s, denoted as fast (Fig. 2A); 3) Ca2+ oscillations with a period ranging from 1 to several minutes and long bursts (Fig. 2B), designated as slow; and 4) mixed (or compound) [Ca2+]c oscillations, characterized by ultrafast or fast [Ca2+]c oscillations superposed on slow oscillations; this is due to periodic bursts, called compound bursting (Fig. 2, C and D) (17).
Ultrafast oscillations can be observed in isolated single β-cells (91, 150). Fast electrical bursting and cytoplasmic Ca2+ oscillations are usually observed in isolated mouse islets (11, 57). Slow and mixed cytoplasmic Ca2+ oscillations were found in single cells, β-cells clusters, and isolated islets at stimulating glucose concentrations (10, 11, 57, 70, 99). Slow and mixed oscillations most likely constitute a physiological oscillatory pattern in β-cells (57, 140).
Gap junctions are responsible for tight electrical coupling at least in mouse islets. This leads to the synchronization of bursting and calcium oscillations in an islet (12, 94, 144). For this reason, as a first approximation we can consider the islet as a community of coupled β-cells with similar electrical behavior.
Experimental data and theoretical concepts support the idea that the AP bursts and the corresponding [Ca2+]c oscillations reflect a periodic depolarization of the PM (7, 11, 37, 48). Whereas a depolarizing component predominates at the beginning of a burst, a progressive increase in outward and/or decrease in inward cation currents take place during the burst, leading to a repolarization and burst termination. Slow depolarization in a resting (silent) phase leads again to a burst initiation (7, 48). Experimental data and theoretical analysis agree that, after the large depolarizing effect following KATP channel closure, the subsequent generation and termination of the bursts can be maintained by small cyclical changes of any PM current (9, 48, 132, 133).
Consequently, initiation and termination of bursts can be connected directly with activation and deactivation of different electrogenic channels, pumps, or exchangers, which can be modulated in turn by numerous intracellular components. Therefore, it is not surprising that a variety of different proposals and corresponding mathematical models have been advanced, underlining the nature of these components in the β-cells. A list of the compounds to be considered here is shown in Table 1. Several of these modulators can act simultaneously, generating AP bursts and corresponding [Ca2+]c oscillations. However, the exact physiological variables and their underlying mechanisms that drive bursting or Ca2+ oscillations in β-cells remain uncertain. Here, we attempt to identify the possible pacemaker candidates for burst activity and cytoplasmic Ca2+ oscillations in the pancreatic β-cells.
Table 1.
Candidates for pacemakers regulating β-cell bursting and [Ca2+]c oscillations
| Compound or Process | Reference No(s). |
|---|---|
| Ca2+-dependent K+ current | 8, 26 |
| Slowly activated Ca2+-sensitive K+ current | 58, 59 |
| Voltage-gated Ca2+ current | 28, 88 |
| [ATP]/[ADP] ratio | 3, 126, 133 |
| Glycolytic oscillations | 17, 19, 142, 145 |
| [Ca2+] in endoplasmic reticulum | 20, 25, 51, 125, 148 |
| Intracellular Na+ | 51, 93 |
| Inositol (1,4,5)-trisphosphate | This article |
| cAMP | 47 |
| Mitochondrial metabolic oscillations | 14, 101 |
[Ca2+]c, cytosolic free calcium concentration.
We define a pacemaker as a component of some pacemaker mechanism that serves to establish a rhythmic physiological activity inside a cell. To distinguish likely pacemaker proposals from less likely hypotheses, we will reject a hypothesis that some component is a part of a pacemaker mechanism if Ca2+ oscillations (or the AP bursting pattern) persist even though the proposed pacemaker mechanism was blocked in an experiment. We will term this condition the main criterion for the rejection of a proposed pacemaker mechanism. Disappearance or a change of bursting or Ca2+ oscillation behavior under the influence of an agent or process we will term a “modulation,” and an agent that creates it we will term a “modulator.”
A pacemaker component can also act as a modulator with a certain concentration dependence, depending on its activity or experimental conditions. However, a modulator in this article is a component that is not a part of a proposed pacemaker mechanism. Several examples of such pacemakers and modulators will be considered.
We performed an analysis of the existing hypothesis, experimental data, and the corresponding mathematical models and compared the simulations with the experimental results. In this way we tested both the validity of the initial hypotheses and the models. Furthermore, predictions for unmeasured quantities could be made, and the model could then be tested. However, many of the mechanisms that could control electrical activity and Ca2+ handling have not been adequately experimentally characterized in pancreatic β-cells, so we can consider them only briefly. Although most of the analyzed experimental work employed mouse islets with some studies in other species, it is difficult to generalize given the different existing animal and insulinoma models of pancreatic β-cells. We have emphasized primary tissues where possible.
There are several reasons why a clear understanding of internal oscillatory mechanisms in β-cells is worth pursuing. First, bursting and [Ca2+]c oscillations are readily observable phenomena in cell culture and in isolated mouse islets. Numerous hormones and small molecule agonists as well as toxins can modulate oscillatory behavior. The study of the changes in bursting or [Ca2+]c oscillations can provide a flexible approach to understand the action of specific modulators on the pancreatic β-cell. However, this approach requires a comprehensive knowledge of the pacemaker mechanisms of these oscillations.
We consider here primarily the internal pacemaker mechanisms for individual β-cells that represent behavior of isolated cells or the electrically synchronized islet. A further consideration of the oscillations in insulin secretion is beyond the scope of the present article. However, islet Ca2+ oscillations appear to be the framework behind the phenomenon of pulsatile insulin release observed in vivo (71, 112, 117, 140). Interestingly, disruptions in rhythmic function may be an important early biomarker of islet dysfunction leading to diabetes in animal models (72, 79, 140) and man (116). Although pulsatility appears to be a natural function of islets both in vivo and in vitro, this emphasizes the need for careful study of the oscillatory phenomena on the cellular level.
EXPERIMENTAL PROCEDURES AND MODELING
Ca2+ imaging measurements of relative cytoplasmic Ca2+ concentrations are presented as the 340/380 nm fluorescence excitation ratio obtained with the indicator fura-2, as described previously (137). Fura-2 was from Invitrogen (Carlsbad, CA). All other chemicals were from Sigma (St. Louis, MO).
The “complex model” of processes (51) was used for the following simulations, excluding the model for slowly activated Ca2+-sensitive K+ channels, that are described in the appendix. This model is available for direct simulation on the web site “Virtual Cell” (www.nrcam.uchc.edu) in the “MathModel Database” on the “math workspace” in the library “Fridlyand” with name “Chicago 1.”
RESULTS AND DISCUSSION
We can distinguish two main types of mechanisms underlying bursting and [Ca2+]c oscillations.
Mechanisms With Ca2+ Feedback Effect
In this case, a fast increase of [Ca2+]c during an active phase should activate (or deactivate) some processes, leading to slow changes in the intermediate pacemaker components. Slow changes of these components should gradually lead to a membrane repolarization down to the threshold potential for spike activity, shutting down the spikes and inactivating the VDCCs. Then Ca2+ influx decreases sharply, leading to decreased PM potential and a resting phase. Processes occur in opposite directions during a resting (repolarized) phase. The [Ca2+]c decreases because cytoplasmic Ca2+ is pumped into the extracellular space and into the endoplasmic reticulum (ER) by specific ATP-consuming Ca2+ pumps. Decreases in [Ca2+]c deactivate (or activate) specific processes of the slow changes in the intermediate pacemaker components, leading to PM depolarization up to the threshold potential, reentry of spike activity, Ca2+ influx, and an active phase.
Ca2+-Independent Mechanisms
This type of mechanism was suggested for oscillations such as glycolytic oscillations that can lead to oscillations in the [ATP]/[ADP] ratio changing the conductance of KATP channels (19, 142). In this case, Ca2+-independent mechanisms create the oscillations of compounds that can lead to cyclic changes in PM potential, generating the bursts and corresponding [Ca2+]c oscillations (101, 142).
[Ca2+]c as the Pacemaker Component and Ca2+-Dependent K+ Channels
Fast-activated Ca2+-dependent K+ (SK1–3 and BK) channels.
Initially, a mechanism with [Ca2+]c as the pacemaker component and a Ca2+ feedback effect was proposed for burst generation and [Ca2+]c oscillations via cyclic activation of a Ca2+-dependent K+ current. According to this hypothesis, Ca2+ influx during the active phase would cause a slow rise in [Ca2+]c, which activates fast Ca2+-dependent K+ (KCa) channels repolarizing the PM potential down to a threshold potential. This would shut down AP spiking and inactivate VDCCs, leading to a resting phase. A decrease in the [Ca2+]c level during the resting period would lead to decreased current through KCa channels, PM depolarization, and burst initiation. According to this proposal, a cyclical change in [Ca2+]c is a candidate islet pacemaker for burst behavior and [Ca2+]c oscillations per se (8). Corresponding mathematical models have incorporated the cyclical activation and deactivation of KCa channels by bursting-induced changes in [Ca2+]c (26).
The principle difficulty with this hypothesis is that [Ca2+]c should slowly increase during a period of depolarization, leading to a slowly increasing current through KCa channels and then to a repolarization only at the end of a burst period. However, subsequent Ca2+ imaging data indicate that the time for the [Ca2+]c increase is short relative to the oscillation period (129). Another problem with this hypothesis was that apamin, a KCa (SK1–3) channel blocker, does not change mouse islet bursting or alter β-cell K+ currents in normal mouse islets (4, 58, 59, 96). Slow [Ca2+]c oscillations were also observed in the presence of 10–20 mM tetraethylammonium (TEA), i.e., in conditions when TEA-sensitive KCa channels should be nearly completely blocked (124, 125). For these reasons, this mechanism for generation of [Ca2+]c oscillation was ruled out (see Refs. 125 and 132). Despite these issues, mathematical models for β-cells continue to appear with slow [Ca2+]c oscillations on the basis of this hypothesis (36, 108).
However, although here we focus on pacemaker mechanisms, some changes in channel conductance may change PM polarization such that oscillation behavior can be modified. For this reason, although KCa (SK1–3 and BK) channels do not directly take part in the creation of the pacemaker mechanism, their inhibition can contribute to PM depolarization and lead to changes in the oscillatory behavior (139).
Slow-activated Ca2+-sensitive K+ channels.
A specific, slowly activated TEA-insensitive Ca2+-sensitive K+ current (SK-like current) may underlie the mechanisms of oscillations (58, 59). This current activates gradually with a time constant of 2.3 s and inactivates with a time constant of 6.5 s (59). It was assumed that this current regulates the duration of intervals between successive AP bursts observed when β-cells are exposed to moderately elevated glucose (59, 151).
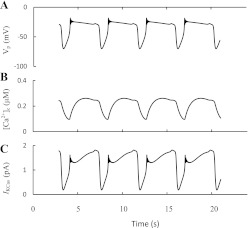
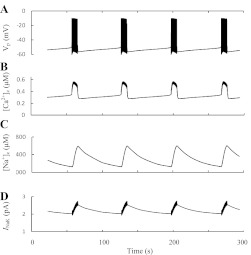
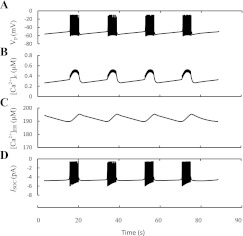
We developed a special mathematical model to simulate this proposal (see appendix). Here, fast KCa channels (SK1–3 and BK; current IKCa in Fig. 1) as well as slowly activated KCa channels (SK-like current; IKCas in Fig. 1), which according to Düfer et al. (38) can be represented partly by SK4 channels, were modeled, and the time constants for activation gating variables reported by Gopel et al. (59) were used for modeling of IKCas. The behavior of [Ca2+]c, Vm, and the IKCas is shown in Fig. 3. The reversible slow cyclical changes in IKCas were obtained, leading to bursting behavior and [Ca2+]c oscillations. The simulated [Ca2+]c increased rapidly in the beginning of burst period, stabilized by activation of the fast KCa (SK1–3) channels and kept at a high level during this period. IKCas increased during a burst period, leading to repolarization, termination of the spikes, and transition to a silent phase. Inhibition of IKCas during a resting period led to repolarization and reentry to an active phase.
Fig. 3.
Slow-activated Ca2+-sensitive K+ channels as pacemaker for ultrafast burst and [Ca2+]c oscillations. Burst behavior of the membrane potential (VP; A), the oscillation pattern of [Ca2+]c (B), and slow Ca2+-sensitive K+ current (IKCas; C). Simulations were made according the model from the appendix.
However, the simulated bursts and [Ca2+]c oscillations had a period of several seconds and corresponded well only to ultrafast bursting and [Ca2+]c oscillations. Therefore, the experimental data on the dynamics of this slow SK-like current and our simulation support the idea that ultrafast bursts and Ca2+ oscillations can be driven by an interaction of these slow-activated KCa channel parameters with [Ca2+]c changes.
Cyclic Changes in KATP Channel Conductance: The Pacemaker Role of [ATP]/[ADP] Ratios
KATP channels contribute the predominant β-cell K+ conductance in resting low-glucose conditions. Following glucose entry and metabolism, their conductance is greatly diminished. However, the small remaining KATP conductance in elevated glucose is still comparable with the conductances of other channels, exchangers, and pumps (133). For this reason, cyclical changes in the KATP channel conductance have been proposed as a possible mechanism underlying oscillatory behavior of β-cells (3, 68, 110, 126, 133). In this conceptualization, the [ATP]/[ADP] ratio decreases slowly when [Ca2+]c increases during a burst, leading to a slow opening of KATP channels and subsequent PM repolarization as the K+ efflux increases. Actually, the opposite should occur since the [ATP]/[ADP] ratio gradually increases during a silent phase in the presence of stimulatory glucose, when [Ca2+]c decreases, leading to the closing of KATP channels, PM depolarization, and burst initiation (34, 86, 87, 103–105, 126). According to our classification, this is a mechanism with a Ca2+ feedback effect, whereas the [ATP]/[ADP] ratio is a pacemaker “compound.” Several mechanisms and corresponding mathematical models for the [ATP]/[ADP] ratio changes and [Ca2+]c oscillations have been proposed.
An empirical equation for [ATP]/[ADP] ratio changes was introduced in an early mathematical model (133) such that [ATP]/[ADP] ratio slowly decreased as [Ca2+]c increased and increased with decreased [Ca2+]c. Oscillatory changes in the [ATP]/[ADP] ratio, KATP channel conductance, bursting, and [Ca2+]c oscillations were simulated using this model (17, 18, 133).
Mechanistic hypotheses underlying the possible influence of [Ca2+]c changes on the [ATP]/[ADP] ratio have also been proposed. Decreased [ATP]/[ADP] ratio during [Ca2+]c rise and an increase of this ratio with [Ca2+]c decline could result from either stimulated ATP hydrolysis or inhibition of ATP production.
[Ca2+]c-activated ATP consumption.
Ca2+ activates Ca2+ pumps on the PM and in the ER as well and certain other intracellular reactions that use ATP. In this case, increased [Ca2+]c can increase ATP consumption and decrease the [ATP]/[ADP] ratio. An opposite process that increases the [ATP/ADP] ratio due to a decline in ATP consumption can also occur with decreased [Ca2+]c (34, 51).
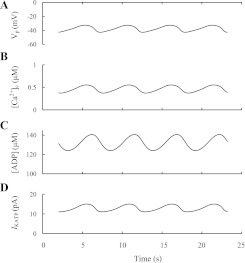
We illustrated this mechanism using our mathematical model (51) that includes a simulation of ATP consumption due to the work of Ca2+ pumps (PM and ER) as well as the Ca2+-activated ATP consumption in some cytoplasmic processes. The simulated phase relations for the conditions when the free ADP (and corresponding ATP) concentration in the cytoplasm is the only slow pacemaker parameter in this complex model are shown in Fig. 4. Other slow parameters such as cytoplasmic concentrations of Na+, inositol 1,4,5-triphosphate (IP3), and Ca2+ in ER ([Ca2+]ER) were frozen at constant levels, blocking other possible mechanisms underlying Ca2+ oscillations in this model. A Ca2+ feedback effect model was responsible for bursting and Ca2+ oscillations; a rise in [Ca2+]c during the active phase leads to increased Ca2+-activated ATP consumption in the cytoplasm and by Ca2+ pumps. As this occurs, free [ADP] increases (and the [ATP]/[ADP] ratio decreases), slowly opening KATP channels. This in turn leads to a slowly increasing IKATP and PM repolarization, damping potential spikes and leading to decreased [Ca2+]c. These processes have the opposite direction after decreased [Ca2+]c in the resting period. KCa channels serve to damp depolarization and terminate the [Ca2+]c increase after initial Ca2+ increase during the active phase.
Fig. 4.
Slow ATP/ADP ratio changes as a pacemaker. Burst behavior of the MP and the oscillation patterns of [Ca2+]c, free ADP ([ADP]), and IKATP are illustrated. It was simulated using a model (51) by a step increase of glucose level. Several variables, [Na+]c, [IP3], and [Ca2+]ER, were frozen at constant levels to eliminate other mechanisms of fast and slow [Ca2+]c oscillations ([Na+]c = 7 mM, [IP3] = 3 μM, and [Ca2+]ER = 20 μM). Several coefficients were set as gmSOC = 2 pS−1 mV, gmKATP = 200,000 pS, gmKCa = 80 pS, gmVCa = 710 pS, gNaCa = 500 pS, kADP = 0.001 ms, kATP = 0.000001 ms, kATP,Ca = 0.0000218 μM/ms, and PNaK = 400 fA. All other parameter settings are as in Ref. 51. A: action potential (VP). B: [Ca2+]c. C: [ADP]. D: IKATP.
Negative [Ca2+]c effects on ATP production.
In several mathematical models the uptake of Ca2+ by β-cell mitochondria has large energy-dissipative effects, leading to decreased oxidative phosphorylation suppressing the production rate of ATP (15, 103–105). This proposal also leads to a decreased [ATP]/[ADP] cytoplasmic ratio with increased [Ca2+]c, as in first case, and the models can simulate [Ca2+]c oscillations through the cyclical changes in [ATP]/[ADP] ratio (103–105). However, recent experimental data convincingly shows that “the primary role of mitochondrial Ca2+ is the stimulation of oxidative phosphorylation” (24), suggesting that [Ca2+]c effects on ATP production are stimulatory rather than inhibitory.
Glycolytic oscillations as a mechanism for cyclical changes in the [ATP]/[ADP] ratio.
A number of hypotheses have been proposed to explain the mechanism of [ATP]/[ADP] ratio oscillations through glycolytic oscillations. The fundamental proposal of this model is that Ca2+-independent glycolytic oscillations that produce [ATP]/[ADP] ratio oscillations are mediated by the positive feedback of fructose 1,6-bisphosphate. This is the product of the glycolytic enzyme phosphofructokinase (PFK), stimulating PFK activity and subsequently depleting substrate (83, 142). Mathematical models for β-cell oscillations have been constructed on the basis of this mechanism (17–19, 81, 145).
However, the direct evidence for glycolytic oscillations in β-cells such as measurements of glycolytic metabolite concentrations is lacking. Periodic variations in mitochondrial membrane potential, NADH, and respiration have been offered as evidence of glycolytic oscillations (18). However, these phenomena can also be a consequence of independent Ca2+ cytoplasmic oscillations (see below). The available evidence supports the idea that glycolytic processes are not a requirement at least for slow cytoplasmic Ca2+ oscillations. Slow [Ca2+]c oscillations can be induced at low glucose levels using K+ and KATP channel blockers (such as TEA and sulfonylureas) in islets and β-cell lines (see Fig. 5 and Refs. 51 and 125). Slow [Ca2+]c oscillations can be generated even in the absence of glucose using such mitochondrial substrates as leucine (64), α-ketoisocaproic acid (69, 106), and methyl pyruvate (69). Fast [Ca2+]c oscillations were found in islets incubated solely in the presence of glyceraldehyde or α-ketoisocaproic acid (31). PFK itself is not required for these oscillations, since [Ca2+]c oscillations remain normal after 95–98% suppression of PFK-M activity in mouse islets (121). These data demonstrate that an oscillatory capacity is preserved when glycolytic flux is small or absent and that the slow components of [Ca2+]c oscillations cannot be fully explained by mechanisms incorporating glycolytic oscillations. However, we cannot entirely rule out that this mechanism could contribute to ultrafast (and possibly fast) [Ca2+]c oscillations, although the metabolic variability is on the order of minutes. Further studies are needed to establish whether there is any role at all for glycolytic-based mechanisms in β-cells regulating Ca2+ or other oscillations as opposed to periodic changes in mitochondrial Ca2+ or membrane potential. On other hand, glycolytic processes can modulate oscillation behavior. For example, bursting and Ca2+ oscillations can change frequency and amplitude and even disappear with changes in glucose concentration (54).
Fig. 5.
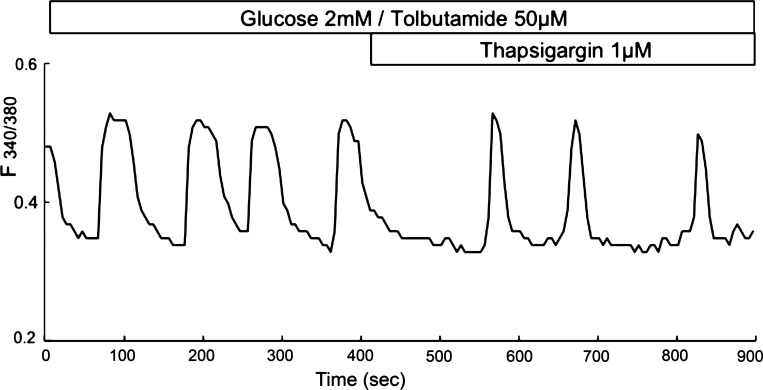
Effect of tolbutamide and thapsigargin on slow Ca2+ oscillations in mouse islets. Mouse islets were loaded with fura-2, and relative [Ca2+]c changes were recorded as the 340/380 nm fluorescence excitation ratio changes obtained with the indicator fura-2 during incubation in 2 mM glucose with 50 μM tolbutamide, with subsequent addition of 1 μM thapsigargin.
Limitations of KATP channel [ATP]/[ADP] ratio-dependent mechanisms of oscillations.
The [ATP]/[ADP] ratio drops when [Ca2+]c rises and increases when [Ca2+]c falls, indirectly supporting the proposal that [Ca2+]c oscillations can therefore evoke oscillations in [ATP]/[ADP] ratio and IKATP (2, 34). These data are in agreement with the hypothesis that the KATP channel conductance changes can generate and maintain oscillations.
We have also considered above the mechanism for ultrafast oscillations determined by changes in the conductance of slow-activated Ca2+-sensitive K+ channels. Based on the effects of tolbutamide, a specific KATP channel blocker, it was concluded that KATP channels contribute a significant fraction (48%) of this mechanism (86). Therefore, we suggest that the mechanism underlying ultrafast bursts and [Ca2+]c oscillations in β-cells can be due partly to the changes in the [ATP]/[ADP] ratio as a pacemaker (and corresponding changes in KATP channel conductivity), in accord with the KATP channel-dependent mechanism.
However, there are several valid arguments against a KATP channel-dependent mechanism for slow bursting and [Ca2+]c oscillations. If KATP channels function as a pacemaker, the conductance of the KATP channels should oscillate during bursting electrical activity following changes in the [ATP]/[ADP] ratio. However, effective KATP channel blockers such as sulfonylureas do not stop slow bursting and Ca2+ oscillations in pancreatic islets and can even induce them in single β-cells or β-cell clusters isolated from mouse islets (see Fig. 5 and Refs. 43, 65, and 109) and in βTC3-neo cells (125). Slow [Ca2+]c oscillations were also found in a mouse lacking functional KATP channels (40, 67, 120, 135). These results suggest that changes in the [ATP]/[ADP] ratio and, consequently, in KATP channel conductivity are unlikely to function as a pacemaker component for coupled slow oscillatory mechanisms.
However, studies are needed to carefully examine whether fast Ca2+ oscillations persist upon blocking KATP channels at low glucose levels or in KATP channel-null mice. Until such studies are reported, it is possible that ultrafast and fast bursting and the corresponding [Ca2+]c oscillations are in part due to [ATP]/[ADP] ratio and KATP channel conductance changes acting as a pacemaker.
Intracellular [Na+] As a Slow Component in Pacemaker Mechanisms
Several components regulate Na+ dynamics in β-cells. The most important is the electrogenic Na+,K+-ATPase that extrudes three Na+ ions in exchange for two K+ ions for each molecule of ATP hydrolyzed, generating a net outward flow of cations through the PM. This pump is highly active, since it determines the high cytoplasmic K+ concentration (113). Like most other cells, the β-cells are also equipped with a PM Na+/Ca2+ exchanger, an electrogenic transporter that couples the exchange of 3 Na+ for 1 Ca2+ (52, 73). Consequently, changes in the cytoplasmic Na+ concentration ([Na+]c) lead to changes of inward and outward currents and the PM potential. Changes in [Na+]c can have a significant effect on generation of slow cytoplasmic Ca2+ oscillations in β-cells (56, 93).
For example, Kitasato et al. (93) proposed a specific oscillatory mechanism, including Na+ pumps and transporters. They suggested that increased [Ca2+]c during an active phase results in an activation of the Na+/Ca2+ exchanger and a corresponding increase in [Na+]c. An increase in cytosolic Na+ would lead to an enhanced ATP consumption at Na+/K+ pump sites and to a decreased ATP/ADP ratio. This in turn could lead to activation of KATP channels followed by membrane repolarization. A decrease in [Ca2+]c results in the opposite order of events during a silent phase. This hypothesis was modeled by Miwa and Imai (110) as the underlying mechanism of [Ca2+]c oscillations. This mechanism is a variant of KATP channel-dependent mechanism for a generation of bursts and [Ca2+]c oscillations. It does not explain the experimental data, suggesting that the [ATP]/[ADP] ratio and KATP channel conductance changes are not the main driving force for slow [Ca2+]c oscillations (see above).
We proposed and modeled a mechanism with a Ca2+ feedback effect where the intracellular [Na+]c is a dynamic pacemaker variable that can govern bursts and slow [Ca2+]c oscillations, although KATP channels do not change their activity (51). Figure 6 illustrates the roles of the Na+,K+-ATPase, the Na+/Ca2+ exchanger, and [Na+]c dynamics in this model. Other slow parameters such as cytoplasmic concentrations of [ADP], [Ca2+]ER, and [IP3] were frozen at constant levels, blocking other possible mechanisms of bursting and [Ca2+]c oscillations. The following mechanism was responsible for bursting and Ca2+ oscillations; increased [Ca2+]c during an active period activates Na+ influx through Na+/Ca2+ exchangers. The resultant increase in intracellular [Na+]c leads to a slow increase in outward current through electrogenic Na+/K+ pumps (INaK in Fig. 1), with corresponding plasma membrane repolarization, so that the cell reenters a silent phase. Decreased [Ca2+]c during a silent phase leads to a slow decrease in [Na+]c because Na+ influx through the Na+/Ca2+ exchanger decreases. This leads to a decreased outward current through Na+/K+ pumps and then in turn to PM depolarization and a generation of bursts and [Ca2+]c oscillations.
Fig. 6.
Slow [Na+]c changes as a pacemaker. Typical computer simulations using the model by Fridlyand et al. (51). Slow bursting and the oscillation patterns of Ca2+ and Na+ are illustrated. The other slow variables were frozen ([ATP] = 3,300 μM, [IP3] = 3 μM, and [Ca2+]ER = 50 μM) at constant levels to eliminate other mechanism of [Ca2+]c oscillations. All other parameter settings are as in Ref. 51. A: VP. B: [Ca2+]c. C: [Na+]c. D: INaK.
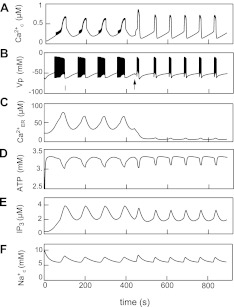
The effect of modulators leads to changes in the shape of simulated [Ca2+]c oscillations, bringing them closer to experimental results. For example, Fig. 7 [which reproduces the third figure from our earlier article (51)] shows slow-simulated [Ca2+]c oscillations that are similar to the experimental data represented in Fig. 2B. In this simulation, as opposed to that in Fig. 6, [ADP], [Ca2+]ER, and [IP3] were not frozen at constant levels and thus played a role as modulators. In this case, cytoplasmic [Na+] as a slowly variable component functioned as the pacemaker mechanism. We will discuss the possible mechanisms of this kind of influence of modulators on the shape of Ca2+ oscillators below.
Fig. 7.
Simulation of glucose-induced slow oscillations and SERCA blocking. Glucose-induced slow electrical bursting and [Ca2+]c oscillations were simulated at a step increase of the rate constant of ATP production from a low to an intermediate value at t = 0. A: [Ca2+]c. B: MP. C: Ca2+ in ER. D: cytosolic ATP. E: cytosolic IP3. F: intracellular Na+ concentration. For simulation of thapsigargin action, the maximal rate of ER (SERCA; PCaER) was decreased from 0.105 to 0.013 μM/ms at arrow in B (adapted from Ref. 51).
Some indirect experimental evidence supports the hypothesis that cyclic [Na+]c changes can act as a pacemaker to induce bursting and slow [Ca2+]c oscillations. For example, in isolated individual β-cells or cell clusters, the slow glucose-induced Na+ oscillations were found under conditions known to induce oscillations of [Ca2+]c. Partial suppression of the Na+/K+ pump by ouabain resulted in an increased amplitude of slow Na+ and Ca2+ oscillations with decreased frequency; slow Na+ and Ca2+ oscillations were converted to a tonically elevated Na+ and Ca2+ level following ouabain inhibition of the Na,K-ATPase (62, 63). Interestingly, slow Ca2+ oscillations were converted to a sustained elevated Ca2+ level following ouabain even in sulfonylurea type 1 receptor (SUR1)-null mouse islets, where KATP channels were blocked (39).
Our computational simulation resulted in a similar picture (see the 7th figure in Ref. 51) showing that these experiments can be modeled exactly by a partial inhibition of the Na+/K+ pumps by oubain. According to this simulation, decreasing the Na+/K+ pump maximal activity reduced the rate of Na+ efflux and corresponding net outward current, leading to increased [Na+]c and PM depolarization. This resulted in increased amplitude of slow Na+ and Ca2+ oscillations with decreased frequency. Greater inhibition of the Na+/K+ pump maximal activity led to a collapse of this Na+-dependent mechanism, the disappearance of bursting and slow Ca2+ oscillations, and tonically elevated [Ca2+]c.
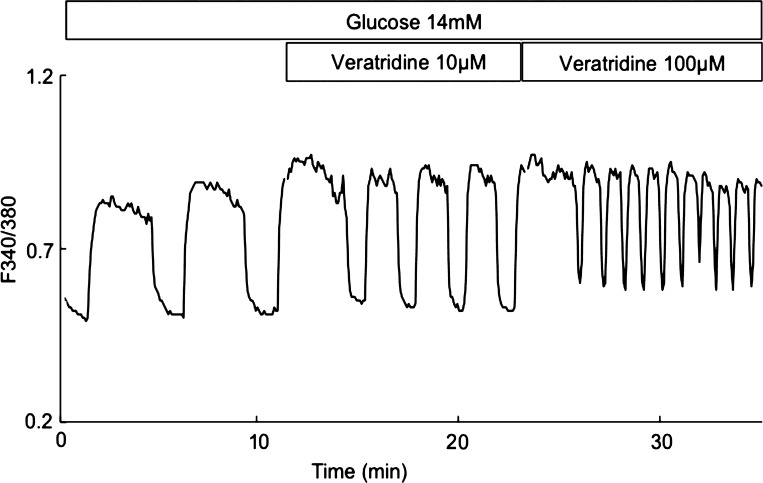
Veratridine causes voltage-dependent Na+ channels to stay open during a sustained membrane depolarization by decreasing inactivation (143). Partial activation of Na+ channels by veratridine resulted in a decreased amplitude and increased frequency of slow Ca2+ oscillations, and slow Ca2+ oscillations were converted to a tonically elevated Ca2+ level in isolated individual β-cells or cell clusters (44). We were able obtain similar results in isolated pancreatic islets (Fig. 8).
Fig. 8.
Effect of veratridine on slow Ca2+ oscillations in mouse islets. The experiments were performed in medium containing 2.5 mM Ca2+ and 14 mM glucose. Veratridine (μM) was added as indicated. The concentration of cytoplasmic Ca2+ is presented as the 340/380 nm fluorescence excitation ratio obtained with the indicator fura-2.
We simulated the effects of veratridine by shifting the half-activation potential for Na+ channels toward a more positive voltage using our general model (51). According to this simulation (Fig. 9), increased Na+ influx through voltage-dependent Na+ channels leads to an additional PM depolarization as a result of increased Na+ inward current and an accelerated Na+ accumulation during an active phase. This resulted in increased amplitude and frequency of slow Na+ and Ca2+ oscillations. The simulations are in reasonably good agreement with experimental data (compare Figs. 8 and 9).
Fig. 9.
Simulated influence of veratridine on slow [Ca2+]c oscillations in β-cells. Addition of veratridine was simulated by decrease of half-activated potential for Na+ channels in the model by Fridlyand et al. (51). (Half-activated potential for Na+ channels was decreased from −104 to −94 mV at arrow 1 and from −94 to −84 mV at arrow 2 in B). A: VP. B: [Ca2+]c. C: [Na+]c. D: INa.
Correlating the model simulations with experimental data shows that cyclic [Na+]c changes can act as a pacemaker to induce bursting and slow [Ca2+]c oscillations as opposed to the proposals on the role of KATP channels. However, this mechanism underlying oscillations remains incompletely investigated. Simultaneous measurements of [Ca2+]c and [Na+]c, although difficult, can directly test this hypothesis.
Role of the ER and [Ca2+]ER as a Slow Pacemaker
The ER is a high-affinity and high-capacity organelle for calcium storage. The β-cell ER sequesters Ca2+ when the cytoplasmic calcium level is high and releases it when [Ca2+]c is low or under the influence of intracellular messengers (55, 122, 123, 141). Ca2+ from the cytosol is transported into the ER by P-type ATPases using ATP and exits through two types of ER Ca2+ channels, the IP3 receptor (IP3R) channels and the ryanodine receptor channels (Fig. 1) (56, 82, 123, 138). However, Ca2+ influx from the extracellular space through VDCCs is the principal regulator of cytoplasmic Ca2+ homeostasis in β-cells under physiological conditions (6, 51, 127, 146).
[Ca2+]ER and store operating currents.
Changes in [Ca2+]ER may regulate PM potential. Depletion of intracellular Ca2+ stores in β-cells activates a special Ca2+ release-activated current [or store operating current (SOC)] through nonselective PM cation channels and can represent an inward cation current, leading to PM depolarization that potentiates glucose-induced Ca2+ influx trough VDCCs (20, 30, 97, 125, 147). This current may be Na+ influx through nonselective PM cation channels, which have been described in insulin-secreting β-cells (30, 97, 125). Transient receptor potential (TRP) ion channels were proposed for this role (74, 78, 125). Although the detailed mechanism for coupling of ER Ca2+ store depletion with the nonselective PM channels activation is uncertain, it likely involves translocation of STIM1 and STIM2 proteins from the ER calcium stores to the PM, where they interact with ORAI1 and related proteins associated with cation influx channels (119, 137).
Several mechanisms of oscillations with [Ca2+]ER as a pacemaker employing a Ca2+ feedback effect have been proposed (20, 25, 51, 53, 107, 125, 148, 150). These proposals were primarily based on the characteristic properties of SOC that lead to cell depolarization with decreased [Ca2+]ER. Several mathematical models have also been developed for these proposals using empirical equations for activation of SOC with decreased [Ca2+]ER (20, 25, 53, 150). SOC increased with decreased [Ca2+]ER and vice versa in simulations using the empirical equations from these models, yielding periodical changes of [Ca2+]ER, bursting, and [Ca2+]c oscillations.
We developed a model where “SOC” includes Na+ influx through nonselective cation channels that open following decreases in [Ca2+]ER (SOC was termed “CRAN current” in our model) (51), following the earlier work of Roe et al. (125).
The proposed mechanism is illustrated in Fig. 10. In this case, other possible pacemaker mechanisms of [Ca2+]c oscillations in the model (51) were blocked by freezing the cytoplasmic concentrations of [ADP], [Na+], and [IP3] at constant levels. In this simulation, a rapid rise in [Ca2+]c at the beginning of the active phase led to increased Ca2+ pumping into the ER and slow [Ca2+]ER accumulation with corresponding closure of PM nonselective cation channels. This decreased inward Na+ influx current (ISOC; Fig. 1) through these channels (i.e., SOC) resulted in PM repolarization, termination of the spiking, and the transition to a silent phase. Slowly decreasing [Ca2+]ER during a silent phase as a result of Ca2+ leak through ryanodine or IP3R then led to increased nonselective cation channel conductance, increased inward Na+ current, and PM depolarization. This resulted in subsequent activation of VDCCs and a new burst. In this case, [Ca2+]ER is a slow pacemaker component for [Ca2+]c oscillations with a Ca2+ feedback effect.
Fig. 10.
Slow [Ca2+]ER changes as a pacemaker. Simulations were made as in Fig. 4. [Ca2+]ER is the only slow parameter at frozen ADP, ATP, Na+, and IP3 concentrations that eliminated other possible mechanisms of bursting and Ca2+ oscillations in the model by Fridlyand et al. (51). ([Na+]c = 6 mM, [IP3] = 1 μM, [ATP] = 3,400 μM, and kADP = 0.00045 ms−1). All other parameter settings are as in Fridlyand et al. (51). A: VP. B: [Ca2+]c. C: [Ca2+]ER. D: ISOC.
However, an explanation of slow oscillations on the basis of [Ca2+]ER-dependent mechanisms involves several difficulties, since it seems to be at odds with data demonstrating that the slow oscillations can persist in the presence of thapsigargin, a SERCA inhibitor (Fig. 5 and Refs. 6, 51, 55, 98, 109, and 136). Slow [Ca2+]c oscillations also persist in islets from a SERCA3 knockout mouse, where fast oscillations disappear (11). These results argue against a role of [Ca2+]ER changes as a pacemaker for slow [Ca2+]c oscillations.
Slow [Ca2+]c oscillations can also persist even though KATP channels and SERCA activity are blocked simultaneously in mouse islets by tolbutamide and thapsigargin (Fig. 5) or in isolated islets from the SUR1-null mouse lacking KATP channels when SERCA is inhibited (39). These complex experimental data show that a mechanism of slow [Ca2+]c oscillations cannot be explained solely by an interaction of KATP channels and ER-dependent mechanisms.
SERCA blockade has led to conflicting results for fast bursts and [Ca2+]c oscillations in β-cells converted to a sustained elevated [Ca2+]c level by thapsigargin (55, 86, 109, 136, 147). However, Tamarina et al. (138) found that an addition of thapsigargin was accompanied by a gradual increase in the amplitude and frequency of fast [Ca2+]c oscillations in some islets. Bertram et al. (20) had previously found that thapsigargin induced a gradual increase in the amplitude plateau fraction and in electrical burst frequency in the β-cell membrane potential. It is possible that in some experiments only partial SERCA blockade was obtained, leading to a partial decrease in [Ca2+]ER, thereby preserving the ability of the β-cells to create an oscillatory mechanism. More profound SERCA block in other experiments could decrease [Ca2+]ER to a threshold level where oscillatory mechanisms with [Ca2+]ER as a pacemaker are suppressed. This suggests that the mechanism discussed above in which [Ca2+]ER is the pacemaker component could be responsible for fast bursting and [Ca2+]c oscillations.
Recently, null mice for one of the TRP ion channels (Trpm5) were found to have islets that had lost the ability to create fast [Ca2+]c oscillations, whereas slow [Ca2+]c oscillations were intact (27). The disappearance of fast [Ca2+]c oscillations in this case is consistent with the hypothesis that Trpm5 channels can be a part of the SOC (or CRAN) mechanism with Na+ influx (75, 118) that is in part responsible for the fast, not slow, [Ca2+]c oscillation (see above).
[Ca2+]ER changes can regulate the shape of slow glucose-induced [Ca2+]c oscillation in pancreatic β-cells (11, 99). Our simulations also support the hypothesis that slow [Ca2+]c oscillation frequency and the generation of the waveform can be modulated by changes in the rates of Ca2+ leak from the ER, although [Ca2+]ER does not account for the pacemaker mechanism for slow oscillations per se (51, 138). For example, Fig. 7 (reproduced from Ref. 51) shows the changes in the shape of [Ca2+]c oscillations during simulation of SERCA block that lead to a decrease in [Ca2+]ER. This is at conditions where the changes in [Na+]c drive the pacemaker mechanism for slow [Ca2+]c oscillations. In this case, Ca2+ is gradually released into the cytosol, and a decrease in [Ca2+]c can be slow at the beginning of the silent period of slow oscillations (Fig. 7). When [Ca2+]ER is small after SERCA inhibition, no additional Ca2+ release occurs during the silent period of slow oscillations, and the [Ca2+]c decrease is sharp. A similar result was obtained experimentally (51, 55).
Pacemaker due to [Ca2+]ER regulated by IP3.
In pancreatic β-cells, as well as in other cell types, external agonists can act on G protein-coupled receptors to stimulate phospholipase C (PLC) activity. Ca2+-activated PLC catalyzes the formation of IP3 from phosphatidylinositol-4,5-bisphosphate (Fig. 1) (23). The resulting rise in IP3 initiates Ca2+ discharge from the ER through IP3R channels (13, 56, 138). IP3 can also activate K+ or Na+ conductances that can lead to PM repolarization (5, 134).
Changes in [IP3]c can play a crucial role in creating Ca2+ oscillations through activation of the ER IP3 receptor in nonelectrically excitable types of cells (13, 130). Several mathematical models employed this mechanism for nonelectrically excitable cells. The first step is that a [Ca2+]c increase is caused by Ca2+ release from the ER. One intracellular signal for this release is IP3, which triggers Ca2+ release by binding to the IP3Rs on the surface of the ER. This opens ER Ca2+ channels, allowing Ca2+ to flow out into the cytoplasm. Subsequent inactivation of the IP3Rs and removal of Ca2+ by ER membrane pumps then reduces the Ca2+ concentration to lower levels. It can initiate a repeating cycle of release and uptake of Ca2+ from the ER, resulting in Ca2+ oscillations if the IP3 concentration is in the correct range (13, 130). However, β-cells are electrically excitable cells, and as discussed above the changes in PM potential and corresponding Ca2+ influx from the extracellular space through VDCCs may be the principal regulator of cytoplasmic Ca2+ homeostasis in β-cells. For this reason, [IP3]c and IP3R interactions are not likely to function as a pacemaker for [Ca2+]c oscillations in β-cells.
We recently investigated the dynamics of IP3 in mouse primary β-cells and in MIN6 mouse insulinoma cells upon stimulation with glucose and a muscarinic agonist (carbamoylcholine) (138). We found that IP3 concentrations in the cytoplasm oscillated in parallel with [Ca2+]c oscillations upon stimulation with glucose. Although this could be interpreted as evidence supporting IP3 oscillations as a pacemaker of Ca2+ oscillations, in this case IP3 oscillations can be readily explained by Ca2+ activation of PLC leading to [IP3]c changes, as simulated in our model (Fig. 7E). This suggests that slow cyclical changes in IP3 concentration may follow from the activation of PLC by independent cyclical [Ca2+]c changes; i.e., IP3 may not be a pacemaker for [Ca2+]c oscillations (51, 138). However, this problem needs further investigation, perhaps by PLC inhibition, to determine the existence of [Ca2+]c oscillations in the absence of IP3 oscillations.
However, the rate of IP3 production can have a dramatic effect on oscillations even though IP3 is not a pacemaker compound; i.e., IP3 can be a strong modulator of oscillatory processes. For example, activation of IP3 synthesis can cause a transformation of slow oscillations into fast ones (20, 138). Although the mechanism is unclear, it may be due to additional PM depolarization following from the opening of SOC or the recently found NALCN channels (134) with decreased [Ca2+]ER, or this could follow from activation of PM K+ channels by IP3.
cAMP as a Pacemaker Component
The cAMP pathway has [Ca2+]c-dependent components such as some isoforms of adenylyl cyclase and phosphodiesterases (PDEs) (Fig. 1) (29, 60). cAMP may also increase Ca2+-induced Ca2+ release from the ER through ryanodine and IP3Rs in mouse pancreatic β-cells and may activate some PM channels via phosphorylation or protein binding (66, 84, 85, 131). The suggestion was made for several types of cells that [Ca2+]c oscillations could result from interactions between cAMP and [Ca2+]c (61, 102). Therefore, an oscillatory mechanism with Ca2+ feedback effect and [cAMP]c as a slow pacemaker component could also occur in β-cells.
However, recent experimental data does not support the hypothesis that cAMP is a pacemaker component for an oscillatory mechanism, at least for slow [Ca2+]c oscillations in β-cells. For example, in insulinoma β-cell lines a PDE inhibitor (IBMX) abolished cAMP oscillations without inhibiting [Ca2+]c oscillations (see the 5th figure in Ref. 95). Dyachok et al. (42) showed that IBMX can stimulate [Ca2+]c oscillations even during elevated, nonoscillating cAMP levels, measured using real-time imaging. For this reason, according to our rules for hypothesis rejection (see introduction), we believe that cAMP oscillations are not part of a pacemaker mechanism, at least for slow [Ca2+]c oscillations. We recently analyzed oscillatory behavior of cAMP using our model of cAMP dynamics and found that slow [Ca2+]c oscillations are a pacemaker for cAMP oscillations in pancreatic β-cells and not the other way around (47).
However, cAMP (as well as IP3) may modulate the dynamics of the intracellular processes and PM potential, leading to the changes in the oscillation pattern. For example, both IBMX and forskolin, an activator of adenyl cyclase, increase the level of cAMP, transforming [Ca2+]c oscillations from slow into fast and further increasing their frequency (10). Other agents that increase the concentration of cAMP, such as glucagon, also promote the appearance of fast [Ca2+]c oscillations (99). The underlying mechanisms of these transformations remain an open question but can be partially explained by altering PM depolarization.
The Pacemaker Role of Metabolic Oscillations
Metabolic cycles can control glucose-stimulated insulin secretion (80), and a number of hypotheses have implicated metabolic oscillations in determining Ca2+ oscillations (101, 142). Oscillations of a metabolic signal in β-cells may result from intrinsic properties of various pathways, although glycolytic oscillations are not likely to account for the mechanism of other metabolic oscillations (see above). We cannot rule out that some Ca2+-independent mechanism can create oscillations of compounds that can change the PM potential, leading to [Ca2+]c oscillations. For example, based on the existence of citrate oscillations in isolated islet mitochondria, it was proposed that there is an independent mitochondrial oscillator and that the exported citrate may feed back and coordinate mitochondrial and cytosolic oscillations (101). Several mathematical models of possible mitochondrial oscillatory mechanisms were discussed recently (14), and these should be testable in β-cells.
Oscillations of the metabolic signals in β-cells may be secondary to oscillations in [Ca2+]c. As was pointed out by Kennedy et al. (89), an appearance of metabolic oscillations does not prove that metabolic variations are the real pacemakers of oscillations, because these metabolic changes can indeed reflect the [Ca2+]c oscillations. For example, variations in [Ca2+]c can change ATP consumption because the rate of work of ATP-consuming Ca2+ pumps depends on Ca2+ concentrations. Using our mathematical model for β-cell processes (49, 50), we found that cyclic [ATP] and [ADP] oscillations in the cytoplasm due to the oscillations in [Ca2+]c can stimulate the oscillations in metabolic processes such as oxygen consumption, the mitochondrial inner membrane potential, the rate of ATP production in mitochondria, and NAD(P)H levels in β-cells, i.e., in the oscillating processes that were found in experiments using β-cells (89, 92, 100, 111). We can also expect oscillations in metabolism if specific metabolic enzymes can be modulated by cyclic Ca2+ concentration changes in cytoplasm or mitochondria. For this reason, the oscillations in metabolic variables mentioned above are most likely secondary and likely follow rather than precede bursting and [Ca2+]c oscillations.
Activation or Deactivation of the Voltage-Dependent Channels As a Pacemaker Component
As we pointed out in the introduction, the cyclic activation and deactivation of several channels can underlie mechanisms that drive bursting and Ca2+ oscillations in β-cells. Here, we consider other possible suggestions related to regulation of ion channels.
For example, it was suggested that PM repolarization and termination of spikes could occur during a burst if some parameters of the voltage-gated Ca2+ current could be slowly changed, leading to a decreased current (28). On the other hand, a regenerative recovery from inactivation and reactivation of Ca2+ currents in the rest period could lead to a depolarization and a beginning of a new burst. This mechanism for burst generation requires mathematical modeling of time-dependent changes in maximal conductance or other coefficients in the equations for VDCC (88). However, this mechanism for the changes in Ca2+ current also lacks sufficient experimental support.
Similarly, we can suggest that slow activation of any K+ currents (other than current through KATP and slow KCa channels, which we have considered above) in the active period can lead to repolarization and burst termination. A regenerative deactivation of these currents in the silent interval can lead to depolarization and to a beginning of a burst. However, the available experimental evidence argues against this hypothesis, at least for slow [Ca2+]c oscillations. For example, stimulation of βTC3-neo or MIN6 insulinoma cells with glucose results only in a modest nonoscillatory increase in [Ca2+]c. However, subsequent addition of TEA (15–20 mM, sufficient to substantially suppress most non-KATP K+ channels) can induce fast and slow [Ca2+]c oscillations (41, 136, 139) so that inhibiting most K+ channels activates rather than suppresses [Ca2+]c oscillations. Slow bursting and [Ca2+]c oscillations are not lost in mouse islets lacking KV2.1 channels (77). According to our rule for rejection, this indicates that KV2.1 channels are not a part of a pacemaker mechanism, but they do have important modulating effects.
Interactions of Mechanisms and Compound Patterns of Bursting and [Ca2+]c Oscillations
Fast and slow modes of oscillation can occur together, as in the mixed pattern, or separately, as in the fast and slow patterns (Fig. 2; see also Refs. 19 and 31). This strongly argues that they stem from distinct mechanisms. These mechanisms can be linked reciprocally and often occur together and can also proceed largely independently of each other. Mixed oscillations also occur in isolated cells, suggesting that this peculiar pattern does not result from the sum of signals produced in distinct β-cells in islets (6).
Modeling approaches show that compound bursting and corresponding mixed [Ca2+]c oscillations can be simulated. The results of the modeling favor a scenario where two or more slow variables interact to produce complex oscillations. For example, Bertram and colleagues (17, 18) simulated the ultrafast and fast oscillations by small variations in KATP conductance using the empirical equation connecting the [ATP]/[ADP] ratio with [Ca2+]c changes. The slow [Ca2+]c oscillations were simulated as metabolic glycolytic oscillations such that the two interact to produce compound oscillations consisting of episodes of bursts separated by long periods of silence, or “accordion” oscillations, that consist of fast bursts with a slowly modulated duty cycle. Similar behavior could be achieved by defining the different slow and fast pacemaker variables (16). For example, slow [Ca2+]c oscillations in a compound picture may be a result of a [Ca2+]ER-dependent mechanism, and a KATP-dependent mechanism may be responsible for fast [Ca2+]c oscillations on the top of the slow (35). According to our analysis, it is most likely that [Na+]c can represent a slow-changing compound for slow oscillations and changes in the [ATP/ADP] ratio and/or [Ca2+]ER for fast oscillations.
Modulators of Oscillation Behavior and External Pacemaker Mechanisms
Changes in channel conductance or Ca2+ handling can change PM polarization or Ca2+ redistribution. This, in turn, may lead to changes in bursting and [Ca2+]c oscillations even though the cellular components do not participate directly in pacemaker oscillatory mechanisms. For example, activation of anion channels may cause depolarization of the β-cell PM (21, 22). Glucose stimulation of β-cells is coupled to an increase in Cl− permeability, and oscillatory Ca2+ signaling may be critically dependent on transmembrane Cl− fluxes (45). This indicates that agents that regulate anion channels may modulate oscillations. Cyclic nucleotide-gated (HCN) channels may also have a modulating effect because they can influence β-cell PM potential (152). External insulin can also be considered a modulator because it may be able to activate KATP channels (90).
Cyclical changes in external modulators can create or synchronize the alterations in PM polarization as well as the corresponding intracellular Ca2+ concentration. This property of β-cells can be important for synchronization of oscillations of insulin release in vivo in the pancreas. This synchronization is likely achieved through intrapancreatic innervation. This is probably due to cholinergie effects synchronizing islets (1, 149). Interestingly, a single cholinergie pulse per several internal [Ca2+]c oscillations can synchronize these oscillations (46, 149).
Other external pacemaker mechanisms can also contribute to islet synchronization. For example, insulin secreted by islets acts on the liver, resulting in a reduction in plasma glucose concentration that can lead to glucose oscillations in blood, synchronizing an insulin secretion in islets (57, 114, 117). Additional synchronizing factors can be external ATP acting on purinergic receptors (115, 128).
Conclusion
Our analysis of several different hypotheses for pacemakers of oscillatory processes in β-cells shows that the following proposals may be most consistent with the existing experimental data. 1) Changes in the conductivity of slow KCa channels and KATP channels can be the pacemakers for ultrafast [Ca2+]c oscillations; 2) changes in [ATP]/[ADP] ratio and/or [Ca2+]ER can be the pacemakers for fast bursts and [Ca2+]c oscillations; and 3) cyclical [Na+]c changes may be important to explain the pattern of slow bursting and calcium oscillations. However, the exact physiological variables and their underlying mechanisms that drive bursting or Ca2+ oscillations in β-cells remain uncertain. Additional dynamic experiments and mathematical models are necessary to better understand this emerging aspect of β-cell physiology.
GRANTS
This work has been partially supported by National Institute of Diabetes and Digestive and Kidney Diseases Grants DRTC P60-DK-020595, DK-48494, and DK-063493 and a Research Grant from the Keck Foundation.
DISCLOSURES
The authors have nothing to disclose.
Supplementary Material
APPENDIX
Modeling of Slow-Activated Ca2+-Sensitive K+ Channel-Dependent Bursting and [Ca2+]c Oscillations
Equations and coefficients for channels and pumps are taken from the previous model (51) or represented here. Slow-activated Ca2+-sensitive K+ channels as well as the fast-activated Ca2+-sensitive K+ channels were modeled, with considerably increased time-dependent parameters for activation reported in Ref. 59.
The units are time in milliseconds (ms), voltage in millivolts (mV), concentration in micromoles/liter (μM), current in femtoamperes (fA), conductance in picosiemens (pS), and capacitance in femtofarads (fF). Numerical integration of the model was carried out using standard numerical methods (51). This model is available for direct simulation on the web site “Virtual Cell” (www.nrcam.uchc.edu) in the “MathModel Database” on the “math workspace” in the library “Fridlyand” with the name “SlowCa+acted Kchan.”
Ca2+ Current (IVCa)
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where gmVCa = 800 pS, ECa = 100 mV.
Delayed Rectifier K+ Current (IKr)
| (6) |
| (7) |
| (8) |
where gmKr = 30,000 pS, τdKr = 23 mc, EK = −75 mV.
Fast Ca2+-Activated K+ Current (IKCa)
| (9) |
| (10) |
where gmKCa = 10 pS.
Slow-Activated Ca2+-Sensitive K+ Channels
| (11) |
| (12) |
| (13) |
where GmKCas = 90 pS and τdKCas = 2,300 mc.
ATP-Sensitive K+ Channel Current (IKATP)
| (14) |
where
| (15) |
| (16) |
where OKATP is the fraction of open KATP channels, [MgADPf]i is the concentration of free Mg-bound ADP, GmKATP = 30,000 pS, and [ADPf]i = 20 μM.
Plasma Membrane Ca2+ Pump Current (ICap)
| (17) |
where PmCap = 4,300 fA.
Na+ Background Current (INab)
| (18) |
where gmNab = 12 pS and ENa = −70 mV.
The differential equation describing time-dependent changes in the PM potential (Vp) is the current balance equation:
| (19) |
where Cm is the whole cell membrance capacitance. The PM currents are listed in Fig. 1.
Based on the consideration in our general model (51), and including only IVCA and ICap, the equations for [Ca2+] dynamics can be written as
| (20) |
where fi is the fraction of free Ca2+ in cytoplasm, F is Faraday's constant, Vi is the effective volumes of the cytosolic compartment, and ksg is a coefficient of the sequestration rate of [Ca2+]c.
REFERENCES
- 1. Ahren B. Autonomic regulation of islet hormone secretion—implications for health and disease. Diabetologia 43: 393–410, 2000 [DOI] [PubMed] [Google Scholar]
- 2. Ainscow EK, Rutter GA. Glucose-stimulated oscillations in free cytosolic ATP concentration imaged in single islet beta-cells: evidence for a Ca2+-dependent mechanism. Diabetes 51, Suppl 1: S162–S170, 2002 [DOI] [PubMed] [Google Scholar]
- 3. Ainscow EK, Rutter GA. Mitochondrial priming modifies Ca2+ oscillations and insulin secretion in pancreatic islets. Biochem J 353: 175–180, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Ammälä C, Bokvist K, Larsson O, Berggren PO, Rorsman P. Demonstration of a novel apamin-insensitive calcium-activated K+ channel in mouse pancreatic B cells. Pflugers Archiv 422: 443–448, 1993 [DOI] [PubMed] [Google Scholar]
- 5. Ammala C, Larsson O, Berggren PO, Bokvist K, Juntti-Berggren L, Kindmark H, Rorsman P. Inositol trisphosphate-dependent periodic activation of a Ca(2+)-activated K+ conductance in glucose-stimulated pancreatic beta-cells. Nature 353: 849–852, 1991 [DOI] [PubMed] [Google Scholar]
- 6. Arredouani A, Henquin JC, Gilon P. Contribution of the endoplasmic reticulum to the glucose-induced [Ca2+]c response in mouse pancreatic islets. Am J Physiol Endocrinol Metab 282: E982–E991, 2002 [DOI] [PubMed] [Google Scholar]
- 7. Ashcroft FM, Rorsman P. Electrophysiology of the pancreatic beta-cell. Prog Biophys Mol Biol 54: 87–143, 1989 [DOI] [PubMed] [Google Scholar]
- 8. Atwater I, Dawson CM, Ribalet B, Rojas E. Potassium permeability activated by intracellular calcium ion concentration in the pancreatic beta-cell. J Physiol 288: 575–588, 1979 [PMC free article] [PubMed] [Google Scholar]
- 9. Atwater I, Ribalet B, Rojas E. Cyclic changes in potential and resistance of the beta-cell membrane induced by glucose in islets of Langerhans from mouse. J Physiol 278: 117–139, 1978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Baltrusch S, Lenzen S. Regulation of [Ca2+]i oscillations in mouse pancreatic islets by adrenergic agonists. Biochem Biophys Res Commun 363: 1038–1043, 2007 [DOI] [PubMed] [Google Scholar]
- 11. Beauvois MC, Merezak C, Jonas JC, Ravier MA, Henquin JC, Gilon P. Glucose-induced mixed [Ca2+]c oscillations in mouse β-cells are controlled by the membrane potential and the SERCA3 Ca2+-ATPase of the endoplasmic reticulum. Am J Physiol Cell Physiol 290: C1503–C1511, 2006 [DOI] [PubMed] [Google Scholar]
- 12. Benninger RK, Zhang M, Head WS, Satin LS, Piston DW. Gap junction coupling and calcium waves in the pancreatic islet. Biophys J 95: 5048–5061, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Berridge MJ. Inositol trisphosphate and calcium signalling mechanisms. Biochim Biophys Acta 1793: 933–940, 2009 [DOI] [PubMed] [Google Scholar]
- 14. Bertram R, Budu-Grajdeanu P, Jafri MS. Using phase relations to identify potential mechanisms for metabolic oscillations in isolated beta-cell mitochondria. Islets 1: 87–94, 2009 [DOI] [PubMed] [Google Scholar]
- 15. Bertram R, Gram Pedersen M, Luciani DS, Sherman A. A simplified model for mitochondrial ATP production. J Theor Biol 243: 575–586, 2006 [DOI] [PubMed] [Google Scholar]
- 16. Bertram R, Li YX. A mathematical model for the actions of activin, inhibin, and follistatin on pituitary gonadotrophs. Bull Math Biol 70: 2211–2228, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Bertram R, Satin L, Zhang M, Smolen P, Sherman A. Calcium and glycolysis mediate multiple bursting modes in pancreatic islets. Biophys J 87: 3074–3087, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Bertram R, Satin LS, Pedersen MG, Luciani DS, Sherman A. Interaction of glycolysis and mitochondrial respiration in metabolic oscillations of pancreatic islets. Biophys J 92: 1544–1555, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bertram R, Sherman A, Satin LS. Metabolic and electrical oscillations: partners in controlling pulsatile insulin secretion. Am J Physiol Endocrinol Metab 293: E890–E900, 2007 [DOI] [PubMed] [Google Scholar]
- 20. Bertram R, Smolen P, Sherman A, Mears D, Atwater I, Martin F, Soria B. A role for calcium release-activated current (CRAC) in cholinergic modulation of electrical activity in pancreatic beta-cells. Biophys J 68: 2323–2332, 1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Best L. Glucose-induced electrical activity in rat pancreatic beta-cells: dependence on intracellular chloride concentration. J Physiol 568: 137–144, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Best L, Brown PD. Studies of the mechanism of activation of the volume-regulated anion channel in rat pancreatic beta-cells. J Membr Biol 230: 83–91, 2009 [DOI] [PubMed] [Google Scholar]
- 23. Biden TJ, Peter-Riesch B, Schlegel W, Wollheim CB. Ca2+-mediated generation of inositol 1,4,5-triphosphate and inositol 1,3,4,5-tetrakisphosphate in pancreatic islets. Studies with K+, glucose, and carbamylcholine. J Biol Chem 262: 3567–3571, 1987 [PubMed] [Google Scholar]
- 24. Brookes PS, Yoon Y, Robotham JL, Anders MW, Sheu SS. Calcium, ATP, and ROS: a mitochondrial love-hate triangle. Am J Physiol Cell Physiol 287: C817–C833, 2004 [DOI] [PubMed] [Google Scholar]
- 25. Chay TR. Effects of extracellular calcium on electrical bursting and intracellular and luminal calcium oscillations in insulin secreting pancreatic beta-cells. Biophys J 73: 1673–1688, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Chay TR, Keizer J. Minimal model for membrane oscillations in the pancreatic beta-cell. Biophys J 42: 181–190, 1983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Colsoul B, Schraenen A, Lemaire K, Quintens R, Van Lommel L, Segal A, Owsianik G, Talavera K, Voets T, Margolskee RF, Kokrashvili Z, Gilon P, Nilius B, Schuit FC, Vennekens R. Loss of high-frequency glucose-induced Ca2+ oscillations in pancreatic islets correlates with impaired glucose tolerance in Trpm5−/− mice. Proc Natl Acad Sci USA 107: 5208–5213, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Cook DL, Satin LS, Hopkins WF. Pancreatic B cells are bursting, but how? Trends Neurosci 14: 411–414, 1991 [DOI] [PubMed] [Google Scholar]
- 29. Cooper DM. Regulation and organization of adenylyl cyclases and cAMP. Biochem J 375: 517–529, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Cruz-Cruz R, Salgado A, Sánchez-Soto C, Vaca L, Hiriart M. Thapsigargin-sensitive cationic current leads to membrane depolarization, calcium entry, and insulin secretion in rat pancreatic β-cells. Am J Physiol Endocrinol Metab 289: E439–E445, 2005 [DOI] [PubMed] [Google Scholar]
- 31. Dahlgren GM, Kauri LM, Kennedy RT. Substrate effects on oscillations in metabolism, calcium and secretion in single mouse islets of Langerhans. Biochim Biophys Acta 1724: 23–36, 2005 [DOI] [PubMed] [Google Scholar]
- 32. Dean PM, Matthews EK. Electrical activity in pancreatic islet cells: effect of ions. J Physiol 210: 265–275, 1970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Dean PM, Matthews EK. Glucose-induced electrical activity in pancreatic islet cells. J Physiol 210: 255–264, 1970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Detimary P, Gilon P, Henquin JC. Interplay between cytoplasmic Ca2+ and the ATP/ADP ratio: a feedback control mechanism in mouse pancreatic islets. Biochem J 333: 269–274, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Diederichs F. Ion homeostasis and the functional roles of SERCA reactions in stimulus-secretion coupling of the pancreatic beta-cell: a mathematical simulation. Biophys Chem 134: 119–143, 2008 [DOI] [PubMed] [Google Scholar]
- 36. Diederichs F. Mathematical simulation of membrane processes and metabolic fluxes of the pancreatic beta-cell. Bull Math Biol 68: 1779–1818, 2006 [DOI] [PubMed] [Google Scholar]
- 37. Dryselius S, Grapengiesser E, Hellman B, Gylfe E. Voltage-dependent entry and generation of slow Ca2+ oscillations in glucose-stimulated pancreatic β-cells. Am J Physiol Endocrinol Metab 276: E512–E518, 1999 [DOI] [PubMed] [Google Scholar]
- 38. Düfer M, Gier B, Wolpers D, Krippeit-Drews P, Ruth P, Drews G. Enhanced glucose tolerance by SK4 channel inhibition in pancreatic beta-cells. Diabetes 58: 1835–1843, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Dufer M, Haspel D, Krippeit-Drews P, Aguilar-Bryan L, Bryan J, Drews G. Activation of the Na+/K+-ATPase by insulin and glucose as a putative negative feedback mechanism in pancreatic beta-cells. Pflugers Arch 457: 1351–1360, 2009 [DOI] [PubMed] [Google Scholar]
- 40. Dufer M, Haspel D, Krippeit-Drews P, Aguilar-Bryan L, Bryan J, Drews G. Oscillations of membrane potential and cytosolic Ca(2+) concentration in SUR1(−/−) beta cells. Diabetologia 47: 488–498, 2004 [DOI] [PubMed] [Google Scholar]
- 41. Dukes ID, Sreenan S, Roe MW, Levisetti M, Zhou YP, Ostrega D, Bell GI, Pontoglio M, Yaniv M, Philipson L, Polonsky KS. Defective pancreatic beta-cell glycolytic signaling in hepatocyte nuclear factor-1alpha-deficient mice. J Biol Chem 273: 24457–24464, 1998 [DOI] [PubMed] [Google Scholar]
- 42. Dyachok O, Isakov Y, Sagetorp J, Tengholm A. Oscillations of cyclic AMP in hormone-stimulated insulin-secreting beta-cells. Nature 439: 349–352, 2006 [DOI] [PubMed] [Google Scholar]
- 43. Eberhardson M, Grapengiesser E. Glucose and tolbutamide trigger transients of Ca2+ in single pancreatic beta-cells exposed to tetraethylammonium. Cell Calcium 25: 355–360, 1999 [DOI] [PubMed] [Google Scholar]
- 44. Eberhardson M, Grapengiesser E. Role of voltage-dependent Na+ channels for rhythmic Ca2+ signalling in glucose-stimulated mouse pancreatic beta-cells. Cell Signal 11: 343–348, 1999 [DOI] [PubMed] [Google Scholar]
- 45. Eberhardson M, Patterson S, Grapengiesser E. Microfluorometric analysis of Cl− permeability and its relation to oscillatory Ca2+ signalling in glucose-stimulated pancreatic beta-cells. Cell Signal 12: 781–786, 2000 [DOI] [PubMed] [Google Scholar]
- 46. Fendler B, Zhang M, Satin L, Bertram R. Synchronization of pancreatic islet oscillations by intrapancreatic ganglia: a modeling study. Biophys J 97: 722–729, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Fridlyand LE, Harbeck MC, Roe MW, Philipson LH. Regulation of cAMP dynamics by Ca2+ and G protein-coupled receptors in the pancreatic β-cell: a computational approach. Am J Physiol Cell Physiol 293: C1924–C1933, 2007 [DOI] [PubMed] [Google Scholar]
- 48. Fridlyand LE, Jacobson DA, Kuznetsov A, Philipson LH. A model of action potentials and fast Ca2+ dynamics in pancreatic beta-cells. Biophys J 96: 3126–3139, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Fridlyand LE, Ma L, Philipson LH. Adenine nucleotide regulation in pancreatic β-cells: modeling of ATP/ADP-Ca2+ interactions. Am J Physiol Endocrinol Metab 289: E839–E848, 2005 [DOI] [PubMed] [Google Scholar]
- 50. Fridlyand LE, Philipson LH. Glucose sensing in the pancreatic beta cell: a computational systems analysis. Theor Biol Med Model 7: 15, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Fridlyand LE, Tamarina N, Philipson LH. Modeling of Ca2+ flux in pancreatic β-cells: role of the plasma membrane and intracellular stores. Am J Physiol Endocrinol Metab 285: E138–E154, 2003 [DOI] [PubMed] [Google Scholar]
- 52. Gall D, Gromada J, Susa I, Rorsman P, Herchuelz A, Bokvist K. Significance of Na/Ca exchange for Ca2+ buffering and electrical activity in mouse pancreatic beta-cells. Biophys J 76: 2018–2028, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Gall D, Susa I. Effect of Na/Ca exchange on plateau fraction and [Ca]i in models for bursting in pancreatic beta-cells. Biophys J 77: 45–53, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Gembal M, Detimary P, Gilon P, Gao ZY, Henquin JC. Mechanisms by which glucose can control insulin release independently from its action on adenosine triphosphate-sensitive K+ channels in mouse B cells. J Clin Invest 91: 871–880, 1993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Gilon P, Arredouani A, Gailly P, Gromada J, Henquin JC. Uptake and release of Ca2+ by the endoplasmic reticulum contribute to the oscillations of the cytosolic Ca2+ concentration triggered by Ca2+ influx in the electrically excitable pancreatic B-cell. J Biol Chem 274: 20197–20205, 1999 [DOI] [PubMed] [Google Scholar]
- 56. Gilon P, Henquin JC. Mechanisms and physiological significance of the cholinergic control of pancreatic beta-cell function. Endocr Rev 22: 565–604, 2001 [DOI] [PubMed] [Google Scholar]
- 57. Gilon P, Ravier MA, Jonas JC, Henquin JC. Control mechanisms of the oscillations of insulin secretion in vitro and in vivo. Diabetes 51, Suppl 1: S144–S151, 2002 [DOI] [PubMed] [Google Scholar]
- 58. Goforth PB, Bertram R, Khan FA, Zhang M, Sherman A, Satin LS. Calcium-activated K+ channels of mouse beta-cells are controlled by both store and cytoplasmic Ca2+: experimental and theoretical studies. J Gen Physiol 120: 307–322, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Gopel SO, Kanno T, Barg S, Eliasson L, Galvanovskis J, Renstrom E, Rorsman P. Activation of Ca(2+)-dependent K(+) channels contributes to rhythmic firing of action potentials in mouse pancreatic beta cells. J Gen Physiol 114: 759–770, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Goraya TA, Cooper DM. Ca2+-calmodulin-dependent phosphodiesterase (PDE1): current perspectives. Cell Signal 17: 789–797, 2005 [DOI] [PubMed] [Google Scholar]
- 61. Gorbunova YV, Spitzer NC. Dynamic interactions of cyclic AMP transients and spontaneous Ca(2+) spikes. Nature 418: 93–96, 2002 [DOI] [PubMed] [Google Scholar]
- 62. Grapengiesser E. Glucose induces cytoplasmic Na+ oscillations in pancreatic beta-cells. Biochem Biophys Res Commun 226: 830–835, 1996 [DOI] [PubMed] [Google Scholar]
- 63. Grapengiesser E. Unmasking of a periodic Na+ entry into glucose-stimulated pancreatic beta-cells after partial inhibition of the Na/K pump. Endocrinology 139: 3227–3231, 1998 [DOI] [PubMed] [Google Scholar]
- 64. Grapengiesser E, Gylfe E, Hellman B. Ca2+ oscillations in pancreatic beta-cells exposed to leucine and arginine. Acta Physiol Scand 136: 113–119, 1989 [DOI] [PubMed] [Google Scholar]
- 65. Grapengiesser E, Gylfe E, Hellman B. Sulfonylurea mimics the effect of glucose in inducing large amplitude oscillations of cytoplasmic Ca2+ in pancreatic beta-cells. Mol Pharmacol 37: 461–467, 1990 [PubMed] [Google Scholar]
- 66. Gromada J, Brock B, Schmitz O, Rorsman P. Glucagon-like peptide-1: regulation of insulin secretion and therapeutic potential. Basic Clin Pharmacol Toxicol 95: 252–262, 2004 [DOI] [PubMed] [Google Scholar]
- 67. Haspel D, Krippeit-Drews P, Aguilar-Bryan L, Bryan J, Drews G, Dufer M. Crosstalk between membrane potential and cytosolic Ca2+ concentration in beta cells from Sur1−/− mice. Diabetologia 48: 913–921, 2005 [DOI] [PubMed] [Google Scholar]
- 68. Hattori M, Kai R, Kitasato H. Effects of lowering external Na+ concentration on cytoplasmic pH and Ca2+ concentration in mouse pancreatic beta-cells: mechanism of periodicity of spike-bursts. Jpn J Physiol 44: 283–293, 1994 [DOI] [PubMed] [Google Scholar]
- 69. Heart E, Smith PJ. Rhythm of the β-cell oscillator is not governed by a single regulator: multiple systems contribute to oscillatory behavior. Am J Physiol Endocrinol Metab 292: E1295–E1300, 2007 [DOI] [PubMed] [Google Scholar]
- 70. Hellman B, Gylfe E, Grapengiesser E, Lund PE, Berts A. Cytoplasmic Ca2+ oscillations in pancreatic beta-cells. Biochim Biophys Acta 1113: 295–305, 1992 [DOI] [PubMed] [Google Scholar]
- 71. Henquin JC. Regulation of insulin secretion: a matter of phase control and amplitude modulation. Diabetologia 52: 739–751, 2009 [DOI] [PubMed] [Google Scholar]
- 72. Henquin JC, Nenquin M, Ravier MA, Szollosi A. Shortcomings of current models of glucose-induced insulin secretion. Diabetes Obes Metab 11, Suppl 4: 168–179, 2009 [DOI] [PubMed] [Google Scholar]
- 73. Herchuelz A, Kamagate A, Ximenes H, Van Eylen F. Role of Na/Ca exchange and the plasma membrane Ca2+-ATPase in beta cell function and death. Ann NY Acad Sci 1099: 456–467, 2007 [DOI] [PubMed] [Google Scholar]
- 74. Hiriart M, Aguilar-Bryan L. Channel regulation of glucose sensing in the pancreatic β-cell. Am J Physiol Endocrinol Metab 295: E1298–E1306, 2008 [DOI] [PubMed] [Google Scholar]
- 75. Huang YA, Roper SD. Intracellular Ca(2+) and TRPM5-mediated membrane depolarization produce ATP secretion from taste receptor cells. J Physiol 588: 2343–2350, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Jacobson D, Philipson L. Ion channels and insulin secretion. In: Pancreatic Beta Cell in Health and Disease, edited by Seino S, Bell G. Japan: Springer, 2008, p. 91–110 [Google Scholar]
- 77. Jacobson DA, Kuznetsov A, Lopez JP, Kash S, Ammälä CE, Philipson LH. Kv2.1 ablation alters glucose-induced islet electrical activity, enhancing insulin secretion. Cell Metab 6: 229–235, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Jacobson DA, Philipson LH. TRP channels of the pancreatic beta cell. Handb Exp Pharmacol: 409–424, 2007 [DOI] [PubMed] [Google Scholar]
- 79. Jahanshahi P, Wu R, Carter JD, Nunemaker CS. Evidence of diminished glucose stimulation and endoplasmic reticulum function in nonoscillatory pancreatic islets. Endocrinology 150: 607–615, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Jensen MV, Joseph JW, Ronnebaum SM, Burgess SC, Sherry AD, Newgard CB. Metabolic cycling in control of glucose-stimulated insulin secretion. Am J Physiol Endocrinol Metab 295: E1287–E1297, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Jiang N, Cox RD, Hancock JM. A kinetic core model of the glucose-stimulated insulin secretion network of pancreatic beta cells. Mamm Genome 18: 508–520, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Johnson JD, Kuang S, Misler S, Polonsky KS. Ryanodine receptors in human pancreatic beta cells: localization and effects on insulin secretion. FASEB J 18: 878–880, 2004 [DOI] [PubMed] [Google Scholar]
- 83. Juntti-Berggren L, Webb DL, Arkhammar PO, Schultz V, Schweda EK, Tornheim K, Berggren PO. Dihydroxyacetone-induced oscillations in cytoplasmic free Ca2+ and the ATP/ADP ratio in pancreatic beta-cells at substimulatory glucose. J Biol Chem 278: 40710–40716, 2003 [DOI] [PubMed] [Google Scholar]
- 84. Kang G, Chepurny OG, Rindler MJ, Collis L, Chepurny Z, Li WH, Harbeck M, Roe MW, Holz GG. A cAMP and Ca2+ coincidence detector in support of Ca2+-induced Ca2+ release in mouse pancreatic beta cells. J Physiol 566: 173–188, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Kang G, Leech CA, Chepurny OG, Coetzee WA, Holz GG. Role of the cAMP sensor Epac as a determinant of KATP channel ATP sensitivity in human pancreatic beta-cells and rat INS-1 cells. J Physiol 586: 1307–1319, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Kanno T, Rorsman P, Gopel SO. Glucose-dependent regulation of rhythmic action potential firing in pancreatic beta-cells by K(ATP)-channel modulation. J Physiol 545: 501–507, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Keizer J, Magnus G. ATP-sensitive potassium channel and bursting in the pancreatic beta cell. A theoretical study. Biophys J 56: 229–242, 1989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Keizer J, Smolen P. Bursting electrical activity in pancreatic beta cells caused by Ca(2+)- and voltage-inactivated Ca2+ channels. Proc Natl Acad Sci USA 88: 3897–3901, 1991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Kennedy RT, Kauri LM, Dahlgren GM, Jung SK. Metabolic oscillations in beta-cells. Diabetes 51, Suppl 1: S152–S161, 2002 [DOI] [PubMed] [Google Scholar]
- 90. Khan FA, Goforth PB, Zhang M, Satin LS. Insulin activates ATP-sensitive K(+) channels in pancreatic beta-cells through a phosphatidylinositol 3-kinase-dependent pathway. Diabetes 50: 2192–2198, 2001 [DOI] [PubMed] [Google Scholar]
- 91. Kinard TA, de Vries G, Sherman A, Satin LS. Modulation of the bursting properties of single mouse pancreatic beta-cells by artificial conductances. Biophys J 76: 1423–1435, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Kindmark H, Kohler M, Brown G, Branstrom R, Larsson O, Berggren PO. Glucose-induced oscillations in cytoplasmic free Ca2+ concentration precede oscillations in mitochondrial membrane potential in the pancreatic beta-cell. J Biol Chem 276: 34530–34536, 2001 [DOI] [PubMed] [Google Scholar]
- 93. Kitasato H, Kai R, Ding WG, Omatsu-Kanbe M. The intrinsic rhythmicity of spike-burst generation in pancreatic beta-cells and intercellular interaction within an islet. Jpn J Physiol 46: 363–373, 1996 [DOI] [PubMed] [Google Scholar]
- 94. Kuznetsov A, Bindokas VP, Marks JD, Philipson LH. FRET-based voltage probes for confocal imaging: membrane potential oscillations throughout pancreatic islets. Am J Physiol Cell Physiol 289: C224–C229, 2005 [DOI] [PubMed] [Google Scholar]
- 95. Landa LR, Jr, Harbeck M, Kaihara K, Chepurny O, Kitiphongspattana K, Graf O, Nikolaev VO, Lohse MJ, Holz GG, Roe MW. Interplay of Ca2+ and cAMP signaling in the insulin-secreting MIN6 beta-cell line. J Biol Chem 280: 31294–31302, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Lebrun P, Malaisse WJ, Herchuelz A. Activation, but not inhibition, by glucose of Ca2+-dependent K+ permeability in the rat pancreatic B-cell. Biochim Biophys Acta 731: 145–150, 1983 [DOI] [PubMed] [Google Scholar]
- 97. Leech CA, Habener JF. A role for Ca2+-sensitive nonselective cation channels in regulating the membrane potential of pancreatic beta-cells. Diabetes 47: 1066–1073, 1998 [DOI] [PubMed] [Google Scholar]
- 98. Liu YJ, Grapengiesser E, Gylfe E, Hellman B. Glucose induces oscillations of cytoplasmic Ca2+, Sr2+ and Ba2+ in pancreatic beta-cells without participation of the thapsigargin-sensitive store. Cell Calcium 18: 165–173, 1995 [DOI] [PubMed] [Google Scholar]
- 99. Liu YJ, Tengholm A, Grapengiesser E, Hellman B, Gylfe E. Origin of slow and fast oscillations of Ca2+ in mouse pancreatic islets. J Physiol 508: 471–481, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100. Luciani DS, Misler S, Polonsky KS. Ca2+ controls slow NAD(P)H oscillations in glucose-stimulated mouse pancreatic islets. J Physiol 572: 379–392, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. MacDonald MJ, Fahien LA, Buss JD, Hasan NM, Fallon MJ, Kendrick MA. Citrate oscillates in liver and pancreatic beta cell mitochondria and in INS-1 insulinoma cells. J Biol Chem 278: 51894–51900, 2003 [DOI] [PubMed] [Google Scholar]
- 102. Maeda M, Lu S, Shaulsky G, Miyazaki Y, Kuwayama H, Tanaka Y, Kuspa A, Loomis WF. Periodic signaling controlled by an oscillatory circuit that includes protein kinases ERK2 and PKA. Science 304: 875–878, 2004 [DOI] [PubMed] [Google Scholar]
- 103. Magnus G, Keizer J. Minimal model of β-cell mitochondrial Ca2+ handling. Am J Physiol Cell Physiol 273: C717–C733, 1997 [DOI] [PubMed] [Google Scholar]
- 104. Magnus G, Keizer J. Model of β-cell mitochondrial calcium handling and electrical activity. I. Cytoplasmic variables. Am J Physiol Cell Physiol 274: C1158–C1173, 1998 [DOI] [PubMed] [Google Scholar]
- 105. Magnus G, Keizer J. Model of β-cell mitochondrial calcium handling and electrical activity. II. Mitochondrial variables. Am J Physiol Cell Physiol 274: C1174–C1184, 1998 [DOI] [PubMed] [Google Scholar]
- 106. Martin F, Sanchez-Andres JV, Soria B. Slow [Ca2+]i oscillations induced by ketoisocaproate in single mouse pancreatic islets. Diabetes 44: 300–305, 1995 [DOI] [PubMed] [Google Scholar]
- 107. Mears D, Sheppard NF, Jr, Atwater I, Rojas E, Bertram R, Sherman A. Evidence that calcium release-activated current mediates the biphasic electrical activity of mouse pancreatic beta-cells. J Membr Biol 155: 47–59, 1997 [DOI] [PubMed] [Google Scholar]
- 108. Meyer-Hermann ME. The electrophysiology of the beta-cell based on single transmembrane protein characteristics. Biophys J 93: 2952–2968, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Miura Y, Henquin JC, Gilon P. Emptying of intracellular Ca2+ stores stimulates Ca2+ entry in mouse pancreatic beta-cells by both direct and indirect mechanisms. J Physiol 503: 387–398, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Miwa Y, Imai Y. Simulation of spike-burst generation and Ca(2+) oscillation in pancreatic beta-cells. Jpn J Physiol 49: 353–364, 1999 [DOI] [PubMed] [Google Scholar]
- 111. Nunemaker CS, Satin LS. Comparison of metabolic oscillations from mouse pancreatic beta cells and islets. Endocrine 25: 61–67, 2004 [DOI] [PubMed] [Google Scholar]
- 112. Nunemaker CS, Zhang M, Wasserman DH, McGuinness OP, Powers AC, Bertram R, Sherman A, Satin LS. Individual mice can be distinguished by the period of their islet calcium oscillations: is there an intrinsic islet period that is imprinted in vivo? Diabetes 54: 3517–3522, 2005 [DOI] [PubMed] [Google Scholar]
- 113. Owada S, Larsson O, Arkhammar P, Katz AI, Chibalin AV, Berggren PO, Bertorello AM. Glucose decreases Na+,K+-ATPase activity in pancreatic beta-cells. An effect mediated via Ca2+-independent phospholipase A2 and protein kinase C-dependent phosphorylation of the alpha-subunit. J Biol Chem 274: 2000–2008, 1999 [DOI] [PubMed] [Google Scholar]
- 114. Pedersen MG, Bertram R, Sherman A. Intra- and inter-islet synchronization of metabolically driven insulin secretion. Biophys J 89: 107–119, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Petit P, Lajoix AD, Gross R. P2 purinergic signalling in the pancreatic beta-cell: control of insulin secretion and pharmacology. Eur J Pharm Sci 37: 67–75, 2009 [DOI] [PubMed] [Google Scholar]
- 116. Polonsky KS. Lilly Lecture 1994. The beta-cell in diabetes: from molecular genetics to clinical research. Diabetes 44: 705–717, 1995 [DOI] [PubMed] [Google Scholar]
- 117. Porksen N, Hollingdal M, Juhl C, Butler P, Veldhuis JD, Schmitz O. Pulsatile insulin secretion: detection, regulation, and role in diabetes. Diabetes 51, Suppl 1: S245–S254, 2002 [DOI] [PubMed] [Google Scholar]
- 118. Prawitt D, Monteilh-Zoller MK, Brixel L, Spangenberg C, Zabel B, Fleig A, Penner R. TRPM5 is a transient Ca2+-activated cation channel responding to rapid changes in [Ca2+]i. Proc Natl Acad Sci USA 100: 15166–15171, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Putney JW. Capacitative calcium entry: from concept to molecules. Immunol Rev 231: 10–22, 2009 [DOI] [PubMed] [Google Scholar]
- 120. Ravier MA, Nenquin M, Miki T, Seino S, Henquin JC. Glucose controls cytosolic Ca2+ and insulin secretion in mouse islets lacking adenosine triphosphate-sensitive K+ channels owing to a knockout of the pore-forming subunit Kir6.2. Endocrinology 150: 33–45, 2009 [DOI] [PubMed] [Google Scholar]
- 121. Richard AM, Webb DL, Goodman JM, Schultz V, Flanagan JN, Getty-Kaushik L, Deeney JT, Yaney GC, Dunaway GA, Berggren PO, Tornheim K. Tissue-dependent loss of phosphofructokinase-M in mice with interrupted activity of the distal promoter: impairment in insulin secretion. Am J Physiol Endocrinol Metab 293: E794–E801, 2007 [DOI] [PubMed] [Google Scholar]
- 122. Roe MW, Lancaster ME, Mertz RJ, Worley JF, 3rd, Dukes ID. Voltage-dependent intracellular calcium release from mouse islets stimulated by glucose. J Biol Chem 268: 9953–9956, 1993 [PubMed] [Google Scholar]
- 123. Roe MW, Mertz RJ, Lancaster ME, Worley JF, 3rd, Dukes ID. Thapsigargin inhibits the glucose-induced decrease of intracellular Ca2+ in mouse islets of Langerhans. Am J Physiol Endocrinol Metab 266: E852–E862, 1994 [DOI] [PubMed] [Google Scholar]
- 124. Roe MW, Worley JF, 3rd, Mittal AA, Kuznetsov A, DasGupta S, Mertz RJ, Witherspoon SM, 3rd, Blair N, Lancaster ME, McIntyre MS, Shehee WR, Dukes ID, Philipson LH. Expression and function of pancreatic beta-cell delayed rectifier K+ channels. Role in stimulus-secretion coupling. J Biol Chem 271: 32241–32246, 1996 [DOI] [PubMed] [Google Scholar]
- 125. Roe MW, Worley JF, 3rd, Qian F, Tamarina N, Mittal AA, Dralyuk F, Blair NT, Mertz RJ, Philipson LH, Dukes ID. Characterization of a Ca2+ release-activated nonselective cation current regulating membrane potential and [Ca2+]i oscillations in transgenically derived beta-cells. J Biol Chem 273: 10402–10410, 1998 [DOI] [PubMed] [Google Scholar]
- 126. Rolland JF, Henquin JC, Gilon P. Feedback control of the ATP-sensitive K(+) current by cytosolic Ca(2+) contributes to oscillations of the membrane potential in pancreatic beta-cells. Diabetes 51: 376–384, 2002 [DOI] [PubMed] [Google Scholar]
- 127. Rutter GA. Nutrient-secretion coupling in the pancreatic islet beta-cell: recent advances. Mol Aspects Med 22: 247–284, 2001 [DOI] [PubMed] [Google Scholar]
- 128. Salehi A, Qader SS, Grapengiesser E, Hellman B. Inhibition of purinoceptors amplifies glucose-stimulated insulin release with removal of its pulsatility. Diabetes 54: 2126–2131, 2005 [DOI] [PubMed] [Google Scholar]
- 129. Santos RM, Rosario LM, Nadal A, Garcia-Sancho J, Soria B, Valdeolmillos M. Widespread synchronous [Ca2+]i oscillations due to bursting electrical activity in single pancreatic islets. Pflugers Arch 418: 417–422, 1991 [DOI] [PubMed] [Google Scholar]
- 130. Schuster S, Marhl M, Hofer T. Modelling of simple and complex calcium oscillations. From single-cell responses to intercellular signalling. Eur J Biochem 269: 1333–1355, 2002 [DOI] [PubMed] [Google Scholar]
- 131. Seino S, Shibasaki T. PKA-dependent and PKA-independent pathways for cAMP-regulated exocytosis. Physiol Rev 85: 1303–1342, 2005 [DOI] [PubMed] [Google Scholar]
- 132. Sherman A. Contributions of modeling to understanding stimulus-secretion coupling in pancreatic β-cells. Am J Physiol Endocrinol Metab 271: E362–E372, 1996 [DOI] [PubMed] [Google Scholar]
- 133. Smolen P, Keizer J. Slow voltage inactivation of Ca2+ currents and bursting mechanisms for the mouse pancreatic beta-cell. J Membr Biol 127: 9–19, 1992 [DOI] [PubMed] [Google Scholar]
- 134. Swayne LA, Mezghrani A, Varrault A, Chemin J, Bertrand G, Dalle S, Bourinet E, Lory P, Miller RJ, Nargeot J, Monteil A. The NALCN ion channel is activated by M3 muscarinic receptors in a pancreatic beta-cell line. EMBO Rep 10: 873–880, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Szollosi A, Nenquin M, Aguilar-Bryan L, Bryan J, Henquin JC. Glucose stimulates Ca2+ influx and insulin secretion in 2-week-old beta-cells lacking ATP-sensitive K+ channels. J Biol Chem 282: 1747–1756, 2007 [DOI] [PubMed] [Google Scholar]
- 136. Tamarina NA, Kuznetsov A, Fridlyand LE, Philipson LH. Delayed-rectifier (KV2.1) regulation of pancreatic β-cell calcium responses to glucose: inhibitor specificity and modeling. Am J Physiol Endocrinol Metab 289: E578–E585, 2005 [DOI] [PubMed] [Google Scholar]
- 137. Tamarina NA, Kuznetsov A, Philipson LH. Reversible translocation of EYFP-tagged STIM1 is coupled to calcium influx in insulin secreting beta-cells. Cell Calcium 44: 533–544, 2008 [DOI] [PubMed] [Google Scholar]
- 138. Tamarina NA, Kuznetsov A, Rhodes CJ, Bindokas VP, Philipson LH. Inositol (1,4,5)-trisphosphate dynamics and intracellular calcium oscillations in pancreatic beta-cells. Diabetes 54: 3073–3081, 2005 [DOI] [PubMed] [Google Scholar]
- 139. Tamarina NA, Wang Y, Mariotto L, Kuznetsov A, Bond C, Adelman J, Philipson LH. Small-conductance calcium-activated K+ channels are expressed in pancreatic islets and regulate glucose responses. Diabetes 52: 2000–2006, 2003 [DOI] [PubMed] [Google Scholar]
- 140. Tengholm A, Gylfe E. Oscillatory control of insulin secretion. Mol Cell Endocrinol 297: 58–72, 2009 [DOI] [PubMed] [Google Scholar]
- 141. Tengholm A, Hellman B, Gylfe E. The endoplasmic reticulum is a glucose-modulated high-affinity sink for Ca2+ in mouse pancreatic beta-cells. J Physiol 530: 533–540, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142. Tornheim K. Are metabolic oscillations responsible for normal oscillatory insulin secretion? Diabetes 46: 1375–1380, 1997 [DOI] [PubMed] [Google Scholar]
- 143. Ulbricht W. Effects of veratridine on sodium currents and fluxes. Rev Physiol Biochem Pharmacol 133: 1–54, 1998 [DOI] [PubMed] [Google Scholar]
- 144. Valdeolmillos M, Gomis A, Sánchez-Andrés JV. In vivo synchronous membrane potential oscillations in mouse pancreatic beta-cells: lack of co-ordination between islets. J Physiol 493: 9–18, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145. Westermark PO, Lansner A. A model of phosphofructokinase and glycolytic oscillations in the pancreatic beta-cell. Biophys J 85: 126–139, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146. Wiederkehr A, Wollheim CB. Impact of mitochondrial calcium on the coupling of metabolism to insulin secretion in the pancreatic beta-cell. Cell Calcium 44: 64–76, 2008 [DOI] [PubMed] [Google Scholar]
- 147. Worley JF, 3rd, McIntyre MS, Spencer B, Dukes ID. Depletion of intracellular Ca2+ stores activates a maitotoxin-sensitive nonselective cationic current in beta-cells. J Biol Chem 269: 32055–32058, 1994 [PubMed] [Google Scholar]
- 148. Worley JF, 3rd, McIntyre MS, Spencer B, Mertz RJ, Roe MW, Dukes ID. Endoplasmic reticulum calcium store regulates membrane potential in mouse islet beta-cells. J Biol Chem 269: 14359–14362, 1994 [PubMed] [Google Scholar]
- 149. Zhang M, Fendler B, Peercy B, Goel P, Bertram R, Sherman A, Satin L. Long lasting synchronization of calcium oscillations by cholinergic stimulation in isolated pancreatic islets. Biophys J 95: 4676–4688, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150. Zhang M, Goforth P, Bertram R, Sherman A, Satin L. The Ca2+ dynamics of isolated mouse beta-cells and islets: implications for mathematical models. Biophys J 84: 2852–2870, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151. Zhang M, Houamed K, Kupershmidt S, Roden D, Satin LS. Pharmacological properties and functional role of Kslow current in mouse pancreatic beta-cells: SK channels contribute to Kslow tail current and modulate insulin secretion. J Gen Physiol 126: 353–363, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152. Zhang Y, Liu Y, Qu J, Hardy A, Zhang N, Diao J, Strijbos PJ, Tsushima R, Robinson RB, Gaisano HY, Wang Q, Wheeler MB. Functional characterization of hyperpolarization-activated cyclic nucleotide-gated channels in rat pancreatic beta cells. J Endocrinol 203: 45–53, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.