Abstract
For many years, subset analysis has been a popular topic for the biostatistics and clinical trials literature. In more recent years, the discussion has focused on finding subsets of genomes which play a role in the effect of treatment, often referred to as stratified or personalized medicine. Though highly sought after, methods for detecting subsets with altering treatment effects are limited and lacking in power. In this article we discuss variable selection for qualitative interactions with the aim to discover these critical patient subsets. We propose a new technique designed specifically to find these interaction variables among a large set of variables while still controlling for the number of false discoveries. We compare this new method against standard qualitative interaction tests using simulations and give an example of its use on data from a randomized controlled trial for the treatment of depression.
Keywords: qualitative interactions, variable selection, personalized medicine, lasso
1 INTRODUCTION
The topics of treatment covariate qualitative interactions and patient subset analysis have seen a good deal of attention throughout the last 30 years (Assmann et al., 2000, Byar and Corle, 1977, Gail and Simon, 1985, Lagakos, 2001, Peto, 1982, Senn, 2001, Shuster and Van Eys, 1983, Yan and Su, 2005, Yusuf et al., 1991), a large amount of it is seemingly controversial. Some segments of the medical field are attempting to move in the direction of individualizing treatment for patients (Evans and Relling, 2004, Sadee and Dai, 2005). While biostatisticians often stress that the search for qualitative interactions should be limited to a small number of pre-specified covariates, many areas of research, including pharmacogenetics, lack prior knowledge or intuition as to which covariates might play an important role in deciding which treatment is optimal. Most clinical scientists feel the search for new qualitative interactions and patient subsets with altering treatment effects is worthwhile and important. However, without proper guidance, these type of analyses are often carried out in an unorganized or error prone fashion.
In this article, we address the problem of determining which of the many possible baseline covariates are likely to qualitatively interact with the treatment. We discuss some of the reasons why this task is difficult and propose a new method for finding these qualitative interactions. We ensure that the method also maintains small susceptibility to finding spurious results. In another paper, Gunter, Chernick and Sun (2011) study a simplification of our method using stepwise selection in place of the approach we describe here. Their purpose is simplification and generalizability to other types of regression models while maintaining low susceptibility to spurious interactions. However, simplicity has a cost in terms of FWER and since it is not expected to be nearly as good as the method we use in this paper for comparison of FWER for linear regression, we did not consider it in our comparisons.
This work is motivated in part by the the Nefazodone CBASP trial data. The Nefazodone CBASP trial (Keller et al., 2000) was a randomized controlled trial conducted to compare the efficacy of three alternate treatments for patients with chronic depression. The study randomized 681 patients with non-psychotic chronic major depressive disorder (MDD) to either Nefazodone, cognitive behavioral-analysis system of psychotherapy (CBASP) or the combination of the two treatments. Analysis of the trial data showed the combination treatment to be superior to the two singleton treatments overall. We wanted to know whether this relationship held true for all major subsets of patients, and if not, to discover which patient characteristics would help to determine the optimal depression treatment for individual patients.
The remainder of this article is organized as follows: Section 2 gives background material on qualitative interactions. Sections 3 and 4 present a new algorithm designed to find variables useful for decision making along with measures to control the familywise error rate. Section 5 details our simulation results comparing the size and power of this new algorithm against two popular qualitative interaction tests. Section 6 illustrates these methods using data from the Nefazodone CBASP study and concluding remarks are given in Section 7.
2 Qualitative Interactions
We consider the search for qualitative interactions in the simplest setting where one must decide between two treatments. Let X = (X1,X2, …,Xp) be covariate observations about a subject and let A represent the treatment. If the response to the treatment is labeled R, then the goal in most clinical studies is to find the treatment a* for which
| (1) |
The idea of a ‘qualitative interaction’ was first introduced by (Peto 1982). Treatment covariate qualitative interactions are important because they result in a reversal of the treatment effect for some subset of patients. More formally, a variable Xj qualitatively interacts with the treatment, A, if there exists at least two distinct, non-empty sets, S1, S2 ⊂ space(Xj) for which
for all xj1 ∈ S1, and xj2 ∈ S2. These variables are useful for prescribing treatment since they help decipher which treatment is optimal for different subsets of patients.
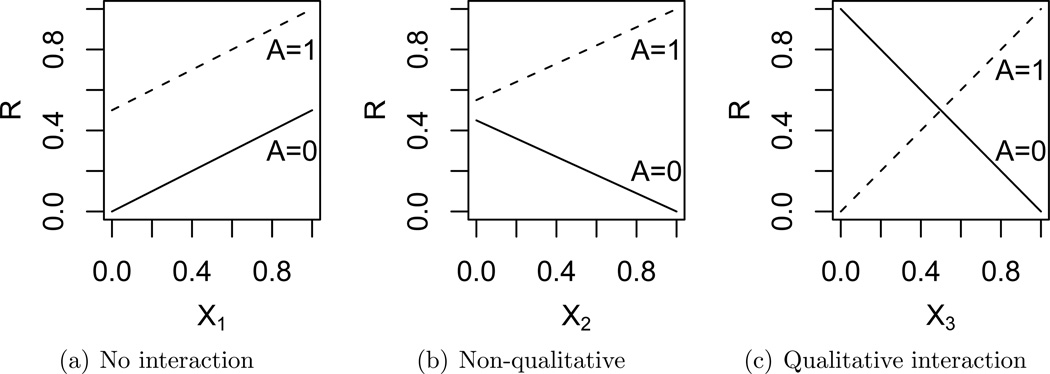
To illustrate this idea, see the plots in Figure 1(c). These plots depict different possible relationships between the conditional mean of R, A and a particular Xj, when averaging over all other Xi, i ≠ j. Figure 1(a), shows a variable, X1, which does not interact with the action. Figure 1(b) shows a variable, X2, that interacts with the action, A, but does not qualitatively interact with the action. Figure 1(c), shows a variable, X3, which qualitatively interacts with the action. This type of interaction is more important since it impacts the best choice of treatment.
Figure 1.
Plots demonstrating qualitative and non-qualitative interactions
There are currently only a few qualitative interaction tests that can be used to test a small number of pre-specified interactions (ALLHAT Collaborative Research Group, 2002, Gail and Simon, 1985, Krystal et al., 2001, Pan and Wolfe, 1997, Reynolds et al., 2006, Shuster and Van Eys, 1983, Silvapulle, 2001, Yan, 2004, Yan and Su, 2005). These tests were not designed to test a large number of variables in one setting. When controlling the error rate for multiple testing, these tests can be quite conservative (Gail and Simon, 1985, Piantadosi and Gail, 1993, Yan and Su, 2005). Yet the number of candidate variables a scientist might want to examine for possible qualitative interactions can be rather large for the average clinical trial. So any variable selection technique that looks for qualitative interactions should deal with this challenge of having to look through or test a large number of covariates.
The easiest way to examine a large group of variables for qualitative interactions is to consider each variable individually. Analyzing the data in this fashion can be misleading, however, if some of the candidate variables are correlated. A better option is to consider subsets of variables. Since the number of candidate variables is often quite large this prohibits considering all possible subsets. Thus, an intelligent way to determine which subsets to consider is needed.
As with most hypothesis tests, the risk of falsely discovering a qualitative interaction increases with the number of variables being tested. Failure to take this into account has lead to a large number clinical trials claiming discovery of new qualitative interactions which are later refuted. To counter this problem, much of the statistical literature suggests that the search for qualitative interactions should be limited to only pre-specified covariates and any qualitative interactions that are found should be initially mistrusted (Lagakos, 2001, Peto, 1982, Senn, 2001, Yusuf et al., 1991). However, this approach limits the ability of scientists to make new scientific discoveries that may be critical toward improving the practice of medicine. Thus, when doing variable selection for qualitative interactions, it is important to control for the number of false discoveries. There are many ways to control the number of false discoveries, but often they dramatically decrease the ability to find true qualitative interactions, especially as the number of variables grows.
Other difficulties arise when trying to do variable selection for qualitative interactions. Most of the qualitative interaction tests currently recommended are designed to test for certain types of qualitative interaction, such as between categorical variables and the treatment. These tests have a difficult time finding other types of qualitative interactions (Gail and Simon, 1985). A good variable selection method needs to successfully handle qualitative interactions with many different types of variables. Also predictive variables are important for estimation and variance reduction when looking for qualitative interactions. Successful variable selection methods should be able to utilize predictive variables, including strong predictive interactions that are not qualitative, in order to improve the power to detect qualitative interactions.
In the next section we present a new method for finding qualitative interactions that demonstrates better power than current methods yet also limits the false discovery rate.
3 AGV LASSO
The new method we propose utilizes methods and concepts from multiple fields of research to deal with the difficulties discussed in the prior section. A variable selection technique designed for prediction is used to sort the data and inform which subsets to try. By using a predictive variable selection technique, important predictive variables are smoothly integrated into the process.
Ideas from computer science and control theory are used to determine which subsets are most likely to contain important qualitative interactions. One way to look for qualitative interactions is to compare different strategies for choosing treatment. These strategies for choosing a treatment are often referred to as policies or individual treatment rules. A policy, π, is just a deterministic decision rule mapping the space of observations, X, to the space of the treatment, A. In other words, π outputs a treatment A = a given the observation X = x.
We compare policies via the expected mean response, called the Value of a policy (Sutton and Barto, 1998). Let the distribution of X be a fixed distribution f, and let the distribution of R given (X,A) be a fixed distribution g. Then when treatments are chosen according to a policy π, the trajectory (X,A,R) has distribution
If Eπ[] denotes the expectation over the above distribution, then the Value of π is
The optimal policy, π*, is defined as
or equivalently
Our variable selection algorithm focuses on the change in Value of the estimated optimal policy when a variable is added to the model:
| (2) |
where a* = arg maxa Ê[R|A = a]. This is similar to the quantity Parmigiani refers to as the value of information (Parmigiani, 2002).
The following is an overview of the algorithm.
Variable Selection Algorithm
Rank the variables: Rank the variables in (X,A * X) using Lasso. Define the variable rank to be the order in which the Lasso coefficients becomes non-zero, with the variable whose Lasso coefficient first becomes non-zero being ranked first.
Create nested subsets of variables: Create 2p nested subsets of the variables based on the rank order of the 2p variables in the previous step. Include Xj in the subset if XjA is included in the subset.
-
Select between subsets using Adjusted Gain in Value Criterion:
-
For each subset k = 1, …, 2p, estimate the maximal Value, e.g.
use subset k, A and a chosen prediction learning algorithm to estimate Ê;
estimate the optimal policy, ;
- estimate the Value of by:
- Select the subset, k*, that has the highest Adjusted Gain in Value (AGV) criterion:
where m = arg maxk V̂k and V̂0 is the estimated Value of the policy .
-
In the first two steps we seek a quick way to navigate through the space of all possible combinations of the variables (X,A * X). First we use Lasso (Tibshirani, 1996) to rank the variables. Lasso is a penalized regression procedure which returns a sparse, piecewise linear coefficient vector. It utilizes the L1-norm of the coefficient vector, |β|1, as its penalty function. The L1-norm causes some of the coefficients to be set exactly to zero. We fit the Lasso on (X, A * X, A), but leave the coefficient of A unconstrained by the L1 penalty function. The rankings for the variables in (X, A * X) are determined based on the order the variables enter the Lasso model. These rankings are then used to create nested subsets of the variables.
We rank all of the variables in the (X, A * X), including the main effects, X, because they may be strongly predictive of the response variable, R, and will help reduce variability in the estimates. Also, when testing for the interaction between Xj and A, researchers often prefer to maintain a hierarchical ordering (Wu and Hamada, 2000) and thus the main effect of the variable Xj is included. This helps to avoid finding spurious interactions that may appear because the main effect is important but is not included in the estimation.
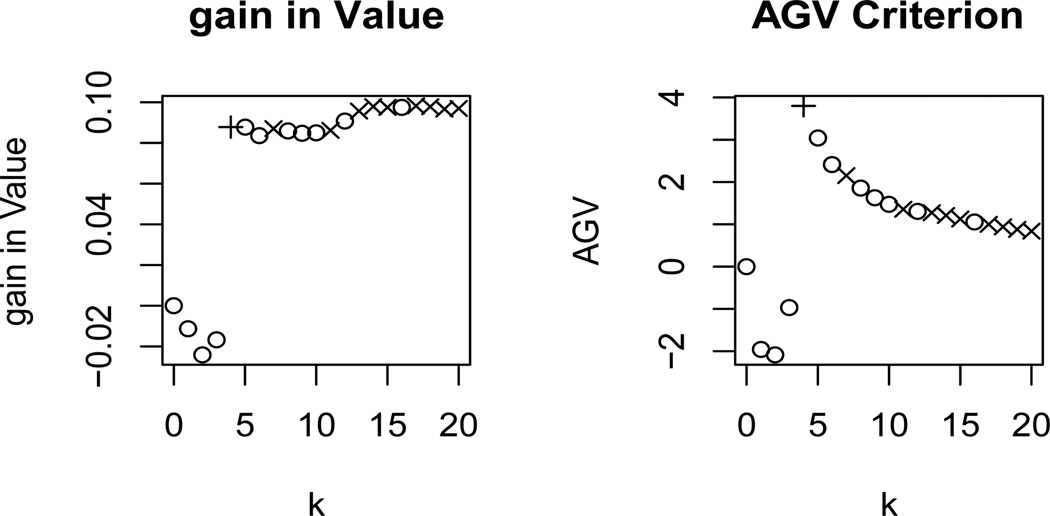
However, Lasso favors variables that are predictive, so we offset this by using the Adjusted Gain in Value (AGV) criterion to select the optimal subset. The AGV criterion provides a trade off between the complexity and the observed Value of each of the models. The criterion selects the subset of variables with the maximum proportionate increase in Value per variable. See Figure 2 for plots demonstrating the AGV criterion. The first plot in the figure shows the average gain in Value, V̂k − V̂0 for a simple toy example and the second plot shows the AGV for the same example. The points marked with a ◦ represent subsets in which a non-interaction variable was added to the model, the points marked with an × represent subsets in which an interaction has just been added to the model and the points marked with a + represent the subset in which the true qualitative interaction has just been added to the model. Ideally the gain in Value stays fairly stationary whenever a predictive variable is added to the model and increases when a qualitative interaction is added to the model. From the plot we see this is mostly true. The quotient, m*/k, acts as a penalty on the inclusion of variables that do not substantially increase the Value. We include main effect variables in the counts m* and k because each main effect variable that is included decreases the degrees of freedom. Also, the inclusion of main effects in the counts quickly deflates the quotient as k increases, leading to a less severe penalty on larger models. This is helpful since there are often many more useful predictive variables than qualitative interaction variables.
Figure 2.
Plots demonstrating the AGV Criterion.
The AGV criterion is similar to an adjusted R2 value as follows. The model with m = arg maxk V̂k variables is akin to a saturated model, because the addition of more variables does not improve the Value of the model. Thus the denominator is the observed maximum gain in value, among the different variable subsets, divided by m, an estimate of the degrees of freedom used to achieve that gain in Value. The numerator then measures the gain in Value of the intermediate model, the model with k variables, divided by k, the estimated degrees of freedom needed to achieve that gain in Value. So the AGV criterion tries to maximize the gain in Value for the current model relative to the maximum observed gain in value while penalizing for too many model parameters, much like adjusted R2 maximizes gain in variance explained by the model relative to the variance left in the residuals while penalizing for too many model parameters.
In the next section we address how to deal with the problem of controlling the number of false discoveries.
4 CONTROLLING THE FAMILY-WISE ERROR RATE
The family-wise error rate (FWER) is the probability of making at least one false discovery among all hypothesis when performing multiple testing procedures (Westfall and Young, 1993, Shaffer, 1995). In the context of variable selection for qualitative interactions the FWER is the probability of selecting at least one spurious qualitative interaction among all interaction variables being considered.
It may be acceptable in some instances to disregard the FWER when testing for qualitative interactions between treatment and a small number of pre-specified variables. That is, controlling just the per test error rate may be sufficient for the desired analysis. When performing a large number of hypothesis tests, however, it becomes a necessity to employ some method which adjusts for the multiplicity of testing to control the FWER or some other measure of multiplicity (e.g. false discovery rate). This is important to consider in variable selection, and in particular, variable selection for qualitative interactions. Naturally, these multiplicity correction methods decrease the power to find qualitative interactions. The failure to incorporate these methods in the variable selection process, however, may result in wasted resources and weakened credibility. We illustrate this issue in the next section.
We suggest a combination of bootstrap sampling and permutation thresholding to help control the FWER when using the algorithm proposed in Section 3. First we use bootstrap sampling (Efron and Tibshirani, 1993) of the original data to give a measure of replicability for each selected variable. The bootstrap samples allow us to determine the percentage of time each interaction variable is selected by the method (this is similar in spirit to Gong, 1986). These selection percentages, with a slight adjustment, can be thought of as pseudo test statistics for each interaction variable. We compute the adjusted selection percentages for each variable as follows.
Take B bootstrap samples of the original data.
Run variable selection algorithm and record the interaction variables that are selected along with the sign of the interaction coefficient for each bootstrap sample.
Calculate the adjusted selection percentage across the B bootstrap samples for each interaction variable: the absolute value of the number of times the interaction is selected with a positive coefficient minus the number of times an interaction is selected with a negative coefficient over the total.
This adjustment used in step 3 helps eliminate variables that, across the bootstrap samples, do not consistently interact in one direction with the action. Computing an adjusted selection percentage for each variable allows us to look at the individual contribution of each variable while taking into account other variables in the model. This provides for individual selection of variables, as opposed to group selection, which is important for controlling the number of false discoveries.
Second, we construct a permutation threshold to control for the number of false discoveries and determine which interaction variables to include in the final model. The threshold estimates the selection percentages we would expect to see if the data contained no interactions. To compute the permutation threshold:
Permute the X values of the X * A interactions in the (X,A,X * A) model matrix P times.
-
On each permuted data set
take B bootstrap samples of the permuted data;
run the variable selection algorithm and record the interaction variables that are selected along with the sign of the interaction coefficient for each bootstrap sample;
calculate the adjusted selection percentage across the B bootstrap samples for each interaction variable: the absolute value of the number of times the interaction is selected with a positive coefficient minus the number of times an interaction is selected with a negative coefficient;
record the maximum selection percentage observed across the p interaction variables.
Define the permutation threshold to be the 100(1 − α)th percentile over the P maximum selection percentages for each permuted data set.
In the first step toward determining this permutation threshold we permute the X values of the X * A interactions to remove all treatment covariate interaction effects on the response variable. We then rerun the bootstrap resampling and variable selection algorithm on the permuted data to determine what the adjusted selection percentages would be if no treatment covariate interactions existed. We record the maximum selection percentage across the p interaction variables to determine the level of selection for which at least one variable would enter the model. We then set the threshold to be the 100(1− α)th percentile over these P maximum selection percentages to ensure that the FWER is maintained at the level α. We chose all interaction variables whose adjusted selection percentage from the original data is greater than the permutation threshold.
Permutation-based multiplicity correction procedures are discussed in detail by Westfall and Young (1993). They have seen widespread use and success in many scientific applications such as micro-array analysis and medicine and even variable selection for prediction (Lindgren et al., 1996, Dudoit, Shaffer and Boldrick, 2003, Simon et al., 2004, Troendle, 2005).
In the next section we show simulation results testing the proposed variable selection algorithm with permutation threshold. We reference this method as AGV Lasso.
5 SIZE AND POWER COMPARISONS
We ran the AGV Lasso on realistically designed simulation data to test its performance and compared the results to two different methods suggested for formally testing for qualitative interactions.
In order to generate realistic simulation data, we randomly selected rows, with replacement from X, the observation matrix from the Nefazodone CBASP trial data. We generated new treatments, A, and new responses, R, that covered a wide variety of models. We report results for the following generative models:
Main effects of X only, no treatment effect and no interactions with treatment;
Main effects of X, moderate treatment effect and no interactions with treatment;
Main effects of X, moderate treatment effect, multiple small non-qualitative interactions, no qualitative interaction;
Main effects of X, moderate to large treatment effect, multiple moderate non-qualitative interactions, no qualitative interaction;
Main effects of X, small treatment effect, no non-qualitative interactions, small qualitative interaction with a binary variable;
Main effects of X, small treatment effect, no non-qualitative interactions, small qualitative interaction with a continuous variable;
Main effects of X, small treatment effect, multiple small non-qualitative interactions with treatment, small to moderate qualitative interaction with a binary variable;
Main effects of X, small treatment effect, multiple small to moderate non-qualitative interactions with treatment, small qualitative interaction with a continuous variable.
For each generative model, we used main effect coefficients for the variables X, estimated in an analysis of the real data set. In generative models 3–8 we randomly selected variables from the Nefazodone CBASP data for each treatment covariate interaction and used these same variables for each repetition. The treatment, qualitative interaction and non-qualitative interaction coefficients were set using a variant of Cohen’s D effect size measure (Cohen, 1988) shown below:
| (3) |
We altered this formula by replacing the marginal variance, V ar(R), with the conditional variance of the response V ar(R|X,A). However, we maintained the definitions of ‘small’ and ‘moderate’ effect sizes suggested by Cohen (1988) as D = 0.2 and D = 0.5 respectively. Thus the effects are slightly smaller than as in the traditional definition.
When implementing AGV Lasso on the data, we used linear models with intercept terms for all Ê[] estimations in Step 3. We also set the number of bootstrap samples to be B = 1000 and the number of data permutations to be P = 100.
We compared AGV Lasso to the likelihood ratio test (LRT) proposed by Gail and Simon (1985). The LRT is designed to test for a qualitative interaction between a binary treatment and a single categorical variable or a combination of categorical variables. Let δi, i = 1, …, I be the true treatment effects for each of the I categories of subjects and let Di, i = 1, …, I be independent normal estimates of those effects with variances .
Define
| (4) |
and
| (5) |
The LRT for testing the null hypothesis that δi ≥ 0 for all i or δi ≤ 0 for all i is then
| (6) |
where the constant c is chosen to ensure a significance level α. Gail and Simon (1985) give several values of c for different I and α. The in Equations 4 and 5 above can be replaced by a consistent estimate in large samples. The LRT test can be applied to interactions between continuous variables and treatment, but the continuous variable must be dichotomized first. This is one of the drawbacks to using the LRT as a variable selection technique.
We also compared AGV Lasso to the qualitative interaction test proposed by Shuster and Van Eys (1983). This test is based on joint confidence intervals and can be used to test for a qualitative interaction between a binary treatment and any type of covariate(s). Assume the response R is a linear function of the treatment and the covariates. For example it might be
| (7) |
where ε is an error term. The treatment difference for subjects with Xj = xj would be D(xj) = β2 + xiβ3. The parameter −β2/β3, is the value of Xj for which the treatments are equal. A asymptotic (1 − α)% confidence interval for −β2/β3 contains all values, xj for which
| (8) |
where Zα is the upper (100α) percent point of the standard normal curve and
| (9) |
is the asymptotic covariance matrix of β̂. All values falling in this confidence interval are values of Xj for which no significant treatment difference exists. The null hypothesis of no qualitative interaction is then rejected if the confidence interval for −β2/β3 is strictly contained in the range of Xj within the data. In other words the null hypothesis is rejected if there exists at least one xij in the range of Xj within the data for which there is a significant positive treatment effect and at least one xkj in the range of Xj within the data for which there is a significant negative treatment effect. We can express this formally as
| (10) |
where
| (11) |
and
| (12) |
The test can also be modified to test multiple covariates at one time (see Shuster and Van Eys, 1983). The Shuster-Van Eys test is more flexible because it allows one to test for qualitative interactions with both continuous and categorical variables, however, Gail and Simon found the test to be overly conservative with binary categorical variables (Gail and Simon, 1985). This is a drawback to using the Shuster-Van Eys test as a variable selection technique.
For each generative model, we ran AGV Lasso and the two qualitative interaction tests with and without corrections for multiplicity. We tried two multiplicity corrections for each qualitative interaction test. The first multiplicity correction method we tried was a Bonferroni correction due to its easy application with non-standard tests such as the LRT (Shaffer, 1995). This correction method tends to be conservative, however, so we also tried a permutation threshold similar to what we used in the new method. The permutation threshold was calculated in the same way except we replaced the selection percentages with the individual T-statistics (Equations 6 and 10) for each variable. We then selected all interaction variables whose T-statistic from the original data was greater than the permutation threshold.
We ran the analysis 200 times. We recorded the percentage of time each method selected one or more spurious interactions and the qualitative interaction (if one existed) to estimate the size and power of each method. The results are listed in Tables 1 and 2. True non-qualitative interactions that were selected were counted as spurious qualitative interactions for all of the methods. The percentage of time one or more spurious qualitative interactions was selected by each method over the 200 repetitions is listed in Table 1. The percentage of time the true qualitative interaction was selected by each method over the 200 repetitions is listed in Table 2. Note that since generative models 1–4 have no qualitative interactions with treatment, power results are not applicable to these models.
Table 1. Size Estimations.
The first two columns list the desired significance level and the method. AGVL stands for AGV Lasso, LRT stands for the Gail-Simon likelihood ratio test and SVE for the Shuster-Van Eys test, Bonferroni stands for a Bonferroni correction and permute stands for the permutation based multiplicity correction. The last eight columns give the percentage of time one or more spurious qualitative interactions was selected over the 200 repetitions for each generative model. Stared percentages fall outside the 95% confidence interval for the desired significance level
| Sig. Level |
Generative Model |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| α = .05 | LRT uncorrected | 13.0* | 7.5 | 5.5 | 0.0 | 22.5* | 17.0* | 20.0* | 14.5* |
| SVE uncorrected | 29.0* | 9.5* | 8.0 | 0.0 | 32.0* | 35.5* | 58.0* | 31.0* | |
| LRT Bonferroni | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | 0.0 | |
| SVE Bonferroni | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | 4.0 | 0.0 | |
| LRT permute | 6.0 | 4.5 | 3.0 | 0.0 | 8.5 | 7.5 | 11.0* | 9.5* | |
| SVE permute | 3.5 | 6.0 | 6.5 | 0.0 | 6.0 | 8.0 | 21.5* | 6.0 | |
| AGVL | 7.0 | 5.5 | 8.0 | 23.5* | 7.5 | 7.0 | 3.5 | 6.0 | |
| α = .1 | LRT uncorrected | 34.5* | 15.0* | 8.5 | 0.0 | 46.0* | 38.5* | 45.5* | 31.0* |
| SVE uncorrected | 54.5* | 29.5* | 29.5* | 1.0 | 65.5* | 62.0* | 74.0* | 56.0* | |
| LRT Bonferroni | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.5 | 0.0 | |
| SVE Bonferroni | 1.5 | 0.5 | 0.0 | 0.0 | 0.0 | 1.5 | 7.5 | 0.5 | |
| LRT permute | 7.0 | 8.5 | 7.0 | 0.0 | 11.5 | 10.0 | 15.0* | 11.5 | |
| SVE permute | 6.5 | 7.5 | 9.0 | 0.0 | 8.5 | 11.5 | 26.5* | 8.0 | |
| AGVL | 11.0 | 9.0 | 14.0 | 32.0* | 10.5 | 11.5 | 5.5 | 10.5 | |
Table 2. Power Estimations.
The first two columns list the desired significance level and the method. AGVL stands for AGV Lasso, LRT stands for the Gail-Simon likelihood ratio test and SVE for the Shuster-Van Eys test, Bonferroni stands for a Bonferroni correction and permute stands for the permutation based multiplicity correction. The last 4 columns give the percentage of time the true qualitative interaction was selected over the 200 repetitions for each generative model. Bolded percentages correlate with settings where the desired significance level was maintained.
| Sig. Level |
Generative Model |
||||
|---|---|---|---|---|---|
| Method | 5 | 6 | 7 | 8 | |
| α = .05 | LRT uncorrected | 12.0 | 8.5 | 52.0 | 12.5 |
| SVE uncorrected | 9.0 | 24.0 | 45.5 | 55.0 | |
| LRT Bonferroni | 0.5 | 0.5 | 8.5 | 0.0 | |
| SVE Bonferroni | 0.0 | 1.0 | 4.5 | 8.5 | |
| LRT permute | 6.5 | 5.0 | 34.0 | 7.5 | |
| SVE permute | 0.5 | 3.0 | 15.0 | 24.0 | |
| AGVL | 14.0 | 13.0 | 44.0 | 20.5 | |
| α = .1 | LRT uncorrected | 21.5 | 13.0 | 59.0 | 20.5 |
| SVE uncorrected | 18.0 | 33.0 | 58.0 | 66.5 | |
| LRT Bonferroni | 0.5 | 0.5 | 8.5 | 0.0 | |
| SVE Bonferroni | 0.5 | 2.5 | 8.5 | 12.5 | |
| LRT permute | 7.5 | 7.0 | 41.0 | 8.0 | |
| SVE permute | 1.0 | 3.5 | 19.0 | 30.0 | |
| AGVL | 17.5 | 16.5 | 49.0 | 26.5 | |
Looking over Table 1 we see that without the multiplicity correction, the two test methods have large Type I error rates. The Bonferroni correction method is far more conservative than the permutation based multiplicity correction. However, the permutation based multiplicity correction fails to maintain the desired significance level in a few of the scenarios for the qualitative interaction tests. Further study of these scenarios showed that this failure was due to moderate correlation between the true qualitative interaction variable and one or two other variables not contained in the generative model. Since both of the qualitative interaction tests allow testing of a qualitative interaction among multiple covariates, one could attempt to solve this problem by trying to test for subsets of variables rather than variables individually. However, there is no apparent way to determine which subsets to test and the tests do not attribute greater significance to different variables within a subset.
AGV Lasso appears to maintain the desired FWER in all settings but one. Under generative model 4 AGV Lasso fails to maintain the desired significance level. Upon closer examination we discovered the failure was due to over selection of the larger true non-qualitative interactions. We believe this is due to a combination of two factors, the importance of the non-qualitative interactions in obtaining an accurate estimate of the Value and the large treatment effect carried over in the permuted data sets leading to a smaller threshold. While this over selection of larger true non-qualitative interaction may not seem ideal, Oxman and Guyatt state that large non-qualitative interactions can be as important as qualitative interactions in many situations (Oxman and Guyatt, 1992). They state that it is important to know about substantial non-qualitative interactions because they can essentially lead to a qualitative interaction when looking at a more comprehensive outcome for treatment.
Table 2 shows that the LRT is better suited to find qualitative interactions with a categorical covariate, as would be expected. Whereas, the Shuster-Van Eys test is much better at finding qualitative interactions with a continuous covariate. The new method seems to have good comparative power for finding both types of qualitative interactions against the methods which control for the FWER.
Overall, we found that the new method performs better than the other two tests when controlling for the FWER. Al of the methods seem to have difficulty universally maintaining FWER, but the new method results in greater power to find the true qualitative interaction. While, the competing methods each have strengths, they seem to lack consistent performance to merit use as a generalized variable selection method for qualitative interactions.
6 EXAMPLE
We applied AGV Lasso along with the LRT test and the Shuster-Van Eys test to the Nefazodone CBASP trial (Keller et al., 2000) data introduced earlier. The trial was conducted to compare the efficacy of three alternate treatments for patients with chronic depression. We applied the methods to pinpoint if any of the patient characteristics might help to determine the optimal depression treatment for each patient.
The study randomized 681 patients with non-psychotic chronic major depressive disorder (MDD) to either Nefazodone, cognitive behavioral-analysis system of psychotherapy (CBASP) or the combination of the two treatments. For detailed study design and primary analysis see (Keller et al., 2000). We considered p = 61 baseline covariates for our observation matrix X. The outcome, R, was the 24-item Hamilton Rating Scale for Depression score (Hamilton, 1967), observed post treatment. As stated earlier, original analysis of the trial data showed the combination treatment to be superior to the two singleton treatments overall. For simplicity, we chose to only compare two treatments, the combination treatment and Nefazodone alone. Thus the data used in this analysis is a subset of the study consisting of the n = 440 patients who were randomized to either the combination treatment or Nefazodone alone.
Using a 90% permutation threshold, AGV Lasso selected two variables. Both variables had the same selection percentage of 21.9%, which was slightly higher than the 90% threshold of 21.1%. These variables were past history of Obsessive Compulsive Disorder and past history of Alcohol Dependence. No variables were selected by the SVE and LRT qualitative interaction tests using either multiplicity correction at α = 0.1.
We do not know whether there exists a true qualitative interaction between treatment and either of these variables since we do not have the generative model. However, closer examination of their relationship using the data set suggests that there is a strong non-qualitative interaction with past history of Obsessive Compulsive Disorder and a qualitative interaction with past history of Alcohol Dependence
7 DISCUSSION
Although multiple tests exist for evaluating qualitative interactions, they are designed to be used on a small number of covariates, often of a particular form. We have proposed a new technique that can be used to find qualitative interactions among a large number of covariates. We have included measures to ensure the FWE error rate is controlled for, an important characteristic for methods used in post-hoc analysis. The methods proposed here can be used with multiple different types of covariates without predetermining the best division into subsets.
In the future we plan to modify the way we permute the data in the permutation threshold so that it targets just the qualitative interactions instead of all interactions. We believe this would eliminate the over selection of non-qualitative interactions in data similar to generative model 4. We also think it would be useful to try replacing the least squares in the algorithm with other types of penalized regression models to allow for different types of response variables such as binary or survival. Our ultimate goal, however, is to develop a variable selection method for sequential decision making applications like SMART trials (Murphy, 2005).
ACKNOWLEDGEMENTS
We wish to thank Martin Keller and the investigators who conducted the trial ‘A Comparison of Nefazodone, the Cognitive Behavioral-analysis System of Psychotherapy, and Their Combination for Treatment of Chronic Depression’, for use of their data, and gratefully acknowledge Bristol-Myers Squibb for helping fund the study. We also acknowledge financial support from NIDA grants P50 DA10075, NIMH grant R01 MH080015 and NSF grants DMS 0505432 and DMS 0705532, and technical support from the Vice-Dean, Prof. A. John Rush, MD at Duke-NUS Graduate Medical School, Singapore
References
- The ALLHAT Officers and Coordinators for the ALLHAT Collaborative Research Group. Major outcomes in moderately hypercholesterolemic, hypertensive patients randomized to pravastatin vs usual care: The antihypertensive and lipid-lowering treatment to prevent heart attack trial(allhat-llt) Journal of the American Medical Association. 2002;288:2998–3007. doi: 10.1001/jama.288.23.2998. [DOI] [PubMed] [Google Scholar]
- Assmann SF, Pocock SJ, Enos LE, Kasten LE. Subgroup analysis and other (mis)uses of baseline data in clinical trials. The Lancet. 2000;355:1064–1069. doi: 10.1016/S0140-6736(00)02039-0. [DOI] [PubMed] [Google Scholar]
- Byar DP, Corle DK. Selecting optimal treatment in clinical trials using covariate information. Journal of Chronic Diseases. 1977;30:445–459. doi: 10.1016/0021-9681(77)90037-6. [DOI] [PubMed] [Google Scholar]
- Cohen J. Statistical Power Analysis for the Behavioral Sciences. 2nd edn. Hillsdale, NJ: Lawrence Earlbaum Associates; 1988. [Google Scholar]
- Dudoit S, Shaffer JP, Boldrick JC. Multiple hypothesis testing in microarray experiments. Statistical Science. 2003;18:71–103. [Google Scholar]
- Efron B, Tibshirani R. An Introduction to the Bootstrap. New York: Chapman and Hall; 1993. [Google Scholar]
- Evans WE, Relling MV. Moving towards individualized medicine with pharmacogenomics. Nature. 2004;429:464–464. doi: 10.1038/nature02626. [DOI] [PubMed] [Google Scholar]
- Gail M, Simon R. Testing for qualitative interactions between treatment effects and patient subsets. Biometrics. 1985;41:361–372. [PubMed] [Google Scholar]
- Gong G. Cross-validation, the jackknife, and bootstrap: Excess error in forward logistic regression. Journal of the American Statistical Association. 1986;81:108–113. [Google Scholar]
- Gunter L, Chernick MR, Sun J. A simple method for variable selection in regression with respect to treatment selection. Pakistan Journal of Statistics and Operations Research. 2011;7 (to appear). [Google Scholar]
- Hamilton M. Development of a rating scale for primary depressive illness. British. Journal of Social and Clinical Psychology. 1967;6:278–296. doi: 10.1111/j.2044-8260.1967.tb00530.x. [DOI] [PubMed] [Google Scholar]
- Keller MB, McCullough JP, Klein DN, Arnow B, Dunner DL, Gelenberg AJ, Marekowitz JC, Nemeroff CB, Russell JM, Thase ME, Trivedi MH, Zajecka J. A comparison of nefazodone, the cognitive behavioral-analysis system of psychotherapy, and their combination for treatment of chronic depression. New England Journal of Medicine. 2000;342:331–336. doi: 10.1056/NEJM200005183422001. [DOI] [PubMed] [Google Scholar]
- Krystal JH, Cramer JA, Krol WF, Kirket GF, Rosenheck R. Naltrexone in the treatment of alcohol dependence. New England Journal of Medicine. 2001;345:1734–1739. doi: 10.1056/NEJMoa011127. [DOI] [PubMed] [Google Scholar]
- Lagakos S. The challenge of subgroup analyses-reporting without distorting. New England Journal of Medicine. 2006;354:1667–1669. doi: 10.1056/NEJMp068070. [DOI] [PubMed] [Google Scholar]
- Lindgren F, Hansen B, Karcher W, Sjostrom M, Erik L. Model validation by permutation tests: Applications to variable selection. Journal of Chemometrics. 1996;10:521–532. [Google Scholar]
- Murphy SA. An experimental design for the development of adaptive treatment strategies. Statistics in Medicine. 2005;24:1455–1481. doi: 10.1002/sim.2022. [DOI] [PubMed] [Google Scholar]
- Pan G, Wolfe DA. Test for qualitative interaction of clinical significance. Statistics in Medicine. 1997;16:1645–1652. doi: 10.1002/(sici)1097-0258(19970730)16:14<1645::aid-sim596>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- Parmigiani G. Modeling in Medical Decision Making: a Baysian Approach. West sussex, England: Wiley; 2002. [Google Scholar]
- Peto R. Statistical aspects of cancer trials. In: Halnan KE, editor. Treatment of Cancer. London, UK: Chapman; 1982. pp. 867–871. [Google Scholar]
- Piantadosi S, Gail MH. A comparison of the power of two tests for qualitative interactions. Statistics in Medicine. 1993;12:1239–1248. doi: 10.1002/sim.4780121305. [DOI] [PubMed] [Google Scholar]
- Oxman AD, Guyatt GH. A consumers guide to subgroup analysis. Annuls of Internal Medicine. 1992;116:78–84. doi: 10.7326/0003-4819-116-1-78. [DOI] [PubMed] [Google Scholar]
- Reynolds CF, Dew MA, Pollock BG, Mulsant BH, Frank E, Miller MD, Houck PR, Mazumdar S, Butters MA, Stack JA, Schlernitzauer MA, Whyte EM, Gildengers A, Karp J, Lenze E, Szanto K, Bensasi S, Kupfer DJ. Maintenance treatment of major depression in old age. New England Journal of Medicine. 2006;345:1130–1138. doi: 10.1056/NEJMoa052619. [DOI] [PubMed] [Google Scholar]
- Sade W, Dai Z. Pharmacogenetics/genomics and personalized medicine. Human Molucular Genetics. 2005;14:R207–R214. doi: 10.1093/hmg/ddi261. [DOI] [PubMed] [Google Scholar]
- Senn SJ. Individual therapy: new dawn or false dawn. Drug Information Journal. 2001;35:1479–1494. [Google Scholar]
- Shaffer JS. Multiple hypothesis testing. Annual Review of Psychology. 1995;46:561–584. [Google Scholar]
- Shuster J, Van Eys J. Interaction between prognostic factors and treatment. Controlled Clinical Trials. 1983;4:209–214. doi: 10.1016/0197-2456(83)90004-1. [DOI] [PubMed] [Google Scholar]
- Silvapulle MJ. Test against qualitative interaction: exact critical values and robust test. Biometrics. 2001;57:1157.e–1165.e. doi: 10.1111/j.0006-341x.2001.01157.x. 2001. [DOI] [PubMed] [Google Scholar]
- Simon RM, Korn EL, McShane LM, Radmacher MD, Wright GW, Zhao Y. Design and analysis of DNA microarray investigations. New York: Springer; 2004. [Google Scholar]
- Sutton RS, Barto AG. Reinforcement Lerning: An Introduction. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B. 1996;58:267–288. [Google Scholar]
- Troendle JF. Multiple comparisons between two groups on multiple Bernoulli outcomes while accounting for covariates. Statistics in Medicine. 2005;24:3581–3591. doi: 10.1002/sim.2202. [DOI] [PubMed] [Google Scholar]
- Westfall PH, Young SS. Resampling-based Multiple testing. New York, NY: John Wiley and Sons; 1993. [Google Scholar]
- Wu CF, Hamada M. Experiments: Planning, Analysis, and Parameter Design Optimization. New York: Wiley; 2000. [Google Scholar]
- Yan X. Test for qualitative interaction in equivalence trials when the number of centers is large. Statistics in Medicine. 2004;23:711–722. doi: 10.1002/sim.1658. [DOI] [PubMed] [Google Scholar]
- Yan X, Su X. Testing for Qualitative Interaction. In: Chow SC, editor. Encyclopedia of Biopharmaceutical Statistics. Informa Health Care; 2005. [Google Scholar]
- Yusuf S, Wittes J, Probstfield J, Tyrole HA. Analysis and interpretation of treatment effects in subgroups of patients in randomized clinical trials. Journal of the American Medical Association. 1991;266:93–98. [PubMed] [Google Scholar]