Abstract
Background Many meta-analyses contain only a small number of studies, which makes it difficult to estimate the extent of between-study heterogeneity. Bayesian meta-analysis allows incorporation of external evidence on heterogeneity, and offers advantages over conventional random-effects meta-analysis. To assist in this, we provide empirical evidence on the likely extent of heterogeneity in particular areas of health care.
Methods Our analyses included 14 886 meta-analyses from the Cochrane Database of Systematic Reviews. We classified each meta-analysis according to the type of outcome, type of intervention comparison and medical specialty. By modelling the study data from all meta-analyses simultaneously, using the log odds ratio scale, we investigated the impact of meta-analysis characteristics on the underlying between-study heterogeneity variance. Predictive distributions were obtained for the heterogeneity expected in future meta-analyses.
Results Between-study heterogeneity variances for meta-analyses in which the outcome was all-cause mortality were found to be on average 17% (95% CI 10–26) of variances for other outcomes. In meta-analyses comparing two active pharmacological interventions, heterogeneity was on average 75% (95% CI 58–95) of variances for non-pharmacological interventions. Meta-analysis size was found to have only a small effect on heterogeneity. Predictive distributions are presented for nine different settings, defined by type of outcome and type of intervention comparison. For example, for a planned meta-analysis comparing a pharmacological intervention against placebo or control with a subjectively measured outcome, the predictive distribution for heterogeneity is a log-normal (−2.13, 1.582) distribution, which has a median value of 0.12. In an example of meta-analysis of six studies, incorporating external evidence led to a smaller heterogeneity estimate and a narrower confidence interval for the combined intervention effect.
Conclusions Meta-analysis characteristics were strongly associated with the degree of between-study heterogeneity, and predictive distributions for heterogeneity differed substantially across settings. The informative priors provided will be very beneficial in future meta-analyses including few studies.
Keywords: Meta-analysis, heterogeneity, intervention studies, Bayesian analysis
Background
Systematic reviews of randomized trials provide the best evidence on the effectiveness of health-care interventions. Within systematic reviews, results from multiple studies are often combined statistically in a meta-analysis. Differences among the results combined in a meta-analysis arise through genuine differences in the study designs, through differences in the conduct of the research and deviation from the planned designs (biases) and through random variation. In the presence of heterogeneity, it is often considered appropriate to perform a random-effects meta-analysis, in which both the underlying average intervention effect and the between-study heterogeneity are estimated.1,2 Many meta-analyses contain only a small number of studies, and this makes it difficult to estimate the between-study variance. A conventional random-effects meta-analysis does not acknowledge the (often substantial) uncertainty in the estimate of the between-study variance.3 A Bayesian meta-analysis offers the benefits of allowing appropriately for this uncertainty, offering a flexible framework for more complex meta-analyses and facilitating prediction of effects in future studies.4–7 Ideally, a Bayesian meta-analysis should be informed by a realistic prior distribution for the between-study variance, based on external evidence.8
In principle, meta-analysts could gather evidence on the extent of heterogeneity observed in previous meta-analyses in similar settings, and construct an informative prior distribution for the degree of heterogeneity in their own meta-analysis. However, this is unrealistic in practice. It would therefore be useful if informative prior distributions relevant to a variety of settings were constructed in advance and made available for all to use.
By modelling the data from a large collection of meta-analyses, we have estimated the influence of meta-analysis characteristics on between-study heterogeneity and have obtained predictive distributions for the degree of heterogeneity expected in particular settings. The distributions presented can be used directly in new meta-analyses as ‘off-the-shelf’ prior distributions.
Methods
The contents of the CDSR (Issue 1, 2008) were provided to us by the Nordic Cochrane Centre for use in this research. Many Cochrane reviews include multiple meta-analyses, which correspond to comparisons of different pairs of interventions or the examination of different outcomes within the same overall research topic. For example, a review evaluating antidepressants could report separate meta-analyses comparing each of several antidepressants against placebo, with respect to depression symptoms and adverse effects. In our analyses, we included all meta-analyses of binary outcomes, which reported data from two or more studies. In some cases, review authors had entered data for a set of studies but had chosen not to combine results numerically in a meta-analysis. We included these ‘potential meta-analyses’ as meta-analyses, to maximize the amount of information available, and because the degree of between-study heterogeneity may have influenced the decision not to perform a meta-analysis.
Our focus was on overall heterogeneity in each meta-analysis, and therefore study data were pooled across subgroups, where these had been defined by review authors. For example, subgroups might be defined by geographical location, or by dose of treatment. In some Cochrane reviews, the ‘subgroups’ defined within a meta-analysis were not mutually exclusive, and the same data from a study were included in more than one ‘subgroup’. We therefore checked for duplications by matching study identifiers, and extracted data for only the first occurrence of each study in each meta-analysis.
Classification process
For each meta-analysis in each systematic review, we classified the type of outcome, the types of intervention compared and the medical specialty to which the research question related. The details of this initial stage of work are described elsewhere.9 The outcomes, interventions and medical specialties were assigned to fairly narrow categories (see Table 1 footnote), which we grouped together later in our analyses. We based outcome categories on those used by Wood10 and those proposed by the Foundation for Health Services Research.11 To classify interventions, we used categories based on the Health Research Classification System developed by the UK Clinical Research Collaboration (UKCRC).12 For medical specialties, we used a taxonomy from the UK National Institute for Health and Clinical Excellence (NICE).13 Our initial sets of categories were modified after testing the classification process in a pilot study that included 50 systematic reviews.
Table 1.
Distribution of outcome types, intervention comparison types and medical specialty types among the 14 886 meta-analyses in the data set
| Number (%) of meta-analyses | |
|---|---|
| Outcome typesa | |
| All-cause mortality | 1132 (8) |
| Semi-objective outcomesb | 4586 (31) |
| Subjective outcomesc | 9106 (61) |
| Intervention comparison types | |
| Pharmacological vs placebo/control | 5599 (38) |
| Pharmacological vs pharmacological | 4118 (28) |
| Non-pharmacologicald vs placebo/ control | 2412 (16) |
| Non-pharmacologicald vs non-pharmacologicald | 2442 (16) |
| Non-pharmacologicald vs pharmacological | 315 (2) |
| Medical specialty | |
| Cancer | 689 (5) |
| Cardiovascular | 1192 (8) |
| Central nervous system/ musculoskeletal | 1210 (8) |
| Digestive system | 1464 (10) |
| Infectious diseases | 780 (5) |
| Mental health and behavioural conditions | 1977 (13) |
| Obstetrics and gynaecology | 3905 (26) |
| Pathological conditions | 414 (3) |
| Respiratory diseases | 1310 (9) |
| Urogenital | 932 (6) |
| Other specialties | 1013 (7) |
aSixty-two meta-analyses were excluded where the outcome did not fit into any of our pre-defined categories and was classified as ‘Other’.
bSemi-objective outcomes include cause-specific mortality, major morbidity event, composite mortality/morbidity, obstetric outcomes, internal structure, external structure, surgical device success/failure, withdrawals/drop-outs, resource use, hospital stay/process measures.
cSubjective outcomes include pain, mental health outcomes, dichotomous biological markers, quality of life/functioning, consumption, satisfaction with care, general physical health, adverse events, infection/new disease, continuation/termination of condition being treated, composite endpoint (including at most one mortality/morbidity endpoint).
dNon-pharmacological interventions include interventions classified as medical devices, surgical, complex, resources and infrastructure, behavioural, psychological, physical, complementary, educational, radiotherapy, vaccines, cellular and gene and screening.
Wherever possible, outcomes and interventions were classified on the basis of short text descriptions provided by the review authors, together with the title of the systematic review. Where additional information was required, we consulted descriptions of the outcomes, interventions and participants in the five studies receiving greatest weight in the meta-analysis. Medical specialties were classified usually on the basis of the title of the systematic review, or on the review abstract if clarification was needed.
Statistical analysis
We used hierarchical models to analyse the study data from all included meta-analyses simultaneously, while investigating the effects of meta-analysis characteristics on the level of between-study heterogeneity. Within each meta-analysis, a random-effects model with binomial within-study likelihoods was fitted to the binary outcome data from each study on the log odds ratio (OR) scale. Across meta-analyses, a hierarchical regression model was fitted to the log-transformed values of underlying between-study heterogeneity variance 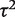 , assuming a normal distribution for the residual variation. As covariates in the regression model, we included indicators of outcome type, intervention comparison type and medical specialty, and number of studies in the meta-analysis (log-transformed, as a continuous covariate). Heterogeneity was assumed to vary across meta-analyses within pair-wise comparisons with separate variances for different outcome types. Heterogeneity was also assumed to vary across pair-wise comparisons, with separate variances for different intervention comparison types. The algebraic form of the models is provided in the Supplementary Appendix S1.
, assuming a normal distribution for the residual variation. As covariates in the regression model, we included indicators of outcome type, intervention comparison type and medical specialty, and number of studies in the meta-analysis (log-transformed, as a continuous covariate). Heterogeneity was assumed to vary across meta-analyses within pair-wise comparisons with separate variances for different outcome types. Heterogeneity was also assumed to vary across pair-wise comparisons, with separate variances for different intervention comparison types. The algebraic form of the models is provided in the Supplementary Appendix S1.
All models were fitted within a Bayesian framework, and estimation was achieved using the WinBUGS software.14 Results were based on 50 000 iterations following a burn-in of 5000 iterations, which was sufficient to achieve convergence. Model selection was performed using the deviance information criterion (DIC).15 We declared N(0,10) priors for all regression coefficients, and declared Uniform(0,2) priors for the standard deviations of the random effects representing variation in heterogeneity across outcomes within comparisons and across pair-wise comparisons.
On the basis of the findings from the above analyses, we chose to focus on a small set of three outcome types and three intervention comparison types. For each pair-wise combination among these, we obtained a predictive distribution for the between-study heterogeneity 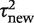 expected in a future meta-analysis in this setting. A log-normal distribution was fitted to each predictive distribution, using the posterior mean and standard deviation for
expected in a future meta-analysis in this setting. A log-normal distribution was fitted to each predictive distribution, using the posterior mean and standard deviation for  . This process provides parametric distributions approximating the predictive distributions obtained from the full Bayesian model, so they can be easily summarized and reported for use in future meta-analyses.
. This process provides parametric distributions approximating the predictive distributions obtained from the full Bayesian model, so they can be easily summarized and reported for use in future meta-analyses.
Results
Characteristics of data set
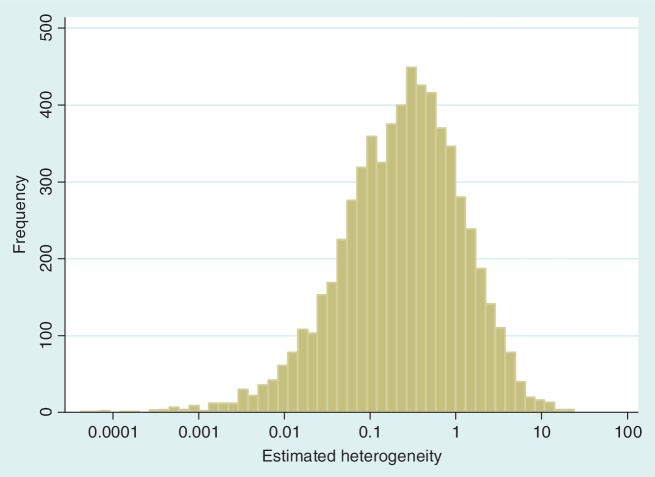
The data set includes 14 886 meta-analyses from 1991 Cochrane reviews, containing data from 77 237 individual studies in total. Table 2 shows the structure of the data set. The number of meta-analyses per pair-wise comparison ranged from 1 to 43 with a median of 2. The median number of studies included in a meta-analysis was 3 with range 2–294 (a meta-analysis had to contain at least two studies to be eligible). The median number of participants in the studies in the meta-analyses varied substantially, from studies of only two individuals to very large studies containing over a million individuals. In 8595 (57%) of the meta-analyses, the method of moments estimate 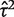 for between-study heterogeneity was set to 0. Figure 1 shows the distribution of the non-zero estimates. We note that zero estimates
for between-study heterogeneity was set to 0. Figure 1 shows the distribution of the non-zero estimates. We note that zero estimates 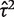 are often obtained when true between-study heterogeneity
are often obtained when true between-study heterogeneity 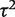 is small but positive.
is small but positive.
Table 2.
Structure of data set: number of pair-wise comparisons per review, meta-analyses per comparison, studies per meta-analysis and size of study
| N | Min | 25% Percentile | Median | 75% Percentile | Max | |
|---|---|---|---|---|---|---|
| Number of comparisons per review | 1991 reviews | 1 | 1 | 1 | 2 | 20 |
| Number of meta-analyses per comparison | 3884 comparisons | 1 | 1 | 2 | 5 | 43 |
| Number of studies per meta-analysis | 14 886 meta-analyses | 2 | 2 | 3 | 6 | 294 |
| Sample size | 77 237 studies | 2 | 50 | 102 | 243 | 1 242 071 |
Figure 1.
Distribution of non-zero estimates for between-study heterogeneity variance (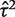 ), plotted on log scale
), plotted on log scale
Table 1 presents the frequencies of different outcome types, intervention comparison types and medical specialties among the meta-analyses included in this data set. We regarded all-cause mortality as the most objectively assessed outcome, and this was used in 8% of the meta-analyses. All other outcome categories were grouped together as ‘semi-objective outcomes’ or ‘subjective outcomes’; the details are given in Table 1. Each meta-analysis compares a pair of interventions, which were classified separately according to a list of 17 categories (pharmacological, psychological, surgical etc.).9 In this article, we group these into broader categories: pharmacological, non-pharmacological and placebo/control. Meta-analyses comparing pharmacological interventions against placebo or control were the most frequent (38%), whereas meta-analyses comparing pharmacological against pharmacological interventions (i.e. head-to-head comparisons) formed the second largest group (28%). The frequency of different medical specialties is shown in Table 1. Obstetrics and gynaecology was the most frequently occurring category (26% of meta-analyses).
Comparing heterogeneity across meta-analysis types
Ratios of heterogeneity variances 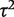 between different types of meta-analysis are presented in Table 3. Meta-analyses in which the outcome was all-cause mortality displayed substantially lower between-study heterogeneity than other meta-analyses; the ratio of variances was estimated as 0.17 (95% CI 0.10–0.26). Heterogeneity was substantially lower in meta-analyses assessing all-cause mortality compared with those assessing subjective outcomes, and also lower in meta-analyses of semi-objective outcomes than in meta-analyses of subjective outcomes.
between different types of meta-analysis are presented in Table 3. Meta-analyses in which the outcome was all-cause mortality displayed substantially lower between-study heterogeneity than other meta-analyses; the ratio of variances was estimated as 0.17 (95% CI 0.10–0.26). Heterogeneity was substantially lower in meta-analyses assessing all-cause mortality compared with those assessing subjective outcomes, and also lower in meta-analyses of semi-objective outcomes than in meta-analyses of subjective outcomes.
Table 3.
Ratios of variances representing comparisons of between-trial heterogeneity 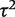 among different types of meta-analysis, according to intervention comparison, outcome, medical specialty and size (number of trials)
among different types of meta-analysis, according to intervention comparison, outcome, medical specialty and size (number of trials)
| Comparisons based on meta-analysis characteristics | Ratio of 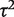 (95% CI) (95% CI) |
|---|---|
| Outcome typesa | |
| All-cause mortality / All other outcomes | 0.17 (0.10–0.26) |
| All-cause mortality / Subjectiveb outcomes | 0.14 (0.07–0.22) |
| Semi-objectiveb outcomes / Subjectiveb outcomes | 0.45 (0.37–0.55) |
| Intervention comparison typesc | |
| Pharmacological vs placebo/control / Non-pharmacologicalb (any) | 0.94 (0.76–1.13) |
| Pharmacological vs pharmacological / Non-pharmacologicalb (any) | 0.75 (0.58–0.95) |
| Medical specialty typesd | |
| Cancer / Obstetrics and gynaecology | 0.95 (0.65–1.35) |
| Cardiovascular / Obstetrics and gynaecology | 0.55 (0.40–0.75) |
| Central nervous system or musculoskeletal disorders / Obstetrics and gynaecology | 0.85 (0.60–1.16) |
| Digestive system / Obstetrics and gynaecology | 1.23 (0.93–1.58) |
| Infectious diseases / Obstetrics and gynaecology | 1.46 (1.05–1.96) |
| Mental health and behavioural conditions / Obstetrics and gynaecology | 1.03 (0.80–1.31) |
| Pathological conditions / Obstetrics and gynaecology | 1.56 (1.09–2.33) |
| Respiratory diseases / Obstetrics and gynaecology | 0.70 (0.51–0.98) |
| Urogenital / Obstetrics and gynaecology | 1.81 (1.28–2.59) |
| Other specialties / Obstetrics and gynaecology | 1.14 (0.86–1.51) |
| Number of studies in meta-analysis: ratio corresponding to 5-study increasee | 1.02 (1.00–1.04) |
aAnalysis adjusted for intervention comparison type and medical specialty type.
bSubjective and semi-objective outcomes and non-pharmacological interventions defined in Table 2.
cAnalysis adjusted for outcome type and medical specialty type.
dAnalysis adjusted for intervention comparison type and outcome type.
eAnalysis adjusted for intervention comparison type, outcome type and medical specialty type.
In terms of intervention types, heterogeneity was on average lowest in pharmacological vs pharmacological meta-analyses, with evidence of a difference compared with meta-analyses involving non-pharmacological interventions. Heterogeneity also tended to be lower in meta-analyses comparing pharmacological vs placebo/control than in non-pharmacological meta-analyses, but the confidence interval for the ratio included the null value 1.
Overall, there was no evidence of differences in between-study heterogeneity among medical areas (inclusion of medical specialty indicators led to worse model fit, as assessed by the DIC). Meta-analysis size was found to have a small effect on between-study heterogeneity; the 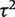 ratio corresponding to a doubling in the number of studies was estimated as 1.11 (95% CI 1.03–1.18).
ratio corresponding to a doubling in the number of studies was estimated as 1.11 (95% CI 1.03–1.18).
To explore sensitivity to our choices in constructing the data set, we performed repeats of the primary analysis reported in Table 3, within three different versions of the data set: firstly, we excluded 529 ‘potential meta-analyses’ which had chosen not to pool results; second, we used data from the first subgroup only, for 5186 meta-analyses including subgroups; third, we excluded 5081 meta-analyses including only two studies. In each analysis, the central estimates for the ratios comparing different types of meta-analyses remained similar to those reported, whereas the 95% CIs widened to reflect the smaller sample size.
Predictive distributions for heterogeneity in future meta-analyses
We first reported a predictive distribution for between-study heterogeneity in a future meta-analysis in a general setting. This was obtained from a hierarchical model fitted to all meta-analyses in the data set, including no meta-analysis characteristics as covariates. The fitted distribution for 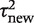 was estimated as log-normal (−2.56,1.742), which has median 0.08 and 95% range 0.003–2.34 on the untransformed
was estimated as log-normal (−2.56,1.742), which has median 0.08 and 95% range 0.003–2.34 on the untransformed 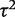 scale.
scale.
Table 4 summarizes a set of log-normal distributions fitted to the predictive distributions for the between-study heterogeneity expected in a future meta-analysis in each of nine different settings, defined by outcome type and intervention comparison type. The differences among these fitted distributions reflect the findings reported in Table 3. There are substantial differences across the three outcome types; the fitted distributions for meta-analyses of an all-cause mortality outcome have much lower medians and 97.5% quantiles, whereas the predictive distributions for a subjective outcome have the highest medians and 97.5% quantiles. Differences among the three types of intervention comparison considered are smaller, but show a consistent pattern within each outcome type: the lowest levels of heterogeneity are expected in meta-analyses of pharmacological vs pharmacological comparisons and the highest levels in comparisons that assess a non-pharmacological intervention.
Table 4.
Predictive distributionsa obtained for the between-study heterogeneity 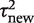 in a future meta-analysis, across nine different settings
in a future meta-analysis, across nine different settings
| Outcome type | Intervention comparison type |
||
|---|---|---|---|
| Pharmacological vs Placebo/Control | Pharmacological vs Pharmacological | Non-pharmacologicalb (any) | |
| All-cause mortality | Log-normal (−4.06,1.452): | Log-normal (−4.27,1.482): | Log-normal (−3.93,1.512): |
| median = 0.017; 95% range = (0.001–0.30) | median = 0.014; 95% range = (0.0008–0.25) | median = 0.020; 95% range = (0.001–0.38) | |
| Semi-objectiveb | Log-normal (−3.02,1.852): | Log-normal (−3.23,1.882): | Log-normal (−2.89,1.912): |
| median = 0.049; 95% range = (0.001–1.83) | median = 0.040; 95% range = (0.001–1.58) | median = 0.056; 95% range = (0.001–2.35) | |
| Subjectiveb | Log-normal (−2.13,1.582): | Log-normal (−2.34,1.622): | Log-normal (−2.01,1.642): |
| median = 0.12; 95% range = (0.005–2.63) | median = 0.096; 95% range = (0.004–2.31) | median = 0.13; 95% range = (0.005–3.33) | |
aFitted distributions reported as 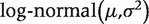 , where µ and σ are the mean and SD on the log scale. We also report medians and 2.5% and 97.5% quantiles on the untransformed scale.
, where µ and σ are the mean and SD on the log scale. We also report medians and 2.5% and 97.5% quantiles on the untransformed scale.
bSubjective and semi-objective outcomes and non-pharmacological interventions defined in Table 2.
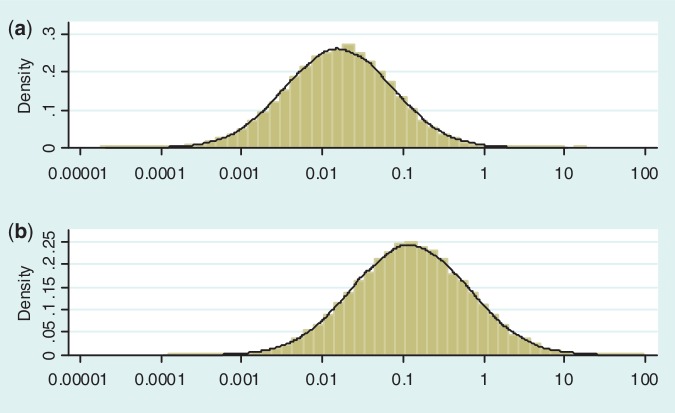
Figure 2 illustrates the predictive distributions for between-study heterogeneity in two very different settings: a pharmacological vs placebo/control meta-analysis with an all-cause mortality outcome; and a non-pharmacological meta-analysis with a subjective outcome. The empirical distribution obtained from the full Bayesian model is plotted as a histogram in each case, whereas the black line represents the fitted log-normal distribution (as summarized in Table 4). For a pharmacological vs placebo/control meta-analysis measuring all-cause mortality, the predictive distribution for 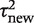 gives little support to values above 0.2, whereas the predictive distribution for a non-pharmacological meta-analysis measuring a subjective outcome gives moderate support to heterogeneity values up to 1. To illustrate the implications for variability in ORs, we calculate expected 95% ranges for underlying ORs in pharmacological vs placebo/control meta-analyses assessing different outcome types. Based on the median-predicted values for
gives little support to values above 0.2, whereas the predictive distribution for a non-pharmacological meta-analysis measuring a subjective outcome gives moderate support to heterogeneity values up to 1. To illustrate the implications for variability in ORs, we calculate expected 95% ranges for underlying ORs in pharmacological vs placebo/control meta-analyses assessing different outcome types. Based on the median-predicted values for  (Table 4), we expect ORs with 95% ranges of 0.77–1.29 for all-cause mortality, 0.65–1.54 for semi-objective outcomes and 0.51–1.97 for subjective outcomes, assuming a central value of 1.
(Table 4), we expect ORs with 95% ranges of 0.77–1.29 for all-cause mortality, 0.65–1.54 for semi-objective outcomes and 0.51–1.97 for subjective outcomes, assuming a central value of 1.
Figure 2.
Predictive distributions for heterogeneity variance (plotted on log scale) in: (a) pharmacological vs placebo/control meta-analysis measuring all-cause mortality; (b) non-pharmacological meta-analysis measuring a subjective outcome
Application to an example meta-analysis
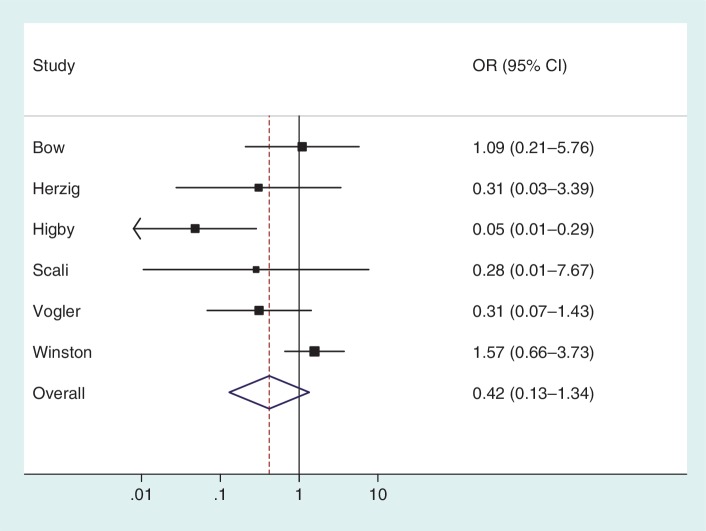
To illustrate the use of an informative prior for heterogeneity, we re-analysed the data from a published meta-analysis including six studies.16 The meta-analysis evaluates the effectiveness of granulocyte (white blood cell) transfusions for treating patients with neutropenia or neutrophil dysfunction, who are at high risk of serious infections and death. In a conventional random-effects meta-analysis of these data (Figure 3), the heterogeneity estimate was high (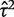 = 1.27, I2 = 65%) but imprecisely estimated (Table 5). Since few studies were available, the
= 1.27, I2 = 65%) but imprecisely estimated (Table 5). Since few studies were available, the 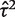 estimate was strongly influenced by the extreme result from the Higby study, and would reduce to 0.13 if this study were excluded.
estimate was strongly influenced by the extreme result from the Higby study, and would reduce to 0.13 if this study were excluded.
Figure 3.
Conventional random-effects meta-analysis combining results from six studies on the effectiveness of granulocyte (white blood cell) transfusions for prevention of mortality in patients with neutropenia or neutrophil dysfunction16
Table 5.
Application to example meta-analyses: comparison of results obtained from conventional and Bayesian approaches to random-effects meta-analysis
| Combined OR estimate (95% CI) | Heterogeneity variance estimate 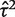 (95% CI) (95% CI) |
|
|---|---|---|
| Granulocyte (white blood cell) transfusions vs no transfusions. Outcome: all-cause mortality | ||
| Conventional random-effects meta-analysis (DerSimonian and Laird estimation) | 0.42 (0.13–1.34) | 1.25 (0.04–8.50)a |
Bayesian random-effects meta-analysis with Uniform(0,5) prior for 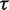
|
0.33 (0.03–1.96) | 2.74 (0.34–18.1) |
Bayesian random-effects meta-analysis with log-normal (−3.93,1.512) prior for 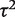
|
0.48 (0.18–1.01) | 0.18 (0.003–1.70) |
| Nortriptyline vs placebo. Outcome: long-term abstinence (6–12 months) from smoking | ||
| Conventional random-effects meta-analysis (DerSimonian and Laird estimation) | 2.26 (1.52–3.37) | 0.02 (0–1.86)a |
Bayesian random-effects meta-analysis with Uniform (0,5) prior for 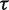
|
2.40 (1.28–4.77) | 0.13 (0.0003–2.50) |
Bayesian random-effects meta-analysis with log-normal (−2.13,1.582) prior for 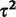 |
2.39 (1.50–3.91) | 0.07 (0.004–0.64) |
aConfidence interval for 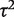 calculated using Q-profile method.19
calculated using Q-profile method.19
Table 5 presents results from a Bayesian meta-analysis using a vague Uniform (0,5) prior for 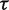 . Estimation was achieved within the WinBUGS software,14 and results were based on 50 000 iterations following a burn-in of 5000 iterations. This analysis produced an extremely wide interval for
. Estimation was achieved within the WinBUGS software,14 and results were based on 50 000 iterations following a burn-in of 5000 iterations. This analysis produced an extremely wide interval for 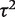 , and a correspondingly widened interval for the combined OR, which reflects the uncertainty in
, and a correspondingly widened interval for the combined OR, which reflects the uncertainty in 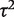 . When so few studies are included, the results are known to be very sensitive to choice of vague prior for
. When so few studies are included, the results are known to be very sensitive to choice of vague prior for 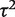 ,17 and little confidence would be placed in these results.
,17 and little confidence would be placed in these results.
The granulocyte transfusions meta-analysis evaluated a non-pharmacological intervention with respect to all-cause mortality, so we used a log-normal (−3.93, 1.512) distribution as an informative prior distribution for 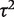 (Table 4). The simple code for fitting the model is available in the Supplementary Appendix S1. When using an informative prior, the central estimate for heterogeneity reduced to 0.18 (95% CI 0.003–1.70), and the interval for the combined OR narrowed substantially (Table 5). Since the informative prior represents our beliefs about likely values of heterogeneity in this meta-analysis, we would consider these results appropriate as a primary analysis of the data.
(Table 4). The simple code for fitting the model is available in the Supplementary Appendix S1. When using an informative prior, the central estimate for heterogeneity reduced to 0.18 (95% CI 0.003–1.70), and the interval for the combined OR narrowed substantially (Table 5). Since the informative prior represents our beliefs about likely values of heterogeneity in this meta-analysis, we would consider these results appropriate as a primary analysis of the data.
As a contrasting example, we have also re-analysed the data from a published meta-analysis of six studies in which the conventional heterogeneity estimate was low (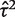 = 0.02, I2 = 6%), but again imprecisely estimated (Table 5). This meta-analysis evaluated the effectiveness of the antidepressant nortriptyline for smoking cessation.18 When performing a Bayesian meta-analysis using an informative prior for
= 0.02, I2 = 6%), but again imprecisely estimated (Table 5). This meta-analysis evaluated the effectiveness of the antidepressant nortriptyline for smoking cessation.18 When performing a Bayesian meta-analysis using an informative prior for 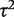 , the central estimate of
, the central estimate of 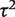 increased slightly to 0.07 whereas its 95% CI narrowed. This Bayesian meta-analysis allows appropriately for the imprecision in
increased slightly to 0.07 whereas its 95% CI narrowed. This Bayesian meta-analysis allows appropriately for the imprecision in  and produces a wider interval for the combined OR in comparison with a conventional random-effects meta-analysis.
and produces a wider interval for the combined OR in comparison with a conventional random-effects meta-analysis.
Discussion
Many meta-analyses synthesize the evidence from only a small number of studies, which makes estimation of the between-study variance difficult. A Bayesian approach to estimation is particularly beneficial in small meta-analyses, since it allows incorporation of external evidence on the between-study variance. In this article, we have analysed a large database of meta-analyses in order to describe the predictors of between-study heterogeneity and construct informative prior distributions for the heterogeneity variance. We have shown how these priors can be used in a future meta-analysis, and provided an example where precision is improved by doing so.
Informative prior distributions for between-study heterogeneity have been proposed previously. Smith et al.4 derived an informative prior distribution for heterogeneity in a binary data meta-analysis by considering the degree of spread of ORs which could reasonably be expected. Higgins and Whitehead8 constructed a prior distribution for a meta-analysis in gastroenterology, by fitting an inverse gamma distribution to the heterogeneity parameters of 18 meta-analyses of similar study types. Pullenayegum20 recently analysed 314 meta-analyses from the CDSR and developed a joint prior for heterogeneity and the pooled log OR, allowing the prior for heterogeneity to depend on the magnitude of the intervention effect. In our models, we allowed heterogeneity to depend only on known meta-analysis characteristics, in order that the priors can be fully specified in advance of the analysis and implementation is straightforward. The size and breadth of the full CDSR data set have enabled us to identify important predictors of heterogeneity and construct a number of priors for specific meta-analysis types.
A limitation of our work is that the data set only includes data entered numerically by the systematic review authors. Meta-analyses reported only in the text of a systematic review may tend to exhibit higher between-study heterogeneity, so we expect our analyses to under-estimate the true levels of heterogeneity. Second, the data set includes only meta-analyses from Cochrane reviews, which are not necessarily representative of meta-analyses in general. Another limitation is that the classifications of meta-analysis characteristics were carried out by only one person, owing to the very large amount of work involved. In our current work, we have analysed meta-analyses of binary outcomes only, and the informative priors cannot be applied directly to other outcome types.
In our analyses, we have modelled total between-study heterogeneity, which is likely to comprise a mixture of variation caused by true diversity among the protocols for the original studies, variation caused by biases and unexplained variation. Assuming that a conventional random-effects model will be used in many future meta-analyses, it is appropriate to focus on total between-study heterogeneity in our predictive findings. However, it would be preferable to separate variation attributable to biases from other sources of between-study variation. In later versions of the CDSR, this will become possible once the recently introduced Cochrane risk-of-bias tool21 has been implemented in a large number of systematic reviews. Our existing hierarchical model for the data from all available meta-analyses could be extended to incorporate the bias model proposed by Welton et al.22 This would allow us to adjust for the bias attributable to a potential source (e.g. inadequate allocation concealment) in all studies judged to be at high risk. In principle, the model could be extended further to adjust for multiple sources of bias simultaneously. Results from this analysis could provide useful information about the degree to which one would expect between-study heterogeneity to reduce, on average, if meta-analysts chose to adjust for known sources of bias, for example, by using empirical evidence or elicited opinion on biases.22,23
In summary, between-study heterogeneity was found to be strongly associated with the type of outcome measured in the meta-analysis, with meta-analyses of all-cause mortality or semi-objective outcomes exhibiting substantially lower heterogeneity than meta-analyses of subjective outcomes. Heterogeneity may also be associated with intervention comparison type, to a lesser extent. Informative priors for heterogeneity would be beneficial in meta-analyses including few studies, and these have been made available in this report. In view of the important influences on heterogeneity observed in the CDSR data set, use of an informative prior for heterogeneity in future meta-analyses would be entirely justifiable.
Supplementary Data
Supplementary Data are available at IJE online.
Funding
Medical Research Council Population Health Sciences Research Network (grant number U.1052.00.011.00003.01).
Supplementary Material
Acknowledgements
We are grateful to the Nordic Cochrane Centre (particularly Rasmus Moustgaard and Monica Kjeldstrøm) and the Cochrane Collaboration Steering Group for providing us with access to the Cochrane Database of Systematic Reviews. We thank David Spiegelhalter, Jonathan Sterne, Tony Ades, Nicky Welton and Sofia Dias for discussions during the development of the project.
Conflict of interests: None declared.
KEY MESSAGES.
Many meta-analyses contain only a small number of studies, which makes it difficult to estimate the extent of between-study heterogeneity.
By analysing a large database of meta-analyses, we have identified important predictors of heterogeneity.
Prior distributions for heterogeneity have been constructed for use in specific topic areas. These would be very beneficial in future meta-analyses including few studies.
References
- 1.DerSimonian R, Laird N. Meta-analysis in clinical trials. Controlled Clin Trials. 1986;7:177–88. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]
- 2.Higgins JPT, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. J Royal Stat Soc A. 2009;172:137–59. doi: 10.1111/j.1467-985X.2008.00552.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jackson D, Bowden J, Baker R. How does the DerSimonian and Laird procedure for random effects meta-analysis compare with its more efficient but harder to compute counterparts? J Stat Plan Infer. 2010;140:961–70. [Google Scholar]
- 4.Smith TC, Spiegelhalter DJ, Thomas A. Bayesian approaches to random-effects meta-analysis: a comparative study. Stat Med. 1995;14:2685–99. doi: 10.1002/sim.4780142408. [DOI] [PubMed] [Google Scholar]
- 5.Sutton AJ, Abrams KR. Bayesian methods in meta-analysis and evidence synthesis. Stat Methods Med Res. 2001;10:277–303. doi: 10.1177/096228020101000404. [DOI] [PubMed] [Google Scholar]
- 6.Higgins JPT, Spiegelhalter DJ. Being sceptical about meta-analyses: a Bayesian perspective on magnesium trials in myocardial infarction. Int J Epidemiol. 2002;31:96–104. doi: 10.1093/ije/31.1.96. [DOI] [PubMed] [Google Scholar]
- 7.Ades AE, Lu G, Higgins JPT. The interpretation of random-effects meta-analysis in decision models. Med Decis Making. 2005;25:646–54. doi: 10.1177/0272989X05282643. [DOI] [PubMed] [Google Scholar]
- 8.Higgins JPT, Whitehead A. Borrowing strength from external trials in a meta-analysis. Stat Med. 1996;15:2733–49. doi: 10.1002/(SICI)1097-0258(19961230)15:24<2733::AID-SIM562>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- 9.Davey J, Turner RM, Clarke MJ, Higgins JPT. Characteristics of meta-analyses and their component studies in the Cochrane Database of Systematic Reviews: a cross-sectional, descriptive analysis. BMC Med Res Methodol. 2011;11:160. doi: 10.1186/1471-2288-11-160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wood L. The Epidemiology of Bias in Randomized (clinical) Controlled Trials: a Meta-epidemiological Study. PhD thesis. University of Bristol; 2006. [Google Scholar]
- 11.Foundation for Health Services Research. Health Outcomes Research: A Primer. http://www.academyhealth.org/files/publications/healthoutcomes.pdf (1 March 2011, date last accessed) [Google Scholar]
- 12.UK Clinical Research Collaboration. Health Research Classification System. http://www.hrcsonline.net/pages/hrcs_download (1 March 2011, date last accessed) [Google Scholar]
- 13.National Institute for Health and Clinical Excellence. NICE Taxonomy (subject encoding scheme). http://www.nice.org.uk/aboutnice/nicewebsitedevelopment/standards/metadata/niceencodingschemes/nice_encoding_schemes.jsp (1 August 2009, date last accessed) [Google Scholar]
- 14.Lunn DJ, Thomas A, Best N, Spiegelhalter D. WinBUGS—a Bayesian modelling framework: concepts, structure, and extensibility. Stat Comput. 2000;10:325–37. [Google Scholar]
- 15.Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit (with discussion) J Royal Stat Soc B. 2002;64:583–640. [Google Scholar]
- 16.Stanworth S, Massey E, Hyde C, et al. Granulocyte transfusions for treating infections in patients with neutropenia or neutrophil dysfunction. Cochrane Database Syst Rev. 2010;(Issue 8) doi: 10.1002/14651858.CD005339. Art. No.: CD005339. [DOI] [PubMed] [Google Scholar]
- 17.Lambert PC, Sutton AJ, Burton PR, Abrams KR, Jones DR. How vague is vague? A simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS. Stat Med. 2005;24:2401–28. doi: 10.1002/sim.2112. [DOI] [PubMed] [Google Scholar]
- 18.Hughes JR, Stead LF, Lancaster T. Antidepressants for smoking cessation. Cochrane Database Syst Rev. 2011;(Issue 8) Art. No.: CD000031. [Google Scholar]
- 19.Viechtbauer W. Confidence intervals for the amount of heterogeneity in meta-analysis. Stat Med. 2007;26:37–52. doi: 10.1002/sim.2514. [DOI] [PubMed] [Google Scholar]
- 20.Pullenayegum E. An informed reference prior for between-study heterogeneity in meta-analyses of binary outcomes. Stat Med. 2011;30:3082–94. doi: 10.1002/sim.4326. [DOI] [PubMed] [Google Scholar]
- 21.Higgins JPT, Altman DG. Assessing risk of bias in included studies. In: Higgins JPT, Green S, editors. Cochrane Handbook for Systematic Reviews of Interventions. Chichester: John Wiley & Sons; 2008. pp. 187–241. [Google Scholar]
- 22.Welton NJ, Ades AE, Carlin JB, Altman DG, Sterne JAC. Models for potentially biased evidence in meta-analysis using empirically based priors. J Royal Stat Soc A. 2009;172:119–36. [Google Scholar]
- 23.Turner RM, Spiegelhalter DJ, Smith GCS, Thompson SG. Bias modelling in evidence synthesis. J Royal Stat Soc A. 2009;172:21–47. doi: 10.1111/j.1467-985X.2008.00547.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.