Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2012 Jul;22(7):1295–1305. doi: 10.1101/gr.129437.111

Physical tethering and volume exclusion determine higher-order genome organization in budding yeast

Harianto Tjong 1, Ke Gong 1, Lin Chen 1,2,3, Frank Alber 1,4
PMCID: PMC3396370  PMID: 22619363

Abstract

In this paper we show that tethering of heterochromatic regions to nuclear landmarks and random encounters of chromosomes in the confined nuclear volume are sufficient to explain the higher-order organization of the budding yeast genome. We have quantitatively characterized the contact patterns and nuclear territories that emerge when chromosomes are allowed to behave as constrained but otherwise randomly configured flexible polymer chains in the nucleus. Remarkably, this constrained random encounter model explains in a statistical manner the experimental hallmarks of the S. cerevisiae genome organization, including (1) the folding patterns of individual chromosomes; (2) the highly enriched interactions between specific chromatin regions and chromosomes; (3) the emergence, shape, and position of gene territories; (4) the mean distances between pairs of telomeres; and (5) even the co-location of functionally related gene loci, including early replication start sites and tRNA genes. Therefore, most aspects of the yeast genome organization can be explained without calling on biochemically mediated chromatin interactions. Such interactions may modulate the pre-existing propensity for co-localization but seem not to be the cause for the observed higher-order organization. The fact that geometrical constraints alone yield a highly organized genome structure, on which different functional elements are specifically distributed, has strong implications for the folding principles of the genome and the evolution of its function.

The structural organization of the genome in its nuclear environment is a key factor in the correct execution of nuclear functions (Misteli 2007; Takizawa et al. 2008; Taddei et al. 2010). For instance, in budding yeast, heterochromatic regions such as telomeres and silent mating-type loci are silenced by anchoring them to the nuclear envelope (NE), presumably through heterochromatin protein factors (Gotta et al. 1996; Hediger et al. 2002; Taddei et al. 2004, 2009; Mekhail and Moazed 2010; Horigome et al. 2011). For some other genes, the location at the NE has also been proposed to play a major role in their transcriptional repression (Csink and Henikoff 1996; Dernburg et al. 1996; Maillet et al. 1996; Brown et al. 1997; Cockell and Gasser 1999; Towbin et al. 2009). However, other genes relocate to the NE upon transcriptional activation (Casolari et al. 2004; Cabal et al. 2006), presumably instigated by forming interactions with nuclear pore complexes, facilitating mRNA export to maximize cellular transcription levels.

The spatial clustering of functionally related loci is also a key characteristic of genome organization. In budding yeast, all heterochromatic centromeres are located in a distinct region of the nucleus. This occurs because throughout interphase they remain attached through microtubules to the spindle pole body (SPB) (O'Toole et al. 1999; Jin et al. 2000). On the other hand, ribosomal DNA (rDNA) repeats appear to be clustered at the NE, opposite to the SPB in the nucleus (Yang et al. 1989; Dvorkin et al. 1991; Bystricky et al. 2005). There they form the core of a distinct subnuclear compartment named the nucleolus, which is the site of RNA pol-I–mediated rDNA transcription and ribosome biogenesis (Yang et al. 1989; Bystricky et al. 2005; Berger et al. 2008; Mekhail et al. 2008; Mekhail and Moazed 2010; Taddei et al. 2010).

There is also growing evidence for a territorial organization of the chromosomes in yeast (Bystricky et al. 2004, 2005; Schober et al. 2008). Large-scale fluorescence imaging experiments on budding yeast have revealed that several individual gene loci are strongly confined into distinct “gene territories” (Berger et al. 2008; Therizols et al. 2010). Also, several genome-wide conformation capture experiments have revealed highly structured chromatin contact patterns: Some chromosome pairs were found to interact rarely, while others interact more often than expected (Rodley et al. 2009; Duan et al. 2010). The contact patterns of chromosomes 3 and 6 in budding yeast agree with a Rabl-like configuration: Both chromosomes appear to be folded backward from their centromeres, so that their telomeres are juxtaposed (Jin et al. 2000; Dekker et al. 2002; Bystricky et al. 2005; Schober et al. 2008). Such a configuration and the resulting territorial chromosome organizations have been previously observed in live fluorescence imaging experiments (Bystricky et al. 2004, 2005; Schober et al. 2008; Taddei et al. 2010).

At the same time, there is ample evidence that the structure of the genome is highly dynamic (Marshall et al. 1997; Heun et al. 2001). Fluorescence imaging shows considerable cell-to-cell variations of gene and chromosome locations (Ferguson and Ward 1992; Csink and Henikoff 1998; Heun et al. 2001; Berger et al. 2008). Also chromosome contacts are observed over a wide range of frequencies, indicating that not all contacts can be present simultaneously (Dekker et al. 2002; Lieberman-Aiden et al. 2009; Duan et al. 2010; Kalhor et al. 2012; Misteli 2012).

Some intrachromosomal contact probabilities are consistent with a diffusion-driven contact formation (Cook and Marenduzzo 2009; de Nooijer et al. 2009; Mateos-Langerak et al. 2009; Bohn and Heermann 2010; Dorier and Stasiak 2010). However, purely random chain behavior as studied in isolated model chromosomes cannot explain many of the specific patterns observed in experiments (Rosa et al. 2010).

To fairly assess the principles of chromosome folding and the possible role of molecular interactions in establishing nuclear order, we must first examine the genome structure that arises when chromosomes are tethered but otherwise randomly configured in the confinement of the nuclear environment. Previous work points toward an important role of nuclear constraints and relative chromosome arm lengths in genome organization (Berger et al. 2008; Taddei et al. 2010; Zimmer and Fabre 2011) as shown for the dynamic relationship of subtelomeric regions (Therizols et al. 2010). However, it remains to be seen if entirely random configurations of tethered chromosomes are sufficient to reproduce in a statistical manner all the available quantitative data about the yeast genome organization and gene loci interactions, including the highly structured contact frequency maps from genome-wide conformation capture experiments (Dekker et al. 2002; Duan et al. 2010), the distribution of gene territories from fluorescence imaging (Berger et al. 2008; Therizols et al. 2010; Zimmer and Fabre 2011), and the clustering of replication start sites as well as tRNA genes.

Our findings demonstrate that purely random configurations of tethered chromosomes do indeed reproduce in a statistical manner a wide range of data related to genome structure: genome-wide chromatin interaction frequencies; the emergence, shape, and location of specific gene territories; the relative distances between telomeres; and even the spatial clustering of functionally related chromosome regions such as early replication start sites and tRNA gene loci. Specific molecular interactions between chromatin regions, although possible, are not required to explain the available experimental data on the higher-order genome organization. Moreover, the large structural variability among individual cell's genome configurations indicates that no single average genome structure can adequately reflect the wide range of structural features relevant to a population of cells.

Results

Population modeling for determining the three-dimensional organization of the genome

To address the challenge of representing highly variable genome structures, we construct a large population of three-dimensional (3D) genome structures, which represent a spectrum of all possible chromosome configurations, and interpret the result in terms of probabilities of a sample drawn from a population of heterogeneous structures (Methods).

All chromosomes are modeled as random configurations that are subject to the following constraints: (1) All chromosomes are confined in the nucleus; (2) all the centromeres are attached to the SPB through microtubules; (3) all the telomeres are located near the nuclear periphery; and (4) the nucleolus is inaccessible to chromosomes, except for those regions containing rDNA repeats (Methods) (Table 1; Fig. 1).

Table 1.

Functional forms of the restraints in the scoring function

graphic file with name 1295tbl1.jpg

Open in a new tab

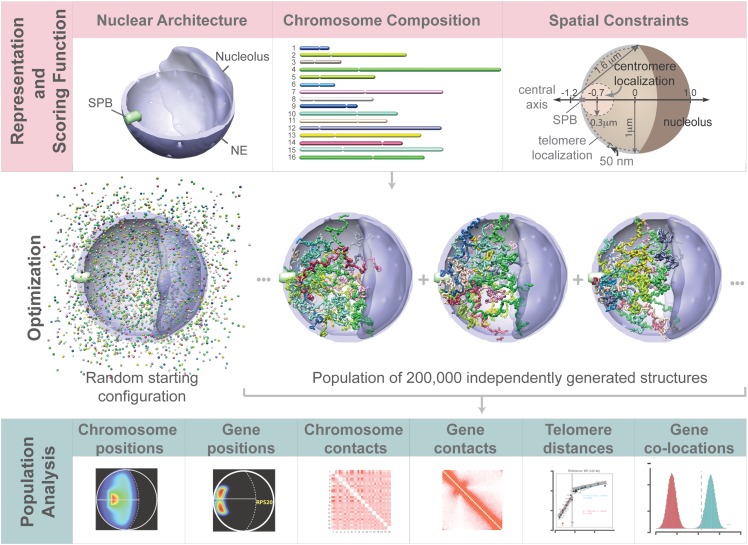
Figure 1.

Figure 1.

Open in a new tab

Population-based analysis of the S. cerevisiae genome organization. To analyze structural features of the genome, we defined an optimization problem with three main components. (Top panels) A structural representation of chromosomes as flexible chromatin fibers (center), a structural representation of the nuclear architecture (left), and the scoring function quantifying the genome structure's accordance with nuclear landmark constraints (right). (Middle panels) An optimization and sampling method, which minimizes the scoring function to generate a population of genome structures that entirely satisfies all landmark constraints. (Bottom panels) The statistical analysis and comparison of structural features from the population of 3D genome structures with all the experimental data.

To generate a population of genome structures, we defined an optimization problem (Methods). In order to sample a representative set of all possible structures, we created a sample of 200,000 independently optimized genome structures, hereafter referred to as the structure population. We also generated a control population with an identical setup but without imposing any landmark constraints (Methods), referred to as the random control. We also calculated a structure population for a nucleus containing only a single chromosome, constrained in a manner identical to the full simulation. We refer to this population as the single chromosome population.

Probabilistic analysis of chromosome structural features

In the following sections, we analyze the spatial properties of the structure population in terms of several statistical quantities: (1) chromosome territory locations, (2) chromosome and gene loci interaction frequencies, (3) locus localization probabilities, (4) telomere distance distributions, (5) physical proximity of functionally associated genomic loci including early and late replication origins, and tRNA genes. Each property of the simulated structure population will be compared with available experimental data.

Chromosome territories as a result of constrained random encounters

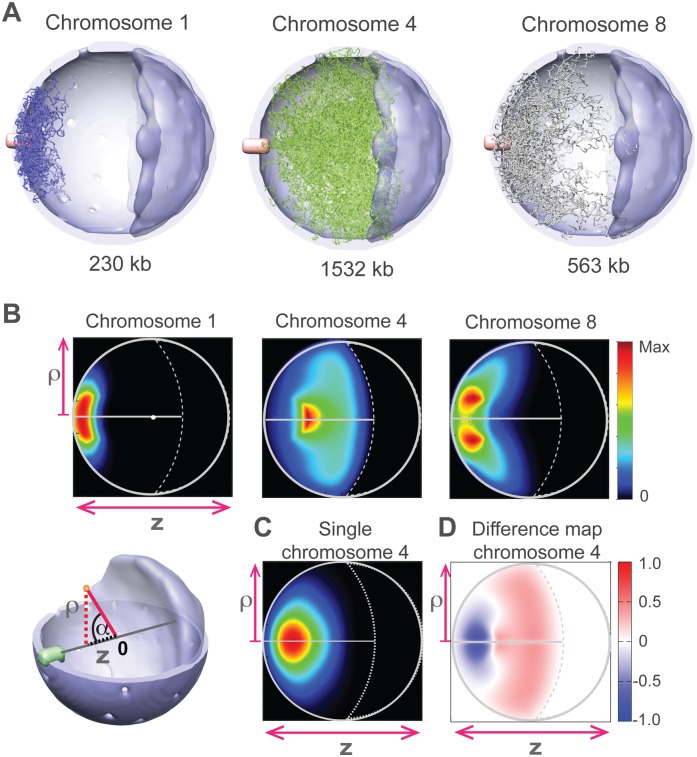
We first ask to what extent the landmark constraints lead to preferred chromosome locations. We calculate the probability that each chromosome occupies any given region of the nucleus (i.e., the localization probability density [LPD] of a chromosome) (Supplemental Material). Based on the LPD, it is evident that all the chromosomes have preferred regions. Smaller chromosomes (e.g., chromosome 1 in Fig. 2) reside preferentially around the central axis, near the SPB. Interestingly medium-sized chromosomes are more likely to reside away from the central axis (e.g., chromosome 8 in Fig. 2A,B; Supplemental Fig. 1), while for large chromosomes (e.g., chromosome 4, whose size is 1.5 Mb), the LPD is highest in the central region of the nucleus again along the central axis.

Figure 2.

Figure 2.

Open in a new tab

Chromosome locations. (A) A sample of 40 chromosome configurations randomly selected from the structure population for the small chromosome 1 (left panel, blue chains), the large chromosome 4 (middle panel, green chains), and the medium-sized chromosome 8 (right panel, gray chains). The chain thickness is reduced to enhance visibility. The chromosomes are depicted in the nucleus with the SPB in pink, the nucleolus in dark blue, and the NE in light blue. (B, top) Chromosome localization probability densities (LPDs) of chromosomes 1 (left), 4 (middle), and 8 (right panel) plotted along the two principal axes ρ and z (Supplemental Material). (Lower left) Reference frame for projecting the positions of chromosome points onto the two principal axes, namely, the projection along the central axis z (connecting SPB, nuclear center, and nucleolus), and the radial distance ρ-axis indicating the absolute distance of a point from the central axis. (C) The LPD of chromosome 4 resulting from the “single chromosome population.” The chromosome is subject to all landmark constraints, but structures are generated without the presence of other chromosomes in the nucleus. The density distribution is significantly different from the situation when all chromosomes are present (see B). (D) Excluded volume effect. The difference map between the LPDs of chromosome 4 from the structure population when all chromosomes are present (B, middle) and the single chromosome population as defined in C.

We then ask what factors are responsible for the chromosomes' preferred locations. For each chromosome, we calculate a new structure population for a nucleus containing only a single chromosome but otherwise constrained in a manner identical to the full simulation (i.e., the single chromosome population) (Fig. 2C). Comparing the two structure populations reveals great differences for each chromosome location (Fig. 2D). For example, in the full simulation, large chromosomes reside substantially farther from the SPB region toward the nucleolus than would be expected based on chromosome tethering alone. The differences are caused by a volume exclusion effect: Because of tethering, the chromosomes must compete for the limited space around the SPB. Smaller chromosomes are naturally more restricted to regions closer to the SPB, which in turn tends to exclude parts of larger chromosomes from these regions. For smaller chromosomes, the opposite effect is observed; in the full simulation, they exhibit an increased probability density around the SPB (Supplemental Fig. 1). Importantly, due to the volume exclusion effect, the preferred location of a chromosome is not defined by tethering alone but also depends on the total number and lengths of all other chromosomes in the nucleus.

Genome-wide chromosome contact patterns

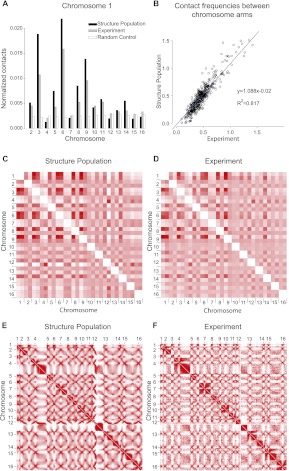
Next, we measure how often any two chromosome chains come into contact with each other over the entire structure population. Interestingly, most chromosomes show distinct preferences for interacting with certain others. For instance, chromosome 1 has a significantly higher chance of interacting with chromosomes 3 and 6 than with any other chromosome. Its interactions with the large chromosomes 4, 7, and 12 are substantially depleted (Fig. 3A). Strikingly, almost identical chromosome interaction preferences are observed in an independent genome-wide chromosome conformation capture experiment (Fig. 3A; Supplemental Fig. 2A; Duan et al. 2010). Pearson's correlation between the chromosome-pair contact frequencies in our structure population and those detected in the experiment is 0.94 (P < 10−15). In the random control, the contact frequencies do not display any significant chromosome-pair contact preferences (Pearson's correlation between experimental data and the random control is −0.57) (Supplemental Fig. 2B).

Figure 3.

Figure 3.

Open in a new tab

Chromosome and gene loci interactions. (A) Histogram of the normalized contact frequencies of chromosome 1 with other chromosomes in the structure population (black bars), chromatin conformation capture experiments (gray bars) (Duan et al. 2010), and the random control population (white bars). Contact frequencies of other chromosomes are shown in Supplemental Fig. 2. (B) Comparison of chromosome-arm–chromosome-arm contact frequencies from the structure population and experiments (Duan et al. 2010). (C,D) Contact frequency heat maps for chromosome arm contacts in the structure population (C) and experiments (D) (Duan et al. 2010). Heat maps of the genome-wide contact frequencies between loci at 32-kb resolution determined from the structure population (E) and in a chromosome conformation capture experiment (F) (Duan et al. 2010). (Color code ranges from white for low to red for high values.) Centromere positions are marked by the ticks. The row-based average Pearson's correlation between the two heat maps is 0.94 (all P-values <10−6). The largest differences between both heat maps involve interactions to the small arm of chromosome 12, which is not surprising because it contains all of the rDNA genes located in the nucleolus, which are not explicitly treated in our simulation. To further improve these interactions it is necessary to include these regions in future simulations (see Supplemental Material).

Next, we compare contact frequencies for all possible pairings of the 32 chromosome arms (Fig. 3B,C). It is evident that some pairs of chromosome arms have a greater propensity to interact than others. In particular, chromosome arms with <500 kb (chromosomes 1, 3, 5, 6, 8, and 9) are more likely to interact with each other than longer arms. For instance, the short arm of chromosome 1R is almost eight times more likely to interact with the short arm of chromosome 3L than with the long arm of 4R. Also these observations are in almost complete agreement with the conformation capture experiments (Pearson's correlation coefficient of 0.93, P < 10−15) (Fig. 3C,D; Duan et al. 2010).

Finally, when chromatin contacts are analyzed at a resolution of 32 kb, the contact frequency heat map of the structure population shows highly organized cross-shaped patterns (Fig. 3E). Also these patterns are in excellent agreement with those observed in the conformation capture experiment (Fig. 3F; Duan et al. 2010). The two contact frequency maps are again strongly correlated, with an average row-based Pearson's coefficient of 0.94 (all P-values <10−6; Supplemental Material). In contrast, the contact frequency map generated from the random control lacks the cross-shaped patterns (Supplemental Fig. 2C). We now analyze the intra- and interchromosomal locus-pair interaction patterns in more detail.

Intrachromosomal locus–locus interactions

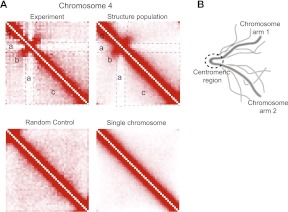
Intrachromosomal contact patterns in the structure population and experiments can be divided into three regions (Fig. 4A). Contact frequencies are enriched between regions in the same chromosome arm, as expected for a constrained random polymer chain (blocks c in Fig. 4A). In general, contact frequencies between regions within the same chromosome arm increase with decreasing sequence separation, which is shown by the strong diagonal in the contact frequency maps (Fig. 4A). However, regions located close to the centromere behave very differently. Contacts between subcentromeric regions on opposite sides of the centromere are clearly enriched in frequency, even with increasing chain distance, as can be seen along the line perpendicular to the main diagonal of the contact frequency map (block b in Fig. 4A). Moreover, contact frequencies between subcentromeric regions and regions from the bulk of both chromosome arms are very low (blocks a in Fig. 4A).

Figure 4.

Figure 4.

Open in a new tab

Chromosome folding. (A) Heat maps showing intrachromosomal contact frequencies for chromosome 4 obtained from conformation capture experiments (top left) (Duan et al. 2010), structure population (top right), random control (bottom left), and single chromosome population (bottom right). The latter is derived from a structure population for a nucleus containing only chromosome 4, constrained in a manner identical to the full simulation. Heat maps of the experiment and the structure population show characteristic folding patterns reminiscent of the back-folding of subcentromeric regions onto themselves. The heat maps of the random control and the single chromosome population lack the characteristic pattern. (B) Scheme showing the particular back-folding of the regions adjacent to both sides of the centromere for several chromosome configurations.

Similar contact patterns have been reported in 3C conformation capture experiments and have been explained by a particular Rabl-like style of chromosome folding (Dekker et al. 2002). The hypothesis is that regions on opposite sides of the centromere are folded toward each other, possibly indicating the existence of a biochemical attraction between loci (Fig. 4B). However, the strong agreement between the experimental contact frequency maps and our structure population demonstrates that such contact patterns are not necessarily caused by specific biochemically mediated interactions between subcentromeric regions. An equally possible explanation is that they represent purely random encounters of constrained chromosome chains.

It remains to be determined which factors are most responsible for the folding. In the “single chromosome population,” the cross-shaped intrachromosomal contact pattern is lost; the contact frequency map is similar to the random control (Fig. 4A, bottom panels). Therefore the particular folding pattern illustrated in Figure 4B is caused by a volume exclusion effect as a result of the presence of all 16 chromosomes. The competition among all centromere-tethered strands for the limited space around the SPB naturally leads to the style of folding described by experiments, and this folding is the proximate cause of the enriched contact frequencies between centromeric regions and the observed shielding of these regions from chromosome arm interactions.

Interchromosomal locus-locus contacts

The interchromosomal contact frequencies in the structure population are correlated with those observed in experiments, with an average Pearson's correlation of 0.54, which is highly significant (P < 10−15) (Fig. 3E,F; Supplemental Fig. 2D). In contrast, the Pearson's correlation between the random control and experiments is close to nil, and the distinctive contact patterns in the experimental data are completely absent in the random control (Supplemental Fig. 2C).

To examine the effect of limited sampling on the accuracy of chromosomal contact patterns, we compared our initial contact frequency map to maps generated from randomly sampling different proportions of these contacts (Supplementary Material; Supplemental Fig. 3D). In contrast, to intrachromosomal contacts, the correlations between interchromosomal contact patterns are greatly affected by limited sampling. At a sampling rate of 0.1%, we find that the Pearson's correlation between the two interchromosomal contact maps (even when assuming an ideal model) cannot exceed 0.5. Similar correlation values are observed in the Hi-C experiment when two interchromosomal contact maps are compared that are generated by using two different restriction enzymes (Yaffe and Tanay 2011). In our analysis, the observed correlation value of 0.54 corresponds to a sampling rate of ∼0.2%, which is also the order of magnitude that is expected for the experiment (Duan et al. 2010). Thus, the observed correlation coefficient of 0.54 represents a remarkably good agreement between the interchromosomal contact patterns, given that the experimental and computational samplings are finite and cannot be exhaustive.

Gene localizations

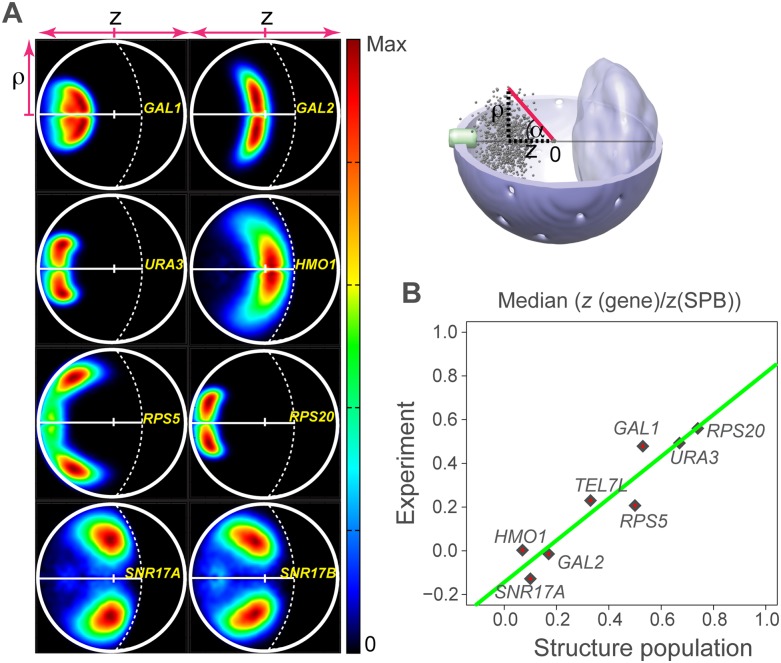
We now focus on the nuclear locations of individual gene loci. The locations of eight genes have been determined by large-scale fluorescence imaging experiments (Berger et al. 2008). These locations are measured with respect to the two principal axes of the nucleus (Methods; Fig. 5A). We determined the two-dimensional (2D) density distributions of the same gene loci in our structure population, allowing for a direct comparison with fluorescence experiments (Berger et al. 2008) (Fig. 5A). The density distribution functions agree well with experiments, in that each locus occupies a well-defined territory. The volumes and shapes of these territories strongly resemble those observed in experiments (Berger et al. 2008). For instance, genes GAL2, HMO1, and SNR17A are located near the nucleolus in the structure population, as seen in the experiment. Interestingly, the structure population places SNR17B (no experiments available) and SNR17A in similar positions near the nucleolus, despite the fact that these genes are located on different chromosomes. Both of these genes are involved in ribosome biogenesis and code the snoRNA U3. Also in agreement with experiments, the distribution patterns of the functionally related genes RPS5 and RPS20 are quite different. For instance, RPS5 positions are significantly more diffuse.

Figure 5.

Figure 5.

Open in a new tab

Gene territories. (A) Projected localization probability densities for the positions of eight gene loci in the structure population. The probability densities are determined with respect to two principal axes of the nuclear architecture (top right panel). The z-axis connects the SPB with the origin at the nuclear center and the nucleolus. The radial axis ρ defines the distance of a point from the central axis (top right panel). The lower half of the projected localization density plot is mirrored from the top half for visual convenience. (B) Median gene loci position along the z-axis calculated from the projected probability localization densities in A and from the experiment (Berger et al. 2008). The two are highly correlated with R2 = 0.9. To allow for comparison with the experiment, the z-axis distance of a gene locus is normalized relative to the SPB–gene distance.

In order to compare quantitatively the relative positions of these eight genes, we measure their median distance along the central axis in the 2D density maps obtained from experimental data and in the structure population. These positions are in excellent agreement (Pearson's correlation is 0.95, P < 10−3) (Fig. 5B).

Pairwise telomere distances

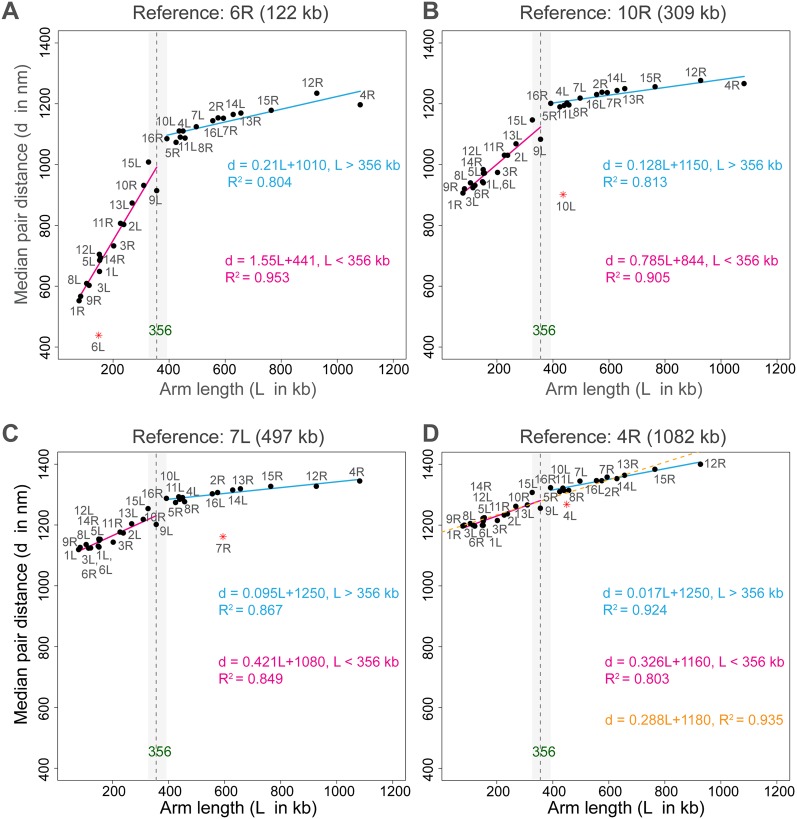
It is well known that telomeres are not positioned randomly on the nuclear periphery (Gotta et al. 1996; Bystricky et al. 2005; Berger et al. 2008; Therizols et al. 2010). Fluorescence imaging has revealed that the distance between any two subtelomeres increases gradually with the arm lengths of their chromosomes (Therizols et al. 2010). For a given subtelomere, this relationship is linear. In the structure population, we observe a very similar behavior. More specifically, after applying a change point analysis (Zeileis et al. 2003), we find that the distance between subtelomere pairs as a function of arm length is divided into two linear regimes (Fig. 6). For chromosome arms with lengths up to ∼360 kb, the distances observed in our structure population increase with a relatively steep slope. Above 360 kb, the slope decreases significantly. This behavior is entirely consistent with experiments, and the change in slope has been explained as follows (Therizols et al. 2010). For small arms, the accessible position of a subtelomere at the NE is entirely restricted by the arm length. Hence, the median distance between two subtelomeres increases rapidly with their accessible areas. However, at a certain arm length, the subtelomere is able to reach all points on the NE. Further increases in arm length do not dramatically increase the median subtelomere distance.

Figure 6.

Figure 6.

Open in a new tab

Median telomere–telomere distances in the structure population. The median distances between a telomere of a reference chromosome arm and all other telomeres are plotted for reference chromosome arms (A) 6R, (B) 10R, (C) 7R, and (D) 4R. (Vertical dashed line) Change point with 95% confidence interval shown by the shaded area.

Interestingly, the change in slope occurs at a slightly different arm length in experiments (∼310 kb) (Therizols et al. 2010) compared to our structure population (356–440 kb) (Supplemental Fig. 5a). However, the incompleteness of the experimental data can explain some of this difference. If we only include those chromosomes that are also analyzed in the experiment (Supplemental Fig. 5b), the change in slope in our simulation shifts to 309–327 kb in remarkably good agreement with the experiment.

Telomere clusters

To identify subtelomere clusters in the structure population, for each subtelomere we calculated the fraction of structures with at least one other subtelomere within 250 nm. In agreement with another experiment (Therizols et al. 2010), such small subtelomere distances are infrequent (1%–3%) for most chromosomes (Supplemental Fig. 6A). However, a few co-locations are observed more frequently between relatively short chromosome arms, namely, 1R:1L, 6R:6L, 1R:9R, and 3L:3R. These pairings occur in 12%-20% of the population, also in agreement with experiments (Bystricky et al. 2005; Schober et al. 2008; Therizols et al. 2010). For example, the pairs 3R:3L and 6R:6L were recently reported to form significant but transient interactions, leading to the formation of chromosome loops (Bystricky et al. 2005; Schober et al. 2008; Therizols et al. 2010). In general, we find that as the length difference between chromosome arms grows more pronounced, the probability of their telomeres being co-localized decreases. Interestingly, the volume exclusion effect has a pronounced effect on the co-location frequency of telomeres. For small and also large chromosomes, the volume exclusion effect increases significantly the co-location frequency, while for medium-sized chromosomes the opposite is observed by decreasing the co-location frequency (Supplemental Fig. 6B). For instance, the fraction of co-located telomeres increases by almost 20% for the small chromosome 6 upon the presence of all other chromosomes in the nucleus, while it decreases by 60% for the medium-sized chromosome 8.

Co-localization of functionally related loci

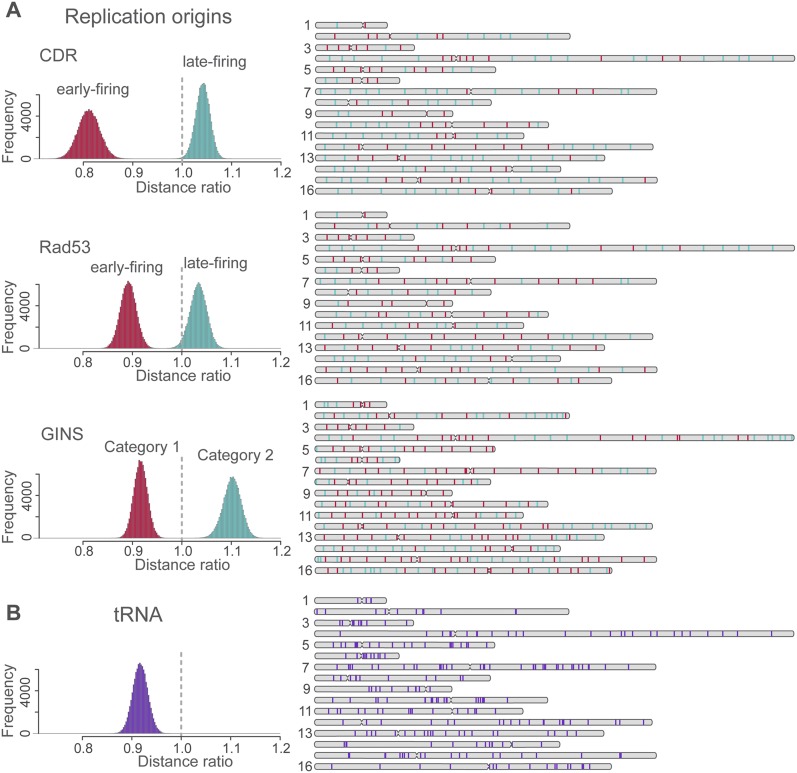
Next, we investigate whether functionally related gene loci are co-localized in the structure population. First, we compare the 3D spatial distributions of early and late replication start sites in the structure population. These sites are distributed across all chromosomes (Fig. 7, right panels). Experimental evidence exists that early replication sites are spatially clustered during interphase (Di Rienzi et al. 2009; Duan et al. 2010).

Figure 7.

Figure 7.

Open in a new tab

Spatial clustering of replication origins and tRNA gene loci. (Left) The histograms show the distribution of the mean pair distance ratio between a set of specific sites (e.g., early replication sites) and all sites in the structures of the population. The histograms are generated as follows: For a given structure in the population, the mean pair distance between a set of specific loci (e.g., all early replication origins) is calculated. This distance is divided by the mean pair distance of all sites in the same structure. The distribution of the distance ratio is then obtained from all structures in the population. If the distribution is centered on 1 (vertical dashed line), the selected sites behave similarly to a random sample of all sites. If the distribution is shifted toward smaller values, their pair distances are smaller than would be expected from the background control. If the distribution is shifted to larger values, the selected sites are more distant from each other than would be expected from the random control background. (A) Distribution of distance ratios of early (red) and late (green) replication start sites as determined by three independent experiments using the CDR (Clb5 Dependent Region), Rad53 checkpoint-mediated regulation, and GINS complex as identifiers. For the latter case, category 1 sites start replication earlier than category 2 sites. (Right panel) The positions of each site in the chromosome sequence. The number of early- and late-firing sites labeled with CDR, Rad3, and GINS are 77 and 123, 101 and 99, and 169 and 135, respectively. (B) Distribution of distance ratios for all 275 tRNAs (loci extracted from SGD, http://www.yeastgenome.org). For all sets of sites in A and B, the shift of the mean pair distances is highly statistical significant (for details, see Supplemental Material and main text).

In each structure of the population, we calculate the mean pairwise distance between all early replication sites. The frequency distribution derived from these mean pairwise distances is compared to a distribution chosen from randomly selected sites in the genome. We observe significant spatial clustering of the early replication sites (Fig. 7A), in the sense that their mean pairwise distances are significantly less than would be expected from randomly selected sites (Stouffer's Z-transform [Stouffer et al. 1949] tests z-scores < −160; Supplemental Material). This observation holds for all three sets of early replication origins identified in the literature (Feng et al. 2006; McCune et al. 2008; Sekedat et al. 2010). Remarkably, for late replication sites we see the opposite effect: a statistically significant increase in the mean pairwise distances between late replication sites compared with the background. It appears that, on average, early replication start sites are closer to the centromere on the chromosome sequence compared with the late start sites (all P-values <10−5 for the three data sets) (Supplemental Material).

We also analyzed the spatial positions of all tRNA gene loci in the genome, which have been observed to cluster in experiments (Thompson et al. 2003; Duan et al. 2010). Again, we observe a statistically significant decrease in the pairwise distances between tRNA loci (Fig. 7B) compared with randomly picked loci.

Our observations clearly indicate that the chromosomal locations of these specific sites are not randomly distributed over the genome; they are positioned in such a way that early replication sites have a higher probability of being co-localized when the chromosome chains behave as random polymer chains that are subject to nuclear landmark constraints.

Discussion

In this paper, we demonstrate that purely random configurations of tethered chromosomes reproduce in a statistical manner all the experimental hallmarks of genome organization in Saccharomyces cerevisiae. Specifically, random configurations generate structural features that agree remarkably well with (1) the highly specific interaction patterns between individual chromosomes, chromosome regions, and chromosome folding patterns obtained by genome-wide conformation capture experiments (Duan et al. 2010); (2) the emergence, shape, and position of individual gene territories revealed by probability maps from fluorescence experiments (Berger et al. 2008); (3) the distribution of median distances between telomeres; (4) the relative frequencies of telomere co-locations observed in imaging experiments (Bystricky et al. 2005; Schober et al. 2008; Therizols et al. 2010); and even (5) the physical proximity of functionally related gene loci, including early replication sites and tRNA gene loci.

In addition to chromosome tethering, the main organizing factor is a volume exclusion effect, as a result of the competition of all the chromosomes for the limited nuclear space. The fact that the chromosome arms have different lengths gives rise to important nuances of organization and implies that the locations of a gene or chromosome territory depends on all the other chromosomes. Therefore, the gene territory position and specific interaction patterns of a given gene locus is determined not only by its chromosome sequence position and the arm lengths of its own chromosome but also by the total number and the relative arm lengths of all other chromosomes. The volume exclusion effect can even create counterintuitive effects. For instance, for small and large chromosomes the volume exclusion effect leads to an increase in the frequency with which subtelomeres on the same chromosome are in proximity to each other, while for medium-sized chromosomes a decrease is observed.

Our findings have several important consequences. First, we show that a small number of purely geometrical constraints on otherwise randomly configured chromosomes can lead to a highly structured 3D genome organization. Second, the hallmarks of genome organization can be explained without calling on specific molecular interactions between chromatin regions or chromatin-bound proteins. For instance, random chromosome encounters can also statistically explain the spatial features often attributed to an apparent Rabl-like chromosome folding, which refers to the back-folding of subcentromeric chromosome regions so that chromosome arms appear juxtaposed. This pattern is mainly caused by the volume exclusion effect (Fig. 4). In response to the competition for the limited space around the SPB, chromosome regions on both sides of the centromere show a statistical preference for bending toward each other. When averaged over the entire cell population, this tendency gives rise to the distinctive cross-shaped intrachromosomal contact patterns observed in experiments and in our structure population. However, most individual structures will not exhibit simultaneously all the features of such an apparent Rabl-like fold. We therefore emphasize that the data should be explained as a statistical preference for chromosome contacts but not necessarily be interpreted as a stable chromosome fold. An interesting predication of this model is that the Rabl-like subcentromeric contact pattern should not be expected in yeast species if the number of chromosomes was considerably smaller even if the chromosomes were all tethered to nuclear landmarks. Although S. pombe and S. cerevisiae have similar genome sizes, the former has only three chromosomes. The prediction is sustained: In genome-wide conformation capture experiments, Schizosaccharomyces pombe yeast does not show the cross-shaped intrachromosomal contact patterns characteristic of this type of folding (Tanizawa et al. 2010).

Another remarkable result is that the early replication sites in our structure population have a high probability of being in close proximity compared with the background distribution of pairwise separations. In contrast, late replication sites have a lower probability of being colocated compared with randomly selected sites. This difference may help regulate a naturally occurring order on replication timing. The existence of these and other co-location patterns may indicate that the relative positions of affected loci in the chromosome were selected by evolution. Due to excluded volume effects, the spatial position of a gene in the nucleus is not only modulated by its relative sequence position in its own chromosome, but also by the relative arm lengths and the total number of all other chromosomes in the nucleus.

We also note that our study provides additional evidence for the existence of a chromatin fiber in the yeast interphase nucleus with length and density properties similar to the 30-nm fiber. We created an alternative structure population consistent with a 10-nm chromatin fiber, and the statistical results do not agree with the described experimental evidence.

Finally, we believe that our results point toward a considerable structural variability of genome structures among individual cells. Each structure in our population not only differs considerably from the “average conformation” but also from all the other structures in the population (<0.3% of loci contacts are shared between any two structures; Supplemental Material). No single-genome structure or population-averaged structure is representative of the population. Although the true structural variability is unknown, our results indicate that a single structural model cannot adequately reflect all the spatial features of the genome. It is crucial to analyze genome structures from a statistical rather than an individual standpoint. Structural analysis should be performed by generating a population of 3D genomes, which represent the spectrum of all possible chromosome configurations consistent with the data. The structural organization of the genome can then be interpreted statistically as a sample drawn from a population of heterogeneous structures. Such an analysis will allow a more accurate statistical description of genome structures and pave the way for structure-function analysis in the future.

Methods

General description

The nuclear architecture is described by the NE, the SPB, the nucleolus, and the 16 individual chromosomes in the haploid yeast genome (Fig. 1). The positions of the NE, SPB, and nucleolus remain fixed, while the configurations of the chromosomes are optimized.

Chromosome representation

The 16 chromosomes are described as flexible chromatin fibers, which in turn are represented as chains of connecting spheres with a radius of 15 nm. The compaction ratio is set to six nucleosomes per 11 nm of length. This figure agrees with other experiments, which have measured the compaction ratio to be between 1.2 and 11 nucleosomes per 11 nm of length (Thoma et al. 1979; Gerchman and Ramakrishnan 1987; Bystricky et al. 2004; Dekker 2008). Thus, each bead accommodates ∼3.2 kb of genome sequence. The ∼12 Mb yeast genome is represented by a total of 3779 beads. Changing the compaction ratio will slightly change the total number of beads but will not affect the outcome of the calculations at the resolution of our analysis.

Nuclear architecture

The nuclear radius is set to 1 micron, as suggested by experiments (Gasser 2002; Chubb and Bickmore 2003; Berger et al. 2008; Meister et al. 2010). The relative position and size of the SPB and nucleolus are taken from imaging experiments (Berger et al. 2008). The SPB and nucleolus are located at opposite ends of the nucleus, while a central axis connects the centers of the SPB, nucleus, and nucleolus (Fig. 1).

Scoring function

The scoring function is defined as a sum of spatial restraints and quantifies the degree of consistency between the structure and the imposed landmark constraints derived from experimental information. To optimize the structure, the scoring function is minimized to a score of zero. The scoring function is written as

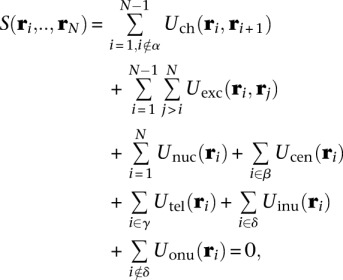graphic file with name 1295equ1.jpg

where 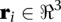Inline graphic is the coordinate vector of bead i, and N is the total number of beads in a model. The restraints are expressed as pseudo potential energy terms u described in Table 1; α, β, γ, and δ are subsets of specific beads in the chromosome chains that share certain properties. More specifically, α is the set of beads assigned to the last bead of every chain, β is the set of beads assigned to centromeres, γ is the set of beads assigned to telomeres, and δ is the set of all beads flanking rDNA repeat regions.

Chromatin chain restraint Uch

Two consecutive beads in a chromosome chain are restrained to be at a distance of 30 nm (Table 1).

Chromatin chain excluded volume restraint Uexc

Overlap between beads is prevented by imposing excluded volume restraints for all bead pairs (Table 1).

NE restraint Unuc

All chromatin beads must remain within the nucleus, defined as a sphere with radius Rnuc = 1 micron (Table 1).

Centromere localization restraint Ucen

All the centromeres cluster near the SPB, which is the microtubule organization center in the yeast nucleus (Jin et al. 2000). The centromeric regions are attached to the SPB through microtubules up to 300 nm in length (O'Toole et al. 1999). Accordingly, all beads representing centromeric regions are restricted to a spherical volume with a radius 300 nm, centered on the SPB (Fig. 1). We follow experimental evidence from fluorescence imaging and place the centromere localization volume on the central axis, close to the NE (Fig. 1, scheme in top right panel; Berger et al. 2008; Therizols et al. 2010).

Telomere localization restraint Utel

Telomeres have a high probability to be located near the nuclear periphery (Berger et al. 2008; Therizols et al. 2010). Beads representing telomeres are positioned in the vicinity of the NE (Table 1; Fig. 1, thin gray shell of 50-nm thickness).

Nucleolus localization restraint Uinu

The rDNA is located on chromosome 12 and consists of 150–200 tandem repeats of 9.1 kb length each (Kim et al. 2006; Taddei et al. 2010). All rDNA regions are found in the nucleolus. Because no conformation capture data or fluorescence imaging data are available for the rDNA genes, we do not explicitly resolve the chromatin fiber within the nucleolus. Instead, we anchor the two beads at the beginning and end of the rDNA repeat region (i.e., positions 458 kb from the left telomere and 620 kb from the right telomere in the sequence of chromosome 12) to the surface of the nucleolus (Table 1; Fig. 1).

Nucleolus excluded volume restraint Uonu

All chromosomal regions except those containing rDNA repeats are excluded from the nucleolus. (Table 1).

Chromatin persistence length

During the optimization process, we imposed an angular restraint between each set of three consecutive beads to reproduce the desired chain stiffness. The constraint is expressed as a harmonic potential:

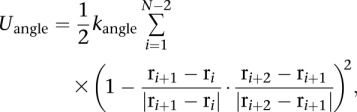graphic file with name 1295equ2.jpg

for i, i + 1, and i + 2 on the same chain.

This restraint is considered only when calculating gradient forces during the optimization process. It makes no contribution to the total score of a model (below). With a force constant of kangle = 0.2 kcal/mol, we obtain chromatin chains that behave like random polymers with a persistence length between 47 and 72 nm (the average is 61.7 ± 7.7 nm) (Supplemental Fig. 7), consistent with experiments. Estimated values for the persistence length from experiments fall between 30 and 220 nm (Cui and Bustamante 2000; Bystricky et al. 2004; Langowski 2006).

Optimization

The optimization is performed using a combination of simulated annealing molecular dynamics and the conjugate gradient methods implemented in the Integrated Modeling Platform (IMP; http://www.integrativemodeling.org) (Alber et al. 2007a,b, 2008; Russel et al. 2012). An individual optimization starts with an entirely random bead configuration, followed by an initial optimization of the structure. Next, we apply simulated annealing protocols to entirely equilibrate the genome configuration. Finally, conjugate gradient optimization ensures that all constraints are satisfied, leading to a structure with score zero. Many independent optimizations are carried out to generate a population of 200,000 genome structures with a total score of zero, hence consistent with all input data. A comparison between the frequency maps of two independently calculated populations, each with 100,000 structures, showed that our genome structure population is highly reproducible (Pearson's correlation between the contact frequency maps of the two populations is 0.999).

Control population

We also generated a control population of 25,000 structures without chromosome tethering constraints and nucleolus excluded volume constraints. Otherwise, the chromosomes are constrained in a manner identical to the full simulation.

Analysis

The analysis of the structure population and all statistical tests are described in great detail in the Supplemental Material.

Acknowledgments

We thank Dr. Oscar Aparicio, Dr. Susan Forsburg, Dr. M.S. Madhusudhan, Dr. Reza Kalhor, Zachary Frazier, Dr. Jasmine Zhou, Dr. Wenyuan Li, and Chao Dai for useful discussions and comments on the manuscript, and the IMP developers for supporting IMP modules. This work is supported by the Human Frontier Science Program, grant RGY0079/2009-C to F.A.; the Alfred P. Sloan Research foundation grant to F.A.; NSF CAREER grant 1150287 to F.A.; NIH grants HL076334, GM064642, and GM077320 to L.C.; NIH grant 1R01GM096089 to F.A.; and NIH grant 2U54RR022220 to F.A. and L.C. F.A. is a Pew Scholar in Biomedical Sciences, supported by the Pew Charitable Trusts.

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.129437.111.

References

  1. Alber F, Dokudovskaya S, Veenhoff LM, Zhang W, Kipper J, Devos D, Suprapto A, Karni-Schmidt O, Williams R, Chait BT, et al. 2007a. Determining the architectures of macromolecular assemblies. Nature 450: 683–694 [DOI] [PubMed] [Google Scholar]
  2. Alber F, Dokudovskaya S, Veenhoff LM, Zhang W, Kipper J, Devos D, Suprapto A, Karni-Schmidt O, Williams R, Chait BT, et al. 2007b. The molecular architecture of the nuclear pore complex. Nature 450: 695–701 [DOI] [PubMed] [Google Scholar]
  3. Alber F, Forster F, Korkin D, Topf M, Sali A 2008. Integrating diverse data for structure determination of macromolecular assemblies. Annu Rev Biochem 77: 443–477 [DOI] [PubMed] [Google Scholar]
  4. Berger AB, Cabal GG, Fabre E, Duong T, Buc H, Nehrbass U, Olivo-Marin JC, Gadal O, Zimmer C 2008. High-resolution statistical mapping reveals gene territories in live yeast. Nat Methods 5: 1031–1037 [DOI] [PubMed] [Google Scholar]
  5. Bohn M, Heermann DW 2010. Diffusion-driven looping provides a consistent framework for chromatin organization. PLoS ONE 5: e12218 doi: 10.1371/journal.pone.0012218 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brown KE, Guest SS, Smale ST, Hahm K, Merkenschlager M, Fisher AG 1997. Association of transcriptionally silent genes with Ikaros complexes at centromeric heterochromatin. Cell 91: 845–854 [DOI] [PubMed] [Google Scholar]
  7. Bystricky K, Heun P, Gehlen L, Langowski J, Gasser SM 2004. Long-range compaction and flexibility of interphase chromatin in budding yeast analyzed by high-resolution imaging techniques. Proc Natl Acad Sci 101: 16495–16500 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bystricky K, Laroche T, van Houwe G, Blaszczyk M, Gasser SM 2005. Chromosome looping in yeast: telomere pairing and coordinated movement reflect anchoring efficiency and territorial organization. J Cell Biol 168: 375–387 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cabal GG, Genovesio A, Rodriguez-Navarro S, Zimmer C, Gadal O, Lesne A, Buc H, Feuerbach-Fournier F, Olivo-Marin JC, Hurt EC, et al. 2006. SAGA interacting factors confine sub-diffusion of transcribed genes to the nuclear envelope. Nature 441: 770–773 [DOI] [PubMed] [Google Scholar]
  10. Casolari JM, Brown CR, Komili S, West J, Hieronymus H, Silver PA 2004. Genome-wide localization of the nuclear transport machinery couples transcriptional status and nuclear organization. Cell 117: 427–439 [DOI] [PubMed] [Google Scholar]
  11. Chubb JR, Bickmore WA 2003. Considering nuclear compartmentalization in the light of nuclear dynamics. Cell 112: 403–406 [DOI] [PubMed] [Google Scholar]
  12. Cockell M, Gasser SM 1999. Nuclear compartments and gene regulation. Curr Opin Genet Dev 9: 199–205 [DOI] [PubMed] [Google Scholar]
  13. Cook PR, Marenduzzo D 2009. Entropic organization of interphase chromosomes. J Cell Biol 186: 825–834 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Csink AK, Henikoff S 1996. Genetic modification of heterochromatic association and nuclear organization in Drosophila. Nature 381: 529–531 [DOI] [PubMed] [Google Scholar]
  15. Csink AK, Henikoff S 1998. Large-scale chromosomal movements during interphase progression in Drosophila. J Cell Biol 143: 13–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Cui Y, Bustamante C 2000. Pulling a single chromatin fiber reveals the forces that maintain its higher-order structure. Proc Natl Acad Sci 97: 127–132 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dekker J 2008. Mapping in vivo chromatin interactions in yeast suggests an extended chromatin fiber with regional variation in compaction. J Biol Chem 283: 34532–34540 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dekker J, Rippe K, Dekker M, Kleckner N 2002. Capturing chromosome conformation. Science 295: 1306–1311 [DOI] [PubMed] [Google Scholar]
  19. de Nooijer S, Wellink J, Mulder B, Bisseling T 2009. Non-specific interactions are sufficient to explain the position of heterochromatic chromocenters and nucleoli in interphase nuclei. Nucleic Acids Res 37: 3558–3568 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Dernburg AF, Broman KW, Fung JC, Marshall WF, Philips J, Agard DA, Sedat JW 1996. Perturbation of nuclear architecture by long-distance chromosome interactions. Cell 85: 745–759 [DOI] [PubMed] [Google Scholar]
  21. Di Rienzi SC, Collingwood D, Raghuraman MK, Brewer BJ 2009. Fragile genomic sites are associated with origins of replication. Genome Biol Evol 1: 350–363 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dorier J, Stasiak A 2010. The role of transcription factories-mediated interchromosomal contacts in the organization of nuclear architecture. Nucleic Acids Res 38: 7410–7421 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Duan Z, Andronescu M, Schutz K, McIlwain S, Kim YJ, Lee C, Shendure J, Fields S, Blau CA, Noble WS 2010. A three-dimensional model of the yeast genome. Nature 465: 363–367 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Dvorkin N, Clark MW, Hamkalo BA 1991. Ultrastructural localization of nucleic acid sequences in Saccharomyces cerevisiae nucleoli. Chromosoma 100: 519–523 [DOI] [PubMed] [Google Scholar]
  25. Feng W, Collingwood D, Boeck ME, Fox LA, Alvino GM, Fangman WL, Raghuraman MK, Brewer BJ 2006. Genomic mapping of single-stranded DNA in hydroxyurea-challenged yeasts identifies origins of replication. Nat Cell Biol 8: 148–155 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ferguson M, Ward DC 1992. Cell cycle dependent chromosomal movement in pre-mitotic human T-lymphocyte nuclei. Chromosoma 101: 557–565 [DOI] [PubMed] [Google Scholar]
  27. Gasser SM 2002. Visualizing chromatin dynamics in interphase nuclei. Science 296: 1412–1416 [DOI] [PubMed] [Google Scholar]
  28. Gerchman SE, Ramakrishnan V 1987. Chromatin higher-order structure studied by neutron scattering and scanning transmission electron microscopy. Proc Natl Acad Sci 84: 7802–7806 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gotta M, Laroche T, Formenton A, Maillet L, Scherthan H, Gasser SM 1996. The clustering of telomeres and colocalization with Rap1, Sir3, and Sir4 proteins in wild-type Saccharomyces cerevisiae. J Cell Biol 134: 1349–1363 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hediger F, Neumann FR, Van Houwe G, Dubrana K, Gasser SM 2002. Live imaging of telomeres: yKu and Sir proteins define redundant telomere-anchoring pathways in yeast. Curr Biol 12: 2076–2089 [DOI] [PubMed] [Google Scholar]
  31. Heun P, Laroche T, Shimada K, Furrer P, Gasser SM 2001. Chromosome dynamics in the yeast interphase nucleus. Science 294: 2181–2186 [DOI] [PubMed] [Google Scholar]
  32. Horigome C, Okada T, Shimazu K, Gasser SM, Mizuta K 2011. Ribosome biogenesis factors bind a nuclear envelope SUN domain protein to cluster yeast telomeres. EMBO J 30: 3799–3811 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Jin QW, Fuchs J, Loidl J 2000. Centromere clustering is a major determinant of yeast interphase nuclear organization. J Cell Sci 113: 1903–1912 [DOI] [PubMed] [Google Scholar]
  34. Kalhor R, Tjong H, Jayathilaka N, Alber F, Chen L 2012. Genome architectures revealed by tethered chromosome conformation capture and population-based modeling. Nat Biotechnol 30: 90–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kim YH, Ishikawa D, Ha HP, Sugiyama M, Kaneko Y, Harashima S 2006. Chromosome XII context is important for rDNA function in yeast. Nucleic Acids Res 34: 2914–2924 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Langowski J 2006. Polymer chain models of DNA and chromatin. Eur Phys J E Soft Matter 19: 241–249 [DOI] [PubMed] [Google Scholar]
  37. Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. 2009. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326: 289–293 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Maillet L, Boscheron C, Gotta M, Marcand S, Gilson E, Gasser SM 1996. Evidence for silencing compartments within the yeast nucleus: a role for telomere proximity and Sir protein concentration in silencer-mediated repression. Genes Dev 10: 1796–1811 [DOI] [PubMed] [Google Scholar]
  39. Marshall WF, Straight A, Marko JF, Swedlow J, Dernburg A, Belmont A, Murray AW, Agard DA, Sedat JW 1997. Interphase chromosomes undergo constrained diffusional motion in living cells. Curr Biol 7: 930–939 [DOI] [PubMed] [Google Scholar]
  40. Mateos-Langerak J, Bohn M, de Leeuw W, Giromus O, Manders EM, Verschure PJ, Indemans MH, Gierman HJ, Heermann DW, van Driel R, et al. 2009. Spatially confined folding of chromatin in the interphase nucleus. Proc Natl Acad Sci 106: 3812–3817 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. McCune HJ, Danielson LS, Alvino GM, Collingwood D, Delrow JJ, Fangman WL, Brewer BJ, Raghuraman MK 2008. The temporal program of chromosome replication: genomewide replication in clb5Δ Saccharomyces cerevisiae. Genetics 180: 1833–1847 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Meister P, Gehlen LR, Varela E, Kalck V, Gasser SM 2010. Visualizing yeast chromosomes and nuclear architecture. Methods Enzymol 470: 535–567 [DOI] [PubMed] [Google Scholar]
  43. Mekhail K, Moazed D 2010. The nuclear envelope in genome organization, expression and stability. Nat Rev Mol Cell Biol 11: 317–328 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Mekhail K, Seebacher J, Gygi SP, Moazed D 2008. Role for perinuclear chromosome tethering in maintenance of genome stability. Nature 456: 667–670 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Misteli T 2007. Beyond the sequence: cellular organization of genome function. Cell 128: 787–800 [DOI] [PubMed] [Google Scholar]
  46. Misteli T 2012. Parallel genome universes. Nat Biotechnol 30: 55–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. O'Toole ET, Winey M, McIntosh JR 1999. High-voltage electron tomography of spindle pole bodies and early mitotic spindles in the yeast Saccharomyces cerevisiae. Mol Biol Cell 10: 2017–2031 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Rodley CD, Bertels F, Jones B, O'Sullivan JM 2009. Global identification of yeast chromosome interactions using genome conformation capture. Fungal Genet Biol 46: 879–886 [DOI] [PubMed] [Google Scholar]
  49. Rosa A, Becker NB, Everaers R 2010. Looping probabilities in model interphase chromosomes. Biophys J 98: 2410–2419 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Russel D, Lasker K, Webb B, Velazquez-Muriel J, Tjioe E, Schneidman-Duhovny D, Peterson B, Sali A 2012. Putting the pieces together: integrative modeling platform software for structure determination of macromolecular assemblies. PLoS Biol 10: e1001244 doi: 10.1371/journal.pbio.1001244 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Schober H, Kalck V, Vega-Palas MA, Van Houwe G, Sage D, Unser M, Gartenberg MR, Gasser SM 2008. Controlled exchange of chromosomal arms reveals principles driving telomere interactions in yeast. Genome Res 18: 261–271 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Sekedat MD, Fenyo D, Rogers RS, Tackett AJ, Aitchison JD, Chait BT 2010. GINS motion reveals replication fork progression is remarkably uniform throughout the yeast genome. Mol Syst Biol 6: 353 doi: 10.1038/msb.2010.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Stouffer SA, Suchman EA, DeVinney LC, Star SA, Williams RMJ 1949. The American soldier: Adjustment during army life. Princeton University Press, Princeton [Google Scholar]
  54. Taddei A, Hedinger F, Neumann FR, Bauer C, Gasser SM 2004. Separation of silencing from perinuclear anchoring functions in yeast Ku80, Sir4 and Esc1 proteins. EMBO J 23: 1301–1312 [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Taddei A, Van Houwe G, Nagai S, Erb I, van Nimwegen E, Gasser SM 2009. The functional importance of telomere clustering: Global changes in gene expression result from SIR factor dispersion. Genome Res 19: 611–625 [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Taddei A, Schober H, Gasser SM 2010. The budding yeast nucleus. Cold Spring Harb Perspect Biol 2: a000612 doi: 10.1101/cshperspect.a000612 [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Takizawa T, Meaburn KJ, Misteli T 2008. The meaning of gene positioning. Cell 135: 9–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Tanizawa H, Iwasaki O, Tanaka A, Capizzi JR, Wickramasinghe P, Lee M, Fu Z, Noma K 2010. Mapping of long-range associations throughout the fission yeast genome reveals global genome organization linked to transcriptional regulation. Nucleic Acids Res 38: 8164–8177 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Therizols P, Duong T, Dujon B, Zimmer C, Fabre E 2010. Chromosome arm length and nuclear constraints determine the dynamic relationship of yeast subtelomeres. Proc Natl Acad Sci 107: 2025–2030 [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Thoma F, Koller T, Klug A 1979. Involvement of histone H1 in the organization of the nucleosome and of the salt-dependent superstructures of chromatin. J Cell Biol 83: 403–427 [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Thompson M, Haeusler RA, Good PD, Engelke DR 2003. Nucleolar clustering of dispersed tRNA genes. Science 302: 1399–1401 [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Towbin BD, Meister P, Gasser SM 2009. The nuclear envelope: A scaffold for silencing? Curr Opin Genet Dev 19: 180–186 [DOI] [PubMed] [Google Scholar]
  63. Yaffe E, Tanay A 2011. Probabilistic modeling of Hi-C contact maps eliminates systematic biases to characterize global chromosomal architecture. Nat Genet 43: 1059–1065 [DOI] [PubMed] [Google Scholar]
  64. Yang CH, Lambie EJ, Hardin J, Craft J, Snyder M 1989. Higher order structure is present in the yeast nucleus: autoantibody probes demonstrate that the nucleolus lies opposite the spindle pole body. Chromosoma 98: 123–128 [DOI] [PubMed] [Google Scholar]
  65. Zeileis A, Kleiber C, Krämer W, Hornik K 2003. Testing and dating of structural changes in practice. Comput Stat Data Anal 44: 109–123 [Google Scholar]
  66. Zimmer C, Fabre E 2011. Principles of chromosomal organization: Lessons from yeast. J Cell Biol 192: 723–733 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES