Predictive regulatory models in Drosophila melanogaster by integrative inference of transcriptional networks

Abstract

Gaining insights on gene regulation from large-scale functional data sets is a grand challenge in systems biology. In this article, we develop and apply methods for transcriptional regulatory network inference from diverse functional genomics data sets and demonstrate their value for gene function and gene expression prediction. We formulate the network inference problem in a machine-learning framework and use both supervised and unsupervised methods to predict regulatory edges by integrating transcription factor (TF) binding, evolutionarily conserved sequence motifs, gene expression, and chromatin modification data sets as input features. Applying these methods to Drosophila melanogaster, we predict ∼300,000 regulatory edges in a network of ∼600 TFs and 12,000 target genes. We validate our predictions using known regulatory interactions, gene functional annotations, tissue-specific expression, protein–protein interactions, and three-dimensional maps of chromosome conformation. We use the inferred network to identify putative functions for hundreds of previously uncharacterized genes, including many in nervous system development, which are independently confirmed based on their tissue-specific expression patterns. Last, we use the regulatory network to predict target gene expression levels as a function of TF expression, and find significantly higher predictive power for integrative networks than for motif or ChIP-based networks. Our work reveals the complementarity between physical evidence of regulatory interactions (TF binding, motif conservation) and functional evidence (coordinated expression or chromatin patterns) and demonstrates the power of data integration for network inference and studies of gene regulation at the systems level.

Transcriptional regulatory networks describe the regulatory program of individual genes by specifying the transcription factors (TFs) that regulate and determine the context-specific expression of a gene. In multicellular organisms, regulatory networks coordinate response to diverse extracellular signals and play a major role in the development and maintenance of living systems. These regulatory programs are often conserved across species, while their differences can form the foundation for morphological changes in animal body plans (Erwin and Davidson 2009). Therefore, regulatory network inference efforts—both experimental and computational—are critical to predicting cellular response and for understanding the role of gene regulation in development, evolution, and disease.

Reconstructed regulatory networks can be broadly categorized into physical regulatory networks and functional regulatory networks. A physical regulatory network is one where edges represent a physical interaction between a TF and a target as detected in chromatin immunoprecipitation (ChIP) assays or predicted using sequence-based DNA binding models (regulatory motifs). The edges in such a network may not necessarily lead to functional changes in gene expression. In contrast, a functional regulatory network is one where edges between TFs and their targets are supported by functional changes of downstream gene expression (Capaldi et al. 2008), even if these relationships may be indirect. The reconstruction of high-quality, genome-scale regulatory networks requires integration of both physical and functional evidence.

Substantial progress has been made in the assembly and analysis of regulatory networks in unicellular organisms such as Escherichia coli and Saccharomyces cerevisiae. For example, RegulonDB provides a literature-curated physical regulatory network for E. coli (Gama-Castro et al. 2008). Integration of the known regulatory interactions with coexpression data and sequence motif–inferred targets have enabled the reconstruction of genome-wide functional regulatory networks for E. coli (Ernst et al. 2008). In S. cerevisiae, physical regulatory networks have been assembled using ChIP for 203 TFs (Harbison et al. 2004) and conserved regulatory sites (MacIsaac et al. 2006), and a genome-wide compendium of physical, metabolic, genetic, and regulatory interactions has been generated using diverse functional data sets (Park et al. 2010).

The fruit fly Drosophila melanogaster provides an ideal model organism for the inference and study of functional regulatory networks in multicellular organisms. First, >100 yr of genetic experiments have resulted in a rich body of literature about regulatory relationships, which have resulted in small, but high-quality networks of known regulatory interactions such as REDfly (Halfon et al. 2008). Second, comparative sequencing of 12 Drosophila species (Drosophila 12 Genomes Consortium 2007; Stark et al. 2007) has provided a wealth of sequence information, which can be used to distinguish regulatory motif instances under purifying evolutionary selection that are thus more likely to be associated with functional edges (Kheradpour et al. 2007). Third, D. melanogaster has been the target of several recent studies mapping the in vivo binding of TFs, providing genome-wide target regions for a growing number of TFs (Zeitlinger et al. 2007; Li et al. 2008, MacArthur et al. 2009; Zinzen et al. 2009). Fourth, the availability of genome-wide data sets measuring mRNA expression levels for all genes across the developmental stages in D. melanogaster enables the identification of functional relationships between TFs and their targets.

These rich data sets saw a further dramatic improvement with the launch of the Drosophila Model Organism Encyclopedia Of DNA Elements (modENCODE) project (Celniker et al. 2009; The modENCODE Consortium et al. 2010). These include high-quality RNAseq time-course data sets measuring genome-wide transcriptional levels during development (Graveley et al. 2010), numerous histone modifications in two cell types (Kharchenko et al. 2011), as well as histone modifications and TF binding across the D. melanogaster developmental stages (Nègre et al. 2011). Together, the modENCODE project has assembled one of the most comprehensive collections of functional data sets for a single organism, which can greatly facilitate our ability to annotate functional elements of an animal genome and understand its regulatory circuitry.

Here, we present a network-based approach for large-scale functional data integration to understand gene regulatory mechanisms. We construct integrative regulatory networks, which leverage both physical and functional data sets to identify regulatory relationships between TFs and target genes, and use these networks for gene function and gene expression prediction. For the network inference component, we develop a machine-learning framework for inferring regulatory edges between TFs and target genes using both physical and functional data sets as input features. We use both supervised and unsupervised inference approaches, the former trained using the REDfly database (Halfon et al. 2008). We further introduce novel metrics to assess the biological relevance of inferred regulatory connections, based on known regulatory relationships, protein–protein interactions (PPIs), gene expression, tissue expression, gene ontology (GO) annotations, and Genome-Wide Chromosome Conformation Capture (Hi-C) contact maps showing three-dimensional contacts between chromosomal segments (Sexton et al. 2012). We use these metrics both to assess the contribution of different types of data sets toward network inference and also to compare the overall quality of both integrative networks and single-feature input networks.

We also leverage the integrative networks to gain insights into the regulatory properties of D. melanogaster. We characterize the topological properties of the resulting networks, evaluate their power for genome-wide prediction of candidate gene functions (GO process annotations), and study whether the expression levels of target genes can be predicted using linear combinations of the expression levels of their regulators, as dictated by the learned regulatory network. In contrast to previous methods for gene expression prediction (Bonneau et al. 2007; Bussemaker et al. 2007; Chikina et al. 2009) and gene function prediction (Zhang et al. 2004; Macskassy and Provost 2005; Sharan et al. 2007; Costello et al. 2009), we take a two-step approach here, in which regulatory networks are first inferred by data integration, and then prediction parameters are learned using the learned network topology. This enables us to learn predictive models using many fewer data sets, once the network topology is fixed.

Our results provide several new insights into gene regulatory networks:

• We find that the two types of evidence used in regulatory network inference are complementary: Physical information (TF binding, motif conservation) and functional information (coordinated expression and chromatin patterns) show little overlap, while their combination captures known regulatory edges the most accurately.

• We find that while physical information (TF binding, motif conservation) is the most informative feature for network inference as benchmarked against the known REDfly network, it alone shows almost no functional enrichments or predictive power for gene expression levels.

• We develop a set of novel validation metrics that can be used to assess the quality of inferred regulatory networks, which go beyond assessment based on known interactions and GO enrichment typical of previous network validation work.

• We provide new functional annotations for hundreds of previously unannotated genes, including several noteworthy examples in nervous system development (NSD) that are independently confirmed by their tissue-specific expression patterns in neuronal precursor tissues.

• We find that a linear regression model of predicting target gene expression level from TF expression level can predict the expression of ∼17% genes, and these “predictable” gene expression patterns are also more reproducible between different experiments.

• We find that the genomic regions of distal coregulated genes tend to be colocalized in three-dimensional chromosome conformation capture experiments, confirming that our regulatory predictions also reveal functional colocalization of genomic segments.

• We make both regulatory networks and the functional predictions available, together with source code for network inference and validation, to enable wider applicability of machine-learning methods in regulatory genomics.

Overall, the framework introduced here is general and should be applicable in any species. While we demonstrate the integrative approach to network reconstruction using the Drosophila modENCODE data sets, our approach will be particularly relevant as the human ENCODE project moves from 1% coverage in its pilot phase (The ENCODE Project Consortium 2007) to genome-wide coverage (The ENCODE Project Consortium 2011), which should enable functional comparisons between flies, worms, and mammals.

Results

Integrative inference of regulatory networks

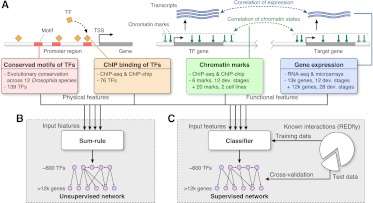
To reconstruct the integrative regulatory network of D. melanogaster, we used a machine-learning framework to combine both functional and physical regulatory interactions (Fig. 1). The physical TF–DNA regulatory interactions consist of (1) evolutionarily conserved instances of TF binding site motifs across 12 Drosophila genomes (Kheradpour et al. 2007; Stark et al. 2007) for 139 TFs with known motifs, and (2) experimentally defined TF binding occupancy profiles from ChIP studies for 76 TFs (Zeitlinger et al. 2007; Li et al. 2008; MacArthur et al. 2009; Zinzen et al. 2009; Nègre et al. 2011). The functional data sets are summarized in Table 1 and consist of (1) profiles of chromatin modifications and general transcriptional regulators in two cell types and across the developmental time-course (Kharchenko et al. 2011; Nègre et al. 2011), and (2) gene expression profiles across the developmental time-course (Hooper et al. 2007; Nègre et al. 2011).

Figure 1.

Overview of inference methodology for supervised and unsupervised functional regulatory networks. (A) The four types of input features to the network inference algorithms are: evolutionary conserved motifs (red) and ChIP-based binding (orange) of TFs near the transcription start site (TSS) of target genes (physical features), and correlation of chromatin (green) and expression (blue) profiles between TFs and target genes (functional features). (B) Unsupervised network inference: An integrative network is formed by adding the evidence from each input feature with equal weight (sum-rule). (C) Supervised network inference: The input features are used in a classifier that predicts for every TF–target pair the presence or absence of a regulatory interaction. The classifier is trained on a literature-curated set of known interactions (REDfly).

Table 1.

Number of genes, conditions, and type of measurements for expression and chromatin modification data sets

To enable integration across these diverse types of data, we represented each data set as a directed, weighted network, with edges from TFs to target genes and weights proportional to the strength of regulation evidence (see Methods). This resulted in six feature-specific networks, which form the basis for the integrative functional regulatory networks. The two physical feature-specific networks, referred to as the motif regulatory network and binding regulatory network, are based on evolutionarily conserved motif instances and TF occupancy data sets, respectively. The weights of the motif network come from the strength of the evolutionary conservation (Kheradpour et al. 2007). The binding network has binary weights, based on the presence of ChIP binding peaks. Both motif instances and ChIP binding peaks are restricted to a window of ±500 bp around the transcription start site (TSS) of a target gene. The four functional feature-specific networks are based on two expression and two chromatin profile data sets (Table 1). Weights in the expression- and chromatin-based networks are given by the correlation between TF and target gene expression profiles and chromatin profiles, respectively (see Methods).

We used both an unsupervised and a supervised method to combine the six feature-specific physical and functional networks to infer an integrative regulatory network (Fig. 1). We estimated an edge “weight” for each possible TF-target pair, as a function of the six feature-specific weights provided by the input networks. For the unsupervised network, we used the average of all the input weights across the six networks (see Fig. 1B; Methods). This approach was chosen for its simplicity, as a baseline for comparison with the supervised network. For the supervised network, we trained a logistic regression classifier based on known regulatory interactions from the REDfly database, version 2.2 (Halfon et al. 2008), using 10-fold cross-validation (see Fig. 1C; Methods). This resulted in two integrative networks, one supervised and one unsupervised, each showing high coverage and connecting ∼600 TFs with over 12,000 target genes (Supplemental File 1).

Network overlap and recovery of known regulatory interactions

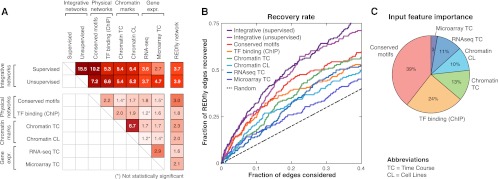
To assess how informative individual feature-specific networks are for predicting regulatory edges between TFs and their target genes, we compared their edges with edges from REDfly. Each feature-specific network showed significant similarity to the REDfly network, with edges present in each network significantly more likely to also be present in the REDfly network than would be expected by chance (Fig. 2A, rightmost column). Among the feature-specific networks, the network based on evolutionarily conserved motif instances showed the strongest enrichment for REDfly edges (threefold enrichment). Note that the motif network is the only feature-specific network that integrates an evolutionary conservation score, which may explain its high enrichment: Evolutionary conservation is known to be a strong predictor of functional regulatory elements (MacIsaac et al. 2006; Kheradpour et al. 2007). The integrative networks that combine the evidence of all feature-specific networks, however, had the strongest enrichment for REDfly edges (supervised, 3.7-fold; unsupervised, 3.9-fold), demonstrating that integration of diverse features leads to higher recovery of true regulatory relationships. The recovery of REDfly edges by the different feature-specific networks (Fig. 2; Supplemental Fig. 1), as well as the weights assigned to these features by the supervised algorithm (Fig. 2C), show that the evolutionarily conserved motifs were the most informative, followed by TF binding (ChIP), chromatin marks, and expression data.

Figure 2.

Comparison of known, predicted, and single-feature networks. (A) Pairwise network comparison based on the enrichment for common interactions among feature-specific networks (physical, chromatin, gene expression), the integrative networks (supervised and unsupervised), and the REDfly network. (Black) Enrichment values that are statistically significant (P < 0.05, hypergeometric); (gray) enrichment values not statistically significant. Enrichment of each feature-specific network with REDfly tends to be stronger than its enrichment to other feature-specific networks of different types (between physical, chromatin, expression), suggesting that these features are capturing complementary sets of interactions. Integrative networks show the strongest enrichment for known edges. (B) Recovery of known REDfly edges at different thresholds for both integrative and feature-specific networks. (Curves) The fraction of the 204 REDfly edges recovered versus the fraction of predicted interactions considered (the expected number of edges recovered by chance [random; dashed line] is kP/T, where k is the number of edges considered, P is the number of REDfly edges, and T is the total number of possible edges). Integrative networks reach significantly higher recovery rates than single-feature networks, highlighting the importance of data integration. (C) Relative importance of the different input features in the supervised integrative network evaluated as the percentage contribution to the increase in scores of the top 10,000 edges (see Methods). Evolutionarily conserved motifs are the strongest contributor, followed by TF binding data (ChIP), chromatin marks, and expression data.

We next compared the feature-specific networks to each other and to the integrative networks (Fig. 2A). The integrative networks showed the strongest enrichment for the motif network, followed by the ChIP binding network and chromatin networks, suggesting that these are the strongest contributors. We found that feature-specific networks were more similar to the integrative networks than to other feature-specific networks, suggesting that our features are complementary and also that our integrative networks have captured their complementary properties. The only exception was a strong pairwise enrichment between the two chromatin networks (6.7-fold vs. 5.2- and 5.4-fold enrichment for the two integrative networks); a moderate enrichment was also found between the two expression data sets (2.9-fold), but this was still smaller than their average similarity to the integrative networks (3.7-fold). Remarkably, the motif-based, chromatin-based, and expression-based feature-specific networks also showed, on average, higher similarity to REDfly edges than to feature-specific networks of different types of evidence (i.e., between expression, chromatin, motifs, and binding), again emphasizing the power of integrating diverse data types for recovering true regulatory edges. The only exception was the TF binding–based networks that showed higher similarity to chromatin networks, likely due to previously reported nonspecific TF binding in regions of accessible chromatin (The modENCODE Consortium et al. 2010).

We also assessed how varying the cutoff for predicting interactions in the feature-specific and integrative networks affected the recovery of edges in the REDfly network. We found that both integrative networks recovered a higher number of REDfly edges than any feature-specific network (Fig. 2B). For example, the top 100 predictions of our integrative networks recover 20 REDfly edges compared with less than four expected at random. In contrast, only five to 13 are recovered in the top 100 predictions of the feature-specific networks.

In summary, the fact that the REDfly edges were among the highest-scoring predicted edges of the integrative networks confirms both the importance of integration of different features for regulatory network inference and that our approach is able to do this successfully.

Functional enrichments of regulatory networks

In addition to the recovery of known regulatory relationships, we assessed the biological relevance of the physical and integrative networks based on the tendency of genes targeted by similar TFs (coregulated targets) to exhibit similar functional properties. For each network, we measured the enrichment of coregulated genes in five independent data sets: (1) GO functional annotations, (2) tissue-specific gene expression patterns, (3) an independent expression time-course that was not used for network inference, (4) PPI networks, and (5) contact maps of three-dimensional chromosome conformation. We also computed these measures for the REDfly network, both to validate our evaluation methodology and to compare the performance of our networks to the gold-standard, but much lower-coverage curated, network.

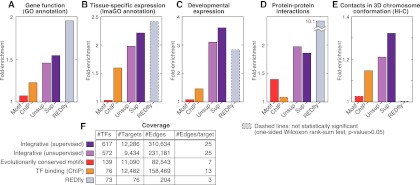
First, we evaluated whether pairs of genes targeted by common regulators show similar GO annotations, reasoning that coregulated genes may participate in similar processes or have similar functions. We extracted pairs of target genes that share >50% of their regulators and computed enrichment for common GO terms (as well as corresponding P-values; see Methods). As expected, the REDfly network showed the highest fold enrichment for cotargeted genes to show similar GO terms (approximately twofold vs. randomized networks), which confirms the relevance of this metric (Fig. 3A). The two integrative networks were also significantly enriched (∼1.5-fold), while including ∼10-fold more TFs and ∼100-fold more targets than REDfly. In contrast, the motif and binding networks show relatively lower enrichment (1.07- and 1.23-fold, respectively). These enrichments in the independent GO data sets support the functional relevance of the integrative networks.

Figure 3.

Functional enrichment and coverage of regulatory networks. Functional enrichment of coregulated genes for annotation with similar functions (A), colocalization in tissues (B), coexpression in an independent developmental time-course (C), physical interactions between coregulated genes (D), and colocalization in three-dimensional chromosome conformation (E). (F) Coverage of the networks. The manually curated REDfly network shows strong enrichment for coregulated genes to be annotated with similar functions, colocalized in tissues, coexpressed in development and to physically interact, thus supporting the relevance of these metrics, although it did not pass the significance test in B,C, and E due to its small size. The integrative networks show significant enrichment for all five metrics, while including ∼10-fold more TFs and ∼100-fold more targets than REDfly. In contrast, the two physical networks (conserved motifs and ChIP binding) show relatively lower enrichment.

Second, we reasoned that coregulated genes might be localized to similar tissues. To assess this, we used the Image Gene Ontology (ImaGO) of 145 distinct tissue terms (Tomancak et al. 2007), which describes the spatial pattern of gene expression based on in situ hybridization on whole-mount embryos. We computed the enrichment of ImaGO annotations among pairs of genes having >50% of their regulators in common (see Methods). Although the REDfly network reaches the highest fold enrichment (2.4-fold vs. randomized networks), it did not pass the significance test due to its small size (Fig. 3B). The two integrative networks had similar, high enrichment (about twofold), while the motif and binding networks had none or weak enrichment, suggesting that our integrative networks are highly relevant for determining tissue-specific expression.

Third, we reasoned that coregulated genes may be more likely to be expressed at similar developmental stages. We computed the average coexpression level of genes with >50% common TFs across a 30-time-point RNA-seq developmental time-course (Graveley et al. 2010), which was not used as an input feature for the network construction. The strongest enrichment was again observed in the two integrative networks and REDfly (about threefold) (Fig. 3C), although for the small REDfly network the enrichment is not statistically significant. In contrast, physical networks showed weak enrichment (<1.5-fold) that was not significant, confirming the relevance of our integrative networks for determining developmental expression.

Fourth, we reasoned that physically interacting genes should tend to be coregulated, as has been previously observed in yeast (Yeger-Lotem et al. 2004). Thus, we evaluated the overrepresentation of PPIs for genes that are coregulated, using a set of high-confidence PPIs from the literature (Pacifico et al. 2006; see Methods). Indeed, the REDfly network showed strong enrichment for PPIs among coregulated genes (10-fold) (Fig. 3D). The two integrative networks were also significantly enriched (∼1.9-fold), while the physical networks showed weak or no enrichment, again supporting the functional relevance of the inferred integrative networks.

Fifth, we evaluated whether the regulatory information captured in our networks relates to three-dimensional chromosome organization in the nucleus. By using chromosome conformation capture followed by high-throughput sequencing (Hi-C), a recent study has produced high-resolution contact maps of fly embryonic chromosomes, revealing that chromosomes are organized hierarchically in a functional manner (Sexton et al. 2012). We used the resulting data sets to evaluate whether the genomic regions of distal coregulated genes are enriched for nuclear colocalization in the Hi-C contact map (see Methods). Indeed, we found that both the supervised and unsupervised integrative networks are significantly enriched for nuclear colocalization of coregulated genes (1.3- and 1.2-fold, respectively) (Fig 3E). In contrast, the motif network and binding networks show none or weak enrichment, and the REDfly did not contain any coregulated genes within colocalized regions.

Taken together, the observed enrichments in all five data sets considered strongly confirm the biological significance of the integrative networks.

Structural properties of regulatory network

We next analyzed the structural properties of the integrative networks. We found that the number of targets for each TF (out-degree) exhibited a scale-free distribution expected for biological networks and similar to those previously observed in E. coli (Balázsi et al. 2005) and S. cerevisiae (Supplemental Fig. 2; Guelzim et al. 2002; Stewart et al. 2009). There are large variations in the number of targets per TF, with some TFs targeting several thousand genes (e.g., ∼6000 targets for Myb) and many others only few genes (Supplemental Files 3,4). The integrative networks also showed high clustering coefficients and small characteristic path lengths (Supplemental Fig. 3) characteristic of small-world networks (Jeong et al. 2000; Ravasz and Barabási 2003; Potapov et al. 2005; Lancichinetti et al. 2010). The genome-scale nature of our regulatory network also enabled us to study the distribution of the number of TFs for each target, which is difficult in TF-centric approaches such as ChIP-seq and ChIP-chip, which analyze only a few TFs at a time. We found that the number of TFs for each target (in-degree) also obeyed a scale-free distribution consistent with E. coli and S. cerevisiae. Most genes are targeted by few regulators (50% have ≤10 regulators), while a handful of genes are heavily targeted by hundreds of regulators (e.g., 180 regulators for predicted zinc-finger regulator CG15514). The heavily targeted genes are enriched in a range of GO biological processes related to gene regulation, including cell cycle, regulation of gene expression, and regulation of metabolic processes (Supplemental File 5). This suggests regulatory feedback and signal integration, as the most heavily targeted genes are themselves regulators. Indeed, these networks were also enriched for feed-forward and feedback loops and other motifs suggesting extensive cooperation and combinatorial control (Supplemental Fig. 4B; Supplemental Note 1), as well as high interconnections with miRNAs (Supplemental Fig. 4A).

Prediction of candidate functions for genes lacking functional annotations

As a demonstration of the utility of the regulatory information captured in the inferred networks, we sought to predict likely GO process terms for previously uncharacterized genes using a “guilt-by-association” approach (Macskassy and Provost 2005). In this approach, GO process categories of unannotated genes are predicted based on the GO categories of other genes with similar functional properties. However, while previous approaches had only used expression evidence (Zhang et al. 2004), protein interaction networks (Sharan et al. 2007), or genetic interactions (Costello et al. 2009), we combined regulatory information and expression information to leverage the “coregulation” information captured by our regulatory networks (see Methods).

To combine coexpression with coregulation, we first grouped genes into 34 similarly expressed clusters using a Gaussian mixture model, where each gene was probabilistically assigned to a cluster based on the similarity of its expression profile with the average expression profile of the cluster. We also defined a regulatory similarity score for every pair of genes based on the proportion of regulators that they have in common. We then computed a score for a given query gene to be a member of a GO process category, based on its regulatory similarity to all genes in that category, weighed by the probability of belonging to the same expression cluster as the query gene (see Methods).

We used this approach to predict candidate functions for genes with no previous GO process annotations, as well as additional candidate annotations for genes that are already annotated with a GO process (Supplemental File 7). Only genes that are part of the integrative networks were considered. At any score cutoff, we estimated the false-discovery rate (FDR) of our predictions for a given GO process category (see Methods; Supplemental Fig. 5). At a FDR ≤ 0.2, using the unsupervised network, our approach predicts GO process annotations for 23% of the genes with no previous annotation and additional annotations for 15% of genes with previous annotations. Our predictions include both general processes, such as oxidative phosphorylation and regulation of gene expression, as well as specific developmental processes, such as NSD and muscle structure development. Compared to using expression information alone, the combination of network information and coexpression was able to predict more GO process terms, especially for low FDR (Supplemental Fig. 5), suggesting that combined evidence leads to improved predictive power.

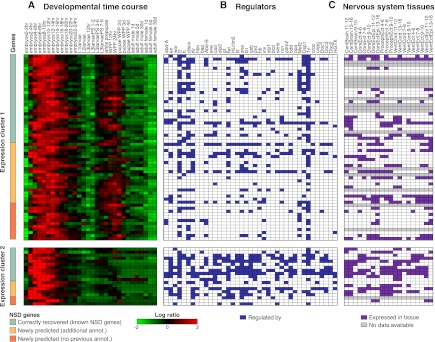
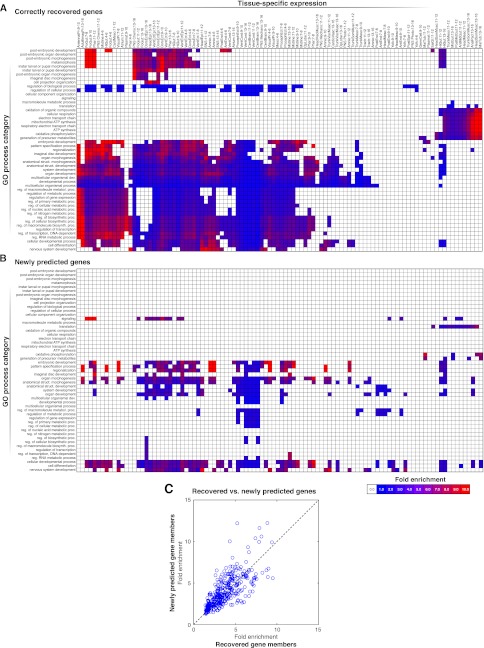
For example, we predicted a function in NSD for 101 genes, which included 42 recovered, known members (true positives) and 59 newly predicted members of NSD. The majority of these genes (80) belong to two main expression clusters (Fig. 4). The first cluster comprises genes that peak in expression at embryo 4–14 h and again in late larval and prepupal stages, as expected for NSD genes (Levine et al. 1995). The second expression cluster comprises genes that peak at the embryonic time points only. Moreover, according to their ImaGO annotation (Tomancak et al. 2007), the newly predicted NSD genes show tissue-specific expression in neural precursor tissues (e.g., central brain, ventral cord, and dorsal, ventral, and procephalic ectoderm), similar to many known NSD genes, even though this information was not used to make the predictions (Fig. 4C). This suggests that many of the new predictions, including 29 genes that lacked any previous functional annotation, are likely to function in NSD.

Figure 4.

Genes predicted to function in nervous system development (NSD). Gene expression (A), regulators (B), and ImaGO tissue annotation (C) for correctly recovered (known) and newly predicted NSD genes. The two expression clusters comprising the majority of the predicted NSD genes are shown. The two clusters are driven by different, but largely overlapping, sets of regulators. Within each of the two clusters, the newly predicted NSD genes show similar expression profiles and similar sets of regulators to those of the recovered, known NSD genes. Moreover, both the recovered and the newly predicted NSD genes show similar expression patterns in nervous system tissues, which were not used as input features.

Inspired by the NSD enrichments for neural tissues, we systematically compared the tissue-specific expression of newly predicted versus the correctly recovered (known) gene members of a GO process category, as an additional validation of our predictions. For every GO process term, we tested both the set of newly predicted and the set of recovered, known gene members for ImaGO tissue enrichments, which were not used to make the GO process predictions and thus provide an independent source of validation. Indeed, we found that the newly predicted gene members were generally enriched in similar tissues as the recovered, known gene members of a given GO term (Fig. 5A,B), supporting the biological relevance of our predictions.

Figure 5.

Tissue-specific expression of correctly recovered (known) versus newly predicted genes of different GO process categories. (A) The heatmaps show, for the set of predicted gene members of each GO category (rows), the enrichment for expression in specific tissues (columns). Only those GO processes that are significantly enriched in at least one tissue (hypergeometric test with FDR < 0.05; Methods) are shown. For most GO categories, the correctly recovered (known) genes are enriched in specific tissues. (B) The newly predicted genes for a given GO category tend to be enriched in fewer, but similar, tissues as the known gene members. (C) The scatter plot compares the fold-enrichment (see Methods), for the ImaGO tissues that were enriched in both the recovered and newly predicted gene members of a given GO category. For these same tissues that the known genes are enriched for, the newly predicted genes have similar or higher enrichment.

For the ImaGO tissues that were enriched in both the novel and the correctly recovered, known gene members of a given GO category, we further compared the fold-enrichment values in the two gene sets. As our method leverages regulatory similarity between unannotated and annotated genes to identify new members of a functional category, we should expect that newly predicted members of a functional category are also more likely to be coregulated, and thus we should expect enrichments that are at least as high. In fact, we found that the ImaGO tissue enrichment for the newly predicted members was actually higher, on average, than the corresponding enrichment for the recovered, known members of the same GO term (Fig. 5C; Supplemental File 8). For example, genes newly predicted to function in the pattern specification process showed a 10-fold enrichment for midline tissues, whereas recovered members of this GO category only showed a 4.3-fold enrichment. These results not only confirm that the newly predicted GO process annotations are consistent with tissue-specific behavior of these genes, but they also demonstrate the power of our integrative regulatory networks for function prediction.

Predicting target gene expression level as a function of TF levels

Numerous studies have shown that multiple regulators can act together in additive and combinatorial ways to determine the expression of a downstream target gene (Bussemaker et al. 2007). These studies have typically focused on a small number of high-confidence regulatory edges, which also are frequently coupled with experimentally determined parameters for activation, repression, and cooperation. It is not clear however, how such studies can scale to genome-wide prediction of gene expression across thousands of genes.

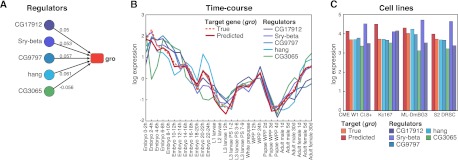
To address this question, we used regulatory relationships captured by the integrative regulatory networks to predict the expression of each target gene as a function of the expression of its predicted regulators. With no access to parameters for regulator activity or motif “grammars” dictating cooperation (Wilczynski and Furlong 2009), we used a simple regression model to predict the expression level of a target gene as a linear combination of the expression levels of its regulators (see Methods). We used expression levels in a 30 time-point developmental time-course obtained using RNA-seq to learn the regression weights (Graveley et al. 2010), a data set that was specifically not used as an input feature to our network inference algorithm, and assessed predictive performance using 10-fold cross-validation. By use of this approach, we learned linear models for all target genes that are part of the integrative regulatory networks and have measured expression in the developmental time-course. The learned weights represent an aggregate effect of trans-acting (Boulesteix and Strimmer 2005; Boorsma et al. 2008) and cis-acting effects (Raveh-Sadka et al. 2009), which would be difficult to explicitly model individually because we do not measure these aspects of regulation. As a representative example, the regulatory model and expression prediction of the gro target gene are shown in Figure 6 (for additional examples, see Supplemental Fig. 6 ). We note that 30 time-points would have probably been insufficient to learn predictive expression models de novo, but in this particular case, we have already learned the topology of the network by data integration, and we are only using these 30 time-points to learn edge weight parameters.

Figure 6.

Expression prediction of the gro target gene. (A) The top five regulators of the gro gene and the magnitude of the regression coefficients. Regulators are colored based on the sign and magnitude of the regression coefficient (green indicates repressors; red, activators; darker, stronger). (B) True expression (dashed orange line) and predicted expression (solid red line) for the gro gene across the developmental time-course. The remaining lines show the corresponding expression profiles of the five regulators, colored according to panel A. (C) True and predicted expression levels of the gro gene in four cell lines, using the same coefficients from panel A as learned on the expression time-course. The expression levels of the five regulators are also shown.

To evaluate the predictive power of the integrative networks compared to other networks, we applied the same approach to predict expression using the feature-specific network based on ChIP binding, the feature-specific network based on conserved sequence motifs, and the REDfly network. For each considered network, we compared the average squared error across all genes to the squared error obtained using the same learning scheme on a randomized network (see Methods). For instance, of the 8433 target genes that were in the unsupervised network and had measured expression in the developmental time-course, expression was predicted substantially better for 1988 genes and worse for 787 genes compared to a randomized network, corresponding to a 2.53-fold enrichment for higher accuracy (Supplemental Table 1). Similar results were obtained for the supervised integrative network (2.03-fold enrichment). In contrast, the ChIP-based and motif-based physical regulatory networks showed almost no enrichment compared with randomized networks (1.04- and 1.08-fold, respectively), even though they were two of the strongest informers of the integrative network, suggesting that they are informative but not predictive in isolation. Lastly, the REDfly network showed the strongest enrichment compared with random networks (3.9-fold enrichment), but due to its small size the expression of only 76 genes was predicted, emphasizing once more the importance of genome-wide network inference.

For each network, we defined a set of “predictable” genes for which expression prediction errors were consistently lower than random networks (six out of 10 random networks), and a set of “unpredictable” genes for which expression prediction errors were consistently higher in six out of 10 random networks. We found that the integrative networks showed more than 1000 predictable genes, for both the unsupervised network and the supervised network, while the motif network had fewer than 200 predictable genes and the ChIP network actually showed an excess of unpredictable genes (Supplemental Table 1). These results were also supported by comparison of the squared error distributions between the true and randomized networks, which were significantly different for the integrative networks (t-test, P < 0.05), but not for the motif and ChIP networks (Supplemental Fig. 7). At a more stringent threshold of eight out of 10 for predictable genes, the supervised and unsupervised networks still show a fourfold enrichment over motif and ChIP networks (8% and 9% vs. <2% of predictable genes).

Last, we evaluated whether the coefficients learned in the developmental time-course were also relevant for target gene expression prediction in independent conditions, which were not used in model learning and were not represented in any other expression data set. We used two hold-out data sets of four RNA-seq (Graveley et al. 2010) and 25 microarray (Cherbas et al. 2011) cell-line experiments. For each predictable gene, we used the model learned in the time-course experiment to predict its expression in the cell lines. We found that for the integrative networks, over 66% of predictable genes remained predictable in the RNA-seq cell line data sets compared with <52% for the ChIP and motif networks (Fig. 6C; Supplemental Table 1). Additionally, for the integrative networks, over 56% of predictable genes were also predictable in the 25 cell line data sets compared with <42% of unpredictable genes, suggesting that both the coefficients learned and the predictability of genes were relevant in independent conditions.

It is possible that genes that were unpredictable with the linear regression model used here could be less tightly regulated. To test this we evaluated the reproducibility of expression patterns across the developmental time-course of predictable and unpredictable genes. For each set of genes, we quantified the correlation of gene expression patterns between the 30-time-point developmental expression data set (Graveley et al. 2010), and the 11-stage time-course data set sampled at longer time intervals (Nègre et al. 2011). We found that predictable genes showed a significantly higher correlation between the two data sets compared with the remaining genes (P-value < 1 × 10⁻⁷ and 1 × 10⁻³⁹ in the unsupervised and supervised networks, respectively) (Supplemental Fig. 8), suggesting that predictable genes are also more reproducible. If we assume that more highly reproducible expression corresponds to less noisy and perhaps more precisely regulated genes, this suggests that our inability to predict gene expression for some genes may be due to intrinsic variability in their expression levels.

Overall, our results demonstrate the potential of regulatory networks for gene expression prediction. While the simple linear model used here could only predict the expression of a subset of the genes, our results suggest that unpredictable genes may in fact be more noisy or less tightly controlled and that predictable genes remain predictable in new cellular conditions, suggesting that the coefficients learned for many of our genes are biologically relevant. While the results here are encouraging, building predictive models of gene regulation remains an enormously difficult problem. Continued advances will likely benefit from more complex models of gene regulation that potentially incorporate genome sequence in determining the weights and combinatorial relationships between regulators in predicting the expression levels of downstream genes.

Discussion

In this article, we integrated diverse genome-wide data sets generated by the modENCODE consortium using a machine-learning framework to reconstruct genome-wide regulatory networks for the model organism D. melanogaster, and investigated both supervised and unsupervised learning paradigms. Our networks can recover many more edges in the curated REDfly network than can physical networks that rely solely on motif or ChIP data. Analysis of input feature importance to the integrative network quality showed that evolutionarily conserved motif instances were the strongest contributor, followed by TF binding and chromatin information, while coexpression information was the weakest contributor. Enrichment of cotargeted genes in common GO functional categories, common developmental and tissue expression, PPIs, and chromosome conformation colocalization further confirmed the biological relevance of the predicted networks. The integrative networks showed comparable enrichments to the manually curated REDfly network for each of the four data sets where its enrichment could be evaluated, while including 10-fold more regulators (∼600 vs. 73), 100-fold more targets (∼10,000 vs. 76) and 1000-fold more edges (>200k vs. 204). Finally, we used the networks to infer GO process annotations for genes lacking a previous annotation and to predict expression levels of target genes as a function of the expression levels of their upstream regulators. In both prediction tasks, integrative networks strongly outperformed all feature-specific networks and the REDfly network.

Comparison with expression-based functional networks

Traditional network reconstruction approaches are unsupervised in nature where the goal is to infer the edges based on the observed expression of a node. While such approaches have been successful in inferring functional networks (Bonneau et al. 2007; Roy et al. 2009), their success in inferring regulatory networks has been hampered by the difficulty of distinguishing direct from indirect interactions from expression data. These indirect links can arise between cotargeted genes of the same TF or between a TF and a target separated by an intermediate TF (Marbach et al. 2010), as indirect links are likely to have a high score in coexpression driven inference. In contrast, in network inference driven entirely by TF binding, indirect links are all automatically discarded in the absence of physical evidence of binding. By combining expression information with experimental and computational evidence of TF binding (ChIP and motifs, respectively), integrative networks limit indirect links and recover known REDfly edges much more accurately than the purely expression-based networks.

Comparison with network inference based on sequence motifs and ChIP binding

A canonical way to reconstruct a regulatory network is to identify instances of known TF motifs in the regulatory regions of genes (Kheradpour et al. 2007). The major difficulty with this approach is that we can infer edges only from well-characterized TFs that have a known binding site associated with them. A complementary approach is to perform ChIP assays for TFs of interest, followed by motif discovery on the bound regions of the genome. While these approaches can infer direct, physical edges, they also identify “nonfunctional” edges that do not result in changes in gene expression (Li et al. 2008). In our setting, we had only 139 TFs with known motifs and 76 TFs with ChIP data, which constitutes about a sixth of the TF space we wanted to span. We leveraged motif and ChIP wherever possible, but we relied on expression and chromatin data to complement the physical evidence. This has the advantage of inferring edges that are both physical and functional and resulted in a global map with similar functional enrichments to the hand-curated REDfly network, while having dramatically higher coverage for TFs, targets, and edges.

Comparison with other integrative approaches

Previous integrative methods for transcriptional network inference were mostly centered on expression-based approaches, either integrating different types of expression data (Greenfield et al. 2010; Gupta et al. 2011) or using an additional data source as a fixed prior for expression-based inference (Bernard and Hartemink 2005). Supervised inference methods were used to integrate known interactions from curated databases as training data, but only used expression data as an input feature to predict interactions (Qian et al. 2003; Seok et al. 2010). A notable exception is the method of Ernst et al. (2008), which uses both sequence motifs and expression data as input features. However, this method trains a local classifier for each individual TF and is thus not well suited for higher organisms, where little or no training data are available for the majority of TFs. In contrast, we trained a global classifier to predict regulatory interactions by integrating motif, binding, chromatin, and expression data as input features. Interestingly, our analysis showed that chromatin profiles were more informative than the commonly used expression profiles (Fig. 2C), suggesting that epigenomic data sets represent a hitherto underappreciated data source for functional network inference.

Comparing supervised and unsupervised learning

While there are many computational approaches to infer networks and to integrate data, it is not clear which particular method is useful for the task of regulatory network reconstruction by integrating different data sets. Supervised learning approaches make efficient use of the available interactions, whereas unsupervised learning approaches are unbiased and applicable to organisms lacking sufficient training data. Here, we investigated both supervised and unsupervised learning frameworks where each data source served as an additional source of regulatory evidence for inferring an edge. Interestingly, we found that the unsupervised approach performed comparably on the REDfly network as did the supervised approach, which was specifically trained on REDfly. This competitiveness of the unsupervised strategy is likely due to the very limited number of known interactions used for training the supervised approach and shows that an unsupervised, integrative network inference approach is a promising direction to pursue for inferring regulatory networks especially for organisms with little or no training data. It also emphasizes the need for continued validation of high-confidence interactions to enlarge the size of gold-standard networks that can be used for training computational methods.

Comparing input features

The value of data integration cannot be overemphasized for the task of regulatory network inference. We used our integrative framework to study the usefulness of different features for regulatory network inference in the context of REDfly. While motifs were the strongest contributors to recovery of the known REDfly network, we found that chromatin profiles of TFs and their targets were also major contributors, enabling us to infer targets of TFs lacking motifs or ChIP information. Previous work has shown that networks derived from different types of data may be affected by different biases in inference (Marbach et al. 2012). Indeed, the feature-specific networks were complementary to each other, namely, those edges that could be predicted by one feature were not necessarily predictable by the other, further demonstrating the need to integrate complementary data sources. While some feature-specific biases may be inherited by integrative networks, for example, stemming from the selection of TFs that have been experimentally profiled or contain known regulatory motifs, the overlap of the different data sources helps reduce these potential biases and add more confidence to the inferred edges. Overall, integrating different types of data sets is critical for reconstructing a reliable picture of the regulatory network, especially for multicellular organisms, which have multiple layers of regulation, and where physical edges are less directly linked to functional edges.

The role of network topology

We found that the integrative Drosophila networks exhibit scale-free degree distributions, high clustering coefficients, short average path lengths, and enrichment for feedback and feed-forward loops. These structural properties have been previously identified in regulatory networks of unicellular organisms such as E. coli and S. cerevisiae, where they have been linked to systems-level properties such as robustness and adaptability (Alon 2007; Tsang et al. 2007). The integrative networks presented here will enable an exploration of the potential role in network dynamics and evolution of such structural properties in Drosophila.

Prediction of gene functions and expression levels

The ultimate test for a regulatory network is the ability to predict attributes of nodes using the network connectivity patterns. Our results demonstrate that integrative regulatory networks can be used to predict biological process annotations and expression levels of target genes. On one hand, integrative networks enable accurate prediction of novel functional annotations for genes based on their “regulatory neighborhood,” resulting in candidate functional annotations for ∼700 previously uncharacterized genes. On the other hand, we leveraged the integrative networks for gene expression prediction, by learning a linear regression model for the expression levels of every target gene based on its set of predicted regulators, demonstrating significantly more accurate predictions than ChIP or motif-based networks. These results demonstrate that integrative networks define “functional regulators” relevant in both function and expression prediction. We found that a linear regression function was predictive for ∼20% of target genes, but we expect that higher-order and combinatorial functions may be prevalent, although they were not tested here. While numerous alternative methods exist to predict gene function (Zhang et al. 2004; Macskassy and Provost 2005; Sharan et al. 2007; Costello et al. 2009) and expression (Bonneau et al. 2007; Bussemaker et al. 2007; Chikina et al. 2009), our goal was to evaluate the predictive power of integrative networks, not to explore the space of possible regulatory functions, which merits further investigation. More complex models of gene regulation (e.g., Boulesteix and Strimmer 2005) may further improve the predictive power of these integrative networks but may require significantly richer training data sets given their increased dimensionality.

Nuclear colocalization of coregulated genes

Our results also have strong implications for the functional hierarchical organization of chromosomes within Drosophila nuclei recently revealed using Hi-C chromosome conformation capture (Sexton et al. 2012). Sexton et al. (2012) reported highly specific chromosomal colocalization hotspots, where the three-dimensional chromosome conformation brings together distal regions driven by functional relationships rather than genomic proximity. The reported hotspots include colocalization of both active and repressed domains and several examples of distal functionally related genes. Our integrative regulatory networks show significantly stronger agreement than motif or ChIP networks, suggesting a global association between colocalization and coregulation, which was eluded to in the Sexton et al. (2012) study but not shown for more than a handful of examples. Our results indeed confirm that this is the case, supporting the hypothesis that nuclear colocalization is involved in coregulation.

Overall, our integrative regulatory networks provide an initial summary view of the regulatory interactions of a multicellular organism, which are undoubtedly more complex than what we have captured here. These networks are likely tissue-specific, stage-specific, and modulated by complex environmental interactions. As genome-wide data sets that capture this additional complexity become available by probing chromatin, TF binding and expression levels from specific tissues and in diverse conditions, we expect that the general network inference techniques presented here will continue to provide useful abstractions and help gain new insights into general principles of eukaryotic and animal gene regulation.

Methods

Input data sets

We assembled a comprehensive compendium of genome-wide data sets that we used as inputs for our integrative reconstruction of the transcriptional regulatory network of Drosophila. Our first inputs were conserved TF motif instances for a set of 139 known TF binding motifs collected from the literature (Kheradpour et al. 2007). Due to the short length of motifs, many instances of motifs in a single genome are expected to be coincidental matches that may not be bound in vivo or have no functional regulatory effect. As evolutionary conservation of an instance is an indication of a functional instance, Kheradpour et al. (2007) used a robust phylogenetic framework that accounts for the evolutionary relationships across 12 sequenced Drosophila species to assign a conservation score to each motif instance measured as 1-FDR and referred to as confidence.

Our second input data set consisted of a compendium of genome-wide TF binding data sets obtained from ChIP-chip and ChIP-seq assays from the modENCODE project and from 14 previously published studies used by the modENCODE Consortium et al. (2010). In total, these data sets include 76 TFs in a range of tissue and cell-line samples.

Our third input data set consisted of genome-wide location data for chromatin marks and chromatin remodeling factors, which was generated by the modENCODE project using ChIP-chip and ChIP-seq. Chromatin profiles were included for six modifications in a developmental time-course of 12 stages (Nègre et al. 2011) and for up to 20 modifications in two cell lines (Kharchenko et al. 2011).

Our fourth data set comprised gene expression profiles generated by RNA-seq and DNA microarrays. The RNA-seq data set consists of a developmental time-course across 11 developmental stages (Nègre et al. 2011). The microarray data sets consists of a developmental time-course of 28 stages (Hooper et al. 2007).

These data sets cover a total of 14,444 genes, out of which 707 were considered to be potential TFs. This set of potential regulators was predicted using InterProScan (Zdobnov and Apweiler 2001) to search for the presence of DNA binding domains assembled from published TF annotation efforts (Reece-Hoyes et al. 2005; Kummerfeld and Teichmann 2006) and further refined using literature curation (SE Celniker, pers. comm.).

Constructing feature-specific networks

We derived feature-specific networks from each input data set by assigning a weight to each TF-target gene pair. The weights range from 0 to 1, where 0 denotes absence of interaction. If a data set had missing values for a TF-target gene pair; the default value of 0.1 was assigned to this interaction. We derived two physical and four functional (two coexpression and two co-chromatin modification) feature-specific networks from our input data sets. Edges in these feature-specific networks have different implications: In the physical networks, edges describe binding of TFs, whereas in the functional networks, edges indicate a functional, possibly indirect, relationship derived from correlated patterns of activity between TFs and their targets.

The two physical networks, motif regulatory network and binding regulatory network, are based on the evolutionarily conserved motif instances and the TF binding data sets, respectively. In these two networks, interactions were added if conserved motifs, or ChIP binding of TFs occurred near the TSS of a target gene (in an interval of 500 bp upstream of or downstream from the TSS, using FlyBase 5.12 genome annotation). Weights in the motif regulatory network are defined by the motif conservation score according to the method described by Kheradpour et al. (2007), which ranges from 0.0 (unconserved motif instance) to 0.9 (strongly conserved motif instance). We increased this score by 0.1 and assigned the value of 0.0 in the case where no motif instance was present (absence of interaction). If a gene had several motif instances of the same TF, we selected the maximum conservation score of these instances. Weights in the binding regulatory network are binary and were set to 0.05 if there was no ChIP binding peak and to 0.95 if there was at least one ChIP binding peak overlapping with the 1-kb window of the target.

The four functional networks include two coexpression networks and two comodification networks, based on the two expression and two chromatin mark data sets (Table 1). In the coexpression networks, the weights of the interactions are given by the squared Spearman's correlation of the TF and target gene expression profiles. In the comodification networks, weights are given by the squared Spearman's correlation of the corresponding chromatin profiles (Fig. 1A). Chromatin modifications are commensurate with transcriptional activity (Ernst and Kellis 2010), and analogous to correlations in expression profiles, correlations in chromatin profiles may thus be used to infer functional relationships between TFs and target genes. Chromatin profiles were defined based on the presence of different chromatin modifications (marks) in five regions for every gene: upstream of TSS, 5′ UTR, coding sequence, 3′ UTR, and downstream transcription end site (Supplemental Fig. 9).

Unsupervised network inference

The unsupervised method uses a sum rule to compute a weight for each edge, which is the average weight of that edge across the six feature specific networks (Fig. 1B). Out of the ∼10 M possible interactions (707 TFs × 14,444 genes), only the top 2% highest confidence edges were selected to constitute the network from the unsupervised method, which corresponds to a similar number of edges as obtained using the supervised method.

Supervised network inference

The supervised network inference method is based on a logistic regression-based binary classifier, where the class label represents the presence or absence of an edge. The logistic regressor is a generalized linear model that predicts the probability of a class variable by combining the input features within a logistic function (Mitchell 1997). For our problem of network inference, the logistic regressor gives the probability w_ij of an edge between a TF and a target:

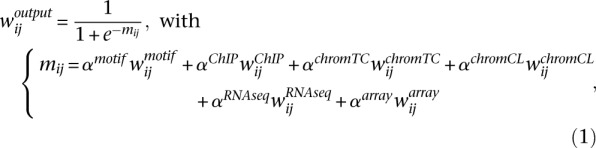where the input features for the classifier are the weights of that edge in the six feature-specific networks.

The training set was obtained from the REDfly network. The REDfly network has 204 edges, connecting 73 TFs with 76 targets. Thus, the training set consists of 5,548 (73 × 76) TF–target gene pairs, out of which 204 are positives (true interactions). The remaining pairs are considered to be negatives (absent interactions).

Learning was performed using 10-fold cross-validation. A challenge in supervised network inference is that the number of negatives and positives is typically not balanced in the training data (there are many more absent than present edges) (Qian et al. 2003). We addressed class imbalance in two ways. First, we used stratified cross-validation, which assures that the ratio of positives to negatives is approximately the same in each fold. Second, we weighted the positive instances in the training set, such that the total weight of positives and negatives is balanced. Specifically, we fixed the weight of negatives at 1 and the weight of positives at N/P, where N is the total number of negatives and P the number of positives in the training data. This is equivalent to oversampling the positives, which is a common approach to balance a learning set (Estabrooks et al. 2004). It forces the classifier to better fit the positive class than the negative class, which is a desirable feature, because negatives may correspond to true interactions that are yet uncharacterized and missing in REDfly. For the final model used to predict the complete set of interactions (beyond REDfly TFs and genes), we used the average weights obtained over 1000 iterations of 10-fold cross validation. Learning was performed using the Weka library (http://weka.sourceforge.net). We included all TF–target pairs that are predicted to interact with a probability of 0.6 or higher in the supervised integrative network (∼300,000 edges).

Network overlap

Enrichment of common interactions between feature-specific networks and the REDfly network (Fig. 2A) was computed as follows. TFs and genes that are not part of REDfly were removed from the feature-specific networks, and only the 10% highest weight interactions were considered present. Enrichment between two networks was defined as the number of interactions that are present in both networks divided by the number of such interactions expected by chance. The number of common interactions expected by chance is given by the mean of the hypergeometric distribution: N₁ × N₂/T, where N₁ and N₂ are the number of interactions in the two networks, and T is the total number of possible interactions. Statistical significance of the observed number of overlapping edges was evaluated at a level of 0.05, using the hypergeometric distribution.

Relative importance of input features

The relative contribution of each input feature for the supervised integrative network (Fig. 2C) was evaluated as the percentage contribution to the increase in scores of the top 10,000 edges as follows: (1) we computed the mean m_all over the scores m_ij (see Equation 1) of the complete list of all possible edges; (2) we computed the mean m_top over the scores of the top 10,000 edges (i.e., the 10,000 highest scores); (3) we computed the difference between the top edges and the complete set of edges d = m_top – m_all; and (4) we determined the percentage that each input feature contributed to the difference d. For instance, the scores m_ij had an increased value of d = 2.58 for the top 10,000 edges, and the term corresponding to the conserved motifs (α^motifw_ij^motif; Equation 1) had an increased value of d_motif = 1.08 for these same edges, thus accounting for 1.08/2.58 = 42% of the difference d that separates the top 10,000 edges from the remaining edges. The relative contribution of each input feature for the unsupervised integrative network was computed analogously (Supplemental Fig. 10).

Functional enrichment of regulatory networks

GO annotations

For each network, we computed the enrichment of coregulated genes for common GO annotations. We considered a gene pair to be coregulated in the given network if the two genes had >50% of their regulators in common. More formally, we computed the Jaccard similarity coefficient between the set of regulators of the first gene and the set of regulators of the second gene (the Jaccard coefficient is defined as the size of the intersection divided by the size of the union of two sets). We considered gene pairs with a Jaccard coefficient >0.5 to be coregulated. For each coregulated gene pair, we then measured the similarity of the set of GO annotations of the first gene and the set of GO annotations of the second gene, again using the Jaccard coefficient. Finally, we took the average of this coefficient over all coregulated gene pairs. The same procedure was done for 100 randomized versions of the network, and enrichment was computed as the ratio of the average coefficient of the original network to the average of the randomized networks. Randomization was done by permuting the labels of all TFs and permuting the labels of all genes. In other words, the network structure remained identical and only the labels of the nodes were changed. This assures that the observed enrichment is not due to potential bias arising from structural properties of the network. Statistical significance was assessed at a level of 0.05 using a one-sided Wilcoxon rank-sum test to compare the Jaccard coefficients from the original network with those from the randomized networks (Bonferroni correction was used to account for multiple testing).

ImaGO annotations

The ImaGO database annotates genes with terms describing their spatial localization patterns in tissues (Tomancak et al. 2007). We computed enrichment of coregulated genes for common ImaGO annotations using the same approach as described above for the GO annotations.

Gene expression in the developmental time-course

Enrichment of coregulated genes for coexpression in the developmental time-course (Graveley et al. 2010) was computed analogously to the GO and ImaGO annotations described above. First, coregulated gene pairs were identified as described. For each coregulated gene pair, we then computed the squared Spearman correlation of the two gene expression profiles. Enrichment compared to randomized networks was evaluated as described.

Protein–protein interactions

We considered a set of high-quality PPIs from the literature (Pacifico et al. 2006), where high-throughput yeast two-hybrid data were excluded. Enrichment of coregulated genes for PPIs was computed analogously to enrichment for coexpression and co-annotation. Specifically, we compared the number of PPIs for coregulated gene pairs to the average number of such PPIs in randomized networks, using the same definition for coregulation and network randomization.

Chromosome conformation colocalization

We evaluated enrichment of coregulated genes for three-dimensional chromosome conformation colocalization using a high-confidence set of intrachromosomal colocalization hotspots identified by Sexton et al. (2012). Colocalization hotspots were defined as pairs of distal chromosomal regions with at least 2.8-fold (log₂ > 1.5) enrichment in contact intensity over a background model accounting for genomic distance and hierarchical domain folding (Sexton et al. 2012). We derived a gene colocalization network by drawing a weighted edge between every pair of genes that are part of two chromosomal regions identified as a colocalization hotspot. Edge weights were defined as the log₂ enrichment in contact intensity (according to the definition of hotspots given above, weights are always >1.5, while absent edges are assumed to have zero weight). Enrichment of coregulated genes for interactions in the colocalization network was computed in the same way as enrichment for PPIs. Specifically, we computed the average weight of edges in the colocalization network over all coregulated gene pairs and compared it to the average weight of such edges over all coregulated gene pairs in randomized networks.

Prediction of GO process terms of unannotated genes

We developed a “guilt-by-association” approach to predict the biological process categories of genes with no previous GO annotations as well as to predict additional functions of genes with known annotations (Macskassy and Provost 2005). The underlying principle of this approach is that genes that have similar biological roles tend to “associate” with each other. We define association between genes based on both the similarity of their regulatory programs and their expression profiles. Thus annotation categories of genes with no known annotation can be predicted based on their regulatory and expression “association” to genes already annotated with a given functional annotation.

To predict the function of a gene, we define a score that relies on (1) a set of probabilistic assignments of a gene for each cluster based on a Gaussian mixture model of clustering, and (2) normalized regulatory similarity for each pair of genes i and j, based on the Jaccard coefficient of the set of regulators associated with each of the two genes (i.e., similarity of regulatory program). The normalization term for a gene i is the sum of the Jaccard coefficients using all other genes j with which it shares at least one regulator. As the regulatory similarity is normalized on a per-gene basis, a gene's contribution to regulatory similarity is split over all genes with which it shares similarity. Thus, genes that are coregulated with many other genes have smaller scores, whereas genes that are coregulated with few other genes have higher scores, given they are both connected to the same number of neighbors annotated with a particular process of interest. Regulators for each gene were obtained from the integrative networks. We first estimate the contribution of every cluster to gene i's score for a functional category by summing the normalized regulatory similarity of all other genes that are known to belong to the category. We then sum the per-cluster scores across all clusters, with the contribution of each cluster weighted by the cluster membership probability of g. Thus, the complete score is defined as follows:

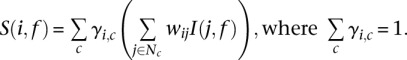Here γ_i,c is the probability of gene i belonging to cluster c. I(j,f) is an indicator function that returns 1 if gene j is annotated with GO process term f; otherwise, it returns 0. w_ij is the normalized regulatory similarity, which was calculated using a metric similar to the Jaccard coeffient between the regulator set of genes i and j, but modified to penalize regulators that have very high out-degree. Let R_i denote the regulator set of gene I, and let d_k denote the total number of targets of regulator k. We define the numerator of the similarity metric between gene i and j's regulator set as and the denominator as 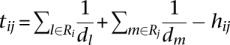. Finally, 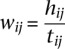. Note, each regulator k contributes an amount that is inversely proportional to the size of its target set, d_k. For the expression-only predictor, we set w_ij to be 1, and for the regulatory network-only predictor, we sum over all genes, ignoring the cluster membership information.

For each gene, this procedure results in a score for each functional category, which we then transform into a FDR value based on the score distribution for previously annotated genes for each functional category. This FDR is calculated based on the fraction of positive predictions for this category among genes from “unrelated” functional categories. We defined pairs of unrelated GO categories as follows. For each GO process term, we created a negative set based on the union of members of all GO terms that shared less than a specified threshold of similarity of its members with the term in question. For each pair of GO terms, t1 and t2, we computed fractions, f1 and f2, respectively, defined as the ratio of the number of common genes between t1 and t2, to the total number of genes in t1 (f1) and t2 (f2). We considered t2 as the negative set of t1 (or t1 as the negative set of t2) if min(f1,f2) was greater than a threshold. We experimented with different values of this similarity threshold (0.01, 0.05, 0.1, 0.15, 0.2) and found 0.15 to give the best performance. This negative set allowed us to define “false positives,” and thus compute an FDR as the ratio of the number of false positives to the sum of the number of true positives and false positives. While estimating the number of genes for which we could predict function, we excluded the following terms that are very general: metabolic process, cellular process, biological process, biological regulation, cellular metabolic process, primary metabolic process, biosynthetic process, and cellular biosynthetic process. We used this approach to predict annotations for all genes that are part of the inferred network, have at least one shared regulator with another gene, and have expression measured in the 30 time point developmental time-course. All predictions at FDR < 0.6 are given in Supplemental File 7.

To test if the predicted members of a GO process were enriched for genes expressed in certain tissues (ImaGO annotations), we used the hypergeometric distribution. We did these tests for the newly predicted and correctly recovered members of a given GO process separately. Let X_p denote the set of newly predicted gene members of GO process p at a particular FDR cutoff. Let Y_t denote the set of genes annotated with tissue t. Let k_pt be the number of genes that are in X_p and Y_t, and let N be the total number of genes in our background. Our test of GO-tissue enrichment then uses the hypergeometric distribution to test the probability of observing k_pt genes of process p to be expressed in tissue t, given that we draw |X_p| genes, and |Y_t| of N genes are known to be expressed in tissue t. The fold enrichment is calculated as the ratio of the foreground (k_pt/|X_p|) to the background fraction (|Y_t|/N). For the newly predicted gene set, we use the background of all genes that have a new prediction in at least one GO process term, whereas for the correctly recovered genes, we consider all genes that have been correctly recovered in at least one GO process term.

Predictive models of expression of target genes from expression of regulators

To predict expression of a target gene from the expression of its regulators, we assume that the expression of a target gene is a linear combination of the expression level of the TFs. We obtain the TFs of every target gene from a given regulatory network and learn the weights of the linear combination from the training expression profiles of the TFs and the target. We use 10-fold cross-validation, where we split the developmental time-course into 10 parts, use nine parts for training, and predict the expression in the tenth. We learned these models for five networks: the ChIP binding network, the motif network, the REDfly network, the unsupervised integrative network, and the supervised integrative network.

We tested each model for its ability to predict the expression of the three time points that it had never observed, and compared the squared errors of the predicted gene expression profiles to the errors found by applying the same prediction scheme to 10 randomized control networks of the same size and degree distribution, generated by permuting the labels of TFs and targets as described in the previous section for the functional enrichment analysis. We performed two types of comparisons against random networks. First, we estimated the average number of genes on which models learned from the original networks had a significantly lower squared error than random networks (one-sided t-test, P-value <0.05). Second, we generated a list of predictable genes and a list of unpredictable genes that had consistently lower or higher errors than random networks. A gene was considered predictable if it had a lower squared error in the true network than in six out of 10 of the random networks and was considered unpredictable if it had a higher squared error in the true network than in six out of 10 random networks.

To assess how well our predictable set of genes were able to predict expression in a completely new setting, we used the learned models from the time-course to predict expression in four RNA-seq and 25 microarray cell-line experiments. For each network, we made a prediction for cell lines for each gene using the models learned from each fold of cross-validation. We did the same for each random network and estimated the number of genes on which the errors from the true networks were significantly lower than the random network, and repeated this for all random networks. We report that the average number of genes on which the models learned from the true networks was better than random (Supplemental Table 1). We repeated this procedure for the unpredictable set.

Network and source code availability

The integrative networks, input and validation data sets, and the source code used for network inference and validation are provided in the online Supplemental Material and on the companion website of this article (http://compbio.mit.edu/flynet).