Abstract
Background
The potential use of magnetic nanoparticles in biomedical applications has witnessed an exponential growth in recent years.
Methods
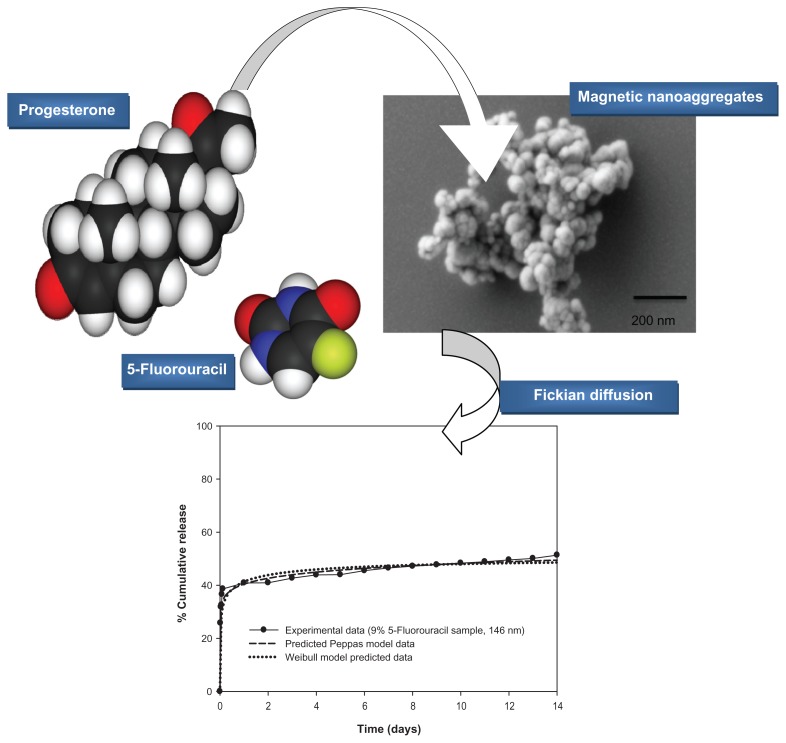
In this study, we used nanoaggregates of magnetic nanoparticles as carriers for controlled drug delivery. The nanoaggregates are formed due to the presence of the block copolymer of polyethylene oxide-polypropylene oxide (Pluronic F-68) and beta-cyclodextrin that surround the magnetic core of the nanoparticles. The administration of the drug carriers occurs by inhalation, and the drug is delivered systemically via the pulmonary route. We tested the delivery of 5-fluorouracil and progesterone, which are used as models of hydrophilic and hydrophobic drugs, respectively.
Results
The estimated nanoaggregates’ diameters are between 293 nm ± 14.65 nm and 90.2 nm ± 4.51 nm, respectively. In-situ and post-synthesis techniques are two approaches for drug loading. The polymer composition of nanoaggregates and initial drug concentration showed a significant effect on both the drug entrapment efficiency and release kinetics. Average drug entrapment efficiencies ranged between 16.11% and 83.25%. In-situ loaded samples showed significantly slower release rates. The drug release mechanism is investigated by mathematical curve fitting to different drug release kinetics models. In most cases, the Peppas model has shown good correlations (coefficients of correlation, R2, between 0.85 and 0.99) with the examined release profiles. The estimated release indices are below 0.5, which indicates the Fickian diffusion mechanism. For samples with an initial burst effect, the modified Peppas model can provide a better understanding of the drug release mechanism, both in the samples loaded with progesterone, or those high polymer concentrations.
Conclusion
Our work showed prolonged delivery of drugs (5-fluorouracil and progesterone) by diffusion from nanoaggregates, with the potential to reduce dose-related adverse effects.
Keywords: Nanoaggregates, 5-fluorouracil, progesterone, release kinetics, Fickian diffusion
Introduction
Pulmonary drug delivery of therapeutic agents is currently an active field of research, which has been progressing rapidly after the approval of insulin dry powder inhaler. The pulmonary delivery of drugs has several advantages over the oral and injection delivery routes.1–4 The ability to circumvent the hepatic first-pass metabolism makes this route very promising for reducing the dose and side effects. Additionally, the delivery of drugs through the pulmonary tract can be modulated to target the drug locally in the respiratory region; it can therefore be applied for the treatment of diseases such as asthma, chronic obstructive pulmonary diseases, and cystic fibrosis.1–3 However, the pulmonary delivery route has been recognized as attractive for systemic delivery, due to the contribution of the large surface area (more than 100 m2) and thin epithelium layer (0.2 μm–1 μm thickness).3 Additionally, the pulmonary route has been associated with an improved bioavailability, which can be attributed to the relatively low enzymatic activity for this region.4
In pulmonary drug delivery, the inhaled particles are subject to an alveolar phagocytosis clearance mechanism by the alveolar macrophage cells. Notably, the alveolar phagocytosis is a more effective mechanism for particles having a geometric diameter of between 1 μm and 2 μm. Inhaled particles with a geometric diameter below 1 μm or larger than 2 μm are subject to reduced macrophage phagocytosis clearance;5,6 thus, nanoparticles offer many advantages to the systemic pulmonary drug delivery field. Hoet et al reported that the optimum particle size of inhalable particles should be below 100 nm in order to maximize the alveolar deposition, and minimize the phagocytic clearance mechanisms.7 In spite of the great advantages offered by nanoparticles in the field of drug development and delivery, their pulmonary application is not straightforward. Significant formulation challenges arise from their high Gibbs free energy, due to the huge surface area. Therefore, prevention of particle agglomeration creates a significant challenge during manufacture.8 To meet this challenge, two strategies have been proposed in the literature: the first approach is to manufacture large, hollow carriers of agglomerated particles which encapsulate the active therapeutic agent. This approach was first introduced by Tsapis et al9 and was later modified by Hadinoto et al.10
The second strategy to meet the challenge of nanoparticles’ high Gibbs free energy is through the addition of surfactants. These can elevate the activation energy of interparticulate agglomeration, through the formation of electrostatic or steric barriers between the particles.8–11
In the present study, we focus on the development of nanocarriers which can be magnetically targeted for the treatment of lung cancer and hormone replacement. Emphasis will be placed on polymers and surfactant self-assembly as a novel approach for the synthesis of well-defined nanoaggregates. Our approach follows directly from the second strategy; however, our method differs from other magnetic nanocarriers, namely by the coating surrounding the magnetic core.12 These nanoaggregates are formed spontaneously by the self-assembly of block copolymers and beta-cyclodextrins, without the application of a crosslinker. They have the advantages of facile preparation without the use of any organic solvents, and of the lack of toxic polymer degradation products. These nanocarriers have the capability of encapsulating both hydrophilic and hydrophobic drugs. Controlled drug delivery can be achieved by variation in the concentration of polymers and/or surfactant. To our knowledge, we are the first group to propose Pluronic F-68 and beta-cyclodextrin for preparation of diffusion-controlled super-paramagnetic nanoaggregates for both hormonal and anticancer drug delivery. The magnetization features (coercivity and retentivity) of our prepared nanoaggregates can also be modulated by varying the surfactant/polymer relative concentrations.13
Drug release by diffusion of biologically active molecules from nanocarriers is an important and commonly-used approach to achieving controlled release. The release from porous systems has been previously reported in several publications.4–16 Depending on the composition of the porous system (both the type of the polymer, and the type of drug), the topology of the nanocarrier (size and shape) and the drug loading technique, one or more of the following physical phenomena affect the drug release kinetics: (1) saturation of the nanocarrier drug delivery system with release medium, (2) penetration of the release medium into the porous structure of the nanoparticles, (3) creation of pores filled with water within the nanoparticles’ structure, (4) drug diffusion through the pores, and (5) drug diffusion to the release medium.
To enable mathematical modeling of drug release kinetics through a porous system, it is crucial to take into account only the dominant process for drug transport. From the transport processes’ point of view, the mechanism of drug release for porous systems consists mainly of exterior and interior diffusion phenomena.15,16
Additionally, the hollow nature of the structure of nanoparticulate carriers is specifically designed to enhance both the aerosolization efficiency, and the therapeutic efficacy.17 Despite the advantages of introducing hollow structure to nanoparticles, many challenges related to drug release profile and drug release kinetics are yet to be addressed. Dailey et al have introduced the possibility of developing surfactant-free nanoparticulate carriers using variable physico-chemical properties for the pulmonary application via nebulization.18 Slow drug release rates have been observed for their nanoagglomerates, especially for hydrophobic drugs. They attributed these results to the large geometric diameter of agglomerated nanoparticles.
The synergistic effect of combining both the hollow nature of nanoaggregates’ structure, and their magnetic properties, appears to be promising for controlled and targeted drug delivery technology.19 For instance, magnetic liposomes and hollow capsules entrapped with magnetic nanoparticles have shown great potential for drug loading and encapsulation efficiency.19–21 In order to produce magnetic nanoaggregates with both controlled drug release kinetics and magnetic retention characteristics, it is necessary to control the collective properties of magnetic nanoaggregates.22 In our study, the magnetic properties of nanoaggregates are dependent on the interparticulate interactions between the block copolymers and the beta-cyclodextrins; these interactions also have a significant effect on the nanoparticles’ aggregation.23
Drugs can be loaded into the nanoparticles’ porous structures using two techniques: (1) postsynthesis, and (2) in-situ loading.15 In the postsynthesis method, the nanoaggregates are synthesized and the drug is subsequently absorbed to the porous structures. In this case, drug diffusion is the major mechanism for drug uptake. In the in-situ loading technique, the drug is mixed with nanoaggregates, polymer precursors. The drug release will be determined by the diffusion or degradation of labile covalent bonds. In this study, both drug loading methods will be analyzed, based on the two techniques’ different drug loading percentages, and different formulation parameters. The drug release kinetics will also be analyzed in terms of experiments and modeling, in order to understand how the release is sustained.
Materials and methods
Materials
The iron precursor ferrous sulphate heptahydrate (FeSO4 · 7H2O) from VWR International, PLC (VWR, Mississauga, Canada), and magnetic nanostructures consisting of polyethylene oxide – lypropylene oxide (Pluronic F-68, Molecular weight 8400) from Sigma-Aldrich, and beta-cyclodextrin (molecular weight 1135), also from Sigma-Aldrich formed the basis of this experiment. The two modeled drugs, progesterone and 5-fluorouracil were purchased from Sigma-Aldrich. The ammonium hydroxide, methylene chloride, acetonitrile and phosphate buffer saline tablets are also all products of VWR.
Preparation of magnetic nanoaggregates
The magnetic nanoaggregates were synthesized according to a modified method reported by Xia et al.24 The reaction involved two iron precursors (ferrous and ferric chloride salts) under nitrogen gas, with vigorous stirring. We used a simple and easy synthetic method. Our experiments were all conducted under an aerobic environment, and by the use of a single iron precursor (ferrous sulphate).
Block copolymer polyethylene oxide-poly propylene oxide (Pluronic F-68, molecular weight 8400, 2.5 mmol, 21 g) was dissolved in 50 mL of distilled water with vigorous magnetic stirring using a VWR 230 magnetic stirrer/hot plate for 30 minutes. The iron precursor (ferrous sulphate heptahydrate FeSO4 · 7H2O, molecular weight 278.01, 5.895 mmol, and 1.396 g) was then added to the reaction mixture. The reaction was mixed again for a further 30 minutes under an aerobic environment. Then beta-cyclodextrin (molecular weight 1135, 5 mmol, 5.675 g) was dissolved in ammonium hydroxide and added, drop-wise, to the reaction mixture. The reaction mixing was then continued for more than 90 minutes until homogeneous stable aqueous suspension occurred. The experiment was conducted without the need for purging nitrogen gas. The concentration of Pluronic F-68 was varied between 0.5 and 3 mmol under fixed experimental conditions.
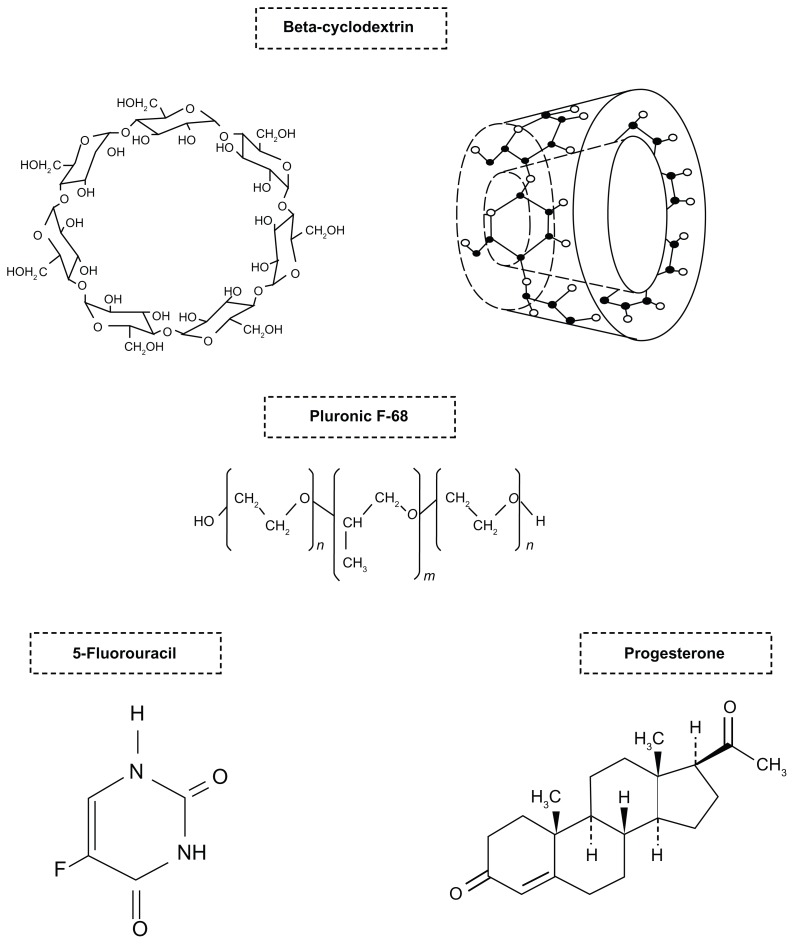
To investigate the magnetic properties and drug release kinetics of the prepared nanoaggregates, the amount of beta-cyclodextrin was varied from 0% to 25% as a fraction of total solids in the formulations. The prepared magnetic nanoaggregates were then thoroughly washed with ethanol, and were then freeze-dried (using a FreeZone Plus 6-Liter freeze dry system, Labconco Corporation, Kansas city, MO). The chemical structure of the drugs and polymers used is presented in Scheme 1.
Scheme 1.
Chemical structures of beta-cyclodextrin, polypropylene oxide/polypropylene oxide block copolymer (Pluronic F-68, HO (C2H4O)n(C3H6O)m(C2H4O)n OH, m = 80 and n = 27) and the two encapsulated drugs: progesterone and 5-fluorouracil.
Drug Loading
In-situ drug loading of 5-fluorouracil
An amount of 50 mg of 5-fluorouracil and a predetermined amount of beta-cyclodextrin were dissolved in 28% ammonium hydroxide solution. In addition, the block copolymer and the iron precursor (FeSO4 · 7H2O) were dissolved in 50 mL of distilled water. The two mixtures were then combined for at least 90 minutes at room temperature. The resulting 5-fluorouracil loaded aggregates were washed, and then oven dried for further characterization.
Drug loading by freeze-drying 5-fluorouracil
The freeze-drying technique for drug loading can be considered as a postsynthetic step. In this method, 10 mg of 5-fluorouracil was mixed with 20 mg of magnetic nanoaggregates in distilled water. The mixture was then stirred mechanically overnight at room temperature. The resulting mixture was then freeze-dried for twenty four hours.
Progesterone loading through inclusion complex formation with beta-cyclodextrin
The progesterone-loaded magnetic nanoaggregates were prepared according to the method reported by Lemos-Senna and colleagues.26 Briefly, progesterone (5 mg) and beta-cyclodextrin (25 mg) were dissolved in methylene chloride (3 mL). The mixture was then added to 28% ammonium hydroxide aqueous solution (50 mL). In a separate beaker, Pluronic F-68 was mixed with an aqueous solution of the iron precursor (1.396 g of FeSO4 · 7H2O in 50 mL of distilled water). The ammonium hydroxide solution containing progesterone and beta-cyclodextrin was added to the iron/block copolymer solution, and vigorously mixed for 90 minutes at room temperature. The precipitated magnetic nanostructures were washed and then oven-dried.
Characterization of 5-fluorouracil- and progesterone-loaded magnetic nanoaggregates
Particle size measurement
The mean diameter of the nanoaggregates and the poly-dispersity index were determined using a dynamic light scattering technique, using a Zetasizer 3000 Has particle sizer, (Malvern Instruments Ltd, Malvern, UK). The size analysis was performed at a scattering angle of 90° and at a temperature of 20°C.
Particle morphology
The morphology of the magnetic nanoaggregates was examined using scanning electron microscopy, with a scanning electron 600F model microscope (Jeol Ltd, Tokyo, Japan). The samples were prepared on aluminum stabs and coated with gold prior to the examination.
X-ray diffractometry
An X-ray diffractometer (Rigaku-Miniflex, The Woodlands, TX) was used to examine the crystal profile of both the loaded and unloaded samples. The samples were exposed to X-ray radiation (CuKα, 40 KV, 20 mA) at a wavelength of 1.54 Å. The samples were scanned over a 2-theta range of between 15° to 70°, and at a step size of 0.02°.
Fourier transform infra-red spectroscopy (FTIR)
FTIR spectra were viewed in the solid state by Bruker-Vector 22 FTIR spectrophotometer (Bruker-Vector, Milton, Canada).
Powder magnetization
The magnetic properties were measured using a model 74035 vibrating sample magnetometer (Lake Shore Cryotronics Inc, Westerville, OH) at 300 K. The magnetic properties of nanoaggregate samples were studied at field range of ±10,000 gauss.
Investigation of drug release profile and kinetics of 5-fluorouracil-loaded magnetic nanoaggregates
Drug loading and entrapment efficiency
The drug loading can be defined as the amount of drug encapsulated per unit mass of nanoparticles. The respective concentrations of 5-fluorouracil and progesterone were determined for all formulations after dissolving a known amount of sample nanoaggregates in acetonitrile. The amount of the supernatants obtained after centrifugation at 15,000 rpm was determined quantitatively for the amount of drug loaded. The ratio of the mass of drug recovered in the nanoparticles to the mass of drug initially loaded can be defined as the drug entrapment efficiency (EE). A summary of experimental data and their effects on drug encapsulation is listed in Table 1.
Table 1.
Entrapment efficiencies of 5-fluorouracil as a function of different initial drug concentrations and nanoaggregates’ average diameters
| Concentration of pluronic F-68 | Particle average diameter (nm ± RSD) | Initial drug concentration (mg drug/mg nanoparticles) | Drug loading (%) | Drug entrapment efficiency (%) | |
|---|---|---|---|---|---|
|
| |||||
| In-situ loading | Freeze-drying loading | ||||
| 0.5 | 293 ± 14.65 | 30 | 10 | 82.65 | 83.25 |
| 1.0 | 207 ± 10.35 | 25 | 9.5 | 50.66 | 63.14 |
| 1.5 | 146 ± 7.30 | 20 | 9 | 48.25 | 56.90 |
| 2 | 124 ± 6.20 | 10 | 5 | 23.69 | 31.56 |
| 2.5 | 98.70 ± 4.93 | 20 | 3 | 16.11 | 19.12 |
| 3.0 | 90.20 ± 4.51 | 20 | 2 | 32.01 | 46.22 |
Abbreviation: RSD, relative standard deviation.
In-vitro release test
A dialysis bag (cellulose membrane, MW cut-off 12400, Sigma-Aldrich Ltd) was used to conduct the in-vitro release experiments. The dialysis in-vitro experiments confirmed that only the free drug molecules diffuse into the release medium without the passage of nanocarriers. The release study was conducted in phosphate buffer saline (pH 7.4), and the samples were withdrawn at predetermined time intervals for 14 days.
Analysis of 5-fluorouracil and progesterone release kinetics
Both the drug release profile and kinetics can be controlled through modulation of the drug delivery architecture.26,27 The 5-fluorouracil and progesterone release data as functions of different formulation parameters were examined, for fitting to the following release kinetics models: zero order, first order, Hixson-Crowell, Higuchi, Peppas, Weibull and Lonsdale models, respectively. Table 1 (Supplementary section) summarizes these functions, together with the corresponding equations.14–16 The data were fitted using SigmaPlot software (v11.0; Systat Software Inc, San Jose, CA), and regression analysis was used for calculation of both the correlation and release parameter coefficients for each function. The student t-test was then applied to calculate which mathematical parameters best fitted each kinetic model. The results were found to be significantly different, based on 95% probability values.
In vitro cytotoxicity study
An in-vitro cytotoxicity study was performed for the purpose of investigating the effect of 5-fluorouracil-loaded magnetic nanoaggregates on lung adenocarcinoma. The human tumorigenic lung epithelial cell line A549 was obtained from the American Type Culture Collection (CCL-185™; Sigma-Aldrich, St Louis, MO). For these experiments, lung cancer cells were plated in 100 μL of tissue culture medium at a density of 2.5 × 104 cells. Examination of the effect of the nanoaggregate formulations on the growth of A549 cell line was carried out by adding serial dilutions of 5-fluorouracil-loaded magnetic nanoaggregates to each well containing cells that had been grown for 1 day. The studied concentrations of 5-fluorouracil were 10−4, 10−3, 10−2, 0.1, 1, 10, 100 and 1000 μL of anti-cancer drug, respectively. The cells were incubated for 4 days at 37°C under a 5% CO2 atmosphere, and then the cell viability was determined using Alamar Blue assay (VWR International, Mississauga, Canada).28 The cytotoxicity data were expressed as percentages of the residual viability, using the plates cultured in absence of 5-fluorouracil as 100% viability samples.
Test of statistical significance
The correlations between our experimental data and the release kinetics models were calculated using SigmaPlot software. The statistical significance of the results was evaluated using a student t-test. The aim of the statistical study was to examine the inter-relationship between the drug release profiles and the studied parameters, ie, the impact of such variables as particle size, drug loading and drug loading technique on the overall correlation results.
Results and discussion
Particle size and morphology
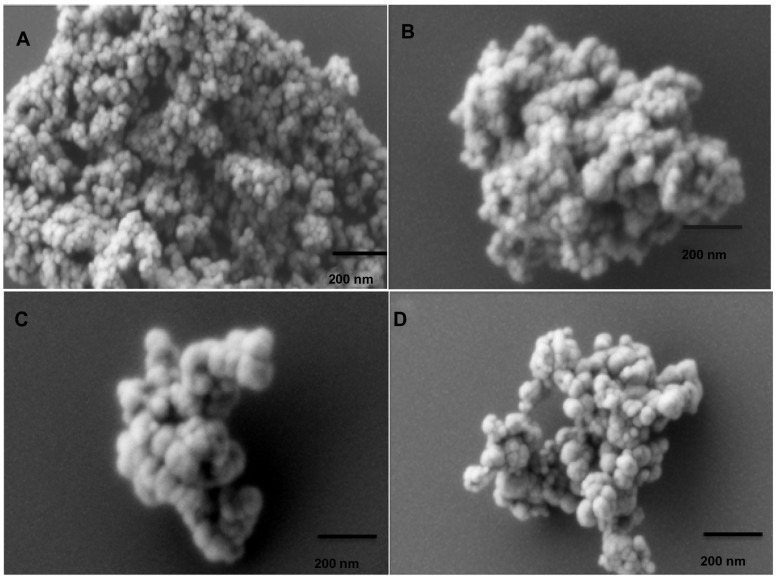
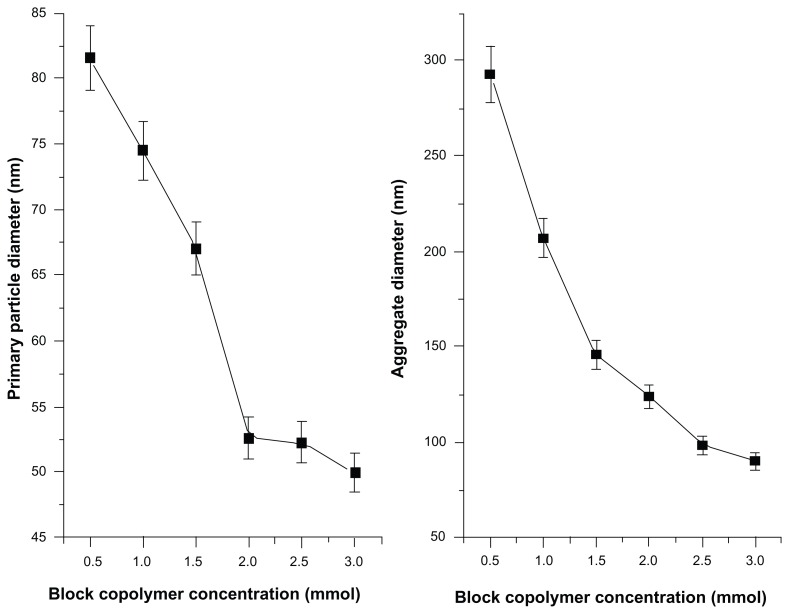
Scanning electron micrograph (SEM) images of magnetic nanoaggregates with loaded drugs are presented in Figure 1. The presented images reveal that the powders consist of uniform, almost spherical primary particles, which are arranged in aggregated nanostructures. In the present work, the produced magnetic nanostructures composed primarily from magnetic nanoparticles (Figure 2). These primary nanoparticles were further aggregated, to yield well-organized nanostructures having an aggregate diameter ranging from 90.20 nm ± 4.51 nm to a maximum of 293 nm ± 14.65 nm. As shown in Figure 1, increasing the concentration of block copolymer does not significantly affect the morphology of nanoaggregates. On the contrary, beta-cyclodextrin does not show a significant effect on the particle diameters; however, it has more influence on the spherical organization of nanoaggregates.
Figure 1.
Scanning electron micrograph (SEM) images for different magnetic nanoaggregate formulations. Effect of polymeric composition on morphology of nanoaggregates: (A) 0.5 mmol block copolymer and 0 wt% beta-cyclodextrin; (B) 3 mmol block copolymer and 0 wt% beta-cyclodextrin; (C) 3 mmol block copolymer and 5 wt% beta-cyclodextrin; and (D) 3 mmol block copolymer and 25 wt% beta-cyclodextrin.
Figure 2.
Effect of block copolymer concentrations on the average primary and aggregated particle diameters.
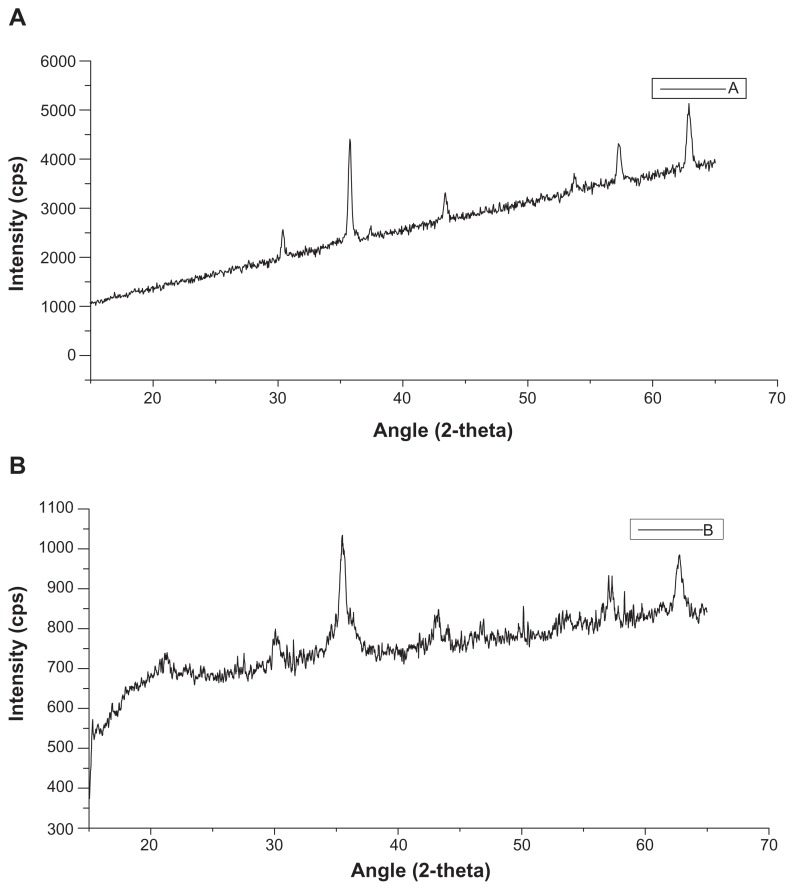
An increase in the concentration of beta-cyclodextrin was associated with an increase in the degree of the hollow nature of nanoaggregate structure. The X-ray diffraction patterns of magnetic nanoaggregates prepared with 0.5 mmol and 3 mmol of Pluronic F-68 is presented in Figure 3. The addition of Pluronic F-68 is usually associated with particle size reduction, which is indicated by the peak broadening. The five characteristic peaks for iron oxide magnetic nanoparticles were at 2-theta angles of 30.95, 35.89, 44.34, 55.06 and 64.51, respectively. These five peaks correspond to the diffraction from each of the 111, 200, 211, 221, 310, 222 planes of face-centered cubic iron oxide crystals.
Figure 3.
X-ray diffraction profiles of magnetic nanoaggregates as a function of block copolymer concentration. (A) 0.5 mmol; and (B) 3 mmol of block copolymer (Pluronic F-68).
Abbreviation: CPS, counts per second.
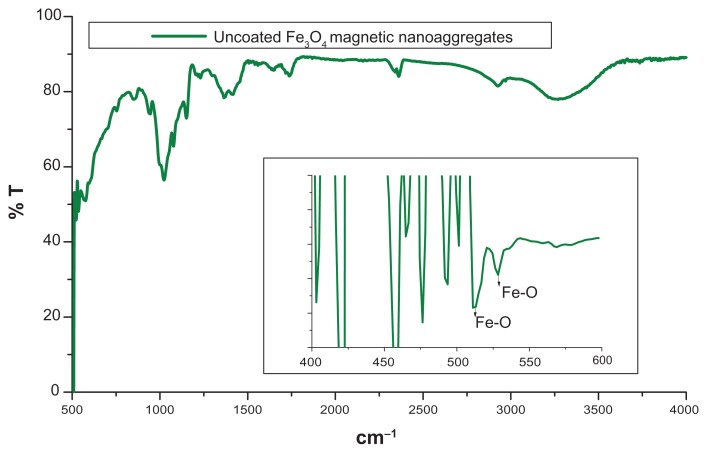
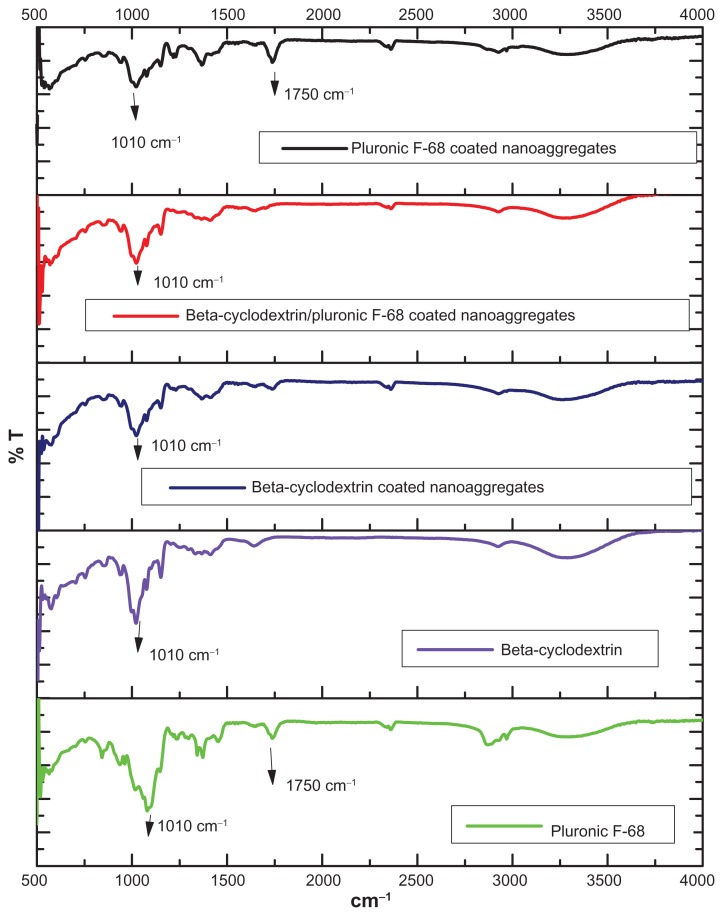
FTIR analysis was performed to confirm the presence of beta-cyclodextrin and Pluronic F-68 on the magnetic nanoaggregates. In the case of uncoated magnetic nanoaggregates, the presence of strong peaks in the region of between 600 cm−1 and 660 cm−1 was attributed to the Fe–O bond of the iron oxide skeleton (Figure 4). Magnetic nanoaggregates were coated with beta-cyclodextrin, and exhibited an intense band at 1010 cm−1, due to the glycoside vibrations (C–O–C). The same peak was observed for nanoaggregate samples coated with Pluronic F-68; this is a result of the C–O–C stretch vibrations of Pluronic F-68. The broad peak in the region of between 3000 cm−1 and 3500 cm−1 corresponded to the multiple hydroxyl groups of both beta-cyclodextrin and Pluronic F-68. A characteristic C–O stretch vibration band was clearly observed at 1750 cm−1 in Pluronic F-68-coated magnetic nanoaggregates, which indicates the presence of the polymer. The magnetic samples coated with both polymers did not show any C–O stretch vibration band at 1750 cm−1, due to the formation of a hydrogen bond between the beta-cyclodextrin and the ether oxygen of the Pluronic F-68 polymeric chain (Figure 5).
Figure 4.
FTIR spectrum of uncoated magnetic nanoaggregates.
Abbreviation: FTIR, fourier transform infrared spectroscopy.
Figure 5.
FTIR spectra of different polymer coated magnetic nanoaggregates.
Abbreviation: %T, % Transmittance.
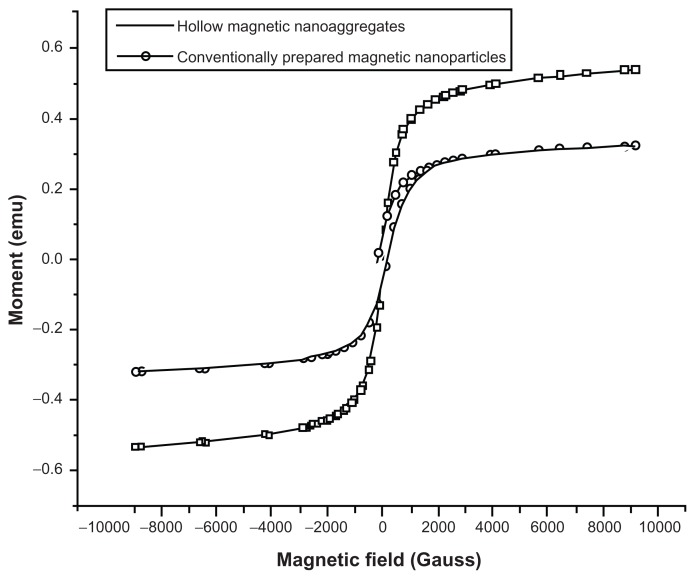
Figure 6 represents the magnetization data for the 293 nm ± 20.51 nm and the primary magnetic core (15 nm ± 0.56 nm), prepared by the conventional thermal decomposition method of iron precursor. The magnetic properties of all samples were studied at a field range of ± 10,000 gauss. The data obtained indicates the super-paramagnetic characteristics for both samples. The mass saturation magnetization values were 26.5 emu/g for the nanoaggregates prepared with 0.5 mmol of Pluronic F-68, compared to 16 emu/g for the as-prepared magnetic core. The significant reduction observed in the coercivity of the nanoaggregate (1.65 gauss for nanoaggregates compared to 168.19 gauss for the as-prepared magnetic core), together with the absence of hysteresis indicates the super-paramagnetic nature of the samples. Additionally, the retentivity data obtained for the primary magnetic nanoparticles prepared by the conventional thermal deposition method was significantly higher than their corresponding nanoaggregated samples (0.59 emu versus 0.0016 emu). This finding also confirmed the super-paramagnetic nature of our nanoaggregated structures. Similar super-paramagnetic behavior was observed for the samples prepared at different concentrations of beta-cyclodextrin.
Figure 6.
Room temperature (300 K) magnetization curves of magnetic nanoaggregates prepared with 3 mmol of block copolymer and 5 wt% beta-cyclodextrin compared to magnetic nanoparticles prepared by conventional method.
Abbreviation: emu, electro-magnetic unit.
Interestingly, increasing the concentration of beta-cyclodextrin from 5 wt% to 25 wt% showed significant improvement in the mass saturation magnetization values of nanoaggregates. The saturation magnetization values for the 5 wt% and 25 wt% beta-cyclodextrin were 38.71 emu/g and 81.22 emu/g, respectively. This value is comparable to the published saturation magnetization value reported by Xia and colleagues,25 and is also comparable to the commercially available magnetite nanoparticles supplied from Sigma-Aldrich. The increased magnetization observed upon increasing the concentration of polymer can be explained by the reduction in the shell thickness. This will consequently lead to an increase in the size of the magnetic core. In other words, the decreased fraction of block copolymer (Pluronic F-68) is associated with an enhancement in the saturation magnetization. The presence of Pluronic F-68 on the surface of magnetic nanoparticles can be considered as a magnetic dead layer, thus affecting the saturation magnetization as a result of quenching of the surface moment.29
Drug release profile through polymeric nanoaggregates as a function of different formulation parameters
The release profiles of 5-fluorouracil- and progesterone-loaded nanoaggregates were investigated. The amount of drug loaded, the loading technique, and the nanoaggregates’ morphology, significantly affected the release patterns. The drug encapsulation efficiency showed significant dependence on the loading technique for all samples smaller than 293 nm ± 14.65 nm. For the samples prepared with 3.0 mmol of block copolymer (nanoaggregate particle size = 90.2 nm ± 4.51 nm), significant reduction in the drug entrapment efficiency was observed upon switching of the drug loading technique from the freeze-drying to the in-situ drug loading method (Table 1).
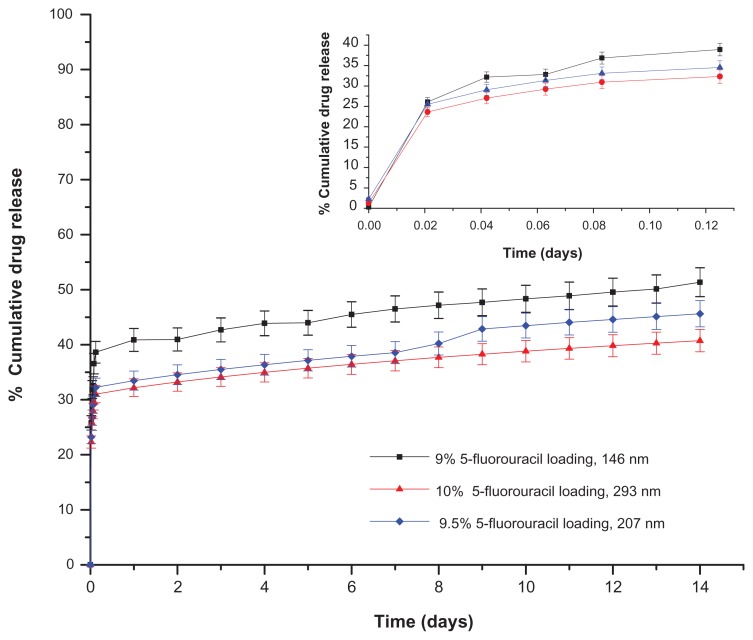
Influence of drug loading and nanocluster size on 5-fluorouracil release
The results of 5-fluorouracil-loaded magnetic nanoaggregates’ release profile as a function of the drug loading and particle diameter are presented in Figure 7. The samples examined in this Figure were prepared at high 5-fluorouracil-loading percentages (9%, 9.5% and 10%, respectively). Increasing the particle diameter from 146 nm ± 3.0 nm to 293 nm ± 14.65 nm resulted in a significant reduction in the drug release rate (Table 2, Supplementary section). In addition, samples prepared at lower percentages of drug loading (2%, 3% and 5%, respectively) showed a higher dependence on the drug loading technique. A comparison between the calculated release rates as a function of the drug loading technique is presented in Table 2. The release rate is significantly higher for all samples loaded using the freeze-drying technique, especially for the sample loaded with 5% 5-fluorouracil. This high release rate could be attributed to the additional drug lost during the decomposition reaction of iron precursor for the in-situ loaded samples.
Figure 7.
Drug release profiles of 5-fluorouracil nanoaggregates prepared by in situ loading method.
Table 2.
Estimated Peppas parameters as a function of drug loading percentages and loading techniques
| Drug loading | In-situ drug loading | Freeze-drying drug loading | ||||
|---|---|---|---|---|---|---|
|
|
|
|||||
| Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) | Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) | |
| 2% 5-FU | 58.75 ± 4.32 | 0.87 | 0.23 ± 0.03 | 66.22 ± 2.94 | 0.91 | 0.18 ± 0.02 |
| 3% 5-FU | 56.78 ± 3.80 | 0.88 | 0.22 ± 0.03 | 67.39 ± 1.55 | 0.95 | 0.14 ± 0.01 |
| 5% 5-FU | 64.08 ± 1.93 | 0.92 | 0.14 ± 0.01 | 94.73 ± 1.55 | 0.96 | 0.15 ± 0.02 |
Abbreviation: 5-FU, 5-fluorouracil.
Upon analysis of the release kinetics of these three samples, the three release profiles showed perfect correlations to the Peppas model of release kinetics. The release calculated indices in all cases are below 0.5, which indicates the presence of the Fickian diffusion mechanism. It should be noted that increasing the drug loading from 2% to 5% was associated with a significant enhancement in the drug release rate. Further increase in the drug loading (from 5% to 9%) results in a drop in the release rate, and consequently in the release index. For example, the calculated release rate based on the Peppas model is 40.43 per day−1; for the sample loaded with 9% 5-fluorouracil compared to 64.08 day−1 at the 5% drug loading capacity. Interestingly, the sample loaded with 2% of 5-fluorouracil showed a good correlation with both the Peppas and first order release models for the two drug loading techniques. The drug release rate for the samples loaded by freeze-drying is significantly higher than the corresponding samples loaded by the in-situ technique.
The influence of drug loading on progesterone release was also investigated. Figure 1 (Supplementary section) shows the release patterns of different progesterone-loaded nanoaggregates produced using the freeze-drying technique. Because of the limited aqueous solubility of progesterone, the drug loading and entrapment efficiency were low for the samples with an average diameter below 293 nm ± 14.65 nm. The release profile of samples prepared with 2% to 10% progesterone is demonstrated in Figure 1 (Supplementary section). The variation in the drug release rate can be attributed to the differences in the average particle diameter, particle morphology, and physico-chemical properties of the drugs. For example, the nanoaggregates loaded with 5% of progesterone demonstrated an average particle diameter of 124 nm ± 6.2 nm, compared to 89.5 nm ± 4.95 nm for the corresponding sample loaded with 5-fluorouracil.
The dependence of the drug release kinetics on the particle diameter can be directly correlated to the variation on the drug loading. Figure S2 (Supplementary material) focuses on the effect of the average particle diameter on 5-fluorouracil release rate through nanoaggregates with approximately equal drug loading. The selected drug loading in all samples was adjusted to be 10%. It should be noted that there is little effect of the particle size on the drug release rate for the samples loaded by the in-situ method. A comparison between the release profiles of both the in-situ loaded and freeze-dried samples prepared at 10% drug loading is shown in Figure 2 (Supplementary section). Based on our previously discussed data, the drug loading, particle size and loading techniques all contribute to the release profile of examined samples. The drug loading techniques exhibited more significant roles in controlling the release rate.
Influence of beta-cyclodextrin mass fraction on the drug release rate and profile
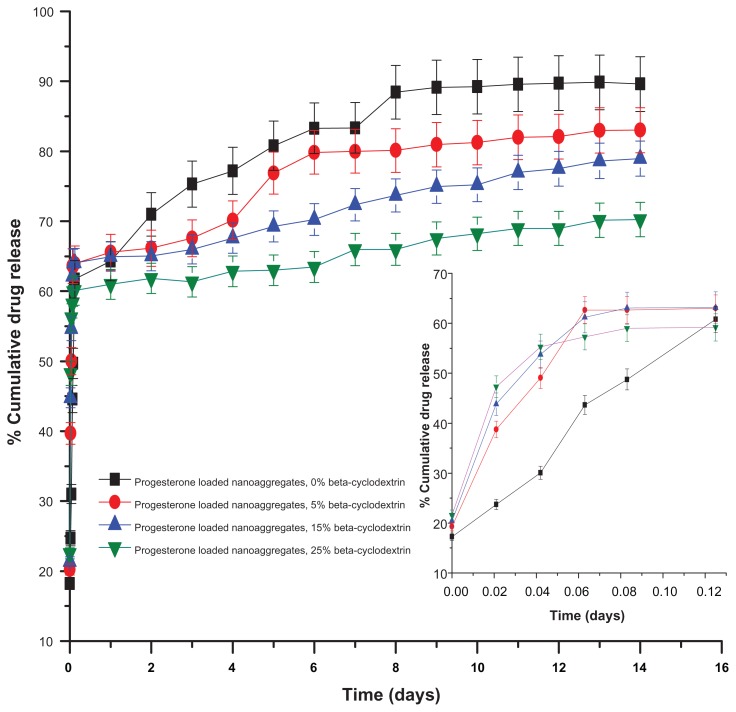
The incorporation of beta-cyclodextrin in the nanoaggregate formulations was found to significantly influence the produced nanoaggregates’ size and morphology. Most crucially, variations in the beta-cyclodextrin concentration added to the nanoaggregate formulations affected the particle aggregation index and the degree of nanocluster hollowness. However, the incorporation of beta-cyclodextrin in the nanocluster formulation had no significant effect on primary particle size distribution. The experiments were conducted for both drugs (progesterone and 5-fluorouracil). The samples with an average diameter of 146 nm ± 7.3 nm and 293 nm ± 14.65 nm were loaded with progesterone (the drug loading was 9% and 10%, respectively). The 5-fluorouracil was then loaded onto the samples with an average diameter of 207 nm ± 10.35 nm. Beta-cyclodextrin was dissolved in 5 mL to 10 mL of 28% ammonium hydroxide solution, and then added to 50 mL of iron precursor–block copolymer solution. The addition of beta-cyclodextrin significantly affected the initial percentage progesterone release for the sample prepared with an average diameter of 293 nm ± 14.65 nm (the initial percentage release increased to 50% within the first hour).
Furthermore, the cumulative amount of progesterone released remained constant for all the samples examined at variable concentrations of added beta-cyclodextrin (ranging from 5% to 25% of the total solid added). After 72 hours of release experiments, the change in the release profiles for these nanoaggregate samples as a function of increasing beta-cyclodextrin concentration became more significant. The cumulative percentage of drug released after 7 days decreased from 83.35% for the nanoaggregate samples prepared in the absence of beta-cyclodextrin to about 72.36% for the samples prepared using a 15% beta-cyclodextrin concentration. Increasing the concentration of beta-cyclodextrin to 25% was associated with the reduction in the cumulative drug release of progesterone to 65.95% after 7 days (Figure 8).
Figure 8.
Effect of beta-cyclodextrin mass fraction on the release of progesterone samples loaded by freeze-drying.
Additionally, the 5-fluorouracil release profile was also investigated as a function of beta-cyclodextrin concentration. The 124 nm ± 6.2 nm nanoaggregate formulation loaded with 2% of the anti-cancer drug was examined for the release rate and profile as a function of increasing the concentration of beta-cyclodextrin. The effect of beta-cyclodextrin concentration on the initial burst was more significant in the case of 5-fluorouracil (Table S3, Supplementary section).
Analysis of release mechanism and mathematical model fitting
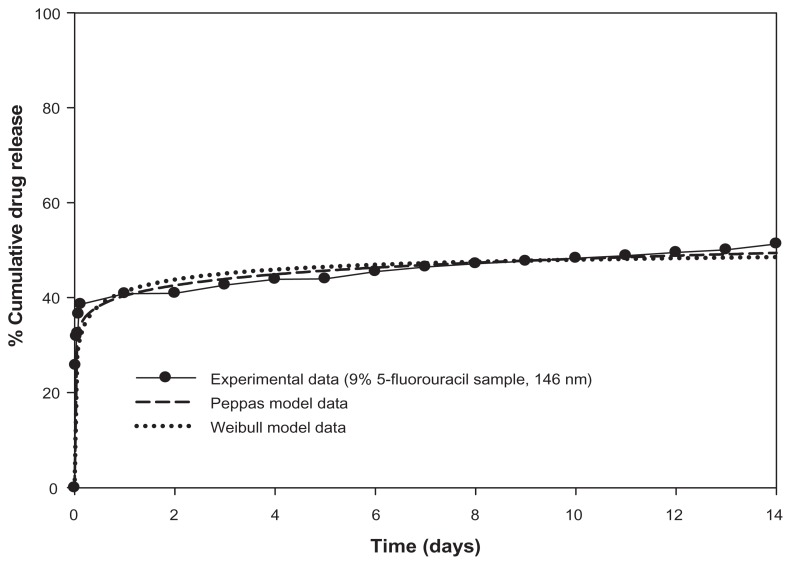
Successful curve fittings were obtained when the Peppas model equation was fitted to the total release curves. A typical example of excellent curve fitting is shown in Figure 9. An overview of the derived estimates for the release index (n) is listed in Table 2. The calculated values of standard error, and the correlation coefficients of the nonlinear regression analysis, are indicative of the optimal fitting of the Peppas model equation to the experimental data (Table 4, Supplementary section). For all examined samples, the estimates for the release index (n) is below 0.5, which indicates pure diffusion controlled release from a sphere.30
Figure 9.
Mathematical modeling of 5-fluorouracil release from 146 nm magnetic nanoaggregates.
Interestingly, good coefficients of correlation were obtained when the Weibull empirical equation was fitted to the release curves for the samples loaded with 5-fluorouracil. The computed parameter, b, for the Weibull curve fitting was 0.74 for the in-situ sample loaded with 9% 5-fluorouracil. This is consistent with the parameter values for the Fickian diffusion reported by Costa et al30 (Figure 9). The mathematical and physical interrelationship between the Peppas and Weibull models have been previously reported; thus, the Weibull function can be considered as further corroboration of the drug release mechanism.
The drug loading technique appears to affect both the release rate and the drug release mechanisms. The Peppas model fitting to the release data of 5-fluorouracil nanoaggregates loaded by freeze-drying showed a significant reduction in the coefficient of correlations for the 293 nm and 146 nm samples. However, good coefficients of correlation were also obtained with the Weibull function. The estimates for the b values were 1.12 and 1.14 (close to 1), which is consistent with the first-order release. In this case, the concentration gradient in the release medium was believed to control the release rate. A typical example of Weibull curve fitting is shown in Figure 8.
The dissimilarity in the fitting parameters between 5-fluorouracil and progesterone could be attributed to the difference in their aqueous solubility. The differences in the estimates of release index (n) were more significant with increasing the mass fraction of beta-cyclodextrin. The Peppas model equation failed to fit the release data for progesterone-loaded samples prepared with either 15% or 25% mass fraction of beta-cyclodextrin. The calculated coefficients of correlations were 0.78 and 0.70, respectively. The correlations for the Weibull model equation showed perfect fitting for these samples. The estimates for the b parameter are 0.09 and 0.1 for samples prepared with 15% and 25% beta-cyclodextrin, respectively. The predicted mechanism in this case is diffusion through highly disordered spaces.
In addition, an increase in the initial burst effect for the progesterone-loaded nanoaggregates prepared with a high percentage of beta-cyclodextrin could be attributed to the enhancement of the drug’s aqueous solubility. Therefore, a modified form of the Peppas model equation was developed to accommodate the initial burst effect. Figures S3 and S4 (Supplementary section) are typical examples for the curve fitting of our experimental release data to the modified Peppas model. A mathematical presentation for the modified Peppas function is presented in the following equation:
| (1) |
where Q is the amount of drug released at time t, a is a constant incorporating structural and geometrical characteristics of the drug dosage form, n is the release exponent and b is a parameter which is indicative of the initial burst effect. In the absence of such initial burst effect, b value would be zero and only the term, at n, is used. Table 3 summarizes the results for the curve fitting parameters for the progesterone-loaded nanoaggregates prepared at two different concentrations of beta-cyclodextrin: 5% and 25%, respectively. The samples prepared with 25% beta-cyclodextrin showed a higher coefficient of correlation to the modified Peppas model. The estimated initial burst parameter is higher for the 25% beta-cyclodextrin sample. This could be attributed to the relatively small fraction of hydrophobic drug that enters the cyclodextrin cavity. At a high concentration of beta-cyclodextrin, it is highly probable that a larger fraction of progesterone interacts with the long aliphatic chain of the polymer. This is consistent with the results obtained by Memisoglu et al.31 In addition, the presence of block co-polymer as the solubilizer influences the rapid initial release of progesterone.
Table 3.
Release parameters for mathematical modeling of progesterone-loaded magnetic nanoaggregates
| Mass fraction of Beta-cyclodextrin | Peppas model | Modified Peppas model with initial burst effect | ||
|---|---|---|---|---|
|
|
|
|||
| Regression coefficient (R2) | Release index (n) | Regression coefficient (R2) | Initial release parameter (b) | |
| 5% Beta-cyclodextrin | 0.83 | 0.07 ± 0.02 | 0.86 | 19.99 ± 0.63 |
| 25% Beta-cyclodextrin | 0.69 | 0.03 ± 0.01 | 0.91 | 22.53 ± 0.31 |
In the present work, we analyzed the effect of different formulation parameters on the viability of A549 lung cancerous cells. First, we examined the effect of different percentages of 5-fluorouracil-loading on the living cells. Thereafter, the effect of different drug loading techniques was also investigated.
In vitro cytotoxicity study
Effect of drug loading percentages on the viability of lung cancer cells
Nanoaggregates loaded with different percentages of 5-fluorouracil were found to exert a cytotoxic effect on the A549 cancerous cell line, in a dose-dependent manner (Figure S5, Supplementary section). The samples exhibited different sensitivity based on their loading percentages. The higher percentage of cytotoxicity was observed for the sample loaded with 5% 5-fluorouracil. Increasing the percentage of drug loaded up to 10% did not result in an enhanced cytotoxicity. The lowest inactivation rate of the cells was observed for the samples loaded with 10% 5-fluorouracil, which could be attributed to the decreased release rate of drug.
Effect of drug loading technique on viability of lung cancer cells
Lung cancer cells were treated with magnetic nanoaggregate formulations, loaded using both the in-situ and freeze-drying techniques. Similarly, all samples induced cytotoxiciy in a dose-dependent manner. The higher cell inactivation rate was recorded for the samples loaded by the freeze-drying technique. In addition, the effect of freeze-dried samples seemed to be extremely strong, with the residual cells’ viability found to be 6.25% at a drug concentration of 100 nM.
Conclusion
Magnetic nanoaggregates based on block copolymer and beta-cyclodextrin can be described as good candidates for controlled drug delivery of both hydrophilic and hydrophobic drugs. The rates of drug loading and encapsulation efficiency can be modulated by controlling different formulation parameters. Significant enhancement in drug encapsulation was observed for the postsynthesis drug-loaded samples. However, by using the in-situ loading method at 0.5% of Pluronic F-68, it was possible to obtain nanoaggregates with high amounts of drug (up to 10% drug loading). Additionally, the drug release mechanism was investigated by mathematical curve fitting to different drug release kinetics models. In most cases, the Peppas model showed good correlations with the examined release profiles, with estimated release indices of below 0.5. In case of drugs with limited aqueous solubility or at high polymer concentrations, the Peppas model failed to fit the entire release curve. Therefore, an estimation of Weibull parameters can provide a hint about the drug release mechanism.
Our designed polymeric magnetic nanoaggregates were verified to be more efficient for encapsulation of both hydrophilic and hydrophobic drugs relative to polyalkylcyanoacrylates, which are the most investigated polymers in the development of 5-fluorouracil magnetic nanocarriers.32 The nanoaggregates that we proposed are advantageous by their facile and organic solvent free method of preparation, and lack of toxic degradation products which comes from polymeric degradation. In addition, these nanoaggregates exhibited superparamagnetic properties at approximately body temperature. In terms of the development of drug carrier systems, the postsynthesis drug loading of both progesterone and 5-fluorouracil showed better drug loading results than the in-situ loading method. Our nanoaggregates were easily loaded with progesterone and 5-fluorouracil. Both the polymer composition and the initial drug concentration were found to play the most effective role in drug loading and release kinetics.
The drug release mechanism was found to be controlled by diffusion. The release profile was sustained for 14 days with considerable release of both drugs within the first few hours. The kinetics of drug release (release rate and indices) was mainly controlled by the type of drug incorporation and the amount of drug loaded. A modified Peppas model with an initial burst effect can provide a better understanding of the drug release mechanism for the samples loaded with progesterone or at high polymer concentrations. The burst effect could be advantageous for drugs that show considerable lag time between the dose administration and therapeutic effect. In addition, we studied the cytotoxic effect of 5-fluorouracil- loaded magnetic nanoaggregates on the viability of A549 lung cancer cells. The cell viability was determined in relation to different percentages of drug loadings. Both in-situ loaded and freeze-dried magnetic nanoaggregates inhibited the proliferation of lung cancer cells. The cytotoxic effect was significantly affected by different polymer concentrations in a dose-dependent manner. These results highlight the biological applicability of our synthesized magnetic nanoaggregates as carriers for anticancer drugs. Further examination of the pulmonary deposition component of our proposed nanoaggregates is being performed.
Supplementary materials
Drug release profiles of 5-fluorouracil-loaded nanoaggregates prepared by in-situ loading method.
Effect of particle size and loading procedures on the release profile of 5-fluorouracil-loaded nanoaggregates at constant percentage of drug loading.
Modified Peppas model equation for prediction of initial burst effect of progesterone-loaded nanoaggregates prepared at 0% beta-cyclodextrin.
Modified Peppas model equation for prediction of initial burst effect of progesterone-loaded nanoaggregates sample prepared at (A) 0%; and (B) 25% beta-cyclodextrin.
Effect of drug loading percentages on the viability of cancerous cells.
Effect of drug loading technique on viability of lung cancer cells.
Abbreviation: 5-FU, 5-fluorouracil.
Table S1.
Mathematical models describing release rates of 5-fluorouracil and progesterone from the hollow nanoaggregates14–16
| Model | Equation |
|---|---|
| Zero order | |
| First order | |
| Hixson-Crowell | |
| Higuchi | |
| Peppas | |
| Modified Peppas | |
| Weibull | |
| Lonsdale and Baker |
Notes: where C is the concentration of drug released, C0 is the initial concentration of drug, K is the release rate constant in units of concentration/time, Q is the amount of drug released in time t, Q0 is the initial amount of drug loaded into the nanoaggregates, and the release index is symbolized as n.
Table S2.
Effect of drug loading on the estimated release rates and release indices according to Peppas model equation
| Drug loading | Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) |
|---|---|---|---|
| 9% 5-fluorouracil | 40.43 ± 0.47 | 0.97 | 0.075 ± 0.005 |
| 9.5% 5-fluorouracil | 35.29 ± 0.39 | 0.92 | 0.069 ± 0.002 |
| 10% 5-fluorouracil | 32.76 ± 0.32 | 0.98 | 0.071 ± 0.004 |
Note: The samples are all loaded by the in-situ method.
Table S3.
Effect of beta-cyclodextrin mass fraction on the release parameters of progesterone and 5-fluorouracil freeze-dried loaded samples
| Drug loading | Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) |
|---|---|---|---|
| Progesterone, 0% beta-cyclodextrin | 64.08 ± 0.14 | 0.92 | 0.14 ± 0.01 |
| Progesterone, 5% beta-cyclodextrin | 67.67 ± 1.72 | 0.83 | 0.07 ± 0.01 |
| Progesterone, 15% beta-cyclodextrin | 65.94 ± 0.05 | 0.78 | 0.05 ± 0.01 |
| Progesterone, 25% beta-cyclodextrin | 61.76 ± 1.42 | 0.70 | 0.03 ± 0.01 |
| 5-Fluorouracil, 0% beta-cyclodextrin | 66.22 ± 2.94 | 0.91 | 0.18 ± 0.02 |
| 5-Fluorouracil, 5% beta-cyclodextrin | 44.29 ± 1.81 | 0.93 | 0.19 ± 0.02 |
| 5-Fluorouracil, 15% beta-cyclodextrin | 39.13 ± 1.34 | 0.95 | 0.21 ± 0.01 |
| 5-Fluorouracil, 25% beta-cyclodextrin | 33.13 ± 1.18 | 0.94 | 0.17 ± 0.02 |
Table S4.
Results for the curve fitting parameters of different model functions for 5-fluorouracil release profiles
| Model function | % 5-FU loading | Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) | Probability (P) |
|---|---|---|---|---|---|
| Lonsdale model | 9% 5-FU | 0.01 ± 0.002 | 0.01 | – | 0.003 |
| Peppas model | 9% 5-FU | 40.43 ± 0.47 | 0.97 | 0.075 ± 0.005 | <0.001 |
| Hixson model | 9% 5-FU | 0.02 ± 0.004 | 0.03 | – | <0.001 |
| Higuchi model | 9% 5-FU | 16.82 ± 1.71 | 0.01 | – | <0.001 |
| First order model | 9% 5-FU | 0.08 ± 0.02 | 0.02 | – | <0.001 |
| Lonsdale model | 9.5% 5-FU | 0.004 ± 0.0001 | 0.79 | – | <0.001 |
| Peppas model | 9.5% 5-FU | 35.29 ± 0.39 | 0.92 | 0.069 ± 0.002 | <0.001 |
| Hixson model | 9.5% 5-FU | 0.02 ± 0.003 | 0.03 | – | <0.001 |
| Higuchi model | 9.5% 5-FU | 14.67 ± 1.42 | 0.09 | – | <0.001 |
| First order model | 9.5% 5-FU | 0.06 ± 0.01 | 0.02 | – | <0.001 |
| Lonsdale model | 10% 5-FU | 0.04 ± 0.01 | 0.01 | – | 0.004 |
| Peppas model | 10% 5-FU | 32.76 ± 0.32 | 0.98 | 0.071 ± 0.004 | <0.001 |
| Hixson model | 10% 5-FU | 0.02 ± 0.002 | 0.03 | – | <0.001 |
| Higuchi model | 10% 5-FU | 13.48 ± 1.41 | 0.01 | – | <0.001 |
| First order model | 10% 5-FU | 0.06 ± 0.01 | 0.02 | – | <0.001 |
Abbreviation: 5-FU, 5-Fluorouracil.
Supplementary materials
Methodology of quantitative drug measurement
5-Fluorouracil HPLC assay: 5-Fluorouracil was quantified by high performance liquid chromatography (HPLC). A Varian HPLC system (Varian ProStar, Santa Clara, CA) with RP C-18 column (250 mm × 4.6 mm, particle size 5 μm) and variable wavelength UV/Vis detector was used. A mixture of methanol and sodium acetate buffer (pH = 4.0) was used as a mobile phase. The eluent was detected by UV detector at 260 nm.
Progesterone UV spectrophotometric assay: Quantitative determination of progesterone was performed using UV spectrophotomeric method at wavelength 254 nm (Varian ProStar).
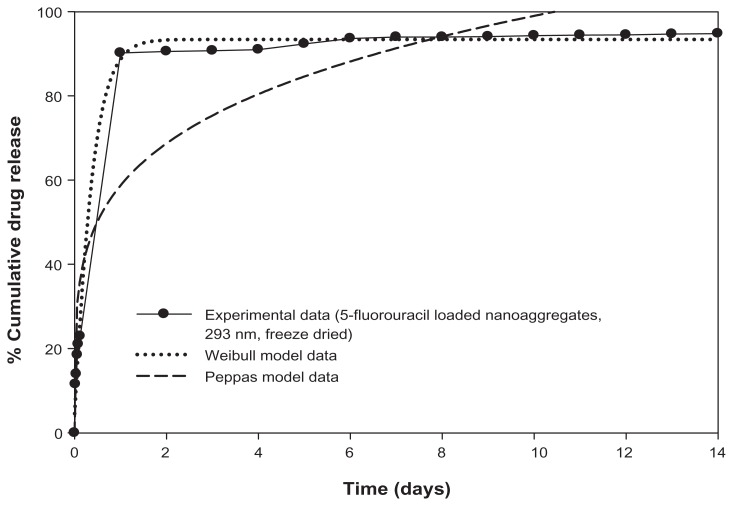
Controlled release of 5-fluorouracil and progesterone from magnetic nanoaggregates.
Figure 10.
Mathematical modeling of 5-fluorouracil release from 293 nm magnetic nanoaggregates.
Acknowledgments
This work was supported by the Pharmaceutical Crystallization and Control of Drug Laboratory, Department of Chemical and Biochemical Engineering, Faculty of Engineering, University of Western Ontario, London, Ontario, Canada.
Footnotes
Disclosure
The authors report no conflicts of interest in this work.
References
- 1.Mansour HM, Rhee YS, Wu X. Nanomedicine in pulmonary delivery. Int J Nanomedicine. 2009;4:299–319. doi: 10.2147/ijn.s4937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Labiris NR, Dolovich MB. Pulmonary drug delivery. Part I: physiological factors affecting therapeutic effectiveness of aerosolized medications. Br J Clin Pharmacol. 2003;56(6):588–599. doi: 10.1046/j.1365-2125.2003.01892.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Patton JS, Byron PR. Inhaling medicines: delivering drugs to the body through the lungs. Nat Rev Drug Discov. 2007;6(1):67–74. doi: 10.1038/nrd2153. [DOI] [PubMed] [Google Scholar]
- 4.Yang W, Johnston KP, Williams RO., III Comparison of bioavailability of amorphous versus crystalline itraconazole nanoparticles via pulmonary administration in rats. Eur J Pharm Biopharm. 2010;75(1):33–41. doi: 10.1016/j.ejpb.2010.01.011. [DOI] [PubMed] [Google Scholar]
- 5.Ahsan F, Rivas IP, Khan MA, Torres Suarez AI. Targeting to macrophages: role of physicochemical properties of particulate carriers – liposomes and microspheres – on the phagocytosis by macrophages. J Control Release. 2002;79(1–3):29–40. doi: 10.1016/s0168-3659(01)00549-1. [DOI] [PubMed] [Google Scholar]
- 6.Makino K, Yamamoto N, Higuchi K, Harada N, Ohshima H, Terada H. Phagocytic uptake of polystyrene microspheres by alveolar macrophages: effects of the size and surface properties of the microspheres. Colloids and Surfaces B: Biointerfaces. 2003;27(1):33–39. [Google Scholar]
- 7.Hoet PH, Bruske-Hohlfeld I, Salata OV. Nanoparticles – known and unknown health risks. J Nanobiotechnology. 2004;2(1):12. doi: 10.1186/1477-3155-2-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rabinow BE. Nanosuspensions in drug delivery. Nat Rev Drug Discov. 2004;3(9):785–796. doi: 10.1038/nrd1494. [DOI] [PubMed] [Google Scholar]
- 9.Tsapis N, Bennett D, Jackson B, Weitz DA, Edwards DA. Trojan particles: large porous carriers of nanoparticles for drug delivery. Proc Natl Acad Sci U S A. 2002;99(19):12001–12005. doi: 10.1073/pnas.182233999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hadinoto K, Phanapavudhikul P, Kewu Z, Tan RB. Dry powder aerosol delivery of large hollow nanoparticulate aggregates as prospective carriers of nanoparticulate drugs: effects of phospholipids. Int J Pharm. 2007;333(1–2):187–198. doi: 10.1016/j.ijpharm.2006.10.009. [DOI] [PubMed] [Google Scholar]
- 11.Van Eerdenbrugh B, Van den Mooter G, Augustijns P. Top-down production of drug nanocrystals: nanosuspension stabilization, miniaturization and transformation into solid products. Int J Pharm. 2008;364(1):64–75. doi: 10.1016/j.ijpharm.2008.07.023. [DOI] [PubMed] [Google Scholar]
- 12.Kim BS, Qiu JM, Wang JP, Taton TA. Magnetomicelles: composite nanostructures from magnetic nanoparticles and cross-linked amphiphilic block copolymers. Nano Lett. 2005;5(10):1987–1991. doi: 10.1021/nl0513939. [DOI] [PubMed] [Google Scholar]
- 13.Ge J, Hu Y, Biasini M, Beyermann WP, Yin Y. Superparamagnetic magnetite colloidal nanocrystal clusters. Angew Chem Int Ed Engl. 2007;46(23):4342–4345. doi: 10.1002/anie.200700197. [DOI] [PubMed] [Google Scholar]
- 14.Tongwen X, Binglin H. Mechanism of sustained drug release in diffusion-controlled polymer matrix-application of percolation theory. Int J Pharm. 1998;170(2):139–149. [Google Scholar]
- 15.Maderuelo C, Zarzuelo A, Lanao JM. Critical factors in the release of drugs from sustained release hydrophilic matrices. J Controlled Release. 2011;154(1):2–19. doi: 10.1016/j.jconrel.2011.04.002. [DOI] [PubMed] [Google Scholar]
- 16.Peppas NA, Bures P, Leobandung W, Ichikawa H. Hydrogels in pharmaceutical formulations. European Journal of Pharmaceutics and Biopharmaceutics. 2000;50(1):27–46. doi: 10.1016/s0939-6411(00)00090-4. [DOI] [PubMed] [Google Scholar]
- 17.Edwards DA, Hanes J, Caponetti G, et al. Large porous particles for pulmonary drug delivery. Science. 1997;276(5320):1868–1871. doi: 10.1126/science.276.5320.1868. [DOI] [PubMed] [Google Scholar]
- 18.Dailey LA, Kleemann E, Wittmar M, et al. Surfactant-free, biodegradable nanoparticles for aerosol therapy based on the branched polyesters, DEAPA-PVAL-g-PLGA. Pharm Res. 2003;20(12):2011–2020. doi: 10.1023/b:pham.0000008051.94834.10. [DOI] [PubMed] [Google Scholar]
- 19.Zhang C, Zhang H, Du B, Hou R, Guo S. Facile organic solvent-free synthesis of size-controlled hierarchically structured magnetic hollow spheres and potential application in adsorption for bovine serum album. J Colloid Interface Sci. 2012;368(1):97–106. doi: 10.1016/j.jcis.2011.10.056. [DOI] [PubMed] [Google Scholar]
- 20.Kuznetsov AA, Filippov VI, Alyautdin RN, Torshina NL, Kuznetsov OA. Application of magnetic liposomes for magnetically guided transport of muscle relaxants and anti-cancer photodynamic drugs. J Magn Magn Mater. 2001;225(1–2):95–100. [Google Scholar]
- 21.Voigt A, Buske N, Sukhorukov GB, et al. Novel polyelectrolyte multilayer micro- and nanocapsules as magnetic carriers. J Magn Magn Mater. 2001;225(1–2):59–66. [Google Scholar]
- 22.Krahne R, Morello G, Figuerola A, George C, Deka S, Manna L. Physical properties of elongated inorganic nanoparticles. Physics Reports. 2011;501(3–5):75–221. [Google Scholar]
- 23.Jin J, Iyoda T, Cao C, et al. Self-Assembly of Uniform Spherical Aggregates of Magnetic Nanoparticles through pi-pi Interactions. Angew Chem Int Ed Engl. 2001;40(11):2135–2138. doi: 10.1002/1521-3773(20010601)40:11<2135::AID-ANIE2135>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 24.Siepmann J, Siepmann F. Mathematical modeling of drug delivery. Int J Pharm. 2008;364(2):328–343. doi: 10.1016/j.ijpharm.2008.09.004. [DOI] [PubMed] [Google Scholar]
- 25.Xia H, Foo P, Yi J. Water-Dispersible Spherically Hollow Clusters of Magnetic Nanoparticles. Chem Mater. 2009;21(12):2442–2451. http://dx.doi.org/10.1021/cm900268z. [Google Scholar]
- 26.Lemos-Senna E, Wouessidjewe D, Lesieur S, Duchêne D. Preparation of amphiphilic cyclodextrin nanospheres using the emulsification solvent evaporation method. Influence of the surfactant on preparation and hydrophobic drug loading. Int J Pharm. 1998;170(1):119–128. [Google Scholar]
- 27.Shuguang Z. Emerging biological materials through molecular self-assembly. Biotechnol Adv. 2002;20(5–6):321–339. doi: 10.1016/s0734-9750(02)00026-5. [DOI] [PubMed] [Google Scholar]
- 28.Al-Nasiry S, Geusens N, Hanssens M, Luyten C, Pijnenborg R. The use of Alamar Blue assay for quantitative analysis of viability, migration and invasion of choriocarcinoma cells. Human Reproduction. 2007;22(5):1304–1309. doi: 10.1093/humrep/dem011. [DOI] [PubMed] [Google Scholar]
- 29.Rana S, Gallo A, Srivastava RS, Misra RDK. On the suitability of nanocrystalline ferrites as a magnetic carrier for drug delivery: Functionalization, conjugation and drug release kinetics. Acta Biomaterialia. 2007;3(2):233–242. doi: 10.1016/j.actbio.2006.10.006. [DOI] [PubMed] [Google Scholar]
- 30.Costa P, Sousa Lobo JM. Modeling and comparison of dissolution profiles. European Journal of Pharmaceutical Sciences. 2001;13(2):123–133. doi: 10.1016/s0928-0987(01)00095-1. [DOI] [PubMed] [Google Scholar]
- 31.Memişoğlu E, Bochot A, Şen M, Duchêne D, Hıncal AA. Non-surfactant nanospheres of progesterone inclusion complexes with amphiphilic β-cyclodextrins. Int J Pharm. 2003;251(1–2):143–153. doi: 10.1016/s0378-5173(02)00593-8. [DOI] [PubMed] [Google Scholar]
- 32.Arias JL, Gallardo V, Ruiz MA, Delgado ÁV. Magnetite/poly(alkylcyanoacrylate) (core/shell) nanoparticles as 5-Fluorouracil delivery systems for active targeting. European Journal of Pharmaceutics and Biopharmaceutics. 2008;69(1):54–63. doi: 10.1016/j.ejpb.2007.11.002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Drug release profiles of 5-fluorouracil-loaded nanoaggregates prepared by in-situ loading method.
Effect of particle size and loading procedures on the release profile of 5-fluorouracil-loaded nanoaggregates at constant percentage of drug loading.
Modified Peppas model equation for prediction of initial burst effect of progesterone-loaded nanoaggregates prepared at 0% beta-cyclodextrin.
Modified Peppas model equation for prediction of initial burst effect of progesterone-loaded nanoaggregates sample prepared at (A) 0%; and (B) 25% beta-cyclodextrin.
Effect of drug loading percentages on the viability of cancerous cells.
Effect of drug loading technique on viability of lung cancer cells.
Abbreviation: 5-FU, 5-fluorouracil.
Table S1.
Mathematical models describing release rates of 5-fluorouracil and progesterone from the hollow nanoaggregates14–16
| Model | Equation |
|---|---|
| Zero order | |
| First order | |
| Hixson-Crowell | |
| Higuchi | |
| Peppas | |
| Modified Peppas | |
| Weibull | |
| Lonsdale and Baker |
Notes: where C is the concentration of drug released, C0 is the initial concentration of drug, K is the release rate constant in units of concentration/time, Q is the amount of drug released in time t, Q0 is the initial amount of drug loaded into the nanoaggregates, and the release index is symbolized as n.
Table S2.
Effect of drug loading on the estimated release rates and release indices according to Peppas model equation
| Drug loading | Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) |
|---|---|---|---|
| 9% 5-fluorouracil | 40.43 ± 0.47 | 0.97 | 0.075 ± 0.005 |
| 9.5% 5-fluorouracil | 35.29 ± 0.39 | 0.92 | 0.069 ± 0.002 |
| 10% 5-fluorouracil | 32.76 ± 0.32 | 0.98 | 0.071 ± 0.004 |
Note: The samples are all loaded by the in-situ method.
Table S3.
Effect of beta-cyclodextrin mass fraction on the release parameters of progesterone and 5-fluorouracil freeze-dried loaded samples
| Drug loading | Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) |
|---|---|---|---|
| Progesterone, 0% beta-cyclodextrin | 64.08 ± 0.14 | 0.92 | 0.14 ± 0.01 |
| Progesterone, 5% beta-cyclodextrin | 67.67 ± 1.72 | 0.83 | 0.07 ± 0.01 |
| Progesterone, 15% beta-cyclodextrin | 65.94 ± 0.05 | 0.78 | 0.05 ± 0.01 |
| Progesterone, 25% beta-cyclodextrin | 61.76 ± 1.42 | 0.70 | 0.03 ± 0.01 |
| 5-Fluorouracil, 0% beta-cyclodextrin | 66.22 ± 2.94 | 0.91 | 0.18 ± 0.02 |
| 5-Fluorouracil, 5% beta-cyclodextrin | 44.29 ± 1.81 | 0.93 | 0.19 ± 0.02 |
| 5-Fluorouracil, 15% beta-cyclodextrin | 39.13 ± 1.34 | 0.95 | 0.21 ± 0.01 |
| 5-Fluorouracil, 25% beta-cyclodextrin | 33.13 ± 1.18 | 0.94 | 0.17 ± 0.02 |
Table S4.
Results for the curve fitting parameters of different model functions for 5-fluorouracil release profiles
| Model function | % 5-FU loading | Release rate constant (K, day−1) | Regression coefficient (R2) | Release index (n) | Probability (P) |
|---|---|---|---|---|---|
| Lonsdale model | 9% 5-FU | 0.01 ± 0.002 | 0.01 | – | 0.003 |
| Peppas model | 9% 5-FU | 40.43 ± 0.47 | 0.97 | 0.075 ± 0.005 | <0.001 |
| Hixson model | 9% 5-FU | 0.02 ± 0.004 | 0.03 | – | <0.001 |
| Higuchi model | 9% 5-FU | 16.82 ± 1.71 | 0.01 | – | <0.001 |
| First order model | 9% 5-FU | 0.08 ± 0.02 | 0.02 | – | <0.001 |
| Lonsdale model | 9.5% 5-FU | 0.004 ± 0.0001 | 0.79 | – | <0.001 |
| Peppas model | 9.5% 5-FU | 35.29 ± 0.39 | 0.92 | 0.069 ± 0.002 | <0.001 |
| Hixson model | 9.5% 5-FU | 0.02 ± 0.003 | 0.03 | – | <0.001 |
| Higuchi model | 9.5% 5-FU | 14.67 ± 1.42 | 0.09 | – | <0.001 |
| First order model | 9.5% 5-FU | 0.06 ± 0.01 | 0.02 | – | <0.001 |
| Lonsdale model | 10% 5-FU | 0.04 ± 0.01 | 0.01 | – | 0.004 |
| Peppas model | 10% 5-FU | 32.76 ± 0.32 | 0.98 | 0.071 ± 0.004 | <0.001 |
| Hixson model | 10% 5-FU | 0.02 ± 0.002 | 0.03 | – | <0.001 |
| Higuchi model | 10% 5-FU | 13.48 ± 1.41 | 0.01 | – | <0.001 |
| First order model | 10% 5-FU | 0.06 ± 0.01 | 0.02 | – | <0.001 |
Abbreviation: 5-FU, 5-Fluorouracil.