Assessing the Accuracy of Protein Structures by Quantum Mechanical Computations of ¹³C^α Chemical Shifts

Conspectus

Two major techniques have been used to determine the three-dimensional structures of proteins: x-ray diffraction and NMR spectroscopy. In particular, the validation of NMR-derived protein structures is one of the most challenging problems in NMR spectroscopy. Therefore, researchers have proposed a plethora of methods to determine the accuracy and reliability of protein structures. Despite these proposals, there is a growing need for more sophisticated, physics-based structure validation methods. This approach will enable us to (a) characterize the “quality” of the NMR-derived ensemble as a whole by a single parameter, (b) unambiguously identify flaws in the sequence at a residue level, and (c) provide precise information, such as sets of backbone and side-chain torsional angles, that we can use to detect local flaws.

Rather than reviewing all of the existing validation methods, this Account describes the contributions of our research group toward a solution of the long-standing problem of both global and local structure validation of NMR-derived protein structures. We emphasize a recently introduced physics-based methodology that makes use of observed and computed ¹³C^α chemical shifts (at the DFT level of theory) for an accurate validation of protein structures in solution and in crystals. By assessing the ability of computed ¹³C^α chemical shifts to reproduce observed ¹³C^α chemical shifts of a single or ensemble of structures in solution and in crystals, we accomplish a global validation by using the conformationally-averaged root-mean-square-deviation, ca-rmsd, as a scoring function. In addition, the method enables us to provide local validation by identifying a set of individual amino acid conformations for which the computed and observed ¹³C^α chemical shifts do not agree within a certain error range and may represent a non-reliable fold of the protein model.

Although it is computationally intensive, our validation method has several advantages, which we illustrate through a series of applications. This method makes use of the ¹³C^α chemical shifts, not shielding, that are ubiquitous to proteins and can be computed precisely from the φ, ψ, and χ torsional angles. There is no need for a priori knowledge of the oligomeric state of the protein, and no knowledge-based information or additional NMR data are required. The primary limitation at this point is the computational cost of such calculations. However, we anticipate that enhancements both in the speed of calculating these chemical shifts coupled with ever increasing computational power should soon make this a standard method accessible to the general NMR community.

1. Introduction

Between the first time that chemical shifts were observed by Arnold et. al., in 1951¹ and the ‘structural genomics’ initiative (that started in 2000) to develop a technology for high-throughput structure determination and expand our understanding of protein structure and function, a vast amount of experimental and theoretical advances in the Nuclear Magnetic Resonance (NMR) field have taken place. Many recent reviews in the field attest to this.^2-8 Despite this formidable progress in NMR spectroscopy, quality assessment remains as a crucial test for NMR-derived protein structures.^9,10 A number of methods have been developed over the years (WHAT IF,¹¹ PROCHECK,¹² RPF,¹³ MolProbity,¹⁴ etc.) because validation of protein structure conformations is essential for both the spectroscopists, since it enables them to focus on aspects of the structure that might contain errors, and for the users, because validation of existing models enables them to determine the quality and suitability of the protein models for any specific purpose. Despite the available tools for assessing the accuracy of NMR-derived proteins, there is consensus that more sophisticated structural validation methods are needed;^15,16 i.e., there is a need for a very sensitive, physics-based, method to detect whether or not a given structure or regions of the structure, at a residue level, is erroneous.

Residual dipolar couplings (RDC) represent a powerful tool with which to identify errors in NMR structures.^6,15-18 Regrettably, as noted by Nabuurs et al.,¹⁶ they are not routinely acquired in most of the structural genomics efforts nor are they available for the great majority of the deposited structures in the BioMagResBank;¹⁹ viz., as noted by Simon et al.,¹⁸ there are 116 RDC data sets compared with 2276 Nuclear Overhauser Effect (NOE) data sets associated with proteins. On the other hand, most chemical shifts are available from any NMR experiment because the first step in NMR spectroscopy, before the collection and analysis of structural restraints such as those derived from NOE, consists of the acquisition of NMR data that lead to the assignment of the chemical shifts for all nuclei (¹H, ¹⁵N and ¹³C) in the molecule. Among all these nuclei, we focus our attention on only one, namely ¹³C^α chemical shifts, because they are exquisitely sensitive to their local environment and provide a conformational ‘finger print’ of each amino acid residue in a protein. The backbone and side-chain conformations of a residue are influenced by interactions with the rest of the protein but, once these conformations are established by these interactions, the ¹³C^α shielding of each residue, but not the shielding from other nuclei such as ¹H, ¹⁵N or ¹³C’, depends mainly on its own backbone^20,21 and side-chain^22-24 conformation, with no significant influence of either the amino acid sequence^21,24,25 or the position of the given residue in the sequence,²⁶ or the oligomerization state of the protein. These properties, together with the facts that this nucleus is ubiquitous in proteins, and that the computation of the ¹³C^α shielding at the quantum chemical level of theory can be carried out with coarse grained parallelization (one residue per processor), make this nucleus an attractive candidate in order to validate protein structures.^26-29

In this Account, we report our efforts to develop a purely physics-based, structure validation method that enables us: (a) to characterize the ‘quality’ of the NMR-derived ensemble, as a whole, by a single parameter; and (b) to unambiguously identify flaws in the sequence, at a residue level.

In section 2, we will focus on the factors affecting the computation, at the quantum mechanical level of theory, of the ¹³C^α chemical shifts in proteins, such as the sensitivity of the shielding/deshielding of ¹³C^α nuclei to changes in the protonation/deprotonation state of distant ionizable groups,³⁰ the values of the bond lengths and bond angles adopted to represent the geometry of the molecule,⁴ etc. In addition, we will demonstrate that the validation method is strong, rather than weak.³¹ Finally, given that our central interest is in the ¹³C^α chemical shifts, not their shielding, computation of an accurate value for the shielding of the reference, namely tetramethylsilane (TMS), is crucial. For this reason, we illustrate how an effective shielding³² value can be computed.

In section 3, we will show, first, how our method can be used, in terms of a new scoring function the ca-rmsd, for validation of two highly-accurate protein structures solved by both NMR and X-ray methods, and, second, how a comparison between observed and computed ¹³C^α chemical shifts (at the DFT level of theory) enables us to determine, at the residue level the existence of local flaws in the sequence. The latter is a very important problem because it is known that ambiguities in the assignment of intra- or intersubunit Nuclear Overhauser Effects (NOE) might result in a wrong fold.^16,33 The increasing number of oligomer structures in biology (~65% of the proteins in every genome are expected to be homo-oligomers³³) may only exacerbate this problem. Hence, the ability of our validation method to detect flaws in the sequence might be of very valuable assistance for determining wrong folds in homodimers, particularly if information regarding the oligomerization state in solution or the structure of homologous monomers, is not available.

Finally, in section 4, a discussion of ongoing progress in our validation method, to speed it up without loss of accuracy, and its impact on progress in the field, is presented, together with a limit of the method, that exists in current applications.

2. General Background

The foundation of the method and the most relevant approximations adopted to make the computation of the ¹³C^α chemical shifts accurate, but feasible, are discussed briefly here.

The computational approach

At the core of the ¹³C^α–based validation method are the following most important approximations adopted to compute chemical shifts. First, all the experimentally determined conformations to be validated were regularized, i.e., all residues were replaced by the standard ECEPP/3³⁴ residue geometry, in which bond lengths and bond angles are fixed (rigid-geometry approximation) and, second, hydrogen atoms were added, if necessary. This problem is central to all the results reported here because it is known that quantum mechanical calculations are very sensitive to bond lengths and bond angles.³⁵ In fact, even proteins solved at a high level of accuracy, as by X-ray diffraction, are not expected to provide the best correlation with the observed ¹³C^α chemical shifts.³⁵ Consequently, we explore the dependence of the ¹³C^α-chemical shift calculations, rather than shielding, on the bond lengths and bond angles.

For this test, we chose the structure of ubiquitin deposited in the Protein Data Bank³⁶ (PDB) [PDB id 1UBQ]; it possesses non-regular geometry and has been solved by X-ray diffraction at 1.8 Å resolution.³⁷ We also examined the corresponding structure with regularized geometry, named here as 1UBQ_reg. Analysis of the differences between computed and observed ¹³C^α chemical shifts for the 1UBQ and 1UBQ_reg structures, in terms of rmsd, leads to 3.28 ppm and 2.38 ppm, respectively. The value obtained for 1UBQ_reg (2.38 ppm) is slightly lower than the previously reported value (2.60)³² because of improvement in the regularization procedure. Further analysis of the agreement of these structures with the deposited electron density data³⁷ of 1UBQ, in terms of the R-factor, leads to 19.2% and 23.1% for 1UBQ and 1UBQ_reg, respectively; and the all-heavy-atom rmsd between these two structures is 0.142 Å. The better agreement obtained with 1UBQ_reg, rather than 1UBQ, in terms of observed and computed ¹³C^α chemical shifts, is consistent with the long-time recognition that the bond lengths and bond angles of both X-ray and NMR-derived structures are not as highly accurately defined as in studies of small molecules,³⁵ with which the ECEPP/3 geometry has been parameterized.³⁴ Hence, we first regularized all the structure for consistent comparison of computed and experimental results.

Second, each amino acid residue X in the protein sequence was treated as a terminally-blocked tripeptide with the sequence Ac-GXG-NMe,²⁶ with X in the conformation of the regularized experimental protein structure, and the ¹³C^α isotropic shielding value (σ) for each amino acid residue X was computed at the OB98/6-311+G(2d,p) level of theory³² with the Gaussian 03 package.³⁸ The remaining residues in each tripeptide were treated at the OB98/3-21G level of theory, i.e., by using the locally dense basis set approach.³⁹

Third, all ionizable residues were considered neutral during the quantum chemical calculations.³⁰ This approximation, based on the analysis of 139 conformations of ubiquitin at pH 6.5, indicated that use of neutral, rather than charged, amino acids is a significantly better approximation of the observed ¹³C^α chemical shifts in solution for the acidic groups, and a slightly better representation, though significantly less expensive in computational time, for the basic groups.³⁰

Fourth, an accurate computation of the reference ¹³C^αchemical shifts, not absolute shielding, is of primary interest for protein structure validation because ¹³C^αchemical shifts, not the shielding, are the quantities determined with high accuracy in NMR experiments. The most common shielding of the reference used in theoretical applications is that for tetramethylsilane (TMS). Although its computation is a nontrivial problem, because of an assorted number of reasons,³² it is possible to derive a very accurate solution by using properties of the Normal (or Gaussian) fit of the frequency of the error distribution (between computed and observed ¹³C^α chemical shift). With this assumption, an effective TMS shielding value can be determined precisely as 184.5 ppm which must be used in combination with ¹³C^α shielding of residues computed at the OB98/6-311+G(2d,p) level of theory.³²

A new scoring function: the ca-rmsd

For a given protein, the observed ¹³C^α chemical shifts represent the contributions from several conformers that coexist in solution. Hence, any scoring function must considerer such dispersion in the conformations of the molecule explicitly in order to be able to reproduce the observed ¹³C^α chemical shifts in solution. As a consequence, we hypothesize that the observed chemical shift ¹³C^α_observed,μ for a given amino acid μ can be interpreted as a conformational average over different internal rotational states represented by a discrete number of different conformations, all of which satisfied NMR restraints such as NOEs, vicinal coupling constants, etc., from which the conformations were derived.²⁶ Thus, the following quantity can be computed: ${{}_{}{}^{13}\mathrm{C}^{\alpha }}_{\text{computed}{,}_{\mu }}={\sum }_{i=1}^{\Omega }{\lambda }_i{}_{}{}^{13}\mathrm{C}^{\alpha }{}_{\mu ,i}$ where ${}_{}{}^{13}\mathrm{C}^{\alpha }{}_{\mu ,i}$ is the computed chemical shift for amino acid μ in conformation i out of Ω protein conformations, and λ_i is the Boltzmann weight factor for conformation i, with the condition ${\sum }_{i=1}^{\Omega }{\lambda }_i\equiv 1$. With existing computational resources, it is not feasible to determine λ_i at the quantum chemical level, and, hence, it is assumed that, under conditions of fast conformational averaging, all Boltzmann weight factors contribute equally and, hence, ${\lambda }_i\equiv 1∕\Omega$. Under this assumptions, the computation of the ca-rmsd for a protein containing N amino acids residues, is straightforward:²⁶ $\mathit{ca}-{\mathrm{rmsd}}^{\alpha }={[(1∕N){\sum }_{\mu =1}^N{({{{}_{}{}^{13}\mathrm{C}}^{\alpha }}_{\text{observed}}{,}_{\mu }-<{{{}_{}{}^{13}\mathrm{C}}^{\alpha }}_{\text{computed},\mu }>)}^2]}^{1∕2}$. Naturally, if Ω = 1, ca-rmsd ≡ rmsd, as for any single structure.

Is the ¹³C^α-based method a ‘strong’ method with which to validate X-ray and NMR structures?

A validation method is considered ‘strong’ if it is able to assess how well a structure, or ensemble of structures, predicts experimental data not used in the structure-determination process; otherwise it should be considered ‘weak’, since it is limited to reproducing the observed experimental data used in the determination of the protein models.³¹ From this point of view, our use of ¹³C^α chemical shifts as a probe for validation is crucial because these experimental data are not used by crystallographers and, hence, our validation method is always ‘strong’, for X-ray-derived structures. However, such a straightforward conclusion cannot be made for NMR-derived structures, because it has been common practice in this field to use information derived from the observed chemical shifts since 1991 when, in a seminal work, Spera and Bax²⁰ pointed out a clear distinction between the ¹³C^α and ¹³C^β chemical shifts in α-helical and β-sheet conformations. But, this Spera & Bax empirical observation provides a set of backbone (ϕ,ψ) dihedral-angle constraints for residues only in the regions of regular secondary structure such as α-helix or β-sheet, i.e., to about 40% of the residues in proteins;⁴⁰ even more important, no torsional constraints for the side chains are provided, although the influence of the side-chain χ torsional angles on ¹³C^α chemical shifts cannot be disregarded.^21,22,24,30 Later, database servers, such as TALOS,⁴¹ provided information about the backbone torsional angles for a larger range (by up to ~75%) of the amino acid residues. Yet, the improvement in the number and accuracy of the backbone torsional angles predicted do not guarantee that the final set of structures will reproduce the observed ¹³C^α chemical shifts as accurately as NMR-derived high-resolution proteins solved without using TALOS information. For example, a comparison of the validation results obtained from an ensemble of conformations derived using TALOS information, e.g., for 2JVD a 48-residue protein (with a ca-rmsd per-residue of 0.032 ppm),²⁹ against validation results obtained from a high-resolution NMR-determined ensemble of conformations obtained without using TALOS information, e.g., for 1D3Z a 76-residue protein (with a ca-rmsd per-residue of 0.029 ppm),³² indicated that the ensemble of conformations of 1D3Z is a better representation, than the ensemble of 2JVD, of the observed ¹³C^α chemical shifts.

Taken as a whole, the concept of ‘strong’ and ‘weak’ is applicable to X-ray structures but is not an issue here, since our validation method deals with reported structures no matter whether an X-ray or NMR technique is used. If chemical-shift derived information was used, as with some structures derived from NMR spectroscopy, our method will also indicate the quality, in terms of the ca-rmsd of the final ensemble of conformations, and if such information is misleading our method will detect it.

3. Global and Local Validation of Proteins Structures

During the last few years, we have applied the ¹³C^α-based validation method to assess the global quality of an assorted number of proteins in all α-helical,^26,27,29 all β-sheet,²⁸ and α/β motifs,²⁶ and spanning a wide range in the number of amino acid residues N, namely in the range 20 ≤ N ≤ 109.^26-30 Among all these applications, we selected two highly-accurate protein structures solved by both NMR and X-ray methods to illustrate the global validation of proteins and to discuss the question of the legitimacy to choose the X-ray structure as the best set of atomic coordinates, i.e., the ‘true structure’, with which to represent the observed ¹³C^α chemical shifts in solution.

Most proteins interact with other proteins, viz., ~80% of ~2,000 yeast proteins were found to be interacting with, at least, one partner.⁴² This might increase the chance of ambiguities in the NOE assignments during protein-structure determination by NMR spectroscopy and, hence, lead to conformational errors. We will also illustrate how the validation of local, rather than global, flaws in the sequence offers an opportunity to spectroscopists for an accurate early detection of the consequences of such possible mis-assignments.

Analysis of the global validation of two selected proteins

The selected set of conformations for the analysis were: (a) 10 conformers of a 76-residue α/β protein ubiquitin, solved by NMR spectroscopy⁴³ [PDB id 1D3Z] and the corresponding X-ray structure, solved at 1.8 Å resolution³⁷ [PDB code: 1UBQ]; and (b) 20 conformers of a 48-residue all-α–helical YnzC protein from Bacillus subtilis solved by NMR spectroscopy⁴⁴ (PDB id 2JVD) and a slightly longer construct of the YnzC protein solved by X-ray diffraction at 2.0 Å resolution²⁹ (PDB id 3BPH, with three chains in the asymmetric unit) showing identical amino acid residue sequence as the 2JVD structure for the first 46 residues.

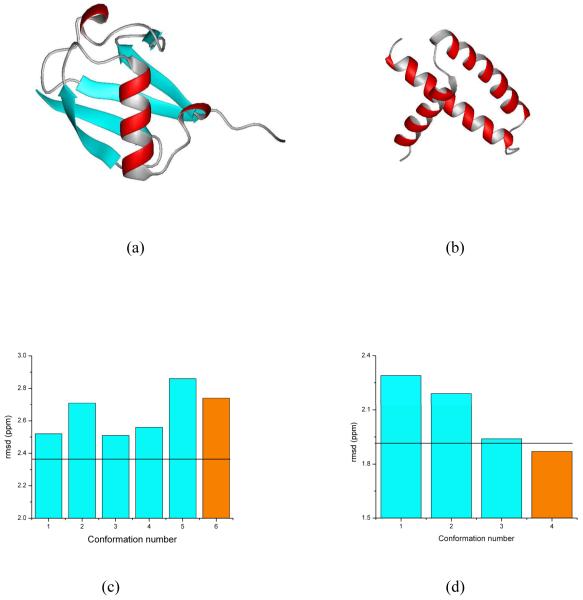
Figures 1a and b show the results for the validation of these two proteins. In both cases, the ca-rmsd (shown as black horizontal line in Figure 1) is a better representation of the observed ¹³C^α chemical shift in solution than is a single X-ray structure (green bar and black, yellow and blue bars in Figure 1a and 1b, respectively). This raises a question as to whether the results reported here are consequences of the ‘single’ model representation of the X-ray data. To answer this question, the room temperature X-ray structures of ubiquitin (PDB id 1UBQ)³⁷ and the RNA-binding domain of the nonstructural protein 1 of the influenza A virus (PDB id 1AIL),⁴⁵ solved at 1.8 Å and 1.9 Å resolution, respectively, were used to investigate whether a set of conformations, rather than a single X-ray structure, provides better agreement with both the X-ray data and the observed ¹³C^α chemical shifts in solution.⁴⁶ Among other important findings, our results show that an ensemble of conformations rather than any single structure (shown in Figures 2a and b) sometimes (Figure 2c), but not always (Figure 2d), is a more accurate representation of a protein structure in the crystal; whether or not an ensemble of conformations is a more accurate representation is determined by the dispersion of the coordinates in terms of the all-atom rmsd among the generated models that satisfied the X-ray data.

Figure 1.

(a) Bar diagram of the rmsd between computed and observed ¹³C^α chemical shifts for 10 experimental NMR-derived models of ubiquitin (red-filled) [PDB id 1D3Z] and the regularized structure of the X-ray-solved model (2.38 ppm; green-filled) [PDB id 1UBQ]. The black solid horizontal line represents the computed ca-rmsd (2.20 ppm) from the 10 NMR conformations; (b) same as (a) for 20 conformations from the NMR-derived models of YnzC (red bars) [PDB id 2JVD] and for each of the three chains in the 2.0 Å crystal structure of YnzC, 3BHP, namely chain A, B and C (black, yellow and blue bars). The amino acid sequence of the YnzC[1-52] (3BHP), YnzC[1-48] (2JVD) structures are identical only for the first 46 residues. Hence, each bar in the figure and the black solid horizontal line representing the computed ca-rmsd (1.54 ppm) were computed from the first 46 residues.

Figure 2.

Panels (a) and (b) show the ribbon diagram of the protein models of ubiquitin and the RNA-binding domain of the nonstructural protein 1 of the influenza A virus, respectively; these models were obtained⁴⁶ after one round of Simulated Annealing Refinement (SAR) starting from the deposited PDB structures of 1UBQ and 1AIL, and represented by the orange bars in (c) and (d); these two panels also show the bar diagram of the rmsd between computed and observed ¹³C^α chemical shifts, as cyan-filled bars, for the generated ensemble of conformations, generated from the SAR PDB models and, at the same time, showing R and R_free factors similar to those of the deposited X-ray structure;⁴⁶ the black solid horizontal lines represent the ca-rmsd for each ensemble (2.36 ppm and 1.92 ppm for UBQ and AIL, respectively).

Testing the sensitivity of the method for local, rather than global, validation

Despite the enormous progress in techniques and methodologies in both NMR spectroscopy and X-ray diffraction, the existence of errors in the determination of protein structures appears to be common to both techniques.^16,47 Besides the assorted reasons leading to such a problem,^16,47 it is commonly accepted that (global) validation is a necessary, but not sufficient condition, with which to prove that a structure is free of (local) errors. There is, indeed, a need for an accurate validation method at the residue level.^16,46

As a test of the ability of the ¹³C^α-based validation method to detect local flaws, we chose to analyze a segment of 27 consecutives residues of a protein structure showing a wrong fold, namely from the protein dynein light chain 2A (DLC2A, from human) PDB id 1TGQ (now obsolete), and another one showing a correct fold, namely from protein PDB id 2B95 (that replaced the obsolete 1TGQ in the PDB). A ribbon diagram of model 1 out of 20 models for protein 1TGQ and 2B95 are shown in Figure 3a and b, respectively. The difference in the folding between these two structures originated in the oligomeric state assumed during the protein structure determination, namely as a monomer for 1TGQ, and homodimer for 2B95. This was first pointed out by Nabuurs et al.¹⁶ who carried out a detailed and extensive validation analysis by using several tools such as WHAT IF¹¹ and PROCHECK¹² for both the protein 1TGQ and the protein DLC2A (from mouse) PDB id 1Y4O (a homolog of 1TGQ since the NMR restraints from 1TGQ were not available). Among other findings, Nabuurs et al.¹⁶ concluded that the use of standard scoring parameters, such as size and number of residual restraint violations, the precision of the structure ensemble, or the fact that most of the residues populate the allowed regions of the Ramachandran map, cannot safely, or unambiguously, assess the accuracy of protein structures. Later, it was shown that structures 1TGQ and 2B95 can be distinguished by comparing how well they fit unassigned NOESY peak list data.⁹

Figure 3.

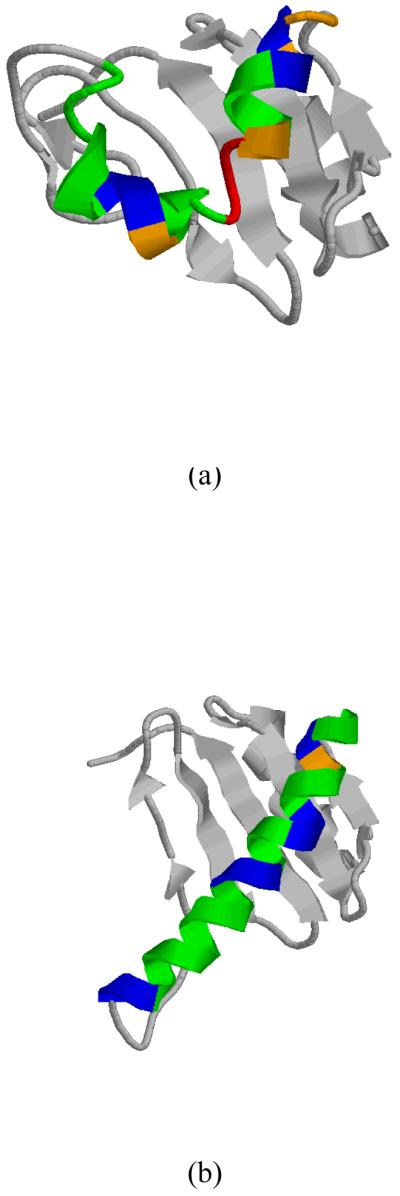
(a) Ribbon diagram of model 1, out of 20 models, for the 106-residue protein 1TGQ; (b) same as (a) for model 1 of chain A, out of 20 models, of the 106-residue protein 2B95. In (a) and (b), we highlight in green, blue, orange and red the 27 residues from residue 45 to 71 of 1TGQ and 2B95, respectively, for which a local validation analysis was carried out. Green color indicates residues with errors within the range of observed standard deviations, i.e., lower than a cutoff value of 2.4 ppm;⁴⁷ blue, orange and red indicate a range of errors greater than the cutoff value, namely $0\lambda \Delta \overline{{\Delta }_{\mu }}\le 1\mathrm{ppm},1\mathrm{ppm}\lambda \Delta \overline{{\Delta }_{\mu }}\le 2.0\mathrm{ppm},\text{and}\Delta \overline{{\Delta }_{\mu }}\left[hsl\right]2.0\mathrm{ppm}$, respectively.

This is an interesting problem for two reasons because it enables us: (a) to determine whether our ¹³C^α-based validation method is able to accurately identify the existence of errors in a segment of 27 residues, from Asp 45 to Asp 71 of protein 1TGQ and the corresponding segment of protein 2B95 (shown in Figure 3); and (b) to illustrate that our validation method is sensitive enough to alert spectroscopists that, even without knowing the correct fold (2B95), or the NMR restraints, the structure of 1TGQ must be revised.

The correlation coefficient R, or Pearson coefficient (Press et al., 1992),⁴⁸ between observed and computed ¹³C^α chemical shifts for the 27 consecutives residues of proteins 1TGQ and 2B95 is 0.74 and 0.90, respectively. Clearly such a significant difference, in terms of R, indicates that careful attention should be paid to the fold of this segment in the protein 1TGQ. Even more important, in the absence of an R value for the correct fold (0.90, for 2B95) the R value obtained from the wrong fold (0.74, for 1TGQ) is low enough to make spectroscopists aware that the conformation of this segment should be carefully revised. In fact, by using the statistical meaning of R², it is straightforward to conclude that ~50% of the observed ¹³C^α chemical shifts cannot be reproduced by the conformation of this segment in the 1TGQ protein model.

Finally, we tested the ability of our validation method to detect residues in the sequence displaying larger errors than a certain cutoff value between observed and computed ¹³C^α chemical shifts. The adopted cutoff value was 2.4 ppm because it is higher than the upper limit of the standard deviation (0.9 ppm ≤ σ ≤ 2.3 ppm) observed by Wang and Jardetzky⁴⁹ for ¹³C^α chemical shifts (from a database containing more than 6,000 amino acid residues in the α-helix, β-sheet and statistical-coil conformations). The average error among the nearest-neighbor residues of μ , $\overline{{\Delta }_{\mu }}$ , was adopted as the error for this residue, namely with $\overline{{\Delta }_{\mu }}=(1∕3){\sum }_{x\in \{\mu -1,\mu ,\mu +1\}}{\Delta }_x$, where Δ_x represents the difference between the observed and computed ¹³C^α chemical shifts for a given residue in the triplet. Departure of this average error from the cutoff value, $\Delta \overline{{\Delta }_{\mu }}=\overline{{\Delta }_{\mu }}-2.4\mathrm{ppm}$, was used for a colored representation of the error distribution (see Figure 3). Blue, orange and red colors were used to designate the range of $\Delta \overline{{\Delta }_{\mu }}$ variations: $0\le \Delta \overline{{\Delta }_{\mu }}\left[hsl\right]1\mathrm{ppm}1\mathrm{ppm}<\Delta {\overline{\Delta }}_{\mu }\le 2.0\mathrm{ppm}$ and $\Delta \overline{{\Delta }_{\mu }}\left[hsl\right]2.0\mathrm{ppm}$, respectively; green color indicates that $\Delta \overline{{\Delta }_{\mu }}<0\mathrm{ppm}$ and, hence, it is free of error since it is within the allowed range of variations. As seen in Figure 3a, the larger errors occur for protein 1TGQ, for Leu 55, Met 56, and His 57 (highlighted in red in Figure 3a). Not surprising, large errors are located in the turn-like region connecting two antiparallel α-helices in protein 1TGQ. On the other hand, all the $\Delta \overline{{\Delta }_{\mu }}$ values in 2B95 are lower than 1ppm, except for Thr 49 with 1.4 ppm, and indicated by the orange color in Figure 3b.

4. Concluding Remarks and Perspectives

While computationally intensive, there are four main advantages of this new methodology: (a) it can be used for proteins of any class or size; (b) it provides a strong methodology with which to validate, at a high-quality level, protein structures as a whole, i.e. by using the ca-rmsd; (c) it has potential value to be adopted as a standard routine for determination of local flaws in the sequence without prior knowledge of the oligomeric state of the protein in solution, the correct fold of the protein, the NMR restraints, or additional NMR data; and (d) it does not use any knowledge-based information and hence, it is a purely physics-based method.

The most relevant limitation of the method is related to the computational cost. However, recent progress in our laboratory shows that ¹³C^α chemical shifts in proteins, computed at the DFT level of theory with a large basis set, can be reproduced accurately (within an average error of ~0.4 ppm) and faster (by ~9 times) by using a small basis set (work in progress). The speed-up of the calculations of the ¹³C^α chemical shifts, together with ever increasing computational power, will significantly alleviate the computational cost of the method and, hence, it could be adopted as a standard by the NMR community with which to validate a significantly large number of deposited and new protein models.

Biography

BIOGRAPHICAL INFORMATION

Jorge A. Vila. Was born in Rivadavia (Mendoza-Argentina) in 1952. He is Professor of the National University of San Luis-Argentina, Researcher of CONICET-Argentina, and Senior Research Associate at Cornell University (USA).

Harold A. Scheraga. Was born in Brooklyn, NY, in 1921. He attended the City College of NY, receiving his B.S. in 1941, and the PhD at Duke University in 1946. Following postdoctoral work at Harvard Medical School, he joined the faculty of Cornell University in 1947 where he is now Todd Professor of Chemistry, Emeritus.