Comprehensive analysis of proton range uncertainties related to patient stopping-power-ratio estimation using the stoichiometric calibration

Abstract

The purpose of this study was to analyze factors affecting proton stopping-power-ratio (SPR) estimations and range uncertainties in proton therapy planning using the standard stoichiometric calibration. The SPR uncertainties were grouped into five categories according to their origins and then estimated based on previously published reports or measurements. For the first time, the impact of tissue composition variations on SPR estimation was assessed and the uncertainty estimates of each category were determined for low-density (lung), soft, and high-density (bone) tissues. A composite, 95th percentile water-equivalent-thickness uncertainty was calculated from multiple beam directions in 15 patients with various types of cancer undergoing proton therapy. The SPR uncertainties (1σ) were quite different (ranging from 1.6% to 5.0%) in different tissue groups, although the final combined uncertainty (95^th percentile) for different treatment sites was fairly consistent at 3.0–3.4%, primarily because soft tissue is the dominant tissue type in human body. The dominant contributing factor for uncertainties in soft tissues was the degeneracy of Hounsfield Numbers in the presence of tissue composition variations. To reduce the overall uncertainties in SPR estimation, the use of dual-energy computed tomography is suggested. The values recommended in this study based on typical treatment sites and a small group of patients roughly agree with the commonly referenced value (3.5%) used for margin design. By using tissue-specific range uncertainties, one could estimate the beam-specific range margin by accounting for different types and amounts of tissues along a beam, which may allow for customization of range uncertainty for each beam direction.

1. Introduction

The major benefit of proton therapy is that protons stop and most of their energy is deposited right before they stop, which allows for the design of a highly conformal dose distribution at the target while sparing normal tissues distal to the target. However, this high-dose-gradient feature also causes proton therapy to be vulnerable to uncertainties (Unkelbach et al., 2009; Urie et al., 1984). There exist various uncertainties in proton treatments, e.g., setup uncertainties, patient motion uncertainties, range uncertainties related to tissue heterogeneities and patient stopping-power-ratio (SPR) estimation, and so on (Lomax, 2008a, b). These uncertainties must be minimized to fully realize the benefit of proton therapy.

One major uncertainty is the range uncertainty related to patient SPR estimation. Patient SPR information is required in the treatment planning process to calculate water-equivalent path lengths (WELs) and determine the proton range. In current clinical practice, range uncertainties related to patient SPR estimation are accounted for by a 3.5% margin at both the proximal and distal end of the target volume (Moyers et al., 2001; Moyers et al., 2009). A large margin causes more normal tissues near the target to receive higher doses.

Treatment-planning computed tomography (CT) images are currently used to derive the SPR distribution on the basis of a predetermined linear relationship between CT numbers (Hounsfield Units) and SPRs, also known as the CT number-to-SPR calibration curve. The calibration curve is determined for each CT scanner used for proton treatment planning, and accuracy of this calibration is critical to the accuracy of dose calculation.

The CT number-to-SPR calibration curve can be determined using various methods, the simplest of which is to directly generate the calibration curve based on the measured CT numbers and SPRs of a number of tissue substitutes of known densities and elemental compositions. Because human tissue substitutes are not truly tissue equivalent, the calibration curve determined using this method is sensitive to the tissue substitutes selected for the calibration (Schneider et al., 1996). Schneider et al. proposed a stoichiometric calibration method to minimize the impact of nonhuman tissue phantoms. In this method, the calibration curve is determined based on theoretical CT numbers and SPRs of human body tissues, which are calculated according to the known elemental compositions of human tissues and the CT-specific parameters determined from the measurements of tissue substitutes. The calibration curve generated using this method was shown to be less sensitive to the tissue substitutes used for the calibration. Currently, the stoichiometric calibration method is considered the most widely used calibration method in proton therapy centers around the world.

One drawback of the current SPR estimation method is the degeneracy issue between CT numbers and SPRs of human tissues. The CT number and SPR describe two different physical properties. Even though both values are dominated by the electron density ratio (EDR), the elemental composition also matters. Thus, no perfect one-to-one correspondence exists between CT numbers and SPRs of human tissues: human tissues with different CT numbers can have similar SPRs and vice versa. The degeneracy issue makes the current SPR estimation method susceptible to variations in human tissue composition. In fact, we previously showed that the uncertainties in estimated SPRs increased substantially with tissue composition variations (Yang et al., 2010).

The goal of this study was to estimate the range uncertainties related to patient SPR estimation in current practice. Compared to previous studies, we performed a systematic analysis of all the uncertainties related to SPR estimation. Our study is also unique in that it accounted for variations in human tissue composition for the first time. We found that uncertainties for tissues of different densities were different; thus, separating uncertainties (1σ) for low-density (lung), soft, and high-density (bone) tissues is important. To calculate the combined uncertainty, we performed a population-based study to determine the composite range uncertainty (95th percentile) for three typical proton therapy sites: prostate, lung, and head-and-neck. These uncertainties could be used as margin considerations in clinical practice.

2. Materials and methods

2.1. Terminology

The following are definitions of frequently used terms in this study:

• theoretical CT number: the CT number calculated based on the elemental composition and CT specific-parameters determined via the stoichiometric calibration procedure (equation (4));

• measured CT number: the CT number measured experimentally;

• true SPR: the actual value of the SPR;

• theoretical SPR: the SPR calculated based on the elemental composition using the Bethe-Bloch equation (equation (5));

• estimated SPR: the SPR estimated from the CT number based on the stoichiometric calibration curve.

2.2. Stoichiometric calibration

The stoichiometric calibration procedure was previously described in detail by Schneider et al. (1996). It is reviewed here briefly to clarify our categorization of uncertainties in SPR estimations using the calibration curve.

The stoichiometric calibration procedure can be divided into four steps: (1) scanning a number of tissue substitutes of known densities and elemental compositions with a treatment-planning CT scanner; (2) calculating scanner-specific parameters (K^ph, K^coh, and K^KN) according to the measurements acquired in Step 1; (3) calculating theoretical CT numbers and SPRs for human body tissues based on the densities and elemental compositions recommended in the literature; and (4) determining the calibration curve using linear regression within each tissue group and connecting them piecewise.

One key step in the stoichiometric calibration procedure is to model the CT scanner and calculate theoretical CT numbers of human body tissues. The CT number (Hounsfield unit or HU) is usually defined as

$$HU=\frac{\langle {\mu }_{\text{x}}\rangle -\langle {\mu }_{\text{w}}\rangle }{\langle {\mu }_{\text{w}}\rangle }\times 1000,$$ (1)

where 〈μ_x〉 and 〈μ_w〉 are the photon linear attenuation coefficients of the object of interest and water, respectively, averaged over the x-ray spectrum. CT number was defined in this study as

$$HU=\frac{\langle {\mu }_{\text{x}}\rangle }{\langle {\mu }_{\text{w}}\rangle }\ast 1000.$$ (2)

In this way, $\frac{\mathit{dHU}}{HU}=\frac{d\langle {\mu }_{\text{x}}\rangle }{\langle {\mu }_{\text{x}}\rangle }$.

For a polyenergetic x-ray beam with a peak energy less than 1.02 MeV, the linear attenuation coefficient (〈μ_x〉) of a composite material can be calculated using

$$\langle {\mu }_{\text{x}}\rangle ={\rho }_{\text{e}}(K^{\text{ph}}{\stackrel{\sim }{Z}}^{3.62}+K^{\text{coh}}{\widehat{Z}}^{1.86}+K^{\text{KN}}),$$ (3)

where ρ_e is the electron density; and K^ph, K^coh, and K^KN are constants for the photoelectric interaction, coherent scattering, and Compton scattering, respectively. Z̃ and Ẑ are the effective atomic numbers, which are defined as $\stackrel{\sim }{Z}={\left[\sum {\lambda }_i{Z}_i^{3.62}\right]}^{1/3.62}$ and $\stackrel{\sim }{Z}={\left[\sum {\lambda }_i{Z}_i^{1.86}\right]}^{1/1.86}$, where ${\lambda }_i=\frac{{\omega }_i{Z}_i}{A_i}/\sum \frac{{\omega }_i{Z}_i}{A_i}$, and Z_i, A_i and ω_i are the atomic number, the atomic weight and the proportion by weight of the ith element. After substituting 〈μ_x〉 and 〈μ_w〉 with equation (3), equation (2) becomes

$$HU=\frac{{\rho }_{\text{e},\text{rel}}}{C_{\text{w}}}(K^{\text{ph}}{\stackrel{\sim }{Z}}^{3.62}+K^{\text{coh}}{\widehat{Z}}^{1.86}+K^{\text{KN}})\ast 1000,$$ (4)

Where ${\rho }_{\text{e},\text{rel}}=\frac{{\rho }_{\text{e}}}{{\rho }_{\text{e},\text{w}}}$ and $C_{\text{w}}=(K^{\text{ph}}{\stackrel{\sim }{Z}}_{\text{w}}^{3.62}+K^{\text{coh}}{\widehat{Z}}_{\text{w}}^{1.86}+K^{\text{KN}})$,

Equation (4) shows that the measured CT number (HU) is a function of six variables, three of which (ρ_{e, rel}, Z̃^3.62, and Ẑ^1.86) are related to only the object of interest and can be determined if the elemental composition of the object is known. The other three variables, the CT scanner-specific parameters (K^ph, K^coh, and K^KN), can be determined if more than three objects with known elemental compositions are scanned. If the scanner-specific parameters are known, the theoretical CT numbers of human body tissues can be calculated using equation (4).

Another key step in the stoichiometric calibration procedure is to calculate theoretical SPRs (S_rel) for human body tissues using the Bethe-Bloch equation, which can be approximated by

$$S_{\text{rel}}={\rho }_{\text{e},\text{rel}}\times \frac{ln\frac{2m_{\text{e}}{c}^2{\beta }^2}{(1-{\beta }^2)I_{\text{m},\text{x}}}-{\beta }^2}{ln\frac{2m_{\text{e}}{c}^2{\beta }^2}{(1-{\beta }^2)I_{\text{m},\text{w}}}-{\beta }^2},$$ (5)

where I_m,x and I_m,w are the mean excitation energies of the object of interest and water, respectively. m_e is the mass of the electron; c is the speed of light; and βc is the speed of the incident proton.

2.3. Our stoichiometric calibration

The following tissue substitutes were selected for stoichiometric calibration in the current study: lung (LN-300), lung (LN450), adipose tissue (AP6), solid water, brain (SR2), liver (LV1), water, B200, CB2-30%, CB2-50%, and cortical bone (SB3), which were all obtained from the RMI 467 tissue characterization phantom (Gammex, Middleton, WI). CT number measurements of the same object may vary substantially with scanning conditions because of the beam hardening effect. To minimize this variability, we scanned one insert at a time and always placed the insert at the center of the phantom during the scan. This scanning condition was referred to as the reference condition. To account for the impact of patient size, we determined the stoichiometric calibration curves for two phantoms sizes (head-and body-size) and used the average one for patient SPR estimation. The diameters of the head- and body-size calibration phantoms were 16 cm and 32 cm, respectively. Both phantoms were made of acrylic (Figure 1).

Figure 1.

Images of (a) the RMI 467 tissue characterization phantom and (b) the head- and body-size calibration phantoms.

Forty-one different human tissues were selected in our stoichiometric calibration: lung (inflated), adipose tissue, adrenal gland, aorta, bladder (filled), blood (whole), brain (grey/white matter 50: 50, by mass), breast (mammary gland), connective tissue, eye lens, gallbladder (bile), gastrointestinal tract (intestine), heart (blood-filled), kidney, liver, lymph, lung (deflated), muscle (skeletal), ovary, pancreas, prostate, skin, spleen, stomach, testis, thyroid, trachea, red marrow, yellow marrow, cartilage, cortical bone, spongiosa, cranium, femur, humerus, mandible, ribs (second and sixth), ribs (10^th), sacrum, vertebral column (C4), and vertebral column (D6, L3). These 41 tissues were classified in three groups: low-density (lung) tissues, soft tissues, and high-density (bone) tissues. The lung tissue group consisted of only inflated lung tissue; the soft tissue group consisted of 29 tissues that did not contain a substantial amount (>1%) of calcium; and the bone tissue group consisted of 11 body tissues that contained a substantial amount of calcium. Their densities and elemental compositions were determined from the literature (Woodard and White, 1982, 1986; White et al., 1987; White et al., 1991; ICRU, 1989).

2.4. Uncertainties in SPR estimation

The uncertainties in SPR estimation in current practice could be divided into five independent categories according to their origins (Error! Reference source not found.Table 1).

Table 1.

Categorization of the uncertainties in SPR estimation.

Uncertainty Category	Uncertainty Source
Uncertainties in patient CT imaging	The deviation of HU value from its calibrated value when imaging a patient. The major contributions of uncertainties are from the scatter condition and beam-hardening effect in patient geometry. Minor contributions are from out-of-field objects, such as a portion of the CT couch, immobilization device, and day-to-day variation etc.
Uncertainties the parameterized stoichiometric formula to calculate theoretical CT numbers	This includes the uncertainties in the definition and measurement of equations (1) – (4) using CT imaging for a tissue substitute phantom, including the parameterization of equation (3).
Uncertainties due to deviation of actual human body tissue from ICRU standard tissue	The uncertainties caused by modeling SPR and variations of tissue composition in patient population. The original stoichiometric calibration assumes tissues to follow ICRU standard tissue compositions, which may introduce uncertainties for a given individual with different age or health status.
Uncertainties in mean excitation energies	The value of mean excitation energy is critical in calculating SPR. We evaluated the impact to SPR by the fact that we always made proton range measurement in water during the commissioning process. Only the relative uncertainties (to water) of the mean excitation energy will contribute towards the SPR calculation for a given tissue.
Uncertainty due to energy dependence of SPR not accounted by dose algorithm	For simplicity, some treatment planning systems ignored the SPR dependency on proton energy. This may be specific to a particular situation, but it shows the uncertainty of dose calculation depends on the implementation of dose calculation algorithms.

The goal of the conversion process is to derive the stopping power of a proton beam based on CT images of a given patient. The process starts at CT imaging. (1) Uncertainties from CT imaging are the first category of uncertainties. (2) The second step of the stoichiometric method involves the prediction of theoretical CT numbers using the tissue substitute phantom. (3) The third step is to use the predicted CT number to derive the SPR for a given biological tissue. In this step, we estimated the uncertainties of human tissue composition. (4) The mean excitation energy in the Bethe-Bloch equation (equation (5)) is an independent factor, which will affect the SPR calculation. We used the worst case scenario to estimate the contribution of this factor. (5) The implementation of treatment planning dose calculation algorithm may also introduce additional uncertainties. In this case, the particular treatment planning system (Eclipse) assumes a fixed proton energy when calculating SPR, which will introduce uncertainties in the final SPR calculation when proton energy changes along the beam path.

The uncertainties were classified into these five categories because they were independent of each other, and it was easier to estimate each uncertainty separately. Our estimation of these five categories of uncertainties is explained in more details in sections 2.4.1.–2.4.5.

2.4.1. Uncertainties in patient CT imaging

Various factors can cause CT number variations. Those considered in this study included time, scanner, patient size, position in the scan, and a special factor: objects outside the field-of-view (FOV).

CT number variations associated with time and the scanner used were estimated on the basis of the monthly quality assurance (QA) data on treatment planning CT scanners at The University of Texas MD Anderson Cancer Center. The same tissue substitute inserts were scanned during monthly QA assessments, which provided a perfect reference for CT number variations associated with time and scanner.

CT number variations associated with patient size were estimated by comparing CT numbers of the same insert when it was scanned at the center of the head and body phantoms, respectively. CT number variations associated with the position in the scan were estimated by comparing CT numbers of the same insert when it was scanned at the center and periphery of the body phantom, respectively. The body phantom was selected for the estimation of CT number variations related to the position in the scan because it offered larger position differences than the head phantom.

The impact of objects outside the FOV on CT measurements inside the FOV were estimated by comparing CT numbers of the same insert when it was scanned with and without certain objects outside the FOV, respectively. One special object to consider is the couch of the treatment planning CT scanner, which can be located either inside or outside the FOV depending on the patient and the treatment site. The impact of the couch position was estimated by scanning the RMI 467 phantom loaded with the same tissue substitutes using two different couch positions: inside the FOV and outside the FOV.

Because of the slope of the calibration curve, 1% relative CT number variation does not necessarily translate to 1% relative SPR variation. The relationship between CT numbers and SPRs on the calibration curve can be essentially described as S_rel = a * HU + b, where a and b are the slope and residue of the calibration curve, respectively. By taking the first derivative, the relative SPR variation ( $\frac{{dS}_{\text{rel}}}{S_{\text{rel}}}$) is related to the relative CT number variation ( $\frac{\mathit{dHU}}{HU}$) as

$$\frac{{dS}_{\text{rel}}}{S_{\text{rel}}}=\frac{\mathit{dHU}}{HU}\ast \frac{HU}{HU+b/a}.$$ (6)

2.4.2. Uncertainties the parameterized stoichiometric formula to calculate theoretical CT numbers

Various factors can contribute to the difference between the CT number measured at reference condition and the CT number calculated based on the model, including the defect of the CT modeling based on equation (3), the uncertainty in the determined parameter set (K^ph, K^coh, and K^KN) in equation (3), the imaging uncertainty when scanning the tissues substitutes for calibration, etc. Directly estimating the differences between the theoretical CT numbers and the CT numbers measured for human tissues was difficult. Thus, we decided to estimate this uncertainty using the data from tissue substitutes. We scanned several tissue substitutes of known elemental compositions and compared their measured and theoretical CT numbers using the scanner-specific parameters (K^ph, K^coh, and K^KN) determined in the stoichiometric calibration procedure.

2.4.3. Uncertainties to calculate SPRs of human tissues

This category of uncertainties was estimated by comparing the theoretical SPRs calculated based on the elemental compositions of human tissues using the Bethe-Bloch equation and the SPRs estimated from the theoretical CT numbers. This category of uncertainties was estimated for both “reference” human tissues (the human tissues with the densities and elemental compositions that were the same as those recommended in the literature) and “individualized” human tissues (the human tissues with densities and elemental compositions that were slightly different from the recommended values). Our previous study showed that this category of uncertainties increases substantially when considering variations in tissue composition (Yang et al., 2010). Therefore, we deemed it necessary to consider human tissue composition variations when estimating this category of uncertainties.

We found that there exist both systematic and statistical uncertainties in the recommended elemental compositions of the reference human tissues. The recommended elemental compositions of the reference human tissues are meant to represent the population average, but in reality they may deviate from the true population average for various reasons, such as a flawed measurement method or a biased sample. The statistical uncertainties are caused by patient-to-patient variations. ICRU Report No. 44 (1989) states explicitly that “the elemental compositions of most body tissues are known to vary considerably between individuals of the same age” and “the composition of a given tissue within one individual may vary from one body site to another.”

For each reference human tissue type, a population of individualized human tissues was generated by introducing variations to only the key factors: the mass density, the hydrogen percentage (H%) for soft tissues, and the calcium percentage (Ca%) for bone tissues. The statistical uncertainties were accounted for by sampling the values of the key factors from a Gaussian distribution, and the systematic uncertainties were accounted for by setting the mean of the Gaussian distribution slightly different from the original value of the key factor. For example, the densities of individualized human tissues were sampled from the Gaussian distribution ~ N (μ * (1 ± δ), μ * σ, where μ were the original recommended values of the density, and δ and σ were the relative systematic and statistical uncertainties. The percentages of key elements were also sampled from a Gaussian distribution ~ N (μ ± δ, σ), where μ was the original recommended percentage, and δ and σ were the systematic and statistical uncertainties, respectively. Table 2 lists the values of δ and σ used in this study; they were determined via a thorough literature search (Appendix). In this study, we generated 2000 individualized human tissues for each tissue type.

Table 2.

Systematic (δ) and statistical (σ) uncertainties in the recommended values of the ‘reference’ human tissues.

	Systematic Uncertainty (δ)	Statistical (Individual) Uncertainty (σ)
Density	2.1%	1.7%
H (%)	0.2%	0.5%
Ca (%)	1.0%	1.0%

2.4.4. Uncertainties in mean excitation energies

Accurately determining the mean excitation energy for a material of known elemental composition is not a trivial task. Even for water, several different values have been suggested in the literature: 67 eV, 75 eV, 78 eV, and 80 eV (ICRU, 2005; Paul et al., 2007; ICRU, 1993; Kumazaki et al., 2007; Emfietzoglou et al., 2009; Bischel and Hiraoka, 1992; Andreo, 2009). The uncertainty in the mean excitation energy of water yields up to 1% uncertainty in the calculated stopping power. The mean excitation energies of human tissues provided in the literature likely carry larger uncertainties than water does, because those values were calculated primarily using the Bragg additivity rule (ICRU, 1993; Seltzer and Berger, 1982) instead of being measured directly, like water. Thus, the uncertainties in the calculated stopping power of human tissues are about 1% as well and the total uncertainties in the calculated SPR of human tissues relative to water are about 1.4%, assuming these two uncertainty factors are independent.

However, we found that these two uncertainties were not completely independent because water is a major constituent of soft tissues (Valentin and Streffer, 2002; Woodard and White, 1986). The mean excitation energies of water and soft tissues should vary in the same direction, so the uncertainties in the calculated SPRs of human tissues should be smaller. We conducted a variation study to estimate the uncertainties in SPR calculations with the correlation considered. The correlation was accounted for by first introducing variations to the mean excitation energies of the elements and then calculating the mean excitation energies of human tissues and water using these varied values. We studied the following three variation scenarios:

• the mean excitation energies of all elements increased or decreased by 10% at the same time;

• the mean excitation energies of all elements except for hydrogen and oxygen increased or decreased by 10%; and

• only the mean excitation energies of hydrogen and oxygen increased or decreased by 10%.

We chose 10% mean excitation energy variation because the largest deviation in the literature for water (67 eV) is approximately 10% from the standard value (75 eV). We used the worst case scenario in our analysis for this factor.

2.4.5. Uncertainties due to energy dependence of SPR not accounted by dose algorithm

For simplicity, some treatment planning systems usually do not account for SPR change associated with proton energy along the beam path. Although the SPR is approximately constant with proton energy, this approximation causes additional uncertainty.

We estimated this uncertainty by comparing proton ranges calculated when proton energy variation were and were not considered. We chose adipose tissue and cortical bone for this comparison, because their mean excitation energies have the largest differences from the excitation energy of water. Their SPRs should vary the most with proton energy, according to the Bethe-Bloch equation. If proton energy variations are not considered, the proton range in human tissues can be calculated by simply multiplying the proton range in water by the SPR at a chosen proton energy. For historical reasons at our institution, the proton energy chosen in this study was 175 MeV. The proton range in human tissues determined when SPR variations associated with energy variations are considered can be found in the online database of the National Institutes of Standards and Technology, the stopping-power and range tables for protons (PSTAR) database, which gives the projected ranges of various materials, including water, adipose tissue, and cortical bone (ICRU, 1993).

2.5. Composite range uncertainties

The uncertainties in SPR estimation were estimated for different tissue groups separately, because their values were found to be substantially different. For each tissue group, an estimate was first determined for each category of uncertainty and then the categorical uncertainties were summed in quadrature to determine the total uncertainty. For treatment planning purposes, it is more convenient to provide a single composite range uncertainty for margin design.

To determine the composite range uncertainty, we selected 15 patients undergoing proton therapy, five each with prostate, lung, or head-and-neck cancer. To determine realistic estimates, we used the beam angles and planning target volume from the original proton therapy plan. The CT voxels were first categorized into lung, soft, or bone tissues according to their CT numbers. Using the CT number histograms of patient CT images, we found that a CT number of 800 could be used to separate lung tissues from soft tissues and a CT number of 1200 could be used to separate soft tissues from bone tissues.

For each beam ray, the composite range uncertainty (σ_R) was calculated as

$${\sigma }_{\text{R}}=w_{\text{L}}\ast {\sigma }_{\text{L}}+w_{\text{S}}\ast {\sigma }_{\text{S}}+w_{\text{B}}\ast {\sigma }_{\text{B}},$$ (7)

where W_L, W_S, and W_B were the relative weights of lung, soft, and bone tissues, respectively, along each ray from the skin to the proximal or distal end of the planning target volume, and σ_L, σ_S, and σ_B were the uncertainties in the SPRs for lung, soft, and bone tissues, respectively. The relative weights of different tissue groups along each ray were determined using a ray-tracing technique developed in house. The values of σ_L, σ_S, and σ_B were sampled from a Gaussian distribution with a mean equal to zero and standard deviation equal to the estimated uncertainty (1 σ) of the corresponding tissue group.

3. Results

3.1. Uncertainties in SPR estimation

3.1.1. Uncertainties in patient CT imaging

The relative variation ratios, $\frac{HU}{HU+b/a}$, were computed for all tissue substitutes used in CT uncertainty measurements (Table 3). Our estimates of uncertainties in patient CT imaging (1 σ) for each factor and its induced SPR uncertainty are listed in Table 4. In general, CT measurements of soft tissues varied less with imaging conditions than CT measurements of lung and bone tissues. For soft tissues, the variation with time and scanner, patient size, and couch position were comparable, whereas patient size was the dominant factor for both lung and bone tissues. We summed the uncertainty estimate for each factor in quadrature to derive the total uncertainty, assuming these factors were independent.

Table 3.

Relative variation ratios calculated for all tissue substitutes used in CT uncertainty measurements.

Tissue Substitute	Ratio
LN-300	1.03
LN-450	1.02
Adipose	0.91
Solid water	0.69
Brain	0.69
Liver	0.70
Water	0.69
B-200	0.55
CB2-30%	0.59
CB2-50%	0.64
Cortical bone	0.69

Table 4.

CT number uncertainties (1 σ) and the induced SPR uncertainties (1σ) for different uncertainty factors and different tissue groups.

	Tissue Group	Major Uncertainty Contributing Factors				Total
		Time and Scanner	Patient Size	Position in the Scan	Couch Position
CT#	Lung	1.0%	2.6%	1.3%	1.1%	3.2%
	Soft	0.3%	0.3%	0.1%	0.3%	0.5%
	Bone	0.6%	1.9%	1.0%	0.5%	2.3%
SPR	Lung	1.0%	2.7%	1.4%	1.1%	3.3%
	Soft	0.3%	0.2%	0.1%	0.2%	0.4%
	Bone	0.4%	1.3%	0.7%	0.3%	1.5%

3.1.2. Uncertainties the parameterized stoichiometric formula to calculate theoretical CT numbers

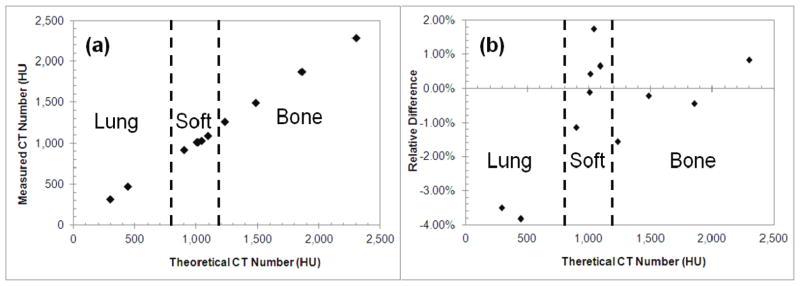
Figure 2 shows the comparison between the measured and theoretical CT numbers of the tissue substitutes used in the calibration. The differences between the measured and theoretical CT numbers for lung tissues were the greatest (Table 5). The spread in the relative difference be etween the measured and theoretical CT numbers was greatest in the soft tissue group.

Figure 2.

(a) Measured versus theoretical CT numbers of the tissue substitutes; (b) the relative difference between the measured and theoretical CT numbers of the tissue substitutes.

Table 5.

Uncertainties in the predicted theoretical CT numbers of the tissue substitutes and the induced errors in estimated SPRs.

Tissue Group	Uncertainties (1 σ)
	CT Number	SPR
Lung	3.7%	3.8%
Soft	1.0%	0.8%
Bone	0.9%	0.5%

3.1.3. Uncertainties to calculate SPRs of human tissues

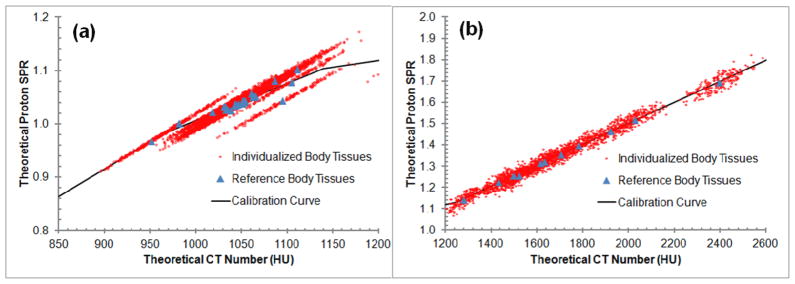
In general, the individualized human tissues fitted worse with the stoichiometric calibration curve than did the reference human tissues (Figure 3). The uncertainties for the individualized human tissues, especially soft and bone tissues, were greater than those for the reference human tissues (Table 6). The uncertainties at least doubled for soft tissues and increased by at least four times for bone tissues. In Figure 3(a), the individualized body tissues (red dots) were found to spread along the direction of density variation centered around the reference body tissues (blue triangles), which indicated the density variation appeared to be the dominant factor for soft tissues. Figure 3(b) has a different vertical scale and shows more vertical spread than Figure 3(a), which demonstrates a large impact from the elemental composition in bony tissue region.

Figure 3.

Uncertainties associated with tissue variations. The stoichiometric calibration curve is shown with the reference (triangles) and the individualized (red cloud) human tissues. (a) and (b) are are magnifications of the soft and bone tissue regions, respectively.

Table 6.

Uncertainties (1 σ) to calculate SPRs of human tissues.

Tissue Group	Uncertainties (1 σ)
	Reference Human Tissues	Individualized Human Tissues
Lung	0.00%	0.18%
Soft	0.43%	1.20%
Bone	0.29%	1.60%

3.1.4. Uncertainties in mean excitation energies

We calculated the theoretical SPRs for the reference human tissues using the elemental mean excitation energies introduced with variations as described in section 2.4.4. and compared them with the SPRs calculated using the original elemental mean excitation energies. For each tissue, the maximal difference among all three scenarios was used to calculate the statistics listed in Table 7. Generally, we found that a 10% variation in the elemental mean excitation energies caused the calculated stopping power of water and human tissues to vary by about 1%, but the ratio of the stopping powers of human tissues relative to water (SPR) varied less than 1.4%. Of note, in lung and soft tissues, the relative SPR differences were only about 0.2%, much smaller than 1.4%, thereby confirming the need to consider the correlation between soft tissues and water.

Table 7.

Relative differences in the calculated theoretical SPRs of the reference human tisssues associated with variations in the elemental mean excitation energies.

Tissue Group	Relative Differences in Theoretical SPRs (1 σ)
Lung	0.17%
Soft	0.23%
Bone	0.65%

3.1.5. Uncertainties due to energy dependence of SPR not accounted by dose algorithm

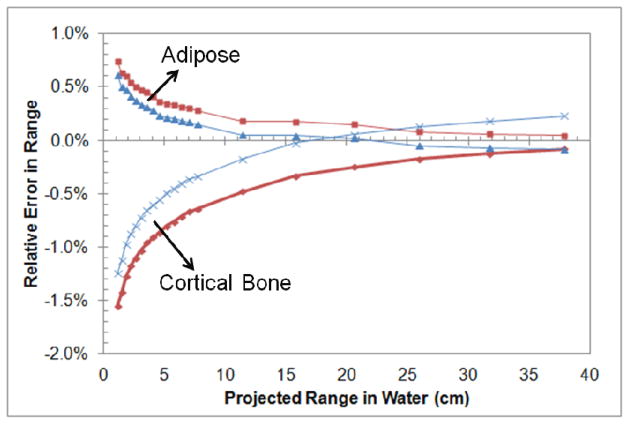
We calculated the relative errors in proton range calculations caused by ignoring proton energy variation for various initial (nominal) proton energies. The initial proton energy chosen in proton treatments depends on the depth of the tumor, so we plotted the relative range error directly against the projected range in water instead of against the proton energy. In our experience, the distal depth of tumors treated at the MD Anderson Proton Therapy Center is typically larger than 5 cm, so we regarded a relative range error at 5 cm as the worst-case estimate (2σ). We found that the relative error in the calculated proton range was small (i.e., less than 0.5% for tumors deeper than 10 cm) at typical tumor depths for both soft (adipose) and bone (cortical bone) tissues. Even for tumors as shallow as 5 cm, the relative range error was still less than 0.5% for soft tissues (adipose tissue). It was also noticed that the SPR uncertainty at the depth of 20.6 cm (the corresponding depth for 175 MeV) is not the smallest when using SPR at 175 MeV. Instead, the use of SPR at an effective proton energy of 100 MeV could minimize the SPR uncertainty at 20.6 cm (at the expense of small increase at much higher energies). Figure 4 shows that SPR uncertainties will decrease at the low energy region (shallow depths) by using the SPR of 100 MeV instead of 175 MeV. The proper selection of SPR value is useful to minimize the uncertainty in the dose calculation algorithm.

Figure 4.

Relative error in the calculated proton range using SPRs based on a single energy of 175 MeV (red) and 100 MeV (blue) versus the projected range in water for adipose and cortical bone tissue.

3.1.6. Summary

Our estimates of the uncertainties in proton SPR estimation are summarized in Table 8. For soft tissues, the dominant contributing factor was the uncertainties to calculate SPRs of human tissues induced by tissue composition variation. Considering the high percentage of soft tissues in the human body, this finding confirms the importance of reducing the impact of tissue composition variation to reduce the overall uncertainties in proton SPR estimation.

Table 8.

Estimates of uncertainties (1 σ) in patient SPR estimation in current clinical practice.

Uncertainty Source	Uncertainties in SPR Estimation (1 σ)
	Lung	Soft	Bone
Uncertainties in patient CT imaging	3.3%	0.6%	1.5%
Uncertainties the parameterized stoichiometric formula to calculate theoretical CT numbers	3.8%	0.8%	0.5%
Uncertainties due to deviation of actual human body tissue from ICRU standard tissue	0.2%	1.2%	1.6%
Uncertainties in mean excitation energies	0.2%	0.2%	0.6%
Uncertainties due to energy dependence of SPR not accounted by dose algorithm	0.2%	0.2%	0.4%
Total (root-sum-square)	5.0%	1.6%	2.4%

3.2. Composite range uncertainties

Table 9 shows our estimates of the composite range uncertainties for prostate, lung, and head-and-neck cancer treatment sites. We found that the variations of the composite range uncertainties among the different treatment sites were smaller (from 3.0% to 3.4%) than the variations among different tissue groups (from 1.6% to 5.0%). The smaller variations among the different treatment sites were due to the dominant percentage of soft tissues in human bodies (i.e., an average of about 80% for all treatment sites). The small variation among different treatment sites suggests that using a single margin value for all treatment sites is reasonable. Our results also showed that the current value used for the margin design, 3.5%, is sufficient for meeting the goal of covering more than 95% of cases at all three treatment sites.

Table 9.

Median, 90th percentile, and 95th percentile of composite range uncertainties and the corresponding percentile when the range uncertainty is 3.5% at different clinical sites.

Tumor Site	Composite Range Uncertainty			Percentile when Range Uncertainty = 3.5%
	Median	90th Percentile	95th Percentile
Prostate	1.3%	2.5%	3.0%	98%
Lung	1.5%	2.9%	3.4%	96%
Head & neck	1.3%	2.6%	3.0%	98%

4. Discussion

4.1. Comparison of our uncertainty estimates with other estimates available in the literature

We performed a systematic analysis of the uncertainties related to SPR estimation in current practice. Our uncertainty categorization scheme differed from those used in previous studies, and we considered some unique uncertainties that were not studied before. In this section, we focused on comparing our estimates to the estimates made by Moyers et al. and other groups (Schaffner and Pedroni, 1998; Trofimov et al., 2010).

Our categorization of the uncertainties in SPR estimation was similar to that by Moyers et al. except in two ways. The first difference was that Moyers et al. classified the difference between the estimated SPR and the theoretical SPR as one category, whereas we divided it into two categories: the difference between the SPR estimated from the measured CT number and the SPR estimated from the theoretical CT number, and the difference between the SPR estimated from the theoretical CT number and the theoretical SPR. By doing this, we could consider human tissue composition variations for the second category. The second difference was that we did not include the uncertainty in the stopping power of water (~1%), because current treatment planning systems use SPR relative to water. The proton range in water is normally measured with high accuracy during the commissioning of the treatment planning system. The precision of proton range measurements in water is about ±0.5 mm, limited by the resolution of a typical water phantom scanning system. At the MD Anderson Proton Therapy Center, the uncertainty in proton range measurements in water is accounted for by an extra 2–3-mm margin in addition to the 3.5% relative margin. However, this 2–3 mm additional margin include other uncertainties, such as the manufacturing of compensator and imperfection of the dose calculation algorithm in modeling scatter etc.

We considered the variation ratio between CT numbers and SPRs ( $\frac{{dS}_{\text{rel}}/S_{\text{rel}}}{\mathit{dHU}/HU}$). For soft and bone tissues, 1% CT number variation translated to approximately 0.7% SPR in our study (Table 3). In contrast, other studies did not consider this relationship.

Another major difference was that we considered tissue composition variations. Their estimate of the uncertainties in converting CT numbers to SPRs was based on the measurements by Schaffner and Pedroni (1998), which included a limited number of animal tissue samples. Our estimate was based on a simulated population-based study, in which we considered both systematic uncertainties in the recommended tissue compositions and tissue composition variations from person to person.

In addition, we considered the correlation between the variations of mean excitation energies of human tissues and water when estimating the uncertainties in theoretical SPR calculation. Moreover, we estimated the uncertainties in range calculations caused by ignoring SPR change associated with proton energy using the difference between proton ranges calculated with and without considering proton energy change.

The estimates by Schaffner and Pedroni (1998) considered two categories of uncertainties: the uncertainties caused by beam hardening and the uncertainties in CT number conversion to SPR. Schaffner and Pedroni measured both CT numbers and SPRs for a number of animal tissues. They then compared the SPRs estimated from the CT numbers based on the calibration curve with the measured SPRs. The differences between the estimated SPRs and the measured SPRs were less than 1%. The strength of Schaffner and Pedroni’s estimates was that they were based on direct experimental measurements. This was also a limitation of their estimates: their study did not include a large number of tissue samples to evaluate the effect of tissue composition variations. The strength of our estimates was that we considered tissue composition variations via a simulated population study. This was also a limitation of our study: we based on simulations instead of direct measurements. As to the uncertainties due to beam hardening, our estimates (1 σ) were similar.

Recently, Trofimov et al. (2010) estimated the relative range uncertainty to be less than 2.5% for patients with prostate cancer. They assigned different uncertainty values for soft and bone tissues separately and then calculated the composite range uncertainties. Our estimated composite range uncertainty value for patients with prostate cancer, 3.0%, was close to their estimated value, 2.5%.

In this study, we demonstrated that different tissue types (lung, soft tissue and bone tissue) carry different uncertainties. A beam-specific PTV approach to incorporate tissue types in the beam path would be more appropriate than the water-equivalent tissue depth approach used in the previous publications (Park et al., 2012).

4.2. Alternative ways to determine proton SPR distribution inside the patient

The uncertainties due to deviation of actual human body tissue from ICRU standard tissue have been found to be the dominant uncertainty contributing factor among all uncertainties, which is largely due to the incapability of single CT-based calibration method to capture the variation between CT number and SPR under the impact of elemental composition variation. Dual-energy CT has been shown to be able to reduce the uncertainty due to tissue composition variation because of simultaneous determination of electron density and effective atomic number (Yang et al., 2010). One disadvantage of the DECT method is that the calculation of electron density and effective atomic number is sensitive to uncertainties in patient CT imaging, which can be minimized by using the combination of kV and MV x-rays for scanning instead of the conventional kV-kV combination (Yang et al., 2011). Active research is currently going on to investigate whether the overall uncertainty in SPR estimation can be reduced by using the kV-MV DECT.

The ideal way to determine proton SPR distribution inside the patient will be to use proton computed tomography (proton CT) to measure SPR distribution inside the patient directly (Schulte et al., 2004; Wang et al., 2011; Talamonti et al., 2010; Civinini et al., 2010; Sipala et al., 2010; Menichelli et al., 2010). One major technical difficulty for proton CT is the numerous small-angle scatterings due to Coulomb interactions along the beam path, which poses an inherent limit on the spatial resolution of reconstructed proton CT images (Li et al., 2006). Another practical difficulty is that proton beams need to have sufficiently high energy to penetrate the body of a patient for imaging purposes.

5. Conclusions

We studied the uncertainties in SPR estimation in current practice thoroughly: 1) we divided them into five categories; 2) we considered their association with tissue composition variations; and 3) we estimated them for lung, soft, and bone tissues separately and then combined them to derive the composite range uncertainties (95th percentile) for three common proton treatment sites (prostate, lung, and head and neck).

The uncertainties (1 σ) in estimated SPRs were shown to be substantially different (from 1.6% to 5.0%) for different tissue groups; however, the combined uncertainty (95th percentile) for different treatment sites was fairly consistent at 3.0%–3.4% because of the dominance of soft tissues in human bodies. The dominant uncertainty contributing factor for soft tissues was the uncertainties due to tissue composition variations, which must be reduced to reduce the overall uncertainties in SPR estimation (e.g., by using the dual-energy CT). The current value used for margin design, 3.5%, was shown to be able to meet the goal of covering more than 95% of cases for all three treatment sites.

Appendix

We conducted a thorough literature review to make a realistic estimate of the systematic and statistical uncertainties in the tissue compositions of human tissues provided in the literature. The systematic uncertainties were estimated using the differences between the tissue compositions of the same tissue type recommended by different published articles. The statistical uncertainties were estimated using several studies by Woodard and White (Woodard, 1964; Woodard and White, 1982, 1986; White et al., 1987; White et al., 1991). Our estimates of the systematic and statistical uncertainties in the recommended values of the key tissue composition factors are provided and explained in detail in the following section. The key factors were the mass density and the percentages of hydrogen (H) and calcium (Ca).

For most human tissues, the recommended densities found in the literature were not determined by direct experimental measurements. Instead, they were calculated using a tissue component model (Woodard and White, 1986; White et al., 1987) that assumed that all human body tissues are made up of a number of fundamental components such as water, lipids, proteins, and minerals. Using that assumption, the density of any human tissue (ρ_x) could be simply calculated by:

$${\rho }_{\text{x}}=\frac{1}{{\sum }_{i=1}^n\frac{w_{\text{i}}}{{\rho }_{\text{i}}}},$$ (A1)

where ρ_i and w_i are the density and weight by mass of the i_th component, respectively. The flaw of this method was that the possible structural changes after mixing these components in vivo were ignored, which could lead to up to 2% error in the calculated density (Woodard and White, 1986). Despite the known possible errors, the calculated densities were still used because the measured values were not available for most human tissue types (White et al., 1991). Table A1 lists the recommended densities of several human tissue types from different sources. The relative differences ranged from 0.0% to 3.6% with the root-mean-square (RMS) value equal to 2.1%. Therefore, 2.1% was chosen as our estimate (1 σ) of the systematic uncertainties in the recommended density values. Table A2 lists the mean and standard deviation of seven human tissues provided by Woodard and White (1986). The relative standard deviation ranged from 0.0% to 3.4% with the RMS value equal to 1.7%, which was used as our estimate (1 σ) of the statistical uncertainties.

Table A1.

Comparison of the recommended density values of the same human tissue type from different sources.

Tissue Type	Density (g/cm3)		Rel. Diff.
	Woodard and White (1986)	ICRU 44 (1989)
Adipose	0.95	0.916	3.6%
Mammary gland	1.02	1.05	2.9%
Liver	1.06	1.053	0.7%
Muscle	1.05	1.04	1.0%
Skin	1.09	1.1	0.9%
Eye lens	1.07	1.1	2.8%
Lung (deflated)	1.05	1.05	0.0%
Ovary	1.05	1.048	0.2%
Red marrow	1.03	1.03	0.0%
Thyroid	1.05	1.05	0.0%
Heart (blood filled)	1.06	1.03	2.8%
Cortical bone	1.92	1.85	3.6%
Root-mean-square (RMS)			2.1%

Table A2.

Mean densities (<ρ>) and standard deviations (σ) of human tissues from Woodard and White (1986). The relative standard deviation (σ_rel) was also calculated.

Tissue Type	<ρ>, g/cm3	σ	σrel
Adipose	0.95	0.02	2.1%
Mammary gland	1.02	0.035	3.4%
Liver	1.06	0.01	0.9%
Kidney	1.05	0.0	0.0%
Muscle	1.05	0.0	0.0%
Skin	1.09	0.0	0.0%
Heart	1.05	0.0	0.0%
Cortical bone*	1.91	0.05	2.4%
Root-mean-square (RMS)			1.7%

^*The mean and standard deviation of cortical bone is from Woodard (1964).

The hydrogen percentages of human body tissues published in the literature were also not measured but calculated using the tissue component model. Three major tissue components in human bodies contain substantial amounts of hydrogen (i.e., water, lipids, and proteins). The hydrogen percentages (H_x) of human body tissues were calculated by

$$H_{\text{x}}={\omega }_{\text{W}}\ast H_{\text{W}}+{\omega }_{\text{L}}\ast H_{\text{L}}+{\omega }_{\text{P}}\ast H_{\text{P}},$$ (A2)

where ω_W, ω_L, and ω_P were the weight by mass of water, lipids, and proteins, respectively, and H_W, H_L, and H_P were the hydrogen percentages by mass in water, lipids, and proteins, respectively. By taking the first derivative of equation A2, the uncertainty in the calculated hydrogen percentage could be calculated by

$${\sigma }_{{\text{H}}_{\text{x}}}=\sqrt{{({\sigma }_{{\omega }_{\text{W}}}\ast H_{\text{W}})}^2+{({\sigma }_{{\omega }_{\text{L}}}\ast H_{\text{L}})}^2+{({\sigma }_{{\omega }_{\text{P}}}\ast H_{\text{P}})}^2+{({\omega }_{\text{W}}\ast {\sigma }_{{\text{H}}_{\text{W}}})}^2+{({\omega }_{\text{L}}\ast {\sigma }_{{\text{H}}_{\text{L}}})}^2+{({\omega }_{\text{P}}\ast {\sigma }_{{\text{H}}_{\text{P}}})}^2},$$ (A3)

where σ_ωW, σ_ωL, and σ_ωP were the uncertainties in the weight by mass of water, lipids, and proteins, respectively, and σ_HW, σ_HL, and σ_HP were the uncertainties in the hydrogen percentages, respectively. Table A3 lists the estimates of the uncertainties in hydrogen percentages provided by Woodard and White (1986), which accounted for only the uncertainties in the relative weights of water, lipids, and proteins in human tissues (i.e., the first three items in equation (A3)). To determine the total uncertainty, we also needed to estimate the uncertainties in the hydrogen percentages of water, lipids, and proteins, the last three items in equation (A3).

The uncertainty in the hydrogen percentage of water (σ_HW) is simply zero because the hydrogen percentage of water is constant. The uncertainties in the hydrogen percentages of lipids (σ_HL) was determined to be 1.0%, based on the standard deviation of the hydrogen percentages of four major biological substances within the lipid category listed in Table A4. The uncertainties in hydrogen percentages of protein (σ_HL) were determined to be 1.8%, based on the standard deviation of the hydrogen percentages of 23 major amino acids, the building blocks of proteins (Table A5). One water molecule will be lost when two amino acids bind to each other. For a relatively long peptide, each amino acid loses approximately one water molecule on average, a factor that was considered in our calculation. After incorporating all the uncertainty estimates back into equation (A3), we calculated the total standard deviation of hydrogen percentage for each tissue type (Table A6). The total standard deviation was 0.5%, which was then used as our estimate (1 σ) of the statistical uncertainties in hydrogen percentages.

Table A3.

Compositions of seven human tissues from Woodard and White (1986) and the calculated standard deviation of hydrogen percentages (σ′_H). Three tissue compositions are provided for each human tissue: mean and mean ± 1 standard deviation (σ). The hydrogen percentage was calculated using the relative weight by mass and the hydrogen percentage of each tissue component.

Tissue Type	Category	Relative Weight by Mass			H	${\sigma }_{\text{H}}^{\prime }$
		Water	Lipid	Protein
Adipose	Mean + σ	30.5%	61.4%	7.9%	11.2%	0.2%
	Mean	21.2%	74.1%	4.4%	11.4%
	Mean − σ	11.4%	87.3%	1.0%	11.6%
Heart	Mean + σ	71.0%	10.0%	18.2%	10.3%	0.0%
	Mean	75.9%	6.2%	17.1%	10.4%
	Mean − σ	80.9%	2.4%	15.9%	10.4%
Kidney	Mean + σ	72.3%	6.9%	19.9%	10.2%	0.1%
	Mean	76.6%	4.8%	17.7%	10.3%
	Mean − σ	80.5%	2.8%	15.8%	10.4%
Liver	Mean + σ	72.8%	7.8%	16.1%	10.1%	0.1%
	Mean	74.5%	4.6%	17.6%	10.0%
	Mean − σ	75.6%	1.5%	19.6%	9.9%
Mammary gland	Mean + σ	30.2%	56.2%	13.3%	10.9%	0.3%
	Mean	51.4%	30.9%	17.4%	10.6%
	Mean − σ	72.6%	5.6%	21.5%	10.2%
Muscle	Mean + σ	70.0%	6.8%	21.3%	10.0%	0.1%
	Mean	74.1%	4.2%	19.8%	10.1%
	Mean − σ	78.6%	1.6%	17.9%	10.2%
Skin	Mean + σ	58.6%	13.5%	27.2%	10.0%	0.1%
	Mean	65.3%	9.4%	24.6%	10.0%
	Mean − σ	72.1%	5.2%	22.0%	10.1%

Table A4.

Hydrogen percentages of major lipid substances from Woodard and White (1986).

Major Lipid Substance	H
Cerebroside	9.8%
Cholesterol	12.0%
Glycerol trioleate	11.8%
Sphingomyelin	11.7%
Standard Deviation	1.0%

Table A5.

Hydrogen percentages of amino acids.

Amino Acid	H
Isoleucine	9.8%
Leucine	9.8%
Lycine	9.4%
Methionine	6.9%
Phenylalanine	6.2%
Threonine	7.0%
Tryptophan	5.4%
Valine	9.2%
Alanine	7.1%
Asparagine	5.3%
Aspartic acid	4.4%
Cysteine	4.9%
Glutamic acid	5.5%
Glutamine	6.3%
Glycine	5.3%
Proline	7.3%
Selenocysteine	3.4%
Serine	5.8%
Tyrosine	5.6%
Arginine	7.7%
Histidine	5.1%
Ornithine	8.8%
Taurine	4.7%
Min	3.4%
Max	9.8%
Mean	6.6%
Standard Deviation	1.8%

Table A6.

Estimates of the uncertainties corresponding to the first three items in equation (A3) given by Woodard and White (1986) (σ′_H); estimates of the uncertainties corresponding to the last three items in equation (A3) (ω_W*σ_HW for water, ω_L*σ_HL for lipid, and ω_P*σ_HP for protein); and the total uncertainty (σ_H) calculated using equation (A3) for seven human tissue types.

Tissue	${\sigma }_{\text{H}}^{\prime }$	(ωW*σHW	(ωL*σHL	(ωP * σHP	σH
Adipose	0.2%	0.0%	0.7%	0.1%	0.8%
Heart	0.0%	0.0%	0.1%	0.3%	0.3%
Kidney	0.1%	0.0%	0.0%	0.3%	0.3%
Liver	0.1%	0.0%	0.0%	0.3%	0.3%
Mammary Gland	0.3%	0.0%	0.3%	0.3%	0.6%
Muscle	0.1%	0.0%	0.0%	0.4%	0.4%
Skin	0.1%	0.0%	0.1%	0.4%	0.5%
Root-mean-square (RMS)					0.5%

The uncertainties in calcium percentages of bone tissues rely heavily on the uncertainties in calcium percentages of cortical bone. The elemental compositions of bone tissues were calculated using the elemental compositions of fundamental bone tissue components such as cortical bone (compact bone), trabecular bone (cancellous bone or spongiosa), cartilage, and bone marrow (Woodard and White, 1982). Among them, only cortical bone and trabecular bone contain a substantial amount of calcium. Cortical bone contains substantially more calcium than trabecular bone: 22.2% by mass versus 7.47%, respectively. Cortical bone is much denser than trabecular bone as well: 1.90 g/cm³ versus 1.18 g/cm³, respectively. In an average adult, approximately 80% of total bone mass is cortical bone, and the remainder is trabecular bone (Valentin and Streffer, 2002). Additionally, the calcium percentage of trabecular bone was actually calculated using the calcium percentage of cortical bone, assuming that trabecular bone is a combination of cortical bone and bone marrow. Therefore, we decided to study only the uncertainty in the calcium percentage of cortical bone and apply it for all bone tissues.

Table A7 lists both the mean value and the range of calcium percentages of cortical bone in adults and children. The relative standard deviation was 0.5% and 0.8% for adults and children, respectively. The calcium percentage in children has a larger spread because bones in children are still growing; therefore, 1.0% was chosen as our estimate of statistical uncertainties in calcium percentages to cover both adult and pediatric patients. The systematic uncertainties in calcium percentages were determined using the difference between the recommended calcium percentages for adults from two publications, which was calculated to be 1.0%.

Table A7.

Calcium percentages in human cortical bone.

Group	Ca %				Source
	Mean	STD	Min	Max
Age 2–19	20.8%	0.83%	19.0%	22.8%	Woodard (1964)
Age 20–74	22.5%	0.50%	21.0%	23.8%
Adult	21.5%				Valentin and Streffer (2002)

One limitation of our estimation was that all our data were taken from studies based on healthy adults. It is known that tissue compositions depend on the state of health, nutrition, sex, age, etc. (White et al., 1991). Most patients with cancer receiving radiation therapy are relatively old in age and in bad health. Therefore, further studies are needed to determine tissue compositions of patients with cancer and compare them with those of healthy adults.