Abstract
Human islet amyloid polypeptide (hIAPP) is a cytotoxic protein that aggregates into oligomers and fibrils that kill pancreatic β-cells. Here we analyze hIAPP aggregation in vitro, measured via thioflavin-T fluorescence. We use mass-action kinetics and scaling analysis to reconstruct the aggregation pathway, and find that the initiation step requires four hIAPP monomers. After this step, monomers join the nucleus in pairs, until the first stable nucleus (of size approximately 20 monomers) is formed. This nucleus then elongates by successive addition of single monomers. We find that the best fit of our data is achieved when we include a secondary fibril-dependent nucleation pathway in the reaction scheme. We predict how interventions that change rates of fibril elongation or nucleation rates affect the accumulation of potentially cytotoxic oligomer species. Our results demonstrate the power of scaling analysis in reverse engineering biochemical aggregation pathways.
Keywords: Scaling analysis, human islet amyloid polypeptide, thioflavin-T fluorescence, fibrillization, pathway reconstruction
1. Introduction
A number of degenerative diseases are associated with abnormal aggregation of protein or peptide to form fibers, plaques, or other deposits. These disorders include Alzheimer’s Disease (AD), Parkinson’s disease, Creutzfeldt-Jakob disease (CJD) and Huntington’s disease. In some cases, misfolded or defective protein causes fibrillization, and results in plaques or deposits associated with cytotoxicity (Kayed et al. 2003, Hall & Edskes 2004). Amyloid, the term commonly applied to such proteins, has been studied in vivo and in vitro in an effort to understand the pathways that lead to fibrillization. In vitro studies commonly follow the time course of aggregation using optical methods such as turbidity measurements or changes in fluorescence of protein solutions. In this paper we consider a protein associated with type 2 diabetes.
Type 2 diabetes is a chronic metabolic disease that affects over 200 million persons worldwide. It is characterized by impairments in both the action of insulin on peripheral tissue and its secretion from the pancreatic islet β cell. Islet insulin production steadily declines as the disease progresses and many patients with this disease require exogenous insulin to maintain blood glucose control. A number of factors may contribute to β cell failure in type 2 diabetes, including the combined cytotoxic effects of elevated glucose and lipids, endoplasmic reticulum stress, the action of pro-inflammatory cytokines, and islet amyloid (Donath et al. 2005). Amyloid deposits have been demonstrated in pancreatic islets of up to 90% of type 2 diabetic patients at autopsy.
Islet amyloid polypeptide (hIAPP or amylin) is produced by pancreatic β-cells and co-secreted with insulin (Hartter et al. 1991, Kautzky-Willer et al. 1994, Charge et al. 1995, Kautzky-Willer et al. 1997) in response to glucose and other secretagogues. Although the physiological role of hIAPP is not well defined, hIAPP is thought to suppress appetite and gastric emptying and to play a role in bone metabolism. Under pathological conditions, namely insulinomas and type 2 diabetes, IAPP may misfold and aggregate into insoluble amyloid plaques. Human IAPP has a natural propensity to aggregate into amyloid fibrils, whereas rodent forms of the peptide are soluble and not toxic. IAPP-derived aggregates are cytotoxic and induce apoptosis of transformed β cells and islet cells from human islets or human IAPP expressing transgenic mice (Padrick & Miranker 2002, Hull et al. 2004). hIAPP fibril cytotoxicity has been inferred from widespread observation of hIAPP fibrils in autopsies of people with type 2 diabetes, and in studies where synthetic hIAPP was applied to β-cell cultures (Marzban et al. 2006, Porat et al. 2003). However, recent studies question the conclusion that mature amyloid fibrils are toxic, and suggest that early stages of fibril development (Hull et al. 2004, Porat et al. 2003) or a distinct pathway of oligomer formation (Powers & Powers 2008) cause toxicity.
Details of the steps involved in fibril formation for hIAPP are still largely unknown, despite recent efforts (Padrick & Miranker 2002, Porat et al. 2003, Tanaka et al. 2006, Lee et al. 2007, Ruschak & Miranker 2007, Powers & Powers 2008). It is important to identify those steps in order to have a clear understanding of the mechanism and to design targeted therapies. In particular, treatments designed to decrease (or increase) fibrillization could increase (or decrease) pathogenic exposure to oligomers, depending on details of the pathway. Once the pathway is identified, simple model predictions could clarify which interventions are likely to be beneficial (reducing exposure to the toxic species) and which are likely to be harmful.
Aggregation pathways for hIAPP have been studied experimentally and theoretically in several recent works. Ruschak et al. used light scattering to detect soluble monomer levels, and showed that monomers are consumed in the production of oligomers and fibrils (Ruschak & Miranker 2007). Using modeling, they were able to quantify the fibril elongation rate and suggest that nuclei form and elongate, without giving details of the pathway. Lee et al. proposed a three stage model of amyloid fibril formation, including monomer assembly into unstable nuclei, and formation and growth of fibrils by addition of monomers or oligomers of any size (Lee et al. 2007). Powers and Powers proposed a similar model in which oligomers and fibrils grow by adding single monomers (Powers & Powers 2008). They proposed a side (“off-pathway”) reaction that diverts oligomers into other forms of aggregates, in competition with fibrilization. Both Ruschak et al. and Powers and Powers argued that such off-pathway kinetics are insignificant in hIAPP fibrillization.
While the above studies have contributed to an emerging concept of hIAPP aggregation, none has as yet confirmed or validated a given hypothetical pathway structure. Here we combine in vitro polymerization data with simple scaling arguments to reconstruct the hIAPP fibrillization pathway. We closely follow the method presented by Flyvbjerg et al. (Flyvbjerg et al. 1996) in a study of tubulin polymerization. Based on our scaling analysis, we are able to dismiss the role of off-pathway kinetics, and infer details of the process including the number of monomers needed to form a stable nucleus, and the number of monomers that are added at each subsequent elongation step. After validation, the model is used to predict effects of interventions that change rate constants, and to determine which treatments are likely to reduce toxic species.
hIAPP is just one of many aggregating proteins with physiological and clinical implications. The kinetics of such proteins is of universal interest, and common features have been recently described (Knowles et al. 2009). In that paper, the focus is on how common features of such oligomer-driven self-assembly result in scaling laws and common dynamical features. In our paper, we exploit such scaling laws to decipher the details of the underlying chemical mechanism.
1.1. Definitions
In the literature, amyloid aggregates of various sizes are known by various names (e.g. oligomers, nuclei, protofilaments, fibrils etc). In this paper, we define the following terminology. An oligomer is a very small aggregate of hIAPP that is smaller than a stable nucleus, which is the smallest aggregate that is detectable by our experimental protocol. Nuclei then grow to form fibrils. We do not use the term protofilament. Caution should be exercised when reading other papers in this area as these terms are not always clearly defined (e.g. see (Zraika et al. 2010) for a longer discussion of identification of oligomeric species).
2. Materials and methods
2.1. Protein Preparation
1mg hIAPP powder (Bachem, Torrance, CA) was dissolved in 1mL hexafluoroisopropanol (HFIP). Solubilized 100 μL aliquots were frozen (−20°C for 2 h, then −80°C overnight) and lyophilized as previously described (Park & Verchere 2001).
2.2. Fluorescence
Fluorescence shift associated with the binding of thioflavin T (Th-T) to amyloid fibrils, but not to monomers, or oligomers (LeVine 1999) was observed to label hIAPP in fibril over time, for concentrations of monomers (20, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, and 100 μM). Aliquots of hIAPP were dissolved in dimethyl sulfoxide (DMSO) and filtered buffer, pH 7.4, in 500 μL 96-well plates with 4 μL Th-T, to the desired concentration of hIAPP. The buffer we used was 10 mM Tris-HCl, 100 mM NaCl, and 0.1% Triton X-100 (Park & Verchere 2001). We assume that following HFIP solubilization and subsequent lyophilization, the peptide is in a monomeric state upon re-solubilization in buffer. Rat IAPP (which does not form fibrils) and blanks (DMSO, Th-T, and buffer) were used as controls. The final concentration of DMSO was 10% and of Th-T was 10 μM. Measurements were taken over a 20 hour period using a Fluoroskan Ascent fluorometer (Thermosystems). As a minimum, each experiment was performed in triplicate and on three separate occasions.
2.3. Fibril elongation assay
hIAPP (50 μM) was allowed to polymerize over 3 h. The mature reaction was vortexed (30 s), and hIAPP monomer at 25, 35, 50 and 100 μM was added and monitored using a Th-T assay. The first 600 s of the elongation kinetics were analyzed, assuming a constant number of fibril ends.
3. Results
3.1. Nucleation-dependent polymerization model
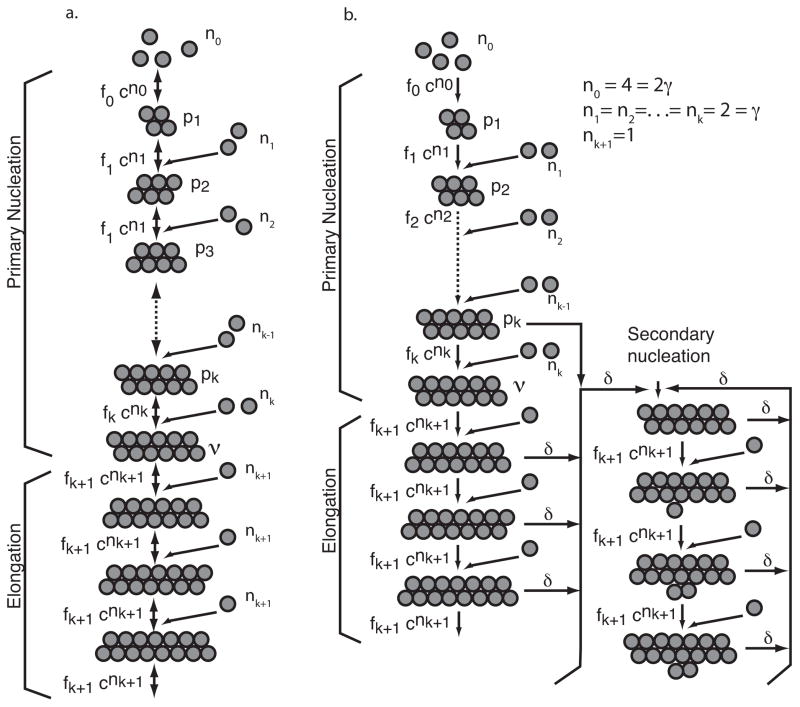
The Nucleation Dependent Polymerization model (NDP) is a basic model for a self assembling polymer. Monomers are assumed to associate and dissociate on a rapid timescale, equilibrating with short-lived oligomer species. Stable nuclei are then formed on a slower time scale by aggregation of oligomers and these nuclei then elongate to form polymers. Such models with rate limiting nucleation have been used to describe actin (Pantaloni et al. 1985) and microtubule (Flyvbjerg et al. 1996, Bonfils et al. 2007) polymerization and generate sigmoidal plots of polymer mass vs. time in simulated aggregation assays. Variants of the NDP model include side reactions (off-pathway reactions, above) that can compete with the main fibril formation pathway to produce other terminal aggregates. Figure 1a shows an NDP aggregation pathway consistent with reactions suggested for hIAPP aggregation.
Figure 1.
a. Representative diagram showing typical nucleation dependent polymerization (NDP) model. b. Pathway for hIAPP fibrillization obtained by our data scaling and modeling methods. In this model, there is the potential for generation of alternative nucleation sites on the largest oligomer specied. First nuclei are labeled ν.
Following Flyvbjerg et al. (1996) we model the IAPP monomer concentration c(t), number concentration of the ith oligomer pi(t), the number concentration of nuclei ν(t) and the monomer mass in fibrils M(t) (excluding oligomers and nuclei). Definitions of variables and model parameters are given in Table 1.
Table 1.
Variable and parameter definitions.
| Symbol | Meaning |
|---|---|
| A(t) | experimentally measured fluorescence |
| A∞ | maximum level of polymerization |
| t50 | time to half-maximal fluorescence |
| c(t) | IAPP monomer concentration |
| pi(t) | number conc. of the ith oligomer (i = 1 … k) |
| ν(t) | number conc. of nuclei |
| M(t) | monomer mass in fibril |
| c0 | initial IAPP monomer concentration |
| ni | number of monomers added to pi to form pi+1 |
| k | number of oligomer species |
| fi | forward rate for the ith oligomer |
| fk | forward rate for nuclei formation |
| fk+1 | forward rate for polymer elongation |
| bi | reverse rate of the ith oligomer |
| di | disintegration rate of the ith oligomer |
| δ | rate of secondary nucleation |
We assume that A(t), the measured fluorescence, represents M(t) (with no time-lag due to delays in ThT binding) and that all mass is initially in monomer form, c(0) = c0. These assumptions, together with the scheme shown in Figure 1a and simple mass-action kinetics, result in the following system of differential equations for nucleated polymerization:
| (1) |
| (2) |
| (3) |
| (4) |
Our notation here is that the parameters fi are on-rates, bi are off-rates, and di are disintegration rates. Here f0cn0 represents the rate of formation of the first oligomer, represented by p1, from the association of n0 monomers. The formation of the ith oligomer from the i − 1 oligomer occurs by the addition of ni−1 monomers to the pi−1 species. Furthermore, oligomers (pi) may be lost by the complete disintegration of the ith oligomer into monomers via the term dipi. Stable nuclei ν form by binding of nk monomers to the pk oligomeric species, the largest oligomer allowed in the model. The mass of fibrils, M then grows by addition of nk+1 monomers to these nuclei, until monomers are used up. As the last monomers are sequestered into polymers, they leave behind oligomeric species.
3.2. Rescaled hIAPP polymerization follows a universal sigmoidal time course
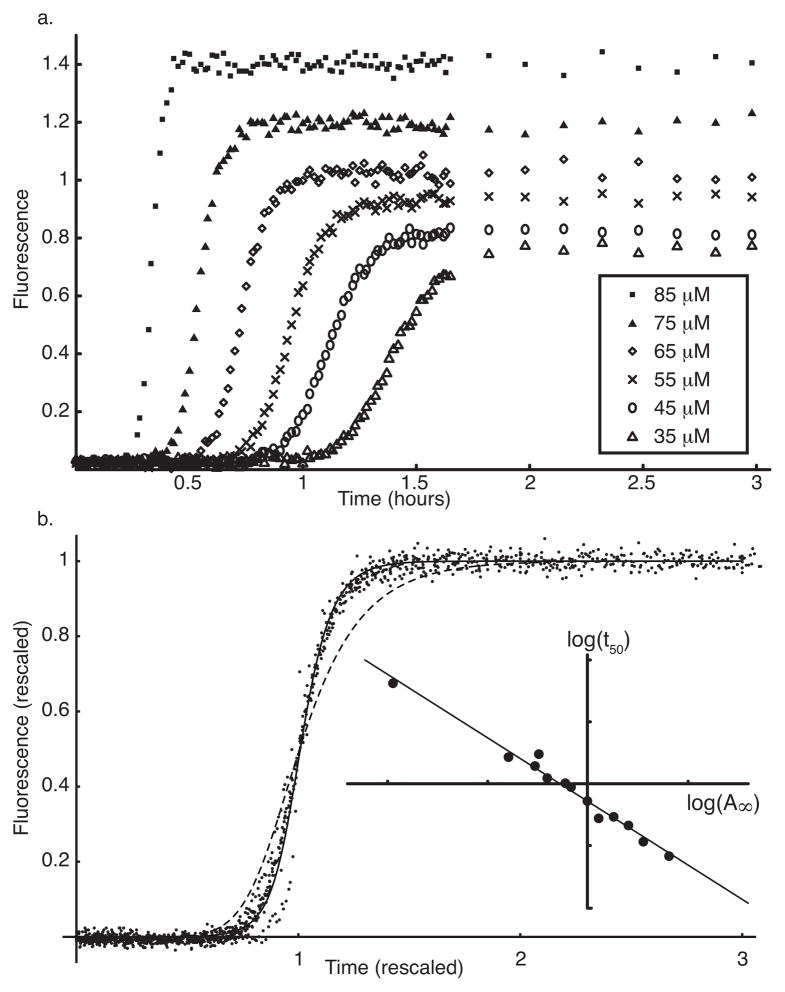
We used the Thioflavin T (Th-T) assay to quantify hIAPP polymerization. Th-T is a benzothiazole dye that exhibits a spectral shift when it binds to hIAPP fibrils but not monomers (LeVine 1999). This specificity makes Th-T useful as a measure of fibrillar hIAPP. While the exact nature of the fibril-Th-T complex is not known, the relative fluorescence intensity correlates well with the degree of aggregation (Ionescu-Zanetti et al. 1999). A sequence of 14 initial monomer concentrations were used, as described in the Methods. Six sample curves are shown in Figure 2a; all data are summarized in Supplementary Figure 1.
Figure 2.
hIAPP fibrillization data and analysis. a. Thioflavin-T fluorescence was measured for 14 initial hIAPP monomer concentrations over 3h. Six sample curves are shown. b. Rescaling each data curve by its maximum fluorescence (A∞) and time to 50% of maximum (t50) collapses the data. All 14 data sets are shown as dots. Dashed line indicates the best fit to the rescaled data using the basic nucleation dependent polymerization (NDP) model; solid line indicates the best fit using the NDP model with an off-pathway branch. Inset: Log-log plot of t50 vs. A∞ for all data sets with the best fit line y = −2.06x − 0.14.
The data were rescaled by the final fluorescence A∞ and the half-time t50. The rescaled data is plotted in Figure 2b and is observed to collapse onto a single universal curve. A log-log plot of t50 vs. A∞ (Figure 2b, inset)) is well fit by the power law relationship
| (5) |
This numerical value agrees with previously published findings (Ruschak & Miranker 2007).
Re-plotting the kinetic profiles on non-dimensional axes in this way (Figure 2b) and obtaining universal behaviour is the first step of our analysis. Crucially, it shows that the rescaled fluorescence is a simple sigmoidal function of the rescaled time, and this behaviour is independent of the monomer concentration. This means that any mathematical model describing the kinetics, when rescaled in the same way, must also be independent of the initial monomer concentration. In the next section we apply this requirement to the NDP model described previously.
3.3. Rescaling analysis
Since the kinetic profiles of hIAPP fibril formation follow a universal sigmoidal curve across initial monomer concentrations, we scale the model equations to eliminate any dependence on c0 (Flyvbjerg et al. 1996). Any model term left which explicitly contains c0 after the scaling must be set to zero for consistency with the observed data scaling of Figure 2b.
We define dimensionless variables as follows:
| (6) |
where the scales X and t0 are to be determined. After a little algebra, the first three governing equations become
| (7) |
| (8) |
| (9) |
We now apply the following two conditions that arise from the data rescaling:
the dynamics described by these rescaled equations must be independent of c0. This is exactly equivalent to requiring that all the curves in Figure 2b are superimposed.
the rescaled data follows (Figure 2b, inset) so we can rewrite where λ is a dimensional constant.
In order for the first coefficient in (7) to be independent of c0, we must choose . We make this choice since X may also carry a dependence on c0, and this allows us to take care of that possibility as well. For the next coefficient in (7), we must choose n1 = γ to make this term independent of c0. Because there is no choice of parameters that can eliminate c0 from the last terms in (7), i.e. from t0 in t0(b2p̂2−d1p̂1), we conclude that, for the scaling to work, we must assign b2 ≈ 0, d1 ≈ 0. This implies that depolymerization and backwards reactions have a negligible effect on the population dynamics of oligomer species. This conclusion is imposed by the two conditions highlighted above.
With these assignments, (7) becomes
| (10) |
Following the same procedure for (8), we must choose ni−1 = γ and ni = γ and again enforce bi = 0, bi+1 = 0, di = 0 for the scaling to work.
We now consider the nuclei equation. Using this becomes
| (11) |
The coefficient in braces is independent of c0 provided nk = n1 = γ. Finally, substituting M = c0M̂ into (4) leads to
| (12) |
To make this independent of c0, we must pick . Then from (1) we have that
| (13) |
implying that n0 = 2γ and the final dimensionless equations are
| (14) |
| (15) |
| (16) |
| (17) |
where the hats are now dropped and we have absorbed λ into the parameters f0, fk, etc.
We have found that 2γ monomers have to come together to form the first oligomer (p1). We have also determined that n1 = n2 = … = nk = γ. Thus, at each step, γ monomers have to be added to form the next oligomer. (p2, p3, etc). After k such steps, the nucleus is formed (ν). The size of the nucleus is then
| (18) |
To summarize, the requirements that we have determined in this section are imposed by the experimental observations, and have the following important consequences:
Neither the off-rates (bi) nor the disintegration rates (di) are relevant to the kinetics and there is no significant flux of monomers into or out of the various oligomer species via these processes, on the timescale of a few hours.
The size of the first oligomer is n0 = 2γ = 4 monomers.
ni = 2 for 2 ≤ i ≤ k. Thus, at each step, two monomers have to be added to form the next oligomer.
The size of the complete nucleus is .
Notably, the final system of equations (14–17) is a lot simpler than the full NDP model (1–4). The simplicity of the final system indicates that the rescaling properties of the data impose strong constraints on the possible kinetics.
3.4. Early-time behaviour allows us to estimate the number of oligomeric species
Close to t = 0, nonlinear terms are small and a good approximation to the model kinetics follows from
| (19) |
| (20) |
| (21) |
| (22) |
Successively solving these approximate equations leads to M(t) ∝ tk+2. Note that this result is derived from the scaling law and is independent of γ. In order to estimate k for hIAPP, we plotted log(A(t)) vs log(t) for each of the 14 data sets, and fit a line to the points between 5% and 30% of the asymptotic fluorescence, omitting three experiments with less than 4 data points in this range. The lower bound of 5% reduces the impact of noise at low fluorescence levels. The values of k obtained by this procedure ranged from 6.3 to 10.4 with a mean of 8.1 (Supplementary Table 1). We therefore estimate that there are k = 8 oligomeric species.
Together with the scaling analysis summarized above, this implies that the first stable nucleus size is N = (k + 2)γ = 20. Four monomers combine to form the first oligomer, after which pairs of monomers are added until a stable nucleus of 20 monomers is formed. This is in general agreement with previously reported estimates of 25–500 monomers (Janson et al. 1999), 20–40 monomers (Anguiano et al. 2002) and > 16 monomers (Green et al. 2004).
3.5. Fibrillar growth rate measured using an elongation assay
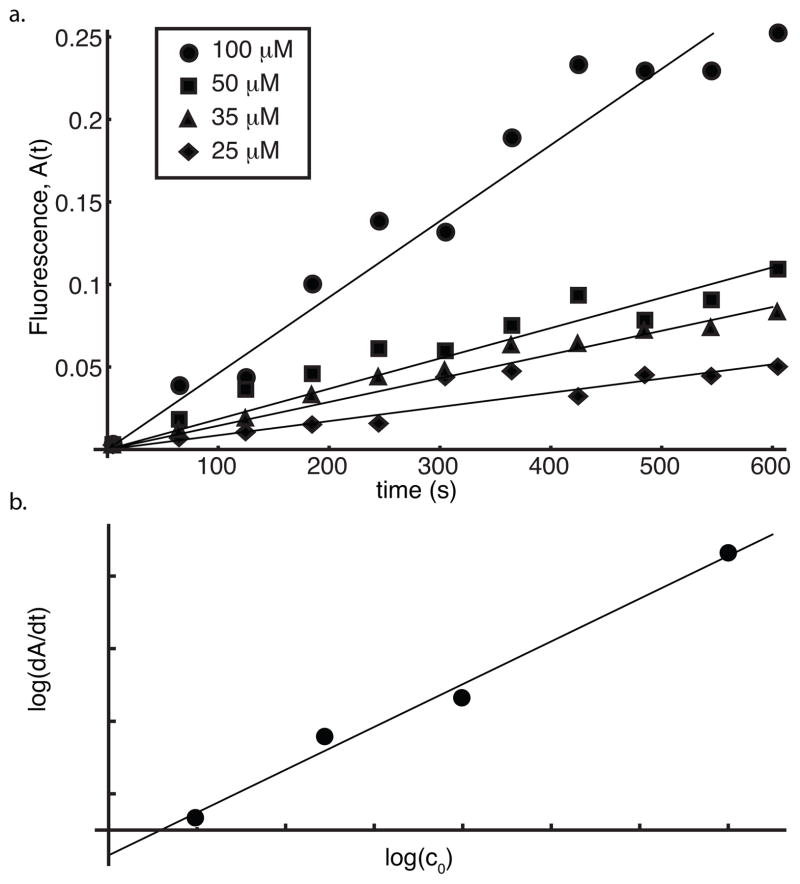
To study the growth of mature fibrils, we performed a fibril elongation assay (see Methods). Different concentrations of hIAPP monomers were added to existing polymer solutions, and monitored using the thioflavin-T assay for 10 minutes. This data is shown in Figure 3a.
Figure 3.
hIAPP elongation kinetics using pre-formed nuclei. a. Fluorescence time course data is plotted for four experiments with different concentrations of hIAPP monomers (25, 35, 50 and 100 μM) and best fit lines are shown for each experiment. b. The slopes of the best fit lines are plotted against the monomer concentration on a log-log plot.
Assays carried out by Ruschak et al. using light scattering reveal that soluble monomer concentration approaches 0 as fibril formation plateaus (Ruschak & Miranker 2007). Assuming that the polymer mass is concentrated in monomers and fibrils, i.e. making the approximation that c0 = c(t) + M(t) we can conclude that in the elongation assay,
| (23) |
where F are the (presumed fixed) number of fibril ends and nk+1 are the number of monomers added per step to a growing fibril. Thus,
| (24) |
A log-log plot of dA/dt (estimated from a best fit line to the elongation rate) vs the monomer concentration c0 has a slope of 1.18, indicating that elongation of fibrils is most likely due to addition of a single monomer at a time, or in our notation, nk+1 = 1 (Figure 3b).
3.6. Oligomer mass is negligible in our assay at all times
We have assumed that the masses of oligomers and nuclei are very small at all times, i.e. that mass is concentrated in monomers and fibrils. This assumption allowed us to relate experimental fluorescence A(t) to initial monomer concentration c0(0). We checked the self-consistency of this assumption using predicted oligomer populations and observed fibril levels. To do so, we computed from the model, scaled both c(t) and M to the same relative units and compared c(t)/c0, A(t)/A∞, and their sum. This calculation based on our model supports the assumption that oligomer masses are very small. Figure 3 of reference (Ruschak & Miranker 2007) also supports this assumption, i.e. it demonstrates that to a good approximation, the declining monomer concentration is converted rapidly into an increase in the fibril mass. Thus, we are able to work in the scaled variable c(t)/c0 and we are justified in assuming that M(t)/M∞ = 1 − c(t)/c0.
3.7. Pathway identification
We performed parameter fitting of the basic NDP model to the observed rescaled data. However, we found a systematic error in such fits: the best-fit NDP model has a smaller lag time, and a shallower rise to the plateau A(t) than does the data (this fit is shown as a dashed line in Figure 2b). Though the NDP model scales appropriately to the data, it fails to accurately describe the formation of hIAPP fibrils.
To address this systematic error, we considered later events in fibril formation. Previously proposed in the literature is a secondary reaction branch: namely, that as fibrils form, a secondary fibril-dependent nucleation occurs by addition of a single monomer to the largest oligomer species. These secondary nuclei form fibrils by unit addition. Based on our elongation assay, we expect that all fibrils grow by single monomer addition. The equations are then as follows, where j is some species that supports the branched pathway,
| (25) |
| (26) |
| (27) |
| (28) |
Observe the new term δfkc(γ−1)pkM in Eq. 27, representing generation of additional growth sites on existing aggregates. We then performed parameter fitting for the modified model. The data are not sufficiently precise to accurately estimate every parameter in the model, and in particular to distinguish between individual polymerization steps. Therefore, to obtain reliable parameter estimates, we simplified our model by assuming equal values of fi for 1 ≤ i ≤ k. The free parameters in the fits were therefore f0, f1 = … = fk−1, fk+1 and δ. The solid line in Figure 2b indicates that the extended model describes the scaled data a little better than the basic NDP model (dashed line). Dimensional parameter estimates for both models are reported in Table 2.
Table 2.
Model parameter estimates. We report dimensional best-fit parameter estimates from the basic and extended NDP models. Note that δ is fundamentally dimensionless.
| Parameter | Estimate |
|---|---|
| Basic NDP model | |
| f0 | 6.4 μM−3hour−1 |
| f1 = f2 = … = fk | 4.2 ×10−5μM−2hour−1 |
| fk+1 | 8.9 ×106μM−1hour−1 |
|
| |
| NDP model with an off-pathway branch | |
| f0 | 5.4 μM−3hour−1 |
| f1 = f2 = … = fk | 5.0 ×10−5μM−2hour−1 |
| fk+1 | 1.2 ×106μM−1hour−1 |
| δ | 3.0 × 103 |
Based on the combined scaling and fitting, and the reasoning above, we identify the final pathway as NDP, modified by a secondary fibril-dependent nucleation. A diagram showing this pathway is given in Fig 1b. The parameter δ controls the rate of this branch, but we cannot comment on possible physical mechanisms for this pathway based only on our kinetic data. We further remark that this pathway is not required to capture the essential features of our data (see Figure 2b).
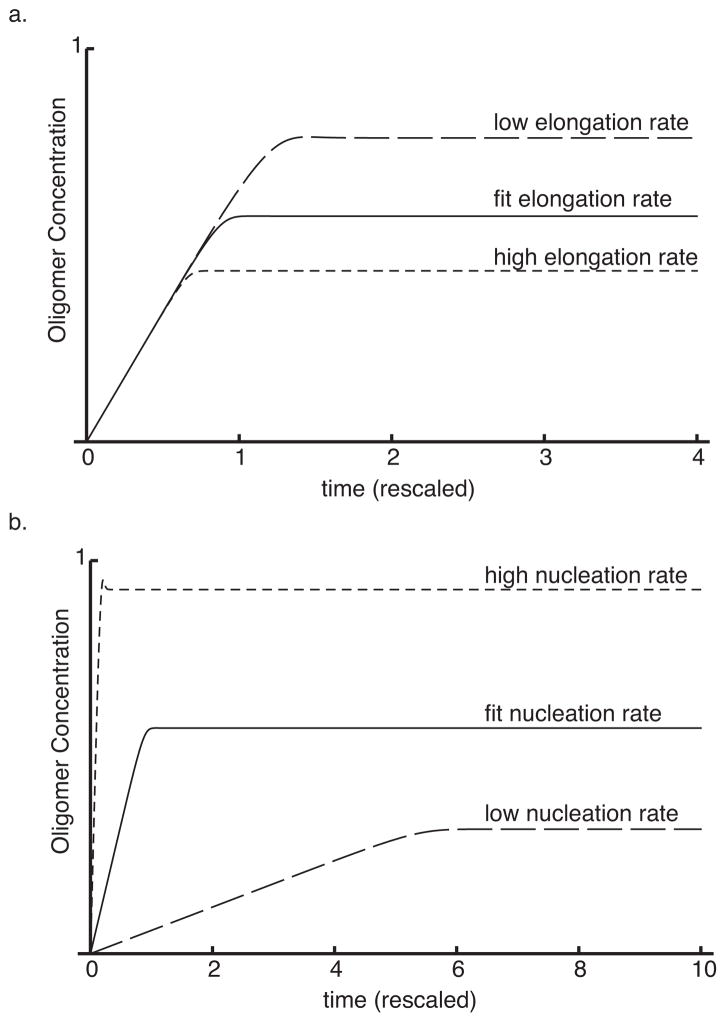
3.8. Interventions
With model and fitted parameters in hand, we can predict the outcomes of interventions. Recall that reducing the exposure to oligomers is one goal of drug targets. We first asked about the effect of altering fibril elongation rates, fk+1 on the various species. We ran the default model as control, and then repeated the simulation for higher and lower values of this parameter. Results, shown in Figure 4a indicate that an increased rate leads to a decrease in the total number of fibrils and in total oligomer levels. Thus, according to our model, accelerating fibril elongation leads to fewer fibrils, increases their mean length, and lowers oligomer level, implying lower cytotoxicity (if oligomers are the toxic species). By contrast, decreasing the fibril elongation rate leads to increased oligomer concentration and more short fibrils. We next investigated treatments that affect rates of formation of nuclei, fk. We similarly compared the default model to simulations in which these parameters were increased and decreased. Results are shown in Fig 4b. We found that accelerating nucleation increases the total number of fibrils (which then have shorter lengths) and simultaneously increases oligomer levels. Conversely, retarding the nucleation rates decreases the numbers of fibers (increases their length) and decreases the level of oligomers.
Figure 4.
Effects of interventions. a. Increasing the fibril elongation rate leads to fewer and longer fibrils and less oligomers. b. Increasing the nucleation rate leads to many short fibrils and also increases oligomer levels. In both panels: low indicates 0.3 times fit value; high is 3 times fit value.
4. Conclusions and outlook
In this study we used in vitro polymerization data, mass action kinetic models and scaling arguments to analyze the pathway of hIAPP nucleation and fibrilization. The final pathway we propose, shown in Figure 1 is a nucleation-dependent polymerization with a secondary branch of nucleation by fibrils. This agrees with conclusions of Ruschak et al (Ruschak & Miranker 2007).
We were able to estimate the nucleus size (20 monomers, in general agreement with previous estimates (Janson et al. 1999, Anguiano et al. 2002, Green et al. 2004)). We find that after a nucleus is formed, aggregate growth occurs by monomer addition. Our analysis shows that aggregation in this assay is essentially a one-way process with negligible impact of monomer unbinding or nucleus disintegration. We checked whether other models of amyloid aggregation could fit our data. In particular, we looked at the three-stage kinetic model of amyloid fibrillization due to Lee et al (Lee et al. 2007), and the NDP model with an off-pathway branch due to Powers and Powers (Powers & Powers 2008), along with generic variations thereof. Detailed analysis is given in the Supplementary Material.
The model of Lee et al. (Lee et al. 2007) assumes that nuclei form as individual monomers and join a growing nucleus (γ = 1). That model is therefore incompatible with our experimental data. The model is nonetheless interesting, as it proposes that fibrils can elongate via the addition of any oligomer. We found that after systematic scaling and application of our experimental observations, the model of Lee et al. reduces to our generic NDP model.
Powers and Powers (Powers & Powers 2008) proposed a model for nucleated polymerization with a competing off-pathway aggregation that sequesters monomers away from the main fibril pathway. However, if aggregates other than on-pathway oligomers exist, the time scale of their formation is likely faster than fibril formation time (due to the “bottleneck” of nucleus formation). This could mean that aggregate populations are in quasi-steady-state with monomers (implying that for our system, the data will not collapse to a single universal curve across initial monomer concentrations). An alternative explanation is that reverse reaction rates in the off-pathway kinetics are trivially small. At the same time, scaling necessitates that aggregate sizes be identical to oligomer sizes (measured in monomer subunits). Altogether, this means that inclusion of off-pathway kinetics in the model will only alter effective rates at the data fitting stage, and will not give insights into the structure of the aggregation pathways. For this reason, we did not find a compelling reason to assume off-pathway kinetics in our preferred reaction scheme for hIAPP.
In summary, using our full model we were able to quantify populations of potentially cytotoxic oligomer species. We used the model to explore how manipulating rate constants artificially (e.g. by chemical agents or drugs) could help to decrease the exposure to a given species (Feng et al. 2009). This has potential implications for therapeutic measures. The model allows for further exploration of interventions, and may be useful for addressing treatments that alleviate symptoms of type 2 diabetes, and preserve β-cell health.
Prevention of IAPP aggregation and toxicity has therapeutic potential in preventing the decline of beta cell function in type 2 diabetes. However, given increasing evidence that smaller oligomeric aggregates of IAPP may be the most toxic form of the aggregated peptide, it is critical that any inhibitor of islet amyloid formation acts at a point in the aggregation pathway that will prevent formation of toxic species. Models such as the present one that predict IAPP aggregation kinetics, assess the potential for off-pathway formation of toxic species, and predict the size of oligomeric species, may have considerable value for in silico testing of drug candidates. To this end, our model predicts that, if indeed the predicted ~20mer oligomer is the primary toxic species, any compound that prevents monomer-monomer interaction and aggregation would be predicted to prevent IAPP toxicity, whereas compounds that inhibit IAPP monomer addition to existing oligomer may increase toxicity. The lack of any off-pathway revealed by our model may also be helpful in drug design.
Preliminary results from cell viability assays suggest an increase in cell toxicity as a function of initial monomer concentration, as well as time exposed to the fibril formation process. We were unable to resolve the toxic component of the system, but it appears that toxic effects are noticeable at early stages, and continue to be present even after completion of fibrillization. This observation, coupled with the observation that mature fibrils did not induce cytotoxicity in the absence of oligomers, supports the idea that the toxic component in hIAPP fibrillization is either the oligomers/aggregate populations or a result of maturing (but not mature) fibrils.
Supplementary Material
Acknowledgments
This work was supported by the Mathematics of Information Technology and Complex Systems National Centre of Excellence and an Accelerate BC internship (to JB). LEK is also supported by a subcontract from NIH grant R01 GM086882. BV is a Senior Scholar of the Michael Smith Foundation for Health Research. LEK was a Distinguished Scholar in Residence of the Peter Wall Institute for Advanced Studies. We acknowledge Raibatak Das and Andisheh Abedini for helpful discussions.
References
- Anguiano M, Nowak RJ, Lansbury PT., Jr Biochemistry. 2002;41(38):11338–43. doi: 10.1021/bi020314u. [DOI] [PubMed] [Google Scholar]
- Bonfils C, Bec N, Lacroix B, Harricane MC, Larroque C. J Biol Chem. 2007;282(8):5570–5581. doi: 10.1074/jbc.M605641200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charge SB, de Koning EJ, Clark A. Biochemistry. 1995;34(44):14588–14593. doi: 10.1021/bi00044a038. [DOI] [PubMed] [Google Scholar]
- Donath MY, Ehses JA, Maedler K, Schumann DM, Ellingsgaard H, Eppler E, Reinecke M. Diabetes. 2005;54(Suppl 2):S108–13. doi: 10.2337/diabetes.54.suppl_2.s108. [DOI] [PubMed] [Google Scholar]
- Feng Y, Yang SG, Du XT, Zhang X, Sun XX, Zhao M, Sun GY, Liu RT. Biochem Biophys Res Commun. 2009;390:1250–1254. doi: 10.1016/j.bbrc.2009.10.130. [DOI] [PubMed] [Google Scholar]
- Flyvbjerg H, Jobs E, Leibler S. Proc Natl Acad Sci U S A. 1996;93(12):5975–5979. doi: 10.1073/pnas.93.12.5975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green JD, Goldsbury C, Kistler J, Cooper GJS, Aebi U. J Biol Chem. 2004;279(13):12206–12. doi: 10.1074/jbc.M312452200. [DOI] [PubMed] [Google Scholar]
- Hall D, Edskes H. J Mol Biol. 2004;336(3):775–786. doi: 10.1016/j.jmb.2003.12.004. [DOI] [PubMed] [Google Scholar]
- Hartter E, Svoboda T, Ludvik B, Schuller M, Lell B, Kuenburg E, Brunnbauer M, Woloszczuk W, Prager R. Diabetologia. 1991;34(1):52–54. doi: 10.1007/BF00404025. [DOI] [PubMed] [Google Scholar]
- Hull RL, Westermark GT, Westermark P, Kahn SE. J Clin Endocrinol Metab. 2004;89(8):3629–3643. doi: 10.1210/jc.2004-0405. [DOI] [PubMed] [Google Scholar]
- Ionescu-Zanetti C, Khurana R, Gillespie JR, Petrick JS, Trabachino LC, Minert LJ, Carter SA, Fink AL. Proc Natl Acad Sci U S A. 1999;96(23):13175–13179. doi: 10.1073/pnas.96.23.13175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janson J, Ashley RH, Harrison D, McIntyre S, Butler PC. Diabetes. 1999;48(3):491–8. doi: 10.2337/diabetes.48.3.491. [DOI] [PubMed] [Google Scholar]
- Kautzky-Willer A, Thomaseth K, Ludvik B, Nowotny P, Rabensteiner D, Waldhausl W, Pacini G, Prager R. Diabetes. 1997;46(4):607–614. doi: 10.2337/diab.46.4.607. [DOI] [PubMed] [Google Scholar]
- Kautzky-Willer A, Thomaseth K, Pacini G, Clodi M, Ludvik B, Streli C, Waldhausl W, Prager R. Diabetologia. 1994;37(2):188–194. doi: 10.1007/s001250050092. [DOI] [PubMed] [Google Scholar]
- Kayed R, Head E, Thompson JL, McIntire TM, Milton SC, Cotman CW, Glabe CG. Science. 2003;300(5618):486–489. doi: 10.1126/science.1079469. [DOI] [PubMed] [Google Scholar]
- Knowles TPJ, Waudby CA, Devlin GL, Cohen SIA, Aguzzi A, Vendruscolo M, Terentjev EM, Welland ME, Dobson CM. Science. 2009;326(5959):1533–7. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- Lee CC, Nayak A, Sethuraman A, Belfort G, McRae GJ. Biophys J. 2007;92(10):3448–3458. doi: 10.1529/biophysj.106.098608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeVine H. Methods Enzymol. 1999;309:274–284. doi: 10.1016/s0076-6879(99)09020-5. [DOI] [PubMed] [Google Scholar]
- Marzban L, Rhodes CJ, Steiner DF, Haataja L, Halban PA, Verchere CB. Diabetes. 2006;55(8):2192–2201. doi: 10.2337/db05-1566. [DOI] [PubMed] [Google Scholar]
- Padrick SB, Miranker AD. Biochemistry. 2002;41(14):4694–4703. doi: 10.1021/bi0160462. [DOI] [PubMed] [Google Scholar]
- Pantaloni D, Hill TL, Carlier MF, Korn ED. Proc Natl Acad Sci U S A. 1985;82(21):7207–7211. doi: 10.1073/pnas.82.21.7207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park K, Verchere CB. J Biol Chem. 2001;276(20):16611–6. doi: 10.1074/jbc.M008423200. [DOI] [PubMed] [Google Scholar]
- Porat Y, Kolusheva S, Jelinek R, Gazit E. Biochemistry. 2003;42(37):10971–10977. doi: 10.1021/bi034889i. [DOI] [PubMed] [Google Scholar]
- Powers ET, Powers DL. Biophys J. 2008;94(2):379–391. doi: 10.1529/biophysj.107.117168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruschak AM, Miranker AD. Proc Natl Acad Sci U S A. 2007;104(30):12341–12346. doi: 10.1073/pnas.0703306104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka M, Collins SR, Toyama BH, Weissman JS. Nature. 2006;442(7102):585–589. doi: 10.1038/nature04922. [DOI] [PubMed] [Google Scholar]
- Zraika S, Hull RL, Verchere CB, Clark A, Potter KJ, Fraser PE, Raleigh DP, Kahn SE. Diabetologia. 2010;53(6):1046–56. doi: 10.1007/s00125-010-1671-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.