Characterization of imaging performance in differential phase contrast CT compared with the conventional CT: Spectrum of noise equivalent quanta NEQ(k)

Abstract

Purpose: Differential phase contrast CT (DPC-CT) is emerging as a new technology to improve the contrast sensitivity of conventional attenuation-based CT. The noise equivalent quanta as a function over spatial frequency, i.e., the spectrum of noise equivalent quanta NEQ(k), is a decisive indicator of the signal and noise transfer properties of an imaging system. In this work, we derive the functional form of NEQ(k) in DPC-CT. Via system modeling, analysis, and computer simulation, we evaluate and verify the derived NEQ(k) and compare it with that of the conventional attenuation-based CT.

Methods: The DPC-CT is implemented with x-ray tube and gratings. The x-ray propagation and data acquisition are modeled and simulated through Fresnel and Fourier analysis. A monochromatic x-ray source (30 keV) is assumed to exclude any system imperfection and interference caused by scatter and beam hardening, while a 360° full scan is carried out in data acquisition to avoid any weighting scheme that may disrupt noise randomness. Adequate upsampling is implemented to simulate the x-ray beam's propagation through the gratings G₁ and G₂ with periods 8 and 4 μm, respectively, while the intergrating distance is 193.6 mm (1/16 of the Talbot distance). The dimensions of the detector cell for data acquisition are 32 × 32, 64 × 64, 96 × 96, and 128 × 128 μm², respectively, corresponding to a 40.96 × 40.96 mm² field of view in data acquisition. An air phantom is employed to obtain the noise power spectrum NPS(k), spectrum of noise equivalent quanta NEQ(k), and detective quantum efficiency DQE(k). A cylindrical water phantom at 5.1 mm diameter and complex refraction coefficient n = 1 − δ + iβ = 1 −2.5604 × 10⁻⁷ + i1.2353 × 10⁻¹⁰ is placed in air to measure the edge transfer function, line spread function and then modulation transfer function MTF(k), of both DPC-CT and the conventional attenuation-based CT. The x-ray flux is set at 5 × 10⁶ photon/cm² per projection and observes the Poisson distribution, which is consistent with that of a micro-CT for preclinical applications. Approximately 360 regions, each at 128 × 128 matrix, are used to calculate the NPS(k) via 2D Fourier transform, in which adequate zero padding is carried out to avoid aliasing in noise.

Results: The preliminary data show that the DPC-CT possesses a signal transfer property [MTF(k)] comparable to that of the conventional attenuation-based CT. Meanwhile, though there exists a radical difference in their noise power spectrum NPS(k) (trait 1/|k| in DPC-CT but |k| in the conventional attenuation-based CT) the NEQ(k) and DQE(k) of DPC-CT and the conventional attenuation-based CT are in principle identical.

Conclusions: Under the framework of ideal observer study, the joint signal and noise transfer property NEQ(k) and detective quantum efficiency DQE(k) of DPC-CT are essentially the same as those of the conventional attenuation-based CT. The findings reported in this paper may provide insightful guidelines on the research, development, and performance optimization of DPC-CT for extensive preclinical and clinical applications in the future.

INTRODUCTION

Motivated to reach higher subject contrast over soft tissues in x-ray CT imaging, the scientific community has devoted increasing effort to the investigation of x-ray tube and grating-based differential phase contrast CT (DPC-CT) for early detection of cancer and other diseases.^{1, 2, 3, 4, 5} The initial exploration was relatively qualitative and demonstrated significant improvement in the contrast of soft tissues in human specimens or very small animals.^{1, 2, 4, 5} Recently, the investigation has become quantitative, and preliminary results on the noise property of DPC-CT,^{6, 7, 8, 9, 10, 11, 12, 13} such as pixel-based gross variance,^{6, 7, 8, 9} contrast-to-noise ratio,^{8, 10} and spatial autocovariance function,⁷ have been reported. It is a fundamental understanding that the subject contrast of soft tissues in an imaging system is intrinsically determined by their interaction with the x-ray beam,^{14, 15, 16} while the system's performance is determined by its signal and noise transfer properties.^{11, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35} In principle, the signal transfer property of an imaging system is dependent on its modulation transfer function MTF(k),^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30} while the noise transfer property can only be thoroughly characterized by its noise power spectrum NPS(k), i.e., the variation of noise intensity as a function over spatial frequency k.^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35} It has been reported that there exists a radical difference in the noise power spectrum NPS(k) between DPC-CT and the conventional attenuation-based CT (referred to as conventional CT hereafter): the NPS(k) of the former manifests itself with the trait 1/|k|, and the latter with |k|.^{11, 12}

In general, an imaging system can be cascaded into two stages—image formation (or record or detection as termed in the literature) and image presentation or display.^{20, 27, 28} Such a separation is straightforward in digital imaging modalities, e.g., the DPC-CT and conventional CT to be investigated in this work, but quite intricate in the early days when only analog imaging modalities, e.g., x-ray screen-film radiography, were available. Quite a few factors may degrade the performance of an imaging system, which include but are not limited to (i) the ubiquitous random fluctuation—noise—in data acquisition, (ii) the anatomic and physiologic variation in patient population, and (iii) the intra- and interobserver variability when a diagnosis is made based on the images presented.^{27, 28} These factors work in concert with one another and thus make the performance assessment of an imaging system extremely challenging. With recourse to Bayesian statistical decision and information theories, a framework for the performance assessment of an imaging system has been established through the tremendous and successful effort of leading scientists in this field,^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28} in which the detection of pathological lesions with a medical imaging system is mathematically treated as a decision making process. An observer makes the decision between two hypotheses—H₁: lesion present (abnormal or positive); H₂: lesion absent (normal or negative)—according to whether the value of a decision function exceeds a threshold or not. If the decision function is the Bayesian likelihood, the decision maker becomes an ideal observer, who minimizes the risks while making the decision, i.e., maximizing the area under the receiver operating characteristics (ROC) curve.^{20, 27, 28}

Suppose the imaging system under study is linear and shift-invariant, and the noise corrupting the system is Gaussian and stationary. Given a signal specified in the spatial frequency domain as ΔS(k), i.e., the signal and background known exactly (SKE/BKE),^{27, 28, 30} the squared signal-to-noise ratio or the detectability index defined by

$${\mathrm{SNR}}_{\mathrm{ideal}}^2=\int {\left|\Delta \mathrm{S}(k\right)|}^2\mathrm{NEQ}(k)dk$$ (1)

is an ideal observer figure of merit (FOM) to assess an imaging system's performance,^{27, 30} wherein the spectrum of noise equivalent quanta NEQ(k) may be in different functional forms over imaging modalities.^{20, 21, 26, 28} An ideal observer is assumed to have prior knowledge of the task and the statistical properties of the noise. Equation 1 is an integration of factorization and implies that, given a specific task |ΔS(k)|², the ideal observer performance of an imaging system can be optimized by maximizing its NEQ(k).^{27, 30} Usually, the task is to differentiate a lesion from the surrounding tissues or organs or simply an object from its background. Therefore, the signal ΔS(k) in Eq. 1 should be perceived as a difference or contrast between the object to be imaged and background.^{20, 21, 27, 30} In practice, Eq. 1 can be extended to deal with more complicated situations, wherein the noise observes the Poisson distribution and is not stationary, the imaging system is nonlinear and shift-variant, or the signal is superimposed on a random background.^{20, 27, 28, 30}

Recognizing the important role played by NEQ(k) as a FOM to assess the ideal observer performance of an imaging system,^{20, 27, 28, 30, 32, 33, 34, 35} we investigate the NEQ(k) and resultant spectrum of detective quantum efficiency DQE(k) of DPC-CT in this work. In a way analogous to the investigation of conventional CT's NEQ(k) and DQE(k), we treat the DPC-CT as a linear and shift-invariant system. Owing to the fact that Gaussian noise approaches Poisson noise if the detected number of photons is large, we assume the noise in the DPC-CT is Gaussian.²⁹ To avoid any interference caused by scatter and beam hardening, a monochromatic x-ray source is assumed in both the DPC-CT and conventional CT in this investigation, though they are actually configured with a polychromatic one in practice. Under the framework of an ideal observer, we derive, analyze, evaluate, and verify the NEQ(k) and DQE(k) of DPC-CT through computer simulation studies and compare the result with that of conventional CT. For clarity in expression henceforth, ΔS(k), SNR²_ideal, NPS(k), MTF(k), NEQ(k), and DQE(k) denote the quantities corresponding to an imaging system in general, which can be either DPC-CT or conventional CT. Specifically, the quantities corresponding to the DPC-CT are denoted with subscript “p,” while those corresponding to the conventional CT are denoted with subscript “a.”

MATERIALS AND METHODS

To characterize the spectrum of noise equivalent quanta NEQ_p(k) and spectrum of detective quantum efficiency DQE_p(k) of DPC-CT, we start out by deriving its functional form and comparing it with that of the conventional CT. Subsequently, we introduce the methods and procedures to evaluate and verify the derived NEQ_p(k) and DQE_p(k) and compare them with their counterparts in conventional CT. We constrain ourselves in this work to conducting computer simulation study only; thereby the systematic and random errors, such as the fabrication accuracy and alignment of gratings, and the effects due to beam hardening and scattering that may exist in a physical DPC-CT and compromise or bias the accuracy and precision of evaluation and verification can be excluded.

Imaging mechanism of DPC-CT implemented with x-ray tube and gratings

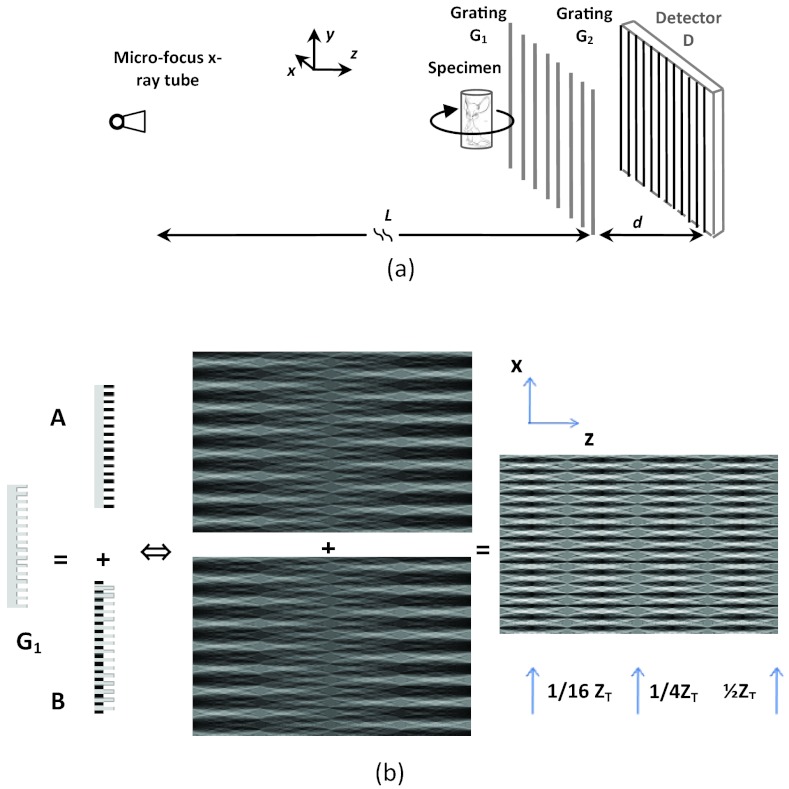
The architecture of DPC-CT implemented with a microfocus x-ray tube and gratings² is shown in Fig. 1a. G₁ is a phase grating and G₂ an absorption grating, which can be fabricated with photolithography, deep chemical etching, and electroplating.³⁶G₁ and G₂ work together as a shearing interferometer^{37, 38, 39} to detect the wavefront alteration caused by the object in x-ray beam. The x-ray tube irradiates the specimen, while the specimen stage rotates by a range satisfying the data sufficiency condition, and the CCD x-ray detector is employed for data acquisition. The key component of the imaging chain is grating G₁, a diffraction interferometer based on the Talbot effect.^{37, 38, 39} Figure 1b shows how G₁ works by virtually decomposing it into gratings A and B. The extra optical path corresponding to grating B relative to that through grating A is half wavelength, which is equivalent to a 180° phase shift. The beams corresponding to gratings A and B recombine after they pass through the gratings, and interference fringe appears if the object to be imaged is in the x-ray beam.

Figure 1.

The diagrams showing (a) the schematic of an x-ray tube and grating-based DPC-CT and (b) the schematic of virtual grating decomposition, in which the upper and lower Talbot patterns are associated with gratings A and B, respectively.

The imaging mechanism of x-ray tube and grating-based DPC-CT is elaborated in Refs. ^{11, 12, 13} and ^{37, 38, 39} and only a concise review is given below. According to Fresnel analysis,^{40, 41} the irradiance I(x, z) at the CCD detector is

$$\begin{array}{ccc}& & {\mathrm{I}}_{\mathrm{A}+\mathrm{B}}(x,z)\sim \varphi \left(x+\Delta \frac{x}{2},y\right)-\varphi \left(x-\Delta \frac{x}{2},y\right)\hfill \\ & & \cong \frac{\partial \varphi (x,y)}{\partial x}\Delta x,\hfill \end{array}$$ (2)

where Δx is a displacement in the x-direction, and ϕ(x, y) is the phase variation over Δx, which is the projection of refractive coeffiecient $\widehat{\delta }(x,y,z)$ along the x-ray path

$$\varphi (x,y)=\frac{2\pi }{\lambda }{\int }_Z\widehat{\delta }(x,y,z)dz.$$ (3)

Note that the refractive coefficient has been denoted by δ(x, y, z) in the literature. However, to avoid its confusion with the Dirac function and Kronecker delta that are used to derive the functional form of NEQ_p(k) later in this paper, $\widehat{\delta }(x,y,z)$ is adopted to represent the refractive coeficient.

Equation 2 shows that the irradiance depends on the derivative of the phase variation along the x axis. After the x-ray passes grating G₂, the irradiance at detector D is⁴¹

$$\begin{array}{c}\hfill {\mathrm{I}}_{u,v}\left(x\right)=a_0(u,v)+\sum _{m=1}^{\infty }{a}_m(u,v)\cos \left(\frac{2\pi mx}{g_2}+{\phi }_m(u,v)\right),\end{array}$$ (4)

where (u, v) is the coordinate of a detector cell and g₂ the period of grating G₂. By linearly shifting grating G₂ along the x axis and carrying out a Fourier analysis, one can determine a₀(u, v), a₁(u, v), and φ₁(u, v) from Eq. 4.⁴¹ In fact, one has

$$\frac{\partial \varphi (x,y)}{\partial x}={\phi }_1(u,v)\frac{g_2}{\lambda z_T},$$ (5)

where z_T is the fractional Talbot distance.^{2, 37, 38, 39, 40, 41} Substituting the ϕ(x, y) defined in Eq. 3 into Eq. 5, one gets

$$\begin{array}{ccc}\hfill {\phi }_1(u,v)& =& \frac{\lambda z_T}{g_2}\frac{\partial \varphi (x,y)}{\partial x}=\frac{2\pi z_T}{g_2}\frac{\partial }{\partial x}{\int }_Z\widehat{\delta }(x,y,z)dz\hfill \\ & =& \frac{2\pi z_T}{g_2}{\int }_Z\frac{\partial }{\partial x}\widehat{\delta }(x,y,z)dz.\hfill \end{array}$$ (6)

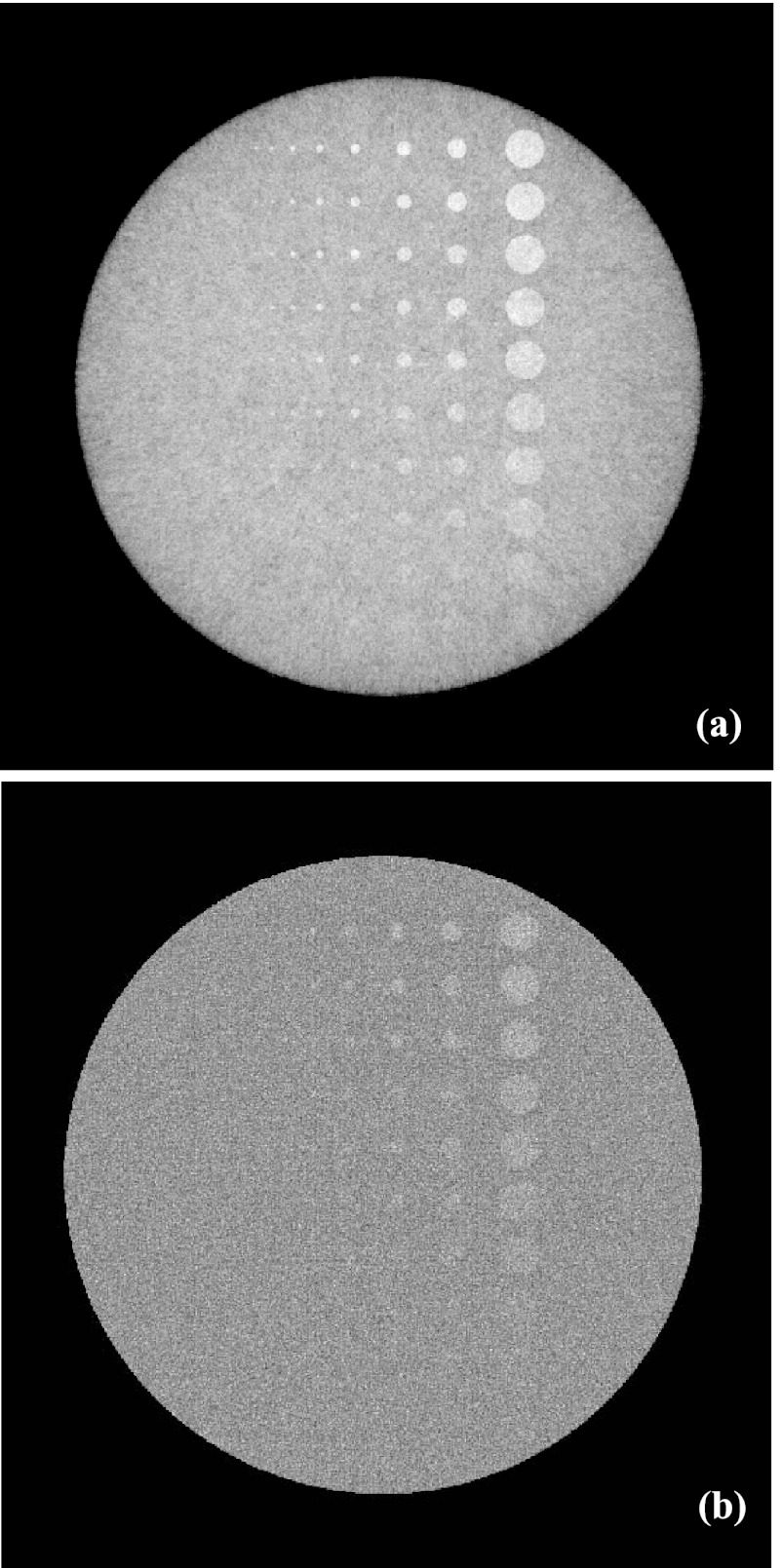
This means that the phase retrieved through a Fourier analysis of Eq. 4 is the projection of the refractive coefficient's derivative, and this is the underlying reason that the phase CT implemented with x-ray tube and gratings is called differential phase contrast CT. Once data φ₁(u, v) are acquired, tomographic images of refraction are reconstructed using the filtered backprojection (FBP) algorithms.^{42, 43, 44, 45} Since the reconstruction is carried out directly from $\partial \widehat{\delta }(x,y,z)/\partial x$, the ramp kernel is replaced with the Hilbert kernel. It should be pointed out that the modeling of data acquisition in the x-ray tube and grating-based DPC-CT through the schematic of Fig. 1b and Eqs. 2, 3, 4, 5, 6 has been evaluated and verified in Ref. 11, which is in principle the same as the five steps detailed in Ref. 13. The well-known contrast-detail (C-D) phantom²⁹ (see Sec. 3) is used to evaluate and verify the correctness and accuracy of the data acquisition modeling and image reconstruction, and the result is presented in Fig. 2.

Figure 2.

Transverse images of the C-D phantom generated by the x-ray tube and grating-based DPC-CT CT (a) and the conventional CT (b) (x-ray exposure 10⁷ photon/cm² per projection, detector cell 48 × 48 μm²).

Spectrum of noise equivalent quanta in DPC-CT and conventional CT

In the early days of conventional CT, an observation of the morphologic difference in the noise of CT images against the white noise suggested that there existed an interpixel correlation. By analyzing the distribution of noise power over spatial frequency k, i.e., the noise power spectrum NPS_a(k), the interpixel correlation is confirmed, even though there is no intercell correlation in the noise of the detector used for data acquisition. Since then, the groundwork of using noise power spectrum NPS_a(k) and spectrum of noise equivalent quanta NEQ_a(k) to analyze the signal and noise behavior of a conventional CT system or CT imaging method has been laid out.^{17, 18, 19, 20, 21, 22, 23, 24, 25} In this section, we follow the mathematic treatment to derive the functional form of NPS_p(k) and NEQ_p(k) in the DPC-CT implemented with x-ray tube and gratings and compare it with that of the conventional CT.

Spectrum of noise equivalent quanta NEQ_a(k) of the conventional CT

A number of strategies, e.g., the method proposed by Barret,¹⁸ the central slice theorem,¹⁹ information theory,²⁰ and statistical detection theory,²¹ have been exercised to obtain the noise power spectrum NPS_a(k) of the conventional CT, and all lead to the same functional form

$$\begin{array}{ccc}\hfill {\mathrm{NPS}}_a\left(k\right)& =& \frac{a\pi }{N_{\theta }\overline{N}}\left|k\right|{\left|{\mathrm{MTF}}_a\left(k\right)\right|}^2\hfill \\ & =& \frac{\pi }{b{N}_{\theta }{I}_0}\left|k\right|{\left|{\mathrm{MTF}}_a\left(k\right)\right|}^2,\hfill \end{array}$$ (7)

where a is the detector pitch, b is the detector height, and k is the radial frequency defined as

$$k=\sqrt{k_x^2+k_y^2}.$$ (8)

N_θ is the number of angular locations at which the projection data are acquired, I₀ is the measured photon flux, and $\overline{N}$ is the mean number of x-ray photons detected at each detector cell. Since no object should be placed in the x-ray beam in the investigation of noise property, $\overline{N}$ is assumed equal across all the detector cells. MTF_a(k) is the overall algorithmic contribution, including the windowing and/or boosting in the frequency domain for an optimization between noise and spatial resolution, to the modulation transfer function.

The multiplication of N_θ and I₀ has been defined as the noise equivalent quanta.^{20, 21, 23} Accordingly, Eq. 7 can be expressed as

$${\mathrm{NPS}}_a\left(k\right)=\frac{\pi }{b{\mathrm{NEQ}}_a}\left|k\right|{\left|{\mathrm{MTF}}_a\left(k\right)\right|}^2.$$ (9)

Consequently, the spectrum of noise equivalent quanta NEQ_a(k) and detective quantum efficiency DQE_a(k) of the conventional CT are^{18, 19, 20, 21}

$${\mathrm{NEQ}}_a\left(k\right)=\frac{\pi }{b{\mathrm{NPS}}_a\left(k\right)}\left|k\right|{\left|{\mathrm{MTF}}_a\left(k\right)\right|}^2,$$ (10)

$${\mathrm{DQE}}_a\left(k\right)=\frac{{\mathrm{NEQ}}_a\left(k\right)}{N_{\theta }{I}_0}.$$ (11)

Spectrum of noise equivalent quanta NEQ_p(k) of the DPC-CT

As indicated above, the phase information φ₁(u, v) can be retrieved by stepping grating G₂ linearly along the x axis (see Fig. 1). At each step

$$x_g=\frac{k}{M}{g}_2,k=1,2,...,M,$$ (12)

the measured x-ray irradiance at (u, v) in a detector represented in Eq. 4 can be rewritten as

$$\begin{array}{c}\hfill N^{\left(k\right)}\left(u,v\right)=\sum _{l=-\frac{M}{2}}^{\frac{M}{2}-1}{N}_l\frac{1+{\delta }_{\mathrm{l}0}}{2}\exp \left[i{\phi }_l\left(u,v\right)+2\pi i\frac{lk}{M}\right],\end{array}$$ (13)

where N_l is non-negative and real and δ_l0 is the Kronecker's delta δ_lm by setting the 2nd subscript m equal to zero, i.e.,

$${\delta }_{l0}=\left\{\begin{array}{cc}\hfill 1& \hfill l=0\\ \hfill 0& \hfill l\ne 0\end{array}\right..$$ (14)

Note that φ_l(u, v) (l = 1) is the phase we want to retrieve for reconstruction of the 3D distribution of refractive coefficient [see Eq. 6].

The discrete Fourier transform of both sides of Eq. 13 gives

$$\begin{array}{c}\hfill \frac{1}{2}M{N}_1\exp \left[i{\phi }_1\left(u,v\right)\right]=\sum _{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left(-2\pi i\frac{k}{M}\right).\end{array}$$ (15)

Since N₁ is non-negative and real, Eq. 15 further gives

$$\exp \left[i{\phi }_1\left(u,v\right)\right]=\frac{{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left(-2\pi i\frac{k}{M}\right)}{\left|{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left(-2\pi i\frac{k}{M}\right)\right|},$$ (16)

or equivalently

$$\exp \left[i{\phi }_1\left(u,v\right)\right]=\frac{{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left(-2\pi i\frac{k}{M}\right)}{{\left\{\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left(2\pi i\frac{k}{M}\right)\right]\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left(-2\pi i\frac{k}{M}\right)\right]\right\}}^{1/2}}.$$ (17)

Differentiating both sides of Eq. 17, one gets

$$\begin{array}{ccc}& & i\exp \left[i{\phi }_1\left(u,v\right)\right]\Delta {\phi }_1\left(u,v\right)\hfill \\ & & =\frac{{\sum }_{k=1}^M\Delta N^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)}{{\left\{\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)\right]\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)\right]\right\}}^{1/2}}\hfill \\ & & {\displaystyle -\frac{1}{2}\frac{{\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)\right]}^2\left[{\sum }_{k=1}^M\Delta N^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)\right]}{{\left\{\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)\right]\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)\right]\right\}}^{3/2}}}\hfill \\ & & {\displaystyle -\frac{1}{2}\frac{\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)\right]\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)\right]\left[{\sum }_{k=1}^M\Delta N^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)\right]}{{\left\{\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)\right]\left[{\sum }_{k=1}^M{N}^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)\right]\right\}}^{3/2}}.}\hfill \end{array}$$ (18)

Substituting Eq. 15 into Eq. 18 yields

$$\begin{array}{ccc}& & i\exp \left[i{\phi }_1\left(u,v\right)\right]\Delta {\phi }_1\left(u,v\right)\hfill \\ & & {\displaystyle =\frac{{\sum }_{k=1}^M\Delta N^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)}{{\displaystyle \frac{1}{2}M{N}_1}}-\frac{1}{2}\frac{\exp \left[2i{\phi }_1\left(u,v\right)\right]2^{-2}{M}^2{N}_1^2\left[{\sum }_{k=1}^M\Delta N^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)\right]}{2^{-3}{M}^3{N}_1^3}}\hfill \\ & & {\displaystyle -\frac{1}{2}\frac{2^{-2}{M}^2{N}_1^2\left[{\sum }_{k=1}^M\Delta N^{\left(k\right)}\left(u,v\right)\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)\right]}{2^{-3}{M}^3{N}_1^3},}\hfill \end{array}$$ (19)

which can be concisely rewritten as

$$\Delta {\phi }_1(u,v)=-i\sum _{k=1}^M\left\{{\displaystyle \frac{\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)}{M{N}_1\exp \left[i{\phi }_1(u,v)\right]}-\frac{\exp \left(2\pi i\frac{k}{M}\right)}{M{N}_1\exp \left[-i{\phi }_1(u,v)\right]}}\right\}\Delta N^{\left(k\right)}(u,v).$$ (20)

Consequently, one has

$$\begin{array}{ccc}\hfill ⟨\Delta {\phi }_1\left(u,v\right)\Delta {\phi }_1\left(u_1,v_1\right)⟩& =& -\sum _{k,k_1=1}^M\left\{{\displaystyle \frac{\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)}{M{N}_1\exp \left[i{\phi }_1\left(u,v\right)\right]}-\frac{\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)}{M{N}_1\exp \left[-i{\phi }_1\left(u,v\right)\right]}}\right\}\hfill \\ & & \times \left\{{\displaystyle \frac{\exp \left({\displaystyle -2\pi i\frac{k_1}{M}}\right)}{M{N}_1\exp \left[i{\phi }_1\left(u_1,v_1\right)\right]}-\frac{\exp \left({\displaystyle 2\pi i\frac{k_1}{M}}\right)}{M{N}_1\exp \left[-i{\phi }_1\left(u_1,v_1\right)\right]}}\right\}⟨\Delta N^{\left(k\right)}\left(u,v\right)\Delta N^{\left(k_1\right)}\left(u_1,v_1\right)⟩,\hfill \end{array}$$ (21)

where (u₁, v₁) represents a location that is different from (u, v) in the detector. Since the measured x-ray flux observes the Poisson distribution and is spatially uncorrelated, one has

$$⟨\Delta N^{\left(k\right)}\left(u,v\right)\Delta N^{\left(k_1\right)}\left(u_1,v_1\right)⟩=N^{\left(k\right)}\left(u,v\right){\delta }_{k{k}_1}\delta \left(\frac{u-u_1}{a}\right)\delta \left(\frac{v-v_1}{b}\right),$$ (22)

where subscripts k and k₁ correspond to different shifting steps of grating G₂. Inserting Eq. 22 into Eq. 21 and substituting N^(k)(u, v) with Eq. 13, one obtains

$$\begin{array}{ccc}& & ⟨\Delta {\phi }_1\left(u,v\right)\Delta {\phi }_1\left(u_1,v_1\right)⟩\hfill \\ & & =-\sum _{k=1}^M{\left\{{\displaystyle \frac{\exp \left({\displaystyle -2\pi i\frac{k}{M}}\right)}{M{N}_1\exp \left[i{\phi }_1\left(u,v\right)\right]}-\frac{\exp \left({\displaystyle 2\pi i\frac{k}{M}}\right)}{M{N}_1\exp \left[-i{\phi }_1\left(u,v\right)\right]}}\right\}}^2{N}^{\left(k\right)}\left(u,v\right)\delta \left({\displaystyle \frac{u-u_1}{a}}\right)\delta \left({\displaystyle \frac{v-v_1}{b}}\right)\hfill \\ & & {\displaystyle =\frac{2}{M^2{N}_1^2}\left\{{\displaystyle \sum _{k=1}^M{N}^{\left(k\right)}\left(u,v\right)-\frac{1}{2}\sum _{k=1}^M\left\{{\displaystyle \frac{\exp \left({\displaystyle -4\pi i\frac{k}{M}}\right)}{\exp \left[2i{\phi }_1\left(u,v\right)\right]}+\frac{\exp \left({\displaystyle 4\pi i\frac{k}{M}}\right)}{\exp \left[-2i{\phi }_1\left(u,v\right)\right]}}\right\}{N}^{\left(k\right)}\left(u,v\right)}\right\}\delta \left({\displaystyle \frac{u-u_1}{a}}\right)\delta \left({\displaystyle \frac{v-v_1}{b}}\right)}\hfill \\ & & {\displaystyle =\frac{2}{M^2{N}_1^2}\left\{{\displaystyle M{N}_0-\frac{M}{4}\left\{{\displaystyle \frac{N_2\exp \left[i{\phi }_2\left(u,v\right)\right]}{\exp \left[2i{\phi }_1\left(u,v\right)\right]}+\frac{N_{-2}\exp \left[-i{\phi }_2\left(u,v\right)\right]}{\exp \left[-2i{\phi }_1\left(u,v\right)\right]}}\right\}}\right\}\delta \left({\displaystyle \frac{u-u_1}{a}}\right)\delta \left({\displaystyle \frac{v-v_1}{b}}\right).}\hfill \end{array}$$ (23)

It is interesting to note that only N₋₂, N₋₁, N₀, N₁, and N₂ survive the last step in getting Eq. 23.

Subsequently, defining

$${\varepsilon }_1=\frac{{\overline{N}}_1}{{\overline{N}}_0},$$ (24)

$${\varepsilon }_2=\frac{{\overline{N}}_2}{4{\overline{N}}_0}\left[\frac{\exp \left(i{\overline{\phi }}_2\right)}{\exp \left(2i{\overline{\phi }}_1\right)}+\frac{\exp \left(-i{\overline{\phi }}_2\right)}{\exp \left(-2i{\overline{\phi }}_1\right)}\right],$$ (25)

Eq. 23 can be concisely rewritten as

$$\begin{array}{ccc}& & ⟨\Delta {\phi }_1\left(u,v\right)\Delta {\phi }_1\left(u_1,v_1\right)⟩\hfill \\ & & =\frac{2\left(1-{\varepsilon }_2\right)}{M{\overline{N}}_0{\varepsilon }_1^2}\delta \left(\frac{u-u_1}{a}\right)\delta \left(\frac{v-v_1}{b}\right).\hfill \end{array}$$ (26)

Note that the random variables N₀, N₁, and N₂ have been replaced with their corresponding mean values ${\overline{N}}_0$, ${\overline{N}}_1$ and ${\overline{N}}_2$, respectively, in a way analogous to that in Ref. 10. Consequently, one gets

$${\sigma }_{\phi }^2=\frac{2\left(1-{\varepsilon }_2\right)}{M{\overline{N}}_0{\varepsilon }_1^2}.$$ (27)

Meanwhile, according to Eq. 6, it is not hard for one to get

$$\begin{array}{ccc}\hfill {\displaystyle \frac{N_{\theta }}{{\sigma }_D^2}}& =& {\left({\displaystyle \frac{\lambda z_T}{g_2}}\right)}^2\frac{N_{\theta }}{{\sigma }_{\phi }^2}={\left(\frac{\lambda z_T}{g_2}\right)}^2\frac{{\varepsilon }_1^2}{2\left(1-{\varepsilon }_2\right)}{N}_{\theta }M{\overline{N}}_0\hfill \\ & =& {\left(\frac{\lambda z_T}{g_2}\right)}^2\frac{{\varepsilon }_1^2}{2\left(1-{\varepsilon }_2\right)}{N}_{\theta }M{I}_{0}ab{q}_0,\hfill \end{array}$$ (28)

where N_θ is the total number of projections in data acquisition, ${\sigma }_D^2$ is the noise at each detector cell, and q₀ = N₀/abI₀. In a way analogous to that of the conventional CT,^{20, 21, 23} we define the noise equivalent quanta as

$${\mathrm{NEQ}}_p=N_{\theta }M{I}_0,$$ (29)

and then Eq. 28 can be rewritten as

$$\frac{N_{\theta }}{{\sigma }_D^2}={\left(\frac{\lambda z_T}{g_2}\right)}^2\frac{ab{q}_0{\varepsilon }_1^2}{2\left(1-{\varepsilon }_2\right)}{\mathrm{NEQ}}_p.$$ (30)

On the other hand, according to Eq. A25 in the Appendix, one has

$$\frac{N_{\theta }}{{\sigma }_D^2}=\frac{a}{4\pi \left|k\right|{\mathrm{NPS}}_p\left(k\right)}{\mathrm{MTF}}_p^2\left(k\right).$$ (31)

By equating the right sides of Eqs. 30, 31, one attains

$$\begin{array}{c}\hfill {\mathrm{NEQ}}_p\left(k\right)={\left(\frac{g_2}{\lambda z_T}\right)}^2\frac{1-{\varepsilon }_2}{2\pi b{q}_0{\varepsilon }_1^2\left|k\right|{\mathrm{NPS}}_p\left(k\right)}{\mathrm{MTF}}_p^2\left(k\right),\end{array}$$ (32)

$${\mathrm{DQE}}_p\left(k\right)=\frac{{\mathrm{NEQ}}_p\left(k\right)}{N_{\theta }M{I}_0}.$$ (33)

Furthermore, as derived in the Appendix, the noise power spectrum NPS_p(k) is

$$\begin{array}{ccc}\hfill {\mathrm{NPS}}_p\left(k\right)& =& {\displaystyle {\left({\displaystyle \frac{g_2}{\lambda z_T}}\right)}^2\frac{a\left(1-{\varepsilon }_2\right)}{2\pi {\varepsilon }_1^2\left|k\right|N_{\theta }M{\overline{N}}_0}{\mathrm{MTF}}_p^2\left(k\right)}\hfill \\ \hfill \begin{array}{ccc}& & \end{array}& =& {\displaystyle {\left({\displaystyle \frac{g_2}{\lambda z_T}}\right)}^2\frac{1-{\varepsilon }_2}{2\pi b{q}_0{\varepsilon }_1^2\left|k\right|{\mathrm{NEQ}}_p}{\mathrm{MTF}}_p^2\left(k\right).}\hfill \end{array}$$ (34)

It should be pointed out that, if N₂ and N₋₂ are assumed to be zero, one gets ɛ₂ = 0 and Eq. 27 becomes exactly the same as that derived in Ref. 10, in which only N₀, N₁, and N₋₁ are considered. In general, however, N₂ and N₋₂ are small but not equal to zero. Hence, the derivation given here is a more general treatment in physics and mathematics. In addition, the factor |k| in the numerator of Eqs. 9, 10 moves to the denominators of Eqs. 32, 34. Readers are referred to the Appendix of this paper for the details related to the derivation of Eq. 34.

Measurement of the modulation transfer function MTF_p(k) of DPC-CT

It has been an established practice in conventional CT to measure the MTF_a(k) with a thin wire phantom.^{29, 46, 47} The wire is usually made of metal, such as tungsten, and placed in either air or water, as long as the attenuation of the thin wire does not exceed the dynamic range of the CT detector. Moreover, it has been well evaluated and verified that, as long as its diameter is substantially smaller than the detector cell dimension, the influence of the wire's thickness on the MTF_a(k) measurement can be ignored.⁴⁷ Unfortunately, however, this approach cannot be directly adopted for measurement of MTF_p(k) in the x-ray tube and grating-based DPC-CT, because the detection of the signal generated by such a thin wire may be substantially compromised.¹³ The major reasons underlying this difficulty are: (i) the signal generated in the DPC-CT is the projection of the refractive coefficient's derivative, which is an odd function in the case of a cylindrical object; (ii) the detection of such a projection can be severely compromised because the integration of an odd function over the finite dimension of a detector cell may be null. As indicated in Ref. 13, a better approach is to utilize a cylindrical object with a diameter substantially larger than the detector cell dimension. The cylinder is placed parallel to the y axis of the DPC-CT and thus it becomes a circle in a reconstructed transverse image. The distribution along a line starting at the center of the circle (namely, a semiradial line) is actually an edge spread function (ESF). In order to reduce random interference, a total of 360 semiradial lines at 1° intervals are engaged, and the intensity profiles reconstructed along these semiradial lines are averaged to get the ESF. The line spread function (LSF) is attained from the ESF via a numerical method, in which an adequate upsampling is carried out to assure that the distance between adjacent pixels along each semiradial line be 4.0 μm for numerical accuracy. Subsequently, the DPC-CT's MTF_p(k) is attained through a 1D discrete Fourier transform of the LSF. To assure a fair evaluation and comparison between the DPC-CT and conventional CT, this ESF → LSF → MTF(k) approach, rather than the conventional method using a thin wire, is also employed to obtain the MTF_a(k) of the conventional CT.

It should be noted that, in theory, the so-called phase wrapping phenomenon, i.e., the detected phase exceeds the unambiguous 2π phase range, can occur in the measurement of DPC-CT's MTF_p(k) with the method specified above. As indicated in the literature [Eq. 19 in Ref. 13], given a cylindrical object, phase wrapping occurs at

$$x_w=\mp \frac{R}{\sqrt{1+{\left(m{g}_2\alpha /\pi \right)}^2}},$$ (35)

where m is the index of fractional Talbot distance, R is the radius of the cylindrical object, and α is the phase shift induced by the object per unit length along the x axis. Since g₂ is very small in comparison to α, [e.g., α ≈ 46 rad/mm in soft tissues at 25 keV (Ref. ¹³)], x_w is almost equal to R, i.e., phase wrapping occurs at the locations immediately adjacent to the cylinder's edge. It is argued in Ref. 13 that, because of the finite size of a detector cell, the phase wrapping in the case of a cylindrical object made of soft tissue may be reduced to an extent that is not detectable in the DPC-CT. This may be perceived as a form of the partial volume effect as we experienced in the conventional CT, and interested readers are referred to Ref. 13 for more details.

Quantitative evaluation of the spectrum of noise equivalent quanta NEQ(k) and detective quantum efficiency DQE(k)

According to Eqs. 9, 34, the noise power spectrum NPS(k) and modulation transfer function MTF(k) are the two prerequisites to obtain the spectrum of noise equivalent quanta NEQ(k). The noise power spectrum can be calculated by taking the Fourier transform of the autocorrelation function that is obtained using a large number of noise images. An alternative approach that is more efficient in computation is to take the average of the squared Fourier transform of a large number of noise images or regions within the images containing noise only.²¹ The obtained 2D NPS(k) is circularly symmetric about its origin, as predicted in Eqs. 9, 34. The modulation transfer function MTF(k) is acquired using the method depicted in Subsection 2C and is also in circular symmetry. Thereby, the spectra of noise equivalent quanta NEQ(k) of the conventional CT and DPC-CT can be obtained using Eqs. 10, 32, which are also in circular symmetry, followed by the spectra of detective quantum efficiency DQE(k) using Eqs. 11, 33, respectively.

EVALUATION VIA SIMULATION STUDIES

The spectrum of noise equivalent quanta NEQ_a(k) of conventional CT specified in Eq. 10 has been evaluated and verified through studies based on computer simulation and physical CT systems.^{20, 21, 23, 33, 34, 35} It is essential for us to evaluate and verify the DPC-CT's spectrum of noise equivalent quanta NEQ_p(k) derived in this paper. We carry out a computer simulation study as the initial effort. For the following reasons, we constrain ourselves to conducting the computer simulation study in the parallel beam geometry: (i) the x-ray beam in differential phase contrast CT satisfies the paraxial condition and thus the beam is almost parallel, (ii) the image reconstruction algorithms in the parallel beam geometry outperform those in the fan beam geometry from the perspective of noise uniformity and thus almost all the clinical CT scanners based on the third generation geometry (fan beam or cone beam) adopt the parallel beam reconstruction algorithms via fan-to-parallel rebinning,^{45, 46} and (iii) most of the simulation studies to investigate the noise power spectrum of CT imaging thus far have been carried out in the parallel beam geometry to exclude the influence of rebinning and weighting schemes. The x-ray source is assumed monochromatic at 30 keV, which irradiates an object by 360° at 1° steps so that no weighting effect can be induced to degrade the noise uniformity. At 30 keV, a 20-fold upsampling is assumed to simulate the x-ray beam's propagation through the gratings G₁ and G₂ with periods 8 and 4 μm, respectively, while the distance between these two gratings is 193.6 mm, i.e., 1/16 of the Talbot distance. The field of view (FOV) in data acquisition and image reconstruction is 40.96 × 40.96 mm². The size of each detector cell is set at 32 × 32 μm², 64 × 64 μm², 96 × 96 μm², and 128 × 128 μm², resulting in the detector consisting of 1280, 640, 426 and 320 cells, respectively. Grating G₂ shifts ten times at step 0.4 μm along the x axis to retrieve the phase information corresponding to the refractive property of the object to be imaged.

Since the purpose of this work is to investigate the potential imaging performance of the DPC-CT and compare it with that of the conventional CT, no windowing or boosting techniques⁴² are adopted in image reconstruction for both the DPC-CT and conventional CT. The data φ₁(u, v) specified in Eq. 6 is used to reconstruct the DPC-CT images, in which the classical FBP (Ref. ⁴²) with the Hilbert transform^{43, 44} is used. The projection data corresponding to the conventional CT are acquired without the G₁ and G₂ gratings in place, and the ramp filter is used to reconstruct the images with the classical FBP algorithm.⁴² It has been claimed in the literature that the data corresponding to the a₀(u, v) in Eq. 4, which are acquired with the gratings G₁ and G₂ in place, are equal to the attenuation projection data acquired in the conventional CT. However, we agree with the discussion presented in Ref. 13 that such a claim only holds approximately, i.e., the a₀(u, v) in Eq. 4 is not exactly the same as the attenuation projection acquired in the conventional CT. Hence, we do not include the results corresponding to the a₀(u, v) in Eq. 4 in this paper.

Prior to analyzing the spectrum of noise equivalent quanta NEQ(k), the C-D phantom²⁴ with outer dimension 37.68 × 28.26 mm² is employed to evaluate and verify the modeling and simulation accuracy of x-ray propagation, data acquisition and image reconstruction of the DPC-CT. The bulk of the C-D phantom is made of water with its complex refractive coefficient equal to n = 1 − δ + iβ = 1 −2.5604 × 10⁻⁷ + i1.2353 × 10⁻¹⁰, which is consistent with that specified in Ref. 2. Other parameters used to simulate the C-D phantom are: rod size (left to right): 16, 32, 64, 96, 128, 192, 256, 384, 512, and 1024 μm; contrast of the rods against phantom body (bottom to top): 5%–50% at step 5%.

To have an accurate and precise measurement of the modulation transfer functions MTF_p(k) and MTF_a(k), a cylindrical water phantom at diameter 5.1 mm is placed in air and thus the edge is sharp and at high contrast. To avoid any interference caused by noise nonuniformity, other than a water phantom, an air phantom, i.e., nothing placed in the x-ray beam, is employed to study the noise power spectra NPS_p(k) and NPS_a(k), and the spectra of noise equivalent quanta NEQ_p(k) and NEQ_a(k). The x-ray flux observing the Poisson distribution is set at 5 × 10⁶ photon/cm² per projection in the simulation study, which is consistent with that of an x-ray micro-CT in preclinical applications. At the detector cell size corresponding to 32 × 32 μm², 64 × 64 μm², 96 × 96 μm², and 128 × 128 μm², ∼360 regions of interest (ROI) at 128 × 128 matrix dimension are used to obtain the noise power spectrum via 2D Fourier transform,¹⁶ in which the technique of zero padding is implemented to convert the data matrix from the dimension 128 × 128 to 256 × 256 so that the noise aliasing effect can be avoided.

By definition, the noise equivalent quanta is the total effective number of x-ray quanta detected per unit of detector area in the data acquisition.^{20, 21, 22, 23, 27, 28, 30, 32} Hence, the specification of the total number of x-ray quanta, i.e., x-ray exposure, is crucial in the investigation of noise equivalent quanta, particularly in the scenario wherein two imaging methods are to be compared. As indicated in Sec. 2A, at each angular position in the data acquisition of DPC-CT implemented with x-ray tube and gratings, grating G₂ needs to linearly shift M steps (M = 10 in this work). To take this fact into account, we set the x-ray exposure corresponding to the conventional CT as M times as that of the DPC-CT at each angular position. Thus, the x-ray exposure in the data acquisition of DPC-CT and the conventional CT are kept identical.

RESULTS

MTF_p(k) of DPC-CT compared with MTF_a(k) of the conventional CT

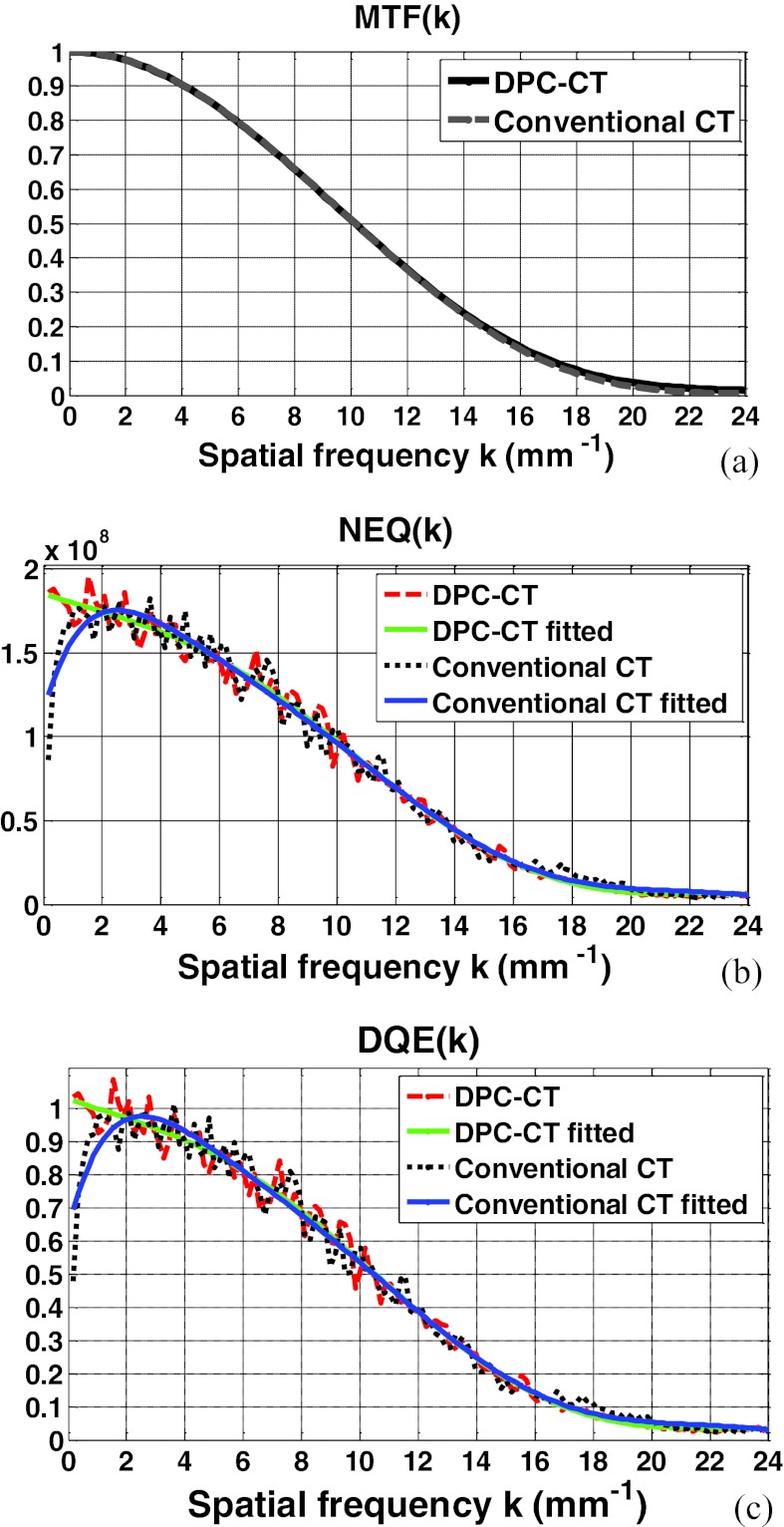
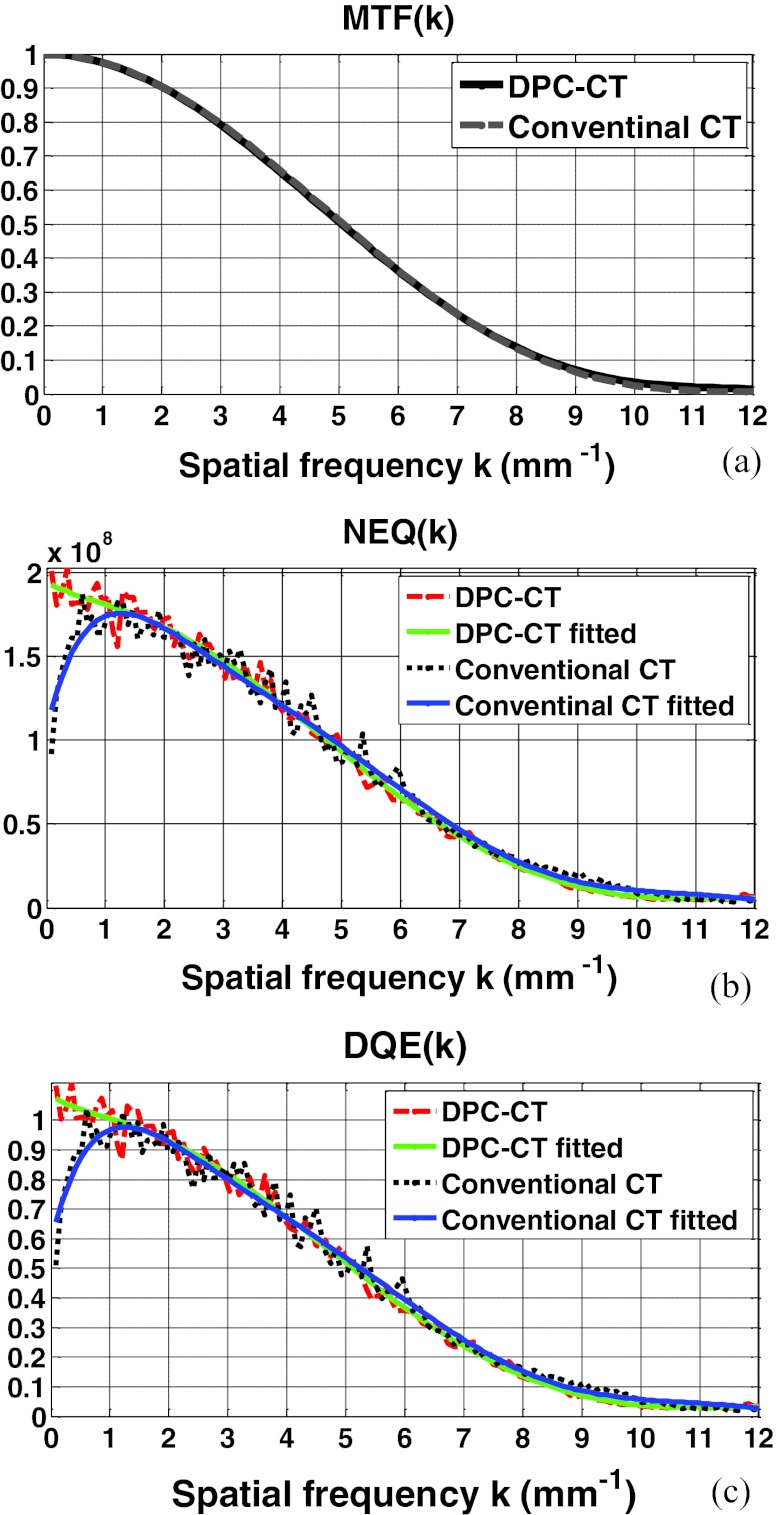
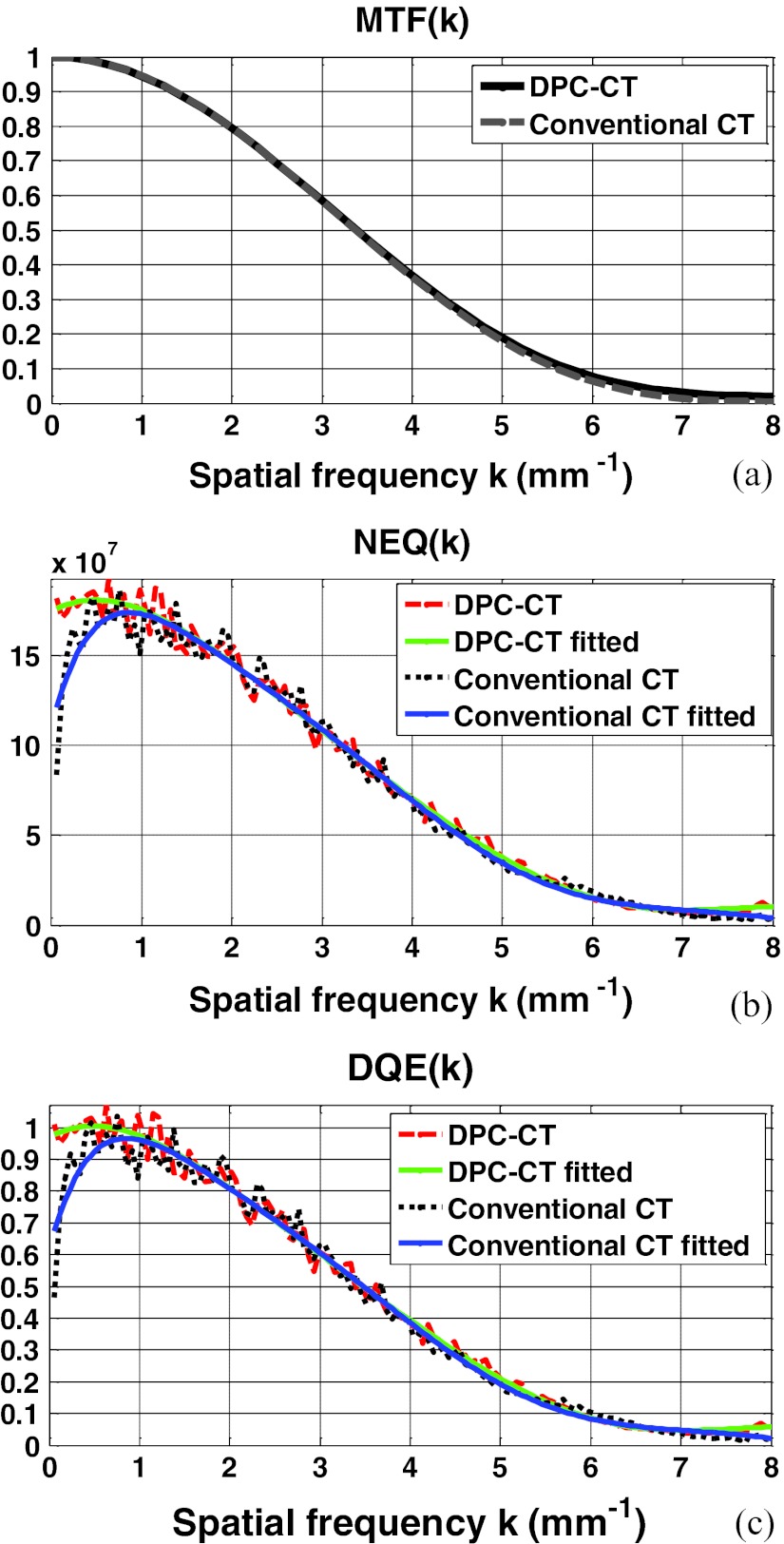
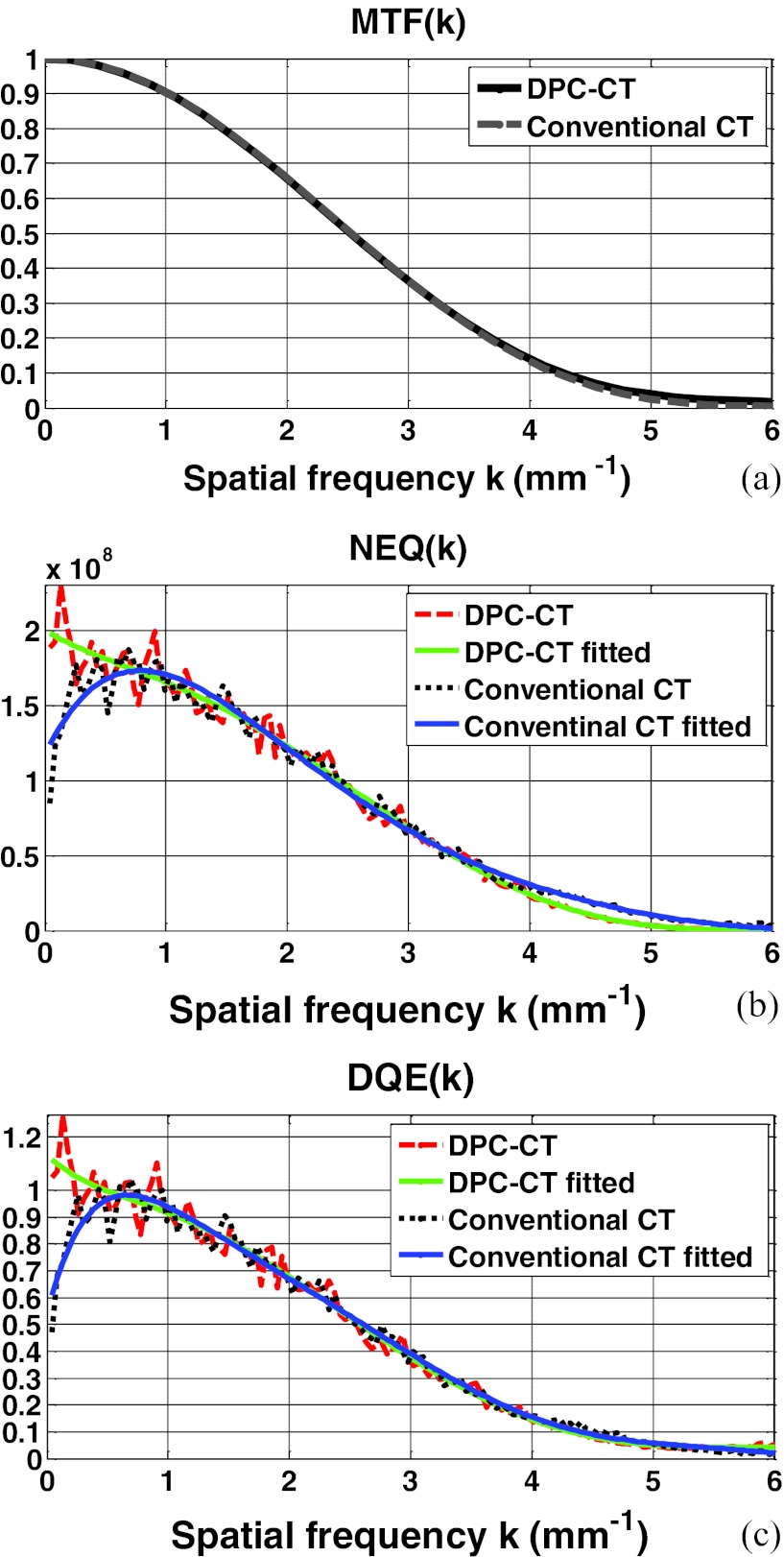
The modulation transfer functions of the DPC-CT and conventional CT have been thoroughly evaluated in our quantitative investigation. Plotted in Figs. 3456a are the MTF_p(k) and MTF_a(k) at detector cell size 32 × 32 μm², 64 × 64 μm², 96 × 96 μm², and 128 × 128 μm², respectively. A close inspection of these plots shows that their spatial resolution measured by the modulation transfer functions MTF_p(k) and MTF_a(k) is almost identical. We have experienced in the conventional CT that a difference in the noise texture/granularity in general means a difference in the spatial resolution. Fortunately, however, this is not the case with regards to the MTF_p(k) and MTF_a(k) between DPC-CT and conventional CT. It is important to note that the equality between MTF_p(k) and MTF_a(k) is of theoretical and practical relevance, and a detailed discussion on this respect is deferred to Sec. 5.

Figure 3.

The imaging performance of DPC-CT compared with that of the conventional CT: (a) MTF_p(k) and MTF_a(k), (b) NEQ_p(k) and NEQ_a(k), and (c) DQE_p(k) and DQE_a(k) (detector cell dimension: 32 × 32 μm²; x-ray exposure 5 × 10⁶ photon/cm² per projection).

Figure 4.

The imaging performance of DPC-CT compared with that of the conventional CT: (a) MTF_p(k) and MTF_a(k), (b) NEQ_p(k) and NEQ_a(k), and (c) DQE_p(k) and DQE_a(k) (detector cell dimension: 64 × 64 μm²; x-ray exposure 5 × 10⁶ photon/cm² per projection).

Figure 5.

The imaging performance of DPC-CT compared with that of the conventional CT: (a) MTF_p(k) and MTF_a(k), (b) NEQ_p(k) and NEQ_a(k), and (c) DQE_p(k) and DQE_a(k) (detector cell dimension: 96 × 96 μm²; x-ray exposure 5 × 10⁶ photon/cm² per projection).

Figure 6.

The imaging performance of DPC-CT compared with that of the conventional CT: (a) MTF_p(k) and MTF_a(k), (b) NEQ_p(k) and NEQ_a(k), and (c) DQE_p(k) and DQE_a(k) (detector cell dimension: 128 × 128 μm²; x-ray exposure 5 × 10⁶ photon/cm² per projection).

NEQ_p(k) of DPC-CT compared with NEQ_a(k) of the conventional CT

The profiles along the radial line that crosses the 2D spectra of noise equivalent quanta NEQ(k) of both DPC-CT and conventional CT at 45° are plotted in Figs. 3456b, corresponding to detector cell dimension 32 × 32 μm², 64 × 64 μm², 96 × 96 μm², and 128 × 128 μm², respectively. As such, the variation of NEQ_p(k) of the DPC-CT as a function over the detector cell dimension can be evaluated. Note that the fluctuation in the profiles of the spectra of noise equivalent quanta NEQ_p(k) and NEQ_a(k) are quite severe, because only 360 ROIs at matrix dimension 128 × 128 in the air phantom are engaged in the measurement. With an increasing number, e.g., more than 1000 (see Ref. 21), of ensemble samples (images or ROIs within the images of the air phantom), smoother profiles corresponding to the noise power spectra can be obtained. Note that the order of the polynomial fitting is determined empirically via trial-and-error to assure that the fitted profile adequately follows the trend in NEQ_p(k) and NEQ_a(k).

DQE_p(k) of DPC-CT compared with DQE_a(k) of the conventional CT

The profiles along the radial line that crosses the 2D spectra of detective quantum efficiency DQE(k) of both DPC-CT and conventional CT at 45° are plotted in Figs. 3456c, corresponding to detector cell dimension 32 × 32 μm², 64 × 64 μm², 96 × 96 μm², and 128 × 128 μm², respectively. It should be noted that the only difference between Figs. 3456b, 6c is the scaling by the x-ray exposure in the DPC-CT and conventional CT, respectively.

DISCUSSIONS

This work is a continuation of our previous investigation focused on the noise power spectrum NPS_p(k) of DPC-CT.¹¹ The primary contribution of this work is derivation of the functional forms of noise power spectrum NPS_p(k), spectrum of noise equivalent quanta NEQ_p(k), and DQE_p(k) of the DPC-CT. By conducting a computer simulation study, we evaluate and verify the derived functional forms and compare them with their counterparts in the conventional CT. To summarize the results, a number of observations and clarifications are given below.

In general, the spectrum of noise equivalent quanta of an imaging system is in the functional form^{20, 21, 26, 27, 28, 29, 30}

$$\mathrm{NEQ}(k)=G^2\frac{{\mathrm{MTF}}^2\left(k\right)}{\mathrm{NPS}(k)}.$$ (36)

By definition, G, MTF(k) and NPS(k) denote the imaging system's transfer characteristics of large area gain, signal, and noise, respectively. In various imaging modalities, Eq. 36 can be in different expressions. For instance, the spectrum of noise equivalent quanta of x-ray radiography and fluoroscopy is expressed in exactly the same way as Eq. 36, whereas that of the conventional CT is expressed in Eq. 10. The spectrum of noise equivalent quanta NEQ_p(k) of the DPC-CT implemented with x-ray tube and grating is specified in Eq. 32. It is interesting and important to note that the term |k| is in the denominator of NEQ_p(k), whereas it is in the numerator of NEQ_a(k).

The computer simulation study shows that, given detector cell dimension, the modulation transfer function MTF_p(k) of the DPC-CT is virtually the same as the MTF_a(k) of the conventional CT [see Figs. 3456a]. It should be indicated that no widowing or boosting technique is utilized to obtain the modulation transfer functions investigated in this work. This means that, despite the difference in the imaging mechanisms between DPC-CT and conventional CT, their modulation transfer functions are essentially determined by dimension of the detector cells used for data acquisition, warranting that the signal transfer characteristics and spatial resolution are in principle identical in these two imaging methods. This result is consistent with what has been published in the literature.^{12, 13} Note that such a fact is of not only theoretical but also practical importance, especially in the scenarios wherein the complementary information drawn from the DPC-CT and the conventional CT are jointly of relevance for applications.

The primary finding of this work is that, except at the spatial frequency close to zero, the spectrum of noise equivalent quanta NEQ_p(k) and detective quantum efficiency DQE_p(k) of DPC-CT are in principle identical to their counterparts NEQ_a(k) and DQE_a(k) in the conventional CT, though there exists a radical difference in their noise power spectrum NPS_p(k) and NPS_a(k). This means that the DPC-CT makes use of x-ray flux as efficiently as the conventional CT if the object to be imaged is of finite size. This fact initially seems surprising since there is a significant difference between NPS_p(k) and NPS_a(k). However, it should become readily understandable if we inspect Eqs. 10, 32 carefully. The term |k| is at the numerator and denominator of NEQ_a(k) and NEQ_p(k), respectively, offsetting the substantial difference in their corresponding NPS_a(k) and NPS_p(k). Hence, NEQ_p(k), DQE_p(k), NEQ_a(k), and DQE_a(k) are essentially determined by MTF_a(k) and MTF_p(k), as analytically specified by Eqs. 10, 11, 32, 33 and experimentally verified by the simulation study as demonstrated in Figs. 3456b, 6c.

By referring to Eq. 1, one may reason that the advantage of DPC-CT in squared signal-to-noise ratio or detectability index over the conventional CT is solely dependent on the extent to which the ΔS_p(f) in DPC-CT is larger than its counterpart ΔS_a(f) in the conventional CT, since the NEQ_p(k) and NEQ_a(k) are essentially identical. Again, this seems inconsistent with our anticipation based on the observation that there exists a radical difference in their noise power spectrum NPS_p(k) and NPS_a(k). However, it should be understood that the SNR²_ideal specified in Eq. 1 is defined under the framework of ideal observer, wherein an ideal observer is assumed to be capable of undoing or removing any correlation in noise, i.e., “pre-whitening” colored noise.^{26, 28} It is interesting and important to note that, the “pre-whitening” is accomplished by the term |k| at the numerator and denominator of NEQ_a(k) and NEQ_p(k), respectively, which offsets the substantial difference in their corresponding NPS_a(k) and NPS_p(k).

We would like to point out and emphasize that a human observer is not an ideal observer, i.e., a human observer is not able to “pre-whiten” colored noise while making a decision. The colored noise plays a significant role in disturbing a human observer's realistic decision-making capacity.^{26, 28} As we have observed, the noise in DPC-CT is abundant at low frequencies (see Fig. 2), while that in the conventional CT occurs at high frequencies. Hence, it is reasonable to anticipate that, if the object to be imaged is of relatively higher frequency, i.e., smaller in size, a human observer may make a better decision based on DPC-CT images than that made based on conventional CT images. This means that, even if ΔS_p(f) = ΔS_a(f), the SNR²_nonideal of DPC-CT can still be higher than SNR²_nonideal of the conventional CT, while the object to be imaged is small in size. In practice, a tomographic imaging method that is less susceptible to high frequency noise has been desired for a long time. The DPC-CT implemented with x-ray tube and grating is just such an imaging modality, which can be of profound significance in clinical and preclinical applications, e.g., the early detection of tumor or atherosclerosis, because a pathophysiological lesion usually starts at a small size.

We have indicated that the root cause for the radical difference between NPS_p(k) and NPS_a(k) is the adoption of the Hilbert filter kernel, rather than the ramp filter kernel, for image reconstruction in the DPC-CT using a filtered backprojection algorithm.¹¹ However, it is interesting to note that such a radical difference between the NPS_p(k) and NPS_a(k) has also been reported in Ref. 12, wherein an integration is carried out on the projection data, followed by the well-known ramp filtering, i.e., no Hilbert filtering is carried out explicitly. In fact, however, a cascading of integration and ramp filtering is equivalent to a Hilbert filtering. Thus, we still believe that the root cause underlying the significant difference between NPS_p(k) and NPS_a(k) and the resultant difference in NEQ_p(k) and NEQ_a(k) is that the data acquired in DPC-CT is the projection of the derivative of the refractive coefficient and in principle only a Hilbert filtering is needed for image reconstruction. In addition, we would like to indicate that, though the image reconstruction scheme used in Ref. 12 may be beneficial in terms of inheriting the filtering strategies established in the conventional CT, the degradation in accuracy and spatial resolution due to the cumulative sum cannot be ignored in practice, especially in the cases wherein the detector cell dimension is not small.

The imaging chain of both DPC-CT and conventional CT is assumed ideal, which should not be confused with the concept of an ideal observer mentioned above, in its system modeling, analysis, and evaluation. For example, the x-ray source is assumed monochromatic in this work and thus the conventional CT investigated in this work is actually a “monochromatic” one. However, the conventional CT in reality usually utilizes a polychromatic x-ray source. Hence, the readers are advised to understand that the imaging performance, including the spectrum of noise equivalent quanta and detective quantum efficiency, of both DPC-CT and the conventional CT may be degraded by the imperfection in its imaging chain in practical situations.

The implementation of a DPC-CT is more challenging, because of the stringent requirements on the optoelectronic accuracy of grating fabrication, mechanical alignment, and stability. The time for data acquisition in the grating-based DPC-CT can be longer if grating G₁ or G₂ needs to shift multiple times. Owing to the phase wrapping phenomenon, the unambiguous phase detection range of DPC-CT is 2π, which may impose limitations on the dynamic range over preclinical and clinical applications. In addition, the noise morphology in DPC-CT images is similar to the texture of some soft tissues. On the other hand, it has been tabulated in Ref. 15 that the refractive coefficients of low atomic number materials are substantially larger than their attenuation counterpart. The preliminary data reported in the literature^{1, 4, 5} have demonstrated that the ΔS_p(f) in soft tissues is significantly larger than its counterpart ΔS_a(f). Moreover, as indicated above, there may exist an extra gain in the DPC-CT's SNR²_nonideal over that of the conventional CT. Hence, it is hoped that the potential of significantly increased contrast sensitivity over soft tissues may outweigh the DPC-CT's implemental shortcomings and enable it to outperform the conventional CT as an imaging modality for extensive preclinical and clinical applications.

CONCLUSIONS

The spectrum of noise equivalent quanta NEQ_p(k) and detective quantum efficiency DQE_p(k) of the DPC-CT is analytically derived in this paper, followed by an evaluation and verification via computer simulation study, as well as its comparison with that of the conventional CT. The signal transfer property of the DPC-CT characterized by the modulation transfer function MTF_p(k) is virtually identical to the MTF_a(k) of conventional CT. Moreover, though there exists a radical difference in their noise property characterized by the noise power spectrum NPS_p(k) and NPS_p(k), the spectrum of noise equivalent quanta NEQ_p(k) and detective quantum efficiency DQE_p(k) of DPC-CT are essentially identical to their counterparts NEQ_a(k) and DQE_a(k) in the conventional CT. It is believed that the NEQ_p(k) and DQE_p(k) characteristics of the DPC-CT unveiled in this study can be of theoretical and practical relevance in the design and optimization of DPC-CT for extensive preclinical and ultimately clinical applications.

APPENDIX: DERIVATION OF THE NOISE POWER SPECTRUM NPS_P(K) IN DPC-CT

Letting the projection of an object function f(x, y) be

$$\begin{array}{c}\hfill P_{\theta }\left(t\right)={\int }_{-\infty }^{\infty }dx{\int }_{-\infty }^{\infty }dyf\left(x,y\right)\delta \left(x\cos \theta +y\sin \theta -t\right),\end{array}$$ (A1)

the object function f(x, y) can be reconstructed from its projection by

$$\begin{array}{ccc}\hfill \widehat{f}\left(x,y\right)& =& {\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }\left|k\right|S_{\theta }\left(k\right)\hfill \\ & & \times \exp \left[2\pi ik\left(x\cos \theta +y\sin \theta \right)\right]dk,\hfill \end{array}$$ (A2)

where the character ^∧ is used to differentiate the reconstructed object function from the original object function. The Fourier transform of projection P_θ(t) is defined as

$$S_{\theta }\left(k\right)={\int }_{-\infty }^{\infty }{P}_{\theta }\left(t\right)\exp \left(-2\pi ikt\right)dt,$$ (A3)

and its inverse Fourier transform can be written as

$$P_{\theta }\left(t\right)={\int }_{-\infty }^{\infty }{S}_{\theta }\left(k\right)\exp \left(2\pi ikt\right)dk.$$ (A4)

According to the property of Fourier transform, if D_θ(t) denotes the derivative of P_θ(t), one has the Fourier transform pair

$$\begin{array}{c}\hfill D_{\theta }\left(t\right)=\frac{\partial P_{\theta }\left(t\right)}{\partial t}={\int }_{-\infty }^{\infty }2\pi ik{S}_{\theta }\left(k\right)\exp \left(2\pi ikt\right)dk,\end{array}$$ (A5a)

$$\begin{array}{c}\hfill D_{\theta }\left(k\right)={\int }_{-\infty }^{\infty }{D}_{\theta }\left(t\right)\exp \left(-2\pi ikt\right)dt=2\pi ik{S}_{\theta }\left(k\right).\end{array}$$ (A5b)

Substituting Eq. A5b into Eq. A2, one obtains

$$\begin{array}{ccc}& & {\displaystyle \widehat{f}\left(x,y\right)=\frac{1}{2\pi }{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }{\displaystyle D_{\theta }\left(k\right)\frac{\left|k\right|}{ik}\exp \left[2\pi ik\left(x\cos \theta +y\sin \theta \right)\right]dk}}\hfill \\ & & \begin{array}{c}={\displaystyle \frac{1}{2\pi }{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }{D}_{\theta }\left(k\right)\left(-i\mathrm{sgn}\left(k\right)\right)\exp \left[2\pi ik\left(x\cos \theta +y\sin \theta \right)\right]dk}\end{array}\hfill \\ & & \begin{array}{c}={\displaystyle \frac{1}{2\pi }{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }{D}_{\theta }\left(k\right)H\left(k\right)\exp \left[2\pi ik\left(x\cos \theta +y\sin \theta \right)\right]dk}\end{array},\hfill \end{array}$$ (A6)

where H(k) represents the Fourier transform of Hilbert filter kernel h(t), i.e.,

$$H\left(k\right)={\int }_{-\infty }^{\infty }h\left(t\right)\exp \left(-2\pi ikt\right)dt,$$ (A7a)

$$h\left(t\right)={\int }_{-\infty }^{\infty }\left(-i\mathrm{sgn}\left(k\right)\right)\exp \left(2\pi ikt\right)dk.$$ (A7b)

In the way similar to Ref. 20, without losing generality, we assume the object function f(x, y) is circularly symmetric, i.e., f(x, y) = f(r, θ) = f(r, 0) = f(r). In the polar coordinate system, one has

$$\widehat{f}\left(r\right)=\frac{1}{2\pi }{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }{D}_{\theta }\left(k\right)H\left(k\right)\exp \left(2\pi ikr\cos \theta \right)dk.$$ (A8)

Note that the subscript θ is kept in D_θ(t) for consistence in expression, though D_θ(t) is actually not a function of θ due to the circular symmetry in f(x, y). It should be easy to show that the Fourier transform F(k) of a circularly symmetric function f(r) is an even function and thus

$$\begin{array}{ccc}\hfill \widehat{f}\left(r\right)& =& {\int }_0^{2\pi }d\theta {\int }_0^{\infty }dk\widehat{F}\left(k\right)k\exp \left(2\pi irk\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_0^{\infty }dk\widehat{F}\left(k\right)k\exp \left(2\pi irk\cos \theta \right)+{\int }_{\pi }^{2\pi }d\theta {\int }_0^{\infty }dk\widehat{F}\left(k\right)k\exp \left(2\pi irk\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_0^{\infty }dk\widehat{F}\left(k\right)k\exp \left(2\pi irk\cos \theta \right)+{\int }_0^{\pi }d\theta {\int }_0^{\infty }dk\widehat{F}\left(k\right)k\exp \left(-2\pi irk\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_0^{\infty }dk\widehat{F}\left(k\right)k\exp \left(2\pi irk\cos \theta \right)-{\int }_0^{\pi }d\theta {\int }_0^{-\infty }dk\widehat{F}\left(-k\right)\left|k\right|\exp \left(2\pi irk\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_0^{\infty }dk\widehat{F}\left(k\right)\left|k\right|\exp \left(2\pi irk\cos \theta \right)+{\int }_0^{\pi }d\theta {\int }_{-\infty }^{0}dk\widehat{F}\left(k\right)\left|k\right|\exp \left(2\pi irk\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dk\widehat{F}\left(k\right)\left|k\right|\exp \left(2\pi irk\cos \theta \right).\hfill \end{array}$$ (A9)

Comparing Eqs. A9, A8, one gets

$$\widehat{F}\left(k\right)=\frac{D_{\theta }\left(k\right)H\left(k\right)}{2\pi \left|k\right|}.$$ (A10)

Letting the object function f(x, y) be a delta function, i.e., f(x, y) = δ(x)δ(y), the magnitude of the Fourier Transform of the reconstructed object function is the modulation transfer function, i.e.,

$${\mathrm{MTF}}_p\left(k\right)=\left|\widehat{F}\left(k\right)\right|\begin{array}{ccc}& \mathrm{while}& f(x,y)=\delta \left(x\right)\delta \left(y\right)\end{array}.$$ (A11)

Noting that

$$\begin{array}{ccc}\hfill D_{\theta }\left(k\right)& =& {\int }_{-\infty }^{\infty }dt\exp \left(-2\pi ikt\right)\frac{\partial P_{\theta }\left(t\right)}{\partial t}=2\pi ik{\int }_{-\infty }^{\infty }dt{P}_{\theta }\left(t\right)\exp \left(-2\pi ikt\right)\hfill \\ & =& 2\pi ik{\int }_{-\infty }^{\infty }dt\exp \left(-2\pi ikt\right){\int }_{-\infty }^{\infty }dx{\int }_{-\infty }^{\infty }dy\delta \left(x\right)\delta \left(y\right)\delta \left(x\cos \theta +y\sin \theta -t\right)\hfill \\ & =& 2\pi ik{\int }_{-\infty }^{\infty }dt\exp \left(-2\pi ikt\right)\delta \left(-t\right)=2\pi ik,\hfill \end{array}$$ (A12)

and substituting Eqs. A11, A12 into Eq. A10, one obtains

$${\mathrm{MTF}}_p\left(k\right)=\left|\frac{ikH\left(k\right)}{\left|k\right|}\right|=\left|i\mathrm{sgn}\left(k\right)H\left(k\right)\right|=\left|H\left(k\right)\right|.$$ (A13)

On the other hand, the autocovariance function of the reconstructed object function is

$$C\left(x,y\right)=⟨\Delta \widehat{f}\left(x,y\right)\Delta \widehat{f}\left(0,0\right)⟩,$$ (A14)

where $\Delta \widehat{f}(x,y)$ represents the deviation of $\widehat{f}(x,y)$ from its mean value.²⁰ Substituting Eqs. A5b, A7a into Eq. A6, one gets

$$\begin{array}{ccc}\hfill \widehat{f}\left(x,y\right)& =& {\int }_0^{\pi }\frac{d\theta }{2\pi }{\int }_{-\infty }^{\infty }dk\exp \left[2\pi ik\left(x\cos \theta +y\sin \theta \right)\right]{\int }_{-\infty }^{\infty }dt{D}_{\theta }\left(t\right)\exp \left(-2\pi ikt\right)\hfill \\ & & \times {\int }_{-\infty }^{\infty }d{t}_{1}h\left(t_1\right)\exp \left(-2\pi ik{t}_1\right)\hfill \\ & =& {\int }_0^{\pi }\frac{d\theta }{2\pi }{\int }_{-\infty }^{\infty }dt{D}_{\theta }\left(t\right){\int }_{-\infty }^{\infty }d{t}_{1}h\left(t_1\right){\int }_{-\infty }^{\infty }dk\exp \left[2\pi ik\left(x\cos \theta +y\sin \theta -t-t_1\right)\right]\hfill \\ & =& {\int }_0^{\pi }\frac{d\theta }{2\pi }{\int }_{-\infty }^{\infty }dt{D}_{\theta }\left(t\right){\int }_{-\infty }^{\infty }d{t}_{1}h\left(t_1\right)\delta \left(x\cos \theta +y\sin \theta -t-t_1\right)\hfill \\ & =& {\int }_0^{\pi }\frac{d\theta }{2\pi }{\int }_{-\infty }^{\infty }dt{D}_{\theta }\left(t\right)h\left(x\cos \theta +y\sin \theta -t\right),\hfill \end{array}$$ (A15)

$$\Delta \widehat{f}\left(x,y\right)={\int }_0^{\pi }\frac{d\theta }{2\pi }{\int }_{-\infty }^{\infty }dt\Delta D_{\theta }\left(t\right)h\left(x\cos \theta +y\sin \theta -t\right).$$ (A16)

Subsequently, the autocovariance function becomes

$$\begin{array}{ccc}\hfill C\left(x,y\right)& =& ⟨{\int }_0^{\pi }\frac{d\theta }{2\pi }{\int }_{-\infty }^{\infty }dt\Delta D_{\theta }\left(t\right)h\left(x\cos \theta +y\sin \theta -t\right){\int }_0^{\pi }\frac{d{\theta }_1}{2\pi }{\int }_{-\infty }^{\infty }d{t}_1\Delta D_{{\theta }_1}\left(t_1\right)h\left(-t_1\right)⟩\hfill \\ & =& {\int }_0^{\pi }\frac{d\theta }{2\pi }{\int }_{-\infty }^{\infty }dth\left(x\cos \theta +y\sin \theta -t\right){\int }_0^{\pi }\frac{d{\theta }_1}{2\pi }{\int }_{-\infty }^{\infty }d{t}_{1}h\left(-t_1\right)⟨\Delta D_{\theta }\left(t\right)\Delta D_{{\theta }_1}\left(t_1\right)⟩.\hfill \end{array}$$ (A17)

Assuming the recorded data D_θ(t) are uncorrelated, i.e.,

$${\int }_0^{\pi }d{\theta }_1{\int }_{-\infty }^{\infty }d{t}_{1}h(x\cos \theta +y\sin \theta -t)h(-t_1)⟨\Delta D_{\theta }\left(t\right)\Delta D_{{\theta }_1}\left(t_1\right)⟩$$ (A18)

$$=\frac{a\pi }{N_{\theta }}{\sigma }_D^{2}h(x\cos \theta +y\sin \theta -t)h(-t)$$ (A19)

where ${\sigma }_D^2$ is the noise at each detector cell, a is the detector pitch, and N_θ is the total number of projection D_θ(t). Then, Eq. A17 becomes

$$C\left(x,y\right)=\frac{a{\sigma }_D^2}{4\pi N_{\theta }}{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dth\left(x\cos \theta +y\sin \theta -t\right)h\left(-t\right).$$ (A20)

Again, without losing generality, we assume a circular symmetry in C(x, y), i.e.,

$$C\left(x,y\right)=C\left(r,0\right)=C\left(r\right)=\frac{a{\sigma }_D^2}{4\pi N_{\theta }}{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dth\left(r\cos \theta -t\right)h\left(-t\right).$$ (A21)

Substituting Eq. A7b into Eq. (A2a), one gets

$$\begin{array}{ccc}\hfill C\left(r\right)& =& -\frac{a{\sigma }_D^2}{4\pi N_{\theta }}{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dt{\int }_{-\infty }^{\infty }dkH\left(k\right)\exp \left[2\pi ik\left(r\cos \theta -t\right)\right]{\int }_{-\infty }^{\infty }d{k}_{1}H\left(k_1\right)\exp \left(-2\pi i{k}_{1}t\right)\hfill \\ & =& \frac{a{\sigma }_D^2}{4\pi N_{\theta }}{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dkH\left(k\right)\exp \left(2\pi ikr\cos \theta \right){\int }_{-\infty }^{\infty }d{k}_{1}H\left(k_1\right){\int }_{-\infty }^{\infty }dt\exp \left(-2\pi i{k}_{1}t-2\pi ikt\right)\hfill \\ & =& \frac{a{\sigma }_D^2}{4\pi N_{\theta }}{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dkH\left(k\right)\exp \left(2\pi ikr\cos \theta \right){\int }_{-\infty }^{\infty }d{k}_{1}H\left(k_1\right)\delta \left(k_1+k\right)\hfill \\ & =& \frac{a{\sigma }_D^2}{4\pi N_{\theta }}{\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dk{\left|H\left(k\right)\right|}^2\exp \left(2\pi ikr\cos \theta \right).\hfill \end{array}$$ (A22)

The noise power spectrum NPS_p(k), defined as the Fourier transform of autocovariance function, is an even function. Thus, the autocovariance function becomes²⁰, ²¹

$$\begin{array}{ccc}\hfill C\left(r\right)& =& {\int }_0^{2\pi }d\theta {\int }_0^{\infty }dk{\mathrm{NPS}}_p\left(k\right)k\exp \left(2\pi ikr\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_0^{\infty }dk{\mathrm{NPS}}_p\left(k\right)k\exp \left(2\pi ikr\cos \theta \right)+{\int }_{\pi }^{2\pi }d\theta {\int }_0^{\infty }dk{\mathrm{NPS}}_p\left(k\right)k\exp \left(2\pi ikr\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_0^{\infty }dk{\mathrm{NPS}}_p\left(k\right)k\exp \left(2\pi ikr\cos \theta \right)+{\int }_0^{\pi }d\theta {\int }_0^{\infty }dk{\mathrm{NPS}}_p\left(k\right)k\exp \left(-2\pi ikr\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_0^{\infty }dk{\mathrm{NPS}}_p\left(k\right)\left|k\right|\exp \left(2\pi ikr\cos \theta \right)-{\int }_0^{\pi }d\theta {\int }_0^{-\infty }dk{\mathrm{NPS}}_p\left(-k\right)\left|k\right|\exp \left(2\pi ikr\cos \theta \right)\hfill \\ & =& {\int }_0^{\pi }d\theta {\int }_{-\infty }^{\infty }dk{\mathrm{NPS}}_p\left(k\right)\left|k\right|\exp \left(2\pi ikr\cos \theta \right).\hfill \end{array}$$ (A23)

Comparing Eqs. A23, A22, one obtains

$${\mathrm{NPS}}_p\left(k\right)=\frac{a{\sigma }_D^2{\left|H\left(k\right)\right|}^2}{4\pi N_{\theta }\left|k\right|}.$$ (A24)

Substituting Eq. A13 into Eq. A24 and reformatting, one finally arrives at

$$\frac{N_{\theta }}{{\sigma }_D^2}=\frac{a}{4\pi \left|k\right|{\mathrm{NPS}}_p\left(k\right)}{\mathrm{MTF}}_p^2\left(k\right).$$ (A25)