Abstract
Phase contrast magnetic resonance imaging (PC-MRI) is subject to numerous sources of error, which decrease clinical confidence in the reported measures. This work outlines how stationary perivascular fat can impart a significant chemical shift induced PC-MRI measurement error using computational simulations, in vitro, and in vivo experiments. This chemical shift error does not subtract in phase difference processing, but can be minimized with proper parameter selection. The chemical shift induced phase errors largely depend on both the receiver bandwidth (BW) and the TE. Both theory and an in vivo comparison of the maximum difference in net forward flow between vessels with and without perivascular fat indicated that the effects of chemically shifted perivascular fat are minimized by the use of high BW (814 Hz/px) and an in-phase TE (HBW-TEIN). In healthy volunteers (N=10) HBW-TEIN significantly improves intrapatient net forward flow agreement compared to low BW (401 Hz/px) and a mid-phase TE as indicated by significantly decreased measurement biases and limits of agreement for the ascending aorta (1.8±0.5 mL vs. 6.4±2.8 mL, P=0.01), main pulmonary artery (2.0±0.9 mL vs. 11.9±5.8 mL, P=0.04), the left pulmonary artery (1.3±0.9 mL vs. 5.4±2.5 mL, P=0.003), and all vessels (1.7±0.8 mL vs. 7.2±4.4 mL, P=0.001).
Keywords: Chemical Shift, Bandwidth, Echo Time, Phase Contrast Magnetic Resonance Imaging
INTRODUCTION
Phase contrast MRI (PC-MRI) is a noninvasive imaging technique that can be used to measure the velocity of flowing blood in a particular blood vessel with flexible spatial and temporal resolution (1,2). PC-MRI is considered the clinical “gold standard” for quantification of blood flow (3,4) for patients with various cardiovascular diseases (5–7). In particular, PC-MRI enables clinicians to measure peak velocity, mean velocity, flow rate, total flow, and pressure gradients throughout the vasculature.
PC-MRI, however, is subject to numerous sources of error, which decrease clinical confidence in the reported measures. These sources of error include eddy currents (8), Maxwell terms (9), gradient field distortions (10), off-resonance (11), variations in intra-thoracic pressure that arise during breath holding (12,13), non-optimized parameter selection, and chemical shift effects. There exist established correction methods for many of these errors (8–10), but chemical shift effects and the concomitant methods to reduce these errors in PC-MRI have not been thoroughly described. Gatehouse et al. describes a 5% error in a stroke volume to be a limit of acceptability in PC-MRI flow measurements (8). Herein we adopt this criterion and state that sources of error must contribute <5% flow measurement error to be clinically insignificant.
Herein we outline the theoretical basis of chemical shift in PC-MRI, and then use computational simulations, in vitro, and in vivo experiments to illustrate how perivascular fat can chemically shift across the vessel wall into the lumen and impart a significant phase measurement error. Importantly, we will show that the chemical shift effects in PC-MRI do not subtract in phase difference processing, but these errors can be reduced to clinically insignificant levels with a judicious choice of bandwidth (BW) and TE. As we will demonstrate, the effects of chemical shift on quantitative PC-MRI measurements are complex as they depend on the field strength, receiver bandwidth, echo time, and the presence or absence of perivascular fat. This has important implications for quantitative, longitudinal, multi-center trials, which require both quantitative imaging clinical endpoints and high methodological reproducibility.
To test the theory, we hypothesized that chemical shift induced phase errors in PC-MRI introduce significant flow measurement errors in vivo. Therefore, the objectives of this study were to: 1) analytically define and quantify the contribution of chemically shifted perivascular fat to quantitative PC-MRI flow measurement errors; and 2) define the BW and TE that reduces errors in PC-MRI net forward flow measurements in the aAo, PA and RPA+LPA to clinically insignificant levels.
THEORY
In PC-MRI, velocity encoded images can be formed from an interleaved set of acquisitions using both flow compensated and flow encoded gradients (14). The complex MRI signals (Z) depend on the signal magnitude (M) from stationary fat (MFat) and flowing blood (MBlood), the signal phase (φ) from stationary fat (φFat) and flowing blood of velocity, v, (φV), as well as off-resonance (φOff):
| [1a] |
| [1b] |
Eq. [1] does not include the effects of eddy currents, Maxwell terms, or other phase errors. From a pair of complex flow images, ZC (flow compensated) and ZE (flow encoded), the measured phase difference (θ) is given by Eq. [2] (15–18).
| [2] |
Where * denotes the complex conjugate and arg yields the angle (i.e. phase) between the two complex vectors (i.e. arg(x+iy) = atan(y/x)):
| [3] |
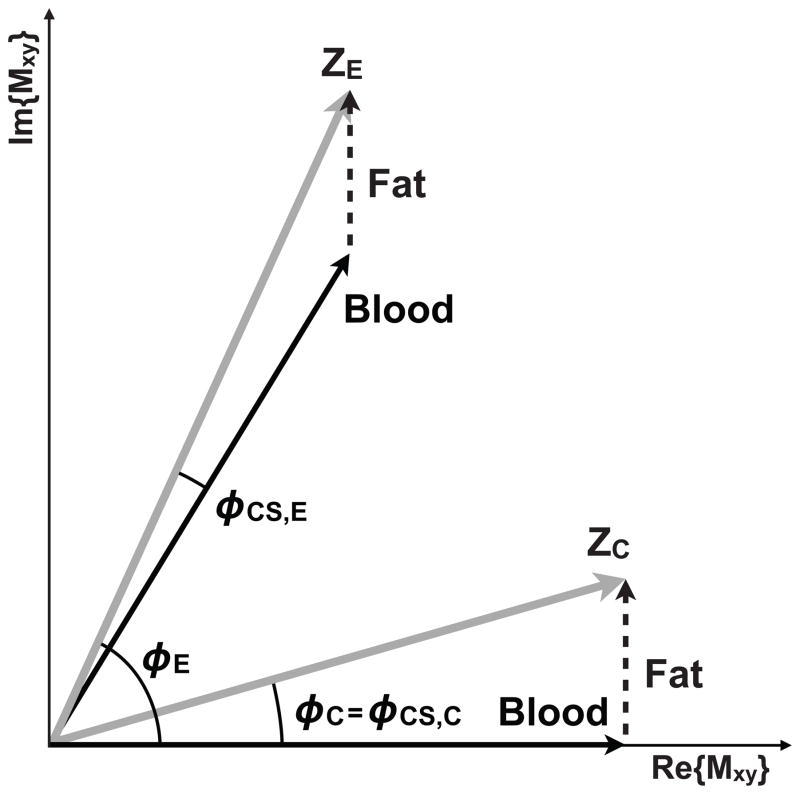
Eq. [3] and Fig. 1 demonstrate that although off-resonance effects due to intravoxel magnetic field inhomogeneity cancel out during phase difference processing, the effects of chemically shifted perivascular fat do not. As a result, stationary perivascular fat contributes to the measurement of θ whenever MFat or φFat is non-zero. Perivascular fat surrounds most vessels and can chemically shift across the vessel wall into the lumen, thereby superposing the off-resonant phase and magnitude of fat onto a pixel containing flowing blood. Depending on the vessel wall thickness, perivascular fat can chemically shift into the vessel lumen and corrupt the complex MRI signal near the vessel wall then adds to the complex blood signal, which can lead to a clinically significant over- or underestimation of blood velocity within a vessel depending upon the magnitude and phase of the fat signal relative to the phase of the blood signal.
Figure 1.
Components of the transverse magnetization from a flow compensated (ZC) and flow encoded (ZE) experiment. In the absence of field inhomogeneity, eddy currents, Maxwell terms, and other phase errors, the blood (i.e. water) signal is encoded with a phase that depends upon the first moment of the velocity encoding gradient and the blood velocity (black arrows). The off-resonant effects of chemically shifted fat (dashed arrow) sum with the complex blood signal to form the ZC and ZE measured signals (gray arrows). Note that the contribution of fat does not cancel with the phase difference method (φ C -φ E) because the two required experiments are differentially affected by chemical shift (φ CS,C ≠ φ CS,E).
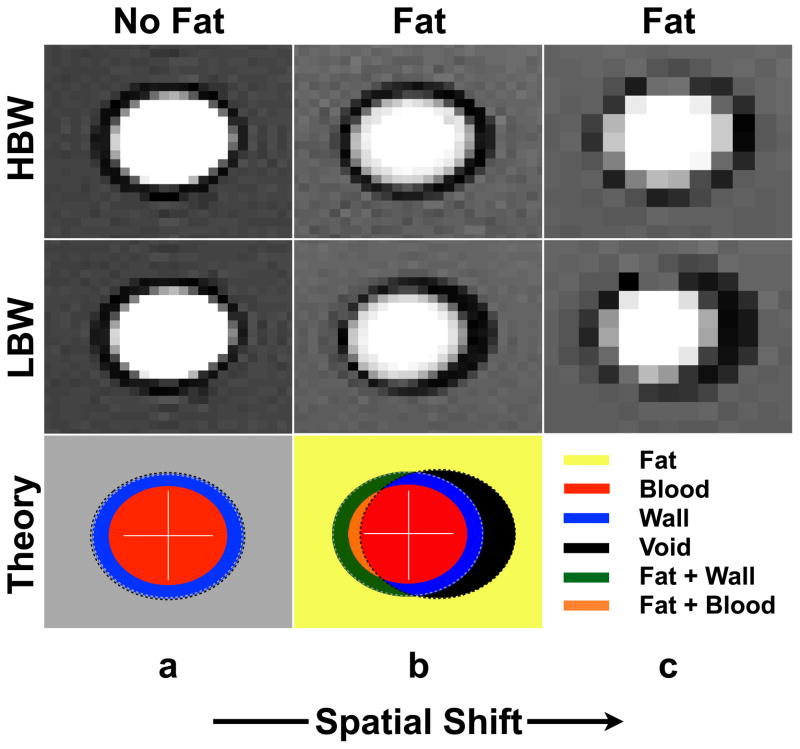
The magnitude of the chemically shifted fat signal depends upon the steady-state signal magnitude of MFat relative to MBlood, the vessel wall thickness, and the percent of chemically shifted fat within a measurement pixel. The percent of chemically shifted fat represents the amount of fat that is spatially shifted into the vessel and is controlled by BW and spatial resolution (Fig. 2) according to the following: pixel shift = δf•BW−1•Δx, where δf is the off-resonance frequency shift between water and fat (δf3T ~420 Hz; scanner reported B0 = 2.89T) and Δx is the spatial resolution in the readout direction. Chemically shifted perivascular fat shifts further into the vessel at low BW (LBW) compared to high BW (HBW) (19). The spatial shift of fat, and thus the percent of chemically shifted fat within a pixel, is greater at lower bandwidths compared to higher bandwidths. The effects of BW on the accuracy of PC-MRI measurements are summarized in Fig. 3a.
Figure 2.
The experimentally measured spatial shift of chemically shifted perivascular fat in a phantom setup depends on the choice of high or low bandwidth (HBW or LBW) and spatial resolution (top two rows). Fat chemically shifts more to the right at LBW (middle row) compared to HBW (top row) and also at lower spatial resolutions (column c). Column a: Images with no “perivascular” fat (“vessel” surrounded by water). Column b: with “perivascular” fat (“vessel” surrounded by oil) at a standard spatial resolution. Column c: with “perivascular” fat at lower spatial resolution. The bottom row is a theoretical representation of the distribution of signal as a consequence of both chemical shift effects and partial voluming at LBW. The black region arises due to fat chemically shifting out of that region (signal void), the green region arises as a result of fat chemically shifting into the vessel wall (signal overlap of wall and fat signal), and the orange region arises due to fat chemically shifting through the vessel wall and into the vessel lumen (signal overlap of blood and fat signal), which leads to chemical shift induced phase errors.
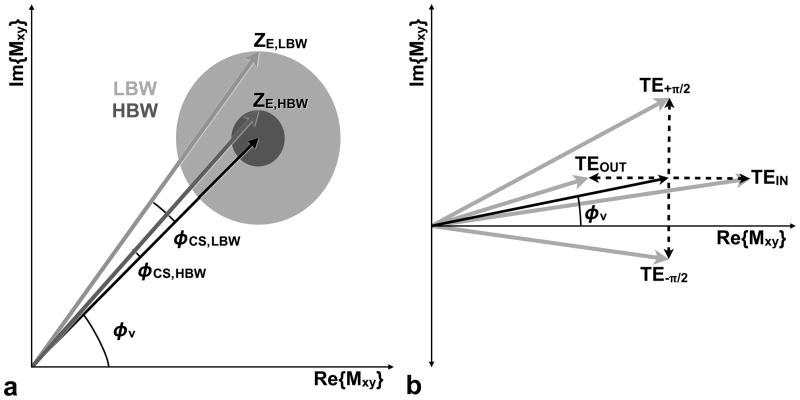
Figure 3.
The effects of chemical shift phase (φ CS) on quantitative PC-MRI measurements. (a) In the absence of chemical shift and other phase errors, flowing spins are encoded with an amount of phase proportional to their velocity (φv, black arrow). When chemical shift effects are taken into consideration the choice of high or low bandwidth (HBW or LBW) scales the magnitude (radius of the gray circles in (a)) of the complex fat factor because it controls the percent of partial-volume fat. HBW results in a lower percent of partial-volume fat (reduced magnitude) than LBW, which for a fixed TE results in φ CS,HBW < φ CS,LBW. In (b) it is apparent that the TE determines the phase of the complex fat factor (dashed arrow), which adds to the blood velocity vector (black arrow) to produce the ZC or ZE complex signal (gray arrow) and subsequently impacts the magnitude of the phase error. TEIN leads the fat vector to be closely aligned with the blood vector when the blood velocity is low, which is typical of the vessel lumen periphery where CS effects are likely to be problematic. The use of TEIN leads to reduced error from chemical shift (φ CS,TE−π/2 < φ CS,TEIN < φ v,Blood < φ CS,TEOUT < φCS,TE+π/2) for slow flowing blood near the vessel lumen periphery. In summary, the chemical shift error (φCS) depends on the magnitude and phase of the fat vector the phase of the water vector (φv). The use of HBW and TEIN can minimize CS effects in PC-MRI.
The phase of fat is determined by δf and the TE:
| [4] |
A careful distinction is to be made between φFat and φCS: φFat is the phase of fat, as determined by Eq. [4], whereas φCS is the chemical shift phase error arising for a given experiment (i.e. φCS,E is the chemical shift induced phase error for the flow encoded measurement in Fig. 1).
A TEIN that orients fat to be in-phase with stationary water (i.e. blood) is referred to as an in-phase TE (TEIN) and, similarly, aand TEOUT that orients fat to be out-of-phase with stationary water is referred to as an out-of-phase TE (TEOUT). From Eq. [4] it can be shown that at 3T, TEIN occurs at 2n•1.23 ms and TEOUT occurs at (2m−1)•1.23 ms, where n=[0,1,2,…] and m=[1,2,3,…]. Similarly, echo times that orient the fat signal perpendicular to the stationary water signal include TE+π/2, which occurs at (2n+0.5) •1.23 ms, and TE−π/2, which occurs at (2m−0.5)•1.23 ms.
Blood near the vessel wall is typically slow flowing (especially under laminar flow conditions) and therefore has a near zero phase. The effects of TE on the phase difference measurements are summarized in Fig. 3b. The use of TE−π/2 causes the phase component of a stationary fat vector to be oriented approximately perpendicular in the negative direction to the slow flowing blood vector, which leads to a decrease in the measured θ. The use of TEIN causes the phase component of a stationary fat vector to be oriented in approximately the same direction as the slow flowing blood vector, which leads to a decrease in the measured θ. The use of TEOUT causes the phase component of the fat vector to be oriented in approximately the opposite direction of the slow flowing blood vector, which leads to an increase in the measured θ. The use of TE+π/2 causes the phase component of the fat vector to be oriented approximately perpendicular to the blood vector, in the positive direction, which leads to an increase in the measured θ.
In summary, Eq. [3] demonstrates that chemical shift differentially affects the flow compensated and flow encoded experiments and, unlike off-resonance effects, does not cancel out during phase difference processing. The chemical shift induced phase error is greater at LBW compared to HBW and also at TE±π/2 compared to TEIN or TEOUT. Collectively, the magnitude of the chemical shift error at different BWs and TEs can be summarized by Eq. [5], where Truth is defined as the net forward flow measured in the absence of chemical shift induced phase errors:
| [5] |
Eq. [5] and Fig. [3] indicate that HBW always reduces chemical shift effects more than LBW for any TE. Additionally, for a given BW, TEIN leads to reduced errors from fat compared to TEOUT because TEIN results in fat being more in-phase with slow flowing blood (φv ≈ 0) near the vessel wall (Fig. 3b).
METHODS
Computational Simulations
A theoretical understanding of chemically shifted perivascular fat in PC-MRI was achieved, in part, through the use of computational simulations. Constant laminar blood flow (v=50 cm/s) and tri-phasic laminar blood flow (vPeak = 50 cm/s; the first 50% of the waveform ranged from 0 to vPeak, the next 25% ranged from 0 to −0.05•vPeak and then back to 0, and the last 25% ranged from 0 to 0.05•vPeak and then back to 0) was modeled using a “vessel” geometry (15.9/1.6 mm inner diameter/wall thickness) that emulated the right or left branch pulmonary artery. The simulations used the following imaging parameters: 8.5/9.1 ms TR (3T/1.5T), 2.80/3.08/3.38/3.69/4.01/4.30/4.60/4.92 ms TEs at 3T and 5.36/5.95/6.55/7.15/2.98/3.57/4.17/4.76 ms TEs at 1.5T (TE+π/4/TE+π/2/TE+3π/4/TEOUT/TE−3π/4/TE−π/2/TE−π/4/TEIN), 1.7 mm × 1.7 mm × 6 mm acquisition voxel, 30° flip angle, BWs of 100, 200, 300, 401 (LBW), 500, 600, 700, 814 (HBW), 900, and 1000 Hz/pixel, and VENC = 50 cm/s. The simulated TEs were chosen based on the achievable TEs within our current pulse sequence. The simulated TRs were chosen as the minimum available TR for the longest TE and lowest BW at each field strength.
The signal magnitude of flowing blood, the vessel wall, and fat for a spoiled gradient echo sequence was determined analytically from the work proposed by Gao et al. (20), which was altered to account for in-flow effects:
| [6a][6b][6c] |
Where, M0 is the equilibrium magnetization, TE and TR are the gradient echo time and repetition time respectively, α is the imaging flip angle, d is the slice thickness, Δx and Δy are the pixel resolutions in the x and y dimensions, v is the tissue velocity, and m, which represents the number of RF excitations a spin experiences, is determined by,
| [7] |
where int indicates the integer value corresponding to the round off quotient. in Eq. [6b] is determined by the following equation:
| [8] |
Values of the T1, T2, and proton density (PD) at 3T (1.5T) for each tissue type were obtained from literature results: T1=1700 ms (T1=1400 ms), T2=275 ms, PD=0.90 (blood); T1=500 ms (T1=350 ms), T2=100 ms, PD=0.98 (fat); and T1=1400 ms (T1=1000 ms), T2=30 ms, PD=1.0 (vessel wall) (21,22). The oil spectrum was measured with spectroscopy at 3T and the frequency shift was found to be 1.4ppm. The chemical shift of the mixture of glycerol and water (“blood”) was estimated to be 4.35ppm, based on proton weighted peak averaging and literature values of glycerol (23). Our computer simulations assume two single resonances, one for “blood” (water and glycerol) and one for fat (vegetable oil) with a frequency difference of 2.96ppm. Similarly, for the 1.5T simulations the blood and fat resonances were simulated with a frequency difference of 1.48ppm. Our simulations were conducted with B0 = 2.89T for 3T B0 = 1.49T for 1.5T based on the scanner reported field strengths.
Eq. [6] describes three flow regimes. Static spins (v =0, Eq. [6a]) are subject to multiple RF pulses, resulting in the development of a steady state signal. For spins moving at a velocity such that they do not fully escape the slice during the TR (v<d/TR, Eq. [6b]), a portion of the spins occupying the selective slice are replenished each TR by fresh inflowing spins with an equilibrium level of magnetization. Lastly, if the spins have a velocity such that they escape the imaging slice during the TR (v ≥ d/TR, Eq. [6c]), then they only experience a single RF pulse and exhibit a maximum signal.
The simulations were conducted with perivascular fat at LBW (high partial volume of fat pixels) and HBW (lower partial volume of fat pixels) as well as with stationary water in place of perivascular fat to yield the true flow result in the absence of chemical shift effects. The simulations were conducted under the assumption of a perfect slice profile. The simulated field of view was 25 × 25 mm with a spatial resolution of 1.7 mm × 1.7 mm. The simulation was conducted under super-resolution conditions to better model partial volume effects. To do this, the image was simulated at 100× the imaging resolution yielding a 1500 × 1500 complex array for blood, fat, and the vessel wall. The signal magnitudes were computed using Eq. [6]. The phase of the blood signal was assigned for each matrix element based on the simulated constant laminar or tri-phasic laminar velocity profiles at each spatial position. The off-resonance phase of fat at 1.5 T and 3T was derived using δf1.5T and δf3T, the simulated TEs, and Eq. [4]. The vessel wall was assumed to be static and on-resonance with blood, thus its phase matrix consisted entirely of zeros.
For the simulations with perivascular fat, the fat array was spatially shifted by 45 (1.5T) and 91 (3T) pixels in the super-resolution domain (equivalent to 0.45 and 0.91 pixels in the imaging domain, respectively) for LBW (401 Hz/pixel) and by 22 (1.5T) and 45 (3T) pixels in the super-resolution domain (0.22 and 0.45 pixels in the imaging domain, respectively) for HBW (814 Hz/pixel) to simulate the chemical shift effect (pixel shift = δf•BW−1•100 spins/pixel). The complex signal from the three simulated tissues was obtained from:
| [9a] |
| [9b] |
| [9c] |
The complex signals for all three tissues within 100 × 100 pixels in the super-resolution domain were added together to constitute one imaging pixel
The net forward flow of blood in the simulated vessel was computed by calculating the velocity of every pixel within the simulated vessel by scaling the phase result by VENC/π (cm/s). The resulting pixel velocities were then multiplied by the spatial resolution (pixel area, cm2) to calculate the flow rate (mL/s) and finally integrated over the cardiac cycle to yield the net forward flow results (mL).
In Vitro Phantom Experiments
The theoretical effects of chemical shift induced PC-MRI errors were compared to those obtained in flow phantom experiments. All imaging was performed on a Siemens Trio 3 Tesla system (Siemens Medical Solutions, Erlangen, Germany) with 40 mT/m maximum gradient amplitude and 200 T/m/s maximum slew rate. PC-MRI data was acquired in a sealed tube (19.1/1.6 mm diameter/wall thickness) surrounded first by water and then by vegetable oil to simulate perivascular fat. Blood-mimicking fluid (40% glycerol, 60% water) was circulated through the phantom by a CardioFlow 1000MR computer-controlled displacement pump (Shelley Medical Imaging Technologies, Toronto, Ontario, Canada) at a constant programmed flow rate of 25 mL/s. Measurements were performed using a 12-element head coil. The flow rate and tubing were selected to approximate the velocity and vessel dimensions of the branch pulmonary arteries.
The PC-MRI protocol used a cine gradient echo phase-contrast sequence with the following sequence parameters: 8.5 ms TR, 4.92/6.15/5.54/6.77 ms TEs (minimum achievable TEIN/TEOUT/TE+π/2/TE−π/2), 192 × 120 encoding matrix, 1.7 mm × 1.7 mm × 6 mm acquisition voxel, 30° flip angle, BWs of 401 Hz/pixel (LBW) and 814 Hz/pixel (HBW) Hz/pixel, 4 views-per-segment, a temporal resolution of 68 ms, 20 phases reconstructed from a 20 second acquisition using retrospective ECG gating, and GRAPPA (24) parallel imaging with an acceleration factor of 2 and 24 central k-space reference lines. An artificial ECG signal was generated using a physiologic signal simulation tool available as part of the scanner’s software environment. The R-R interval was adjusted to 1000 ms (60 beats per minute). Through-plane velocity encoding was performed using interleaved flow-compensated and flow-sensitive encoding with a VENC of 70 cm/s.
In Vivo Imaging Experiments
Based upon the theoretical and experimental findings, in vivo experiments were performed to demonstrate the effects of chemical shift errors in PC-MRI in healthy volunteers (N=10). The university’s Institutional Review Board (IRB) approved the study and informed consent was obtained for each subject prior to MRI scanning. After addressing each subject’s concerns, each subject was positioned head first in the supine position on the scanner bed and imaged using a 6-element body matrix and 6-element spine matrix coils for signal reception. Blood flow was measured using PC-MRI in the aAo, PA, RPA, and LPA of ten (N=10) volunteers (3 female, 7 male; age 25.9±4.7 years) with no previous history of cardiovascular disease. High-resolution black blood turbo spin echo (TSE) images were also acquired with and without fat saturation (25,26) during end-systole in order to define the presence (or absence) of perivascular fat for the vessel of interest in the same slices used for PC-MRI flow measurement.
The imaging plane for aAo flow was located in the ascending aorta distal to the aortic valve and coronary ostia. The imaging plane for flow in the PA was located downstream from the pulmonary valve and proximal to the bifurcation. The imaging planes for the LPA and RPA were located ~1 cm distal to the pulmonary bifurcation. All imaging planes were prescribed on the cine images during end-systole with end-expiratory breath holds.
PC-MRI flow measurements were obtained using the same sequence parameters as in the in vitro phantom experiments with the following changes: 8.5 ms TR, 4.92/5.54 ms TEIN/TE+π/2, 340 × 233 FOV, 256 × 160 matrix, 1.3 mm × 1.3 mm × 6 mm acquisition voxel, BWs of 399 Hz/pixel (LBW) and 814 Hz/pixel (HBW), and a VENC of 125 cm/s for all flow territories.
Note that the minimum available TR at LBW was used during HBW scans in order to ensure the resulting differences in the PC-MRI measurements were only due to the change in BW, and not due to changes in TR.
Image Processing
Data were processed offline using MATLAB (The MathWorks, Natick, MA) and a DICOM viewing tool (Osirix, www.osirix-viewer.com). Eddy current correction was conducted through the use of a stationary phantom (8,27–29) for in vivo studies after the subject was removed from the scanner and, in the case of the in vitro phantom studies, with the flow turned off. For quantitative flow assessment, a region-of-interest (ROI) was drawn in Osirix for each vessel territory. This same ROI was copied into the stationary eddy current phantom images and background phase errors were subtracted in MATLAB. The net forward flow was calculated as described in the Methods section for the computational simulations.
Statistical Analysis
Chemical Shift Effects on Net Forward Flow
An analysis of the maximum difference (ΔMax) in the measured net forward flow for measurements obtained in the aAo, PA, RPA, and LPA at LBW-TEIN, HBW-TEIN, HBW-TE+π/2, and LBW-TE+π/2 for ten patients was conducted. Pulmonary to systemic blood flow ratios (Qp/Qs, PA flow divided by aAo flow) were calculated for each individual. A two-sample t-test with Holm-Sidak post hoc correction was used to measure the statistical significance of the differences in ΔMax between vessels with and without perivascular fat and Qp/Qs at HBW-TEIN vs. LBW-TE+π/2. Additionally, the mean ΔMax was calculated for each patient’s flow territory in mL and also as a percentage (percent mean ΔMax).
Relative Blood Flow Comparison
For the in vivo experiments, according to Eq. [5] and Fig. 3, we expect the net forward flow measurements to be ordered as follows:
| [10] |
Blood Flow Comparison Between Flow Territories
Bland-Altman (30) plots were constructed to show that the reduction of chemical shift induced flow errors improved the intra-patient agreement of flow in the various territories as evidenced by a decrease in the measurement bias (mean difference between the two measurements) and limits of agreement (95% confidence intervals, 95%-CI) between the net forward flow in the aAo and PA, aAo and RPA+LPA, and PA and RPA+LPA at HBW-TEIN and LBW-TE+π/2. In addition, the measurement bias was evaluated using a paired t-test with Holm-Sidak post hoc correction.
RESULTS
Computational Simulations versus In Vitro Phantom Studies
Figure 4a demonstrates that constant laminar flow computational simulations and in vitro phantom studies show nearly identical chemical shift effects over a range of BWs and TEs. Net flow results follow the expected trends of Eq. [5], with HBW-TEIN being closest to programmed volume flow rate (“Truth”=48mL) and LBW-TE+π/2 being furthest from “Truth.” The 3T tri-phasic laminar flow computational simulations (Fig. 4c) overestimate the net forward flow compared to “Truth” at LBW-TE+π/2 (54mL vs. 48 mL, 12%) compared to HBW-TEIN (47.9 mL vs. 48 mL, 0.2%), whereas the 1.5T tri-phasic laminar flow computational simulations (Fig. 4e) overestimate the net forward flow LBW-TE+π/2 (50mL vs. 48 mL, 4%) compared to HBW-TEIN (47.9 mL vs. 48 mL, 0.2%).
Figure 4.
Impact of receiver bandwidth (BW) and echo time (TE) on PC-MRI flow measurements. (a) Constant laminar flow computer simulations (dots) and in vitro (bars) 3T results show nearly identical chemical shift effects (“Truth”=48mL). Computer simulations of constant laminar flow (b,d) and tri-phasic flow (c,e) at 3T and 1.5T demonstrate that the use of HBW-TEIN is closest to the known flow of 48mL and has the least chemical shift induced PC-MRI errors. Other BW and TE combinations at 3T (1.5T) can lead to as much as a 12% (3%) underestimate (LBW-TE−π/2) or a 12% (4%) overestimate (LBW-TE+π/2) for tri-phasic flow.
In Vivo Studies
Chemical Shift Effects on Net Forward Flow
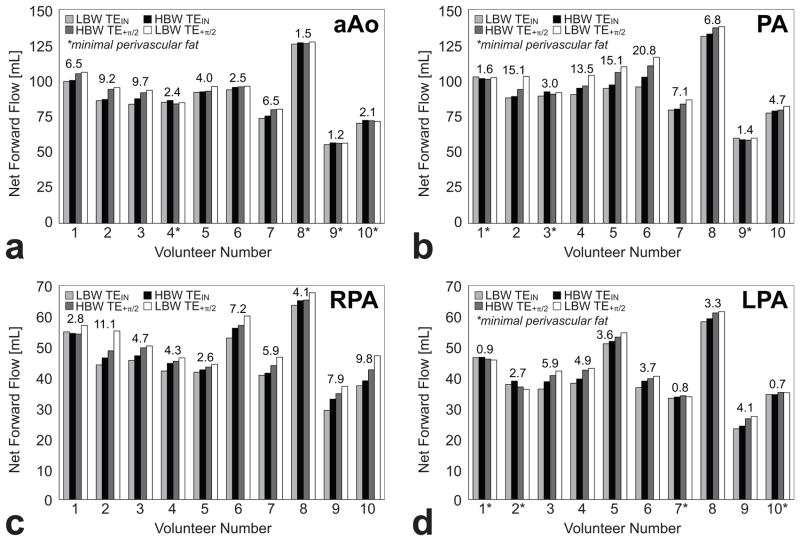
Not every volunteer had visible perivascular fat surrounding every measured vessel (Fig. 5). To qualitatively illustrate the effects of chemical shift the net forward flow data from the aAo, PA, RPA, and LPA at LBW-TEIN, HBW-TEIN, HBW-TE+π/2, and LBW-TE+π/2 for all ten patients were arranged in a bar-chart to show that changing the BW and TE can systematically lead to changes in measured flow. The results for each vessel are arranged in order of their theoretically expected trend (Fig. 6). For vessels in which minimal perivascular fat was observed in the TSE images (annotated with an * below each dataset) the bar-charts appear much flatter (low ΔMax) than vessels wherein perivascular fat was detected. In the presence of perivascular fat the bar-charts step upward from LBW-TEIN (smallerΔMax) to LBW-TE+π/2 (larger ΔMax) as expected in Eq. [5].
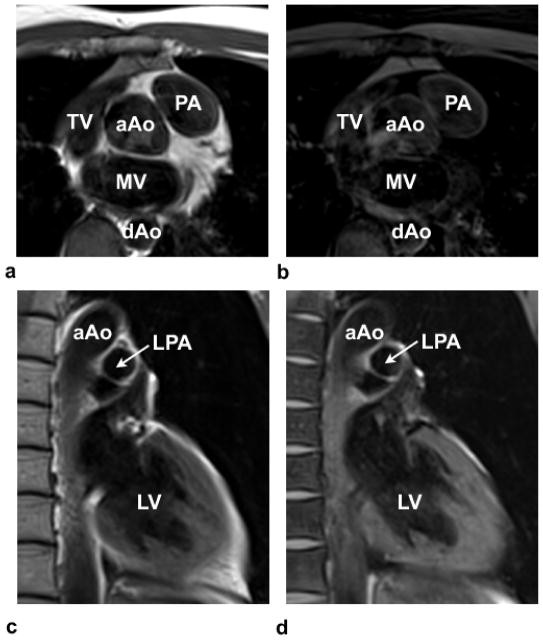
Figure 5.
Turbo spin-echo (TSE) (a,c) and TSE with Fat-Sat images (b,d) highlight the presence of perivascular fat, especially around the PA in (a) and (b) and the lack of perivascular fat around the LPA in (c) and (d). TV-Tricuspid valve; MV-mitral valve; aAo-ascending aorta; and dAo-descending aorta; PA-pulmonary artery; LPA-left pulmonary artery; LV-left ventricle.
Figure 6.
Net forward flow (mL) data from the ascending aorta (aAo), main pulmonary artery (PA), right pulmonary artery (RPA), and left pulmonary artery (LPA) at LBW-TEIN, HBW-TEIN, HBW-TE+π/2, and LBW-TE+π/2 in normal subjects (N=10). The maximum difference (ΔMax) in the measured net forward flow is presented above each dataset. An asterisk (‘*’) is used to indicate that minimal perivascular fat was observed in the TSE images. In general, the trends follow the trend expected from Eq. [5]. a) The mean ΔMax in the aAo are small compared to other vascular territories due to the small amounts of observed perivascular fat and a thicker vessel wall. b) The chemical shift induced flow measurement errors in the PA can be large due to the presence of perivascular fat and a relatively thin vessel wall. c) Note that no subject had an RPA that was identified as having minimal perivascular fat, whereas this was common in the aAo, PA, and LPA. Additionally, the thin wall of the RPA makes it easy for perivascular fat to spatially shift into the vessel lumen. Therefore, all subjects’ RPAs were susceptible to chemical shift induced flow errors. d) Perivascular fat was not as consistently observed in the LPA compared to the RPA. Additionally, the thin wall of the LPA makes it easy for perivascular fat to spatially shift into the vessel lumen.
The ΔMax in aAo, PA, LPA, and all vessels with fat is significantly greater than ΔMax in those vessels with minimal perivascular fat (Table 1). The analysis could not be conducted in the RPA because every vessel had visible perivascular fat.
Table 1.
Comparison of the maximum difference between LBW-TEIN, HBW-TEIN, HBW-TE+π/2, and LBW-TE+π/2 forward flow measurements in the aAo, PA, RPA, and LPA in normal subjects.
| ΔMax No Fat [mL] | ΔMax Fat [mL] | n/m | * P-Value | |
|---|---|---|---|---|
| aAo | 1.8 ± 0.5 | 6.4 ± 2.8 | 4/6 | 0.01 |
| PA | 2.0 ± 0.9 | 11.9 ± 5.8 | 3/7 | 0.04 |
| RPA | -- | 6.0 ± 2.9 | 0/10 | -- |
| LPA | 1.3 ± 1.0 | 4.3 ± 1.0 | 4/6 | 0.003 |
|
| ||||
| All Vessels | 1.7 ± 0.8 | 7.2 ± 4.4 | 10/30 | 0.001 |
Data is expressed as mean ± standard deviation in mL.
n is the number of vessels where minimal perivascular fat was observed.
m is the number of vessels where perivascular fat was observed.
P-values<0.05 show a significant difference in ΔMax indicating the presence of perivascular fat leads to significant flow errors in PC-MRI.
The mean ΔMax and percent mean Δ Max for the aAo, PA, RPA, and LPA is summarized in Table 2. The mean Δ Max was greatest in the PA (8.9±6.7 mL) and smallest in the LPA (3.1±1.8 mL). The percent mean Δ Max was greatest in the RPA (13.8±7.9%) where every vessel had observed perivascular fat and the vessel wall was thinnest. The percent mean Δ Max was smallest in the aAo (5.3±3.7%) where perivascular fat was not observed in 4 of the 10 vessels and had the thickest vessel walls.
Table 2.
Comparison of the mean maximum difference between LBW-TEIN, HBW-TEIN, HBW-TE+π/2, and LBW-TE+π/2 forward flow measurements in the aAo, PA, RPA, and LPA in normal subjects (N=10).
| Mean ΔMax [mL] | Percent Mean ΔMax | |
|---|---|---|
| aAo | 4.6 ± 3.2 | 5.3 ± 3.7 |
| PA | 8.9 ± 6.7 | 9.4 ± 6.8 |
| RPA | 6.0 ± 2.9 | 13.8 ± 7.9 |
| LPA | 3.1 ± 1.8 | 8.0 ± 5.5 |
Data is expressed as mean ± standard deviation in mL.
Relative Blood Flow Comparison
The measured phase at LBW-TEIN, HBW-TEIN, HBW-TE+π/2, and LBW-TE+π/2 follow the expected trends of Eq. [10] for all of the volunteers. Note that when there is not an apparent trend this is always associated with a lack of observable perivascular fat in the black blood TSE images, hence the trend is still as expected. The Qp/Qs ratios were closer to one with lower variance when measured with HBW-TEIN and compared to LBW-TE+π/2 (1.05±0.03 vs. 1.08±0.09, p=0.10), but not statistically different.
Blood Flow Comparison Between Flow Territories
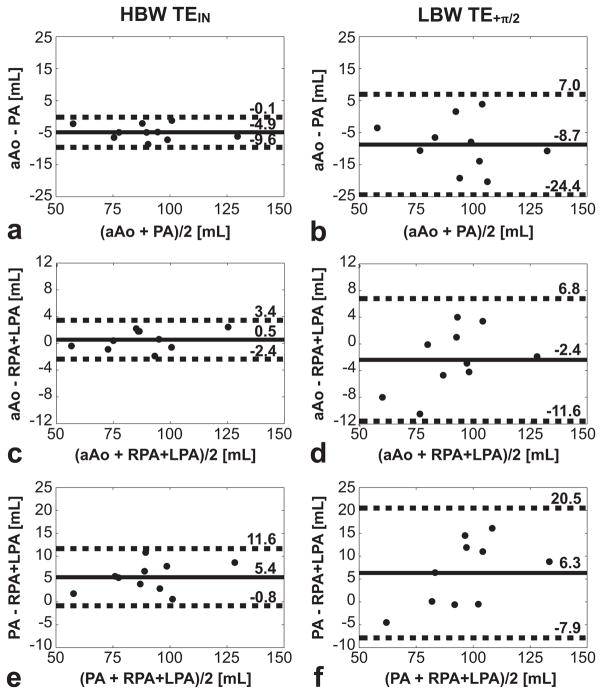
The Bland-Altman plots and statistics (Fig. 6) show higher internal consistency (lower bias and smaller 95%-CIs) at HBW TEIN compared to LBW TE+π/2 across all flow territories.
The magnitude of the bias in net forward flow between the aAo and PA, aAo and RPA+LPA, and PA and RPA+LPA demonstrates a larger flow discrepancy in different subjects when using LBW-TE+π/2 compared to HBW-TEIN (Table 3). The PA vs. RPA+LPA comparison failed to reach a significant statistical difference due to the fact that seven of the thirty vessels in this comparison did not have notable perivascular fat.
Table 3.
Comparison of the bias (mean difference) between HBW-TEIN and LBW-TE+π/2 forward flow measurements in the aAo vs. PA, aAo vs RPA+LPA, and PA vs. RPA+LPA in normal subjects (N=10).
| HBW-TEIN | LBW-TE+π/2 | * P-Value | |
|---|---|---|---|
| aAo vs. PA | 4.9 ± 2.4 | 9.8 ± 6.4 | 0.01 |
| aAo vs. RPA+LPA | 1.3 ± 0.8 | 4.0 ± 3.2 | 0.03 |
| PA vs. RPA+LPA | 5.4 ± 3.1 | 7.4 ± 5.9 | 0.25 |
| †PA vs. RPA+LPA | 2.0 ± 0.3 | 5.0 ± 2.9 | 0.03 |
Data is expressed as mean ± standard deviation in mL.
Excludes seven vessels that contained minimal perivascular fat.
P<0.05 show a significant difference in the measurement bias indicating HBW-TEIN is less susceptible to chemical shift flow errors compared to LBW-TE+π/2.
The bias in net forward flow between the aAo and PA, aAo and RPA+LPA, and PA and RPA+LPA was shown to be significantly lower at HBW-TEIN compared to LBW-TE+π/2 (Table 3). The PA vs. RPA+LPA comparison failed to reach a significant statistical difference likely due to the fact that seven of the ten vessels in this comparison contained no notable perivascular fat. If these seven vessels were excluded from the statistical comparison, the comparison reaches statistical significance. The internal consistency between the net forward flow in the aAo and RPA+LPA was higher at both HBW-TEIN (0.5 mL bias) and LBW-TE+π/2 (−2.4 mL bias) compared to across any other vessel combination.
DISCUSSION
Both theory and an in vivo comparison of the maximum difference in net forward flow between vessels with and without perivascular fat indicated that the effects of chemically shifted perivascular fat are minimized by the use HBW-TEIN. In healthy volunteers (N=10) HBW-TEIN significantly improves intrapatient net forward flow agreement as indicated by decreased measurement biases and limits of agreement across the ascending aorta, pulmonary artery, left pulmonary artery, and all vessels (Table 3 and Fig. 7).
Figure 7.
Bland-Altman analysis of the net forward flow in the ascending aorta (aAo), main pulmonary artery (PA), and right and left pulmonary branches (RPA and LPA) in normal subjects (N=10). The solid lines represent the measurement bias while the dashed lines represent the limits of agreement (95%-CIs). (a) Bland-Altman statistics for aAo versus PA at HBW-TEIN; (b) aAo versus PA at LBW-TE+π/2; (c) aAo versus RPA+LPA at HBW-TEIN; (d) aAo versus RPA+LPA at LBW-TE+π/2; (e) PA versus RPA+LPA at HBW-TEIN; (f) PA versus RPA+LPA at LBW-TE+π/2. The measurement bias and limits of agreement are reduced at HBW-TEIN (a, c, e) compared to LBW- TE+π/2 (b, d, f) for all flow territories. The HBW-TEIN measurements are less susceptible to chemical shift induced errors and demonstrate better internal consistency.
In these experiments we suggest that the use of HBW-TEIN mitigates chemical shift induced phase errors, but increasing the spatial resolution will also help, all other things being equal. Throughout the description of chemical shift effects on quantitative PC-MRI measurements we have assumed that fat has a single resonant peak, which belies the spectral complexity of fat. Additionally, this means that even at TEIN, not all spectral components of fat are in phase with water.
It is important to note that perivascular fat is not always present; therefore not all PC-MRI flow measures are subject to errors from chemical shift effects. Additionally, the presence or absence of perivascular fat can lead to spurious agreement or disagreement in PC-MRI flow measures between territories. For example, the presence of perivascular fat could erroneously leads to a good or poor agreement in flow across the aAo, PA, and RPA+LPA. Although the internal consistency may be observed to be high, the flow in each territory could be over- or underestimated due to chemical shift errors.
The observed error arising from the chemical shift effect is greater in our in vivo studies and tri-phasic laminar computational simulations compared to our in vitro studies (Fig. 4 and Table 1) due to differences in the velocity profiles. The chemical shift induced flow error is larger for dynamic flow when compared to constant laminar flow and the largest for TE+π/2, when the total true forward flow is the same. This effect is evident in Fig. 4 and arises as a consequence of the fact that dynamic flow has more low-velocity pixels, which are the most effected by these chemical shift induced errors.
Fat-water separated PC-MRI should be considered to solve for both the phase of fat and the phase of water, thereby eliminating the contamination of the water phase by perivascular fat phase (31). The physics and mathematics of this problem are interesting, but the clinical utility of this approach is uncertain. This approach requires the acquisition of additional imaging data, which may prohibitively increases breath hold duration or significantly decrease spatial and/or temporal resolution.
In addition, fat saturation techniques could be combined with PC-MRI to minimize chemical shift induced phase errors. Fat saturation techniques, however, are spatially inhomogeneous and provide inconsistent fat saturation throughout the cardiac cycle and therefore may require multiple saturation pulses to be effective.
The results of this study focused entirely on Cartesian based trajectories. Non-Cartesian trajectories, such as radial and spiral, lead to distortion and blurring of the fat signal (31,32). This blurring effect may not be as resilient to the proposed chemical shift reduction strategy (HBW-TEIN) and may necessitate the use of spatial-spectral pulses (33) or non-Cartesian based multipoint fat-water separation techniques (e.g. IDEAL (31) or Dixon (34))
Breathing artifacts and parallel imaging reconstruction artifacts, for example, can cause the signal from fat in regions distant from a vessel (e.g. subcutaneous fat) to alias into a vessel and corrupt the phase. Under these conditions the magnitude of the error is governed by the relative magnitudes and phases of the superposed fat and flowing blood signals and can lead to large errors in both velocity and flow.
Limitations
This study compared the results at TEIN and TE+π/2 as a means of characterizing and quantifying the effects of chemical shift. In clinical practice, it is common to use the minimum available TE, which may or may not be near the TEs chosen for this study. In our clinical setting, the minimum TE used at 1.5T and 3T are 2.67ms and 1.99ms, respectively. These TEs differ from TEIN by 202° (approximately TEOUT) and 291° (approximately TE−π/2), implying that the use of these minimum clinical TEs can lead to a significant deviation in net forward flow, especially at 3T.
The use of HBW leads to a reduction in chemical shift induced phase errors, but also leads to an inherent reduction in both SNR and velocity-to-noise (35,36). Based on our theoretical description of chemical shift induced phase errors, future work is needed to define the imaging BW that provides optimal quantitative PC-MRI accuracy. Westenberg et al. reported previously that a 55% reduction in SNR (187±116 vs. 84±60) did not lead to flow inaccuracies in measurements across the mitral valve (37). Our SNR measurements indicate that both the LBW (103±6) and HBW (72±4) data are similar to Westenberg’s acceptable and lower SNR measures. Therefore, the trends in our net forward flow results were largely chemical shift related and not SNR related. The use of HBW at 1.5T may lead to an SNR below these acceptable levels.
The in vitro and in vivo studies were conducted at 3T field strength. The spatial shift of chemically shifted perivascular fat at 1.5T is half of that at 3T because δf1.5T ≈ ½δf3T (38), which leads to ~1/2 the spatial shift and half the off-resonance phase accumulation for fat at 1.5T. Therefore, the chemical shift induced phase error is lower at 1.5T when spatial resolution and SNR effects are not considered (Fig. 4d–e). The SNR performance of 1.5T, however, is ~1/2 that of 3T and to compensate for this, larger imaging voxels and/or lower bandwidths are typically employed; both of which increase chemical shift induced phase errors. Therefore, depending on the specific imaging parameters, quantitative PC-MRI measurements conducted at 1.5T are susceptible to similar chemical shift induced flow quantification errors.
All subjects included in this study were normal healthy volunteers. We propose that HBW and TEIN parameters in PC-MRI minimize the phase corrupting effects of chemical shift, but this needs to be clinically validated in patients. In doing so, the assumption that flow at the vessel lumen periphery is near-zero, may not be true due to complex flow patterns, areas of turbulent flow, and partial volume effects. In future studies involving clinical patients with complex flow patterns, the optimum TE for the minimization of chemical shift effects may be different than TEIN, because the flow won’t meet the requirement of being near-zero near the vessel wall. Under these circumstances fat-water separated or fat-saturation PC-MRI techniques may be necessary.
Acknowledgments
The authors thank J. Paul Finn, Abbas Moghaddam, Yutaka Natsuaki, and Meral Reyhan for their feedback and discussion as well as Francine Cobla, Sergio Godinez, and Glen Nyborg for their MRI planning assistance and cooperation. This work is supported in part by NIH/NHLBI K99-R00 HL-087614 and Siemens Medical Solutions to D.B.E.
References
- 1.Lotz J, Meier C, Leppert A, Galanski M. Cardiovascular flow measurement with phase-contrast MR imaging: basic facts and implementation. Radiographics. 2002;22(3):651–671. doi: 10.1148/radiographics.22.3.g02ma11651. [DOI] [PubMed] [Google Scholar]
- 2.Pelc NJ. Flow quantification and analysis methods. Magn Reson Imaging Clin N Am. 1995;3(3):413–424. [PubMed] [Google Scholar]
- 3.Firmin DN, Nayler GL, Klipstein RH, Underwood SR, Rees RS, Longmore DB. In vivo validation of MR velocity imaging. J Comput Assist Tomogr. 1987;11(5):751–756. doi: 10.1097/00004728-198709000-00001. [DOI] [PubMed] [Google Scholar]
- 4.Attili AK, Parish V, Valverde I, Greil G, Baker E, Beerbaum P. Cardiovascular MRI in childhood. Arch Dis Child. doi: 10.1136/adc.2009.179051. [DOI] [PubMed] [Google Scholar]
- 5.Wang ZJ, Reddy GP, Gotway MB, Yeh BM, Higgins CB. Cardiovascular shunts: MR imaging evaluation. Radiographics. 2003;23(Spec No):S181–194. doi: 10.1148/rg.23si035503. [DOI] [PubMed] [Google Scholar]
- 6.Devos DG, Kilner PJ. Calculations of cardiovascular shunts and regurgitation using magnetic resonance ventricular volume and aortic and pulmonary flow measurements. Eur Radiol. 20(2):410–421. doi: 10.1007/s00330-009-1568-2. [DOI] [PubMed] [Google Scholar]
- 7.Kilner PJ, Geva T, Kaemmerer H, Trindade PT, Schwitter J, Webb GD. Recommendations for cardiovascular magnetic resonance in adults with congenital heart disease from the respective working groups of the European Society of Cardiology. Eur Heart J. 31(7):794–805. doi: 10.1093/eurheartj/ehp586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chernobelsky A, Shubayev O, Comeau CR, Wolff SD. Baseline correction of phase contrast images improves quantification of blood flow in the great vessels. J Cardiovasc Magn Reson. 2007;9(4):681–685. doi: 10.1080/10976640601187588. [DOI] [PubMed] [Google Scholar]
- 9.Bernstein MA, Zhou XJ, Polzin JA, King KF, Ganin A, Pelc NJ, Glover GH. Concomitant gradient terms in phase contrast MR: analysis and correction. Magn Reson Med. 1998;39(2):300–308. doi: 10.1002/mrm.1910390218. [DOI] [PubMed] [Google Scholar]
- 10.Markl M, Bammer R, Alley MT, Elkins CJ, Draney MT, Barnett A, Moseley ME, Glover GH, Pelc NJ. Generalized reconstruction of phase contrast MRI: analysis and correction of the effect of gradient field distortions. Magn Reson Med. 2003;50(4):791–801. doi: 10.1002/mrm.10582. [DOI] [PubMed] [Google Scholar]
- 11.Bernstein MA, Ikezaki Y. Comparison of phase-difference and complex-difference processing in phase-contrast MR angiography. J Magn Reson Imaging. 1991;1(6):725–729. doi: 10.1002/jmri.1880010620. [DOI] [PubMed] [Google Scholar]
- 12.Ferrigno M, Hickey DD, Liner MH, Lundgren CE. Cardiac performance in humans during breath holding. J Appl Physiol. 1986;60(6):1871–1877. doi: 10.1152/jappl.1986.60.6.1871. [DOI] [PubMed] [Google Scholar]
- 13.Paulev P, Wetterqvist H. Cardiac output during breath-holding in man. Scand J Clin Lab Invest. 1968;22(2):115–123. doi: 10.3109/00365516809160955. [DOI] [PubMed] [Google Scholar]
- 14.Bernstein MA, Shimakawa A, Pelc NJ. Minimizing TE in moment-nulled or flow-encoded two- and three-dimensional gradient-echo imaging. J Magn Reson Imaging. 1992;2(5):583–588. doi: 10.1002/jmri.1880020517. [DOI] [PubMed] [Google Scholar]
- 15.Bryant DJ, Payne JA, Firmin DN, Longmore DB. Measurement of flow with NMR imaging using a gradient pulse and phase difference technique. J Comput Assist Tomogr. 1984;8(4):588–593. doi: 10.1097/00004728-198408000-00002. [DOI] [PubMed] [Google Scholar]
- 16.Nayler GL, Firmin DN, Longmore DB. Blood flow imaging by cine magnetic resonance. J Comput Assist Tomogr. 1986;10(5):715–722. doi: 10.1097/00004728-198609000-00001. [DOI] [PubMed] [Google Scholar]
- 17.Polzin JA, Alley MT, Korosec FR, Grist TM, Wang Y, Mistretta CA. A complex-difference phase-contrast technique for measurement of volume flow rates. J Magn Reson Imaging. 1995;5(2):129–137. doi: 10.1002/jmri.1880050202. [DOI] [PubMed] [Google Scholar]
- 18.Spritzer CE, Pelc NJ, Lee JN, Evans AJ, Sostman HD, Riederer SJ. Rapid MR imaging of blood flow with a phase-sensitive, limited-flip-angle, gradient recalled pulse sequence: preliminary experience. Radiology. 1990;176(1):255–262. doi: 10.1148/radiology.176.1.2353099. [DOI] [PubMed] [Google Scholar]
- 19.Soila KP, Viamonte M, Jr, Starewicz PM. Chemical shift misregistration effect in magnetic resonance imaging. Radiology. 1984;153(3):819–820. doi: 10.1148/radiology.153.3.6494479. [DOI] [PubMed] [Google Scholar]
- 20.Gao JH, Holland SK, Gore JC. Nuclear magnetic resonance signal from flowing nuclei in rapid imaging using gradient echoes. Med Phys. 1988;15(6):809–814. doi: 10.1118/1.596197. [DOI] [PubMed] [Google Scholar]
- 21.Edden RA, Smith SA, Barker PB. Longitudinal and multi-echo transverse relaxation times of normal breast tissue at 3 Tesla. J Magn Reson Imaging. 32(4):982–987. doi: 10.1002/jmri.22306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med. 2005;54(3):507–512. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- 23.Govindaraju V, Young K, Maudsley AA. Proton NMR chemical shifts and coupling constants for brain metabolites. NMR Biomed. 2000;13(3):129–153. doi: 10.1002/1099-1492(200005)13:3<129::aid-nbm619>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 24.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002;47(6):1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 25.Tanaka S, Yoshiyama M, Imanishi Y, Nakahira K, Hanaki T, Naito Y, Imai M, Tanaka M. MR measurement of visceral fat: assessment of metabolic syndrome. Magn Reson Med Sci. 2006;5(4):207–210. doi: 10.2463/mrms.5.207. [DOI] [PubMed] [Google Scholar]
- 26.Tanaka S, Yoshiyama M, Imanishi Y, Teragaki M, Kasayuki N, Shimizu N, Nakahira K, Hanaki T, Naito Y, Tanaka M, Inoue Y. Measuring visceral fat with water-selective suppression methods (SPIR, SPAIR) in patients with metabolic syndrome. Magn Reson Med Sci. 2007;6(3):171–175. doi: 10.2463/mrms.6.171. [DOI] [PubMed] [Google Scholar]
- 27.Gatehouse PD, Rolf MP, Graves MJ, Hofman MB, Totman J, Werner B, Quest RA, Liu Y, von Spiczak J, Dieringer M, Firmin DN, van Rossum A, Lombardi M, Schwitter J, Schulz-Menger J, Kilner PJ. Flow measurement by cardiovascular magnetic resonance: a multi-centre multi-vendor study of background phase offset errors that can compromise the accuracy of derived regurgitant or shunt flow measurements. J Cardiovasc Magn Reson. 12:5. doi: 10.1186/1532-429X-12-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holland BJ, Printz BF, Lai WW. Baseline correction of phase-contrast images in congenital cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 12:11. doi: 10.1186/1532-429X-12-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Miller TA, Landes AB, Moran AM. Improved accuracy in flow mapping of congenital heart disease using stationary phantom technique. J Cardiovasc Magn Reson. 2009;11:52. doi: 10.1186/1532-429X-11-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1(8476):307–310. [PubMed] [Google Scholar]
- 31.Johnson KM, Wieben O, Samsonov AA. Phase-contrast velocimetry with simultaneous fat/water separation. Magn Reson Med. 2010;63(6):1564–1574. doi: 10.1002/mrm.22355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Brodsky EK, Holmes JH, Yu H, Reeder SB. Generalized k-space decomposition with chemical shift correction for non-Cartesian water-fat imaging. Magn Reson Med. 2008;59(5):1151–1164. doi: 10.1002/mrm.21580. [DOI] [PubMed] [Google Scholar]
- 33.Meyer CH, Pauly JM, Macovski A, Nishimura DG. Simultaneous spatial and spectral selective excitation. Magn Reson Med. 1990;15(2):287–304. doi: 10.1002/mrm.1910150211. [DOI] [PubMed] [Google Scholar]
- 34.Moriguchi H, Lewin JS, Duerk JL. Dixon techniques in spiral trajectories with off-resonance correction: A new approach for fat signal suppression without spatial-spectral RF pulses. Magn Reson Med. 2003;50:915–924. doi: 10.1002/mrm.10629. [DOI] [PubMed] [Google Scholar]
- 35.Pelc NJ, Sommer FG, Li KC, Brosnan TJ, Herfkens RJ, Enzmann DR. Quantitative magnetic resonance flow imaging. Magn Reson Q. 1994;10(3):125–147. [PubMed] [Google Scholar]
- 36.Anderson A, Kirsch J. Analysis of noise in phase contrast MR imaging. Med Phys. 1996;23(6):857–869. doi: 10.1118/1.597729. [DOI] [PubMed] [Google Scholar]
- 37.Westenberg JJ, Roes SD, Ajmone Marsan N, Binnendijk NM, Doornbos J, Bax JJ, Reiber JH, de Roos A, van der Geest RJ. Mitral valve and tricuspid valve blood flow: accurate quantification with 3D velocity-encoded MR imaging with retrospective valve tracking. Radiology. 2008;249(3):792–800. doi: 10.1148/radiol.2492080146. [DOI] [PubMed] [Google Scholar]
- 38.Lufkin R, Anselmo M, Crues J, Smoker W, Hanafee W. Magnetic field strength dependence of chemical shift artifacts. Comput Med Imaging Graph. 1988;12(2):89–96. doi: 10.1016/0895-6111(88)90002-x. [DOI] [PubMed] [Google Scholar]