Coil Compression for Accelerated Imaging with Cartesian Sampling

Abstract

MRI using receiver arrays with many coil elements can provide high signal-to-noise ratio and increase parallel imaging acceleration. At the same time, the growing number of elements results in larger datasets and more computation in the reconstruction. This is of particular concern in 3D acquisitions and in iterative reconstructions. Coil compression algorithms are effective in mitigating this problem by compressing data from many channels into fewer virtual coils. In Cartesian sampling there often are fully sampled k-space dimensions. In this work, a new coil compression technique for Cartesian sampling is presented that exploits the spatially varying coil sensitivities in these non-subsampled dimensions for better compression and computation reduction. Instead of directly compressing in k-space, coil compression is performed separately for each spatial location along the fully-sampled directions, followed by an additional alignment process that guarantees the smoothness of the virtual coil sensitivities. This important step provides compatibility with autocalibrating parallel imaging techniques. Its performance is not susceptible to artifacts caused by a tight imaging fieldof-view. High quality compression of in-vivo 3D data from a 32 channel pediatric coil into 6 virtual coils is demonstrated.

Introduction

With the development of parallel imaging (PI) (1–3), MRI data acquisitions have been significantly accelerated. This has made many lengthy MR exams clinically feasible. PI uses receiver arrays with multiple coils (4) to simultaneously acquire data. The different coil sensitivities of the receiver coils are used to partially replace traditional k-space encoding and reduce scan time. In addition to PI, there is a growing trend towards utilizing constrained reconstructions in MRI, such as compressed sensing (CS) (5). These techniques use prior information to achieve better image quality, enhanced resolution, and improved signal-to-noise ratio (SNR). Higher accelerations in data acquisition can be achieved by combining CS with PI (6–8). These reconstructions are often iterative and therefore much more computationally intensive.

Because of the obvious benefits of large coil arrays for SNR and acceleration, both researchers and manufacturers have been developing and building large dedicated arrays (9–12). These large coil arrays enable even faster data acquisition with high SNR. However, the reconstruction and data storage of these large datasets are becoming increasingly problematic, especially for 3D and dynamic acquisitions. To reduce the computation cost with large receiver arrays, coil compression (13–15) can be used. Coil compression linearly combines the raw data from multiple coils into fewer virtual coils. Since the computation required for PI reconstruction and constrained reconstruction is highly dependent on the number of coils, reconstruction time can be significantly reduced by coil compression.

Coil compression was first applied in hardware (15, 16). The original multiple coils are linearly combined into fewer eigencoils using the knowledge of the noise covariance of the receiver array. However, since this hardware combiner does not take into consideration the spatially varying coil sensitivities or the received data, the compression is often not optimal. This leads to large compression signal loss.

Software coil compression algorithms are more flexible and provide higher accuracy. Several techniques have been developed so far. The method by Buehrer et al. requires the explicit knowledge of the coil sensitivities (13). Compression is achieved by optimizing the SNR in a region of interest (ROI) in the reconstructed image. This type of coil compression is suitable for sensitivity-based PI reconstructions like SENSE (1). Doneva et al. presented a different approach based on automatic selection of the “best” subset of coils (17). The individual coils are selected by a ranking that quantifies the contribution of each coil element to the reconstructed image. This type of coil compression requires the coil sensitivity measurements as well. Similar coil subset selection was applied to channel-by-channel parallel reconstruction by Feng et al. (18). Huang et al. proposed a data-based coil compression that does not require the coil sensitivity measurements and is solely based on the acquired data (14). This method is fast, and it works well with autocalibrating PI (ACPI) and CS. Channel-by-channel parallel reconstruction can also be speeded up by reconstructing a single direct virtual coil (19) or a synthetic target coil (20). A generalized hybrid method of compressing both the source channels and target channels has been recently proposed by Huang et al. (21).

All these software coil compression methods have been well demonstrated for 2D Cartesian data acquisitions. Coil compression for non-Cartesian BLADE acquisitions has been studied by Stemmer et al. (22). For 3D datasets, the direct extension of these coil compression methods is usually applied (14). The original coils are combined by the same linear coil compression weights for the entire 3D dataset. Since the coil sensitivities vary spatially in 3D, this direct extension needs more virtual coils to achieve a negligible compression loss. Huang et al. studied a spatially varying coil compression for 3D datasets with one phase encoding direction fully sampled (23), but no major advantages were reported.

In this work, a data-based coil compression method for accelerated Cartesian acquisitions is introduced. It is based on a geometric decomposition of the data. In Cartesian acquisitions, there are often one or more dimensions that are fully sampled (e.g., the readout direction), and the variation of the coil sensitivities along these dimensions is not utilized to accelerate data acquisition. The proposed method minimizes the number of virtual coils (hence the reconstruction time) using a spatially varying coil compression. Coil compression is performed separately for each location along the fully sampled dimensions by a singular value decomposition (SVD). Then the spatially varying compression matrices are carefully aligned so that the virtual coils have smooth coil sensitivities. The smoothness of the coil sensitivities is crucial for the calibration step in ACPI methods, where the unacquired data are synthesized from data at multiple adjacent locations in the readout direction (24). In addition, because the coil compression is performed in k-space, this approach is not susceptible to tight imaging field-of-view (FOV) artifacts (25). Using in-vivo data acquired with a 32 channel dedicated pediatric coil array, we demonstrate near lossless geometric-decomposition coil compression (GCC) from 32 original coils to 6 virtual coils. The ACPI and CS reconstruction of data in the 6 virtual coils requires approximately 14 times less computation than that of the original data, without image quality degradation.

Theory

Data Redundancy and Coil Compression

In PI, the different coil sensitivities of the receiver array coils are used to accelerate data acquisition by subsampling k-space and reconstruct the missing data (1–3). Square root of sum-of-square (SSOS) images are usually used to combine individual coil images (4). Assume N is the number of the original coils used for data acquisition. At each location k = [k_x , k_y , k_z]^T in k-space, define a vector $v^o\left(k\right)={[v_1^o\left(k\right),v_2^o\left(k\right),\cdots ,v_N^o\left(k\right)]}^T$ that represents data at this location from all the original coils. The acquired raw data v^o(k) is usually contaminated with noise that can be modeled as a zero mean Gaussian random noise with covariance matrix Ψ. Define a new set of coils with data vectors v(k) = [v₁(k), v₂(k), ..., v_N(k)]^T:

$$v\left(k\right)={\Psi }^{-1∕2}{v}^o\left(k\right),$$ (1)

Then the noise in this set of coils is independently identically distributed (IID) (15). For simplicity, this set of coils (v(k)) is considered as the original set of coils for the rest of this paper.

In most cases, the different coil sensitivity functions do not form an orthogonal basis and often span a subspace with dimension much smaller than the number of coils. This limits the possible acceleration factor of PI. At the same time, this results in large amount of redundant and highly correlated multicoil data. Coil compression algorithms reduce this data redundancy by combining the original multicoil data into fewer virtual coils. The ultimate goal of coil compression is to minimize the number of virtual coils while preserving as much of the signal as possible. Let $A\in {\mathcal{C}}^{M\times N}$ represent a coil compression matrix and the data vector $v^{\prime }\left(k\right)={[v_1^{\prime }\left(k\right),v_2^{\prime }\left(k\right),\cdots ,v_M^{\prime }\left(k\right)]}^T$ represent data at location k from the M virtual coils. Coil compression can be formulated as (13,14):

$$v^{\prime }\left(k\right)=Av\left(k\right),$$ (2)

where we need to find the coil compression matrix A. In this work, we are only interested in the data-based coil compression that does not assume explicit knowledge of the coil sensitivities. Previous studies have shown that the compression matrix A can be found by PCA in data-based coil compression (14). One good property of this compression matrix by PCA is that AA^H = I. Assume n_v(k) is the IID Gaussian noise in v(k), then the noise in v^′(k) is $n_v^{\prime }\left(k\right)=A{n}_v\left(k\right)$. When the acquired data has sufficient SNR (usually true for dedicated coils), this compression matrix A is not sensitive to noise n_v(k) and $n_v^{\prime }\left(k\right)$ is close to IID noise. Sufficient SNR in auto calibration signals (ACS) is assumed for the rest of the paper. SNR measurements in SSOS images can be found in reference (26). The intensity at each pixel in the SSOS image is noncentral chi distributed. Noise in SSOS images can be reduced by coil compression because of the decreased numbers of coils. This is also known as the denoising effect (27).

Since the set of the virtual coils and the set of the original coils approximately span the same space, each original coil can also be approximated by a linear combination of the virtual coils:

$$v\left(k\right)=A^H{v}^{\prime }\left(k\right)+∊,$$ (3)

where ε is the approximation error. If the number of virtual coils is fixed, the coil compression problem can be written as a minimization of the compression error:

$$\begin{array}{cc}\hfill \underset{A}{\text{minimize}}& \sum _k{\Vert (A^{H}A-I)v\left(k\right)\Vert }^2\hfill \\ \hfill \text{subject to}& A{A}^H=I,\hfill \end{array}$$ (4)

The solution for Eq. (4) can also be found by PCA or SVD (13–15).

Geometric-decomposition Coil Compression for Cartesian Sampling

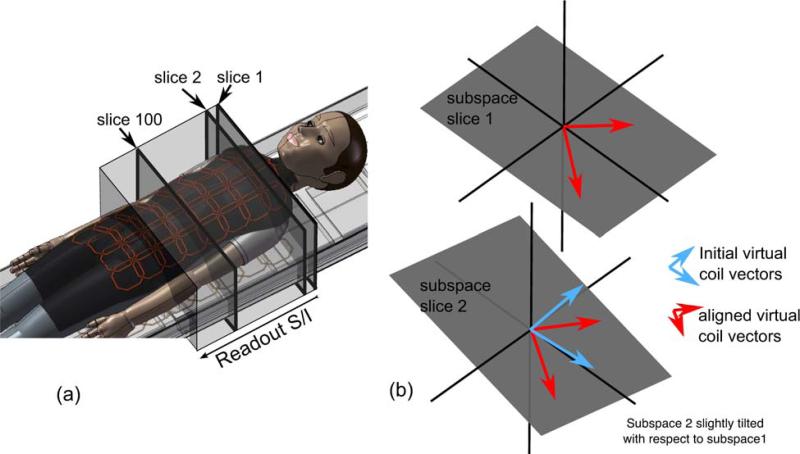
To illustrate the idea behind GCC, let us consider for example the 3D Cartesian case in Fig. 1(a). The figure shows a body coil array, the imaging volume and the readout direction. In general, 3D k-space data obtained using this array will contain non-negligible signal in all the coils. Therefore, straightforward coil compression in k-space using the same compression matrix will often require a substantial number of virtual coils.

Figure 1.

The geometry of GCC and virtual coil alignment in 3D Cartesian imaging. (a) The imaging setup showing a body coil array and the imaging volume with S/I readout. Slices 1 and 2 along the readout “see” the same coils with slightly different sensitivities. On the other hand, slice 100 “sees” a completely different set of coils. This enables better compression after geometric decomposition. (b) Illustration of virtual coil alignment: Data in each slice lies in a smaller subspace (illustrated by planes in 3D) spanned by the compressed virtual coil vectors (arrows). The subspaces of nearby slices are close, but not the same. There are many sets of orthogonal vectors that span each subspace and the ones given by SVD can be arbitrary. The alignment finds new sets of orthogonal vectors in one subspace that are closest to the ones spanning the other. This process guarantees smoothness of the virtual coil sensitivities.

However, slice 1 and slice 100 are seen by a completely different subset of coils in the coil array. One slice represents one spatial location in the readout direction. Since the readout direction is fully sampled, the original data can be spatially decomposed into separable 2D k-spaces by a Fourier transform along the readout direction. Data in each new coordinate (x, k_y, k_z) have non-negligible signal in fewer coils, and can be compressed into a smaller number of virtual coils if different compression matrices are applied at each spatial location. This concept can be extended to decomposition in additional fully sampled dimensions. For simplicity, we will limit most of the discussion to geometric-decomposition only along the readout direction. GCC for 3D Cartesian datasets can be formulated as:

$$\begin{array}{cc}\hfill \underset{A_x}{\text{minimize}}& \sum _{x,k_{yz}}{\Vert (A_x^H{A}_x-I)v\left(k_{yz}\right)\Vert }^2\hfill \\ \hfill \text{subject to}& A_x{A}_x^H=I,\hfill \end{array}$$ (5)

Here, $A_x\in {\mathcal{C}}^{M\times N}$ are a family of compression matrices at different spatial locations along the x axis (the readout direction) and $v_x\left(k_{yz}\right)\in {\mathcal{C}}^{N\times 1}$ are data at some spatial location x and 2D k-space coordinate k_yz = [k_y , k_z]^T in the y — z plane.

This optimization is separable. The compression matrices A_x can be separately calculated by SVD at each x location using the following steps:

1. Compute an inverse Fourier transform of the k-space multicoil data along the readout direction into [x, k_y, k_z] coordinates.

2. At each x location, construct a data matrix X_x in which each row consists of all the v_x(k_yz) from an individual original coil. Often, just ACS data are sufficient.

3. Perform SVD of X_x:

   $$X_x=U_x{\Sigma }_x{\left(V_x\right)}^H,$$ (6)

   Take the first M rows of (U_x)^H to form an initial compression matrix $A_x^0$.

4. Repeat Step 2 and 3 until compression matrices are calculated for all slices.

Virtual Coil Alignment

The SVD method is good at selecting the signal subspace. However, the compression matrices are not unique. In fact, for any unitary matrix $P\in {\mathcal{C}}^{M\times M}$, the product,

$$A_x=P{A}_x^0,$$ (7)

is a valid solution to Eq. (5). Directly using the solution $A_x^0$ obtained by SVD as the compression matrices is likely to introduce non-smooth virtual coil sensitivities along the x direction. This can lead to failure of the ACPI reconstructions, particularly when 3D synthesis kernels are used (28). To address this problem, we introduce an additional alignment stage in which we find new compression matrices $A_x=P_x{A}_x^0$ such that the resulting virtual coils are smooth in the x direction.

Figure 1(b) illustrates the basic idea behind this alignment. Data in each slice along the readout direction lie in a smaller subspace that is spanned by the physical coils. In the figure, the subspaces of slice 1 and 2 are illustrated as planes in 3D. The subspaces of nearby slices are very close but not the same since the physical coil sensitivities vary slightly from slice to slice. In Fig. 1(b), the subspace of slice 2 is slightly tilted with respect to the subspace of slice 1. The compressed virtual coils can be any orthonormal vectors that span the subspace. Aligned virtual coils are sets of virtual coils in each subspace that are closest in Euclidean distance.

This alignment can be achieved by solving the following optimization problem:

$$\begin{array}{cc}\hfill \underset{A_x,P_x}{\text{minimize}}& \sum _x{\Vert A_x-A_{x-1}\Vert }_F^2\hfill \\ \hfill \text{subject to}& A_x=P_x{A}_x^0,\hfill \\ \hfill & P_x{\left(P_x\right)}^H={\left(P_x\right)}^H{P}_x=I,\hfill \end{array}$$ (8)

where the variables are P_x and A_x, and ||A_x — A_{x — 1}||_F is the Frobenius norm of the matrix (A_x — A_{x — 1}). This problem does not have a unique solution either. However, if we set P_x = I at a specific slice x, the optimal solution of P_x at the other slices is then unique. From now on, without loss of generality, we assume P₁ = I. This problem actually has an analytical solution. The orthogonal alignment matrices P_x for all slices can be found sequentially by the following steps:

1. Given A_{x— 1}, define the matrix $C_x\in {\mathcal{C}}^{M\times M}$ to be $C_x=A_x^0{\left(A_{x-1}\right)}^H$.

2. Compute SVD: $C_x=U_x^C{\Sigma }_x^C{\left(V_x^C\right)}^H$.

3. Set $P_x=V_x^C{\left(U_x^C\right)}^H$ and $A_x=P_x{A}_x^0$. This A_x minimizes ${\Vert A_x-A_{x-1}\Vert }_F^2$.

4. Repeat steps 1-3 until the alignment is done for all slices.

Since each P_x minimizes ${\Vert A_x-A_{x-1}\Vert }_F^2$, ${\sum }_x{\Vert A_x-A_{x-1}\Vert }_F^2$ is ultimately minimized (see Appendix A). After the compression matrices are carefully aligned, the coil compression can be simply performed according to Eq. (2) at each x location. The final step is to compute the Fourier transform of the virtual coil data along x direction. At this point, the original 3D data from N physical coils have been compressed into M spatially smooth virtual coils. For 2D Cartesian acquisitions, similar steps can be applied: GCC is applied in (x, k_y) space, and all the acquired data at each slice can be used to formulate matrix X_x.

Relationship to Walsh's Adaptive Coil Combination

In the extreme case when k-space is fully sampled and there is no acceleration, we can perform geometric-decomposition in all three dimensions. Computing the coil compression for every spatial location is not possible since one measurement at each location is not enough to determine the subspace by SVD. However, since the sensitivities are smooth, we could use a neighborhood around a particular location to compute the compression matrix. This is exactly the approach described by Walsh et al. (29). The “best” possible coil compression is of course compressing data into a single virtual coil using compression matrices that span the sensitivity maps.

Image Reconstruction Using Compressed Virtual Coils

Any PI or constrained reconstruction method can be directly applied to the virtual coils for reconstruction. In this paper, we simulate GE Healthcare product ACPI method (28), which belongs to the GRAPPA (3) family of reconstructions. We also use ${\ell }_1\text{-SPIRiT}$ (8), which is an iterative autocalibrating parallel imaging compressed sensing reconstruction. Both reconstructions are coil-by-coil methods that generally include two sequential steps in the reconstruction: calibration and data synthesis. The total computation complexity of both reconstruction methods is approximately O(N²), where N is the number of coils. Brief computational analysis of the two reconstructions can be found in reference (24) and Tab. 1. With coil compression applied to the acquired data, the number of coils is significantly reduced and the reconstruction is highly accelerated.

Table 1.

Approximate major computation required for ${\ell }_1\text{-SPIRiT}$ with and without GCC. The major computation of each step is measured by the number of complex-valued multiplications. The numerical example is calculated from the parameters used in the second dataset in Fig. 7. The number of samples in x, y, z directions are N_x = 308, N_y = 230, N_z = 156, the total ACS points in one coil N_t = 480, number of coils N = 32, number of virtual coils M = 6, SPIRiT kernel size G_x = 5, G_y = G_z = 7, reduction factor R ≈ 4, and the number of iterations in data synthesis N_i = 50.

Method		${\ell }_1\text{-SPIRiT}$	${\ell }_1\text{-SPIRiT}\mathrm{GCC}$
GCC SVD	Generalized Formula	-	NxNtN 2
	Numerical Example	-	1.5 × 108
	Actual Time (seconds)	-	2
GCC Compression	Generalized Formula	-	$\frac{1}{R}{N}_x{N}_y{N}_{z}NM$
	Numerical Example	-	5.3 × 108
	Actual Time (seconds)	-	3.5
Calibration	Generalized Formula	NNt(GxGyGzN)2	MNt(GxGyGzM)2
	Numerical Example	9.4 × 1011	6.2 × 109
	Actual Time (seconds)	516	4
Data Synthesis	Generalized Formula	NiNxNyNzN 2	NiNxNyNzM 2
	Numerical Example	5.7 × 1011	2.0 × 1010
	Actual Time (seconds)	130	22

PI is sometimes limited in cases with a tight imaging FOV, where the reconstructed FOV is smaller than the object being imaged. ACPI methods (e.g., GRAPPA or SPIRiT (8)), which do not rely on the direct measurements of the coil sensitivities, are not sensitive to a tight FOV (25). The proposed coil compression is also not susceptible to tight FOV artifacts for two reasons. First, the k-space ACS are independent of the actual imaging FOV. The tight FOV only increases the spacing between k-space lines, but does not change the k-space lines. Thus the calculations of the compression matrices are not affected by a tight FOV. Second, at each slice, the entire 2D k-space data from each coil are combined with the same compression weighting to construct the virtual coils. This compression is also independent of the imaging FOV. Therefore, although the virtual coils may have a tight imaging FOV, the construction of the virtual coils is not affected. As long as the ACPI or CS methods that follow the coil compression are not susceptible to a tight FOV, the related artifacts will not appear in the final reconstruction.

Materials and Methods

The proposed GCC was evaluated on two 3D datasets. Both of them were acquired on a 3T GE MR750 scanner (GE Healthcare, Waukesha, WI, USA) with Cartesian sampling using a 32 channel pediatric coil. The pediatric coil contains two 4×4 coil arrays, with one on top of the subject and the other embedded in the table (9). The first dataset was fully sampled, and acquired with the following imaging parameters: TE/TR = 0.944 ms/3.832 ms, flip angle (FA) = 15°, bandwidth (BW) = ± 64 kHz, FOV = 35 cm, slice thickness = 2 mm, and matrix size = 192 × 224 × 184. The second dataset was accelerated in both phase encoding directions. The acquisition sampling was chosen according to a poisson-disc distribution (30) with an overall reduction factor R ≈ 4. The imaging parameters were: TE/TR = 1.128 ms/4.832 ms, FA = 15°, BW = ± 64 kHz, FOV = 38 cm, slice thickness = 2 mm, matrix size = 308 × 230 × 156, and ACS = 24 × 20.

Coil Compression Methods Comparison

The first dataset was used to compare two coil compression methods: (1) single coil compression (SCC) and (2) the proposed GCC. For SCC, the same compression matrix was applied to compress the entire 3D dataset. The compression matrix was calculated using a 24 × 24 × 24 ACS in the center k-space. For GCC, the proposed steps were applied, including the alignment of the compression matrices. In both cases, various numbers of virtual coils were examined. SSOS images were used in all cases for coil combination. The SSOS images from the 32 original coils were used as the reference. The difference images between the reference and coil compression results were calculated in each case. The normalized root mean squared error (nRMSE) of SSOS images was also calculated using the formula:

$$nRMSE=\frac{1}{\text{max}\left(x\right)-\text{min}\left(x\right)}\sqrt{\frac{1}{N_p}\sum _{i=1}^{N_p}{(x\left(i\right)-\tilde{x}\left(i\right))}^2},$$ (9)

where x is the reference, x̃ is the coil compression result, and N_p is the number of image pixels.

To compare the denoising effect of SCC and GCC, the following experiment was performed. The first dataset was normalized first (maximum intensity normalized to 1). IID Gaussian noise (SNR = 20 for each original coil) was added to the normalized dataset. The new dataset with the added noise was referred to as the noisy dataset, and the original dataset was referred to as the noiseless dataset. Coil compression matrices for SCC with 6 and 16 virtual coils and GCC with 6 virtual coils were calculated from the noisy dataset. These compression matrices were then used to compress both the noisy dataset and only the added noise. The SSOS images of the noiseless dataset, noisy dataset, GCC results of the noisy dataset and SCC results of the noisy dataset were compared. The histograms of the added noise in these reconstructions were also compared to demonstrate the denoising effect. The noise covariance matrices of the added noise in 32 coils, 6 virtual coils after GCC, 6 virtual coils after SCC and 16 virtual coils after SCC were calculated.

To test the robustness of GCC and SCC, the denoising experiment was repeated 300 times. The coil compression matrices were different each time due to the different random noise added. The noiseless dataset was compressed by these compression matrices, and the SSOS images of GCC and SCC results were recorded each time. The pixelwise signal standard deviations (PSTD) of GCC and SCC results were calculated, and their histograms were compared.

GCCs with different number of virtual coils were simulated with three different readout directions: superior/inferior (commonly used as the readout direction), left/right and anterior/posterior. The relationship of nRMSE versus the number of virtual coils was studied in all cases.

To demonstrate the importance of the alignment of the compression matrices in GCC, 6 virtual coils before and after alignment were compared for the first dataset. Magnitude and phase images of single virtual coils in both cases were studied.

Image Reconstruction using Virtual Coils

To demonstrate the feasibility of combining GCC with ACPI and CS reconstruction, three experiments were carried out. First, the fully sampled dataset was uniformly undersampled by a factor of 2 in both phase encoding directions with ACS 28 × 28. The total reduction factor R was 3.7. The undersampled dataset was reconstructed by: (1) simulated GE Healthcare product ACPI method (28) using 32 original coils; and (2) GCC followed by the same ACPI method using 6 virtual coils. The ACPI kernel size was 5 × 7 × 7 (k_x × k_y × k_z). SSOS images were reconstructed in both cases. Differences between the two reconstructions were compared. The theoretical computation of each steps in this ACPI method can be found in reference (24).

Second, the fully sampled dataset was used to simulate cases with a tight imaging FOV. The FOV in k_y phase encoding direction was reduced by 20 percent, resulting in an overlapped reconstructed FOV. The dataset with a tight FOV was then undersampled by a factor of 2 in both phase encoding directions with ACS 28 × 28. Similar to the previous experiment, the same ACPI reconstruction method with the same kernel size using both the 32 original coils and 6 virtual coils were performed.

Third, the pseudo-randomly undersampled dataset was reconstructed by the following methods: (1) ${\ell }_1\text{-SPIRiT}$ using 32 original coils; (2) SCC followed by ${\ell }_1\text{-SPIRiT}$ using 16 virtual coils; (3) GCC followed by ${\ell }_1\text{-SPIRiT}$ using 6 virtual coils; (4) GCC without the alignment of the coil compression matrices followed by ${\ell }_1\text{-SPIRiT}$ using 6 virtual coils. The SPIRiT kernel size was 5 × 7 × 7 (k_x × k_y × k_z). SSOS coil combination was used in all cases. Theoretical computation, numerical examples, and actual reconstruction time in each step of ${\ell }_1\text{-SPIRiT}$ were calculated and compared.

In the coil compression methods comparison, two coil compression methods were implemented in MATLAB (The MathWorks, Natick, MA, USA) on a 8-core 2.8GHz Intel Xeon E5462 PC with 32 GB DRAM. The GE Healthcare product ACPI reconstruction method was also simulated in Matlab. For ${\ell }_1\text{-SPIRiT}$ reconstructions, SCC and GCC were implemented in C++, and ${\ell }_1\text{-SPIRiT}$ was implemented in CUDA on the same PC with a 30-core, 8-SIMD 1.48 GHz GTX285 GPGPU with 2 GB GDRAM (30,31).

Results

Coil Compression Methods Comparison

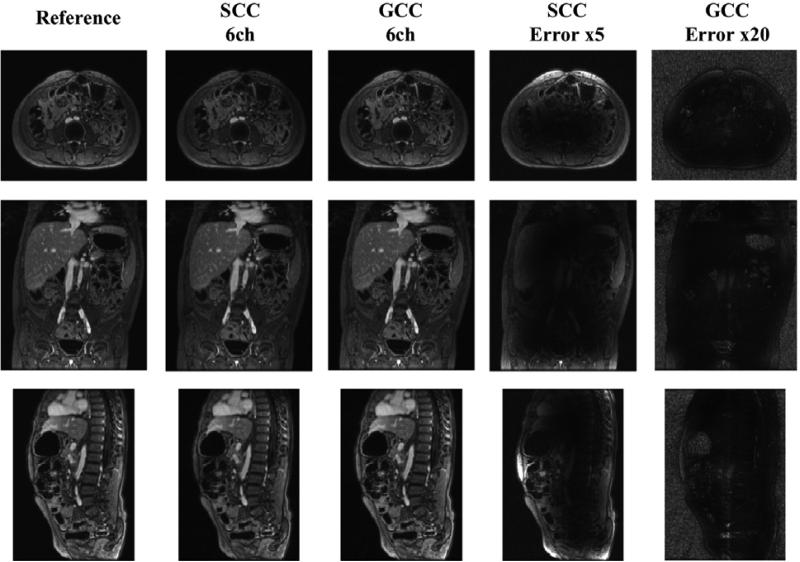
The number of virtual coils was first set to 6 for both SCC and GCC. The experimental results on the first dataset are shown in Fig. 2. Compared with the reference images, the SCC compression results had more compression loss while the results of GCC looked very similar to the reference images. The 5× difference images between the SCC images and the reference images further showed large compression error due to the non-optimal coil compression. However, the compression error was very small and negligible in GCC. The nRMSE values were 0.020 for SCC and 0.005 for GCC. The experimental results showed that GCC had much better compression performance than SCC for a fixed number of virtual coils.

Figure 2.

Comparison of SCC and GCC. SSOS images (axial/coronal/sagital) were compared. The original images in the first column were used as the reference. The compression results of SCC and GCC with 6 virtual coils were shown in the second and third column respectively. Compression errors (5× in SCC and 20× in GCC) were shown in the fourth and last column. GCC had very little compression loss even with only 6 virtual coils, while SCC suffered from much larger compression loss.

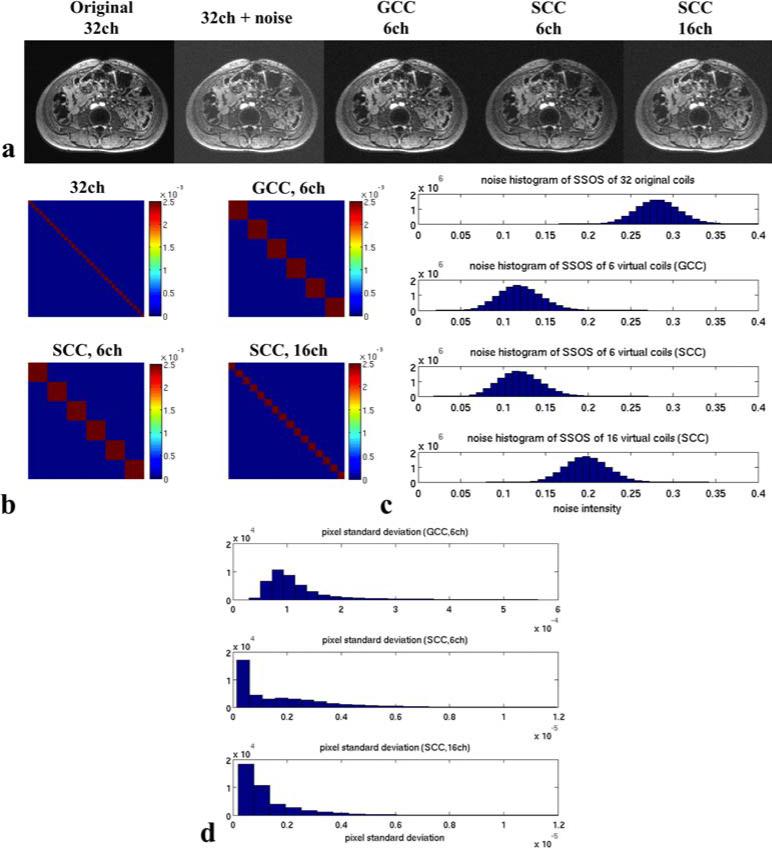
In the denoising experiment, the SSOS images of all the reconstructions are shown in Fig. 3a. The denoising effect of GCC and SCC can been seen as the reduced background noise after coil compression. The noise covariance matrices of the added noise in 32 coils, 6 virtual coils after GCC, 6 virtual coils after SCC and 16 virtual coils after SCC are shown in Fig. 3b. The added noise in the virtual coils was very close to IID, and the noise standard deviation of each virtual coil was approximately the same as that of each individual coil before coil compression. The histograms of the added noise in all SSOS images (Fig. 3a) are shown in Fig. 3c. The SSOS of the added noise approximately followed a chi distribution. The denoising effect of coil compression can be considered as the removal of those virtual coils that did not contain significant signal and were dominated by IID noise.

Figure 3.

Results of the denoising and Monte Carlo experiment. (a) SSOS images of the noiseless dataset, noisy dataset, GCC results of the noisy dataset and SCC results of the noisy dataset. The denoising effect can be seen as the reduced background noise after GCC and SCC. (b) Noise covariance matrices of the added noise in 32 coils, 6 virtual coils after GCC, 6 virtual coils after SCC and 16 virtual coils after SCC. Noise was close to IID after GCC or SCC. (c) Histograms of the SSOS of the added noise. The noise level was dependent on the number of virtual coils. The fewer the number of virtual coils, the less noise there was in SSOS images. (d) Histograms of PSTD of GCC with 6 virtual coils and SCC with 6 and 16 virtual coils. PSTD was very small (up to 0.0005) in GCC. SCC of the noiseless dataset was even less sensitive to the added noise due to larger ACS.

The histograms of PSTD over 300 SSOS images in the Monte Carlo experiment are shown in Fig. 3d. The PSTD of GCC results was very small (up to 0.0005). This indicated that GCC results of the noiseless dataset did not change much over 300 experiments, and were not very sensitive to noise in ACS. Compared with the added noise (σ = 0.02 for each coil), we can see that if GCC is applied to the noisy dataset, the dominant signal variation of GCC results would directly come from the added noise in the dataset instead of the variation of compression matrices. On the other hand, PSTD of SCC results was even smaller since the size of ACS was larger in SCC than GCC. In cases where ACS is highly corrupted by noise, SCC would be more robust than GCC.

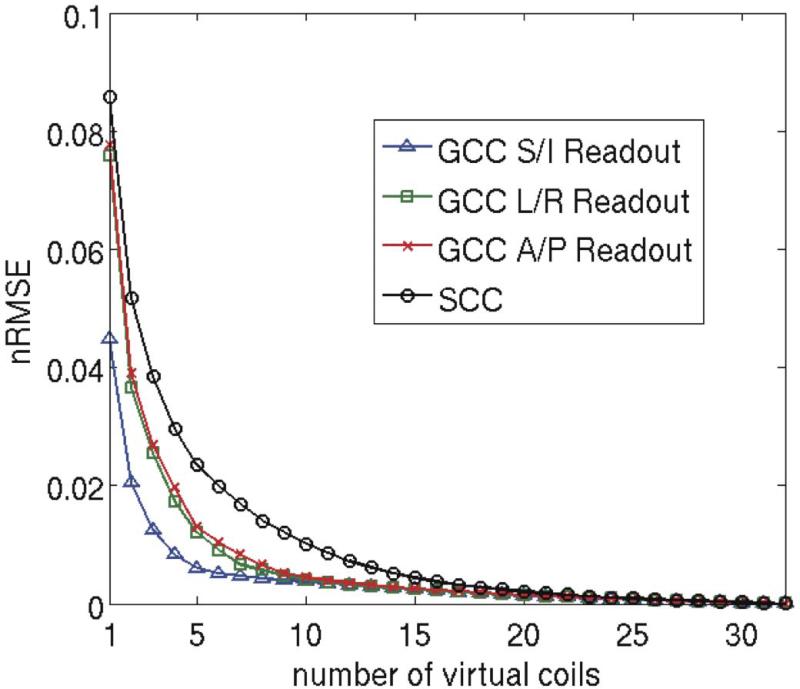
Next, the number of virtual coils was set from 1 to 32, and the corresponding nRMSE values were calculated for both coil compression methods. Similar experiments were carried out with three readout directions. The nRMSEs were plotted as a function of the number of virtual coils in Fig. 4. In Fig. 4, we can see that SCC always had larger compression error than GCC. In order to achieve the same level of compression error as GCC, more virtual coils were needed for SCC. This is due to the fact that SCC can not effectively exploit the spatially varying data redundancy. Figure 4 also shows that the nRMSE performance of GCC depended on the readout direction used in the data acquisition. Acquisition with the common superior/inferior readout direction only needed 6 virtual coils to represent the same information from 32 original coils, while SCC needed approximately 16 virtual coils.

Figure 4.

Compression with different numbers of virtual coils and the corresponding nRMSE. The entire 3D dataset was used for nRMSE calculation. Data from 32 original coils were used as the reference. GCC had less compression loss than SCC. To achieve similar nRMSE as in GCC, more virtual coils were needed in SCC.

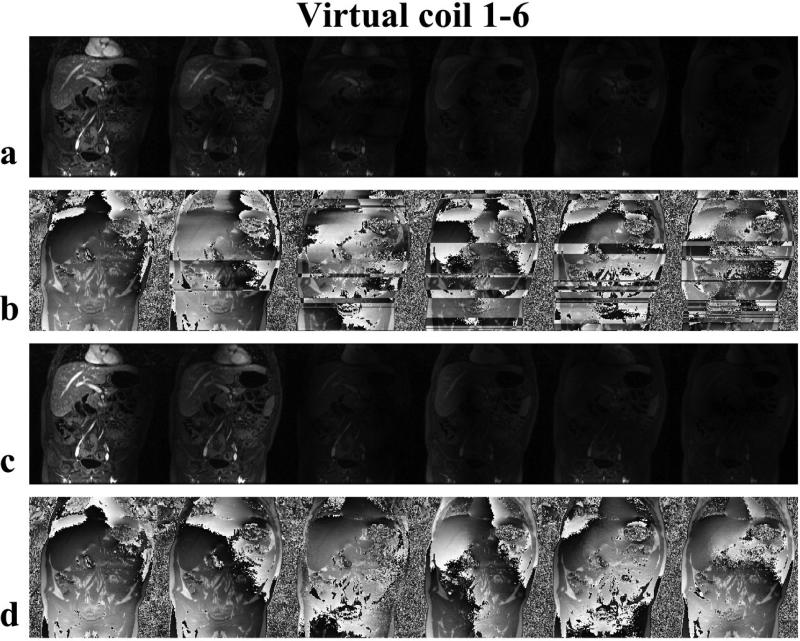
The magnitude and phase images of the 6 virtual coils from GCC with and without proper alignment are shown in Fig. 5. From Fig. 5(a,b), we can notice abrupt changes along x direction (superior/inferior) in both magnitude and phase images without the alignment of the coil compression matrices. This indicates that the coil sensitivities of the virtual coils were not smooth. Non-smooth coil sensitivities can cause significant problems for the calibration step in ACPI reconstructions. With proper alignment, the magnitude and phase images (Fig. 5(c,d)) were smooth enough for calibration. It is important to note that the alignment affects both the phase and the magnitude images of the virtual coils.

Figure 5.

Compression matrices alignment comparison. (a,b) Magnitude and phase images of the individual virtual coil from 1 to 6 by GCC without alignment. (c,d) Magnitude and phase images of the virtual coil from 1 to 6 by GCC after alignment. After proper alignment of the compression matrices, the images from individual virtual coil no longer have random abrupt phase changes or discontinuous coil sensitivities.

Image Reconstruction using Virtual Coils

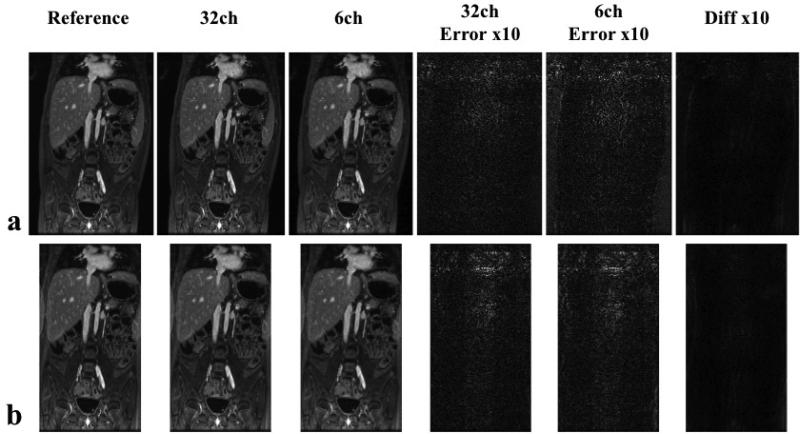
The simulated product ACPI reconstruction was applied in the experiment with uniform undersampling of the first dataset. The reconstructions with 32 original coils and 6 virtual coils were carried out separately. The total reconstruction times (including coil compression) were 876 seconds and 55 seconds respectively. Coil compression accelerated the reconstruction by approximately a factor of 16. Compared with the fully sampled data as the reference, the nRMSEs of the ACPI reconstructions (R = 3.7) were 0.008 with 32 original coils and 0.010 with 6 virtual coils. The reconstruction errors were very small in both cases.

Results for the experiment with a tight imaging FOV simulation are shown in Fig. 6b. As expected, both the proposed coil compression and the ACPI reconstruction were not sensitive to the tight FOV. The reconstructions were robust and had similar reconstruction errors to the previous experiment with the normal imaging FOV. The nRMSEs of the ACPI reconstructions (R = 3.7) were 0.008 with 32 original coils and 0.011 with 6 virtual coils.

Figure 6.

Reconstruction results by the simulated product ACPI method with and without GCC. Reference images of the fully sampled data using 32 original coils were shown in the first column. ACPI reconstruction results of 32 original coils and 6 virtual coils were shown in the second and third column respectively. 10× error images in both reconstructions were shown in the fourth and fifth column. The last column is the difference between two ACPI reconstructions. (a) In the normal imaging FOV case, the nRMSE was 0.008 for reconstruction with 32 original coils, and 0.010 for the reconstruction with 6 virtual coils. (b) In the tight imaging FOV case, the nRMSE was 0.008 for reconstruction with 32 original coils, and 0.011 for the reconstruction with 6 virtual coils. ACPI reconstructions with GCC and with original data had very similar image quality independent of the imaging FOV.

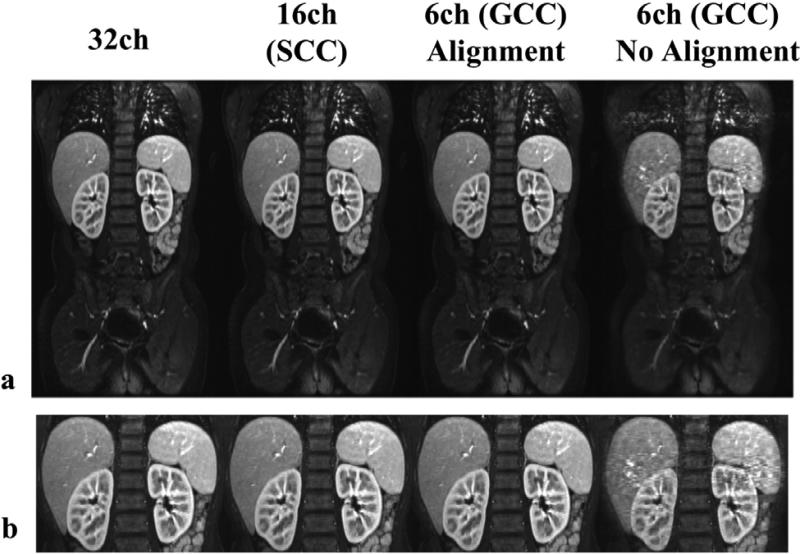
The second dataset with random undersampling was reconstructed by ${\ell }_1\text{-SPIRiT}$ both with and without GCC. The analytical formula, numerical examples, and actual reconstruction time of each step in ${\ell }_1\text{-SPIRiT}$ are shown in Tab. 1. From Tab. 1 we can see that coil compression theorectically reduces the calibration computation by a factor of over 100, and data synthesis by a factor of 28. Data synthesis was performed on GPGPU, and the actual time spent was reduced by a factor of 6. GCC did require extra computation, but it was very fast, and negligible compared to ${\ell }_1\text{-SPIRiT}$ reconstruction. The total reconstruction time was reduced from 652 seconds to 46 seconds. The reconstruction time was speeded up by approximately a factor of 14. This is fast enough to be clinically practical. The reconstruction results with GCC were also compared with those with SCC (16 virtual coils). The total reconstruction time with SCC was 134 seconds (approximately 3 times of that with GCC). The reconstruction results (shown in Fig. 7) had very similar image quality. Without the alignment of the coil compression matrices, the reconstructed images suffered from artifacts due to non-smooth virtual coil sensitivities and inaccurate SPIRiT kernel calibration.

Figure 7.

In-vivo reconstruction results by ${\ell }_1\text{-SPIRiT}$. (a) Reconstruction results of ${\ell }_1\text{-SPIRiT}$ with 32 original coils, with 16 virtual coils after SCC, with 6 virtual coils after GCC with the alignment of the coil compression matrices, and with 6 virtual coils after GCC without the alignment of the coil compression matrices; (b) Zoomed-in images of (a). The difference between ${\ell }_1\text{-SPIRiT}$ with 32 original coils, with 16 virtual coils after SCC, and with 6 virtual coils after GCC with the alignment of the coil compression matrices was very small and negligible. Without proper alignment of the coil compression matrices in GCC, the ${\ell }_1\text{-SPIRiT}$ reconstruction suffered from artifacts due to inaccurate calibration.

Discussion

GCC uses the fact that the coil sensitivity variation in the readout direction is not used for acceleration in Cartesian data acquisition. The acquired data can be spatially separated in the readout direction. Therefore at each slice, GCC can effectively minimize the number of virtual coils, and hence the PI or CS reconstruction time. The performance of GCC depends on several factors including the original coil geometry and the readout direction used in the data acquisition. Generally speaking, the optimal readout direction is the direction where the number of effective virtual coils is maximized, so that largest acceleration can be achieved for PI. However, the actual readout direction is practically chosen for several clinical imaging considerations. The number of effective virtual coils in GCC can be determined by thresholding the singular values in SVD. The nRMSE is another useful indication for choosing the number of effective virtual coils.

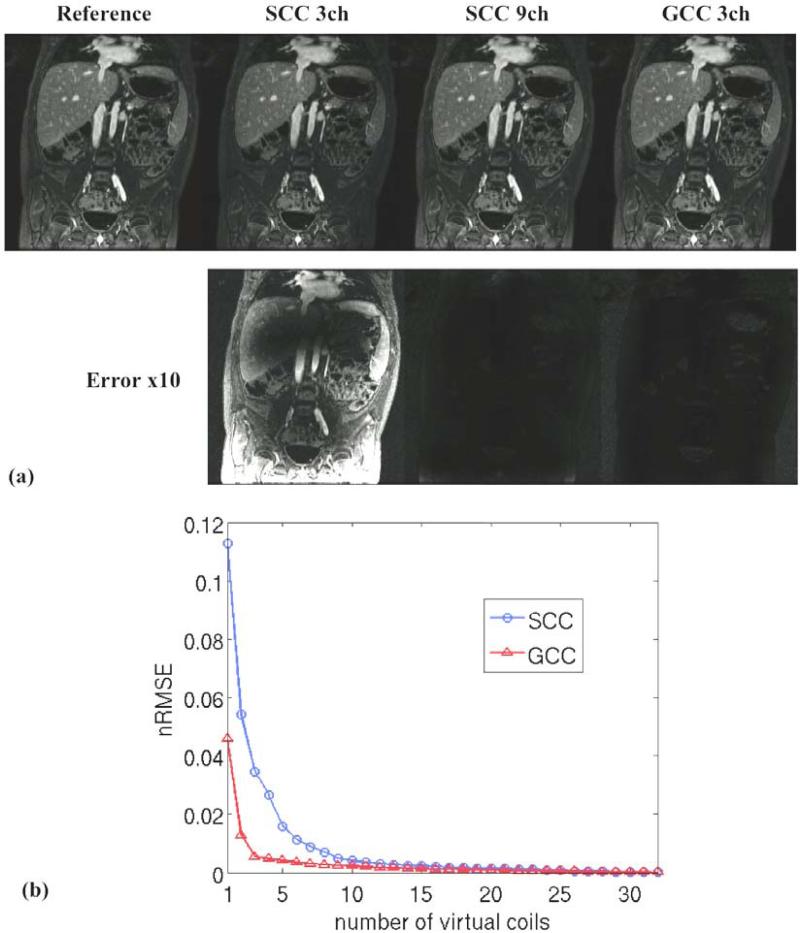
The proposed GCC can also effectively compress 2D Cartesian datasets. Figure 8 shows the results of SCC and GCC on a simluated 2D fully sampled dataset. For a similar nRMSE (less than 0.01), only 3 virtual coils were needed in GCC compared to 9 virtual coils in SCC. This can be used to effectively compress time-series data from large arrays that appear, for example, in many fMRI experiments.

Figure 8.

Simulation of a 2D fully sampled Cartesian dataset (S/I readout direction) with SCC and GCC. (a) Coil compression results and errors (×10) of SCC with 3 and 9 virtual coils and GCC with 3 virtual coils; (b) Compression error (nRMSE) with different numbers of virtual coils using SCC and GCC. Only 3 virtual coils were needed in GCC compared to 9 in SCC.

The initial compression matrices in GCC are calculated from the center k-space. In 3D ACPI datasets, the size of ACS at each x location is sufficiently large for this calculation. Further discussion of the required inputs of coil compression matrix calculation can be found in reference (14). However, in 2D datasets, the size of ACS at each x location is not usually big enough for the calculation. In this case, all the acquired data at one x location can be used to calculate the compression matrices; or the ACS in the adjacent x locations can be included to calculate the compression matrices based on the fact that the original coil sensitivities are smooth.

Both SCC and GCC require two major steps to achieve coil compression. The first step is to find the appropriate coil compression matrices; and the second step is to apply the coil compression matrices to the original coils and construct the virtual coils. Assuming the same number of virtual coils is chosen for both SCC and GCC, then the second step in SCC and GCC requires the same amount of computation (shown in Tab. 1). Take 3D ACPI datasets as an example. The first step in SCC only requires a SVD of the 3D ACS, which is a O(N_ACS,xN_tN²) computation, where N_ACS,x is the number of data points chosen in the k_x direction for calibration, and N_t is the number of ACS points in two phase encoding directions. The first step in GCC requires two operations: the initial coil compression matrices calculation and the alignment of the compression matrices. The calculation of the initial compression matrices is a O(N_xN_tN²) computation, and can be accelerated by parallel computing; the alignment of the compression matrices is a O(N_xNM²) computation. The computation of the alignment is negligible compared to the initial compression matrices calculation. Since usually the number of virtual coils in GCC is less than SCC, the actual computation time of SCC and GCC is close and much smaller than the ACPI or CS reconstruction time. If a synthetic target coil, a direct virtual coil or flexible virtual coils is used as the ACPI reconstruction, GCC can speed up the reconstruction by replacing the source channels with the virtual coils.

Note that after the operation in Eq. 1, the noise in each coil is IID. When the coil compression matrices are calculated from ACS with sufficient SNR, they are usually not sensitive to noise. As a result, the noise in each virtual coil is close to IID. In GCC, different coil compression matrices are applied at different spatial locations, but the noise distribution does not change significantly in the entire set of virtual coils.

For multi-echo or multi-phase data acquisition, the spatially varying coil compression matrices can be calculated from data in the first echo or the first phase. The same compression matrices should be applied to data in the other echoes or phases so that GCC is consistent in the entire dataset.

The proposed method can also address the data storage problem. However it requires the access of raw data during data acquisition. To store the virtual coil data directly, ACS has to be first acquired so that the compression matrices can be calculated. Then for each of the other acquisitions, an inverse Fourier transform along the readout direction needs to be done before coil compression. Depending on the reconstruction method used, the compressed data can be stored either in k-space, which requires another Fourier transform along the readout direction, or (x, k_y, k_z) space.

Conclusion

Data-based coil compression can transform signals from a large number of physical coils into fewer virtual coils without the direct measurements of coil sensitivities. A geometric-decomposition coil compression technique for Cartesian datasets has been proposed in this work. The proposed method can minimize the number of virtual coils without noticeable compression loss. The compression matrices are properly-aligned to achieve smooth virtual coil sensitivities. Autocalibrating parallel imaging and compressed sensing reconstruction can be directly carried out on the virtual coils, which significantly reduces reconstruction time. The image quality of reconstructions using the virtual coils is comparable to that of reconstructions using the original coils. Based on the experimental results, 3D datasets from a 32 channel pediatric coil can be effectively compressed into 6 virtual coils. The proposed coil compression is also robust in cases with tight imaging FOVs.

Appendix A: Analytical solution of the alignment of the compression matrices

The objective function in Eq. (8) can be minimized sequentially at each slice. Assume P_x—1 (and A_x—1) is known at slice x — 1, we can then minimize ${\Vert A_x-A_{x-1}\Vert }_F^2$ at slice x.

$$\begin{array}{cc}\hfill {\Vert A_x-A_{x-1}\Vert }_F^2={\Vert P_x{A}_x^0-A_{x-1}\Vert }_F^2& =Tr\left[{(P_x{A}_x^0-A_{x-1})}^H(P_x{A}_x^0-A_{x-1})\right]\hfill \\ \hfill & =Tr\left[{\left(P_x{A}_x^0\right)}^H{P}_x{A}_x^0\right]+Tr\left[{\left(A_{x-1}\right)}^H{A}_{x-1}\right]-Tr\left[2{\left(A_{x-1}\right)}^H{P}_x{A}_x^0\right]\hfill \\ \hfill & =Tr\left[{\left(A_x^0\right)}^H{A}_x^0\right]+Tr\left[{\left(A_{x-1}\right)}^H{A}_{x-1}\right]-2Tr\left[A_x^0{\left(A_{x-1}\right)}^H{P}_x\right]\hfill \\ \hfill & =Tr\left[{\left(A_x^0\right)}^H{A}_x^0\right]+Tr\left[{\left(A_{x-1}\right)}^H{A}_{x-1}\right]-2Tr\left[C_x{P}_x\right]\hfill \\ \hfill & =Tr\left[{\left(A_x^0\right)}^H{A}_x^0\right]+Tr\left[{\left(A_{x-1}\right)}^H{A}_{x-1}\right]-2Tr\left[U_x^C{\Sigma }_x^C{\left(V_x^C\right)}^H{P}_x\right]\hfill \\ \hfill & =Tr\left[{\left(A_x^0\right)}^H{A}_x^0\right]+Tr\left[{\left(A_{x-1}\right)}^H{A}_{x-1}\right]-2Tr\left[{\Sigma }_x^C{\left(V_x^C\right)}^H{P}_x{U}_x^C\right]\hfill \end{array}$$ (10)

with the use of $C_x=U_x^C{\Sigma }_x^C{\left(V_x^C\right)}^H$ and the property of T r[M₁ M₂] = T r[M₂ M₁].

To minimize ${\Vert A_x-A_{x-1}\Vert }_F^2$ is equivalent to maximize $2Tr\left[{\Sigma }_x^C{\left(V_x^C\right)}^H{P}_x{U}_x^C\right]$. Define $Q={\left(V_x^C\right)}^H{P}_x{U}_x^C=\left[q_{ij}\right]$. Since $V_x^C$, $P_x$, and $U_x^C$ are all orthogonal matrices, then Q is also an orthogonal matrix, and |q_ij| ≤ 1. Define ${\Sigma }_x^C=\text{diag}({\sigma }_{11},{\sigma }_{22},\dots ,{\sigma }_{MM})$, then $Tr\left[{\Sigma }_x^C{\left(V_x^C\right)}^H{P}_x{U}_x^C\right]={\sum }_{k=1}^M{\sigma }_{kk}{q}_{kk}\le {\sum }_{k=1}^M{\sigma }_{kk}$. To maximize $Tr\left[{\Sigma }_x^{C}Q\right]$, we have Q = I, and $P_x^{opt}=V_x^C{\left(U_x^C\right)}^H$. Thus, the closed form solution for A is $A_x^{opt}=V_x^C{\left(U_x^C\right)}^H{A}_x^0$.

Define another set of unitary matrices R_x , where $R_x=P_{x-1}^H{P}_x$. Then ${\Vert A_x-A_{x-1}\Vert }_F^2={\Vert P_x{A}_x^0-P_{x-1}{A}_{x-1}^0\Vert }_F^2={\Vert R_x{A}_x^0-A_{x-1}^0\Vert }_F^2$. To prove the global optimality of $A_x^{opt}$, let us reformulate Eq. (8) into the following form,

$$\begin{array}{cc}\hfill \underset{R_x}{\text{minimize}}& \sum _x{\Vert R_x{A}_x^0-A_{x-1}^0\Vert }_F^2\hfill \\ \hfill \text{subject to}& R_x{\left(R_x\right)}^H={\left(R_x\right)}^H{R}_x=I,\hfill \end{array}$$ (11)

Define $D_x=A_x^0{\left(A_{x-1}^0\right)}^H$ and assume the SVD of D_x is $D_x=U_x^D{\Sigma }_x^D{\left(V_x^D\right)}^H$. Similar to the previous proof, it is easy to show that the optimal solution of the reformulated problem (Eq.(11)) is $R_x^{opt}=V_x^D{\left(U_x^D\right)}^H$. In fact, $R_x^{opt}$ is the global optimal solution of Eq. (11), since for different slices x₁ and x₂, ${\Vert R_{x_1}{A}_{x_1}^0-A_{x_1-1}^0\Vert }_F^2$ and ${\Vert R_{x_2}{A}_{x_2}^0-A_{x_2-1}^0\Vert }_F^2$ are independent. Notice C_x = D_x(P_{x — 1})^H, then $D_x=U_x^C{\Sigma }_x^C{\left(V_x^C\right)}^H{P}_{x-1}$. Without loss of generality, we can assume $U_x^D=U_x^C$, ${\Sigma }_x^D={\Sigma }_x^C$ and $V_x^D={\left(P_{x-1}\right)}^H{V}_x^C$. Therefore, $R_x^{opt}=V_x^D{\left(U_x^D\right)}^H={\left({\left(P_{x-1}\right)}^{opt}\right)}^H{P}_x^{opt}$. When $R_x^{opt}$ achieves the global minimum of ${\sum }_x{\Vert R_x^{opt}{A}_x^0-A_{x-1}^0\Vert }_F^2$, $P_x^{opt}\left(A_x^{opt}\right)$ achieves the same global minimum of ${\sum }_x{\Vert P_x^{opt}{A}_x^0-A_{x-1}^{opt}\Vert }_F^2={\sum }_x{\Vert R_x^{opt}{A}_x^0-A_{x-1}^0\Vert }_F^2$. In other words, the previous solution to Eq. (8) $(P_x^{opt}=V_x^C{\left(U_x^C\right)}^H\text{and}{A}_x^{opt}=P_x^{opt}{A}_x^0)$ is global optimal.