Engineering metallic nanostructures for plasmonics and nanophotonics

Abstract

Metallic nanostructures now play an important role in many applications. In particular, for the emerging fields of plasmonics and nanophotonics, the ability to engineer metals on nanometric scales allows the development of new devices and the study of exciting physics. This review focuses on top-down nanofabrication techniques for engineering metallic nanostructures, along with computational and experimental characterization techniques. A variety of current and emerging applications are also covered.

1. Introduction: status and challenges

Technological advances often catalyze scientific breakthroughs and accelerate discovery by enabling experiments at previously inaccessible regimes with improved precision. In his prescient 1959 speech, Feynman envisioned the revolutionary impact of nanofabrication technologies—the ability “…to drill holes, cut things, solder things, stamp things out, mold different shapes all at an infinitesimal level…”—on physics, biology, and engineering (Feynman). Today, scientists and engineers have access to a wealth of technologies such as electron-beam lithography (“write”), focused ion beam lithography (“drill,” “cut,” and “solder”), nanoimprint (“stamp”), nano-molding, and scanning probe lithography (“rearranging the atoms”) to build nanostructures at unprecedented scales, resolution, and throughput. Some examples are shown in figure 1. Indeed, broad scientific disciplines have been transformed by the ability to define functional devices on nanometric scales, a development largely facilitated by Moore's law (Moore, 1998) in the microelectronics industry and the resulting technological infrastructure. The extraordinary and ubiquitous success of silicon microelectronics is the most impressive feat of modern nanotechnology, and researchers are continuously pursuing more breakthrough technologies in a wide range of disciplines.

Figure 1.

Various metallic nanostructures. (a) Periodic nanohole arrays, period 600 nm, in a metallic film exhibit extraordinary optical transmission effects (Ebbesen et al., 1998). Picture used with permission, Elsevier Publishing, from (Krishnan et al.) (b) Metallic bull’s eye structure for channeling light from the concentric rings into the central, subwavelength aperture. The groove periodicity is 500 nm. From (Lezec et al., 2002) Reprinted with permission from AAAS. (c) Silver grating structure with 500 nm periodicity. (d) A sharp metallic tip can concentrate light below the diffraction limit. Image courtesy Lukas Novotny. Used with permission (www.nano-optics.org). (e) Metal-insulator-metal nanogap plasmon cavity. Scale bar 500 nm. Inset: the 3.3 nm insulating layer. Scale bar 20 nm. Reprinted figure with permission from (Miyazaki and Kurokawa, 2006). Copyright 2006 by the American Physical Society.

Given this, and for a tractable scope, this review paper focuses on the physics and technology of engineered metallic nanostructures—i.e. metallic structures made by top-down fabrication methods with critical dimensions below 100 nm. Metallic devices are ubiquitous in science and technology. Crisscrossing copper interconnects with sub-micron dimensions carry information in modern microprocessors. Metallic gratings, antennas, waveguides, and resonators have been extensively studied and used in radiofrequency, microwave, terahertz, and optical domains. More recently, the progress in our ability to model, fabricate, and characterize metallic structures at the nanoscale have galvanized material, optical, and chemical sciences. In particular, Ebbesen’s discovery (Ebbesen et al., 1998) of extraordinary optical transmission through subwavelength apertures in thin metallic films inspired new research activities for harnessing optical nanostructures in the emerging field of plasmonics (Barnes et al., 2003; Atwater, 2007, Polman, 2008, Ozbay, 2006, Lal et al., 2007, Brongersma and Shalaev, 2010, Engheta). The characterization and application of the optical properties of metallic nanostructures will be extensively covered.

Indeed, it is only with metallic nanostructures that the subwavelength control and manipulation of optical energy is possible. Dielectric structures suffer from diffractive effects, but metallic nanostructures that support surface plasmon polaritons (SPP) offer a solution. As shown in figure 2a, plasmonics promises to break the diffraction limit of dielectric photonics while still operating at optical frequencies. Physically, SPPs are collective wave oscillations of the conduction electrons at the surface of a metal (Pitarke et al., 2007; Ritchie, 1957; Ritchie, 1973), shown in figure 2b. As they are hybrid electron-photon electromagnetic waves, SPPs are thus able to combine photonics, nanotechnology, and electronics. Given this, the field of plasmonics promises to develop many new technologies and exciting physics.

Figure 2.

(a) Combined with state-of-the-art nanofabrication (<100 nm resolution), nanoplasmonics promises to break the diffraction limit (~ 0.5 µm) at optical frequencies. From (Brongersma and Shalaev, 2010) Reprinted with permission from AAAS. (b) An SPP is an oscillation of the conduction electrons that propagates along the surface of a metal. These hybrid electron-photon waves can be generated and manipulated with metallic nanostructures.

Historically, the driving force behind the growth of nanofabrication and specifically the semiconductor industry has been the miniaturization of transistors. This process has led to the development of a vast array of new equipment and techniques. In the context of plasmonics, these mature technologies are now being utilized for the miniaturization of metallic nanostructures. Since Maxwell’s equations are invariant to frequency scaling, many phenomena in microwave engineering, based on millimeter-length scales, have analogs at optical wavelengths if one can properly shrink the dimensions of the device. Many technological challenges, however, have to be addressed. First, while metals act like an ideal conductor at lower frequencies, they suffer from considerable ohmic losses at optical frequencies, degrading the performance of nanoscale resonators and waveguides. In this regard, it is critical to find suitable materials. In particular, noble metals such as gold and silver are able to sustain SPP waves at optical frequencies with fewer losses than other materials. Second, simple fabrication techniques to pattern millimeter-scale features, which are sufficient for microwave devices, need to be replaced with expensive and delicate micro and nanofabrication instruments to demonstrate devices in the optical regime. Nano-optical structures require deep-sub-wavelength dimensions, on the order of ~10 nm. These problems are compounded since most as-deposited metal films are inherently rough due to polycrystallinity, which can sharply degrade their optical properties and performance.

While many techniques used in integrated circuit (IC) manufacturing can be readily utilized in building metallic nanostructures, inherent challenges exist such as the high capital cost of nano-resolution lithography tools, the roughness of as-deposited metal films, and the contamination resulting from many standard patterning techniques. Nanofabrication of silicon-based devices commonly rely on a combination of lithography followed by plasma etching (also called “dry etching” since it does not require wet solvents) of the silicon or of dielectric films (SiO₂, Si₃N₄). The versatility of silicon processing is augmented by the availability of chemical vapor deposition (CVD) of polycrystalline silicon, which provides excellent conformality and step coverage. Unfortunately, most CVD-deposited metal films, especially those useful for plasmonics, have degraded optical properties due to inherent contaminants from the precursor materials. Evaporated or sputtered metal films are polycrystalline and thus exhibit surface roughness and grain-boundary SPP scattering. Furthermore, unlike silicon, most metals are not amenable to dry etching. In particular, gold and silver cannot be easily plasma etched because their etch byproduct is nonvolatile. Physical patterning such as ion milling is thus often required but may worsen surface roughness and contaminate the metallic surface with implanted ions.

Besides the difficulties in nanofabrication, characterization of light-matter interactions in metallic nanostructures poses additional challenges. Unlike free-space light or conduction electron motion in metals, surface plasmons are evanescent in space, are characterized by femtosecond electron-electron-phonon interactions, and often interact with materials in a highly nonlinear fashion. To probe plasmon-mediated light-matter interactions, the characterization technique should, ideally, possess both nanometer scale spatial resolution and ultra-fast temporal resolution. To these ends, significant progress has been made. Methods such as time-resolved ultrafast spectroscopy, near-field optical microscopy, cathodoluminescence, electron-energy loss spectroscopy, and photoemission spectroscopy are summarized in this review.

Despite these challenges, exciting physics and novel applications based on engineered metallic nanostructures have been demonstrated. For instance, the discovery of surface-enhanced Raman scattering from metallic substrates established a new branch of spectroscopy (Jeanmaire and Van Duyne, 1977). Harnessing optical, electrical and magnetic properties of metallic structures will likely lead to a new generation of tools and devices for optoelectronics (Tang et al., 2008), biosensing (Homola et al., 1999), imaging (Liu et al., 2007), data storage (Challener et al., 2009), photovoltaics (Atwater and Polman, 2010), non-linear optics (Danckwerts and Novotny), and optical antennas (Novotny and Hulst, 2011) to name a few. By combining metallic nanostructures with materials systems, such as semiconductors, quantum dots, organic materials, biomolecules, and soft matter, one can better understand and harness light-matter interactions at the nanoscale. Clearly, nanotechnology will benefit tremendously from the development of affordable and reproducible techniques for designing, building, and characterizing metallic nanostructures. On the one hand, the silicon IC industry continues to develop high-capital-cost instruments for making faster, smaller, and cheaper transistors, even toward achieving nearly atomistic precision. On the other hand, emerging technologies for unconventional and lower-cost fabrication enables more researchers to access nanofabrication technologies (Gates et al., 2005). The availability of nanofabrication techniques that enable both high-resolution patterning at low costs will advance basic research as well as lead to new applications. Toward such goals, this review offers an overview of the processing sciences related to metallic nanostructures, presents a snapshot of the state-of-the-art in characterization, and covers some promising applications of engineered metallic nanostructures. We also focus this review on top-down nanofabrication techniques (i.e. not self-assembly) and to specific techniques demonstrated to be capable of patterning substrates with sub-100 nm features.

The review is broken into the following sections. First, we discuss standard and emerging top-down nanofabrication techniques such as optical lithography, electron-beam lithography, focused ion beam lithography, atomic layer deposition, soft lithography, and template stripping. We then present background on understanding the optical physics of these metallic nanostructures, particularly with computational modeling techniques. Following this, we outline several experimental methods for characterizing metallic nanostructures. Finally, we present some exciting current and emerging applications of plasmonic nanostructrues.

2. Fabrication techniques for metallic nanostructures

Metallic nanostructures offer the correct combination of material properties for the subwavelength control of optical energy. In this section, after discussing the need for metals, we outline standard nanofabrication techniques and then describe some exciting new approaches to metallic nanostructure engineering.

2.1. Materials choice

Choosing the proper material for a plasmonic device is critical to ensuring its optimal performance. While silver and gold have been the primary materials in almost all plasmonic devices demonstrated to date, these materials still suffer from relatively large losses in the optical frequency range.(West et al., 2010) Recently, several experimental and theoretical studies on alternative materials for plasmonic devices have appeared (West et al., 2010, Boltasseva and Atwater, 2011). Below, we provide a brief background on the optical properties of plasmonic materials and survey recent work exploring new materials.

The electrical permittivity or dielectric function describes how a material is polarized by an electric field. Furthermore, the polarization of a material by the electric field is not an instantaneous process and therefore always lags behind the applied field. This means that the permittivity of actual materials depends on the frequency of the applied electric field. Permittivity is typically written as a complex function in order to represent the phase difference between the electric field and the polarization response of the material. Permittivity can be defined by the following equation:

$$D_o{e}^{-i\omega t}=\epsilon (\omega )E_o{e}^{-i\omega t}$$ (1)

Where D_o represents the displacement field, E_o the electric field, ω the angular frequency, t is time and i is the imaginary unit. ε(ω) can be further described by the complex function:

$$\epsilon (\omega )=\epsilon \prime (\omega )+i\epsilon ″(\omega )$$ (2)

where the real part of the permittivity, ε′(ω), describes how strongly a material is polarized by an external electric field and the imaginary part, ε″(ω), describes the losses in the material due to the polarization and ohmic losses (West et al., 2010).

In the context of this review, SPP waves can exist at the interface between two materials only if the real part of the permittivity undergoes a sign change at the interface (Yeh, 1988). As alluded to in the introduction, SPPs represent quantized oscillations in the density of the electron plasma at the interface (Ritchie, 1973). Due to their abundance of free electrons (West et al., 2010), metals provide a negative real permittivity that ensures a sign change in permittivity at a metal / dielectric interface. Incident electromagnetic energy can be used to excite surface plasmons by coupling the incident photons to the free electron plasma by the use of patterned metallic surfaces, as shown throughout this review.

Unfortunately, metals suffer from high ohmic losses in the visible and ultra-violet (UV) regions that can strongly degrade the performance of plasmonic devices. These ohmic losses can be separated into two groups—losses from conduction electrons and losses from bound electrons. Conduction electron losses arise from electron-electron interactions, electron-phonon interactions, and scattering from lattice defects and grain boundaries. Bound electron losses, also known as interband transitions, result from the excitation of electrons into higher energy levels by the absorption of photons. Interband transitions are a considerable source of loss for metals at optical frequencies (West et al., 2010). Together, these combine to give high losses in current materials and present a significant roadblock to the practical advancement of plasmonic devices. The need for lower loss has fueled research aimed at developing new materials for plasmonics. Here, we survey the latest activities in this area.

2.1.1. Pure metals

The large number of free electrons in metals ensures a high plasma frequency and a negative real permittivity over a wide frequency range. Table 1 gives a brief sampling of some of the important properties of metals that are used in plasmonics and nanophotonics. Figure 3 shows plots of the real and imaginary permittivity in the visible and near-infrared (NIR) regions for aluminum (Rakić, 1995), copper (Palik, 1985), gold (Johnson and Christy, 1972), and silver (Johnson and Christy, 1972). To date, silver and gold are the most commonly used materials in plasmonics. Silver exhibits the lowest losses of current materials in both the visible and NIR (West et al., 2010). Some plasmonic devices fabricated with silver include a sub-diffraction limited superlens (Fang et al., 2005, Melville and Blaikie, 2005), a far-field optical hyperlens (Liu et al., 2007), a negative-index metamaterial in the visible range (Dolling et al., 2007), a subwavelength hole array that exhibits extraordinary optical transmission (Ebbesen et al., 1998), ultra-thin-film amorphous silicon solar cells with enhanced absorption (Ferry et al., 2010, Haug et al., 2008), and three-dimensional (3-D) nanofocusing sharp tips (Lindquist et al., 2010). However, silver is not well suited for telecommunication devices due to corrosion from sulfur and chlorine species in the natural environment (Graedel, 1992). It is possible, however, to deposit thin protective films over nanostructured silver using atomic layer deposition (see section 2.9) (Zhang, 2006; Im, 2010b). These protected films can then be used for biosensing or in other harsh environments. Unless a seed layer is used (Logeeswaran et al., 2009), silver films under 30 nm in thickness can also be discontinuous, although localized surface plasmons on discontinuous silver island films have found use in sensors and photovoltaics (Wei et al., 2009, Pillai et al., 2007, Beck et al., 2009). Applications utilizing propagating surface plasmons, such as waveguides (De Leon and Berini), require thin continuous films. Unfortunately, the added cost of thicker continuous films could hinder the adoption of devices in cost-conscious applications such as solar cells.

Table 1.

Selected properties of metals. Bulk resistivity from (Meaden). Density of conduction electrons from (Kittel). Price is as of Sept. 2011.

	Bulk Resistivity (µΩ-cm)	Melting Point (°C)	Price (US$ / troy ounce, September 2011)	Density of conduction electrons (1022 cm−3)
Au	2.2	1064	1618	5.9
Ag	1.61	962	30	5.85
Cu	1.7	1085	0.22	8.45
Al	2.74	660	0.07	18.06
Pt	10.4	1768	1534	6.62
W	5.3	3410	1.6	12.6

Figure 3.

(a) Real part and (b) imaginary part of the complex dielectric functions for Al (Rakić, 1995), Cu (Palik, 1985), Au (Johnson and Christy, 1972), and Ag (Johnson and Christy, 1972). For plasmonic applications, the real part must be negative. For low loss operation, the imaginary part must be small.

Gold exhibits the next lowest losses in the visible region after silver. However, an interband transition at ~470 nm greatly increases the losses in gold at wavelengths below 600 nm (Etchegoin et al., 2006). Gold has the advantage over silver of being chemically stable in natural environments making it well suited for plasmonic biosensors (Homola, 2003), discussed in section 5.1. Indeed, plasmonic biosensors have been fabricated from thin gold films (Homola et al.), patterned gold nanohole arrays and gold nanoparticles (Brolo et al., 2004, He et al., 2000, Lyon et al., 1998, Menezes et al., 2010, Shon et al., 2009), discussed in section 5.2. Additionally, gold forms continuous films with thicknesses of even 10 nm or less (Svorcik et al., 2006). However, these advantages have to be weighed against significantly higher material costs than silver (table 1).

Along with gold and silver, copper and aluminum have also been used in plasmonics, albeit to a lesser extent. Copper has the second lowest resistivity of all metals (table 1). Both the real and imaginary permittivities of copper are similar to gold for wavelengths above 600 nm. Copper has about 40% lower electrical resistance than aluminum. In addition, copper wires are more robust against electromigration caused by high currents in microprocessors than aluminum wires, thus copper has replaced aluminum as the interconnect material in silicon integrated circuits. These desirable properties would make copper a low-cost alternative to gold. Unfortunately, the surface of copper is readily oxidized in air to form CuO and CuO₂(Kim et al., 2004). Chan et al. showed that the optical properties of copper nanoparticles were significantly degraded by this surface oxide layer (Chan et al., 2007). Gao et al. measured dispersion diagrams for copper nanopyramidal gratings fabricated by soft interference lithography (sections 2.2 and 2.6). Both of these works concluded that oxide-free copper and gold displayed analogous optical properties (Gao et al., 2008). Such results suggest that copper could be a viable alternative to gold where the metal surface is not exposed to air. Alternatively, thin protective layers may also be added, as discussed above for silver (Im, 2010b; Zhang, 2006), and later in section 2.9.

Aluminum outperforms both gold and silver in the blue and UV regions. Aluminum displays a negative real permittivity at wavelengths less than 200 nm with relatively low losses in this region. Gold and silver do not display the required negative real permittivity until approximately 327 and 207 nm, respectively (West et al., 2010). In the UV-blue region, nanostructured aluminum films have been shown to enhance fluorescence and Raman scattering (Ray et al., 2007, Dörfer et al., 2007). Extraordinary optical transmission (section 3.2) in the UV has been observed in an aluminum nanohole array (Ekinci et al., 2007) and aluminum has been used to fabricate a deep-UV superlens (Schilling et al., 2009). Because aluminum was the workhorse metal for interconnects in silicon-based integrated circuits before being replaced with copper, many sophisticated techniques have been developed to deposit and pattern aluminum-based alloys. However, despite aluminum’s good performance in the UV and blue region, it has not been widely used in plasmonics. This is primarily due to challenges from oxidation, as with silver and copper, and large losses in the visible region. Aluminum is rapidly oxidized in air to form a ~3 nm layer of Al₂O₃ at the surface (Langhammer et al., 2008). This oxide layer has been found to red shift the local SPR (Chan et al., 2008). In addition, even pure aluminum suffers from large losses at visible wavelengths due to an interband transition at 800 nm.

In principle, alkali metals are even better than silver, gold, and aluminum since they have the strongest free electron behavior of any metals. Both potassium and sodium exhibit negative permittivity in the visible and NIR with lower losses than silver in the visible. Unfortunately, these metals are extremely reactive to even trace amounts of water, presenting major challenges. Consequently, alkali metals will not be reviewed here. The reader is directed to theoretical works by Blaber et al.(Arnold and Blaber, 2009, Blaber et al., 2007)

For applications at longer wavelengths, other metals have also been considered for plasmonic applications. In particular, the area of thermal plasmonics has been explored. While light has typically been the primary excitation source for SPPs in the materials discussed above, they can also be excited thermally (De Wilde et al., 2006). This possibility was initially discussed with heavily doped silicon structures (Hesketh et al., 1986, Hesketh et al., 1988a, Hesketh et al., 1988b). Tungsten was quickly found to be superior to doped silicon due to its high melting temperature (Heinzel et al., 2000) (table 1). Depending on the precise application, moderate optical losses are not necessarily problematic in thermal plasmonics. For example, surface gratings on tungsten—often fabricated (Heinzel et al.) via holographic or interference lithography (section 2.2)—can facilitate control over thermal emission through SPP and standing wave resonances.(Sai et al., 2005) In this case, Kirchhoff’s law states that the thermal emission and optical absorption spectra are directly related. Therefore, tailoring the spectrum and directionality of the thermal emission from a patterned refractory material requires some optical losses. Such control over the thermal emission spectrum of a material has been proposed as a route to improved thermophotovoltaic devices (which convert heat into electricity) (Sai et al., 2005, Chen and Zhang, 2007, Coutts, 1999, Licciulli and et al., 2003, Han and Norris, 2010), high-efficiency incandescent light sources (Waymouth, 1992), and micro/nano mechanical engineering (Sai et al., 2005). Beyond tungsten, such effects can also be observed in other refractory metals, such as molybdenum and tantalum, but these materials have higher losses than tungsten in the mid-infrared region (figure 4).

Figure 4.

(a) Real part and (b) imaginary part of the complex dielectric functions for W (Palik, 1985), Mo (Palik, 1985), and Ta (Weaver, 1974) in the IR range.

2.1.2 Metal alloys

Expanding the list of possible plasmonic materials, metal alloys have also been explored. They offer the potential to tune the optical and physical properties of pure metals for optimal performance. For plasmonics, two classes of metal-alloy systems have been studied—transition-noble metal and alkali-noble metal alloys. Transition-noble metal alloys have been explored both theoretically and experimentally while, to the best of our knowledge, alkali-noble metal alloys for plasmonics have only been considered theoretically. The reader is directed to Blaber et al. for further reading on alkali-noble metal alloys for plasmonics (Blaber and et al., 2010).

Doping a noble metal with a transition metal provides one to two extra electrons to the free electron gas. This n-type doping raises the Fermi level, increases the plasma frequency, shifts interband transitions, and ultimately alters the absorption and reflection properties of the noble metal (Ehrenreich and Philipp, 1962, Bobb et al., 2009). Bobb et al. reported a decrease in the imaginary permittivity of gold at certain wavelengths when it was alloyed with cadmium (Bobb et al., 2009). However, at other wavelengths the imaginary permittivity increased. This work illustrates how band engineering of noble metals can potentially be used to enhance their plasmonic performance over certain spectral regions.

2.1.3. Beyond metals

Another approach to avoid the limitations of metals is to explore semiconductors (Boltasseva and Atwater, 2011, West et al., 2010). Under certain conditions, semiconductors can also display negative permittivity values in the IR region (Lai et al., 2007, West et al., 2010). To achieve this, the concentration of free carriers is typically increased through impurity doping. If the carrier concentration is sufficiently high, the semiconductor essentially acts as a metal. Thus, heavily doped semiconductors (also known as degenerate semiconductors) provide a potential alternative to metals.

Current dopant levels in semiconductors such as tin-doped indium oxide (or indium tin oxide, ITO) and Ga-doped ZnO result in a maximum free carrier concentration (Boltasseva and Atwater, 2011) of 10²⁰ carriers/cm³. Negative permittivity in the NIR is possible at this free carrier concentration. Achieving negative permittivity values in the visible region would require even higher doping levels. This becomes increasingly difficult due to the solubility limit of the dopant in the host material. Wide band gap semiconductors are preferred since they ensure no interband transitions and thus lower losses (West et al., 2010). Therefore, transparent conducting oxides (TCO) such as ITO and doped ZnO are promising plasmonic semiconducting materials. Lau et al. and West et al. have reported that ITO films annealed in nitrogen display negative permittivity in the NIR region (West et al., 2010, Lai et al., 2007). Negative permittivity values have also been reported in non-TCO semiconductor materials. Hoffman et al. reported a negative index of refraction metamaterial in the long-wavelength IR region fabricated from interleaved layers of InGaAs and AlInAs (Hoffman et al., 2007). A superlens operating in the mid-IR region has also been fabricated using SiC (Taubner et al., 2006). The ability to tune the properties of semiconductors through varying their growth conditions makes these materials promising candidates for future plasmonics. In the context of this review, however, in the next sections we will focus on the nanofabrication of metals.

2.2. Optical and interferometric lithography

Once a specific material has been chosen, a nanofabrication technique is typically required to pattern the necessary nanostructure. For nearly half a century, the semiconductor industry has developed a suite of sophisticated equipment and processing recipes to engineer silicon transistors with near perfection, including the growth of crystalline silicon wafers, atomic-scale deposition of thin films, and nanoscale patterning using photolithography and plasma etching. Figure 5 shows some impressive examples of modern silicon transistors featuring sub-50-nm gate lengths, nanometer-thin gate insulators, and multilayer copper interconnects. Transistors are arguably the most precise and sophisticated man-made nanostructures.

Figure 5.

(a) A silicon transistor in the 65-nm generation IC technology (Tyagi, 2005). Image courtesy Intel. Reprinted with permission. (b) A silicon transistor in the 45-nm generation IC technology: Gate insulator is grown by atomic layer deposition, followed by a deposition of a metal gate (Mistry, 2007). Image courtesy Intel. Reprinted with permission. (c) Cut-away image showing metal vias. Image courtesy IBM. Reprinted with permission. (d) Multi-layer copper interconnect lines are patterned using a technique known as “damascene”—a combination of copper electroplating followed by chemical-mechanical polishing. Image courtesy IBM. Reprinted with permission.

In principle, these state-of-the-art manufacturing techniques may also be utilized for engineering optical metallic nanostructures. In practice, however, considerable challenges exist for patterning metals (in particular noble metals such as Au and Ag) due to materials properties as well as processing and equipment issues. In conventional lithography (figure 6), a wafer is spin-coated with photoresist (a hydrocarbon mixture that changes chemical structure upon exposure to light), followed by an exposure via an optical source through a photomask. A developer will then either remove the exposed areas (positive photoresist) or the unexposed areas (negative photoresist). If the exposed region can then be directly patterned with plasma etching, as with Si, SiO₂, or Si₃N₄, well-defined nanostructures can be easily created (figure 6, option 1). However, most metals are not amenable to direct plasma etching because the byproducts of their plasma reaction are non-volatile, thus protecting the surface. Therefore, patterning of metallic structures has relied on other methods such as lift-off, ion milling, electroplating, or shadow evaporation. In lift-off processing (figure 6, option 2), the metal is evaporated on to the exposed region, followed by photoresist removal, thereby eliminating the need for plasma etching altogether. While lift-off has been widely used in research, it has many shortcomings and relatively poor yield for nano-patterning. For example, the metal that is lifted off remains in the solvent bath, and is likely to redeposit on the surface. In addition, due to shadowing and sidewall deposition effects, edges can often be rough and ill-defined.

Figure 6.

Lithographic patterning: Option 1: If the substrate is amenable to dry etching (e.g. Si or SiO₂), the pattern in the photoresist is readily transferred. Option 2: If the substrate is not amenable to dry etching like most metallic films, a lift-off process is used instead.

In semiconductor manufacturing, copper lines, which cannot be easily etched in plasma, are instead patterned using a complex and delicate process known as the damascene process. Here, negative patterns (trenches) are first made in a dielectric film, followed with copper electroplating. The structure is then planarized using chemical-mechanical polishing (Andricacos et al.). While the end result (figure 5d) looks very impressive, this process requires expensive equipment and considerable process optimization, and thus cannot be easily practiced in basic research.

Optical lithography still remains the only viable technology for mass production of microprocessors, and the minimum resolution continues to scale down even below 45 nm today, assisted by techniques such as phase-shift masks and optical proximity correction. However, state-of-the-art lithography systems cost well over $10M and cannot be readily utilized in basic research, which is typically low volume, low budget, and requires many design revisions. Also, the cost of a high-resolution photomask for lithography is prohibitive ($1K~$100K per mask). For low-throughput, proof-of-concept experiments, therefore, electron-beam lithography (section 2.3) or focused ion beam lithography (section 2.5) has been used.

Overall, lithography is the single most expensive step in nanofabrication. Patterning a dense array of nanostructures repeatedly over large areas, which is necessary for systematic and statistical investigation of physical phenomena or practical applications, remains a significant challenge. The high capital cost of optical lithography tools is partly due to the requirements to project arbitrary nano-patterns from a photomask to a photoresist layer, followed by additional aligned exposures with nanometric precision. Many important structures in nanotechnology, however, consist of simple periodic patterns (e.g. periodic arrays of nanoparticles, wires, apertures, or line gratings) and do not require multiple aligned exposures for fabrication. In that case, a technique known as optical interferometric lithography (also called interference lithography or holographic lithography) provides a unique option for researchers to produce structures with nanometric resolution while achieving high-throughput, large-area patterning (Beesley and Castledine, 1970, Brueck, 2005). In this technique, coherent optical beams incident from different directions generate interference patterns in a photoresist without using any photomask or advanced exposure optics. With two-beam interference, as shown in figure 7, for an interference half-angle of θ, the periodicity of the final structure is given by the following formula (Brueck, 2005) for the intensity I given a field amplitude E:

$$I(x,z)=|E{|}^2{\left|\overrightarrow{n_1}{e}^{\mathit{\text{ikx}}\text{sin }\theta }+\overrightarrow{n_2}{e}^{-\mathit{\text{ikx}}\text{sin }\theta }\right|}^2=2|E{|}^2\left|1+{\sigma }_{\mathit{\text{pol}}}\text{cos}(2\mathit{\text{kx}}\text{sin }\theta )\right|$$ (3)

where k = 2πn/λ₀ with n the refractive index of the medium (air or immersion liquid) and λ₀ the vacuum wavelength, n₁ and n₂ are unit polarization vectors, and σ_pol = [1, cos(2θ)] for [transverse-electric, transverse-magnetic] polarization, respectively. In fact, many commercial diffraction gratings are manufactured with this method. When combined with a water immersion technique, a 193 nm ArF excimer laser can achieve dimensions as low as ~34 nm (Brueck). A variety of 1-D, 2-D, and 3-D nanostructures patterned by interference lithography have been used for diffractive optics, photonic crystals (Berger, 1997; Campbell, 2000), spintronics (Ross et al., Field et al., Martin et al., Brueck), plasmonics (Henzie, 2007; Tetz, 2006; Odom, 2009; Gao, 2010), and metamaterials (Zhang, 2005a). While interference lithography cannot be applied to arbitrary patterns, for periodic structures—e.g. line gratings, nanohole or nanoparticle arrays—this technique becomes a very practical option because (1) it is relatively inexpensive in capital costs, (2) an expensive photomask is not required, and (3) patterning can be done with high throughput over a large area.

Figure 7.

(a) Interference lithography can be used to create large-area periodic structures, as shown in the photograph. Reprinted by permission from Macmillan Publishers Ltd: Nature Nanotechnology, (Henzie et al., 2007), copyright 2007. (b) Two interfering coherent beams will generate standing waves to expose the resist. (c) Scanning electron micrograph (SEM) of a 234 nm line pattern in a SiO₂ mask on Si. The Si has been partially etched. Image courtesy Ning Cao and Brian Thibeault at the University of California at Santa Barbara Nanofabrication Facility and the National Nanotechnology Infrastructure Network (NNIN). Reprinted with permission.

2.3. Electron-beam lithography

For patterning arbitrary-shaped, e.g. non-periodic, structures with nanometric resolution, electron-beam (e-beam) lithography has been widely used. It was first developed as a lithography method in the 1970’s when researchers noticed that certain types of materials would be damaged under e-beam exposure. Through the use of modified electron microscopes for pattern generation, intense effort was also put into developing a suitable resist material. To date, poly(methyl methacrylate) (PMMA) remains the resist of choice due to its high resolution and chemical stability. E-beam lithography is similar in basic principle to optical lithography—in that both can selectively alter a layer of resist material—but instead of a flood-exposure of light through a patterned mask, a focused beam of electrons is scanned over a layer of electron-sensitive material.

E-beam writing systems have been used as a production tool in the microelectronics industry for many years to make photomasks for optical lithography. E-beam lithography is also used for application-specific integrated circuits and other small-volume device work. In addition to these more established uses, an emerging application of high-resolution e-beam lithography is for directly making nanoimprint molds and template stripping templates (section 2.10). For its flexibility and superb patterning resoltion, e-beam lithography has been the method of choice for advanced research and development in the physical sciences and devices communities (Vieu et al., 2000).

Typical e-beam writing tools use 10–100 kV acceleration voltages, and thus the de Broglie wavelength of the electrons in these tools is below 1 Å. At this scale, diffraction effects do not impose the resolution limit, which is more a function of other mechanisms such as Coulomb repulsion between electrons and electron scattering in the resist. Even in 1976, feature sizes smaller than 10 nm had been demonstrated using an e-beam system, although the patterns were in thin metal-organics and couldn’t be transferred to an underlying substrate (Broers et al., 1976). Obtaining transferable patterns with resolutions below 10 nm using e-beam lithography, while feasible, is not trivial and it requires extensive photoresist processing, cold development (Hu et al.), and precise beam shaping (Cord, 2007; Cord, 2009). However, e-beam lithography techniques can still provide sufficient resolution to meet the needs of most applications in the nanosciences (Broers et al., 1976). E-beam lithography can also be used as an additive technique via e-beam-induced metal deposition (Koops et al., van Dorp et al., De Angelis et al.).

While e-beam lithography has been successfully utilized in a wide range of pioneering research in physical sciences, it is a serial process that has a low throughput, is relatively expensive compared to other methods covered in this review, and cannot realistically be used for patterning arbitrary, dense arrays over a large-area substrate. Thus e-beam lithography systems have been typically used for fabricating small quantities of devices for proof-of-concept demonstrations. Some examples of arbitrary, high-resolution patterns are shown in figure 8.

Figure 8.

SEM of the text of Feynman’s 1959 speech (Feynman) in hydrogen silsesquioxane resist, written with a high-resolution e-beam lithography system. Images courtesy Bryan Cord at the University of Minnesota Nanofabrication Center.

2.4. Etching

After patterning a resist layer with optical or e-beam lithography, the pattern must then be transferred to the substrate via wet etching, dry etching, ion milling, lift-off, or electro deposition. Here we discuss the pros and cons of various etching techniques that are commonly employed for patterning metallic nanostructures. For more details, the reader is refereed to comprehensive textbooks on the topic (Plummer, 2000; Campbell, 2008; Madou).

Both wet and dry etching can be used for pattern transfer. Wet etching is chemical in nature and can dissolve different materials in a highly selective manner. While wet etching was used for device fabrication in the early days of the IC industry, most wet etch processes are isotropic, i.e. etch equally in all directions, which causes a lateral undercut of the resist mask and degrades the patterning resolution. Also, the etching time in a liquid bath cannot be controlled very precisely. For these reasons, wet etching is generally not acceptable for nano-patterning, but is mostly used to remove blanket films. Wet etching of crystalline materials, however, can be highly directional and anisotropic. In a Si crystal, for instance, the density of bonds in the (111) crystal plane is higher than in the (100) or (110) planes. Some etchants such as potassium hydroxide (KOH) will etch Si along the [111] direction more slowly, revealing the slowly etching (111) planes. (Note: With Miller index notation, {100} denotes the set of equivalent planes and [100] denotes the direction of a normal vertor.) The differences in etch rates (Campbell, 2008) between the [100] and [111] directions can be larger than 100:1. If a standard Si wafer with a (100) surface is etched in a mixture of KOH and water, then V-shaped grooves (from a rectangular opening) or inverted pyramids (from a square or circular opening) will eventually form, as illustrated in Figure 9. The (111) planes will intersect the top surface at a 54.7° angle. Because 3-D trenches with well-defined facets can be made using simple and inexpensive wet etching, this technique has been widely used for applications in micromachining, scanning probe microscopy, and plasmonics. Furthermore, these inverted pyramids or V-shaped grooves (figure 9b) can be turned into protruding sharp metallic pyramids or wedges by depositing metals and subsequently dissolving the Si wafer or a sacrificial layer to dislodge pyramidal particles (Henzie, 2005) (figure 9c) or wedges (Boltasseva, 2008). Alternatively, by depositing a metal film and peeling it off (figure 9d) as in template stripping (section 2.10)(Nagpal, 2009), the template may be reused. The angle between opposing facets is 70.6 deg (figure 9a) and the size of the tip can be made smaller than ~10 nm.

Figure 9.

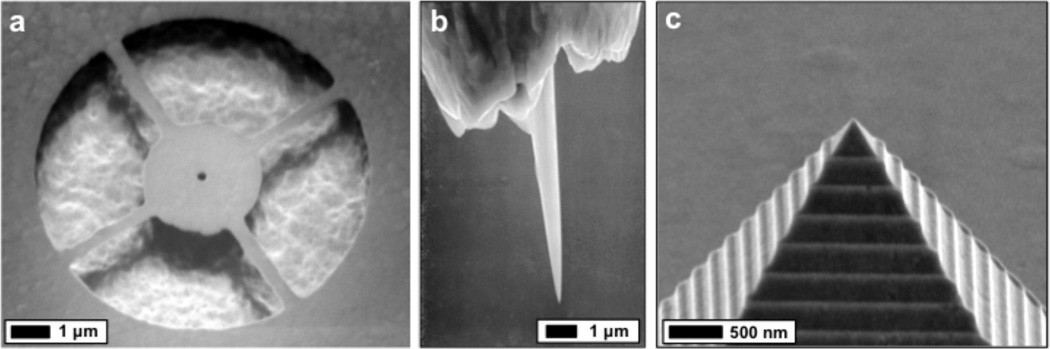
(a) Crystal plane orientation. Pyramidal divots with a tip angle of 70.6 are produced with anisotropic KOH etching of a crystalline silicon wafer. (b) SEM of sharp inverted wedges in a silicon wafer. From (Nagpal et al., 2009). Reprinted with permission from AAAS. (c) Small Au-Ni bilayer pyramid structures released from the silicon mold. Reprinted with permission from (Henzie et al., 2005) Copyright 2005 American Chemical Society. (d) Template stripping (section 2.10) of an upright silver pyramid. From (Nagpal et al., 2009). Reprinted with permission from AAAS.

In contrast to wet chemical etching, ion-beam milling is a physical etching technique. Here, accelerated ion beams, typically Ar or other inert ions, bombard the sample surface and sputter atoms in a highly directional, anisotropic manner for virtually any material. Material-independent etching, however, is also a drawback. For example, if the etch rate of the resist mask and the underlying substrate to be etched is similar, the photoresist will erode and degrade the patterns in the substrate. Also, redeposition of the mask material on the sample surface can be problematic.

Plasma etching, or dry etching, has been the dominant technique used in the microelectronics industry because it can combine the benefits of both chemical etching (selectivity) and physical etching (directionality). A large suite of plasma etch recipes have been developed for Si, SiO₂, Si₃N₄, Al, silicides, and GaAs. Compared with wet etching in a bath, plasma etching is easier to start (i.e. ignite) and stop, more reproducible, highly directional, less susceptible to particle contamination, and produces less chemical waste. In silicon microfabrication, reactive ion etching (RIE) in a plasma system has been predominantly used to simultaneously achieve anisotropic etching with high selectivity. Chlorine-based plasma RIE processes have been commonly employed for anisotropic etching of Si, GaAs, and aluminum-based alloys. Details of RIE etch processing can be found elsewhere (Plummer, 2000; Campbell, 2008). However, RIE also has drawbacks. It physically damages the sample surface, via ion injection, and also leaves chemical impurities near the surface. While plasma etching has been a workhorse in the IC industry, selective and directional plasma etching of metals, in particular noble metals such as gold and silver, is extremely challenging. For example, copper, which is the choice for IC interconnects, cannot be easily etched in plasmas because the etch residues are difficult to remove and corrode easily. The challenges of manufacturing multi-layer copper interconnects for microprocessors was eventually overcome (Andricacos et al.) in late 1990’s. Interestingly, it turned out that the industry solution, known as the damascene process (figure 5d), was to avoid direct plasma etching. For the same reason, patterning of noble metals relies on physical ion milling or lift-off. Template stripping, described in section 2.10, provides an alternative solution for patterning noble metal films. In that case, nanostructures are patterned in crystalline Si wafers using the well-established methods described above, e.g. anisotropic wet etching of crystalline Si, ion-beam milling, or RIE etc., and the pattern is replicated in deposited metallic films, which can be peeled off on demand. This way, one can eliminate the need for direct plasma etching of metallic films while retaining the smoothness of crystalline Si templates (Nagpal, 2009).

2.5. Focused ion beam nanofabrication

Focused ion beam (FIB) lithography is used extensively for the direct fabrication of metallic nanostructures. This section gives a brief outline of the FIB nanofabrication technique for physically patterning a substrate (Langford, 2007; Orloff, 1993; Melngailis, 1987). FIB can also be used for depositing various metals with ion-beam induced deposition (Tao, 1990), for doping semiconductors (Melngailis, 1987, MoberlyChan, 2007), or for preparing transmission electron microscope (TEM) samples (Reyntjens and Puers, 2001; Mayer, 2007). These methods are extremely useful to test device designs and geometries, fix masks or electrical traces, or produce high-resolution ion-beam images, and have been essential in the emerging field of plasmonics.

Focused ion beams impinging on a surface offer a very different form of nanopatterning compared to conventional methods that use a resist, exposure, and development. Typically, the ions have accelerating potentials of tens of kilovolts, with beam currents ranging over many orders of magnitude from picoamps to several nanoamps. Depending on the column optics, ion source, and beam current, the beam spot sizes can range from ~5 nm up to a micron. Numerous ion species are available, such as Al, Au, B, Be, Cu, Ga, Ge, Fe, In, Li, P, Pb, and Si, the most commonly used being the semiconductor dopants (Orloff et al., 1993, Melngailis, 1987). In particular, Ga is widely used due to its low melting temperature (30° C), low volatility, and low vapor pressure (Volkert and Minor, 2007).

To produce the smallest and brightest ion beam, FIB systems use a liquid metal ion source (Volkert and Minor, 2007). A metal source is heated up, such that it flows down and wets a sharp tungsten needle. As an extraction voltage is applied between the metal source and an extraction aperture, the liquid metal is pulled into an extremely sharp “Taylor-Gilbert” cone (Volkert and Minor, 2007, Forbes and Djuric). By balancing the electrostatic forces produced by the extraction voltage and the liquid surface tension forces (Orloff, 1993), the liquid source can have a tip size on the order of several nanometers (Melngailis, 1987). Ions are then extracted from the tip of this cone by field emission. As opposed to electron-beam imaging systems, the “lenses” in a FIB column are typically electrostatic and not magnetic because the Lorenz force acting on ions, which are much heavier and slower than electrons, is much lower than that for electrons with the same kinetic energy (Volkert and Minor, 2007). Some other similarities and differences are pictured in figure 10a. A fast beam blanker is then used for patterning. Commercial instruments usually have many patterning options within the control software, such as drawing simple bitmaps or using more complicated proprietary CAD files. Effects such as chromatic aberration, i.e. beams of ions with a range of different energies, limit the final size and resolution of the focused beam, which to a good approximation is Gaussian in profile. The minimum beam size is on the order of ~5 nm. A schematic of the ion source is shown in figure 10b.

Figure 10.

(a) Schematic showing the similarities and differences between typical e-beam and FIB systems. (b) Schematic of the gallium liquid metal source.

Using a FIB for milling a substrate produces many effects, with approximately one to five atoms removed per incident ion depending on the substrate and ion energies. Additionally, electrons are released that can be used for imaging, chemical reactions may be induced, and atoms can be displaced from their equilibrium positions. Interestingly, the shape of a milled groove depends on several factors, and not just the Gaussian beam profile (Melngailis, 1987). Re-deposition and self-focusing effects can lead to large geometrical differences depending on whether the patterns were milled in a single step or with multiple repetitions, even with the same overall ion dose. Also, milling a trench with large total ion doses deviates from the Gaussian profile, giving an unexpectedly deep, V-shaped groove (Melngailis, 1987). The FIB milling process depends on the material, ion beam incident angle, redeposition of sputtered materials, and even the crystal orientation, as outlined in figure 11. Grain-orientation-dependent FIB sputtering can also lead to severe surface roughness on polycrystalline samples, as discussed in section 2.10 and figure 11a, b. However, care can be taken to produce well-defined structures as shown in figure 12.

Figure 11.

The crystal orientation of a sample can affect the FIB sputtering rates, shown in (a) and (b). (c) The sputtering rate is also affected by the mass of the atoms (orange atoms are more massive), and (d) by the local geometry of the sample. Figure from (Volkert and Minor, 2007) Reprinted with the permission of Cambridge University Press. Copyright 2007.

Figure 12.

(a) Single nanohole in a suspended 200 nm thick Ag circular pad. The underlying SiO₂ was etched after patterning the Ag via FIB. (b) SEM image of a sharp gold tip fabricated by FIB milling. Image courtesy of Lukas Novotny, from www.nano-optics.org. (c) A silver pyramid with integrated gratings. The gratings were patterned into a KOH-etched silicon mold via FIB and the mold was then used for template stripping (section 2.10). Reprinted with permission from (Lindquist et al., 2010). Copyright 2010 American Chemical Society.

An important additional benefit of a FIB tool is its ability to use a gas injection system (GIS) for the deposition of various materials (such as W, Pt, C, and Au) via site-specific CVD (Volkert and Minor, 2007). By carefully adjusting the gas precursor flow rates and the ion beam current density, high-efficiency deposition is achieved with ~µm per minute accumulation rates. The reaction of the ion beams with the precursor materials offers the ability to weld micromanipulators to specific parts of a substrate in situ. With subsequent FIB milling and thinning, those parts are cut free, and are often mounted to a TEM imaging grid (Mayer et al., 2007). Unfortunately, metals deposited via FIB are highly contaminated with carbon. With other GIS systems, instead of depositing materials, it is also possible to enhance the inherent FIB milling etch rate.

As a direct-write, maskless, high-resolution nanofabrication tool with the ability to sputter, image, analyze, and deposit, a FIB instrument offers many significant advantages. Both 2-D and 3-D patterning is possible (Langford, 2007). However, as a patterning tool, particularly for metals, some limitations also exist. Unlike optical lithography that patterns the whole wafer with one short exposure, FIB milling is a serial lithography technique, like e-beam lithography, patterning only one spot or device at a time. Large-area patterning is not feasible. For high-resolution (<100 nm) features, FIB milling can also be slow since very low currents (~pA) must be used. Along with FIB-induced sample damage (Mayer, 2007), Ga ions are implanted at atomic fractions of 1% to 50% near the sample surface (Volkert and Minor, 2007). This can degrade the plasmonic properties of the patterned metal film. As mentioned in other parts of this review (sections 2.10 and 4.1), increased surface roughness of metals degrades the SPP propagation lengths. As such, the advantages and disadvantages of FIB milling need to be taken into account when fabricating new optical or electronic devices. When combined with a template stripping technique (Section 2.10), many of these roughness and contamination issues are minimized, since FIB is then used to only pattern a reusable template, leaving the resulting metal films smooth and contamination-free.

2.6. Soft lithography

Soft lithography is part of a newer breed of “unconventional” nanofabrication methods (Gates, 2005, Gates, 2004) wherein soft elastic stamps (Xia and Whitesides, 1998) are used for printing or molding nanoscale patterns. This encompasses techniques such as molding, microcontact printing, microtransfer printing, and nano-imprint lithography, as illustrated in figure 13.

Figure 13.

Various soft lithography techniques. (a) replica molding, (b) microcontact printing, (c) micromolding in capillaries, and (d) microtransfer printing.

For fabricating metallic nanostructures, two different methods are available: (1) utilizing patterns of self-assembled monolayers (SAM) of molecules as an etch mask (Kumar and Whitesides, 1993), or (2) using a soft polymer template (Xia, 1996b, Zhao, 1996, Kim, 1995, Kim, 1997, Rogers, 1997, Terris, 1996, Chou, 1995). The first fabrication scheme, called microcontact printing (figure 13b), involves using a polymer stamp made from a master mold and coating it with a suitable SAM. The stamp is then brought into contact with the flat metal film to be patterned, transferring the SAM. The soft stamp is then released, leaving the SAM behind as an etch mask. Different SAM molecules have been used, depending on the metal. For example, alkanethiols have been used for gold (Delamarche, 1996), silver (Fenter, 1991), copper (Schlenoff, 1995), and palladium (Lee, 1991); alkanephosphonic acids for aluminum (Goetting, 1999); alkylisonitriles for platinum (Hickman, 1992); carboxylic acids for metal oxides (Tao, 1993); and alkanesulfinates (Chadwick, 1993) and alkylphosphines (Uvdal, 1995) for gold patterning. Typically, the inked polymer stamp is in contact with the metal film for only a short time because the SAM is formed quickly upon contact (Larsen, 1997). Longer contact with the polymer stamp results in the spreading of SAM molecules outside the contact regions, thereby destroying the pattern (Xia and Whitesides, 1995). Following the formation of the highly ordered SAM, the exposed metal film is then etched in a suitable chemical etchant, resulting in large areas of patterned metallic nanostructures. Suitable wet etchants include K₂S₂O₃ / K₃Fe(CN)₆ / K₄Fe(CN)₆ or cyanide solutions in water saturated with oxygen for gold and silver with an alkanethiol SAM (Kumar, 1994, Xia, 1995), or FeCl₃ and HCl for copper (Xia, 1996a) films.

The second fabrication scheme involves patterning a polymer template on top of the metal film (as in figure 13c), and then using the patterned polymer as mask for chemical, plasma, or ion etching (section 2.4). The polymer can be patterned using a host of techniques such as replica molding (Xia, 1996b), microtransfer molding (Zhao, 1996), micromolding in capillaries (Kim, 1995), solvent-assisted micromolding (Kim, 1997), phase-shift lithography (Rogers, 1997), cast molding (Terris, 1996), and embossing (Chou, 1995). All of these techniques involve some variation of either stamping or embossing an evenly coated polymer film on the metal film (with or without solvent), or selectively coating parts of the metal film with the polymer using either liquid polymer inside patterned polydimethylsiloxane (PDMS) microfluidic channels, or removing selected areas of polymer using PDMS wetted with a solvent layer. Irrespective of the fabrication scheme used in soft lithography, the PDMS mold is an integral part of the templating process.

One limitation of these fabrication schemes is that the resolution and aspect ratio of the patterns formed is limited by sagging or contact between different pattern areas on the PDMS mold. This results from the flexibility and mechanical properties of the soft PDMS polymer. This has been minimized by using a two-part PDMS stamp—a stronger and more mechanically robust h-PDMS (Schmid and Michel, 2000) followed by a second softer PDMS backing support. This prevents nearby patterns from coming into contact, while simultaneously providing a flexible backing layer to prevent cracking of the rigid stamp (Odom et al., 2002). This technique has been used extensively to fabricate high-resolution, large-area nanopatterned films. Another limitation of this fabrication technique is the contamination of the metal film while patterning. The use of either SAM or polymer masks results in residual contamination on the metallic surfaces, which may be problematic for some applications. Moreover, direct patterning via chemical etchants or ion etching can also embed contaminants in the metal film, and degrade its optical (Nagpal et al., 2009) or mechanical (Stanishevsky et al., 2002) properties.

Another variation of the polymer-based soft lithographic patterning techniques is nanoimprint lithography. This technique utilizes a hard nanopatterned mold (e.g. patterned silicon) to transfer the desired patterns in a soft polymer either using heat (thermoplastic nanoimprint lithography), or ultraviolet light to cure the polymer (photo nanoimprint lithography). In thermoplastic nanoimprint lithography, a hard mold is pressed against a heated polymer film (above its glass transitions temperature) to transfer the desired pattern into the polymer using “hot embossing” (Chou, 1996). Desired nanopatterns can also be transferred into a polymer by curing the polymer using ultraviolet light, while the photocurable polymer resist is in contact with the silicon mold. Since this patterning relies in reusing a hard nanopatterned mold, it is not affected by some of the aforementioned limitations of low resolution due to mechanically soft molds. However, silicon molds can often get damaged from application of high pressure, or contamination from liquid photocurable resist, while transferring the pattern to the polymer template.

Although these soft lithography techniques can pattern metals over large areas, these techniques have some drawbacks in producing smooth patterned metals that are required for plasmonics (more details in section 2.10) with high throughput. For example, if the molds are etched away to release the patterned metals, one has to produce the expensive mold each time. In addition, because of poor wetting of metals on polymers, the patterned metals can exhibit rough surfaces.

2.7. Stencil lithography

Stencil lithography is an alternate mode of patterning wherein a shadow mask (typically a free-standing Si or Si₃N₄ film perforated with the desired patterns) is used to physically block an incident beam of atoms or ions instead of light as in photolithography (figure 14). This method has been used for selectively depositing metals, etching the underlying surface, projection e-beam lithography, implanting ions, and making tunnel junctions (Dolan and Dunsmuir, 1988, Ono et al., 1996, Deshmukh et al., 1999, Brugger et al., 2000, Vazquez-Mena et al., 2008, Yan et al., 2005).

Figure 14.

(a) Illustration of the stencil lithography process. Reprinted with permission from (Vazquez-Mena et al., 2008) Copyright 2008 American Chemical Society. (b) Silicon nitride membranes with 50-nm nanoholes. Image is taken after Pt deposition, showing some clogging. (c) Resultant Pt stencil patterns on the substrate. Panels (b) and (c) Reprinted with permission from (Yan et al., 2005) Copyright 2008 American Chemical Society.

Stencil lithography is particularly useful for patterning substrates that are not compatible with standard photoresist processing. For example, substrates coated with organic semiconductors or polymers may be damaged during a photoresist process, because it requires spin-coating followed by baking at ~100°C, and dissolution of the polymeric photoresist in a developer. As another example, if the adhesion between a deposited metal film and the substrate is poor, subsequent wet processing may delaminate the metal film. Stencil lithography can overcome these issues by eliminating the use of photoresist, wet solvent processing, and high-temperature baking steps. Lithographic patterning is also difficult on non-planar surfaces since photoresist cannot uniformly coat structures with topography. As a versatile direct deposition technique, stencil lithography is particularly useful for patterning metals on top of such unusual substrates and non-planar structures. Furthermore, in contrast to ion milling, the stencil lithography process does not implant unwanted ions into the substrate.

A stencil mask is typically made with a free-standing Si3N4 film supported by a Si wafer, a silicon-on-insulator film or a metallic film. For nanoscale patterning, the stencil masks are typically made using e-beam lithography or FIB. The mask surface may be coated with other materials to improve its durability and reduce unwanted metal deposition. The size of the patterned apertures in the stencil mask can be reduced by a conformal coating with SiO₂, Al₂O₃, or other films (Yan et al.). Atomic layer deposition (section 2.9) can be used for such coating, improving the durability of the mask while decreasing the minimum patterning resolution. For the metal deposition step, a highly collimated beam, i.e. an evaporation process, is desired. Various metallic nanostructures such as dots, lines, wires, optical antennas, and tunnel junctions have been fabricated via stencil lithography (Dolan and Dunsmuir, Champagne et al., Vazquez-Mena et al., 2008, Vazquez-Mena et al. 2011).

Toward reliable and reproducible fabrication, several challenges should be overcome. High-resolution (sub-100-nm resolution) patterning requires the use of a thin stencil mask, but such a thin suspended membrane can be easily broken. Furthermore, the evaporation of metal through the stencil mask gradually clogs the apertures as shown in figure 14b (Yan, 2005). The patterning resolution depends on the precise control of the mask-substrate distance and the patterns still retain the nominal roughness of as-deposited metal films. Since a collimated evaporation beam is required, sputtering cannot be easily used, and multilayer pattern fabrication is difficult. Furthermore, the use of the stencil prohibits the use of patterns that cannot be made into a free-standing film, such as annulus or ring devices. The bottleneck for patterning dense features is the fabrication of the stencil mask itself, if it relies on e-beam lithography or FIB. Alternatively, interference lithography, nanoimprint lithography, or other high-throughput patterning technique may be used to produce high-resolution stencil masks that can then be repeatedly used.

2.8. Cold welding and pattern transfer

Cold welding (Bowden and Tabor, 1964) developed as an important fabrication method following the report by Whitesides et al. on selectively transferring one layer of gold to another by simply applying pressure and forming a “cold weld” (Ferguson, 1991). The gold transfer layer was grown or deposited on a patterned or unpatterned substrate with poor adhesion to the gold film. The second gold layer was on a surface with good adhesion to gold. This technique has been widely used for patterning a variety of metal nanostructures ranging from metal electrodes for devices (Zaumseil, 2003b) to three-dimensional periodic gold nanostructures built from a single elastomeric PDMS stamp (Loo, 2002, Zaumseil, 2003a, Menard, 2004, Jeon, 2004, Schmid, 2003). Although most of the work done on cold welding and pattern transfer has used gold as the metal of choice, other ductile metals have also been examined (Alcantar, 2003).

While this printing method was initially developed using gold cold welding, it has been extended using SAMs to either enhance or reduce the adhesion of the gold films, thereby eliminating the need for the second gold layer (Menard, 2004, Zaumseil, 2003a, Jeon, 2004). Metal on the “non-stick” surface can thus be transferred to a “sticky” surface. This novel technique can be widely used for fabricating complex metal nanostructures as shown in figure 15. The pattern-transfer methodology has also been extended to other metals, polymers and other inorganic surfaces (Jiang, 2002, Childs and Nuzzo, 2002). This pattern transfer technique is very general, and can lead to fabrication of large-scale, low-cost devices for applications in photonics, electronics, plasmonics, and metamaterials.

Figure 15.

A wide variety of patterned metal nanostructures and 3-D stacks can be fabricated using pattern transfer of thin gold layers from molds followed by cold welding with another gold layer or self-assembled monolayer. The 3-D structure shown in figure (c) is difficult to fabricate by other means. Reprinted with permission of John Wiley & Sons, Inc., Copyright 2004, from (Jeon et al., 2004)

One drawback of this fabrication technique is that the thickness of the transferred layer should be small. Typically, only ~20 nm thick gold films can be transferred with cold welding by exploiting the differences in adhesion on the two substrates (Jeon, 2004). Moreover, growing metal films on surfaces with organic SAMs or other coatings can lead to increased surface roughness. While nanoscale inhomogeneities are acceptable for most photonic and electronic applications, applications in plasmonics and metamaterials benefit from smooth metal interfaces to reduce losses (Raether, 1988; Nagpal, 2009).

2.9. Atomic layer deposition

Atomic layer deposition (ALD) is a special variant of CVD that utilizes repeated cycles of self-limiting surface reactions to deposit conformal thin films in a layer-by-layer fashion with angstrom-scale thickness control. This method was originally called atomic layer epitaxy (Ahonen et al.). Among its many applications, ALD has been used for commercial production of thin-film electroluminescent flat-panel displays (Leskela and Ritala). More recently, ALD processes for HfO₂, ZrO₂, and Al₂O₃ have been studied for applications in the microelectronics industry to replace an ultra-thin SiO₂ gate oxide insulator, which leaks unacceptably high tunneling currents below 10 Å thickness (Wilk, 2001). Following the adoption of ALD by the microelectronics industry (Mistry, 2007; Bohr, 2007), this versatile technique now finds a series of novel applications in the nanosciences. Many excellent review articles describe the growth mechanism and chemistry of ALD processes (Leskela and Ritala, 2003, Puurunen, 2005, George, 2010). Here, we summarize key features and focus on applications for metallic nanostructures in particular.

A complete ALD cycle for the deposition of a compound film, e.g. a binary film such as Al₂O₃, consists of the following sequence: (1) expose the first precursor (trimethylaluminum, or TMA, in the example of Al₂O₃) and perform one self-limiting surface reaction; (2) purge the reaction chamber of nonreacted material; (3) initiate a self-limiting reaction of the second reactant (H₂O for Al₂O₃ deposition); and (4) purge. Ideally, each surface reaction in ALD is self-limiting and complementary, i.e. the completion of each reaction presents a substrate for the alternate reaction. These reactions are then cycled repeatedly to grow compound films with a desired thickness. Because the film thickness in ALD is controlled in discrete steps given by the number of self-limiting deposition cycles, rather than by the exact temperature or growth time, this layer-by-layer deposition scheme is more robust against variations in temperature and flux of reactant species than conventional CVD and molecular-beam epitaxy. Additionally, since two reactant gases are injected separately after purging the reaction chamber, ALD prevents the possibility of unwanted gas-phase reactions that can lead to particle generation and poor film quality. Thus ALD-grown thin films are dense and pinhole-free, and exhibit conformality over extremely challenging, high-aspect-ratio 3-D topography such as nanoholes or nanogaps often encountered in plasmonics.

ALD can grow many pure or compound thin films on a diverse set of substrates including silicon, glass, oxide, polymer, and even inert materials such as graphene (George, 2010). Among these, the ALD-grown alumina (Al₂O₃) has been studied as a model system applied to metallic nanostructures. For microelectronic applications, ALD-grown alumina has a dielectric constant (George) of ~7, which is higher than the dielectric constant of SiO₂ (3.9), and can be used to reduce tunneling current when used as a gate insulator. Because ALD alumina can be deposited at low temperatures (<100°C) (Groner et al., 2004) and act as an excellent barrier against gas diffusion (Groner et al., 2006), it is well-suited for robust device encapsulation. Several groups have used ALD-grown alumina films for tuning the resonances of optical devices (Yang et al., 2007, Qian et al.), layer-by-layer characterization of surface-based biosensors (Whitney et al., 2005, Im et al., 2010b), protecting patterned metallic surfaces against oxidation (Zhang et al., Im et al., 2010b), or patterning functional devices with ultra-thin gaps (Im et al., 2010a). Some examples are pictured in figure 16. In general, hydroxylated surfaces are amenable to the ALD process, but it has been shown that TMA, which is a precursor of ALD alumina process, also adheres well to silver, which is nonhydroxylated (Standridge et al.).

Figure 16.

(a) SEM of an alumina-coated silver nanosphere array. Reprinted with permission from (Zhang, 2006) Copyright 2006 American Chemical Society. Only two ALD cycles were used to deposit a sub-1-nm thick film. (b) Cross-sectional image of a gold nanohole array film after encapsulation with ALD silica. Inset: The top surface and vertical sidewall of each nanohole is uniformly coated with 20-nm-thick silica (Im, 2010c). Reproduced by permission of The Royal Society of Chemistry. (c) Vertical nanogap array with a 7-nm gap size fabricated using ALD-grown alumina. Inset: zoomed view showing the 7-nm-gap around the circumference. Reprinted with permission from (Im, 2010a) Copyright 2010 American Chemical Society.

The materials and processing options for ALD keeps expanding. Gordon et al. demonstrated a conformal deposition of SiO₂ that incorporates a small amount of Al₂O₃ (Hausmann et al.). This process has been used for surface modification of plasmonic sensors (Im, 2010c). ALD-grown TiO₂ has also been used to functionalize metallic nanoparticles for photovoltaics (Standridge, 2009). Metallic ALD films have been demonstrated for W (Klaus, 2000), Cu, Co, Fe, Ni (Lim, 2003), and Ag (Maarit Kariniemi). While ALD-deposited metal films may be useful for plasmonics, their optical and electrical properties tend to be degraded due to residual impurities compared with pure evaporated or sputtered metal films.

Thin film deposition techniques such as CVD and ALD can achieve a level of nanometric precision that cannot be achieved using even the most advanced e-beam lithography (section 2.3). Consequently, various schemes have been devised to convert the deposited thin films into a lithography-independent critical dimension (Choi, 2002; Hergenrother, 2002; Odom, 2002; Im, 2010a; Kubo and Fujikawa). Since ALD is one of the more precise and robust thin-film processing methods available, ALD may be used to define sub-10-nm, or even sub-1-nm, critical device dimensions. For instance, an ALD-based patterning technique was used to produce vertical metallic nanogap structures with 5-nm gap sizes at the wafer-scale (Im, 2010a). Moreover, no fundamental reason prohibits this technique from yielding gap sizes below 1–2 nm, making it a unique top-down fabrication technique with potential angstrom-scale patterning resolution.

While ALD has been successfully used in production, further improvements can be considered. Low throughput may be problematic for depositing thicker films. Materials choice needs to expand further to enable ALD for a wider variety of pure metals or other compounds. Overall, ALD tools have been reliably deployed in many research laboratories, and beyond its already successful usage in the microelectronics industry, will continue to enable progress in the nanosciences.

2.10. Template stripping

As discussed in previous sections, as-deposited polycrystalline metal films are inherently rough. Furthermore, the metallic films must then be patterned, which can exacerbate the surface roughness. For example, FIB can be used, but the roughness is increased as the grains are exposed. For example, on an as-deposited silver film, a typical rough FIB bull’s eye pattern is shown in figure 17a, b. To avoid this roughness, extremely small grains can be grown with fast sputtering (Yin et al., 2005) or single crystals can be grown by the Czochralski process (Vesseur et al., 2008, Kuttge et al., 2008) or with chemically-synthesized flakes (Huang et al.). However, subsequent FIB patterning, in addition to being a slow, serial fabrication process, will still introduce ion impurities (section 2.5).

Figure 17.

(a) Top-view and (b) zoomed in SEMs of a bull's eye pattern milled into an as-deposited silver film via FIB. The graininess of the pattern is evident. (c) Top-view FIB image and (d) side-view SEM of a bull's eye pattern milled into an ultrasmooth template-stripped silver film. Though the surface is smooth, patterning via FIB still exposes the grains, leading to pattern roughness and degrading the optical performance of the device.

With these problems in mind, this section focuses on a novel scheme based on template stripping for the fabrication of ultrasmooth patterned metallic substrates (Nagpal, 2009). Although template stripping from ultrasmooth, unpatterned silicon or mica surfaces is a well-known technique (Hegner, 1993), it can also be done with patterned templates. This simple procedure opens up a path towards high-throughput fabrication of a wide range of high-quality plasmonic devices that are not plagued by surface roughness, sample-to-sample variability, or ion contamination and implantation.

2.10.1. Unpatterned metal films

Template stripping is a well-known method for producing unpatterned, ultrasmooth metal surfaces over large areas (Hegner, 1993). The process exploits the poor adhesion but good wettability of noble metals on ultrasmooth templates such as freshly cleaved mica or silicon wafers. A metal film is first deposited onto the clean template. Subsequently, an epoxy or adhesive backing layer is attached to the topside of the metal film. By peeling off the backing layer, the metal will be released from the template (demonstrated in situ in figure 18), clinging to the backing layer and revealing the ultrasmooth surface. The roughness of the template-stripped films can approach that of the template itself. For example, a silicon wafer with an root-mean-square (RMS) roughness of 0.19 nm was shown to yield a corresponding silver film with a surface roughness of 0.34 nm (Nagpal, 2009). This approach also provides other benefits. For example, prior to template stripping, the metal films can be annealed to increase the grain size. On a typical exposed metal surface, such annealing would increase the surface roughness. However, the hard template constrains the surface roughness of the buried surface during annealing. Therefore, after template stripping, a smooth, large-grain film can be obtained.

Figure 18.

By micro-welding via a platinum gas-injection-system (GIS) inside a FIB chamber, it is possible to perform in situ template stripping of a 200-nm-thick Ag film with a sharp tungsten probe. The smooth underlying silicon surface is clearly seen. Both (a) unpatterned and (b) patterned films can be peeled out (Lindquist et al., 2011).

2.10.2. Patterned metal films

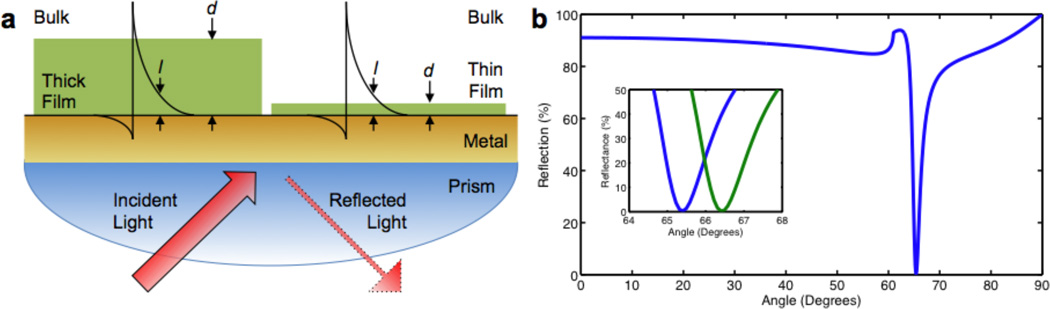
With a flat template, the resulting smooth template-stripped metallic surface must still be patterned. However, even on a smooth surface, FIB milling will still introduce roughness (figure 17c,d) and implant impurities. To solve this problem, it was recently realized that the template-stripping process could also be used with a patterned template to produce ultrasmooth metals (Nagpal, 2009). Modern micro and nanofabrication techniques such as photolithography or e-beam lithography are able to pattern entire single-crystal silicon wafers on nanometric scales with very little roughness and high precision. Furthermore, FIB milling may also be used without worrying about grains or ion contamination, since only the silicon is being patterned. With template stripping, high-quality patterns can then be transferred to a metal film, as shown in figure 19. The template can then be reused, unlike other templating methods where the high-quality (and possibly expensive) template must be etched away and destroyed to reveal the patterned metals (Henzie et al., 2005, Boltasseva et al.). Alternatively, polymeric replica molds have been used, but surface roughness is still an issue (Gates, 2005).

Figure 19.

Template stripping takes advantage of the poor adhesion and good wettability of noble metals on silicon. The top, as-deposited side of the metal films remain rough, but when the film is stripped from the template, the ultrasmooth, patterned interface is exposed. SEMs from Nagpal, et al.(Nagpal et al., 2009) Reprinted with permission from AAAS.

Furthermore, with template stripping, it is possible to fabricate complex patterns, as shown in figure 20. Different metals, such as copper, are also possible, as long as the low-adhesion requirement is met (Nagpal, 2009). By combining silicon microfabrication techniques, such as FIB, optical lithography, nanosphere lithography, reactive ion etching, or anisotropic potassium hydroxide (KOH) ething, a wide variety of structures can be created (Nagpal, 2009, Sun, 2007, Yang, 2010, Lindquist, 2010). If the silicon template is properly structured, apertures, bumps and grooves can be template-stripped (Im, 2011; Lindquist, 2011), all integrated into a single device. Due to the deposition process, both the top and bottom sides are patterned. Additionally, the template can be reused ~100 times, giving high-throughput, low-cost fabrication of high-quality repeatable plasmonic devices. To fabricate the patterned pyramid structure in figure 20d, anisotropic KOH etching of silicon (section 2.4) was used followed with aligned FIB patterning (Lindquist, 2010). The resulting template-stripped pyramid tip has a radius of curvature of ~10 nm.

Figure 20.

Template stripping of patterned surfaces. (a) An array of silver bumps from a FIB-patterned Si template. From (Nagpal, 2009) Reprinted with permission from AAAS. (b) Multilayer structures, here with silver and alumina, are also possible. From (Nagpal, 2009) Reprinted with permission from AAAS. (c) An array of periodic nanoholes in an optically thick Ag film, still on the silicon mold. Since the deposited film is discontinuous, nanoholes are formed. Reprinted with permission from (Im, 2011) Copyright 2011 American Chemical Society. (d) Patterned silver pyramid made from a Si template etched with KOH and patterned via FIB milling. Reprinted with permission from (Lindquist, 2010) Copyright 2010 American Chemical Society.

It should be noted that template-stripped metal films, while ultra-smooth (Hegner, 1993), still consist of polycrystalline grains and resultant SP damping due to grain-boundary scattering and ohmic loss cannot be eliminated (Nagpal, 2009). If a metal film in contact with a silicon template is annealed at a high temperature, the metal grains can grow without any causal increase in film roughness (as it is constrained by the smoothness of the silicon template). It was shown that the average grain size in template-stripped Ag film can be increased from ~80 nm to over ~1 um after annealing at 150 °C, which resulted in 12 fold decrease in losses due to grain boundary scattering of SPPs (Nagpal, 2009). This eliminates grain boundary scattering as a dominant loss mechanism in propagation of SPs on smooth films, and the losses in the metal films are now limited by the ohmic losses encountered by the conduction electrons. Other groups have used single-crystalline metal films grown by the Czochralski process (Vesseur et al.) and chemically synthesized thin crystalline Au flakes (Huang et al.) to fabricate high-quality plasmonic devices. As with template stripping, wherein FIB is used to mill single-crystal silicon wafers to obtain smooth patterns, single-crystal metal films can also lead to smooth patterns while eliminating grain-boundary scattering of SPs. On the other hand, in addition to surface contamination resulting from the implanted Ga ions, the patterns must be directly milled one-by-one.

3. Computational modeling

Following the fabrication of a particular plasmonic metallic nanostructure, its optical properties must be determined. This review will now shift its focus from fabrication to computational and theoretical modeling of metallic nanostructures in section 3 and experimental characterization in section 4. Theoretically, the classical optical behavior of a metallic nanostructure is determined by Maxwell’s equations. Unfortunately, Maxwell's equations can only be solved analytically for a small set of relatively simple geometries, such as spherical metallic nanoparticles, planar metallic films, or simple SPP waveguide structures. For other geometries, these equations must be solved numerically. This section outlines one of the most common domain-discretization algorithms, finite-difference time-domain (FDTD) (Taflove and Hagness). Another common domain-discretization technique is Finite Element Modeling (FEM). One of its main advantages is the use of unstructured grids. However, FEM time-domain (broadband) simulations can be inefficient (Smajic et al., 2009). For this review, only FDTD will be covered.

3.1. Finite-difference time-domain

The FDTD algorithm is one of the most widely used domain-discretization methods for performing numerical experiments with plasmonic devices by calculating the distribution and propagation of electromagnetic fields through complex materials with arbitrary geometries. The FDTD algorithm is a direct solution to Maxwell's equations, with no approximations except for the discrete nature inherent to all numerical methods. It is easily derivable without much mathematical rigor, and is therefore fairly simple to implement in computer code.

The domain of the problem of interest must be discretized, and, for Maxwell's equations, a convenient grid structure is the Yee cell (Yee, 1966). In this method, the electric and magnetic field components are offset by half a grid step both in space and in time. The “curl” nature of the electric and magnetic field relationships are then easily accounted for. For a three-dimensional problem in Cartesian coordinates, the spatial grid is assumed to have mesh step sizes of Δx, Δy, and Δz. Additionally, since Maxwell's equations dictate that a temporal change in the electric field E is related to a spatial change in the magnetic field H and vice versa, a time step Δt is also defined. Due to the nature of the FDTD algorithm, the fairly restrictive Courant stability condition must be met:

$$c\mathrm{\Delta }t\le {\left(\frac{1}{\mathrm{\Delta }{x}^2}+\frac{1}{\mathrm{\Delta }{y}^2}+\frac{1}{\mathrm{\Delta }{z}^2}\right)}^{-\frac{1}{2}}$$ (4)

which generally states that a wave or electromagnetic disturbance may not propagate more than one grid point per time step. To obtain accurate results, the spatial grid must also be small enough to resolve the wavelength of the light, SPP, or smallest structural feature. For plasmonic applications, where subwavelength structures and evanescent fields are involved, care must be taken. Using non-uniform grids, with more grid points surrounding the smallest features can help by balancing simulation accuracy and efficiency (Fullwave, 2008). Some implementations also use sub-gridding and sub-pixel smoothing. Since the entire grid cannot be excessively large, special care must also be taken in the appropriate choice of boundary conditions. The most common are periodic, symmetric/anti-symmetric, and perfectly matched layer (PML) absorbing boundary conditions.

FDTD methods are widely used in the field of plasmonics, since they can accurately account for all the properties of dispersive materials (Taflove and Hagness, Pernice et al.). Real material can be incorporated by fitting Drude and Lorentzian dispersion models to experimentally measured optical constants of noble (Johnson and Christy, 1972) and transition (Johnson and Christy, 1974) metals. Nonlinear effects can also be implemented. Additionally, since FDTD is a time-domain technique, a wide range of frequency components can be solved in a single simulation.

Several important limitations exist for the FDTD algorithm, the most severe being the intensive computational resources required for a full 3-D calculation. Even for relatively simple geometries and small computational volumes, it is not uncommon to be limited by tens of gigabytes of computer memory, or for a single simulation to run for several days or weeks on modern workstations. Furthermore, the entire computational domain must obey the Courant stability condition given above, which is tightened further for dispersive materials. Thus, the smallest structural features limit the computational speed of other larger and simpler structures. Fortunately, since it is a nearest-neighbors discretization, the FDTD algorithm lends itself to parallel computation and the use of multiple processors, significantly reducing computation time. Another major limitation is the need for discretization of the simulation volume on regular or simple graded grids. Although sub-gridding is possible, it can require fractional time steps and can be difficult to implement. Unless conformal gridding is used (Dey and Mittra, 1997, Yu and Mittra, 2000), the square grids of the Yee cell can also lead to staircasing effects—where an angled surface is represented as a series of cubes instead of a smooth slope—and reduced accuracy. As with any method, care must be taken when comparing to experiment (Barnes, 2009).

As an example of the utility of FDTD calculations for simulating the electromagnetic behavior of metallic nanostructures, figure 21 demonstrates the simple situation of SPP generation from a single groove in a silver film as the depth of the groove is changed. Depending on the depth, the photon-to-SPP coupling efficiency is modulated, offering insight into the best design parameters. For example, launching an SPP from such the groove is more efficient at a depth of 65 nm than a depth of 150 nm. Such resonances are also observed with transmission through slits (Xie et al., 2004, Xie et al., 2005). The next section covers FDTD simulations of a more complicated plasmonic phenomenon, outlining the utility of FDTD to shed light on underlying physical mechanisms.

Figure 21.

Sample FDTD calculation of a single metallic groove. (a) A groove in a metal film will scatter incident light into many channels, both propagative and evanescent. The long-range persistent evanescent wave is an SPP. (b) Monitoring the electric field a distance of 5 µm from the center of the groove with 600 nm plane-wave illumination shows that, for a groove width of 100 nm, the optimal coupling efficiency occurs for a groove depth of 65 nm. (c) A snapshot of the scattered field amplitude at the optimal coupling efficiency. The full electromagnetic field is computed in an FDTD simulation, which includes the incident wave and all scattered waves. For clarity, it is often convenient to subtract the field generated in the absence of the groove, giving only the field scattered by the groove itself. For this simple case, the electromagnetic fields are fully described with a 2-D transverse-magnetic FDTD simulation. Figure from (Lindquist, 2010).

3.2. Extraordinary optical transmission as a case study in FDTD modeling

Light will interact differently with periodic structures depending on the ratio of its wavelength λ to the period a. In the long-wavelength limit, λ ≫ a, the periodic structure can be understood as being an effective homogeneous medium, just as each individual atom is not considered when describing the refractive index n of a given material. The opposite limit, λ ≪ a, is the region of geometric ray optics, although the phase of the light field will still generate interference effects. The distinct wave nature of light becomes fundamentally important when λ ~ a. When metals are patterned at such a length scale, both diffractive and plasmonic effects become important, with often striking results. As will be shown here, FDTD modeling can provide one way to illucidate the physical mechanisms present in these plasmonic structures.

From its initial discovery by Ebbesen et al., (Ebbesen et al., 1998) the Extraordinary Optical Transmission (EOT) effect has initiated significant interest, not only for potential applications in novel nanophotonic devices, but also for understanding the underlying physical mechanism. This effect manifests itself as unexpectedly large light transmission at specific wavelengths through a periodic array of subwavelength nanoholes perforating a thin metal film. The amount of transmitted light is larger than that predicted by conventional Bethe aperture theory, which states that the transmission trough a single aperture in a thin perfectly conducting screen drops off as (b/λ)⁴, where b ≪ λ is the radius of the opening (Bethe, 1944). If the aperture is through a thicker film, the transmission decreases exponentially further (Roberts, 1987). When Ebbesen and coworkers performed their experiments, however, the transmission was greater than unity when normalized to the area of the open nanoholes, indicating that even light incident on the flat metal regions between the nanoholes was somehow “extraordinarily” transmitted. Geometric factors were found to play a critical role, such as the periodicity of the nanohole array (Ebbesen et al., 1998), the film thickness (Martin-Moreno et al., 2001), and the shape and orientation of the nanoholes with respect to the incident polarization (Koerkamp et al., 2004, Gordon et al., 2004, Degiron et al., 2004b).

Initial explanations (Ebbesen et al., 1998, Ghaemi et al., 1998, Martin-Moreno et al., 2001) of the EOT mechanism involved the generation of SPPs via a grating coupling mechanism from the nanoholes array. With this SPP model, the transmission peaks are approximated by the SPP grating-coupling equation:

$${\lambda }_{\mathit{\text{peak}}}\approx \frac{a}{\sqrt{i^2+j^2}}\sqrt{\frac{{\epsilon }_d{\epsilon }_{\mathit{\text{metal}}}}{{\epsilon }_d+{\epsilon }_{\mathit{\text{metal}}}}}$$ (5)

where a is the periodicity, i and j are grating orders, and ε_metal and ε_d are the dielectric functions of the metal and the surrounding dielectric medium, respectively (Ebbesen, 1998). For a sufficiently thin yet still opaque metal film, the SPPs on both sides of the perforated film were found to be strongly coupled, especially for symmetric, free-standing metal films (Martin-Moreno, 2001, Krishnan, 2001, Ghaemi, 1998). For asymmetric structures, e.g. ones fabricated on a glass substrate, the transmission spectra were identical regardless of which side of the film is illuminated, confirming an anomalously strong coupling between both side of the metal film (Ghaemi, 1998). Furthermore, the transmission maxima also correlated with absorption maxima, indicating strong generation of the lossy SPP waves (Barnes, 2004). Direct near-field imaging of a nanohole array structure (Gao, 2006) and the necessary existence of a metallic interface (Grupp, 2000) also confirmed the role of SPP waves in the EOT process, as did mapping the transmission spectrum as a function of incident angle (Ebbesen, 1998, Ghaemi, 1998, Barnes, 2004). With real metals at optical frequencies, SPP models closely fit experimental data and numerical calculations (Martin-Moreno, 2001, Liu and Lalanne, 2008, Lalanne, 2009).

Interestingly, similar effects were also observed in structures where SPP waves are not directly supported, such as unity transmission through a perfect conductor (Garcia de Abajo et al.), or EOT at millimeter wavelengths (Beruete, 2004). Additionally, under certain conditions, the excitation of SPPs was shown to suppress (Cao and Lalanne, 2002), enhance (Porto, 1999, Schroter and Heitmann, 1998), or, in a re-visitation of Young's double slit experiment, either suppress or enhance (Schouten, 2005) the transmission through subwavelength slits. Indeed, the grating-coupled SPP equation for λ_peak more accurately predicts the transmission minimum (Chang, 2005, Cao and Lalanne, 2002, Lezec and Thio, 2004, Pacifici, 2008). Along with these findings, it was discovered that non-SPP diffracted evanescent waves (Lezec and Thio, 2004, Cao and Lalanne, 2002, Weiner and Lezec, 2006, Gay et al., 2006a, Gay et al., 2006b) and interference between surface waves (Pacifici, 2008) and the incident light standing wave (Weiner, 2011) also play a significant role in such subwavelength optical effects (Weiner, 2009).

Understanding the shapes and positions of the transmission peaks lies beyond the pure-SPP model given by λ_peak ≈ λ_SPP above. To this end, there are two types of anomalies present in a diffraction grating (Fano, 1941, Hessel and Oliner, 1965). For a non-resonant surface, e.g. without SPP excitation, a purely geometrical effect called the non-resonant Rayleigh-Wood (Rayleigh, 1907) anomaly. This manifests itself as a transmission (or reflection) minimum that arises from the special case where an incident beam is diffracted tangent to the surface. Through extensive calculations, the non-resonant Rayleigh-Wood anomalies are seen to not correlate with EOT minima (Sarrazin et al., 2003), but are merely hidden within the broader spectral features (Chang et al., 2005). Resonant Rayleigh-Wood anomalies occur for gratings that can sustain SPPs or other surface modes. Furthermore, the red-shift of the actual transmission peak λ_peak from that predicted by λ_SPP as well as the asymmetric peak profiles can be explained by the presence of Fano-type interference effects (Fano, 1961) between the directly transmitted light and the grating-coupled SPPs (Genet and Ebbesen, 2007, Sarrazin et al., 2003, Genet et al., 2003). At the transmission minimum (maximum), there is destructive (constructive) interference between these two channels. As such, it is the resonant surface modes that most directly influence the optical transmission. To illustrate these ideas, figures 22 through 24 present FDTD simulations of a simple EOT case-study: 200 nm diameter holes with a 600 nm period perforating a 100 nm thick suspended Ag film. Electromagnetic field distributions, spectral features, geometric array effects, and SPP contributions are all shown. Similar results were first demonstrated by Chang, et al. (Chang et al., 2005)

Figure 22.

Simulated EOT spectrum. (a) Schematic and (b) FDTD transmission spectrum for a simple EOT test case. The suspended silver film is 100 nm thick, and is perforated with 200 nm diameter holes spaced by 600 nm. Periodic boundary conditions were used in x and y, and the xyz grid size was 4×4×4 nm in and around the area of the holes and Ag film and 4×4×10 nm in free space. PML boundary conditions absorbed all reflected and transmitted light in the ±z directions. A time-pulsed plane-wave was incident from the topside, and the transmitted power was Fourier transformed to calculate the transmission spectrum in a single simulation run. The locations of Wood's anomaly λ_Wood = a = 600 nm, the transmission minimum at 625 nm which corresponds closely with λ_SPP = 622 nm, and the transmission maximum λ_peak at 678 nm are all marked with dashed lines. The peaks are also labeled with the (m,n) grating orders and interfaces on which they occur. Figures 23 and 24 below show electric field maps at these wavelengths. Figure from (Lindquist, 2010).

Figure 24.

Simulated EOT electric field lines. A snapshot of the total electric field is shown, with field lines overlayed. (a) At a transmission minimum, λ=625 nm, the SPP field lines and inferred charge distributions are anti-symmetric, arising from Fano-type destructive interference between the grating-coupled SPPs and the local excitation of the nanohole. (b) At a transmission maximum, this interference is constructive, building up significant field intensity within the nanoholes and boosting the transmission. The field intensities are scaled by 2 and 1 for (a) and (b), respectively. The transmission maximum has the most intense surface fields. Figure from (Lindquist, 2010).

Finally, the total electromagnetic field surrounding a single subwavelength aperture is a combination of multiple scattered waves, some of which will be SPPs (if supported), other freely propagative, and others evanescent (Visser, 2006). All these waves are coherently scattered, and all contribute to the transmission process (Garcia de Abajo, 2007, Lalanne et al., 2009). Therefore, the exact role of the SPP itself is often difficult to separate out (Chang et al., 2005). However, with real metals at optical frequencies, the involvement of SPPs in the transmission process has been firmly established. At longer wavelengths, an SPP-only model becomes less and less accurate (Liu and Lalanne), and a surface diffracted wave dominates the transmission process. In the extreme case of perfect conductors (where SPPs are not allowed), such resonant surface modes are sometimes called “spoof” plasmons (Pendry et al., 2004). Essentially, hybrid-wave models (Liu and Lalanne, 2008) that include the microscopic interactions of both surface diffracted waves as well as SPPs will capture the physics of the transmission process.

4. Optical nanostructure characterization

Once a plasmonic device has been fabricated, characterization techniques are required to measure how it interacts with light or other materials. Fully characterizing and understanding the light-matter interactions in metallic nanostructures often requires techniques beyond conventional far-field optical imaging because of their subwavelength dimensions. For example, to detect the optical near field, the detector must be brought very close to the metallic surface, viz. within ~100 nm. However, the strong sample-detector interaction often perturbs the optical properties and produces measurement artifacts. Furthermore, characterizing the dynamic interactions of surface plasmons with other materials often requires ultrafast time resolution. Following optical absorption in metallic nanostructures, the photo-excited hot electrons can cool down rapidly via interactions with other electrons or phonons. These interactions are often mediated by imperfections of the metal surface (e.g. grain boundaries or roughness). Since these nanoscale energy transfer processes occur with very short lifetimes, characterizing the fundamental interactions between conduction electrons, photons, and phonons can be challenging. To address these characterization requirements in both the temporal and spatial dimensions, researchers have employed sophisticated measurement techniques, as summarized in this section.

4.1. Measurements of plasmon propagation and damping

Ideally, propagating SPPs are non-radiative waves that travel and remain along the interface. However, when the surface deviates from being perfectly flat, SPPs can be scattered in-plane (into other SPPs) or out-of-plane (into light). (Raether, 1988) This scattering reduces the field amplitude of the SPP, resulting in propagation lengths shorter than calculated theoretically. For a perfectly flat film, the propagation length l_ohm is limited only by ohmic losses in the metal. Considering other sources of loss, the total propagation length l_tot of the SPP can be given as:

$$\frac{1}{l_{\mathit{\text{tot}}}}=\frac{1}{l_{\mathit{\text{ohm}}}}+\frac{1}{l_{\mathit{\text{rad}}}}+\frac{1}{l_{\mathit{\text{scat}}}}$$ (6)

where l_rad and l_scat are the propagation length contributions from out-of-plane SPP scattering into radiation and in-plane SPP scattering into other SPPs, respectively. For perfectly flat, single-crystal films, l_rad and l_scat are infinite meaning that they do not contribute to SPP propagation losses. The propagation lengths of SPPs on such idealized gold and silver films, using dielectric constant data from Johnson and Christy (Johnson and Christy, 1972), are outlined in table 2 at several laser wavelengths. Other SPP loss channels may also be considered, such as l_grain, describing losses due to scattering grain boundaries. For as-deposited rough Ag films, losses associated with l_rad and l_scat can be of the same order as the intrinsic losses l_ohm, severely limiting the total propagation length l_tot of the SPP. (Nagpal et al., 2009) As-deposited Au films are inherently smoother, but still see SPP propagation length reduced due to roughness. Clearly, a smooth metallic surface would increase the SPP propagation and greatly benefit the performance of any plasmonic device. As described above, template stripping is a well-known method for producing ultrasmooth metal surfaces over large areas. (Hegner et al., 1993) The roughness of the template-stripped films can approach that of the template itself.

Table 2.

Calculated SPP propagation lengths (micrometers) on various metal / air and metal / water (Hale and Querry, 1973) interfaces and at different wavelengths. The permittivity data is from figure 3 in section 2.1.1.

Interface/Wavelength	514 nm	633 nm	752 nm	1550 nm
Au - Air	0.2 µm	10.0	36.5	292.7
Au - Water	0.05	3.8	14.6	126.7
Ag - Air	25.0	61.4	264.8	1260
Ag - Water	9.3	24.3	107.7	546.1

Directly measuring the total SPP propagation length l_tot is possible by creating a surface-wave slit-groove interferometer (Temnov et al., 2007, Pacifici et al., 2007, Kalkum et al.). This concept is presented in figure 25. When illuminated from below with white light, SPP waves are launched from the slit and propagate towards the groove, where they partially scatter into radiation. The intensity of the light scattered from the groove is directly proportional to the intensity of the SPP at the groove. Measurements of the scattered light from several slit-groove pairs with various separations will therefore allow a direct measurement of the decay of the SPP intensity versus distance and thus the propagation length l_tot. Figure 26 shows SPP propagation length data from several silver films. On an ultrasmooth template-stripped silver film, the measured propagation length l_tot approaches that of l_ohm calculated from the dielectric constant of the silver film measured via ellipsometry. Control measurements from a rough as-deposited film, along with previously reported data (van Wijngaarden et al., 2006) are also shown.

Figure 25.

Two-dimensional FDTD simulation of a slit-groove interferometer. The time-averaged Poynting vector is plotted on a log scale. A fraction of the SPPs that propagate from the slit to the groove are scattered into far-field radiation, and are detectable with an imaging spectrometer. Figure from (Lindquist, 2010).

Figure 26.

Propagation length measurements with a slit-groove interferometer. (a) SEM of a single slit and a single groove milled with FIB through a 200 nm thick Ag film. (b) Propagation length measurements. The diamonds show l_tot measured from a template-stripped 200 nm thick silver film. The solid line depicts l_ohm calculated from ellipsometry data. Control measurements were also made on a rough as-deposited film for comparison (dots), along with previously reported data (squares)(van Wijngaarden, 2006). From (Nagpal, 2009) Reprinted with permission from AAAS.

4.2. Time-resolved and ultrafast spectroscopy

Some optical and electronic processes in metallic nanostructures, such as dephasing of plasmons, can occur within just a few periods of the optical waves. To take “snapshots” and characterize these ultrafast processes, an equally fast probing technique is required, meaning the excitation or probing should be done using an ultrashort pulse with duration of only a few periods. In fact, many fast chemical reactions or electronic processes in semiconductors have been probed using time-resolved spectroscopy techniques with short (ps) and ultrashort (fs) optical pulses. In the context of plasmonics, these techniques can reveal the fast damping mechanisms of plasmons following their photoexcitation and other ultrafast light-matter interactions. Because time scales for thermal processes, e.g. electron cooling in metals, are generally much longer than the duration of ultrashort pulses, excitation with ultrashort pulses can differentiate thermal vs. electronic processes in metals. In addition to enriching a fundamental understanding of plasmon dynamics, such techniques are of practical importance for potential applications in ultrafast plasmonic modulators and switches, nonlinear plasmonic devices and quantum dot plasmonics (section 5.5), to name a few.

Femtosecond pump-probe spectroscopy is one commonly used technique to characterize these ultrafast processes. In a typical ultrafast measurement, a coherent ultrafast laser beam (a Ti:Sapphire laser is commonly used) is split into two optical paths, corresponding to a “pump” and a “probe” beam, with adjustable time delays. Following the absorption of a photon from a sharp laser pulse (pump), a second coherent beam with desired photon energy (probe) is used to monitor the changes in the absorption properties of the sample as a function of time delay and photon energy. The probe beam often goes through a non-linear crystal (e.g. beta barium borate, BBO) wherein frequency conversion processes occur to shift the frequency of the probe beam or to generate a white-light continuum probe beam (Klimov and McBranch, 1998). By generating probe beams with frequencies from UV-visible to the infrared, the pump-probe technique can monitor various cooling processes following photoexcitation of the sample. With precise motion control (accuracy of ~1 µm), the additional time delay Δt introduced in the path of light is measurable with femtosecond resolution:

$$\mathrm{\Delta }t\approx \raisebox{1ex}{$1\mu \mathrm{m}$}\!\left/ \!\raisebox{-1ex}{$3\times {10}^{14}\mu \mathrm{m}/\mathrm{s}$}\right.\approx {10}^{-15}\mathrm{s}$$ (7)

For plasmonic structures, the pump beam generates excited electrons that then relax due to several mechanisms: electron-electron scattering, electron-phonon scattering, electron-surface scattering, electron-defect scattering, and phonon-phonon scattering. For example, in metal nanoparticles, after an electron thermalization, the time-resolved spectrum is dominated by the coherently excited acoustic phonon modes. This and the other relaxation pathways have been investigated extensively in the literature for different metal nanoparticle sizes, shapes, and compositions to derive conclusions about the time scales and relative importance of each pathway.

The mean free path of electrons in silver and gold is 40~50 nm (Ashcroft and Mermin, 1976). As the nanoparticle size decreases, the frequency of electron-surface collisions increases. In metallic nanostructures, the presence of surface roughness and grain boundaries can enhance electron-defect scattering or modulate electron-phonon scattering. While these effects can be strongly correlated, assuming uncorrelated effects the electron relaxation time τ can be described as (Kreibig and Vollmer, 1995, Kreibig and Genzel, 1985)

$$\gamma =\frac{1}{\tau }=\frac{1}{{\tau }_{e-e}}+\frac{1}{{\tau }_{e-\mathit{\text{ph}}}}+\frac{1}{{\tau }_{e-\mathit{\text{defect}}}}+\frac{\alpha {\nu }_F}{R}$$ (8)

where the τ’s are the respective time constants for electron-electron, electron-phonon, and electron-defect scattering, v_F is the Fermi-velocity, α is the proportionality constant, and R is the radius of the nanoparticle. The last term accounts for electron-surface scattering, which is important especially for nanostructured metals. Using the Drude model and incorporating the electron relaxation frequency γ, the frequency-dependent dielectric response is approximated as (Ashcroft and Mermin, 1976)

$${\epsilon }_{\mathit{\text{free}}}(\omega )=1-\frac{{{\omega }_p}^2}{{\omega }^2+i\gamma \omega }$$ (9)

where ω_p is the plasma frequency of the metal. Since ε_metal (ω) = ε_free (ω) + ε_bound (ω), the optical properties of both bulk and nanostructured metal depend strongly on these individual electron interactions. Moreover, while the individual time constants affect the dielectric properties and hence all the optical interactions, specifically for generation and propagation of SPPs on the metal surface, these time constants can affect both the position and width of the plasmon resonance (Kreibig and Vollmer, 1995). Therefore, a careful study of time constants and their variation with size, shape, surface morphology, and grain structure can give invaluable insights into various damping mechanisms of surface plasmons.

The most dominant contribution for electron relaxation comes from electron thermalization, i.e. electron scattering via phonons and other electrons (Smith and Ehrenreich, 1982, Link and El-Sayed, 1999, El-Sayed, 2001, Hodak et al., 2000c, Voisin et al., 2001). While a strong dependence of relaxation dynamics on nanoparticle size and shape can be expected, most studies indicate similar transient absorption data for different nanoparticles, as shown in figure 27. Further evaluation of electron relaxation indicates that electron-electron scattering times for different metals (Au ~500 fs (Link et al., 1999) and Ag ~350 fs (Voisin et al., 2000)) and electron-phonon scattering times (Au ~1.6 ps (Hodak et al., 2000c, Link et al., 1999, Hodak et al., 1999, Hodak et al., 2000b) and Ag ~0.85 ps (Hamanaka et al., 1999, Del Fatti et al., 2000a, Halte et al., 1999a, Halte et al., 1999b)), match their respective bulk value (Au (Sun et al., 1994) and Ag (Del Fatti et al., 2000b)), especially for nanoparticles with dimensions greater than 5 nm. Following fast electron thermalization with a ~1 ps time delay, thermal equilibrium is established between electrons and phonons. These previous studies have mainly employed isolated single-crystalline nanoparticles. In patterned metal films, electron cooling also depends on surface roughness and grain boundaries (Nagpal et al., 2009, Critchley et al., 2010).

Figure 27.

(a) Time-resolved transient absorption measurements on different sized metal nanospheres showing identical electron relaxation dynamics Reprinted with permission from (Link and El-Sayed, 1999). Copyright (1999) American Chemical Society. (b) Electron thermalization time for small silver nanospheres showing identical (~310 fs) relaxation times for large particles (>5 nm), but a sharp decrease in thermalization time for nanoparticles between 2–5 nm (Voisin, 2000). Reprinted figure with permission from (Voisin, 2000) Copyright (2000) by the American Physical Society. (c) Coherent acoustic phonon oscillations launched due to a sharp increase in lattice temperature following electron-phonon cooling. The oscillation period strongly depends on mechanical properties of metal nanoparticle and surrounding media (Pelton, 2009). Reprinted by permission from Macmillan Publishers Ltd: Nature Nanotechnology (Pelton, 2009), copyright (2009).

Following thermal equilibrium between electrons and phonons, phonon-phonon interactions dissipate energy to the surrounding medium on a ~100 ps time scale. Since most of these studies were performed on smooth metallic nanocrystals, no significant electron-defect interaction was observed. Moreover, theoretical studies predict that due to the small number of valence electrons and large atomic mass of transition metals, electron-surface scattering has a relatively small contribution to the overall electron energy loss (Hodak et al., 2000b, Belotskii and Tomchuk, 1992). For particles with dimensions larger than 5 nm, electron relaxation is similar to that of bulk metal films. However, for small silver particles (2 nm ≤ R ≤ 5 nm), it has been shown that electron-electron scattering [Umklapp scattering (Gurzhi, 1959)] can decrease strongly with size (figure 27b), and hence electron-thermalization times will be affected (Voisin et al., 2000).

Another dominant signal in ultrafast time-resolved absorption measurements is excitation of coherent acoustic phonon modes, following electron thermalization and energy transfer to phonons (Hartland, 2006, Hodak et al., 1999, Pelton et al., 2009). After transfer of energy to the lattice via phonon coupling, the lattice temperature increases and the nanoparticles expand rapidly, exciting phonon modes (Hodak et al., 1999, Del Fatti et al., 1999). The period of acoustic vibrations gives information about the intrinsic elastic properties of the nanoparticle as well as the damping of the surrounding medium (Pelton et al., 2009, Hodak et al., 2001, Hodak et al., 2000a).

The ultrafast electron and phonon cooling times result in large changes in the absorption of metallic nanoparticles at picosecond time scales, mainly due to their large absorption cross-sections. These ultrafast processes may be used for ultrafast plasmonic switches, modulators, or active plasmonics.

4.3. Near-field optical microscopy

The resolution of a far-field optical imaging system based on a conventional lens is diffraction-limited to ~λ/2n (λ is the wavelength of the light and n is the refractive index of a medium) according to the Rayleigh criterion. Physically, this limit arises because a conventional lens can capture only propagating waves. High-spatial-frequency Fourier components of an object, which contain the fine details required for perfect image reconstruction, remain as non-radiative evanescent waves in the near field and cannot propagate to the detector in the far field. Thus, the transfer of information from the near-field to the far-field has a limited bandwidth, i.e a limited resolution (Pendry).

SPPs are also non-radiative evanescent waves, in this case bound to the metal surface. Consequently, they cannot be probed directly by a far-field imaging system. Near-field scanning optical microscopy (NSOM), also known as scanning near-field optical microscopy (SNOM), can overcome this diffraction limit by capturing the evanescent waves to extend the spatial bandwidth. Typically a scanning probe with a sharp metallic tip or a metallic aperture probe is brought close to the sample to capture its optical near field (Synge, Ash and Nicholls, Pohl et al., Lewis et al., Harootunian et al., Fischer and Pohl, Betzig et al., Trautman et al., Inouye and Kawata, Xie and Trautman, Novotny and Hecht). Comprehensive reviews and historical perspectives on near-field optics can be found elsewhere (Dunn, Hecht et al., Lewis et al., Novotny and Stranick, Novotny, Bharadwaj et al., Schuller et al.).

Aperture NSOM probes are usually prepared by metallizing tapered optical fibers or hollow AFM tips to make a subwavelength aperture, ~100 nm or less in diameter, at the end of the tip. Near-field scans can be obtained using this microscopy technique (Lopez-Tejeira, 2007, Laluet, 2007, Bouhelier, 2007, Kihm, 2009, Choi, 2008, Maier, 2003a, Zia and Brongersma, 2007), as the lateral imaging resolution largely depends on the size of the aperture used for guiding and/or collecting light and the skin depth of the metallic coating. Aluminum has been typically used for coating aperture NSOM probes, since it has the smallest skin depth among all metals in the visible regime (Novotny and Hecht). The collected light is analyzed to obtain a wealth of information by analyzing its frequency (Achermann, 2007, Park, 2008, Bakker, 2007) and polarization (Schnell, 2009, Burresi, 2009a, Burresi, 2009b, Lee, 2007). Recently, this technique has also been utilized for analyzing near-field photoluminescence, two-photon photoluminescence (Imura and Okamoto, 2009; Okamoto and Imura, 2009), and other multiphoton processes (Breit et al., 2007).

Apertureless NSOM, on the other hand, utilizes light scattered from sharp metallic tips to characterize the near-field optical response of a sample (Keilmann and Hillenbrand, 2004, Schnell, 2009, Huth, 2011, Kuhn et al., Anger et al.). In this case, it is the diameter of the tip that determines the resolution. This technique has been utilized to probe a wide variety of metallic nanostructures such as disks (Esteban, 2008), antennas (Schnell, 2009) (see figure 29), slits, tapered strips (Schnell, 2011), nanoholes (Rindzevicius, 2007), nanorods (Schnell, 2009, Jones, 2009, Dorfmuller, 2009), and nanotriangles (Rang, 2008). Apertureless tips can also be fabricated by attaching a colloidal gold nanoparticle to the tip of a pulled optical fiber (Kalkbrenner, 2005, Kalkbrenner, 2001). Such a system has been used for single-molecule fluorescence spectroscopy (Anger, 2006, Kuhn, 2006). Recently, apertureless NSOM was also combined with a thermal source for infrared-spectroscopic imaging to map free-carrier concentration in doped silicon with nanometer-scale resolution (Huth, 2011). Thus nano-imaging can be extended to retrieve spectroscopic identification of chemical or electrical domains.

Figure 29.

Phase-resolved near-field intensity measurements that map nanowire antennas, with gaps of increasing separation in the middle. In each panel, the top image shows the topography, the middle image shows the near-field light amplitude, and the lower image shows the phase of the scattered light collected using a silicon apertureless NSOM. Finally, the bottom graphs plot high-resolution electric-field intensity maps, which show optical hot spots and experimentally confirm the plasmon modes expected in the antennas. Reprinted by permission from Macmillan Publishers Ltd: Nature Photonics, (Schnell, 2009), copyright 2009.

Other variations of NSOM have also been used. In particular, photon scanning tunneling microscopy (PSTM), also known as scanning tunneling optical microscopy (STOM), has been used (Courjon et al., Reddick et al., de Fornel et al., Dawson et al., Balistreri et al., Bozhevolnyi et al., Ditlbacher et al., Jose, 2008; Jose, 2011) to study SPP propagation in metallic nanostructures (figure 30). In this technique, the sharp tip of a pulled optical fiber picks up an evanescent field on the sample surface and converts it into a propagating wave. In another setup, a scanning tunneling microscope (STM) has been used to induce the emission of photons (Silly et al., 2000, Myrach et al., 2011) to map the optical modes of nanoparticles.

Figure 30.

(Left) Scanning electron micrographs of a 18.6 µm long silver nanowire with diameter of 120 nm. (Right) NSOM image, via PSTM method, shows surface plasmon propagation along the silver nanowire. Reprinted figure with permission from (Ditlbacher et al.) Copyright 2005 by the American Physical Society.

As with all techniques, however, NSOM has limitations. While it is often particularly useful to probe optical fields at a surface with increased resolution, the evanescent near-field decays exponentially, necessitating close probe proximity. NSOM can thus only probe surfaces, unlike 3-D imaging techniques such as confocal microscopy. More importantly, the proximity of the metallic tip leads to coupling between the tip and the sample, distorting the near-field and complicating the data analysis. Exact determination of unperturbed fields of the sample is difficult since probe-sample interactions leads to many imaging artifacts (Hecht). These artifacts can be partly compensated for by independently characterizing the tip (Fischer, 2008) or by scanning some distance away from the metal nanostructures to reduce the perturbation (Babayan, 2009, Zhou, 2009). However, diminishing signal-to-noise and resolution make it difficult to remove the tip artifacts completely from the collected data. Indeed, only resonant modes extend far enough into space to allow appreciable tip-sample separation (Babayan, 2009, Zhou, 2009).

Apertureless NSOM also suffers from probe-sample coupling and perturbation of the near field. This can be addressed by replacing a strongly scattering probe with a sharp but weakly scattering localized probe that has dimensions similar to the object of interest. For example, carbon nanotubes have been used (Wilson and Macpherson, 2009, Nakata and Watanabe, 2011). An alternative method is to use cross-polarized light for excitation and detection, thereby eliminating background scattered light (Schnell, 2009, Kim and Leone, 2008).

While near-field perturbations produced by scanning probe tips can be problematic in mapping the inherent field of a metallic nanostructure, they can also be used for selectively enhancing electrical (or optical) fields near the probe (Moerland, 2008). Variations of apertureless NSOM techniques have also been used to selectively probe nanoscale moieties on the surface (Stockle, 2000, Knoll and Keilmann, 1999, Anderson, 2000, Pettinger, 2004, Ichimura, 2004) as in tip-enhanced Raman scattering (TERS), which is discussed in sections 5.3 and 5.4. The tips, modified either via a metal coating or by attaching a metal nanoparticle at its apex, can also be used to study enhanced fields via coupling of the modified tip to the metallic nanostructure via non-linear optical effects (Bouhelier, 2003a) like four-wave mixing (Danckwerts and Novotny, 2007). Such tip-enhanced fields and coupling of a metal nanoparticle at the tip to either another metal nanostructure, fluorophore (Moerland, 2008, Anger, 2006), or semiconductor nanoparticle has been investigated in several recent studies.

Time-resolved NSOM has also been developed, using ultrafast laser pulses, for spatial and temporal mapping of nanoplasmonic structures (Balistreri, 2001, Sandtke, 2008). The technique combines an NSOM probe with a time-delayed probe beam as discussed in section 4.2 above. The sample is excited through a pump beam from the laser. Scanning the NSOM probe over the entire sample builds a map of the time evolution of electron relaxation across the entire metal nanostructure with nanometer-scale resolution. This technique can provide a rich four-dimensional map of space and time following electron excitation. However, since the technique involves probing each nanoscale spot for many different delay times, the technique is slow.

Arguably, reproducible fabrication of precisely tuned metallic probes is at the core of the NSOM technique. It is difficult to fabricate tips with identical aperture diameters or tip radii. Emerging nanofabrication techniques described in section 2 will further improve reproducible high-throughput fabrication of both aperture NSOM probes and apertureless NSOM probes with the goal of higher plasmonic field enhancements, better near-field resolutions, and more reproducible measurements.

4.4. Cathodoluminescence

In most examples discussed in previous sections, SPPs in metallic nanostructures are generated using optical sources coupled with a prism, diffraction grating, or patterned metals. Alternatively, since surface plasmons are density fluctuations in a conduction-electron plasma, these waves can also be excited by irradiating the metal surface with an electron beam. Theoretical studies of plasmon excitations in metal films were performed by Ritchie using fast electrons as an excitation source (Ritchie, 1957). Electron energy loss was used to demonstrate experimentally the existence of SPP waves (Blackstock et al., 1955, Rudberg, 1930, Ruthemann, 1948, Lang, 1948). Over the years, this approach has been used to excite surface plasmons on a variety of structures including flat interfaces (Ritchie and Eldridge, 1962, Cram and Arakawa, 1967), patterned films,(Bashevoy, 2007, Degiron, 2004a, Kuttge, 2008, Kuttge, 2009, Vesseur, 2008, Vesseur, 2009, van Wijngaarden, 2006) and nanoparticles. (Yamamoto, 2001, Vesseur, 2007, Yamamoto, 2006, Chaturvedi, 2009) In a typical e-beam system such as an SEM, accelerated electrons with 10–100 kV energies can obtain De Broglie wavelengths of just a few Ångstroms. When these high-energy electrons bombard a sample surface, light can be emitted from the excited atoms in a phenomenon called cathodoluminescence, which has been widely used in cathode ray tubes (CRT). (Ozawa, 1990) As an imaging technique, cathodoluminescence (CL) employs a scanning electron beam to excite the sample locally while simultaneously collecting luminescence signals. Because this technique is based on electron beams, it has potential to achieve a sub-micron imaging resolution.

As illustrated in figure 31a, a typical CL imaging setup consists of an electron-beam source, collimated using magnetic lenses, and then focused onto the sample through an aperture in a parabolic mirror. The mirror then collects light emitted from the sample over a large solid angle and redirects it to a spectrometer. The light emission from the sample depends not only the material, but also on the shape and size of the patterned structure or nanoparticle. In a typical SEM or TEM system, the electron beam can be focused down to a very small spot, as small as ~1 nm. As discussed in sections 2.3 and 2.5, the spot size is a function of the acceleration voltage and the beam current: a higher acceleration voltage or a lower current leads to a smaller spot size. The overall spatial resolution of CL imaging depends not only on the spot size of the focused e-beam, but also on the spreading of the electrons inside the sample as well as diffusion of the secondary carriers therein. By mapping the emission intensity as a function of the e-beam excitation location, high-resolution images can be obtained. Moreover, secondary electrons map the topography of the sample that can be correlated to the plasmonic local density of states (figure 31b).

Figure 31.

(a) Schematic of a typical CL setup consisting of a parabolic mirror with an aperture. (b) High resolution scans of a metal nanorod imaged with a CL setup. The top image shows the topography, and the bottom image depicts the density of states excited by the fast electrons incident on the metal nanostructure. CL imaging provides correlated topography and plasmonic local density of states excited by the electrons, scanned with high precision. Reprinted with permission from (Vesseur et al., 2007) Copyright 2007 American Chemical Society.

Electron beams bombarding on metallic nanostructures can generate both propagating SPPs and localized surface plasmon resonance (LSPR). Thus CL imaging has been used to characterize SPPs on silver gratings (Bashevoy, 2007, Kuttge, 2008, van Wijngaarden, 2006) as well as LSPRs on silver nanoprisms (Chaturvedi, 2009), nanorods (Vesseur, 2007), and nanoholes in metal films (Degiron, 2004a). Other plasmonic structures studied with CL include nanoparticle dimers (Yamamoto, 2006), high-order plasmon modes in silver nanospheres (Yamamoto, 2001), Fabry-Perot resonators (Kuttge, 2009), and ridge waveguides (Vesseur, 2008) in single-crystal gold films.

Other non-linear imaging techniques, such as confocal Raman spectroscopy or second-harmonic generation (SHG) imaging, can also provide plasmonic “hot spot” maps for metallic nanostructures. However, the CL imaging technique is not limited by diffraction and thus it can provide additional information that cannot be obtained by optical excitation techniques. For example, CL imaging has been used to map individual higher-order plasmon modes (Yamamoto, 2001, Hofmann, 2007, Vesseur, 2007), which were only predicted theoretically. Besides providing experimental evidence for predicted plasmon modes and coupling between nanoparticles (Yamamoto, 2006), CL studies have been utilized for measuring SPP propagation lengths on polycrystalline (van Wijngaarden, 2006) and single-crystal (Kuttge, 2008) metal films. These measurements identified grain boundaries (Kuttge, 2008) and metal ions implanted during device fabrication (Vesseur, 2008) as scattering centers impeding SPP propagation. Moreover, high-resolution plasmon mapping enabled by CL also leads to the visualization of stationary plasmon modes and plasmonic confinement effects. Hyperspectral imaging (Bashevoy, 2007) using CL have also been used to correlate the nanoscale geometry and plasmon mapping.

Ultrafast time-resolved CL studies have been conducted, where a fast pulsed laser is used to excite a photocathode under bias, releasing a burst of electrons which are then focused down to the sample using magnetic lenses (Merano et al., 2005, Sonderegger et al., 2006). This technique combines the high spatial resolution of electron beams with the fast time response of the pulsed lasers. Zero-time delay is assigned taking into account the time of flight for electrons from the photocathode to the sample. A spatial resolution of ~50 nm and a time resolution of ~10 ps have been simultaneously achieved for imaging quantum dots and quantum wells. These time-resolved CL studies give the possibility of precisely mapping the spatio-temporal dynamics of electron excitation and plasmon propagation in metal nanostructures.

Like any other characterization techniques, CL imaging is not free of artifacts. Spurious signals can result from contaminants on the sample surface. Prolonged e-beam irradiation on the sample may cause charging, e-beam-induced sample heating, or even e-beam-induced materials depsition (discussed in section 2.3).

4.5. Electron-energy loss spectroscopy

Electron-energy loss spectroscopy (EELS) measures the energy loss of fast electrons (Hillier and Baker, 1944) as they transmit through metallic nanostructures. In a scanning transmission electron microscope (STEM), the inelastically scattered electrons lose energy to the metal film (Ritchie, 1957, Blackstock, 1955), giving a detailed map of the excited surface plasmon modes (Nelayah, 2007; Koh, 2011; Sigle, 2009; Sigle, 2010; Nelayah, 2009; Chu, 2009; N'Gom, 2009; Schaffer, 2009; Arslan, 2009; Batson, 1982; Batson, 1985; Eggeman, 2007; Little, 1984; Sarid, 1981; Vincent and Silcox, 1973; Pettit, 1975; Sander, 2001). With the advent of high-resolution electron monochromators, energy resolutions of ~50 meV can be obtained (Brink, 2003) giving high spatial and energy resolution maps for scanned samples. STEM-EELS images of a silver triangular nanoprism (Nelayah, 2007) in figure 32 show the detailed plasmon mode peaks and the spatial distribution in a given nanostructure. Surface plasmon modes on a metal nanoparticle can vary in nature based on the particle geometry and arrangement of charge oscillations on the surface. Generation of oscillating charge waves (due to localized surface plasmons) on a nanoparticle surface can result in a net dipole, which dissipates part of the energy as plasmon-mediated light emission. This mode, with a radiating dipole, is commonly referred as a “bright” plasmon. However, if the net dipole moment due to a plasmon wave cancels out, it results in no net emission from excitation of a localized surface plasmon. Such a plasmon is known a “dark” plasmon mode. Since EELS maps not just the local electric-field intensity but also the plasmonic local density of states, it can be used to map both radiative and nonradiative plasmon modes (figure 32c). This can provide valuable information regarding dark plasmon modes which are difficult to observe via other near-field imaging techniques, but useful for applications where energy loss through radiative outcoupling of localized surface plasmons can be detrimental (e.g. for photovoltaics refer to section 5.7, or for coupling to other semiconductors refer to section 5.5). An important difference between investigation of plasmonic density of states using cathodoluminescence (section 4.4) and EELS is that CL can be used only to probe “bright” plasmon modes.

Figure 32.

(a) High-resolution EELS scans showing higher-order plasmon modes in silver nanotriangular prisms (Nelayah et al., 2007). (b) STEM-EELS mapping depicts the plasmonic local density of states (LDOS) excited by electrons. The energy of the LDOS is measured by the energy loss and the spatial distribution is mapped by the EELS image after removal of the zero-loss peak (Nelayah et al., 2009). (c) LDOS depicting plasmonic hot spots in coupled metal nanostructures. Both bright and dark (i.e. nonradiative) plasmon modes can be mapped using EELS (N'Gom et al., 2009).

The main drawback of EELS stems from the elastically scattered electrons or the “zero-loss peak.” Depending on the energy distribution of the source of the electron radiation, the zero-loss peak can be as wide as 0.6 eV, thereby limiting the use of this technique to low-energy excitation. However, with the introduction of new emitters, the range of energies has been expanded. Also, precise measurements of the spatial energy-loss spectra allow an estimate of the local density of states to be made (de Abajo and Kociak, 2008). Therefore, a wide variety of structures ranging from silver triangular nanoprisms, nanoholes in films (Sigle et al., 2009), elongated nanoparticles (Schaffer et al., 2009), coupled (Chu et al., 2009, N'Gom et al., 2009) and isolated (Arslan et al., 2009) nanorods, nanospheres (Batson, 1982, Batson, 1985), nanoshells (Eggeman et al., 2007), and ellipsoids (Little et al., 1984) have been characterized using this technique.

Other useful advances made using EELS include determination of plasmon-guided modes in buriedmetal (Sarid, 1981, Vincent and Silcox, 1973), metal-insulator (Pettit et al., 1975), and other patterned/nanoparticle geometries (Sander et al., 2001). Spatial energy maps also give detailed information about hybridized plasmon modes in coupled nanoparticles (Schaffer et al., 2009), nanorods (N'Gom et al., 2009), triangular nanoprisms (Nelayah et al., 2009), and other geometries with very small spatial separation between nanostructures (Sigle et al., 2009).

4.6. Photoemission spectroscopy

Most nanoscale near-field characterization techniques depend on either emission of electrons or photons following local electron absorption, or using small probes to spatially pick near-field photons. In contrast, photoemission spectroscopy involves measuring the energy of emitted electrons following multiphoton absorption of intense laser radiation (Kubo et al., 2005, Kubo et al., 2007b, Kubo et al., 2007a, Hrelescu et al., 2011, Peppernick et al., 2011, Mikkelsen et al., 2009, Aeschlimann et al., 2010, Stockman et al., 2007, Cinchetti et al., 2005, Douillard et al., 2008, Aeschlimann et al., 2007, Berndt et al., 2009, Chelaru and Heringdorf, 2007, Heringdorf et al., 2007, Lin et al., 2009). The emitted electron energy is measured with an energy resolution better than 50 meV while the laser beam is scanned over the sample to generate a spatial profile. The spatial resolution is determined not by the multiphoton process, but by electron imaging optics, and hence this method can also achieve subwavelength spatial resolution.

Ultrafast time-resolved photoemission data can be obtained by using time-delayed pump and probe (section 4.2) beams as multiphoton sources (typically two-photon). The temporal resolution of the process arises from a time delay induced by a precision motion delay stage, which staggers the pump and probe pulses with femtosecond resolution. Subtle variations of this technique use different colored coherent pump and probe beams (Aeschlimann et al., 2010), which can be obtained by using frequency doublers or optical parametric amplifiers. This photoemission electron microscopy (PEEM) can be used for high-resolution four-dimensional (space and time) mapping of nanoplasmonic near-field processes.

Two-photon photoemission microscopy has been used for recording the time evolution of localized and propagating SPP waves in silver gratings (Kubo et al., 2005, Kubo et al., 2007a, Kubo et al., 2007b), rough metal films (Kubo et al., 2005, Stockman et al., 2007), gold nanostars (Hrelescu et al., 2011), a sun-shaped silver nanostructure (Aeschlimann et al., 2010), and metal nanorods (Douillard et al., 2008, Chelaru and Heringdorf, 2007). An example is shown in figure 33. PEEM has also been used to study the time evolution of hot-spot formation in rough samples (Stockman et al., 2007, Kubo et al., 2007a) and symmetry-broken structures (Berndt et al., 2009), which yields valuable physical insights into the formation of stagnant intense electric fields following electron excitation via light absorption. Also, the correlation between the mapped topography and the electric-field intensity provides information about plasmon localization following the excitation of SPP waves.

Figure 33.

(a) Schematic depicting the setup used for time-resolved photoemission electron microscopy using different colored beams. (b) Topography of the imaged metal nanostructure. (c–e) PEEM images with different beams and time delays on the pump-probe measurement. The scans show the richness of the data obtained with high resolution in time and space for nanoplasmonic systems (Aeschlimann et al., 2010). (f) PEEM images showing both localized and propagating surface plasmons in metal gratings. (g) Time-resolved measurements showing dephasing of excited state electrons vs. time for surface plasmon polaritons. Reproduced with permission from (Kubo et al., 2007a). Copyright (2007) IOP Publishing, Ltd.

5. Current and emerging applications

In various formats, metallic nanostructures have been used in applications such as sensing, imaging, and spectroscopy. For example, some commercial pregnancy-test kits use colloidal gold nanoparticles as labeling agents, because their localized surface plasmon resonance (LSPR) enables large scattering crosssections compared with conventional fluorescence dyes (Bangs, 1996). The surface plasmon resonance (SPR) instrument (Liedberg et al.), which has been commercialized by Biacore™ (GE Healthcare), is a successful product that utilizes SPP waves in thin gold films. We begin this section with SPR instruments as a case study for applications of plasmonics, and then discuss surface-enhanced spectroscopy and other emerging applications.

5.1. SPR affinity biosensors

Modern biology has been transformed by the ability to describe biological phenomena quantitatively, due in part to new technologies such as fluorescence-activated cell sorting, mass spectrometry, microarrays, and SPR biosensing (Hood et al.). With the completion of the Human Genome Project, the next challenge in the life sciences is to catalogue proteins, the workhorse in our bodies, and to understand how they interact with other biomolecules. A new generation of instruments capable of quantifying protein interaction kinetics will play an important role in this emerging field of proteomics and drug discovery (Cooper, 2002; Ramachandran et al.). In general, the function of a biosensor is to transduce specific molecular interactions (e.g. binding, cleavage, or transport) into a signal that can be read out using optical, electrical, or mechanical methods. To do this, solid-state sensing surfaces are typically decorated with “receptor” molecules, whose binding with target “analyte” molecules generates a signal change (e.g. impedance, mass, luminescence, or refractive index). It is desirable to monitor protein recognition events without labeling the target analytes with fluorescent or radioactive tags because the chemical labeling process is expensive, time-consuming, and often perturbs the binding interactions. Furthermore, to understand molecular recognition mechanisms, thermodynamic constants and key biophysical parameters should be measured directly. As the analyte binds to the receptor, these biomolecules accumulate on the surface. In a simple model, the change in the relative amount R(t) of analytes on the surface as a function of time t can be obtained by subtracting the dissociation rate from the association rate:

$$\begin{array}{cc}\hfill \mathit{\text{dR}}/\mathit{\text{dt}}& =r_{\mathit{\text{association}}}-r_{\mathit{\text{dissociation}}}=k_a{c}_A(1-R)-k_{d}R\hfill \\ \hfill R(t)& =\left(\frac{k_a{c}_A}{k_a{c}_A+k_d}\right)(1-e^{-(k_a{c}_A+k_d)t})\hfill \end{array}$$ (10)

where k_a (mol⁻¹ L s⁻¹) is the association constant, c_A is the analyte concentration, and k_d (s⁻¹) is the dissociation constant. The equilibrium constant K_A = k_a/k_d (M⁻¹) is for the association reaction and K_D = k_d/k_a (M) is for the dissociation reaction. A large K_A means high affinity, i.e. large binding strength. When dR/dt = 0, equilibrium coverage R_eq is obtained, as described by the equation below. This equation is known as the Langmuir equation or Langmuir isotherm (Figure 34):

$$\frac{R_{\mathit{\text{eq}}}}{R_{\text{max}}}=\frac{k_a{c}_A}{k_a{c}_A+k_d}=\frac{1}{1+K_D/c_A}$$ (11)

Figure 34.

(a) Simulated binding responses with “typical” values of c_A (200 nM, 50 nM, 20 nM, and 5 nM), k_a (10⁵), and k_d (10⁻³). With such real-time measurements, the on-off rates (kinetics) and affinity of a reaction can be measured. All three parameters (K_A, k_a, and k_d) are important, since two reactions can have the same affinity k_a/k_d, but have different kinetics. (b) The Langmuir isotherm equation is plotted for receptor-analyte pairs with different K_D values (1 pM and 1 nM). As an example, consider a 1 µm × 1 µm sensor chip that is coated with 10⁴ receptor molecules, and assume that K_D = 1 nM between the receptor and analyte. If the analyte concentration is 1 pM, R_eq/R_max ~10⁻³ according to Eq. 11, thus only 10 molecules will be bound to the sensor in equilibrium. As this example shows, the kinetics and equilibrium constants guide the design of surface-based affinity biosensors. For further details, see (Squires et al.).

Relatively few surface-sensitive techniques exist that allow label-free measurements of protein binding affinity and kinetics. Among various transduction mechanisms for detecting thin biological films, optical techniques have been particularly successful because they are robust in the presence of background fluctuations in pH, viscosity, or conductivity of the solution. The effective refractive index—a function of the amount R(t) of molecules on the surface—of a sensing surface will change with time as analytes bind to receptors. This can be read out using various optical techniques. Label-free optical sensing of biomolecules, however, is challenging since a monolayer of biomolecules is only a few nanometers in thickness, i.e. a tiny fraction of the optical wavelength. To enhance the sensitivity, one has to increase the optical path length, i.e. the light-matter interaction distance in the biological film. SPR instruments accomplish this by redirecting optical energy to travel laterally along the interface and thereby increasing the effective film thickness seen by the SPP wave. The use of tightly confined SPP waves can further increase the sensitivity for thin films. In a simplified model, the effective refractive index of a thin film seen by the SPP waves can be approximated as (Jung et al., 1998)

$$n_{\mathit{\text{eff}}}=n_{\mathit{\text{bulk}}}+(n_{\mathit{\text{film}}}-n_{\mathit{\text{bulk}}})(1-e^{-2d/l})$$ (12)

where n_film and n_bulk are the refractive indices of a thin film and of the surrounding liquid, respectively, d is the film thickness, and l is the SPP decay length into the medium. Since SPPs are coupled to free electrons, for a given energy they have a larger momentum than light, necessitating a mechanism to increase the momentum of the exciting light, such as the use of a high-index prism, metallic grating, or subwavelength pattern (Homola et al., 1999). In a commercial Biacore™ SPR instrument, a convergent light cone illuminates the detection spot (~1 mm in size) on a gold film via prism coupling in a total internal reflection mode (figure 35). The SPP excitation condition in this case is given by:

$$k_x=\sqrt{{\epsilon }_{\mathit{\text{prism}}}}\text{sin }{\theta }_i=\text{Re}\left(\sqrt{\frac{{\epsilon }_d{\epsilon }_{\mathit{\text{metal}}}}{{\epsilon }_d+{\epsilon }_{\mathit{\text{metal}}}}}\right)$$ (13)

where k_x is the in-plane momentum of an SPP wave, ε_d and ε_metal are the dielectric constant of the medium and metal, respectively. In metals such as Au or Ag, Re (ε_metal) is negative and large in magnitude, and Im(ε_metal) is small in comparison. The SPP excitation condition can then be simplified to:

$$\text{sin }{\theta }_i\approx \sqrt{{\epsilon }_d/{\epsilon }_{\mathit{\text{prism}}}}=n_d/n_{\mathit{\text{prism}}}$$ (14)

Figure 35.

(a) Schematic depicting evanescent SPP waves and their excitation with a prism in a total internal reflection setup. The decay length l of the SPP determines its sensitivity to a film of different thicknesses. When the film thickness d is small compared to l, the SPP will probe the refractive indices of both the film and the bulk solution above the film. (b) Simulated SPR excitation. At the correct angle, SPPs are excited at 850 nm illumination for a 50 nm thick Au film. The inset shows a 1° shift in the SPP resonance dip when the bulk refractive index above the Au film changes from 1.32 to 1.33. This sensitivity of 100 deg/RIU (Refractive Index Unit) is typical for prism-based SPR instruments (Pang et al.).

The excitation of an SPP wave can be monitored by a sharp dip in the reflected light at the resonant angle (figure 35b). As more analytes bind to the receptors on the surface, this resonant angle changes. The angular distribution of the reflected light can be measured by a photodiode array or a CCD camera in real time, scanning for the steep drop in intensity that indicates the excitation of SPR (figure 35a). For an SPP excitation source, a light emitting diode, a broadband lamp, or a laser can be used (Shumaker-Parry et al., 2004). In a prism-based SPR setup, the angular sensitivity is typically ~100 deg/RIU (refractive index unit). Assuming an angular resolution of 10⁻⁴ degrees, the corresponding minimum resolution (Pang et al., 2007) for refractive index changes is Δn/n ~10⁻⁶. Recently groups have reported refractive index resolution approaching even 10⁻⁷ using SPR sensors (Piliarik and Homola, 2009).

The SPR peak width is determined by both ohmic loss and radiative out-coupling, which is a function of the dielectric constants, roughness, film thickness, and the wavelength of operation. While any metallic films that can sustain SPP waves can be used for SPR sensing, Au and, to a lesser degree, Ag, have been mainly employed. The use of smooth metallic films with increased SPP propagation lengths can improve the sharpness of the SPR peak. Single spot measurements can be taken, or, if the entire sensor chip is illuminated, the reflection dips can be imaged onto a camera, providing parallel imaging of multiple sensing spots (Brockman et al.). An SPR instrument is indeed a sophisticated system that integrates optics, surface chemistry, signal processing, and microfluidics. Advances in nanofabrication (section 5.2), utilization of SPPs in the near-infrared (Nelson et al., 1999) or of long-range SPPs (Wark et al., 2005), parallel SPR imaging (Shumaker-Parry et al., Smith and Corn), microfluidic multiplexing (Luo et al., Ouellet et al., 2010), and integration with other analytical methods such as mass spectroscopy (Cooper, 2002) will benefit the next generation of SPR instruments.

5.2. Metallic nanoparticles and nanoholes for biosensing

Emerging technologies based on metallic nanostructures provide new design freedoms to improve SPR biosensors in terms of sensitivity, multiplexing, tunability, resolution, and biological interfacing. Among various options, we focus on two categories: (1) metallic nanoparticles and (2) the inverse structure, i.e. metallic nanohole arrays. A desirable feature of these non-planar structures is their ability to directly convert incident light directly into SPRs, eliminating the need for a bulky coupling prism. On the curved surface of a metal nanoparticle, light can directly couple into a localized surface plasmon resonance (LSPR). Likewise, an array of subwavelength nanoholes or even a single isolated nanohole can act as a source of SPP waves. Furthermore, light scattering from nanoparticles or optical transmission through nanoholes exhibit tunable spectral resonances, unlike the flat Au films used in the Biacore™ system. While both systems harness SPR effects, the LSPR in nanoparticles and the propagating SPP wave in a metal film perforated with nanoholes exhibit very different characters.

5.2.1. Noble metal nanoparticles for biosensing

Metallic nanoparticles have been widely used for biological labeling, sensing, and spectroscopy because of their large optical scattering cross-section and photostability. Comprehensive reviews on this topic can be found elsewhere (Oldenburg et al., Schultz, Wang et al., Jain et al., Pelton et al.). Colloidal metal nanoparticles with various sizes and shapes can be chemically synthesized (Jin et al., Sun and Xia, Nikoobakht and El-Sayed, Tao et al., Wang et al., Xia, 2009). Alternatively, metallic nanoparticles can be patterned on a substrate using techniques such as e-beam lithography (Maier, 2003b, Hentschel et al., Felidj et al.) or nanosphere lithography (Haynes and Van Duyne, 2001). A key advantage of chemical synthesis is that monocrystalline particles can be obtained. For example, it was shown that the SPP propagation length—and thereby its sensitivity—along a crystalline Ag nanowire was increased compared with that of a polycrystalline Ag nanowire (Ditlbacher, 2005).

With dark-field optical microscopy techniques, light scattering can be monitored from a single metallic nanoparticle. To achieve this, typically reflection mode (angled incidence) or evanescent mode (via total internal reflection) illumination is used to block out the incident light (Schultz, 2003, Pelton, 2008).

The spectral sensitivity of LSPR sensors to bulk refractive index change is typically 100–400 nm/RIU in the visible regime, which is lower than the sensitivity of prism-based SPR instrument utilizing propagating SPPs. On the other hand, the LSPR decay length (10~50 nm) into the surrounding medium is much shorter than that of SPPs (100~300 nm), and thus provides advantages for the detection of small molecules according to Eq. 12 (McFarland and Van Duyne, 2003). The reduced bulk index sensitivity in LSPR sensors is not necessarily a disadvantage, since it also reduces the background noise due to temperature variations, which could eliminate the need for an on-chip temperature controller. However, one of the challenges for practical applications of LSPR sensors is fabrication reproducibility. Because their spectral resonances are very sensitive to nanometric shape changes or surface roughness, device-to-device or particle-to-particle reproducibility is more difficult to achieve with LSPR structures compared with SPP-based sensors. Also, the short probing range (tens of nanometers) of LSPR sensors may be problematic for studying large antibodies or thick films.

5.2.2. Nanohole SPR biosensors

While noble metal nanoparticles exhibit strong LSPR effects, the inverse structure, nanoholes in a metal film, also show unique SPR characteristics because of the EOT effect discussed in section 3.2. An obvious distinction between a nanohole array patterned in a continuous metal film and an array of disconnected nanoparticles is that the former can support propagating SPP waves, whereas the latter can only sustain the short-range LSPRs. Like a noble-metal nanoparticle, a single nanometric hole in a metal film can couple incident light into SPP waves. When many of these nanoholes, or SPP sources, are arranged in a periodic array, the SPP waves constructively interfere at the resonance wavelengths giving rise to the EOT effect. Molecules on the gold surface or inside the nanoholes can sharply modulate the resonance wavelength and the optical transmission process (figure 36). Because of the commercial success of SPR instruments, researchers have extensively studied label-free biosensing applications of metallic nanoholes (Brolo, 2004; Williams et al.; Stark et al.; Dahlin et al.; Tetz et al.; Stewart et al.; Lesuffleur, 2007; Lesuffleur, 2008; De Leebeeck et al.; McMahon et al.; Yang, 2008; Yang, 2010; Lindquist et al.; Chen et al.; Im, 2009; Masson et al.; Murray-Methot et al.; Escobedo et al.; Menezes et al.), as illustrated in figures 37 and 38.

Figure 36.

(a) A periodic array of nanoholes milled through a thin Au film. (b) At resonant wavelengths, the incident light is efficiently transmitted, giving a sharp transmission peak. As molecules bind, the peak shifts, modulating the transmission. (c) Side view: 3-D FDTD simulation of the EOT effect through a nanohole array. Intense optical energy is observed, confined within ~100 nm from the surface. Molecular binding on or near the surface modulates this field distribution, and the optical transmission process, providing the basis for measuring binding events.

Figure 37.

(a) EOT peak shifts due to binding of molecules Reprinted with permission from (Brolo et al., 2004) Copyright 2004 American Chemical Society. (b) Sharp apexes in a double-hole aperture enhance the detection sensitivity. Reprinted with permission from (Lesuffleur et al.) Copyright 20047, American Institute of Physics. (c) An array of 3×3 nanoholes occupying ~1 um² footprint can be used as a sensing element (Lindquist et al.). Image reproduced by permission of Sang-Hyun Oh and The Royal Society of Chemistry from [Lab Chip 9, 382 (2009)]. (d) Multiscale patterning of nanoholes using soft interference lithography. Reprinted by permission from Macmillan Publishers Ltd: Nature Nanotechnology, (Henzie et al.) Copyright 2007.

Figure 38.

(a) SPR imaging with nanohole arrays. Reprinted with permission from (Yang, 2008) Copyright 2008 American Chemical Society. (b) Nanohole arrays made with interference lithography with Fano-type lineshapes for SPR sensing in the NIR regime. Reprinted with permission from (Tetz, 2006) Copyright 2006, The Optical Society (OSA).

In a periodic nanohole array, the spectral resonances can be tuned by changing the array periodicity, as discussed in section 3.2. The peak transmission wavelength, given in equation (5) and here again for convenience, is approximated by (Ebbesen et al., 1998)

$${\lambda }_{\mathit{\text{peak}}}\approx \frac{a}{\sqrt{i^2+j^2}}\sqrt{\frac{{\epsilon }_d{\epsilon }_{\mathit{\text{metal}}}}{{\epsilon }_d+{\epsilon }_{\mathit{\text{metal}}}}}$$ (15)

where a is the periodicity of the array, i and j are the grating orders and ε_metal and ε_d are the dielectric constants of the metal and dielectric, as before. Using this equation, Pang et al. derived an analytical expression for the spectral sensitivity of periodic nanohole arrays (Pang et al., 2007):

$$S=\frac{d\lambda }{\mathit{\text{dn}}}=\frac{a}{\sqrt{i^2+j^2}}\sqrt{{\left(\frac{{\epsilon }_{\mathit{\text{metal}}}}{n^2+{\epsilon }_{\mathit{\text{metal}}}}\right)}^3}$$ (16)

For sensing in the visible and NIR regimes, the typical array periodicity ranges from 400–1000 nm with a hole diameter of 100–500 nm. The sensitivity is a function of the array periodicity, the SPP grating order, and the wavelength. The spectral response and local electric-field enhancement of nanoholes can also be tuned by changing the hole shape (Gordon et al., 2004, Lesuffleur et al., 2007) as elliptical holes display strong polarization effects (Zakharian et al.). Additional mechanisms such as plasmonic Bragg mirrors have been implemented to enhance the functionality of nanohole-based devices and suppress unwanted crosstalk between sensing elements (Lindquist et al., Lindquist et al., Marthandam and Gordon).

The figure of merit (FOM) of nanoplasmonic sensors is often measured in terms of the spectral sensitivity (nm/RIU) divided by the resonance linewidth (nm). In periodic hole arrays in optically thick metal films, the linewidth is mainly determined by the radiative loss, i.e. SP scattering via nanoholes and ohmic loss. (Tetz et al., Kim et al., Genet and Ebbesen) Reducing the hole size leads to sharper resonance peaks, although the overall transmission also decreases. Because the linewidth can be significantly broadened when the hole array is immersed in water, the figure of merit should be measured and compared in water. Overall, the sensitivity of nanohole array sensors typically ranges from 300 nm/RIU to 1500 nm/RIU, which is generally lower than that of prism-based SPR sensors. However, Tetz et al. demonstrated that linewidth-optimized nanohole sensors can possess very high figures of merit, e.g. 410 RIU⁻¹ in air and 120 RIU⁻¹ with water broadened transmission in the NIR, compared with typical prism-based SPR instruments that show 108 RIU⁻¹ in water at 850 nm (Tetz et al.).

Both periodic and aperiodic nanohole systems have been utilized for SPR biosensing. A random array of nanoholes in metallic films can be inexpensively fabricated by colloidal lithography (Dahlin et al., 2005). However, since no long-range ordering exists to support hole-to-hole SPP interference effects, the optical transmission is determined by the LSPR of individual holes, which tends to be broader in spectral width and weaker in intensity than the EOT spectra of periodic nanohole arrays (Garcia-Vidal et al.).

Gold and silver nanohole arrays have been predominantly used in most sensing studies in air and water. When a silver film is used, a thin dielectric shell can be used to protect the silver surface against oxidation (Jonsson et al., 2007, Im et al., 2010b). Teeters-Kennedy et al. used commercial nickel meshes patterned with a microarray of subwavelength holes in the IR regime for sensing and infrared spectroscopy (Teeters-Kennedy et al., 2007).

The EOT spectrum through a metallic nanohole array can be easily measured using a simple co-linear optical transmission setup. Because SPP waves in the nanohole arrays are generated without using a bulky coupling prism, this setup considerably simplifies the optical design, assembly, and alignment. For microarray applications, this is particularly important since high-resolution imaging optics are required for multiplex detection, which is not straightforward to implement in the prism-based SPR setup (Chinowsky et al., 2004, Lindquist et al., 2009).

Most existing work on nanohole arrays has utilized direct patterning of metal films using FIB milling (section 2.5) or e-beam lithography (section 2.3). These serial patterning techniques, however, cannot be used for routine production of large-area nanohole array chips, which is required for practical applications. Interference lithography (IL), discussed in section 2.2, nanosphere lithography (NSL), or nanoimprint lithography have been employed to address these issues (Stewart, 2006, Tetz et al., 2006, Henzie, 2007, Lee, 2009). While the NSL technique can eliminate the need to use a photomask and an exposure system, precise tunability and long-range patterning order is not easily achieved. Rather, the periodic nanohole arrays possess an ideal, repetitive geometry that is amenable to large-area patterning with IL (Tetz, 2006, Zeineldin, 2006). Furthermore, IL can also be combined with other replication methods such as nanoimprint or template stripping (section 2.10).

5.2.3. Future direction: biomimetic sensing with cellular membranes

Integrating SPR biosensors with soft matter, in particular lipid membranes and membrane proteins, can tremendously enhance their applications in biology and medicine. Membrane-bound receptors such as neurotransmitter receptors, ion channels, and G protein-coupled receptors (GPCR), serve as communication gateways between a cell and its environment. Importantly, drugs acting on these receptors can modulate a broad spectrum of diseases including cancer, cardiovascular disease, depression, diabetes, obesity, inflammation, and pain(Filmore). In fact, almost half of the 100 best-selling drugs target membrane-bound receptors (Cooper, 2004), including well-known brands(Ma and Zemmel, 2002) such as Claritin^®, Lopressor^®, Pepcid^®, Prozac^®, and Zantac^®. As discussed in section 5.1, one of the big advantages of SPR sensing is their ability to measure the binding kinetics between drugs and their targets. Thus, the development of a reliable in vitro sensing technology for membrane-bound receptors is highly desirable for drug discovery and medicine, but is not easily addressed by existing SPR instruments. A major challenge has been the nontrivial integration of solid-state sensors with lipid membranes and proteins integrated therein. These membrane receptors are notoriously hard to purify and do not fold properly outside the lipid bilayer membrane. In addition, the metallic surface, which is required for SPR sensing, does not provide a natural environment to study membrane proteins, as the procedures of isolating and immobilizing membrane proteins often adversely affect their function.

Metallic nanoparticles and nanoholes present potential routes to incorporate these clinically important membrane proteins into SPR sensors. Instead of a flat surface, these 3-D nanostructures can be utilized to better mimic cellular environments (figure 39). Metallic nanoparticles have been mainly combined with supported lipid membrane systems for LSPR sensing (Galush et al., 2009). On the other hand, metallic nanohole arrays provide the unique options for integrating SPR sensing with both supported (Dahlin, 2005; Jonsson, 2007) and freely suspended lipid membranes (Im et al., 2010c). For example, Dahlin et al. used metallic nanoholes that exposed an underlying silica substrate to overcome the challenge of reconstituting a supported lipid bilayer membrane on gold films and performed label-free measurements of lipid-membrane-mediated reaction kinetics. (Dahlin, 2005) Nanohole arrays made in free-standing metallic films provide another interesting option, since a thin lipid bilayer can be suspended over the nanopores while maintaining mechanical stability (because of the small pore dimensions) and being surrounded by a solution on both sides. This nanoscale free-standing lipid membrane configuration, known as a pore-spanning lipid bilayer or nano-black lipid membrane (nano-BLMs), on gold-covered nanoporous arrays have been introduced by Steinem and coworkers (Hennesthal and Steinem, 2000), and has been used to study electrical properties of lipid membranes and ion channels using AFM or impedance measurements (Hennesthal and Steinem, Reimhult and Kumar, Han, 2007). The integration of pore-spanning lipid membranes and membrane proteins (alpha-hemolysin) with label-free SPR sensor has been realized recently (Im, 2010c) (figure 39c, d). Metallic nanopore arrays are ideally suited for SPR biosensing of membrane proteins since they concurrently provide (1) stable mechanical support for porespanning membranes, since smaller diameter free-standing lipid membranes are more stable than larger diameter lipid membranes, and (2) a means to detect molecular binding kinetics, since the gold film sustains SPR effects via the EOT effect. Membrane proteins can thereby be integrated with the SPR sensing capability of gold nanohole arrays, preserving their functionality in an environment that more closely mimics their natural state. Furthermore, membrane proteins integrated in the free-standing lipid bilayer can be accessed from both sides, making this approach more attractive for studying membrane protein interactions than planar lipid bilayers supported on a flat substrate (Im et al., 2010c).

Figure 39.

Membrane biosensing schemes: (a) LSPR sensor has been integrated with lipid membranes by utilizing localized rupture of phospholipid vesicles on silicon dioxide in the bottom of nanometric holes in a thin gold film Reprinted with permission from (Dahlin et al., 2005). Copyright 2005 American Chemical Society. (b) Pore-spanning lipid membrane (nano-black lipid membrane) covering an anodic aluminum oxide (AAO) nanopores. Reprinted with permission from (Lazzara, 2011). Copyright 2011 American Chemical Society. (c) Colorized SEM of a nanopore array made on a suspended Au/Si₃N₄ membrane. (d) The ability to fill both sides of the membrane with a buffer makes this geometry a unique platform to study transmembrane proteins. From (Im et al., 2010c) Both (c) and (d) reproduced by permission of the Royal Society of Chemistry.

Several other interesting schemes have been demonstrated to using the metallic nanoholes as nanofluidic channels for molecular transport and “flow-through” biosensing (Eftekhari, 2009; Jonsson, 2010), the translocation of DNAs (Chansin et al.), or as scaffolding to incorporate lipid vesicles or natural cell membranes (Dahlin, 2008; Wittenberg, 2011). Finally, metallic films can concurrently act as electrodes, presenting opportunities to build a multi-functional sensing platform that combines SPR sensing with electrochemistry and impedance spectroscopy (Hook, 2008; Andersson, 2008; Shan, 2010; Sannomiya, 2010).

It should be emphasized that the overall performance of SPR sensors depends not only on the physical instrument but also on molecular recognition elements. In this way, SPR biosensing research is an exciting multidisciplinary field that merges engineering, physics, chemistry, and biology. Furthermore, since SPR instruments have been one of the first successful products utilizing plasmonic principles, this field will continue to entice researchers toward developing next generation biosensors with improved sensitivity, throughput, and integration, towards tackling new and exciting problems in the life sciences.

5.3. Surface-enhanced and tip-enhanced Raman spectroscopy (SERS and TERS)

While label-free SPR biosensing is a very useful technique for measuring protein binding kinetics, it cannot identify bound molecules because only refractive index changes are recorded. Many applications in diagnosis, pathogen detection, or environmental sensing from complex samples require some form of chemical fingerprinting or identification such as Raman spectroscopy. In Raman scattering, which is analogous to amplitude modulation (AM) used in radio communications, the carrier wave (laser) is modulated by the signal coming from the vibrational and rotational motion of chemical species in the gas, liquid, or solid state. Typically these vibrational transition frequencies are in the infrared (IR) regime such that direct measurements of these transitions normally require expensive IR detectors made from compound semiconductors. Fortunately, in Raman spectroscopy, as in radio broadcasting, the frequency of the carrier wave (laser) can be much higher than that of the encoded signal, meaning that IR spectroscopy can be conveniently performed at visible frequencies using visible light sources and silicon-based detectors, which are more sensitive yet less expensive. In addition, Raman spectroscopy possesses some distinct advantages compared with other vibrational spectroscopy techniques such as Fourier-Transform Infrared Spectroscopy (FTIR). Because Raman selection rules are different than for IR absorption, some transitions that are not IR-active can be probed using Raman spectroscopy. When chemical imaging of a sample is required, Raman imaging with a visible or NIR laser can achieve a far better lateral imaging resolution than FTIR-based imaging. Perhaps the most notable example of high-resolution Raman imaging is tip-enhanced Raman spectroscopy (TERS), in which Raman spectroscopy is combined with NSOM (section 4.3) for nano-resolution chemical mapping, as described later in this section. Moreover, Raman spectroscopy can be readily performed in water, which has a very small Raman scattering cross-section. On the other hand, mid-IR radiation is strongly absorbed by water, thus hydrated samples (e.g. biological specimen) cannot be easily probed via FTIR (Krafft, 2009). For these reasons, Raman spectroscopy has been an extremely valuable analytical technique in physical, chemical, and materials science.

Unfortunately, Raman scattering itself is a very feeble (Raman and Krishnan, 1928) phenomenon, since a typical non-resonant Raman scattering cross-section (~10⁻³⁰ cm²) is about 14–15 orders of magnitude lower than that of fluorescence (~10⁻¹⁵ cm²)(Haynes, 2005). However, when a molecule is very near to a roughened or nanostructured noble metal substrate, the Raman signal can be greatly increased (Jeanmaire and Van Duyne, 1977), usually around 10⁴ to 10⁹ times (Haynes, 2005). This Surface Enhanced Raman Spectroscopy (SERS) carries both a “chemical” enhancement (Kambhampati and Campion, 1999) of roughly 10 – 100 times, and an “electromagnetic” enhancement (Schatz, 2006) due to the excitation of LSPRs and large field intensities in and around nanostructured metal substrates (Van Duyne and Haynes, 2001).

SERS is a powerful label-free method that can identify proximate molecules (Van Duyne and Haynes, 2001, Jeanmaire and Van Duyne, 1977, Stiles et al., 2008, Moskovits, 1985, Haynes et al., 2005, Jackson and Halas). Indeed, single-molecule sensitivity has been reported (Kneipp et al., Nie and Emory). Since SERS relies on the excitation of localized plasmonic hot spots, it can be a unique addition to SPR biosensing. Bound molecules are effectively “fingerprinted,” naturally complementing the label-free methods of SPR biosensing. For example, SERS has recently been used to detect a diverse set of biomolecules (Shafer-Peltier, Grubisha, Faulds, Wabuyele and Vo-Dinh, Kneipp, Qian, Barhoumi, Lim, Bantz) as well as trace amounts of anthrax (Zhang, 2005b), nuclear waste (Bao, 2003), and pesticides (Weissenbacher, 1997). Additionally, a SERS signal can also be used as a tool for optically characterizing a plasmonic device, for example, by pinpointing the locations and the intensities of maximum field enhancement. Raman spectroscopy has several important advantages, in that it is a vibrational spectroscopy technique, unlike fluorescence, providing much more information about molecular structure and orientation. For the basics of SERS, Raman, and applications, the reader is referred to other review articles (Van Duyne and Haynes, 2001, Moskovits, 1985, Kneipp, 2002, Bantz, 2011, Stiles, 2008).

Since SERS occurs on roughened metallic substrates with the production of localized hot spots, we can understand the electromagnetic enhancement by modeling the roughness as small metallic nanoparticles whose diameters are much smaller than the wavelength of the incident light. Under the influence of an external electromagnetic field, the electron plasma of a metallic nanoparticle will oscillate, greatly enhancing the local field. Due to such a strong field, the Raman signals are enhanced by many orders of magnitude. In fact, the nanoparticle boosts the signal in two ways. First, the incident field is localized and intensified by the nanoparticle, increasing the field seen by the Raman-active molecule. Second, the scattered light, i.e. the Raman spectrum, is localized and intensified in turn by the nanoparticle. Even though the Raman light is frequency-shifted from the incident light, the resonance (LSPR) of the nanoparticle is sufficiently wide to enhance both the incoming and scattered fields. Thus, the SERS signal is proportional to the incident field intensity squared, i.e. the SERS Enhancement Factor (EF) is proportional to the electric field to the fourth power. This process is outlined in figure 40.

Figure 40.

Basic SERS electromagnetic enhancement. A gold nanoparticle will enhance both (a) the incident field, as well as (b) the scattered field, greatly boosting the Raman signal from a proximate molecule. Since the intensity is enhanced twice, i.e. the nanoparticle acts as both a receiver and a transmitter, the SERS signal is proportional to the intensity of the incident field squared.

To quantify the enhancement, the SERS signal is compared to a normal, bulk Raman signal. Additionally, quantification must account for the number of molecules in bulk versus adsorbed on the surface. For accurate calculations of EF, the number of surface molecules must be estimated knowing the packing density of the molecules, and the surface area and local geometry of the metal. This is a difficult calculation with many assumptions, often resulting in wildly varying estimates of the maximum EF.

Local enhancement of the optical field is a primary factor for a strong SERS signal (Moskovits, 1985). However, measurements are typically performed on roughened or randomly structured metallic substrates with poor control over the location and intensity of the enhanced fields, or hot spots (Kneipp, 2008). A SERS substrate that is both highly reproducible and that can offer high signal enhancement due to controlled field localization can offer immediate benefits to a broad range of disciplines where efficient and accurate chemical detection is necessary. Using some of the nanofabrication techniques outlined in this review, such as template stripping (section 2.10) of ultrasharp metallic pyramids or ALD-based lithography for sub-5-nm nanogap formation (section 2.9), may lead to more practical SERS devices.

Going forward, several technical problems should be addressed before SERS can be more widely adopted for real-world applications. In particular, high-throughput fabrication of substrates with reproducible performance has been lacking. Often, the SERS hot spots are randomly distributed. While Ag is an effective SERS substrate and has larger enhancement factors than gold or other elements, it suffers from oxidation. Delicate handling or coating with Al₂O₃ ALD (section 2.9) is required to prolong the lifetime of Ag substrates. Furthermore, unwanted fluorescence background can be a problem. This is partially solved by using longer (e.g. 785 nm) excitation wavelengths, but the Raman scattering intensity drops significantly with increasing wavelength. Finally, the cost of instrumentation is still an issue. While the cost of Raman spectrometers have been going down, it is still prohibitive to many laboratories.

TERS is an emerging branch of SERS, wherein a sharp metallic tip, such as the probe of an scanning tunneling microscope (STM) or atomic force microscope (AFM) is brought in proximity to analytes to enhance their Raman scattering cross-section (Wessel, Sanchez et al., Stockle et al., Anderson, Hayazawa et al., Yeo et al.). In this configuration, the sharp (~10 nm) apex of a laser-irradiated metallic tip confines optical energy well below the conventional diffraction limit, as discussed in section 5.4. TERS is useful because it empowers SERS, usually detected using a far-field spectroscopy tool, with the sub-wavelength imaging resolution enabled by plasmonics. The combination of Raman chemical fingerprinting and near-field optical imaging has numerous applications in physics, chemistry, and biology (Deckert et al., Hartschuh et al., Hartschuh et al., Pettinger et al., Roth et al., Anderson et al., Anderson et al., Berweger et al., Weber-Bargioni et al.). Single-molecule sensitivity has been demonstrated for TERS (Domke et al., Neacsu et al., Zhang et al.). In addition to its nanoscale resolution, TERS can extend the capability of SERS in many interesting ways. Here the SERS “substrate” is fabricated on or mounted to the probe of a scanning probe microscope, and SERS signals can be extracted from analytes that cannot be brought into contact with a metallic substrate. Also, the Raman enhancement factor can be measured as a function of tip-sample distance, which can provide valuable information on the near-field response of the tip (Roth et al.). While aperture probes have been useful in NSOM, they are difficult to use for TERS due to the low optical throughput from subwavelength apertures. Thus apertureless probes, i.e. sharp metallic tips, are better suited for TERS. However, reliable and reproducible fabrication of sharp TERS tips (10 – 20 nm radius) using conventional fabrication methods remains a significant challenge (Yeo et al.). For TERS, both the sharpness of the tip and the smoothness of the surrounding surface are important, and can lead to precise control over the location and intensity of the hot spot, which is explained in the next section.

5.4. Plasmonic nanofocusing

All nanoscale metallic tips exhibit local field enhancements due to an electrostatic optical “lightning rod” effect. Plasmonic nanofocusing, on the other hand, uses diffraction limited optics to launch SPPs into engineered metallic nanostructures that deliver the plasmonic energy into nanoscale volumes. Certain metallic nanostructures are able to confine SPPs into deeply subwavelength volumes. For instance, confining red light (700 nm) into 3 nm thick metal-insulator-metal (MIM) stack has been experimentally demonstrated (Miyazaki and Kurokawa, 2006). This vertical confinement increases the wavevector k_spp of the SPP by, in that case, about a factor of 10. Nanoscale confinement can also be achieved by allowing an SPP to propagate towards a sharp tip (Stockman, 2004, Babadjanyan et al., 2000), narrow gap (Choi et al., 2009, Seo et al.), within an aperture (Lee et al., 2010), or along a wedge (Nerkararyan, 1997). If the lateral dimensions of the metallic structure are tapered, the propagating SPPs is squeezed, effectively, into the non-propagating LSPR at the tip. This can be achieved by continuously changing the thickness of the insulator in an MIM stack, or the thickness of the metal in an insulator-metal-insulator (IMI) stack. As the SPP propagates along the tapered waveguide, it will be squeezed laterally or vertically, which will increase k_spp. Correspondingly, the field intensity will also increase, sometimes by several orders of magnitude. The final tip or gap size can be on the order of only several nanometers.

Adiabatic nanofocusing techniques (Stockman, 2004, Babadjanyan et al., 2000) taper the waveguide slowly compared to the wavelength of the SPP, minimizing reflections. If dissipation of the SPP is sufficiently weak, very large (~1000×) field amplitude enhancements can be produced. However, as the SPP becomes more and more confined, the field will be largely located within the metal, increasing the dissipation. Furthermore, if the taper angle is very small (e.g. few degrees) the taper length will be quite long, also increasing the total dissipation of the SPP as it travels towards the tip. Conversely, non-adiabatic nanofocusing schemes use a relatively large (e.g. 30 degrees) taper angle in an effort to minimize propagative SPP dissipation. Unfortunately, significant reflections may result, decreasing SPP delivery to the tip. With these two competing effects, it may be possible to design a structure with an optimal taper angle (Pile and Gramotnev, 2006).

For simplicity and to provide a qualitative description, a one-dimensional theoretical case is presented here. An SPP propagating along an IMI structure can have either even or odd symmetry with respect to the electric field (Economou, 1969, Maier, 2007). The odd mode (with symmetric charge distributions) will give the desired nanofocusing effect. This can be thought of as two SPPs, one on each side of the taper, arriving with their charges in phase, and interfering constructively at the tip. The even mode is the so-called long-range SPP (Sarid, 1981) since as the thickness of the metal film decreases, the mode resembles more and more that of free-space light. These modes are illustrated in figure 41a.

Figure 41.

Plasmonic nanofocusing. (a) Two types of modes exist for an IMI tip. An even-field mode (odd charge distribution) will have zero charge at the tip, and as the SPP travels down the metal taper to the sharp tip, the field distribution resembles that of a wave propagating in the dielectric, and no plasmonic nanofocusing occurs. However, an odd-field mode (even charge distribution) will have large charge density at the tip. The SPPs traveling on either side of the taper will arrive to the tip with their charge distributions in phase. With this mode, the propagating SPP becomes a localized at the tip, focusing its energy into a nanoscale volume. As the tip tapers to a finite size, the resulting high-intensity field is oriented longitudinally, i.e. along the tip axis. (b) Plotting the dispersion of the odd-mode SPP shows that the wavenumber k_spp at a given frequency increases with decreasing metal thickness. Once the metal thickness becomes on the order of the skin depth δ_m, the two SPPs on the top and bottom of the thin metal film will couple. The mode with odd field symmetry will generate the large wavevectors suitable for plasmonic nanofocusing. Figure from (Lindquist, 2010).

For a certain thickness a of the guiding IMI metallic structure, the odd-mode SPP will have the following dispersion relationship (Pitarke et al., 2007):

$$\text{tanh}\left(\frac{a}{2{\delta }_m}\right)=-\frac{{\epsilon }_d{\delta }_d}{{\epsilon }_m{\delta }_m}$$ (17)

where δ_m and δ_d are the SPP field penetration depths and ε_m and ε_d are dielectric functions of the metal and the dielectric, respectively. This dispersion relation is plotted and discussed in figure 41b for several thicknesses a. It is this IMI dispersion relation—and similarly for MIM devices—that makes extreme sub-wavelength plasmonic confinement of optical energy possible. This also works for cylindrically-symmetric geometries (Takahara et al.).

Previously, it has been shown that gratings milled into the side of an electrochemically etched gold wire tip, when illuminated, will deliver SPPs to the tip (Ropers et al., 2007). Likewise, nanofocusing using nanohole gratings in a thin gold film next to a region with a lateral taper has also been demonstrated (Verhagen et al., 2007, Verhagen et al., 2008), with only the odd-field mode focusing at the tip. Curved slits, grooves, or holes can focus plasmons to an in-plane bright spot (Lopez-Tejeira et al., 2007, Chen et al., 2009c, Kim et al., 2010, Liu et al., 2005, Yin et al., 2005), and the focus position can even be controlled actively (Gjonaj et al., 2011). In all these cases, the plasmons were focusing on one side of a wire, a flat tapered film, or in plane. Full three-dimensional nanofocusing is also possible, with, for example, radially polarized plasmons propagating along a circularly symmetric tapered waveguide (Stockman, 2004, Chen et al., 2009d, Issa and Guckenberger, 2007). Most metallic tips and tapers are fabricated with metal deposition (Verhagen et al., 2007), the metallization of fibers (Wang et al., 2008), or with electrochemical etching (Ropers et al., 2007). Often, the devices are then patterned with FIB milling (Ropers et al., 2007, Verhagen et al., 2008, Wang et al., 2008).

Tapered-wire nanofocusing schemes require the use of radially polarized light (Zhan and Leger). As the plasmons travel towards and intensify near the tip, the associated fields should interfere constructively (Bouhelier et al., 2003b), as shown in figure 41, resulting in a field oriented along the tip axis, i.e. longitudinally. Simple linear polarization does not have the necessary symmetry to excite a longitudinal field. Breaking the symmetry of linearly polarized light requires illumination at a large tilt angle (Roth et al., 2006), or the use of an asymmetric tip (Sanchez et al., 1999). Alternatively, the edges of tightly focused Gaussian beams are also able to excite the longitudinal mode of the tip(Bouhelier et al., 2003a). If a single metallic nanoparticle is used at the end of dielectric waveguide or AFM probe, efficient optical coupling and excitation of longitudinally polarized fields still requires illumination with the correct polarization, radial modes, or at large angles. More recently, a 3-D plasmonic nanofocusing structure that is excited with normally incident linearly polarized light was demonstrated (Lindquist et al., 2010). In these pyramid structures shown in figure 42, 3-D plasmonic nanofocusing as achieved by placing gratings on the pyramidal faces, converting normally-incident linearly polarized light into plasmons that propagate towards and converge at the ~10 nm apex. The nanofocusing effect depended on an asymmetric placement of the gratings (figure 42c, d) as well as on the smooth metallic interfaces produced via template stripping.

Figure 42.

SEMs of a (a) symmetrically and (b) asymmetrically patterned silver pyramids produced via template stripping. (c,d) FDTD simulations of the same structures. The asymmetry is necessary to convert linearly polarized light into a longitudinal (along the z-axis) field at the tip. For 710 nm wavelength illumination, the hotspot is calculated to be 28×32×14 nm³. Panels reprinted with permission from (Lindquist, 2010) Copyright 2010 American Chemical Society.

5.5. Quantum dot plasmonics

Plasmonic devices can also take advantage of nanometer-scale semiconductor crystallites, known as nanocrystals or colloidal quantum dots. These materials can now be prepared from many semiconductors using liquid-phase syntheses (Murray; Klimov). The resulting colloidal particles are highly crystalline, very uniform in size, and coated with surfactants to prevent aggregation. Thus, they can be manipulated and processed in solution. Due to their small dimensions, these nanocrystals can also exhibit efficient and robust fluorescence with a wavelength that is tunable with the nanocrystal diameter. By changing the size or the material, nanocrystals with emission from the ultraviolet to the infrared are now available. Understanding and controlling the light-matter interactions between these quantum emitters and SPPs can open up new avenues in basic research and practical applications. It is well known that metal surfaces can influence the spontaneous emission of fluorophores. Even in 1946, Purcell discussed that the local electromagnetic environment of a dipole could influence its emission rate (Purcell, 1946). Subsequent theoretical and experimental work has considered the emission of dipoles near metal films in detail.

To date, quantum dots have been integrated with plasmonic nanostructures in two main classes: as emitters and as absorbers. Coupling of quantum dots to SPPs has been examined to improve quantum-dot properties such as the absorption cross-section and the radiative emission rates. Likewise, positioning quantum dots within the evanescent fields of SPPs can boost the propagation of SPPs. Because of the Purcell effect, the fluorescence of molecular dyes can be enhanced significantly due in part to coupling to SPPs. Indeed, enhanced quantum dot emission has already been demonstrated on metallic colloids, thin films, or patterned metals (Kulakovich et al., Shimizu et al., Song et al., Gryczynski et al., Pompa et al., Biteen et al., Okamoto et al., Liu et al., Wei et al., Wu et al., Curto et al.). Substantial changes in both radiative decay rates and non-radiative quenching (Shimizu et al.), such as enhanced Auger decay, have been observed by coupling quantum dots with SPPs, leading to brighter or quenched emission, depending on the distance between the fluorophore and metal nanostructure. The fact that the radiative rate of the quantum dot is increased next to the metal can lead to additional benefits. Because the quantum dots are in their excited state so briefly, undesirable photochemistry should be reduced, increasing photostability even further. In addition, fluorescence “blinking” from individual quantum dots—an effect in which quantum dot emission turns on and off periodically—can be suppressed (Shimizu et al.). This opens opportunities to investigate the behavior of stable nanocrystals next to patterned metal films down to single particles. The metal structures can also be designed to make quantum dot emission highly directional (figure 43)(Brolo, 2006; Curto et al., Kosako et al.).

Figure 43.

Highly directional emission of photons from a single quantum dot coupled to a metal nanostructure (a Yagi-Uda antenna). The image shows comparisons between the directionality of emission from a reference quantum dot (“Ref”), grating, and directional Yagi-Uda antenna (“YU”) at visible wavelengths. Such high-efficiency coupling of quantum dots with SPPs can potentially be utilized for on-chip generation of single-photon sources for quantum computing. From (Curto et al., 2010) Reprinted with permission from AAAS.

Strong coupling of surface plasmons with confined excitons in quantum dots or quantum wells can enhance their absorption cross-sections, which is manifested in frequency-resolved photodetector measurements (Wu et al., 2010a, Chang et al., 2010, Chang et al., 2007a). While the size-tunable optical properties make quantum dots useful, variations in size or shape broadens their emission inhomogeneously. In conventional ensemble-averaged measurements, therefore, it difficult to extract and analyze decay rates that are distinct to individual quantum dots. To overcome this limitation, single-quantum-dot measurements have been performed in the context of plasmonics (Shimizu et al.). In addition, while many experiments have been performed with quantum dots on roughened metal films, using smooth metallic nanostructures can lead to simpler and more reproducible measurements for understanding the interactions between quantum dots and surface plasmons (Wu et al.).

In parallel, researchers have been trying to utilize plasmonic coupling with quantum dots to improve the properties of the SPPs. Even on perfectly smooth films, SPPs can suffer from significant Ohmic losses intrinsic to the metal. To compensate for this, several strategies have been proposed to provide gain to the SPPs (Nezhad et al., Grandidier et al.), including Surface Plasmon Amplification by Stimulated Emission of Radiation (SPASER) and lasing SPASERS (Bergman and Stockman, 2003). Here colloidal quantum dots have been proposed as the ideal gain medium due to their stability and strong fluorescence in the near-field. Recently, it was demonstrated that dye molecules can also be used to provide gain in metal nanostructures which can be used for SPP nanolasers (Noginov et al., 2009). Beyond the SPASER (Oulton et al., 2009), coherent coupling between surface plasmons and excitons in quantum dots has enabled interesting studies like single-photon optical transistors (Chang et al., 2007b, Wu et al., 2010b, Falk et al., 2009), single-photon sources (Vion et al., 2010), quantum optics with SPPs (Chang et al., 2006), and effects in cavity quantum electrodynamics like Rabi splitting (Gómez et al., 2009, Passmore et al., 2011).

Plasmonic effects may also be utilized for enhancing the performance of quantum-dot-based solar cells (Atwater and Polman, 2010). The use of SPPs to increase photocurrent is an effect that has already been reported in other materials (Pryce et al., 2010). SPP-based quantum-dot photovoltaics can gain from the enhanced photon cross-section in two ways: (i) the film thickness required to absorb the solar radiation will be reduced leading to a decrease in the material costs and (ii) the charge collection in a thin-film system will be enhanced allowing charge transport limitations in the power conversion efficiency to be overcome. See section 5.7 for more details.

5.6. High-density data storage

As discussed above, the optical behavior of subwavelength metallic nanostructures—such as holes, grooves, bumps, or particles—is largely determined by the excitation of SPRs. These resonances are strongly influenced by the local geometry of the metallic nanostructures themselves and any neighboring nanostructures. The complex resonant behaviors, spectral features, and polarization dependence of arrangements of such metallic nanostructures may have applications in next-generation optical data-storage applications (Mansuripur, 2009, Zijlstra, 2009, Ditlbacher, 2000).

Figure 44 outlines an optical data storage technique adapted from Mansuripur, et al.(Mansuripur, 2009) In transmission mode operation, a focused, diffraction-limited spot is scanned over each metallic bit-cell on a substrate. Each bit-cell is composed of different arrangements of nanobumps and nanoholes. By carefully positioning the nano-features, multi-dimensional data can be recorded within each bit-cell, i.e. by using different spacings and combinations of the nanobumps and nanoholes, or by exploiting polarization-dependent geometries, such as using elliptically shaped features or asymmetric spacings. The spectrum of the incident light is thus encoded with the multi-bit information stored in each bit-cell, allowing high-density data storage due to the nanoscopic field distributions. Arrangements of nano-apertures can also be recorded in mutiple metallic tracks (figure 44c). Ditlbacher et al. demonstrated spectral encoding with various arrangements of polarization-dependent nanoparticle (Ditlbacher, 2000). By illuminating with either red or blue light, the scattered light produced different images. More recently, Zijlstra et al. demonstrated multi-dimensional photothermal recording and two-photon luminescence readout with gold nanorod substrates (Zijlstra, 2009). By arranging nanostructured elements to form a completed bit-cell, multi-dimensional data can be encoded at several different wavelengths and with two orthogonal polarizations (figure 45). Along a different vein, a flying plasmonic head was used for high-density maskless lithography (Srituravanich et al.) with possible data storage applications. However, for plasmonic data storage to be a feasible option, fabrication and instrumentation costs must be reduced. Typically, expensive tunable pulsed lasers have been used, or low-throughput fabrication methods such as FIB.

Figure 44.

Plasmonic optical data storage. (a) Proposed optical data storage technique, with each bit-cell composed of multiple arrangements of nanobumps or nanoholes. (b) In reflection-mode operation. (c) The data can also be recorded in multiple tracks on a metal film. Scheme adapted from (Mansuripur et al., 2009) Used with permission of The Optical Society (OSA), Copyright 2009.

Figure 45.

Demonstration of five-dimensional plasmonic optical recording. The 18 different images are read-out from the same 100-by-100 µm area using two different laser polarizations (indicated by arrows at bottom) and three different wavelengths (indicated on the left). Reprinted by permission from Macmillan Publishers Ltd: Nature, from (Zijlstra et al., 2009), copyright 2009.

5.7. Plasmonics for photovoltaics

Recently, several review articles have appeared that detail how plasmonic nanostructures can be used to reduce the material usage and improve the efficiency of photovoltaics (PV)(Atwater and Polman, 2010, Pillai and Green, 2010). The two primary ways plasmonic devices have been utilized to enhance the performance of solar cells are through local enhancement of the electric field in the absorber and by increasing the path length of light through the absorber. The layers in solar cells need to be optically thick to allow for complete light absorption. Crystalline silicon (c-Si), which accounts for 85% of the PV market (Wolden, 2011), is a weak indirect-band-gap absorber. Therefore c-Si solar cells typically require thicknesses of ~100 µm to be sufficiently thick. High quality c-Si is also required for minority carriers to successfully diffuse across such a thick layer. The cost of high quality c-Si represents the largest fraction of the manufacturing cost for c-Si solar cells (Wolden, 2011). Scattering light from metallic nanoparticles or coupling photons to SPPs are two routes that offer to increase the path length through the absorber. Several options are shown in figure 46.

Figure 46.

(a) A typical thin-film PV structure. (b) Metallic nanoparticles can enhance light-trapping efficiency by increasing optical path lengths within PVs; Since nanoparticles cannot act as electrodes, transparent contacts (e.g. ITO) are needed. (c) LSPR effects using embedded nanoparticles. Used in tandem OPVs etc. Field enhancement is short-range (~10 nm). (d) Replace expensive ITO with ultra-thin metallic films with or without patterning. (e) Patterned metal contact on the backside can launch SPPs and increase optical path lengths. (f) Combined schemes (d) and (e) and potentially utilize coupling between top and bottom electrodes.

Sub-wavelength scale metal nanoparticles, with high free-electron density, placed on the top of c-Si solar cells have been shown to increase efficiency (Pillai, 2007) by up to 19%. Metal nanoparticles placed on top of an amorphous silicon solar cell (Derkacs, 2006) have also provided an 8.3% increase in efficiency in a design similar to Figure 46b, e. Stuart and Hall were the first to discover that scattering from nanoparticles could lead to increased absorption in a SOI photodiode (Stuart and Hall, 1996). Since then, several groups have reported enhanced absorption and photocurrent on a variety of solar cell designs by placing metal nanoparticles near the absorber (Pryce, 2010; Nakayama, 2008; Chen, 2009a; Qu, 2011; Schaadt, 2005; Derkacs, 2006; Derkacs, 2008). The nanoparticles act as dipoles with scattering cross-sections as high as 10 times their geometric cross-sections near their resonant frequency (Bohren, 1983). Light striking the metal nanoparticle is preferentially scattered into the material with higher permittivity (Mertz, 2000). The incident light is scattered over a large solid angle, facilitating coupling into the waveguide modes of the absorber. If the scattering angle is below the critical angle for the absorber material, then the scattered light will not escape (Atwater and Polman, 2010). Furthermore, preferential scattering allows the nanoparticle arrays to act as an anti-reflective coating. Spinelli et al. found that ordered arrays of silver nanoparticles placed on top of high-refractive index substrates showed higher transmittance than standard anti-reflection coatings over almost the entire spectrum (Spinelli, 2011). For frequencies above the plasmon resonance of the metal nanoparticles, interference effects, known as Fano resonance, cause increased reflection (Spinelli, 2011; Beck, 2009). Fano resonance can be avoided by moving the metal nanoparticles to the back contact of the solar cell (Beck, 2009, Ferry, 2010). The size of the metal nanoparticles must be optimized depending on the semiconductor material with which they are in contact. In general, ~100 nm particles are best due to their large degree of scattering. Smaller sizes are highly absorbing and are therefore not generally desirable (Pillai, 2007, Pillai and Green, 2010, Spinelli, 2011). Fabrication of randomly spaced nanoparticles has typically involved vacuum evaporating a thin film of silver followed by annealing. During annealing, the thin silver film breaks up under surface tension and results in randomly spaced 100–150 nm diameter silver nanoparticles (Beck, 2009). However, Spinelli et al. found that the transmittance through nanoparticle arrays was most sensitive to the array pitch. Therefore, random placement of nanoparticles may not be ideal. More control over nanoparticle size and spacing can be achieved by using porous alumina templates as shadow masks (Nakayama, 2008).

Another route to increase the absorption path length, depicted in figures 46e and 46f, is to couple incident photons to SPPs by nanostructuring the back metal contact of the solar cell. Through this coupling, the incident photon flux is essentially re-directed horizontally, therefore extending the path length through the absorber layer (Atwater and Polman, 2010). However, in order for the photons to be coupled to SPP, the momentum mismatch in the photons must be considered, as explained in section 5.1, necessitating either prism or grating couplers. Recently, grating couplers have been found to be an efficient method for coupling photons to surface plasmons (Renger, 2007, Andkjær, 2010). Periodic wavelength-scale structuring of a silver back contact in a solar cell has been shown to facilitate the excitation of surface plasmons and increase absorption in the absorber layer (Wang, 2010, Haug, 2008, Zhu, 2010). Structuring the front or back contact of the solar cell has intrinsic advantages over other plasmonic solar cell designs since the metal back contact is already an integral part of a solar cell. For example, a plasmonic nanocavity array electrode in an organic PV cell resulted in an increase in power conversion efficiency compared to an unpatterned electrode (Lindquist, 2008). One of the primary factors affecting the performance of this plasmonic solar cell design is choosing the appropriate metal/absorber combination. Metals have high losses in the visible regime. Therefore, it is important to choose a metal/absorber combination that provides minimal absorption in the metal (Atwater and Polman, 2010). Highly absorbing, direct-band-gap semiconductors or organic absorbers coupled with a silver back contact have shown the most promise (Slooff, 2007, Ferry, 2009).

Beyond increasing the light path in the absorber, metal nanoparticles can also provide local enhancement of the electric field in the absorber (Etchegoin et al., 2003) (see figure 46c). Absorption is directly proportional to the magnitude of the electric field squared (Yaghjian, 2007). Therefore, even small enhancements to the local electric field can have a strong effect on absorption. Small metal nanoparticles with low scattering cross section have been shown to act as antennas increasing the local electric field and absorption in the adjacent semiconductor absorber layer (Rand et al., 2004). By changing the spacing between the metal nanoparticles, the local electric field can be further enhanced. Rand et al. reported that interparticle coupling effects between embedded 5 nm silver nanoparticles were primarily responsible for near field enhancement and the higher-than-normal efficiency observed in tandem bi-layer organic PV cells (Rand et al., 2004). The direct generation of electron-hole pairs by plasmon excitation has also been reported as a route for absorption enhancement. Westphalen et al. showed that excited plasmons in silver nanoparticles could emit an electron in a preferential direction if they were placed inside an oriented electric field (Westphalen et al., 2000). Computer simulations have also shown that small metal nanoparticles embedded within silicon absorbers can facilitate the direct generation of electron-hole pairs (Kirkengen et al., 2007, Guilatt et al., 2010). Beyond metal nanoparticles, other designs exist for optical antennas (Heidel et al., 2007, Lindquist et al., 2008, Luhman, 2011).

6. Conclusion and outlook

This review has covered the nanofabrication, characterization, and emerging applications of engineered metallic nanostructures. A large suite of top-down nanofabrication methods, which have been the core technologies behind scaling of silicon transistors, now finds new and exciting applications in plasmonics to manipulate optical waves at the nanoscale and potentially combine the benefits of nanoelectronics and nanophotonics. Perhaps the most notable characteristics of plasmonics is the broad range of potential applications including drug discovery, biosensing, nano-imaging, spectroscopy, optoelectronics, data storage, and photovoltaics. Plasmonics indeed has much to offer to the nanoscience and the larger scientific community. While reproducible and precise nano-patterning of metals with high throughput is a formidable task, the emerging technologies described herein will continue to improve in terms of their resolution, throughput, and reproducibility to address those challenges that lie ahead.

Figure 23.

Simulated EOT field maps. Continuous plane-wave illumination is incident from the +z direction. The time-averaged amplitude of the z component of the electric field is pictured. (a) λ=600 nm generates a non-resonant Rayleigh-Wood anomaly in which the field is de-localized from the SPPs and is diffracted tangent to the silver film. (b) λ=625 nm corresponds to the transmission minimum. SPPs are excited, but weakly, especially on the bottom side of the film. (c) λ=678 nm corresponds to a transmission maximum. The SPPs are excited symmetrically and are very intense. The field intensities are scaled by 4, 2, and 1 for (a), (b), and (c), respectively, for the same intensity scale bar. The transmission maximum has the most intense SPP fields. Figure from (Lindquist, 2010).

Figure 28.

Aperture probes and apertureless probes for NSOM. (a) SEM of a 70-nm aperture surrounded on all sides by 100-nm-thick aluminum. From (Betzig and Trautman) Reprinted with permission from AAAS. (b) A pulled fiber tip carrying a single gold nanoparticle used for apertureless NSOM. Reprinted figure with permission from (Kuhn et al.) Copyright 2006 by the American Physical Society. (c) SEM showing a gold particle attached to the end of an optical fiber. Reprinted figure with permission from (Anger et al.) Copyright 2006 by the American Physical Society (d) SEM of an asymmetrical gold tip made with FIB. Reprinted figure with permission from (Sanchez et al.) Copyright 1999 by the American Physical Society. (e) SEM of an aluminum nano-antenna sculpted with FIB. Reprinted by permission from Macmillan Publishers Ltd: Nature Photonics, (Taminiau et al.), copyright 2008. (f) SEM of a conical metallic tip with a grating SPP coupler made by FIB. Reprinted with permission from (Ropers et al.) Copyright 2007 American Chemical Society.