Scaling of form and function in the xenarthran femur: a 100-fold increase in body mass is mitigated by repositioning of the third trochanter

Abstract

How animals cope with increases in body size is a key issue in biology. Here, we consider scaling of xenarthrans, particularly how femoral form and function varies to accommodate the size range between the 3 kg armadillo and its giant relative the 300 kg glyptodont. It has already been noted that femoral morphology differs between these animals and suggested that this reflects a novel adaptation to size increase in glyptodont. We test this idea by applying a finite element analysis of coronal plane forces to femoral models of these animals, simulating the stance phase in the hind limb; where the femur is subject to bending owing to longitudinal compressive as well as abduction loads on the greater trochanter. We use these models to examine the hypothesis that muscles attaching on the third trochanter (T3) can reduce this bending in the loaded femur and that the T3 forces are more effective at reducing bending in glyptodont where the T3 is situated at the level of the knee. The analysis uses traditional finite element methods to produce strain maps and examine strains at 200 points on the femur. The coordinates of these points before and after loading are also used to carry out geometric morphometric (GM) analyses of the gross deformation of the model in different loading scenarios. The results show that longitudinal compressive and abductor muscle loading increases bending in the coronal plane, and that loads applied to the T3 reduce that bending. In the glyptodont model, the T3 loads are more effective and can more readily compensate for the bending owing to longitudinal and abductor loads. This study also demonstrates the usefulness of GM methods in interpreting the results of finite element analyses.

1. Introduction

Scaling of animal form is a key issue in comparative biology [1,2]. With regard to the musculoskeletal system, large variations in size demand that the skeleton and muscles be proportioned differently at different scales in order to maintain the same function. Alternatively, if bone stresses are to be maintained, then the manner in which the skeleton is loaded by body mass and muscles must be varied. Thus, Biewener [2,3] notes that while one might expect limb bone cross-sectional areas to scale relative body mass, such that constant stresses are maintained, in fact scaling is often geometrically similar among small-to-medium-sized taxa. Thus, animals often adopt different postures, rather than different skeletal proportioning to maintain similar skeletal stresses.

A closely related alternative to modification of posture is to adapt the form of the skeleton so as to vary muscle and tendon attachment sites to minimize the skeletal effects of greater loading. The xenarthran femoral third trochanter (T3) has been suggested to vary in a way that is consistent with such a stress reducing strategy [4]. Living armadillos range from the pink fairy armadillo (Chlamyphorus) at 85 g to the giant armadillo (Priodontes) at 30 kg [5]. Their fossil relatives, the glyptodonts, have a rigid carapace and an armoured tail, and range in estimated size from 100 kg in the Miocene propalaeohoplophorines, to over 1000 kg for the Pleistocene giants, Panochtus and Deodicurus [6]. Fossil ground sloths reached sizes of several tons [6]. This group, especially the armadillos and glyptodonts (Cingulates), provides a natural laboratory where aspects of scaling and limb stress can be analysed.

In smaller armadillos T3 projects from the upper half of the femoral shaft, whereas in larger armadillos, small glyptodonts and sloths it is near the middle, and in the larger glyptodonts and sloths T3 is close to the lateral femoral epicondyle. This led Milne et al. [4] to suggest that muscles attaching to T3 can reduce coronal plane bending stress in the femur, and that the stress reducing effect of the muscle pull on T3 occurs in the femoral shaft above the trochanter. In larger xenarthra, the T3 is more distal, leading to the hypothesis that bending stress reduction is greater; affecting the whole femoral shaft. Thus, a recent study of allometric variation in xenarthran femoral shape [4] found features which indicate that the femora of larger xenarthrans are more subject to bending in the coronal plane. Larger specimens have relatively larger medial femoral condyles and increased curvature of the medial femoral border. The longitudinal forces passing through the femur pass from the femoral head to the medial femoral condyle. This has been reported for Pleistocene sloths [7] didelphids [8] and tupaiids [9], and is also shown by the relative increase in medial condyle size seen in larger xenarthrans [4]. The line of action of these forces passes medial to the femoral shaft and so probably leads to coronal plane bending forces acting on the femur; these are probably greater in larger specimens [4]. However, in the single support phase of locomotion (i.e. when the contralateral limb is off the ground, and the loads on the femur are maximal), the hip abductors of the stance/supporting limb are probably active to prevent uncontrolled adduction at the hip as occurs in humans [10,11]. The action of the abductors (gluteus medius and minimus) probably increases coronal plane bending stresses in the femur. It is at this stage in the locomotor/gait cycle that we propose that muscles attaching on the T3 act to modulate the bending stresses in the femur.

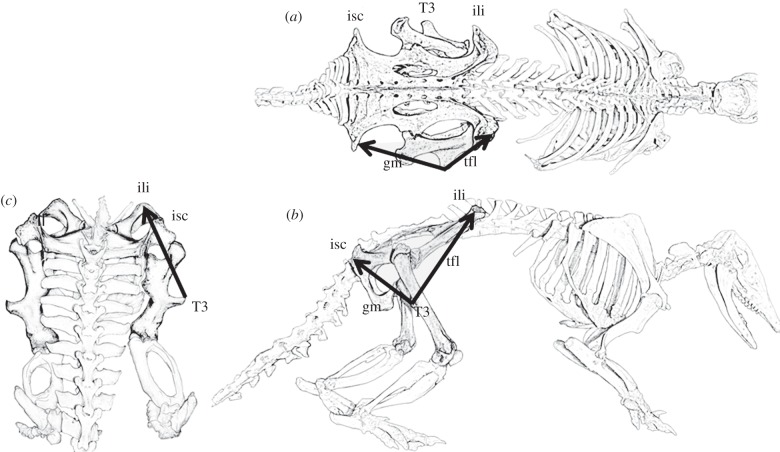
The muscles that attach to T3 in xenarthrans are the gluteus maximus (gluteus superficialis; [12]) and the tensor fasciae latae (TFL) muscles (with TFL extending its attachment into the fascia lata). These form a superficial sheet that arises posteriorly from the dorsal tuberosity of the ischium, and anteriorly from the tuberosity of the ilium and from the fascial sheet that connects these points (figure 1) [12–14]. These are the same muscles that insert into the iliotibial tract in humans. Rybicki et al. [15] showed that tension in the iliotibial tract can effectively counteract bending stresses in models of the human femur. It may be that these same muscles have a similar function in the xenarthran specimens under study here.

Figure 1.

Diagrams of a mounted armadillo specimen (Dasyopus hybridus). The gluteus maximus (gm) and tensor fasciae latae (tfl) muscles and their attachments to the tuberosities of the ischium (isc) and ilium (ili) are indicated in the (a) superior and (b) lateral views. (c) The posterior view shows the probable combined direction of pull of the muscles attaching to the third trochanter (T3).

This study therefore aims to apply finite element analysis (FEA) to test in an armadillo and glyptodont femur the null hypotheses that: (i) longitudinal forces acting on the femur do not induce coronal bending strains in the femur; (ii) if falsified, that abductor muscles acting on the greater trochanter do not increase these coronal bending strains; (iii) muscles acting on the T3 do not reduce bending strains in the femur; and (iv) if (i–iii) are falsified, in the glyptodont specimen, where the T3 is located more distally, the action of T3 muscles has no greater effect in reducing bending in the femur. If these hypotheses are falsified, then the study will have identified a novel mechanism, whereby a simple variation in musculoskeletal form effectively mitigates the impact of increased body mass on bony stress magnitudes.

2. Material and methods

One femur from an armadillo (Chaetophractus villosus, 69 mm long) was computed tomography (CT) scanned (1 mm slices with a resolution of 0.1145), and a fossil femur from a glyptodont (Neosclerocalyptus sp. MACNPv 18107, about 394 mm long) was CT scanned (2 mm slices with a resolution of 0.586 mm). The CT stacks were segmented in Amira v. 4.1.1 (Mercury Computer Systems Inc., USA). A low threshold was used so that much of the cancellous bone in the epiphyses was treated as solid material, but the model retained the empty space in the shaft. Extraneous features, including remnants of the cruciate ligaments in the armadillo scans and sediment that had accumulated in the diaphysis of the glyptodont femur were removed. The glyptodont femur also had a small crack on the upper end of the shaft posteriorly, and the cortical bone had been eroded over an area near the knee. These regions were repaired in the segmentation and reconstruction process. The digitally reconstructed armadillo and glyptodont femora were down-sampled to make models with similar numbers of voxels; 0.4 and 2 mm cubic voxels, respectively. The three-dimensional volume data for the two models were exported as bitmap stacks and then converted to eight-noded linear brick finite element meshes by direct voxel conversion. The resulting armadillo femur model had approximately 83 000 elements and the glyptodont 129 000 elements (figure 2). Prior exploratory studies, using the armadillo femur indicated that the results obtained from FEA, were almost identical with variations in voxel side length between 0.2 and 0.8 mm.

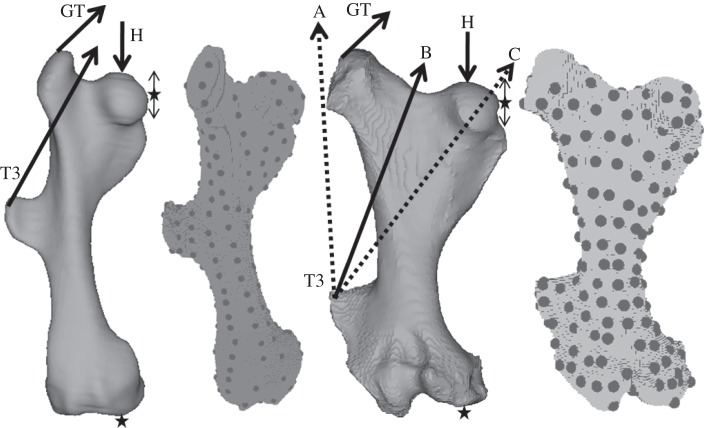
Figure 2.

The armadillo and glyptodont femur models showing the constraints (stars) and forces applied (arrows). Also shown are the finite element models with the 200 landmarks placed on the surface. The dotted arrows (A and C) are alternative force directions for the T3 load.

The FEAs were performed using the non-commercial FEA software Vox-FE [16]. The models were assigned isotropic material properties within the range of published values for bone (17 GPa for Young's modulus and a Poisson's ratio of 0.3). They were constrained in the x-, y- and z-directions at an area on the distal surface of the medial femoral condyle, and also in the x- and y-directions on the medial surface of the femoral head, thus enabling the head to move up and down under load. A compressive force was applied to the upper surface of the femoral head, and that force was directed through the centre of the constrained area of the medial femoral condyle. A force representing the lesser gluteal muscles was applied to the superolateral part of the greater trochanter and that force was directed superomedially in the coronal plane at an angle of 45° above the horizontal (figure 2). Forces were also applied to the lateral aspect of the T3 and directed in a line that passed between the head and the greater trochanter (figures 1 and 2 force ‘B’). Figure 1 shows lateral, posterior and superior views of an articulated armadillo skeleton (Dasypus hybridus). The muscles attaching to the T3 (gluteus maximus and TFL) are marked, and in the posterior view the proposed net line of pull of the T3 muscles is shown. In addition, to assess sensitivity, two additional lines of action for these muscles were used in the finite element modelling (see later text).

The three forces applied were the same magnitude within each model: 60 N for the armadillo and 3000 N for the glyptodont. A force of 60 N was chosen for the armadillo because that is approximately twice the body mass. The estimated body mass of Neosclerocalyptus is about 300 kg, but the force of 3000 N (equal to estimated body mass) was chosen so that the load on the femora produced similar levels of strain (deformation) in the femoral shaft to that seen in the armadillo. The extent to which loads are comparable between models is not important in relation to this study because we are concerned with bending and unbending irrespective of degree. The constrained or loaded areas in the armadillo and glyptodont specimens were selected to be similar in anatomical location and relative area in each model. The models were solved to equilibrium on a personal computer.

Two hundred landmarks were placed on the surface of the models using Amira (figure 2). After each load case was applied the new coordinates of each landmark were extracted. For each model, three load cases were used; first, the head load was applied, next the greater trochanter load was added and finally the T3 load was added. With the glyptodont model, some additional sensitivity analyses were carried out where the loads were each applied individually and also where the direction of the T3 load (B) was altered to pass outside the line of the greater trochanter (A) and through the femoral head (C; see figures 1 and 2 for explanation of loads A, B and C).

The results are presented in the form of strain maps for each model and load condition, and the three-dimensional coordinates of the 200 landmarks in each load case were submitted to geometric morphometric (GM) analysis to compare the sizes and shapes of unloaded and loaded models in each femur separately. The approach is described in detail by O'Higgins et al. [17] but here we use a modified approach that simultaneously accounts for differences in both size and shape. This is because under loading, landmarks displace, leading to differences in the form (size and shape components) of the configuration; the forces generate changes in both components of form. In terms of mechanics, differences in both size and shape arising from loading are of equal interest; indeed, it makes little sense to partition form into these components. Thus, to preserve the weighting of both, we omit the scaling step prior to registration and carry out analyses using the resulting size and shape variables [18,19]. While this omission of the scaling step does not lead to specimens being represented in the well-behaved shape space that results from Procrustes superimposition, the fact that the deformations resulting from FEA are very small mitigates the impact of variations in size on such things as the estimation of means.

We carried out a registration of coordinate data in which we translated and rotated landmark configurations to minimize the sum of squared distances among landmarks. This removes rigid body displacements arising from FEA and produces size and shape variables. Size and shape distances among unloaded and loaded models are computed by Pythagoras, and principal component analysis (PCA) of size and shape variables is carried out to complement the strain based analyses. The aspects of size and shape variation described by each principal component (PC) can be visualized, facilitating interpretation of PC plots in terms of deformations of the models. We visualized these deformations as warped rendered surface models together with a transformation grid computed using a triplet of thin plate splines [18]. It should be noted that the grid is simply a device to facilitate interpretation of the deformation induced by loads; it does not reflect the true deformation throughout the material between landmarks. Morphologika² [20] and the Evan toolbox (www.evan-society.org) were used for the GM analysis.

In order to directly compare the deformations in the armadillo and glyptodont models, a subset of 40 homologous landmarks [4] was used. In this case, the landmark coordinates were first scaled translated and rotated (GPA) to register the load cases for each model together. The remaining differences between the coordinates of the 40 landmarks in each loaded condition and the unloaded state were then added to the mean shape of the armadillo and glyptodont unloaded model to facilitate exploratory visualization, and the resulting shapes were rescaled according to the ratio of centroid sizes between loaded and unloaded to ‘restore’ size changes owing to loading. The resulting coordinates representing isometrically scaled displacements in each model were then submitted to a size and shape PCA of both femora.

3. Results

Strain maps for the three load cases of the armadillo and glyptodont models (figure 3) show that the head load (column 1) induces bending in the femoral shaft (compressive strains medially, tensile laterally). When the greater trochanter load is added to the head load (column 2), the bending of the femoral shaft is increased, as indicated by high tensile strains on the lateral side and compressive strains on the medial side of the shaft, both in the armadillo and the glyptodont. The third column in figure 4 shows that when the T3 load is added to the head and greater trochanter loads, the bending in the femoral shaft is reduced. This reduction in bending of the femoral shaft is reflected in the reduced strain gradients across the femoral shaft at the level above the T3. In columns 2 and 3 of figure 3 there are, of course, high local strains associated with the forces applied to the trochanters. In the armadillo where the T3 is halfway along the femoral shaft the T3 loads do not effectively reduce the bending loads below the level of the T3.

Figure 3.

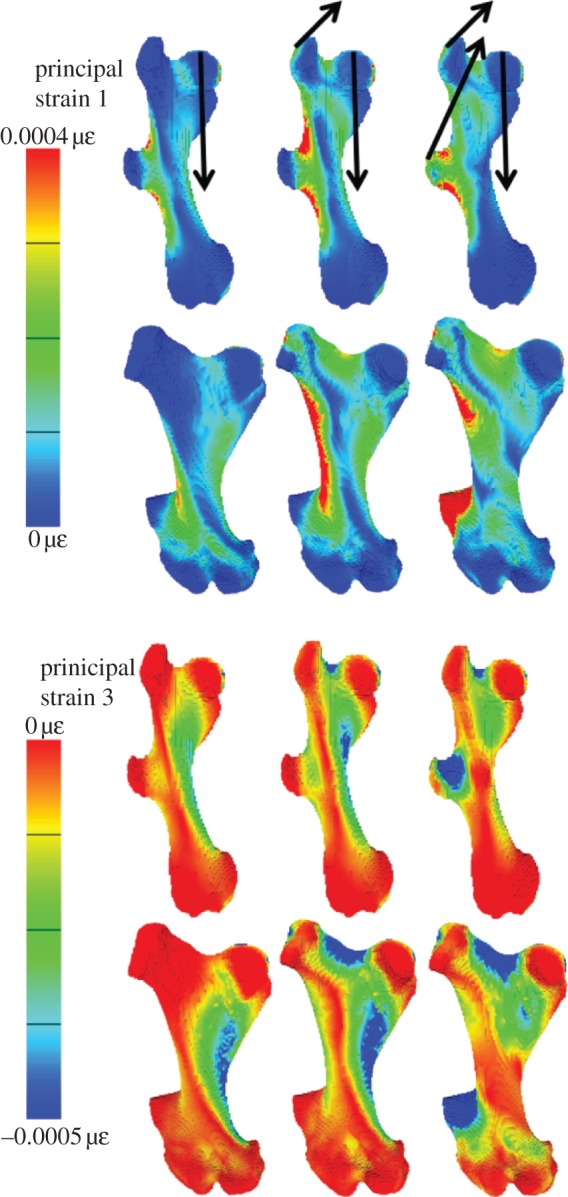
Strain maps of principal strains 1 (tension) and 3 (compression) for the armadillo and glyptodont femoral models. The arrows in the top row indicate the loading conditions for each column. For the armadillo, the forces are all 60 N and for the glyptodont they are 3000 N. Note that in the strain magnitudes colour key, more tensile strains are red and more compressive, blue.

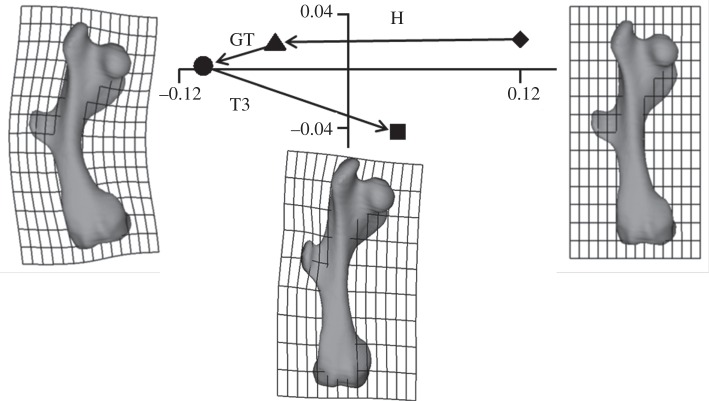
Figure 4.

Gluteus maximus analysis of the armadillo load cases. PC1 (90.3%) and PC2 (9.6%) from a size and shape space analysis of the coordinates of the 200 landmarks. The shapes to the left and right show the shape change in the model associated with PC1, and the shape below the plot indicates the deformation related to PC2. These deformations are exaggerated by a factor of approximately 100 to aid visualization. Diamond denotes unloaded; triangle denotes head load; circle denotes head plus greater trochanter load; square denotes head load plus greater trochanter plus T3 load.

The GM analyses of the deformation of the armadillo (figure 4) and glyptodont (figure 5) femoral models show that while the head and greater trochanter loads cause the femur to bend, addition of the T3 load reduces this. Further, this effect is larger in the glyptodont model than the armadillo model. That is, in the glyptodont model, the T3 loads produce a deformation that is larger than the combined head and great trochanter loads, whereas in the armadillo the deformation caused by the T3 load is smaller than the deformation resulting from the head load alone and much smaller than the effect of combined head and greater trochanter loads. Both in figures 4 and 5, there is a substantial effect seen in PC2. Both in the armadillo and glyptodont models, this deformation involves local bending within, and in the immediate vicinity of, the greater and third trochanters.

Figure 5.

Gluteus maximus analysis of the glyptodont load cases. PC1 (80.4%) and PC2 (16.7%) from a size and shape space analysis of the coordinates of the 200 landmarks. The shapes to the left and right show the shape change in the model associated with PC1, and the shape below the plot indicates the deformation related to PC2. These deformations are exaggerated by a factor of approximately 100 to aid visualization. Diamond denotes unloaded; triangle denotes head load; circle denotes head plus greater trochanter load; square denotes head plus greater trochanter plus T3 load.

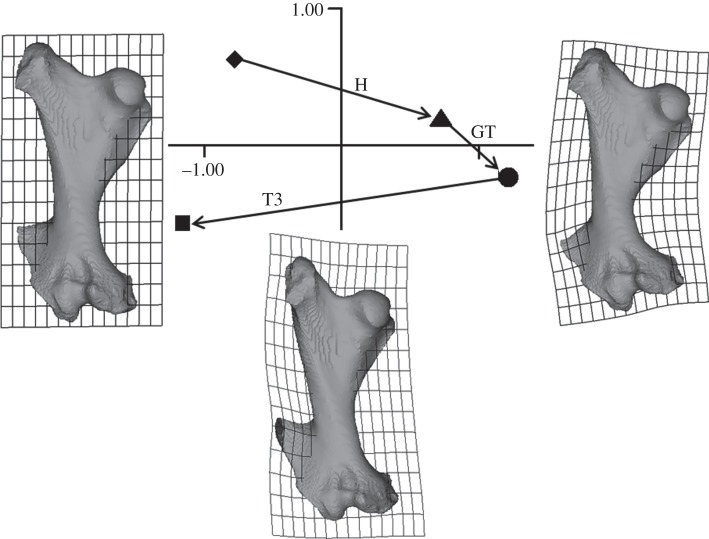
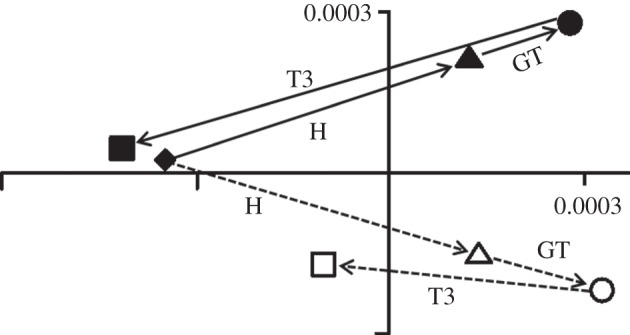
Figure 6 shows the effects of altering the direction of the T3 force. It also shows how combined loads are the vector sum of simple loads. For example, the point representing the combined head and greater trochanter load (open circle) is located at the point that is the sum of vectors H and GT (closed triangle and circle). Similarly, the open squares are located at the vector sums of the loads applied. Vectors H and T3B combined to produce the eventual form of the femur represented by the leftmost open square, and vectors H, GT and T3B, the rightmost open square. Changing the direction of the T3 load to either pass through the femoral head or lateral to the greater trochanter has an effect on the deformation caused by this load (figure 6). The load passing through the femoral head (C) is most effective, and the load passing lateral to the greater trochanter (A) is least effective at countering the bending produced by head and greater trochanter loads. The greater trochanter force direction used in the remainder of this study (and the open squares in figure 6) is the intermediate (B) direction.

Figure 6.

Simple and complex loads on the glyptodont femur. PCs 1 and 2 (91.8% and 5.4%) from a size and shape analysis of head load (filled triangle and vector H), greater trochanter load (filled circle and vector GT) and T3 loads (filled squares and T3 vectors for the three force directions indicated in figure 2). The open shapes represent the deformations caused by compound loads: greater trochanter load in addition to a head load (open circle) and T3 loads (T3B) added to head load or head load plus greater trochanter load (open squares). All the loads applied are the same (3000 N). The shapes with transformation grids show the shape change in the model from the unloaded state (diamond, shape not shown) to the loaded states with deformed grids representing shape change on PC1 on the left and right of the plot. These deformations are exaggerated by a factor of approximately 100 to aid visualization.

When the deformations caused by the armadillo and glyptodont load cases are viewed in the same GM analysis (figure 7), the results confirm the findings in the separate analyses (figures 4 and 5). The figure shows that the 60 and 3000 N head, and greater trochanter loads on the armadillo and glyptodont models, respectively, produce similar amounts of bending (along PC1) in the two models, however, their directions in the plot of PC1 versus PC2 are somewhat different, indicating differences in aspects of how they bend. T3 loads produce much more (un)bending in the glyptodont than the armadillo model. Thus, T3 load in the armadillo (open shapes) reduces the amount of bending produced by the head and greater trochanter loads, whereas in the glyptodont model (closed shapes), the T3 load completely reverses the bending produced by the other loads.

Figure 7.

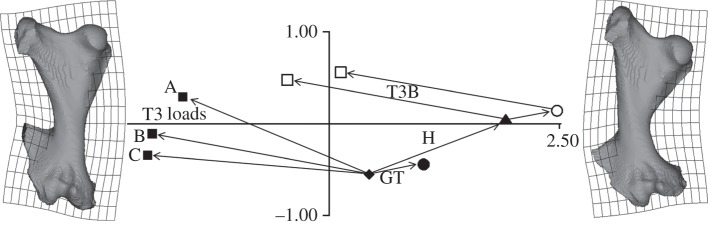
Armadillo and glyptodont deformations compared. PC1 (63.8%) and PC2 (18.6%) from a size and shape space analysis of the displacements of the 40 homologous landmarks on both armadillo and glyptodont femora. The unloaded states were averaged and the deformations recalculated to show a direct comparison of the two models. Diamond denotes unloaded (for both Glyptodont and armadillo); triangle denotes head load; circle denotes head plus greater trochanter load cases; square denotes head plus greater trochanter plus T3 loads. The filled shapes and solid lines are the glyptodont, and the open shapes and dotted lines are the armadillo models.

4. Discussion

In our models of armadillo and glyptodont femora, forces simulating the muscles applied to the T3 counter the femoral bending caused by the action of longitudinal forces acting through the head and abductor forces on the greater trochanter. This effect is more pronounced in the glyptodont where the T3 is located closer to the knee than in the armadillo where the T3 is located proximal to the mid-shaft. The findings falsify our initial null hypotheses and are consistent with the predictions of Milne et al. [4].

The medial condyle was chosen as the site of the knee constraint, because in xenarthrans, the medial condyle appears to bear the majority of the load at the knee [4,7–9,12]. The sliding constraint on the medial side of the femoral head represents the pelvis and prevents the femoral head from being deflected medially by the forces applied. The line of action of the T3 loads was chosen based on observations of mounted skeletons of armadillos (figure 1) and glyptodonts. The TFL and gluteus maximus force directions are angled in front of and behind the coronal plane, but this study considers only their actions in the coronal plane. Given the uncertainty in determining the coronal plane force direction of muscles attaching to the T3, we assessed the effects of alternative force directions, and all tended to reduce bending strains in the femoral models. Clearly, the more horizontal force directions (B and C) produced more bending strain relief.

During the single support phase of locomotion, when the opposite hindlimb is off the ground, gravity and ground reaction forces produce strong adduction moments at the hip. These adduction moments are countered by the abductors of the hip that attach to the greater trochanter. Our study assesses the extent to which the muscles attaching to the T3 (if also active at this time) act to reduce the coronal plane bending caused by the action of the longitudinal forces on the femur together with the hip abductors. No electromyographic studies have been conducted on living armadillos, whereas in humans it is well established that the lesser gluteal muscles attaching to the greater trochanter are active [10,11], and the iliotibial tract is tense owing to contraction of TFL [21,22] during the stance phase of locomotion. In the human femur, the tension in the iliotibial tract reduces bending stresses that result from axial loading and the action of the abductors [15,23,24]. Indeed, it has been widely suggested that bones are adapted to have minimal bending or torsional stresses during normal function, and that the net effect of muscles and loading produces axial compression with minimal bending [25–27].

The head loads applied to the two models were chosen to produce similar deformations of the femoral model. Head and greater trochanter loads result in similar strain magnitudes in both femora (figure 3). Large-scale bending is also comparable in degree as can be seen in figures 4 and 5 and in the combined PCA (figure 7). It is interesting that the very different relative magnitudes of the loads used in each model produced similar deformation in both models. Thus, the head load in the armadillo, 60 N, represents about twice the body weight of C. villosus [5], whereas in the glyptodont, 3000 N was required to produce a similar degree of bending. This load represents the estimated body weight of Neosclerocalyptus [28–30]. Clearly, if loads equivalent to body mass were applied to models, then the glyptodont femur would be bent much more than the armadillo. This suggests that the glyptodont femur is much less stiff in relation to its body mass than is the armadillo. This discrepancy is interesting from the perspective of scaling [1,2] in that the robusticity/cross-sectional area of the shaft does not increase according to the scaling relationship expected with body mass to maintain constant stress. As Biewener [2,3] has noted, this expected scaling is commonly not found to be the case because larger animals often adopt different postures that result in lower bending stresses. Thus, the differences we find in relative loads required to generate similar bending in the armadillo and glyptodont may, in part, indicate differences in hind limb posture. However, our findings demonstrate an additional, but related, mechanism, whereby larger animals may reduce stress and thus economize on bone mass. Thus, T3 loads produce much greater ‘unbending’ of the femur in the glyptodont than in the armadillo as a result of the different position of the T3 in the two specimens. This is because in the armadillo the T3 projects from the femoral shaft a little above the midpoint, whereas in the glyptodont it projects from the distal end of the shaft close to the knee. The Neosclerocalyptus specimen used in the present study is by no means the largest glyptodont. Other fossils have been found that are up to six and half times heavier (28–30) and in those the T3 is also close to the knee. It would be interesting to apply the present kind of analysis to a femoral specimen of, for example, Glyptodon clavipes [28]. This is particularly the case because Fariña [28] has reported that this glyptodont may have used bipedal locomotion at least some of the time; subsequently, another study [30] has explored the possibility that other glyptodonts were also capable of facultative bipedalism.

When the deformations relating to each load case are examined using GM analyses, large-scale deformations can be usefully compared. Thus, it is easy to see that greater trochanter loads deform the models at large scales in a similar way to the longitudinal loads applied to the femoral head (figures 4–7). It is also easy to see that the T3 loads act in opposition to head and greater trochanter loads. By placing the two models in the same GM analysis (figure 7), it is straightforward to compare the effects of the loadings in the two models and adjust loads so that they produce similar deformations. Further, figure 6 shows that the GM analysis of the deformations has some interesting properties. For example, the load case where two forces are applied plots in a location in the graph that is the vector sum of the two forces applied individually. The same is true if three forces are applied as seen in figure 6 and the associated description in §3. As a corollary of this observation, if the force applied is doubled, then the vector of deformation in the size and shape space shows doubling of the distance from the undeformed model while the direction is unchanged. Doubling and summing as described for the GM analysis of deformations also applies to stresses and strains when comparing results from models with isotropic materials and the same constraints. However, using strain maps, while it is easy to see the regions of maximum strain, it is more difficult to translate this information into a visualization of large-scale deformations and to appreciate the subtle differences in deformation that are clearly evident in the PCA. Conversely, GM methods do not easily lead to appreciation of regions where deformation is maximal (strains largest). The methods are complementary.

This study aimed to test a number of hypotheses pertaining to bending and ‘unbending of an armadillo and a glyptodont femur. Our findings falsify hypotheses that: (i) longitudinal forces acting on the femur do not induce coronal bending strains in the femur; (ii) abductor muscles acting on the greater trochanter do not increase these coronal bending strains; and (iii) muscles acting on the T3 do not reduce bending strains in the femur. As such our models have shown that the bending that would otherwise be induced in the femora of these animals during the stance phase by body weight and the lesser gluteals can be mitigated by simultaneous action of the muscles attached to T3. Further, we falsify hypothesis (iv) by showing that in the glyptodont specimen, where the T3 is located distally, the action of T3 muscles has a greater effect in mitigating bending in the femur than in the armadillo, where T3 is more proximal. Given that the T3 in glypotodonts is more distal than that in armadillos, our findings point to a novel mechanism whereby the need for a stiffer femur to resist medial bending is met through muscle action, rather than increased bone mass in larger animals, thus minimizing skeletal mass.