Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2012 May 23;279(1742):3491–3500. doi: 10.1098/rspb.2012.0683

Phylogenomic datasets provide both precision and accuracy in estimating the timescale of placental mammal phylogeny

Mario dos Reis 1, Jun Inoue 1,2, Masami Hasegawa 3, Robert J Asher 4, Philip C J Donoghue 5,*, Ziheng Yang 1,*
PMCID: PMC3396900  PMID: 22628470

Abstract

The fossil record suggests a rapid radiation of placental mammals following the Cretaceous–Paleogene (K–Pg) mass extinction 65 million years ago (Ma); nevertheless, molecular time estimates, while highly variable, are generally much older. Early molecular studies suffer from inadequate dating methods, reliance on the molecular clock, and simplistic and over-confident interpretations of the fossil record. More recent studies have used Bayesian dating methods that circumvent those issues, but the use of limited data has led to large estimation uncertainties, precluding a decisive conclusion on the timing of mammalian diversifications. Here we use a powerful Bayesian method to analyse 36 nuclear genomes and 274 mitochondrial genomes (20.6 million base pairs), combined with robust but flexible fossil calibrations. Our posterior time estimates suggest that marsupials diverged from eutherians 168–178 Ma, and crown Marsupialia diverged 64–84 Ma. Placentalia diverged 88–90 Ma, and present-day placental orders (except Primates and Xenarthra) originated in a ∼20 Myr window (45–65 Ma) after the K–Pg extinction. Therefore we reject a pre K–Pg model of placental ordinal diversification. We suggest other infamous instances of mismatch between molecular and palaeontological divergence time estimates will be resolved with this same approach.

Keywords: divergence time, fossil, mammal, Bayesian analysis

1. Introduction

Controversy over the timing of placental mammal diversification relative to the Cretaceous–Paleogene, (K–Pg) mass extinction event ignited debate over the veracity of palaeontological versus molecular approaches to divergence time estimation [1]. Fossil representatives of crown placental orders appear in the 16 Myr (million years) interval following the K–Pg extinction [2], indicating a diversification peak between 65 and 60 Ma (millions of years ago) [3], and consistent with a Paleogene radiation of placentals after the sudden disappearance of non-avian dinosaurs and other species during the mass extinction event [4]. Early molecular studies (most notably [5], see also [6]) found ancient dates of origination of placental mammals, pre-dating the K–Pg extinction. Although it is expected that the earliest fossil evidence for a divergence will postdate the event itself, the time lag between these molecular time estimates and the placental mammal fossil record has been considered unacceptably large [7,8].

Archibald & Deutschman [2] proposed three models of placental mammal diversification with respect to the K–Pg event and their relationship to the fossil record. In the explosive model, the last common ancestor of Placentalia originated and diversified in the Paleogene. In the long-fuse model, the ancestor of Placentalia originated in the Cretaceous but intraordinal diversification (the evolution of new families and genera within orders) occurred in the Paleogene, agreeing with fossil finds of modern orders postdating the K–Pg event, but acknowledging an ancient origin for Placentalia. Finally, in the short fuse model, several placental orders diversified in the Cretaceous shortly after the origination of Placentalia, with the others diversifying in the Paleogene. This last model implies that Middle- and even Early Cretaceous crown placental mammals existed, but have not yet been recovered from an otherwise diverse mammalian fossil record. Palaeontological interpretations of crown placental lineages deep within the Cretaceous [9,10] have been contested on phylogenetic and anatomical grounds [11–13].

Nevertheless, the fossil record provides only a minimum estimate for the antiquity of a given clade, and molecular clock studies contradict the explosive model of a Paleogene origin for Placentalia. Some of these studies date the origin of Placentalia at more than 100 Ma, deep within the Cretaceous [5,14–17]. Others indicate a younger (ca 80–90 Ma) Cretaceous last common ancestor for Placentalia [18,19]. Although molecular studies have agreed on a Cretaceous origin for Placentalia, they disagree on the extent of ordinal level diversification relative to the K–Pg event. For example, a supertree-based molecular study of over 4000 mammal taxa by Bininda-Emonds et al. [16] found that half of the placental orders originated deep in the Cretaceous, much earlier than any known fossil record of those groups. However, this study employed a heuristic time estimation method that does not account appropriately for lineage rate variation, used a point fossil calibration for the mammalian root, and did not account for uncertainty in branch length estimation. More recently, Meredith et al. [17] used a supermatrix of 164 taxa and 26 genes, and found younger dates of intraordinal diversification, with five placental orders presenting large credibility intervals extending from the Early Cretaceous to the Late Paleocene. However, the limited statistical power afforded by the small sequence dataset resulted in error margins on divergence time estimates that are too broad to determine whether placental diversification occurred mainly in the Cretaceous or in the Paleocene (i.e. short versus long fuse models).

Here we take advantage of the whole genome sequence data now available for tens of mammal species [20], together with multiple, fossil-based temporal constraints encompassing the breadth of mammalian phylogeny [21], to establish a refined timescale for the placental mammal evolution. We use a Bayesian approach that integrates over the uncertainty in rate variation along the phylogeny and facilitates analysis of very large alignments [22–24]. In a Bayesian analysis, fossil constraints impose a theoretical limit on the precision of posterior time estimates [22,25]. We set out to determine whether current genome scale data are enough to approach this theoretical limit, and whether the precision achievable in divergence time estimation is sufficient to confidently reject the hypothesis of post K–Pg diversification of placental mammal orders.

2. Methods

Our analysis was performed in two stages. First, we performed Bayesian estimation of divergence times on a set of 14 632 nuclear gene alignments (20.6 × 106 base pairs) for 36 mammalian species (33 placentals, two marsupials and one monotreme). In the second stage, the posterior probability of divergence times obtained in the first stage was used to construct the time prior for an analysis of the 12 protein genes encoded on the heavy strand of the mitochondrial genome of 274 mammal species, and Bayesian estimation of divergence times proceeded on this dataset. The result is effectively a combined analysis of nuclear and mitochondrial genomes.

(a). Taxon sampling, molecular data and tree topology

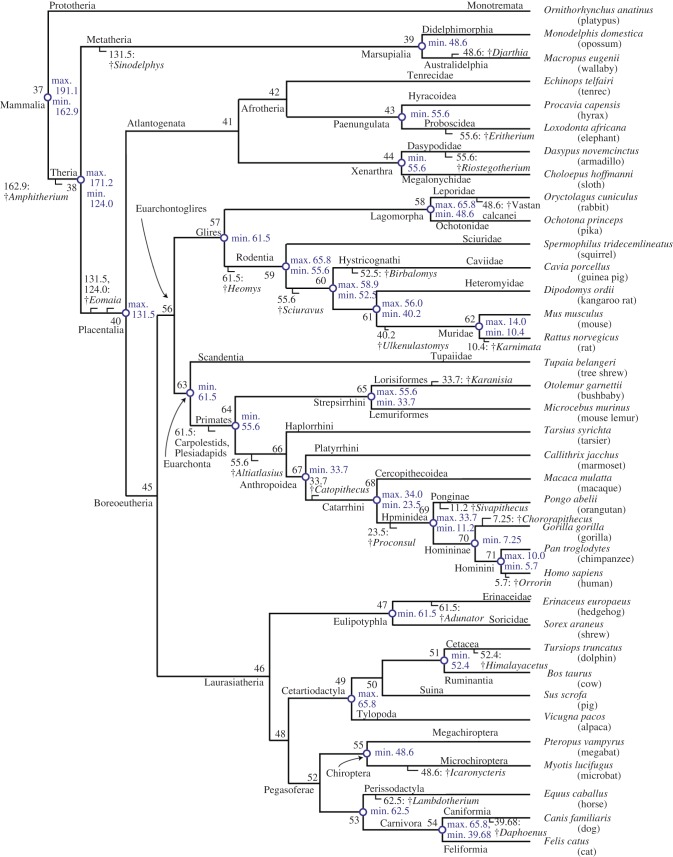
Confirmed and predicted copy DNA (cDNA) sequences for the 36 mammalian genomes were downloaded from Ensembl v. 56. The Ensembl database provides detailed information about orthology and paralogy for the mammalian genome [20]. A rooted tree was constructed based on the literature [26,27]. The tree and species list are presented in figure 1. Only gene sequences identified as one-to-one orthologues between human and the remaining 35 species were analysed, and only the longest splicing variant for each cDNA sequence was considered. The mitochondrial genome sequences from 274 mammal species were downloaded from GenBank. The list of 274 mammal species and their tree topology are given in the electronic supplementary material, figure S1.

Figure 1.

Figure 1.

Open in a new tab

The tree of 36 mammal species showing fossil calibrations. Calibration bounds are soft; that is, the probability that the true divergence time is outside the bounds is small but non-zero. Internal nodes are numbered from 37 to 71. The tree topology follows the literature [26,27]. The ‘dagger’ symbol shows a species which is extinct.

Amino acid sequences for the nuclear genomes were aligned using PRANK [28] according to the rooted guide tree. The following gene alignments were discarded: genes that did not have a mouse orthologue, genes for which sequences could be found for fewer than 10 of the 36 species and genes shorter than 100 codons. Furthermore, for each gene alignment, a phylogentic tree was estimated by maximum likelihood (ML) using RAxML v. 7.2.1 [29]. Alignments where at least one sequence was associated with an unusually long external branch (that accounted for more than 60% of total tree length) were also removed. This left a dataset of 14 632 nuclear gene alignments. The amino acid sequences were reverse translated to generate DNA alignments. For the mitochondrial genomes, only the 12 protein genes encoded on the heavy strand were analysed. Amino acid and DNA alignments were generated as for the nuclear gene dataset. The tree topology for the 274 species was estimated with RAxML using the 36 species tree as a guide tree. Well-supported marsupial, bovid, carnivoran, pholidote, euarchontan and chiropteran clades identified from the literature were fixed into the guide tree [26,30–34].

The 14 632 nuclear gene alignments were divided into 20 partitions based on the relative substitution rate, with about the same number of genes in each partition. Because the number of species within each alignment varies from 10 to 36, we measured the relative rate by the p-distance between amino acid sequences of human and mouse. The 12 protein genes in the mitochondrial alignment of 278 species were treated as a single partition. Third codon positions in both the nuclear and mitochondrial alignments were excluded from all dating analyses.

(b). Bayesian divergence time estimation

The analysis of divergence times was conducted using the program MCMCTree v. 4.4e [35]. Exact calculation of the likelihood function during Markov chain Monte Carlo (MCMC) iteration is computationally expensive, and so we used the approximate method [24,36]. First we calculated the maximum-likelihood estimates of the branch lengths, the gradient vector and Hessian matrix, using the BaseML and CodeML programs [35]. We used branch-by-branch optimization, as it provided quick convergence for the large datasets. We used the HKY + Γ4 model [37,38] for the DNA datasets, the WAG + F + Γ4 model [39] for the nuclear encoded proteins and the MTMAM + F + Γ4 model [40] for the mitochondrial proteins. The second step uses an MCMC algorithm to estimate divergence times on the tree topology. The gradient vector and Hessian matrix are used to generate the Taylor expansion of the log-likelihood. This approximation saves much computation time during the MCMC on large alignments.

The auto-correlated rates model [22,36] was used to specify the prior of rates. The time unit was 100 Myr. We used a diffuse gamma prior G(1, 1) for the overall substitution rate, with mean 1, meaning 10−8 changes per site per year. The rate drift parameter σ2 was assigned G(1, 1). Parameter σ2 reflects the amount of rate variation across lineages or how seriously the molecular clock is violated. The parameters of the birth–death process with species sampling were fixed at λ = μ = 1 and ρ = 0. We tested a series of informative priors on the overall rate based on rough rate estimates obtained by fitting a molecular clock to the sequence data using point calibrations. However, these priors did not affect estimated posterior times noticeably, possibly because the fossil calibrations, which occur throughout the phylogeny, constrain the time prior. The number of iterations, the burn-in and the sampling frequency were determined in test runs of the program. Every analysis was conducted at least twice to ensure convergence of the MCMC.

(c). Fossil calibrations and time prior

We used 26 fossil calibrations on the 36 species tree: 12 joint (maximum and minimum), two maximum and 12 minimum bounds (figure 1 and electronic supplementary material, table S1). Both minimum and maximum bounds were ‘soft’, that is we set the probability that the true divergence time is outside the bounds to be small, but non-zero, allowing molecular data to correct for conflicting fossil information [25]. Minimum bounds are represented using truncated Cauchy distributions [41] with a left tail probability of 0.1 per cent. For maximum and joint bounds, the default 2.5 per cent tail probability was used. MCMC runs were carried out without using the sequences to estimate the time prior and to check for consistency with the fossil calibrations.

The marginal posterior of divergence times obtained from the 14 632 nuclear gene dataset was used to construct the time prior for the 274 species mitochondrial gene dataset. A Skew-t distribution was fitted by ML to each posterior node age in the 35 species tree (sm package, R), and used as calibrations for the appropriate nodes in the 274 species tree. The Skew-t distribution is very flexible, and can approximate a range of unimodal distributions with arbitrary skewness and kurtosis. This effectively results in a combined analysis of nuclear and mitochondrial genes to estimate divergence times. A simultaneous multi-partition analysis, with the mitochondrial proteins in one partition, and the 14 632 nuclear genes arranged in several partitions, would have been the ideal way to estimate divergence times for all 274 species. However, such an analysis would have been computationally expensive (many months) with the current MCMCTree implementation.

(d). Data partitioning

A total of 857 of the nuclear genes are present in all 36 mammalian genomes. We used this data subset for several exploratory analyses and so we analysed these genes in a single partition as an amino acid alignment and as a nucleotide alignment. We then explored two partitioning strategies. In the first, we divided the 857 genes into 10 or 20 partitions with approximately the same number of genes according to their relative substitution rate, measured by the tree length (sum of branch lengths) on the tree of figure 1. Branch lengths for each gene were estimated with RAxML using the GTR + Γ model.

In the second strategy, we used principal component analysis (PCA) on the branch lengths, and k-means clustering on the PCA components to generate the partitions. For each nucleotide alignment of first and second codon positions, the branch lengths were estimated by ML with RAxML using the GTR + Γ substitution model on the fixed tree. We constructed a matrix of absolute branch lengths, B = (bij), with 857 rows and 2 × 36 − 3 = 69 columns (trees are unrooted), and a matrix of relative branch lengths, R = (rij) where 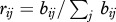Inline graphic. 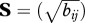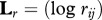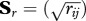Four transformed matrices were constructed L = (log bij), Inline graphic, Inline graphic and Inline graphic. On each one of the four transformed matrices, a PCA was performed to try to identify patterns in branch length variation across orthologues. The first principal component in the analyses using absolute branch lengths was highly correlated with total tree length. A robust version of the k-means clustering algorithm (PAM [42]) was used to group the 857 alignments into 10 partitions using the first two axes of the PCA.

3. Results and discussion

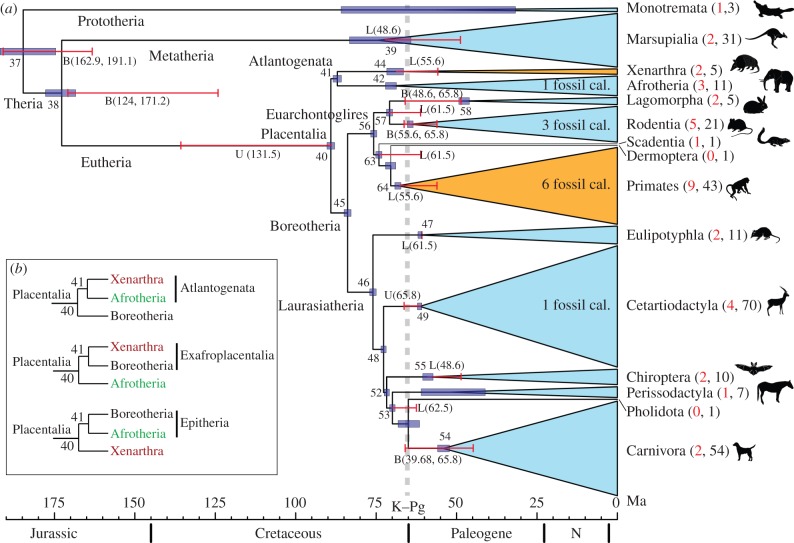
Our results are summarized in figure 2a and table 1. Detailed time estimates for the divergences in the 274-species tree are given in the electronic supplementary material, figure S1. We estimated the origin of placentals at 88–90 Ma, substantially younger than some previous estimates [5,14–16], but congruent with others [17–19]. With the exception of Xenarthra and Primates, placental orders diversified in the 20 Myr interval following the K–Pg extinction event. For example, within Laurasiatheria, the ancestral lineages of cats, dogs, bears, bats, horses, rhinoceros, whales, ruminants, pigs, camels, hedgehogs, moles and shrews are estimated to have originated by 45 Ma. However, the divergences of each of their crown parent clades (Cetartiodactyla, Carnivora, Chiroptera and Eulipotyphla) did not occur until after 62 Ma (figure 2a and the electronic supplementary material, figure S1). Similarly, diversification of the crown clades within Afrotheria, Euarchontoglires (except Primates) and even Marsupialia are estimated to have occurred soon after the K–Pg extinction event, with the establishment of morphologically diverse lineages within approximately 20 Myr (figure 2a and the electronic supplementary material, figure S1). Crown Primates and crown Xenarthra are estimated to have diverged just before the K–Pg event, at 69–67 Ma and 72–67 Ma, respectively, with the fundamental splits within these groups occurring well within the Paleogene (electronic supplementary material, figure S1).

Figure 2.

Figure 2.

Open in a new tab

The timetree of mammals. (a) Blue horizontal bars represent the posterior 95% CI for the node ages. Red horizontal bars represent fossil calibrations: U for upper (maximum), L for lower (minimum) and B for both. The number of species analysed is presented within brackets: red for nuclear and black for mitochondrial genomes. The two mammal orders that diversified before the K–Pg event are shown in orange. All orders within Afrotheria and Marsupialia diversified after the K–Pg event. The tree topology follows [26,27]. (b) The three possible topologies concerning the divergence of early Placentalia.

Table 1.

Prior and posterior divergence times for selected nodes in the mammal tree.

node marginal priora,d
 combined, 14 K + Mitb,d
 14 K, Atlantogenatac,d
 14 K, Epitheriac,d
 14 K, Exafroplacentaliac,d
37 root 177.7 (163.1, 191.2) 184.6 (174.1, 191.9) 185.0 (174.5, 191.8) 188.8 (182.5, 192.6) 184.1 (173.1, 191.7)
38 Theria 149.4 (125.7, 170.9) 172.8 (168.4, 177.8) 175.4 (170.4, 181.7) 184.9 (178.1, 190.4) 173.4 (169.0, 179.2)
39 Marsupialia 90.6 (50.8, 139.4) 75.1 (64.4, 84.0) 66.7 (50.7, 83.7) 64.9 (50.3, 86.0) 67.7 (51.4, 83.4)
40 Placentalia 124.1 (102.1, 139.2) 89.1 (87.9, 90.4) 89.9 (88.3, 91.6) 92.2 (90.4, 93.8) 92.2 (90.6, 93.8)
41 *e 113.3 (77.9, 134.4) 87.1 (85.8, 88.4) 87.5 (85.9, 89.1) 90.5 (88.8, 92.1) 90.2 (88.7, 91.7)
42 Afrotheria 95.1 (59.9, 129.2) 70.4 (68.7, 72.1) 70.4 (68.5, 72.4) 71.1 (69.1, 73.3) 73.1 (71.1, 74.8)
43 Paenungulata 75.9 (56.1, 117.3) 60.3 (58.4, 62.2) 59.8 (57.7, 61.8) 61.8 (59.7, 64.1) 64.5 (62.4, 66.2)
44 Xenarthra 86.5 (56.9, 126.0) 69.4 (66.5, 71.8) 70.0 (67.3, 72.4) 75.4 (72.3, 77.3) 72.7 (70.7, 74.8)
45 Boreotheria 120.5 (97.8, 136.6) 83.8 (82.8, 84.9) 82.4 (81.1, 83.8) 82.1 (80.7, 83.5) 82.7 (81.4, 84.0)
46 Laurasiatheria 114.6 (87.0, 133.9) 76.0 (74.9, 77.0) 76.0 (74.8, 77.1) 75.6 (74.4, 76.7) 75.7 (74.6, 76.8)
47 Eulipotyphla 91.7 (62.9, 126.4) 61.5 (60.9, 62.0) 61.3 (60.6, 61.8) 61.4 (60.6, 61.9) 61.5 (61.0, 62.1)
48 cow/horse 105.7 (74.1, 130.8) 72.7 (71.9, 73.6) 73.1 (72.0, 74.2) 72.8 (71.7, 73.8) 73.1 (72.1, 74.1)
49 Cetartiodactyla 63.6 (55.8, 70.4) 61.4 (60.8, 62.3) 61.4 (60.7, 62.3) 61.2 (60.5, 61.9) 61.1 (60.5, 61.8)
50 pig/cow 60.0 (53.4, 67.4) 58.1 (57.5, 58.9) 58.0 (57.4, 58.8) 57.8 (57.3, 58.5) 57.8 (57.3, 58.5)
51 dolphin/cow 56.6 (52.5, 64.5) 52.8 (52.3, 53.9) 52.7 (52.2, 53.7) 52.6 (52.2, 53.4) 52.5 (52.1, 53.2)
52 horse/cat/bat 96.0 (66.4, 126.7) 71.7 (70.8, 72.5) 72.2 (71.2, 73.3) 71.9 (70.9, 72.9) 72.1 (71.2, 73.2)
53 horse/cat 80.6 (63.0, 115.4) 69.9 (69.1, 70.8) 70.1 (69.1, 71.1) 69.8 (68.8, 70.8) 70.1 (69.2, 71.1)
54 Carnivora 53.2 (39.7, 65.7) 54.2 (52.3, 56.0) 54.1 (52.0, 55.9) 53.6 (51.6, 55.4) 52.9 (50.7, 54.9)
55 Chiroptera 71.1 (49.6, 111.0) 59.1 (57.7, 60.6) 59.3 (57.6, 60.8) 59.4 (57.9, 60.9) 60.3 (58.8, 61.7)
56 Euarchontoglires 114.0 (87.4, 133.3) 75.8 (74.9, 76.7) 75.8 (74.6, 77.0) 75.4 (74.2, 76.6) 75.5 (74.3, 76.6)
57 Glires 90.8 (64.0, 125.2) 70.8 (69.9, 71.8) 70.7 (69.6, 71.8) 70.5 (69.4, 71.6) 70.8 (69.7, 71.8)
58 Lagomorpha 57.5 (48.6, 65.8) 47.9 (46.0, 49.3) 47.8 (45.8, 49.3) 47.5 (45.4, 49.1) 46.7 (44.4, 48.6)
59 Rodentia 61.1 (56.0, 65.8) 64.4 (63.5, 65.3) 64.5 (63.4, 65.5) 64.2 (63.1, 65.2) 64.2 (63.1, 65.2)
60 guinea pig/rat 55.8 (52.5, 58.9) 61.3 (60.5, 62.2) 61.3 (60.3, 62.2) 61.1 (60.0, 62.0) 61.1 (60.1, 62.1)
61 kangaroo rat/rat 47.7 (40.2, 55.6) 56.0 (55.1, 56.8) 55.6 (54.4, 56.5) 55.3 (54.1, 56.3) 55.1 (53.9, 56.2)
62 mouse/rat 12.2 (10.4, 14.0) 14.0 (13.5, 14.4) 13.9 (13.2, 14.3) 13.9 (13.2, 14.3) 13.9 (13.4, 14.4)
63 Euarchonta 100.8 (69.4, 128.8) 74.1 (73.2, 75.1) 74.2 (73.0, 75.3) 73.8 (72.6, 75.0) 74.0 (72.9, 75.1)
64 Primates 81.9 (57.7, 115.1) 68.2 (67.3, 69.1) 69.0 (67.8, 70.1) 68.6 (67.4, 69.7) 68.4 (67.3, 69.5)
65 Strepsirrhini 44.9 (33.7, 55.7) 55.1 (53.4, 56.8) 54.3 (52.3, 55.8) 54.4 (52.5, 55.9) 54.9 (53.2, 56.2)
66 human/tarsier 64.1 (42.5, 99.5) 65.0 (64.0, 65.9) 65.0 (63.9, 66.0) 64.7 (63.6, 65.8) 64.7 (63.6, 65.7)
67 Anthropoidea 48.2 (34.3, 76.4) 37.4 (35.9, 39.0) 36.6 (34.9, 38.3) 36.1 (34.5, 37.7) 35.6 (34.1, 37.3)
68 Catarrhini 29.5 (23.7, 34.1) 26.4 (25.3, 27.4) 25.6 (24.4, 26.8) 25.3 (24.2, 26.5) 25.0 (24.0, 26.3)
69 human/orang 21.5 (11.7, 31.6) 17.1 (16.2, 18.1) 17.3 (16.2, 18.4) 17.1 (16.1, 18.1) 16.8 (15.8, 17.9)
70 human/gorilla 12.8 (7.7, 23.2) 10.4 (9.8, 11.0) 10.2 (9.6, 11.0) 10.1 (9.5, 10.8) 9.9 (9.3, 10.6)
71 human/chimpanzee 7.7 (5.7, 10.0) 8.2 (7.6, 8.8) 8.7 (8.1, 9.4) 8.5 (8.0, 9.2) 8.4 (7.8, 9.0)
Open in a new tab

aThe marginal prior of a node is constructed from the fossil calibrations or from a birth–death process for nodes with no fossil calibration.

bPosterior time estimate for the combined analysis of 14 K nuclear genes and mitochondrial data for 274 species.

cPosterior time estimates for 14 K nuclear genes for 36 species, assuming each of the three different basal Placentalia topologies (figure 2b).

dValues are mean and 95% CI (in brackets). Clade ages are the ages of the corresponding crown groups.

eNode 41 represents basal Atlantogenata, Epitheria or Exafroplacentalia, according to the placental topology considered (figure 2b). Node numbers correspond with those in figure 1.

Bininda-Emonds et al. [16] dated the age of 9 of 18 crown placental orders to be before the K–Pg event. They proposed a delayed rise model of placental diversification to explain the large time gap between the origination of crown orders in the Cretaceous and their lineage diversification in the Paleogene. For example, they dated crown Chiroptera at 74.9 Ma, Primates at 87.7 Ma, Lagomorpha at 66.8 Ma and Rodentia at 85.3 Ma, while there are no Cretaceous fossil representatives for these groups [7]. Our estimates suggest a post K–Pg origination for ordinal level crown groups, consistent with the fossil record. For comparison, we date Chiroptera at 59.1 Ma, Primates at 68.2 Ma, Lagomorpha at 47.9 Ma and Rodentia at 64.4 Ma. We conclude that there is no evidence to support a delayed rise model.

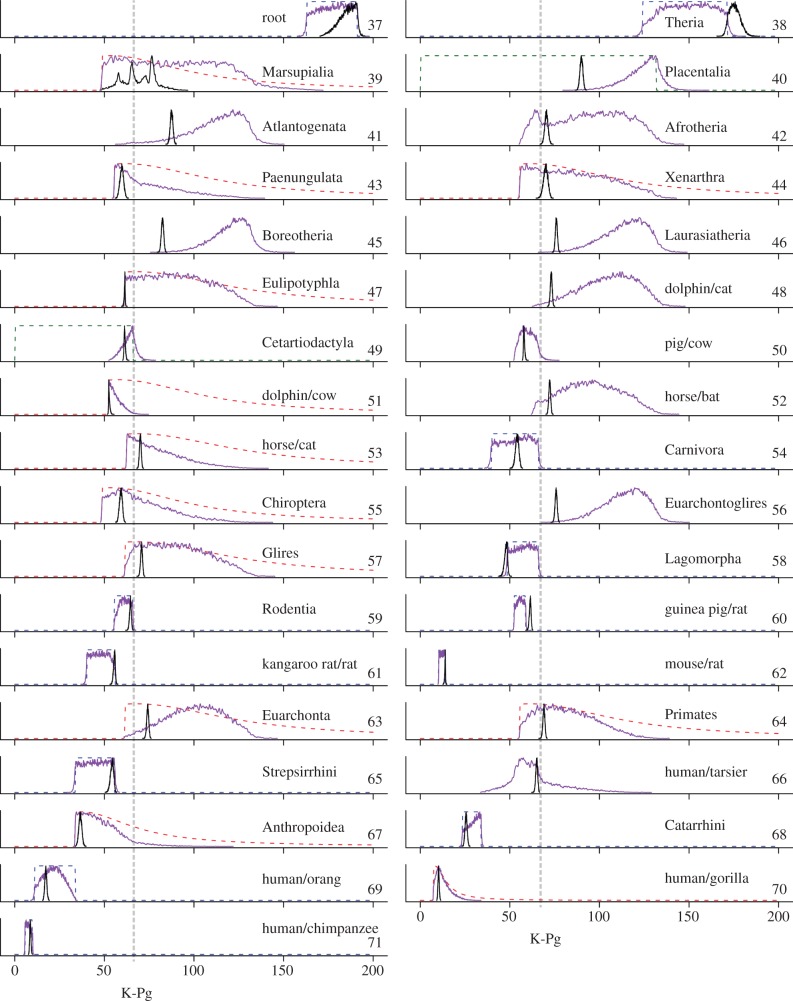
Our large genome scale alignment is very informative, contributing to a concentrated posterior time distribution for almost all ordinal placental divergences (table 1 and figure 3). Our credibility intervals are much narrower than those reported in other studies ([17], electronic supplementary material, figure S2), even though the time prior is rather diffuse, encompassing both pre and post-K–Pg divergences for many ordinal level crown groups (table 1). Construction of the time prior is a complex process as it accounts for the fossil age constraints, the birth–death process and the age constraints required by the hierarchical ordering of nodes in the tree (electronic supplementary material, text). In particular, the marginal prior of a node may differ from its fossil calibration [43]. We note the importance of estimating the time prior explicitly so that it can be compared with the time posterior and the fossil calibrations (figure 3).

Figure 3.

Figure 3.

Open in a new tab

Calibrations, prior and posterior densities. The marginal posterior density of divergence times estimated from the 14 346 nuclear genes is shown in black. The marginal prior density of times is shown in purple. The fossil calibrations are shown as dashed lines in red (minimum bound), green (maximum bound) and blue (joint). Nodes with no calibrations (41, 42, 45, 46, 48, 50, 52, 56 and 66) have their marginal priors generated using the birth–death process conditioned on the ages of the calibration nodes [25] (see the electronic supplementary material, text). Note how the marginal prior densities may differ from the corresponding fossil calibration densities. All densities are scaled so that their maximum is one. Time scale is in million years ago. Clade ages are the ages of the corresponding crown groups.

The use of soft calibration densities allows the data to correct for conflicting fossil-based time constraints. For example, the estimated age of crown Theria (node 38), 178–168 Ma, violates our fossil-based soft maximum age constraint for this node (figure 3 and table 1). However, our posterior estimate is in accord with a recently described eutherian fossil dated approximately 153 Ma [44] (electronic supplementary material, figure S3). This highlights the robustness of soft fossil-based age constraints and large informative sequence datasets to palaeontological uncertainty. The posterior ages of nodes 58 (lagomorphs) and 60 (guinea pig/rat) also violated their corresponding fossil calibrations (figure 3). To assess the robustness of our estimated times to the presence of these problematic calibrations [45], we performed an additional analysis on the 36 species tree where we removed the maximum age constraints on nodes 38 (crown Theria) and 60 (guinea pig/rat), and the joint constraints on lagomorphs (node 58). We found that the estimated age of crown Theria became older (the posterior mean and credibility interval (CI) changed from 175, 170–182 Ma to 186, 181–191 Ma), while the guinea pig/rat clade (node 60) became younger (the posterior mean and CI changed from 47.8, 45.8–49.3 Ma to 45.6, 42.9–48.2 Ma). The ages of all other nodes (including guinea pig/rat; node 60) were only marginally affected (electronic supplementary material, figure S4). Thus our estimated times are robust to the presence of this conflicting fossil evidence for calibrations.

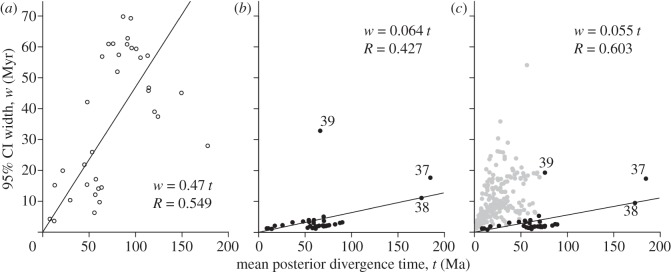
We tested whether current genomic data are sufficient to reduce uncertainty in time estimates towards its theoretical limit. With a relaxed clock, as the number of sites and loci approach infinity, a scatter plot of posterior mean times (divergence) versus their corresponding CI widths (uncertainty) approaches a straight line [22]. Figure 4a shows the scatter plot for the time prior, showing the high level of uncertainty owing to the soft fossil constraints: for every 100 Myr of divergence, 47 Myr of uncertainty is added to the prior CI width. For the time posterior calculated using 36 species and 14 632 genes, the scatter plot is close to a straight line (figure 4b). The addition of molecular data reduces uncertainty substantially, and for every 100 Myr of divergence, only 6.4 Myr of uncertainty is added to the posterior CI width (figure 4b). Marsupialia (node 39) is a clear outlier, exhibiting much greater uncertainty than expected, given the age of the clade. Increased taxon sampling through the inclusion of the mitochondrial data reduced substantially the uncertainty on the age of Marsupialia (figure 4c). Our analysis indicates that current genome scale sequence data yield results close to the theoretical limit of uncertainty for the ages of mammalian ordinal and supraordinal clades. However, the uncertainty associated with divergences at family and genus levels is high (grey points in figure 4c), and increased density of taxon-sampling at genome scale will probably improve their age estimates substantially.

Figure 4.

Figure 4.

Open in a new tab

Infinite-sites plot. The 95% CI width is plotted against the mean of the divergence time. (a) Prior calculated from a MCMC without sequence data on the 36-species tree. (b) Posterior calculated using 14 632 nuclear genes in 20 partitions, 36 species. (c) Posterior from combined analysis of 14 632 nuclear genes in 20 partitions and 12 mitochondrial genes for 274 species in one partition. In (c), black dots indicate nodes shared with the 36-species tree, and grey dots indicate nodes that are exclusive to the 274-species tree. Only black dots are used to fit the line and calculate R.

Extensive tests indicate that our divergence time estimates are robust to the substitution model (protein versus nucleotide), to variations in the number of genes and gene partitions, and to various partitioning strategies based on multivariate analysis and clustering of branch lengths (electronic supplementary material, figure S5). In particular, sophisticated partitioning strategies based on PCA did not perform better than the simpler rate-based partition strategy. Our results are also robust to tree topology. The three main groups of placental mammals (Boreotheria, Xenarthra and Afrotheria) diverged almost simultaneously [27] and there is uncertainty regarding the position of the placental root [27,46]. Our principal analyses assumed the Atlantogenata hypothesis of placental divergence (figure 2b). Estimated divergence times using the two alternative Placentalia trees (figure 2b) yield very similar clade ages (table 1), indicating that our divergence time estimates are robust to these topological differences. The three superorders are thought to reflect the radiation of early placentals among the three principal continental land masses resulting from the break-up of Pangaea: Boreotheria in North America, Asia and Europe; Xenarthra in South America; and Afrotheria in Africa [26,27,47]. However, our age estimate for crown Placentalia postdates the critical episode of continental fragmentation, 148–110 Ma [27,48], questioning this hypothesis of vicariance driving placental mammal diversification.

A comprehensive divergence time study should account for three sources of uncertainty: the degree to which fossil calibrations approximate or encompass the time of divergence [25], the randomness in the molecular rate [22,36] and the variance of branch length estimates [49]. The variance in branch length estimates can be substantial for small sequence datasets leading to exceedingly large CIs for divergence times as has been observed in some studies [17]. These sources of uncertainty were not adequately addressed in molecular clock studies that supported particularly ancient dates of placental diversification [5,16]. Our Bayesian approach integrates genome-scale data with a conservative interpretation and realistic implementation of fossil-based time constraints [21], overcoming the limitations of previous analyses, and ameliorating this notorious instance of discord between molecular and palaeontological estimates of evolutionary time.

4. Conclusions

Palaeontologists have long understood that the first record of crown placentals in the early Paleogene is an underestimate of the age of Placentalia. Along with other studies, we confirm that the explosive model, in which the last common ancestor of placentals postdates the K–Pg event, is incorrect. However, our results allow us to decisively reject a pre-extinction diversification, indicating instead the diversification of placental orders in a 20 Myr post-extinction interval. These results accord with the long fuse model [2] and are therefore consistent with the current interpretation of the mammalian fossil record. Our study is oriented around the genomic diversity of extant mammals. An important direction for future research concerns the extent to which the lack of genomic data from extinct groups, some of which were diverse shortly after the K–Pg boundary, may influence our ability to understand mammalian divergences generally. Nevertheless, we hypothesize that other instances of mismatch between molecular clocks and the fossil record, such as the origins of animal phyla, flowering plants, and modern birds, may be similarly reconciled without assuming extensive cryptic episodes of evolutionary history preceding their fossil records. Access to genome scale datasets through next generation sequencing makes realistic the prospect of an accurate and precise timescale for the Tree of Life.

References

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES