Integrated Multiscale Modeling of the Nervous System: Predicting Changes in Hippocampal Network Activity by a Positive AMPA Receptor Modulator

Abstract

One of the fundamental characteristics of the brain is its hierarchical organization. Scales in both space and time that must be considered when integrating across hierarchies of the nervous system are sufficiently great as to have impeded the development of routine multilevel modeling methodologies. Complex molecular interactions at the level of receptors and channels regulate activity at the level of neurons; interactions between multiple populations of neurons ultimately give rise to complex neural systems function and behavior. This spatial complexity takes place in the context of a composite temporal integration of multiple, different events unfolding at the millisecond, second, minute, hour, and longer time scales. In this study, we present a multiscale modeling methodology that integrates synaptic models into single neuron, and multineuron, network models. We have applied this approach to the specific problem of how changes at the level of kinetic parameters of a receptor-channel model are translated into changes in the temporal firing pattern of a single neuron, and ultimately, changes in the spatiotemporal activity of a network of neurons. These results demonstrate how this powerful methodology can be applied to understand the effects of a given local process within multiple hierarchical levels of the nervous system.

I. Introduction

Multiscale modeling historically has been explored primarily in the fields of engineering, computer sciences, and physics, where multiple scales of observation have motivated the extensive use of this approach. With the growth of computational neuroscience, recent years have seen the emergence of multiscale modeling in this field as well. Clearly, the nervous system represents a complex integrated system, and multiscale modeling is now recognized as being essential for a better understanding its function, and in particular, how events taking place at the molecular level are modifying brain function at the neuronal and circuit levels [1], [2].

Most instances of neuronal multiscale simulation attempts have started with a relatively high-order modeling, spanning mostly from cellular to systems levels [see Fig. 1(a)]. Simulators that allow multiscale modeling of neural function include NEURON [3], GENESIS [4], NEST, and CSIM [5].

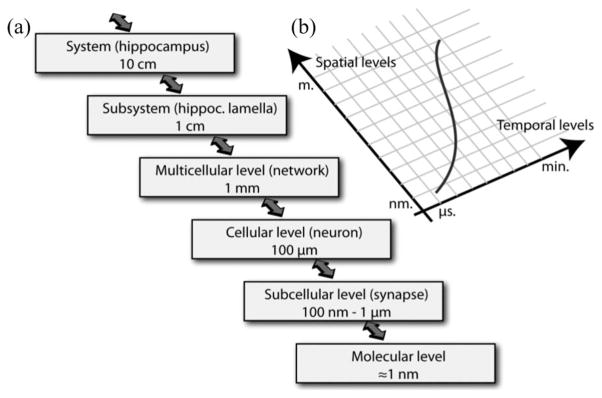
Fig. 1.

Schematic representation of the spatial and temporal integration taking place in the nervous system. (a) Adapted from [7]: spatial scales necessary for multiscale modeling ranging from the molecular (nanometer scale) to the systems level (centimeter scale). (b) In parallel to spatial complexity, the nervous system exhibits temporal complexity, as events take place from the microsecond range to the minute and hour range. Determining the appropriate LOD (red line) both in terms of spatial and temporal accuracy allows for reasonable approximation, while covering a wide range of spatiotemporal scales.

While recent computational efforts have been devoted mainly to expanding from the neuron toward large-scale network simulations, we have developed a bottom-up approach starting from the molecular level consisting of the integration of molecular events into synaptic and neuronal architectures. The platforms implemented Elementary Objects of the Nervous System (EONS)/Rhenovia Modeling and Simulation (RHENOMS) take into account a large number of biochemical processes (numerous synaptic mechanisms including second-messenger pathways and modulations) as well as their complex spatiotemporal interactions [6]. In this study, we illustrate this approach by analyzing how a perturbation at the molecular level (modification of kinetic parameters of the AMPA receptor-channel simulating the effects of a positive modulator) is translated into modifications of the temporal pattern observed at the neuronal level (firing rate of a pyramidal neuron) (see Fig. 2). Our results indicate that small modifications of critical parameters at the molecular level may have significant impact at the neuronal level, and illustrate the power of our approach to understand physiological as well as pathological mechanisms.

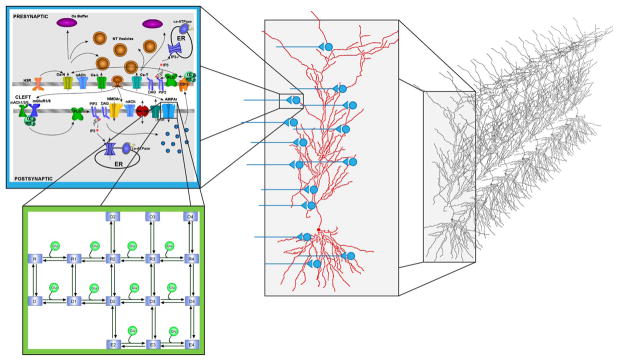
Fig. 2.

Schematic representation of the different levels of complexity addressed in the current multiscale modeling platform. Molecular mechanisms, such as the AMPA receptors, are represented by a 16-state kinetic model [12]. At the subcellular level, these mechanisms are geometrically coupled, based on their location in the cell (presynaptic, extracellular, postsynaptic, or along the dendritic tree); the resulting changes in postsynaptic currents are then injected in a CA1 pyramidal cell neuron [13], which can be studied in isolation, or within a network.

II. Methods

A. Spatiotemporal Scales

The central nervous system is a highly hierarchical structure that integrates several spatial levels of complexity (see Fig. 1). The “lowest” level of the system considered here is the molecular level. This is the level where biochemical reactions, ion exchanges, and diffusion, and protein/protein interactions occur. Above this, the second level consists in the spatial clustering of some of these molecular events, e.g., at a presynaptic terminal, which incorporates all the events taking place in this spatially defined compartment. The third level consists in the integration of all the subcellular compartments into a cell. The fourth level is the structured organization of cells into cellular networks. Right above this, those networks are organized in subsystems (i.e., hippocampal subfields or cortical columns), which are then compounded into anatomical structures of systems (i.e., hippocampus, prefrontal cortex).

An additional and critical multiscale dimension is time. The nervous system integrates mechanisms that occur extremely rapidly, within microseconds (e.g., release and diffusion of neurotransmitters in the synaptic cleft [8] and their binding to receptors), with other mechanisms taking place at a much slower time scale (i.e., seconds for induction of long-term potentiation, and minutes or longer for signal-transduction mechanisms, and other regulatory processes). Computational simulation of mechanisms spanning such broad scales (Fig. 1(b)) inherently imposes constraints on the numerical and computational methods used to integrate these multiscale events. To satisfy those constraints, we have used two main concepts: 1) temporal level of details (LOD) and variable step numerical methods and 2) event-constrained asynchrony. The implementation of these concepts will be described in the following sections before presenting results of a specific application of our approach.

B. Molecular Level

At the level of elementary models (molecular level), the first concept consists in channeling the computational power where and when it is needed most; to reach this goal, we use variable-step numerical methods to calculate the dynamic evolution of elementary models. Since the models are highly dynamic, they exhibit periods of intense activity (in the tens of microsecond range), yet may remain silent for long periods of time. Using a solver with variable-step numerical methods guarantees a high level of accuracy at all times, while decreasing the computational demand at times when it is not needed.

C. From Molecular to Synaptic Level: The EONS/RHENOMS Platforms

The second concept utilized is an asynchronous event-constrained communication protocol between elementary models, which ensures that, at each and every moment of the simulation, only the results of models that are essential at that particular moment are calculated. However, as higher spatial levels are analyzed, elementary models become highly interconnected, i.e., they depend on each other for their temporal evolution. To take into account this high level of interconnectivity and interdependence, events are generated so that results from a model are recalculated if significant changes occur in the values of the input variables of that model. Similarly, if a model requires an input value at a specific time point, but this value does not exist (as the model that generates this value was not updated due to the utilization of variable-step algorithm), the input value is interpolated based on the previous outputs of the input model.

The EONS/RHENOMS platforms we have developed integrate a very large number of complex and highly interconnected models (thousands of differential equations) that represent and regulate synaptic function in the presynaptic terminal, in the synaptic cleft (even incorporating diffusion processes [8] and astrocytic modulation) and in the postsynaptic spine (read [6], [9] for details). All elementary models are written in the Systems Biology Markup Language standard. The simulation engine in the synaptic platform is based on the event-constrained asynchronous principle described earlier, allowing us to reach reasonable computation speeds while maintaining acceptable accuracy.

D. From Synaptic to Neuronal Level

In order to incorporate these levels most efficiently, we elected to combine well-established modeling tools—each in its area of proficiency (level), and to define a communication protocol in such a way that they can perform their calculations in parallel and communicate with each other as the simulation evolves. At the molecular and synaptic levels, we use the EONS/RHENOMS integrated synaptic modeling platforms that we developed; for the rest of the neuron, we use the NEURON simulator; communications between EONS/RHENOMS and NEURON are handled using a protocol that we developed based on MPJ express [10] on the Java side (a message-passing library implementation for Java), and Python for NEURON. The frequency at which NEURON and EONS/RHENOMS communicate (1000 Hz) is much lower than the temporal sampling frequency used at the subcellular level (<microsecond), as dynamics of synaptic currents and potentials have lower time constants and, therefore, slower variations than intrasynaptic mechanisms (see Fig. 3).

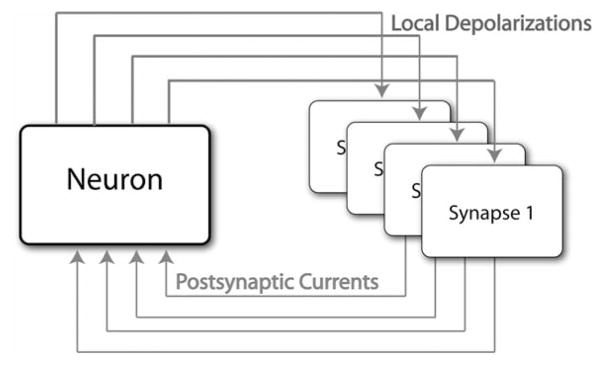
Fig. 3.

Conceptual diagram describing the bidirectional communication between instances of the EONS/RHENOMS synaptic platform and an instance of the NEURON simulator on the high performance cluster. Each box represents a computing node. Synapses send to the neuron the calculated changes in postsynaptic conductances (resulting from the integration of all complex biochemical/biophysical calculations occurring at the synaptic level). Those changes are then integrated at the neuron level, which leads to a global change in potential. Resulting local depolarizations are then sent back to the synapses according to their distribution and spatial location. Communication overhead is minimized as temporal sampling frequency is decreased going from the synaptic to the neuronal level.

E. From Individual Neurons to Network

The framework presented earlier, as it is implemented on our high performance cluster can be directly extended to the network level; connection points between neurons (synapses) can consist of either an entry point in which input signals can be entered in the system, or exit points, allowing an action potential generated by a neuron to be sent to another layer of neurons. This structure allows complete flexibility in terms of network connectivity (in parallel or series) with very little overhead.

III. Results

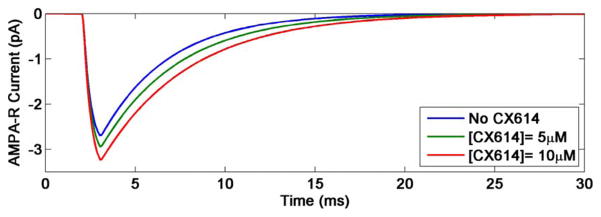
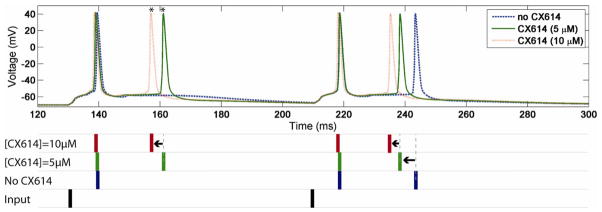
To illustrate how perturbations at the molecular level impact function at the neuronal level, we determined the effects of a positive AMPA receptor modulator (CX614) [11] at various levels of complexity. The stimulation protocol consisted in presenting a train of random interspike interval action potentials at a mean frequency of 4 Hz as the presynaptic input; our observable readouts were molecular, synaptic (excitatory post-synaptic current and voltage), and neuronal (somatic potential and firing pattern). The kinetic model of the AMPA receptor we used is the one proposed by [12]; it was adapted to fit the results presented in [11] in the presence of 5 and 10 μM of a positive AMPA receptor modulator, CX614 (see Fig. 4). The NEURON model used in our simulations was a CA1 pyramidal cell, as described in [13]. The results presented in Fig. 5 indicate that the increase in current through the AMPA receptor channels induced by CX614 at the molecular level has complex effects on neuronal excitability. As the concentration of modulator increases, two phenomena in particular can be observed: 1) neuronal spike timing is shifted, as spikes occur earlier than in control conditions, and 2) additional spikes were evoked by the same stimulation protocol. Other simulations (results not presented here) in which higher concentrations of modulator were applied generated a much stronger increase in excitability even reaching continuous spiking, suggesting potential initiation of epileptiform activity.

Fig. 4.

Effects of different concentrations of the positive AMPA receptor modulator, CX614, on the current going through AMPA receptor channels in the synaptic modeling platform resulting from a 1-ms long single pulse of 1-mM glutamate.

Fig. 5.

Top: Effects of different concentrations of the positive AMPA receptor modulator, CX614, on postsynaptic somatic potential of a CA1 hippocampal neuron in response to random interpulse interval stimulation at a mean frequency of 4 Hz. Responses are shown for a 300-ms window. In the presence of CX614, note the increase in frequency of action potentials (*). Bottom: Timing of the postsynaptic spikes at various concentrations of CX614; presynaptic action potential (input) is compared to the timing of the postsynaptic spikes. Note that spikes occur earlier with increasing CX614 concentration.

IV. Discussion

We presented a novel multiscale modeling approach that incorporates complex nonlinear dynamics ranging from the molecular level up to population events at the network level, thus creating a framework spanning four levels of observables. This framework allows for incorporation of a high LOD at the molecular level into larger scale simulations. Results presented here include molecular, synaptic, and neuronal level; given the underlying structure we introduced, network-level simulations represent a straightforward extension of this paper. We highlighted the main principles of our approach starting at the molecular level using adaptive LOD concepts emphasizing 1) variable step numerical methods, 2) event-constrained asynchrony, and 3) temporal relaxation, as higher modeling levels are reached. This approach was successfully used to determine the effects of perturbations of parameters at the molecular level on the functional properties observed at the neuronal level. One particularly useful application of our approach is study of the effects of drugs on the nervous system, as it provides for the integration of drug effects (or combinations thereof) into a multiscale pathophysiological modeling framework. In the example presented earlier, our results indicate how a glutamatergic receptor modulator can produce a beneficial effect at low concentrations (increased synaptic responses) but also potentially harmful effects at high concentrations (continuous spiking).

Future perspectives consist of 1) further increasing the temporal range to include slower mechanisms (i.e., signal transduction) and 2) expanding the neuronal level to a simplified mini-hippocampal network. As the level of complexity increases, it will become crucial to develop in parallel to the multiscale simulation platform a multiscale, multiobjective optimization framework to facilitate calibration of all models and parameters.