Generation of 42-fs and 10-nJ pulses from a fiber laser with self-similar evolution in the gain segment

Abstract

A double-clad Yb-doped all-normal-dispersion fiber laser with a narrow intra-cavity spectral filter is demonstrated to produce 22 nJ pulses at 42.5 MHz repetition rate. These pulses are characterized and compressed via mulitphoton intrapulse interference phase scan to as short as 42 fs and 10 nJ/pulse. Adaptive compression underlies the achievement of 250-kW peak power, which enables efficient second and third harmonic generation with spectra spanning 30 nm and 20 nm, respectively.

1. Introduction

The promise of rugged, compact, and robust femtosecond pulsed sources with excellent mode quality has been driving innovation in ultrafast fiber laser technology for the last 20 years [1–9]. Recent developments have enabled fiber lasers to deliver high pulse energy or short pulse duration comparable to solid state lasers. Among the most impressive results are the demonstration of 28 fs pulses with 0.7 nJ per pulse obtained from a Yb-doped fiber laser with intra-cavity dispersion compensation [10] and 31 nJ per pulse before compression to 80fs from a dissipative soliton fiber laser with double-clad Yb gain fiber [11].

Dissipative solitons allow the highest stable pulse energies and peak powers reached by mode-locked fiber lasers to date. These are nearly static and highly-chirped pulses in all-normal-dispersion cavities [6]. The 200-kW peak power in Ref [11]. was achieved using single-mode fiber with 10 μm mode-field diameter. Scaling to higher pulse energy and peak power has been achieved by using large mode area (LMA) fibers, such as LMA photonic crystal fiber (PCF) [12,13]. Unfortunately, current LMA PCF fibers are relatively rigid (bending radius has to be greater than 30 cm) and are not easy to splice. Both of these drawbacks work against the promise of fiber lasers being compact and alignment-free.

Self-similar pulse propagation is an alternate route to high-performance fiber lasers. Self-similar pulse evolution was first observed in a fiber amplifier [14]. Later, self-similar pulse propagation in a passive fiber section of a fiber oscillator was demonstrated [15]. The passive similariton pulses stretch in time while their spectral bandwidth stays nearly constant. Similaritons can tolerate greater pulse energy than solitons without wave-breaking, thus enabling the generation of ~100 fs pulses with over 10 nJ per pulse. Recently, Oktem et al. [16], Renninger et al. [17], and Aguergaray et al. [18] have reported similariton formation in the amplifier sections of lasers. Amplifier similaritons undergo strong spectral and temporal breathing in the cavity. In the report of amplifier similariton formation in an all-normal-dispersion cavity [17], the authors focused on the new pulse evolution, not the performance limits. Amplifier similariton pulses having 3-nJ per pulse and compressed down to 55-fs were generated from an Yb fiber laser [17], but there was no attempt to maximize the pulse energy. The short pulses and smooth spectra of amplifier similariton lasers will be attractive for applications, so it is desirable to see if these solutions will be stable at higher energies.

Here we demonstrate scaling of pulse the energy for an amplifier similariton laser to the 20-nJ level, which is comparable to the highest pulse energies obtained in instruments based on single-mode fiber (SMF). The pulse energy is limited by multi-pulsing. Pulse characterization and adaptive compression are achieved using multiphoton intrapulse interference phase scan (MIIPS) [19–21]. Following compression, pulses as short as 42 fs are obtained, with the peak power of approximately 250 kW. To our best knowledge, this is the shortest pulse duration reported to date for an Yb fiber laser without any intra-cavity dispersion compensation. It has also produced the highest peak power from a fiber laser without the use of LMA fiber. Second and third harmonic generation spectra obtained when using the output of this high order dispersion corrected fiber laser are the evidence of the high peak power and proper pulse compression. This type of lasers promises to be very useful for nonlinear optical applications, such as multi-photon imaging.

2. Design and simulations

An all-normal-dispersion laser cavity [Fig. 1 ] is designed to support similariton formation in the gain medium, based on the amplifier-similariton fiber laser [17]. The cavity is based on SMF with 10-µm core diameter, compared to the 6-µm core diameter use in Ref [17]. The larger core should allow ~3 times higher maximum pulse energy, while retaining the practical features of standard fiber. The intra-cavity spectral filter is formed by the combination of a grating and a collimator [17]. Here, the collimator connected to SMF-I is about 13 cm away from the grating (300 groves per millimeter) and acts as a ~3 nm spectral filter. It is aligned to couple the 1st order diffraction beam from the grating back into the laser cavity. Only a small amount of the 1st order beam couples into the 10 µm core diameter fiber as illustrated in Fig. 1. Following the collimator, there is 1.7 m long 10 µm/125 µm single mode passive fiber (SMF-I) including the extension fiber of the collimator and combiner. A 0.35 m long section of single mode passive fiber (SMF-II) follows the gain fiber. The ends of the 2.5m Yb doped double-clad gain fiber (CorActive DCF-YB-10/128) are spliced to SMF-I and SMF-II, respectively. The gain fiber is pumped by a CW diode laser at 976 nm. The polarizing beam splitter (PBS), isolator, and waveplates (half- and quarter-waveplate on the left side, quarter-waveplate on the right side in Fig. 1) act as an artificial saturable absorber, due to the nonlinear polarization evolution of the laser pulse propagating through the fiber [22]. By adjusting these waveplates, passive mode-locking can be achieved. The half-waveplate preceding the grating helps to maximize the efficiency of the 1st order diffraction. The 0th order diffraction beam is directed onto a photodiode, connected to an oscilloscope and Radio Frequency (RF) spectrum analyzer.

Fig. 1.

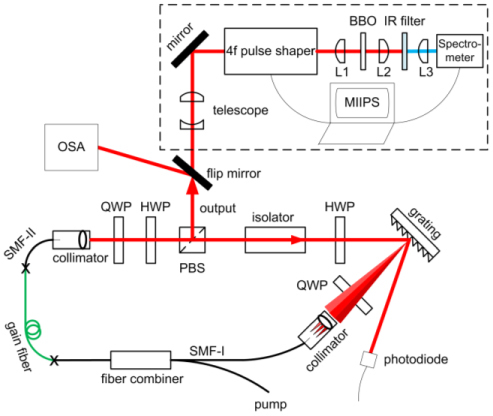
Schematic of the double-clad Yb all-normal-dispersion fiber laser cavity and the setup for pulse characterization and adaptive compression via MIIPS (dash-line box). SMF-I and SMF-II: single mode passive fiber section I and II; QWP and HWP: quarter- and half-waveplates; PBS: polarizing beam splitter; OSA: optical spectrum analyzer; L1, 2, 3: plano-convex lenses.

The PBS acts as the output coupler. The output spectrum is measured by an Optical Spectrum Analyzer (OSA, HP70451). A flip mirror near the output is used to direct the beam into the MIIPS-enabled pulse shaper (MIIPS Box 640, Biophotonic Solutions Inc.). Before entering the shaper, the beam is expanded by a 3x telescope. The output of the pulse shaper is focused on a 10 µm BBO crystal by L1 (see Fig. 1). The resulting SHG signal is detected by a fiber-coupled spectrometer (Ocean Optics USB4000). The MIIPS software measures the spectral phase of the pulses at the nonlinear crystal and adaptively compensates high order dispersion to obtain transform limited pulses. A number of tests and shaper-assisted interferometric autocorrelation are performed to ensure that the obtained results are consistent with independent theoretical calculations.

To verify the presence of amplifier similaritons in the cavity, numerical simulation based on the non-linear Schrödinger equation using split-step Fourier method [23] are performed with the actual fiber parameters. An instantaneous saturable absorber is used, corresponding to the nonlinear polarization evolution. Group-velocity dispersion β₂ = 23 fs²/mm and non-linearity coefficient γ = 0.0016 (W m)⁻¹ are used. Starting from white noise, a stable solution of 23 nJ pulse energy is obtained with a 3 nm intra-cavity spectral filter [Fig. 2 ]. The pulses experience both large temporal and spectral breathing in the gain segment. The saturable absorber and spectral filter shape the pulse and make it self-consistent over the cavity round-trip. The spectral breathing ratio is up to 15 throughout the cavity, similar to that in ref [17]. Comparison between the simulated laser spectrum at the end of the second SMF and the spectrum experimentally taken from the 0th order diffraction of the intra-cavity grating shows a good match [Fig. 2(b)]. The simulated pulses at the end of 2nd SMF also show very good fit to the parabolic profile in time domain [Fig. 2(c)], which is a key characteristic of amplifier similaritons [17]. Based on these numerical results, we conclude that amplifier similaritons are formed in the cavity.

Fig. 2.

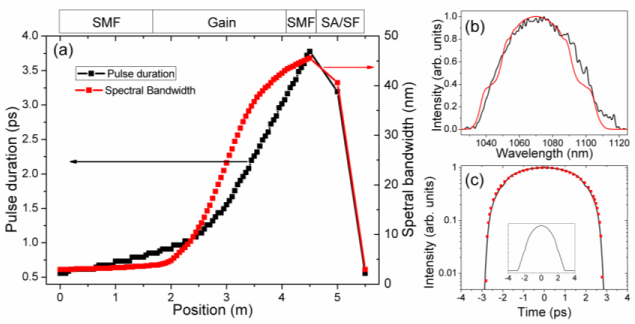
Numerical simulation results. (a) Evolution of pulse duration (black) and spectral bandwidth (red) through the laser cavity. SA: saturable absorber; SF: spectral filter. (b) Comparison of the spectrum at the end of the 2nd SMF (red) and the spectrum of the 0th order diffraction from the intra-cavity grating (black). (c) The pulse temporal profile at the end of the 2nd SMF in log-10 scales (black line) and parabolic fit (red dots). Insert: the same pulse temporal profile in linear scale.

3. Experiments and results

The performance parameters of the laser are summarized in Fig. 3 . Various mode-locked states are possible depending on the diode laser pump power and the orientation of the wave plates. When pumping at 4.1 W, a stable mode-locked state with an average output power of 930 mW is obtained [Fig. 3(a)], corresponding to 21.9 nJ pulses emitted at 42.5 MHz rep. rate [Fig. 3(c)]. When the output pulses are compressed to their transform limit, interferometric measurements are performed [24], resulting in the full-width-half-maximum (FWHM) of 57 fs [Fig. 3(b)]. Based on Fourier transform of the experimental laser spectrum and autocorrelation simulations using commercial ‘FemtoPulse Master’ software (Biophotonic Solutions Inc.), the deconvolution factor should be 1.37. This is the factor we have used to determine the experimental FWHM duration of 41.6 fs for the compressed pulses.

Fig. 3.

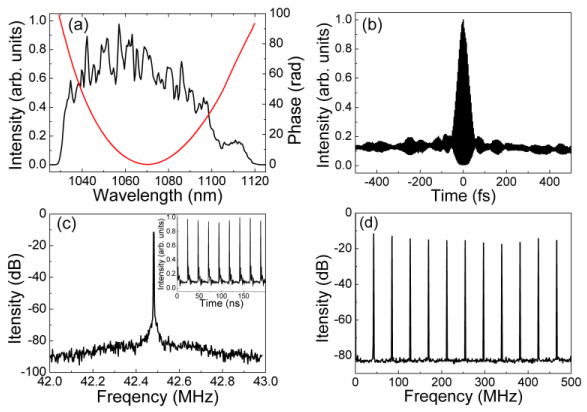
(a) Output laser spectrum (black) and measured phase of the output pulses (red). (b) Experimental interferometric autocorrelation, AC FWHM 57 fs. (c) RF spectrum analyzer result, 1 MHz frequency span. Insert: pulse train form oscilloscope. Repetition rate 42.5 MHz, energy per pulse 21.9 nJ. (d) RF spectrum analyzer result, 500 MHz span.

The output pulse train is monitored by a fast photodiode on the oscilloscope and examined using the RF spectrum analyzer. With a 1 MHz frequency span, the RF spectrum analyzer gives a single peak at 42.48 MHz with ~70 dB signal-to-background ratio [Fig. 3(c)]. The inset in Fig. 3(c) shows the response from a fast photodiode confirming single-pulse operation. No sidebands are observed for the fundamental and higher harmonics over the 500 MHz span [Fig. 3(d)], which confirms stable mode-locking.

Pulse dispersion measurement and compression are accomplished using the pulse shaper. The MIIPS software scans a sinusoidal spectral phase function across the spectrum of the pulse, collects the resulting SHG spectra and derives the corresponding spectral phase distortion [19–21]. Typically, seven iterations are run for the measurements presented here in order to obtain compensation within 99.7% of the theoretical transform limit, defined by the input laser spectrum. The phase function required to achieve transform limited pulses is the complementary phase obtained after double integration of the shaper-measured second-derivative.

To account for phase distortions due to optics in the pulse shaper and thereby measure the pulse phase directly at the laser output, we have independently measured the phase distortions due the pulse shaper itself by putting it in line with another pulse shaper. The measured phase at the laser output pulses is shown in Fig. 3(a). Polynomial fitting up to the third order gives ~35,000 fs² of the second order dispersion (SOD) and ~166,000 fs³ of the third order dispersion (TOD). Note that the observed SOD is much less than the cavity dispersion of ~100,000 fs², calculated based on the total fiber length and the fiber group-velocity dispersion β₂ = 23 fs²/mm. This is one of the characteristic signatures of the similariton formation in the gain medium [17].

After the pulse compression, the pulse shaper has been used to create two pulse replica and scan one of them in time to obtain interferometric autocorrelations [24]. The measurements show excellent agreement with calculations using ‘FemtoPulse Master’ software [Fig. 4(c) ]. Similarly, we have also compared the experimental SHG spectrum for compressed laser pulses with the calculated SHG spectrum based on the measured fundamental spectrum of the laser and a flat spectral phase [Fig. 4(a)]. Excellent agreement between theoretical and experimental results for both linear and logarithmic scales gives us confidence in the measured parameters and that the laser pulses at the BBO crystal are transform limited.

Fig. 4.

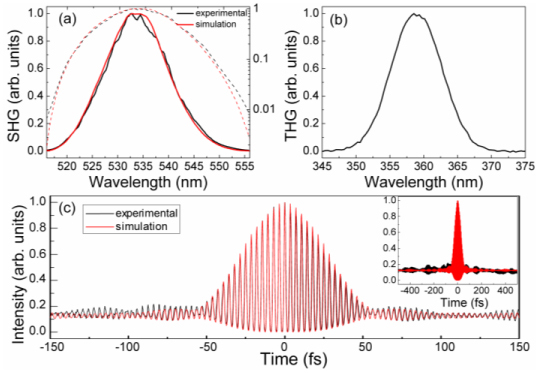
(a) Experimental and calculated SHG spectra shown in linear (solid line) and log-10 (dash line) scales. (b) Experimental THG spectrum obtained by focusing TL pulses at the surface of a glass slide. (c) Experimental and calculated interferometric autocorrelation traces for compressed laser pulses on the range of −150 fs to 150 fs. Insert: Same data on the range of −500 fs to 500 fs.

Taking into account the throughput of our pulse shaper (~50% due to the reflection efficiency of the grating and mirrors), we calculate the peak power for compressed pulses to be about 250 kW. This peak power is sufficient to obtain third harmonic generation (THG) signal at the interface of air and glass [25], see Fig. 4(b). For these measurements, the output from the pulse shaper is first focused via a 10x objective on a BBO crystal. Then the pulses are compressed at the objective focus. Once pulse compression is achieved, the BBO crystal is replaced by a 1-mm-thick glass slide. The observed THG spectrum spans ~20 nm bottom-to-bottom. The broad THG spectrum indicates that the third order dispersion is fully corrected. It is necessary to point out that, higher peak power can be obtained by improving the throughput efficiency of the pulse shaper.

We have also observed that for a fixed filter bandwidth, the spectral breathing ratio through the cavity is proportional to the pump power. When the pump power is increased over 4.1 W, the output laser spectrum continues to broaden but is no longer stable and fully coherent. Only partial pulse compression has been achieved and the resulting SHG signal is observed to be much weaker than when the output is fully coherent. When the pump power is reduced to 3.85 W, the output laser spectrum becomes narrower. Under these conditions, pulses with FWHM duration of 44.4 fs have been obtained with the average output power of 850 mW. The pulse duration increases to 57 fs with pumper power of 3.1 W.

The filter bandwidth, a key factor of the laser cavity, certainly affects the laser performance. When the collimator is moved closer to the grating and spectral filter bandwidth is increased to ~4 nm, the compressed pulses as short as 52 fs are obtained. A birefringent spectral filter of 12 nm bandwidth has also been used. With this large bandwidth filter, output spectra with steep edges and ‘cat-ears’ are obtained, which are the characteristics of dissipative soliton pulses [5,6,11]. The output pulses are compressed to 80 fs.

According to numerical simulations, the transition from dissipative soliton to amplifier-similariton happens when the filter bandwidth is reduced below ~6 nm. The simulation results are in agreement with experimental results for several filter bandwidth conditions. Our numerical simulations also predict that, it is difficult to achieve stable mode-locking when the filter bandwidth is smaller than 3 nm.

A systematic study of the amplifier similariton laser will be needed to determine the limits on the pulse energy. Considering that the energy was not maximized in Ref [17], the 7-fold increase in pulse energy that we find is in rough agreement with the 3-fold increase that would be expected based on the fiber core areas difference alone. The experimental results presented here can be viewed as initial experimental data in the effort to determine the maximum performance of these lasers.

4. Conclusion

In conclusion, we have fully characterized and compressed the output of an Yb all-normal-dispersion fiber laser with an intra-cavity spectral filter. Pulse energy as high as 22 nJ is reached, and after being de-chirped, 42-fs and 10-nJ pulses are generated. Efforts in our lab will focus on scaling up the pulse energy using LMA fibers.