Abstract
Background
Despite their notorious diversity, biological cells are mechanically well characterized by only a few robust and universal laws. Intriguingly, the law characterizing the nonlinear response to stretch appears self-contradictory. Various cell types have been reported to both stiffen and soften, or “fluidize” upon stretch. Within the classical paradigm of cells as viscoelastic bodies, this constitutes a paradox.
Principal Findings
Our measurements reveal that minimalistic reconstituted cytoskeletal networks (F-actin/HMM) exhibit a similarly peculiar response. A mathematical model of transiently crosslinked polymer networks, the so-called inelastic glassy wormlike chain (iGwlc) model, can simulate the data and resolve the apparent contradiction. It explains the observations in terms of two antagonistic physical mechanisms, the nonlinear viscoelastic resistance of biopolymers to stretch, and the breaking of weak transient bonds between them.
Conclusions
Our results imply that the classical paradigm of cells as viscoelastic bodies has to be replaced by such an inelastic mechanical model.
Introduction
Cells stiffen upon stretch [1]–[3]. But cells also soften upon stretch [4], [5]. We call this the stiffening-softening paradox of cell mechanics, since both apparently contradictory effects are attributed to the same structural entity or “functional module” [6] of the cell, the cytoskeleton [7]. The cytoskeleton is essentially a semidilute meshwork of semiflexible biopolymers, calling for an explanation by a mechanistic polymer-physics based model [8], [9]. Indeed, in-vitro reconstituted cytoskeletal networks were also found to stiffen [10]–[12] and soften [12]. Within the classical mechanical paradigm of cells and biopolymer networks as viscoelastic bodies, such contradictory responses constitute a paradox, as they elude attempts of a unified explanation. Accordingly, the different behaviors were previously attributed to distinct network architectures [10]. In the following, we want to challenge this view by revealing that even a passive in-vitro cytoskeletal model network exhibits a two-faced mechanical response. Using a simple mathematical model for the inelastic mechanics of a transiently crosslinked biopolymer network, we explain how the apparently paradoxical behavior may naturally emerge from a unified mechanism. Taken together, our results thus show a plausible way of how to resolve the stiffening-softening paradox within a unified framework of inelastic network mechanics, with important implications for cell function, development, and disease [13], [14].
We performed shear rheometry with a biomimetic cytoskeletal model system, an F-actin network isotropically and transiently crosslinked by rigor heavy meromyosin (HMM). The F-actin/HMM system was chosen for its structural simplicity and experimental reproducibility, not for its physiological significance. Its frequency-dependent linear rheology has been well characterized before [15]. Our aim was to demonstrate that even such simple model networks, which are arguably accessible to a schematic mathematical modeling, exhibit a complex two-faced nonlinear rheological response akin to that reported for living cells.
Results
Nonlinear Rheology of F-actin/HMM Networks
We applied a staircase of sinusoidal shear excitations. For small amplitude  , the resulting stress-strain curves have elliptical shapes (Fig. 1a). This means that the stress response
, the resulting stress-strain curves have elliptical shapes (Fig. 1a). This means that the stress response 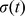 is sinusoidal, like the stimulus
is sinusoidal, like the stimulus 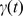 , but shifted in phase, as characteristic of a linear viscoelastic (dissipative) response. Upon raising the oscillation amplitude
, but shifted in phase, as characteristic of a linear viscoelastic (dissipative) response. Upon raising the oscillation amplitude  step by step after every 30 cycles (Fig. 2a), deviations from the elliptical shape become increasingly pronounced (Fig. 1b), in line with previous observations for F-actin/
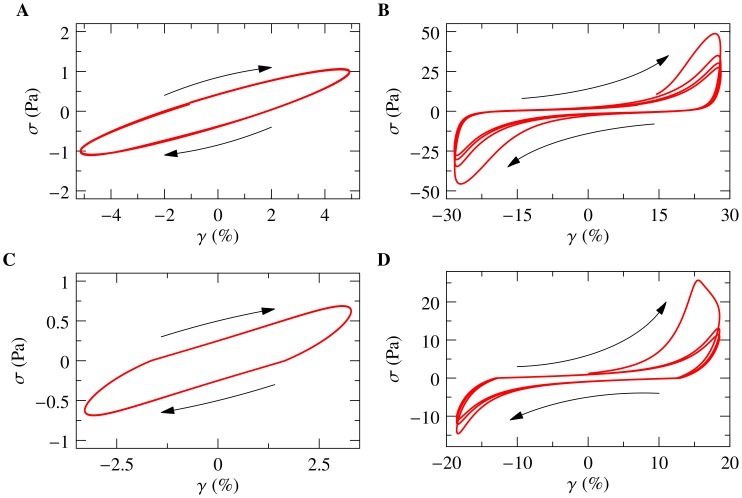
step by step after every 30 cycles (Fig. 2a), deviations from the elliptical shape become increasingly pronounced (Fig. 1b), in line with previous observations for F-actin/ -actinin networks [16] and even pure F-actin solutions [17]. Within each cycle, the material stiffens appreciably, which manifests itself in convex stress-strain relations, i.e. the ellipses bending upwards. This is the equilibrium viscoelastic stiffening commonly attributed to the nonlinear resistance of individual semiflexible polymers to stretch [9]–[11], [18]. But note that, at the same time, the sample exhibits signatures of softening near the maximum strain
-actinin networks [16] and even pure F-actin solutions [17]. Within each cycle, the material stiffens appreciably, which manifests itself in convex stress-strain relations, i.e. the ellipses bending upwards. This is the equilibrium viscoelastic stiffening commonly attributed to the nonlinear resistance of individual semiflexible polymers to stretch [9]–[11], [18]. But note that, at the same time, the sample exhibits signatures of softening near the maximum strain  , where the stress-strain curves become concave. As a consequence of such repeated softening phases, the maximum stress
, where the stress-strain curves become concave. As a consequence of such repeated softening phases, the maximum stress 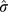 reached in subsequent identical loading cycles decreases continuously until the stress-strain curve settles on a limit cycle. This phenomenon, known as “shakedown” or dynamic softening, is the hallmark of inelastic behavior.
reached in subsequent identical loading cycles decreases continuously until the stress-strain curve settles on a limit cycle. This phenomenon, known as “shakedown” or dynamic softening, is the hallmark of inelastic behavior.
Figure 1. Stress-strain curves for an oscillatory shear strain 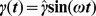 .
.
(a, b) Experiment: passive transient F-actin/HMM gels (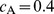 mg/ml,
mg/ml, 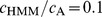 ) sheared at strain amplitudes of
) sheared at strain amplitudes of 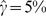 and
and 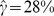 , corresponding to a weakly/strongly non-linear response, respectively. The upward bending of the ellipses signals stiffening, their concave regions near maximum strain imply softening. The softening and the ensuing “shakedown” of the stress-strain curves towards a limit cycle are indicative of inelastic fluidization. (c, d) Corresponding theory curves from the inelastic glassy wormlike chain (i Gwlc) model [25] (parameters
, corresponding to a weakly/strongly non-linear response, respectively. The upward bending of the ellipses signals stiffening, their concave regions near maximum strain imply softening. The softening and the ensuing “shakedown” of the stress-strain curves towards a limit cycle are indicative of inelastic fluidization. (c, d) Corresponding theory curves from the inelastic glassy wormlike chain (i Gwlc) model [25] (parameters 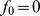 ,
,  ,
, 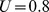 ,
,  Hz; single-polymer displacement and force were converted to network strain and stress as described in Methods). The absolute stress and strain scales in theory and experiment are compatible on the present (mean-field) level of modeling, but the theory somewhat overestimates the stiffening during the initial large-amplitude loading cycle, and, as a consequence, also the peak force and the strength of the shakedown.
Hz; single-polymer displacement and force were converted to network strain and stress as described in Methods). The absolute stress and strain scales in theory and experiment are compatible on the present (mean-field) level of modeling, but the theory somewhat overestimates the stiffening during the initial large-amplitude loading cycle, and, as a consequence, also the peak force and the strength of the shakedown.
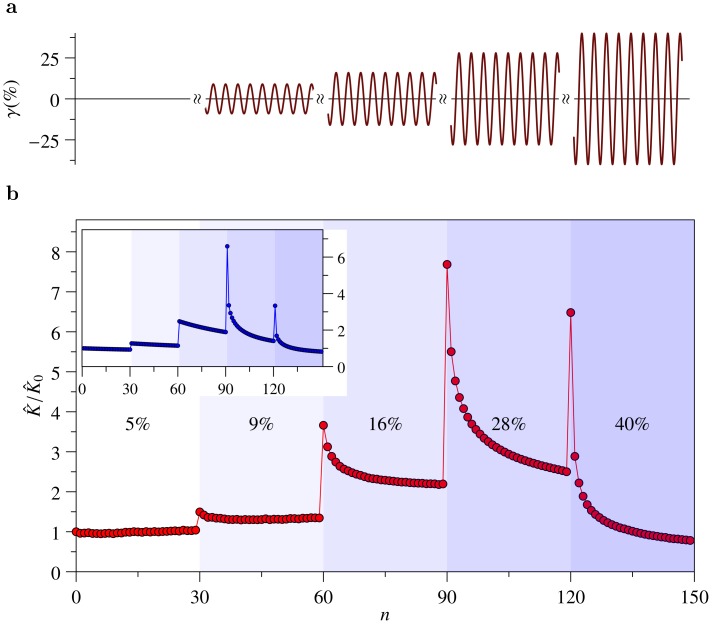
Figure 2. Nonlinear inelastic response of F-actin/HMM networks.
(a) Schematic of the oscillatory driving protocol (the strain amplitude  is increased in steps after every 30 cycles, driving frequency
is increased in steps after every 30 cycles, driving frequency 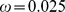 Hz). (b) Measured reduced nonlinear modulus
Hz). (b) Measured reduced nonlinear modulus 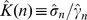 (peak stress over peak strain) as a function of the cycle number
(peak stress over peak strain) as a function of the cycle number  . The shaded background indicates the monotonic increase of the strain amplitude
. The shaded background indicates the monotonic increase of the strain amplitude  (indicated in percent). Note that the modulus responds nonmonotonically to both transient and stationary loading, hinting at antagonistic mechanisms with multiple time scales. Inset: Theory curve from the i Gwlc model [25] reproducing the key features, transient and stationary stiffening and softening with the parameters from Fig. 1 (see also Methods and Fig. E in Supporting Information S1).
(indicated in percent). Note that the modulus responds nonmonotonically to both transient and stationary loading, hinting at antagonistic mechanisms with multiple time scales. Inset: Theory curve from the i Gwlc model [25] reproducing the key features, transient and stationary stiffening and softening with the parameters from Fig. 1 (see also Methods and Fig. E in Supporting Information S1).
To better illustrate how stiffening and dynamic softening interfere, we reduce the full information contained in the nonlinear stress-strain curves in Fig. 1 by introducing a reduced description in terms of the maximum amplitudes 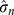 and
and 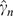 of stress and strain, respectively, for each cycle
of stress and strain, respectively, for each cycle  . Their ratio
. Their ratio 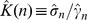 defines a nonlinear modulus as a function of the oscillation frequency and the cycle number
defines a nonlinear modulus as a function of the oscillation frequency and the cycle number  , hence of the cycle-to-cycle history of the sample. It captures the essence of stiffening and dynamic softening, while discarding some finer details encoded in the individual stress-strain cycles. The oscillatory staircase protocol with its monotonically increasing amplitude
, hence of the cycle-to-cycle history of the sample. It captures the essence of stiffening and dynamic softening, while discarding some finer details encoded in the individual stress-strain cycles. The oscillatory staircase protocol with its monotonically increasing amplitude  (Fig. 2a) results in a non-monotonic evolution of
(Fig. 2a) results in a non-monotonic evolution of 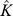 (Fig. 2b). One can distinguish a “transient response” to sudden steps in the driving amplitude
(Fig. 2b). One can distinguish a “transient response” to sudden steps in the driving amplitude  ––generically a rapid stiffening followed by a gradual shakedown––from a “stationary response” prospectively attained when the shakedown has ceased after many identical driving cycles. Note that this implies that the modulus
––generically a rapid stiffening followed by a gradual shakedown––from a “stationary response” prospectively attained when the shakedown has ceased after many identical driving cycles. Note that this implies that the modulus 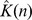 reveals underlying dynamics on multiple time scales. It is a non-monotonic function of the cycle number
reveals underlying dynamics on multiple time scales. It is a non-monotonic function of the cycle number  both for the transient and for the stationary response. Such behavior could not easily be explained by a mere elastic stiffening [18]–[20] or softening [21], [22], alone.
both for the transient and for the stationary response. Such behavior could not easily be explained by a mere elastic stiffening [18]–[20] or softening [21], [22], alone.
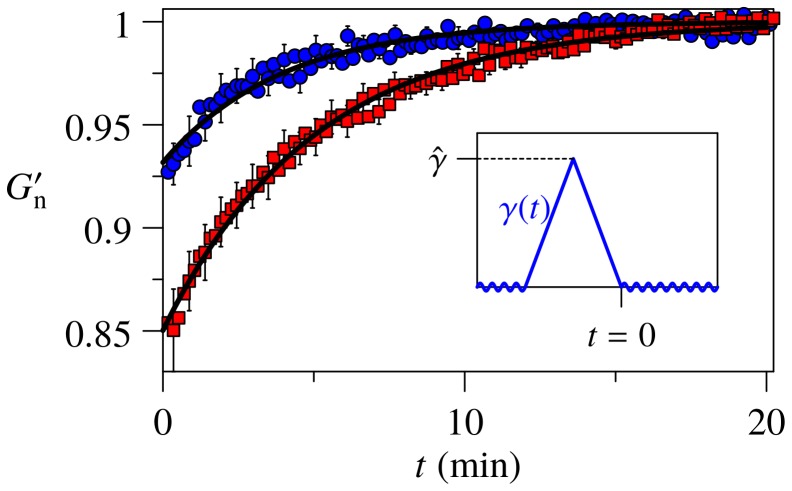
It finds a very natural interpretation in terms of an inelastic response, though. To demonstrate this, we adopted a cell rheology protocol aimed at isolating the inelastic contributions to the response by minimizing viscoelastic contributions [4]. The protocol consists of a transient shear pulse of a given amplitude, followed by a recovery phase during which the linear mechanical material properties are monitored over time, as illustrated in the inset of Fig. 3. The main figure depicts the dynamic evolution of the sample stiffness, characterized by the linear storage modulus 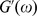 , after the application of the strain pulse. Right after the pulse, the stiffness of the F-actin/HMM networks is systematically reduced. Similarly to what was previously reported for cells, the effect is sensitive to the amplitude of the pulse (at fixed duration), and the mechanical recovery is slow. The softening is moreover accompanied by an increase in the loss angle (see Fig. F in Supporting Information S1). In accordance with the cell-mechanical terminology we thus speak of “fluidization” [4], [23].
, after the application of the strain pulse. Right after the pulse, the stiffness of the F-actin/HMM networks is systematically reduced. Similarly to what was previously reported for cells, the effect is sensitive to the amplitude of the pulse (at fixed duration), and the mechanical recovery is slow. The softening is moreover accompanied by an increase in the loss angle (see Fig. F in Supporting Information S1). In accordance with the cell-mechanical terminology we thus speak of “fluidization” [4], [23].
Figure 3. Fluidization and slow mechanical recovery of an F-actin/HMM gel after a transient strain pulse 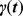 (inset).
(inset).
Stiffness is quantified by the normalized (“n”) real part 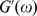 of the linear shear modulus, measured by small sinusoidal oscillations at fixed oscillation frequency
of the linear shear modulus, measured by small sinusoidal oscillations at fixed oscillation frequency 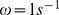 , before and after the stretch. The softening immediately after the stretch is found to be sensitive to the maximum strain
, before and after the stretch. The softening immediately after the stretch is found to be sensitive to the maximum strain  (circles) and
(circles) and 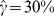 (squares) of the pulse, albeit less pronounced as for cells, where the same pattern is observed at 3–4 times smaller strain amplitudes [4]. Error bars are SE, ensemble size is
(squares) of the pulse, albeit less pronounced as for cells, where the same pattern is observed at 3–4 times smaller strain amplitudes [4]. Error bars are SE, ensemble size is 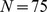 ; lines represent theoretical (exponential) fits by the i Gwlc model [25]; see Methods and Supporting Information S1 for further explanations.
; lines represent theoretical (exponential) fits by the i Gwlc model [25]; see Methods and Supporting Information S1 for further explanations.
Mathematical Model
The notion of fluidization unifies four of the features described so far: the dynamic softening or shakedown (Figs. 1, 2), the reduction and slow recovery of the modulus after stretch (Fig. 3), and the stationary softening observed in Fig. 2 over long times. For the physical origin of fluidization the transient breaking of weak bonds provides a plausible microscopic mechanism [24]. To support this interpretation, we now turn to a quantitative analysis of our data, based on the inelastic glassy wormlike chain model [25]. The glassy wormlike chain (Gwlc) model is a minimalistic phenomenological model for the Brownian dynamics of biopolymer solutions. It is rooted in the standard polymer-physics model for a semiflexible chain molecule in solution, the wormlike chain (Wlc). But it effectively accounts also for the caging and enthalpic trapping of such a polymer by the surrounding polymer matrix, resulting in a microscopic mechanical susceptibility 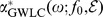 , depending on the frequency
, depending on the frequency  , prestressing force
, prestressing force 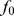 , and a stretching parameter
, and a stretching parameter 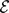 , interpreted as a characteristic bond breaking enthalpy in units of the thermal energy
, interpreted as a characteristic bond breaking enthalpy in units of the thermal energy 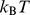 . The Wlc and the Gwlc can parametrize a wealth of mechanical data obtained in single molecule experiments [26] and rheometric measurements of biopolymer solutions, networks and cells [27]. The inelastic Gwlc (i Gwlc) adds to this an effective description of bond kinetics [25], i.e. it is applicable to nonequilibrium situations characterized by an appreciable dynamical evolution of the bond network mutually connecting the polymers (see Fig. D in Supporting Information S1 for an illustrative sketch). This is realized by introducing a dependence of the microscopic susceptibility
. The Wlc and the Gwlc can parametrize a wealth of mechanical data obtained in single molecule experiments [26] and rheometric measurements of biopolymer solutions, networks and cells [27]. The inelastic Gwlc (i Gwlc) adds to this an effective description of bond kinetics [25], i.e. it is applicable to nonequilibrium situations characterized by an appreciable dynamical evolution of the bond network mutually connecting the polymers (see Fig. D in Supporting Information S1 for an illustrative sketch). This is realized by introducing a dependence of the microscopic susceptibility 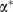 on the mean fraction
on the mean fraction  of closed bonds,
of closed bonds, 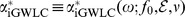 . To keep the model as simple as possible, we limit our discussions to “inelastic” (as opposed to “plastic”) deformations by requiring reversible binding-unbinding kinetics. Broken bonds ultimately reform in their original equilibrium states after the external load has been released. This means that we refrain, at the present stage, from distinguishing between the breaking of sacrificial bonds that triggers a transient domain unfolding [28] and the breaking and reforming of cytoskeletal filaments [29] or the unbinding and rebinding of their mutual sticky contacts [30], crosslinkinking molecules [15], [16], or actin-myosin cross bridges [31].
. To keep the model as simple as possible, we limit our discussions to “inelastic” (as opposed to “plastic”) deformations by requiring reversible binding-unbinding kinetics. Broken bonds ultimately reform in their original equilibrium states after the external load has been released. This means that we refrain, at the present stage, from distinguishing between the breaking of sacrificial bonds that triggers a transient domain unfolding [28] and the breaking and reforming of cytoskeletal filaments [29] or the unbinding and rebinding of their mutual sticky contacts [30], crosslinkinking molecules [15], [16], or actin-myosin cross bridges [31].
A more detailed description of the model is given in Supporting Information S1. For the sake of our present discussion, its essential predictions for the shear modulus 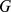 are (i) a roughly linear increase with prestress if bond-breaking is negligible,
are (i) a roughly linear increase with prestress if bond-breaking is negligible, 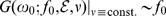 , (ii) a reciprocal relation to the number of bonds at constant stress,
, (ii) a reciprocal relation to the number of bonds at constant stress, 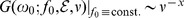 , with
, with 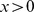 , and (iii) bond softening under stress. The latter is implemented by a Bell-type exponential force dependence of the bond opening and closing rates,
, and (iii) bond softening under stress. The latter is implemented by a Bell-type exponential force dependence of the bond opening and closing rates, 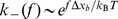 ,
, 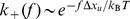 with the widths
with the widths 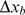 and
and 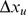 of the bound and unbound state.
of the bound and unbound state.
Discussion
The interplay between the nonlinear mechanical response of individual polymers and the slow but stress-sensitive bond dynamics gives rise to a rich and complex mechanical behavior of the i Gwlc. It naturally predicts the bent stress-strain curves and their softening characteristics and gradual shakedown, as exemplified in Fig. 1d, and the fluidization and slow recovery after a transient strain pulse (Fig. 3, lines). Even the stiffness evolution on multiple time scales, depicted in Fig. 2, is well reproduced by the model (inset). Here, we always considered the prestressing force 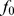 as a (small) constant. It represents frozen-in stresses in the network, which are supposedly weak for our passive reversibly crosslinked networks. But we note in passing that
as a (small) constant. It represents frozen-in stresses in the network, which are supposedly weak for our passive reversibly crosslinked networks. But we note in passing that 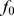 might play a much more dynamic role in applications of the i Gwlc to cell rheological data, where it might under certain circumstances be needed to represent an active contractile cell response.
might play a much more dynamic role in applications of the i Gwlc to cell rheological data, where it might under certain circumstances be needed to represent an active contractile cell response.
Beyond providing an economical parametrization of our own data and known literature results [4], [5], [10]–[12], [30], [32], the i Gwlc makes a plausible and intuitive quantitative proposal for the underlying molecular mechanism. More precisely, by analyzing the model equations, stiffening can be attributed directly to the characteristic nonlinear stretch response of individual semiflexible biopolymers, causing a prompt viscoelastic response to an applied stress. Softening emerges as an aftermath to an applied strain from the slow and stress-sensitive dynamical evolution of the mutual bonds between the biopolymers, and is therefore better characterized as an inelastic fluidization. The time-scale separation between viscoelastic stiffening and bond softening turns out to be at the heart of the observed complex nonlinear dynamical response, because large internal stresses can build up before eventually relaxing via inelastic bond breaking. The stationary effects, in contrast, rely on a static balance between polymeric stiffening and bond breaking. The model quantitatively relates these essential properties to each other and also to other characteristic features of the mechanical response of biopolymer networks and cells. For example, scale-free power-law spectra, as observed in cell rheology [33], are a characteristic feature of the model (see Ref. [27] and Supporting Information S1). Finally, the i Gwlc makes a number of interesting testable predictions for future investigations. For instance, as a direct consequence of the Bell-type stress-dependence of the bond strength, we find that the peak force reached in a large strain ramp or pulse grows essentially logarithmically with the characteristic rate at which the force increases. Conversely, the fraction of broken bonds––and therefore the resulting fluidization of the sample––is quite insensitive to the duration of the stimulating pulse, over a broad range of time scales. This particular feature has indeed already been demonstrated for live cells [5]. However, beyond a certain effective “yield threshold”, the bond fraction sensitively depends on the (imposed or attained) maximum strain, no matter what the yield force is (see Supporting Information S1 for a quantitative description).
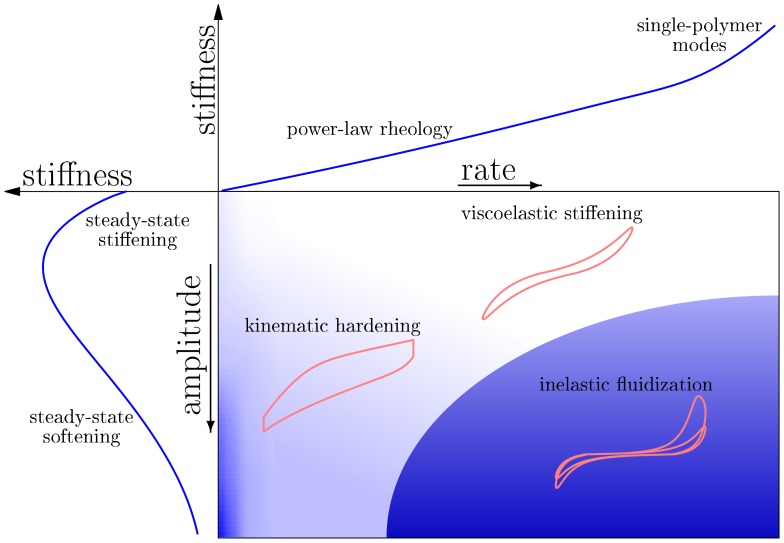
The observation that the rate and amplitude of an imposed deformation affect the nonlinear response so differently suggests to delineate a non-equilibrium constitutive diagram in the reduced parameter plane spanned by the rate and amplitude of an imposed deformation (Fig. 4 central panel). The background shading and the small representative stress-strain cycles distinguish domains of deformation rate and amplitude with a qualitatively distinct mechanical response. The limiting behaviors at vanishing rate and vanishing amplitude, i.e. near to the coordinate axes, are further characterized in the side panels (note the different labelings on their outer axes). The upper panel depicts the rate-dependent viscoelastic response for vanishing amplitude, hence essentially the linear frequency-dependent shear modulus on a log-log scale, exhibiting power-law rheology. The left panel (linear axes) shows the nonlinear shear modulus in the limit of slow driving. Note the turnabout from inelastic stiffening to softening in response to a quasi-static driving, which is responsible for the initially ascending and later descending plateaus in the nonlinear modulus 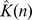 in Fig. 2. This non-monotonic stationary stress-stiffness relation originates in the sigmoidal sensitivity of the bond fraction to the force (see Supporting Information S1). For slightly larger rates, the stiffening becomes steeper, which gives rise to a “kinematic-hardening” type behavior (central panel). Finally, if the deformation rate and amplitude of the loading are both large, the response features steep initial stress stiffening and ensuing dynamic fluidization, as caused by the amplitude steps in Fig. 2, as well as the fluidization-recovery pattern illustrated in Fig. 3. The depicted representative stress-strain cycle exhibits shakedown, as in Fig. 1. Though it should not be confused with a thermodynamic state diagram, the constitutive diagram in the central panel of Fig. 4, if judiciously interpreted, can serve as a compact characterization of the multifaceted nonlinear mechanical response of transiently crosslinked biopolymer networks and as a potentially useful road map for cell rheologists.
in Fig. 2. This non-monotonic stationary stress-stiffness relation originates in the sigmoidal sensitivity of the bond fraction to the force (see Supporting Information S1). For slightly larger rates, the stiffening becomes steeper, which gives rise to a “kinematic-hardening” type behavior (central panel). Finally, if the deformation rate and amplitude of the loading are both large, the response features steep initial stress stiffening and ensuing dynamic fluidization, as caused by the amplitude steps in Fig. 2, as well as the fluidization-recovery pattern illustrated in Fig. 3. The depicted representative stress-strain cycle exhibits shakedown, as in Fig. 1. Though it should not be confused with a thermodynamic state diagram, the constitutive diagram in the central panel of Fig. 4, if judiciously interpreted, can serve as a compact characterization of the multifaceted nonlinear mechanical response of transiently crosslinked biopolymer networks and as a potentially useful road map for cell rheologists.
Figure 4. Constitutive diagram for the iGWLC model.
The central panel gives a qualitative graphical summary of the mechanical response predicted by the model as a function of the amplitude and characteristic rate of an imposed deformation pulse. At low amplitudes, in the linear regime, it exhibits power-law rheology (upper panel, log-log scale). At low rates, in the quasistatic regime, it exhibits stiffening at low amplitudes, where entropic stiffening of the polymer backbone dominates, and softening at high amplitudes, where the stiffening is eventually overruled by the exponential bond softening (left panel, linear scale). This mechanism underlies the initially ascending and later descending steps in the nonlinear modulus in Fig. 2. At high rates and high amplitudes, a steep initial stiffening with subsequent fluidization and slow recovery governs the response (central panel). The schematic stress-strain curves for oscillatory driving exemplify the salient features of the nonlinear response in the various parameter regions.
In summary, we have explored the stiffening-softening paradox of cell mechanics, both by rheological measurements of minimal cytoskeletal model systems (F-actin/HMM) and by theory. The nonlinear nonequilibrium mechanical response of the reconstituted networks was found to provide a close match to previous cell rheological measurements, albeit at 3–4 times larger amplitude. It was moreover well parametrized by the inelastic glassy wormlike chain model, which suggests a unified mechanistic explanation. Stiffening, as a direct viscoelastic response to an applied stress, is attributed to the characteristic nonlinear stretch resistance of individual semiflexible biopolymers. Conversely, softening emerges as an aftermath to an applied strain from the dynamical evolution of the mutual bonds between the biopolymers, and it is better characterized as an inelastic fluidization. By emphasizing the key role played by inelastic processes, the proposed polymer-physics based explanation of the stiffening-softening paradox clearly transcends the classical mechanical paradigm of biopolymer networks and cells as viscoelastic bodies. Our unifying explanation based upon inelastic processes is specific concerning the basic mechanism, yet robust against details of its implementation. It makes reference to microscopic elements in the molecular structure of the cytoskeleton, such as biopolymers and their mutual transient bonds, and relates them quantitatively to a wide range of rheological responses. It would also be straightforward to accommodate more sophisticated physical constituents accounting for dynamic prestresses generated by molecular motors, stress-induced domain unfolding, or catch bonds. In the minimalistic implementation discussed here, our model is, at the same time, still schematic and deliberately employs bold simplifications. In particular, it does not address network and crosslinking geometries, nor is it parametrically fine-tuned to a particular molecular architecture, as would be required for extracting reliable parameter values (such as binding affinities of crosslinkers) from fits to experimental data. In return, one may hope that it can qualitatively capture major elements of the mechanical phenomenology of both networks and cells, irrespective of their utterly different degrees of molecular complexity.
Methods
Protein Preparation and Rheology
Passive rigor F-actin/HMM networks at various concentrations were prepared as previously described [34], except that no gelsolin was added. Nonlinear oscillatory experiments were performed at actin concentration 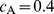 mg/ml and HMM molar ratio
mg/ml and HMM molar ratio 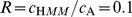 . Data for pulsed loading were pooled over two different actin concentrations
. Data for pulsed loading were pooled over two different actin concentrations 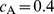 mg/ml and
mg/ml and 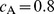 mg/ml and values of
mg/ml and values of 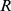 ,
, 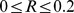 , see Table A in Supporting Information S1 for details. We used a commercial AR G2 shear rheometer (TA Instruments, New Castle, USA) in cone-plate geometry (40 mm diameter, cone opening angle 1°). About 370
, see Table A in Supporting Information S1 for details. We used a commercial AR G2 shear rheometer (TA Instruments, New Castle, USA) in cone-plate geometry (40 mm diameter, cone opening angle 1°). About 370  l sample were loaded within 1 minute into the rheometer. The transition to rigor HMM upon ATP depletion is followed by recording the elastic response of the F-actin/HMM network over time (see Fig. B in Supporting Information S1). Two different rheological protocols were applied. The first protocol, termed “nonlinear oscillations”, consisted of shear oscillations at 0.025 Hz with a staircase increase in the amplitude. The amplitude was kept constant for 30 cycles and then increased to a higher value, where it again was kept constant for 30 cycles, and so forth. Amplitude values were 5
l sample were loaded within 1 minute into the rheometer. The transition to rigor HMM upon ATP depletion is followed by recording the elastic response of the F-actin/HMM network over time (see Fig. B in Supporting Information S1). Two different rheological protocols were applied. The first protocol, termed “nonlinear oscillations”, consisted of shear oscillations at 0.025 Hz with a staircase increase in the amplitude. The amplitude was kept constant for 30 cycles and then increased to a higher value, where it again was kept constant for 30 cycles, and so forth. Amplitude values were 5 , 9
, 9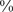 , 16
, 16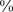 , 28
, 28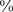 , and 40
, and 40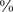 (cf. Fig. 2a). The second protocol, termed “fluidization protocol”, was chosen to specifically probe the inelastic contribution to the response, as pioneered in cell rheology [4]. A triangular shear pulse of four minutes duration and variable amplitude was applied to the sample, followed by a waiting time of at least 20 minutes. During the waiting time, the linear frequency-dependent modulus was constantly recorded by applying small shear oscillations of 1
(cf. Fig. 2a). The second protocol, termed “fluidization protocol”, was chosen to specifically probe the inelastic contribution to the response, as pioneered in cell rheology [4]. A triangular shear pulse of four minutes duration and variable amplitude was applied to the sample, followed by a waiting time of at least 20 minutes. During the waiting time, the linear frequency-dependent modulus was constantly recorded by applying small shear oscillations of 1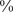 amplitude at frequencies of 2 Hz (cf. Fig. 3).
amplitude at frequencies of 2 Hz (cf. Fig. 3).
Data Analysis
For the nonlinear oscillations, raw data were extracted from the rheometer. Spline smoothing was applied to the data using a custom-made Python script. Torque  and angle
and angle  were converted to stress
were converted to stress  and strain
and strain  using
using 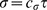 and
and 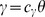 , with conversion factors of
, with conversion factors of 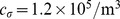 and
and 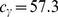 , respectively, which are calculated from the cone geometry. From the resulting stress-strain data, a nonlinear modulus
, respectively, which are calculated from the cone geometry. From the resulting stress-strain data, a nonlinear modulus 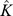 was calculated as described in the main text. The response to the nonlinear oscillations was qualitatively reproducible among different samples (Fig. E in Supporting Information S1). No averaging over samples was performed.
was calculated as described in the main text. The response to the nonlinear oscillations was qualitatively reproducible among different samples (Fig. E in Supporting Information S1). No averaging over samples was performed.
To relate theoretically calculated filament forces 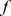 to network strains
to network strains  , we used the relation [35]
, we used the relation [35]
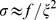 , with the mesh size [36]
, with the mesh size [36]
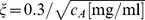 ; an estimate for the strain was obtained by normalizing the displacement by the mesh size
; an estimate for the strain was obtained by normalizing the displacement by the mesh size  .
.
For the pulsed loading experiments, the linear stiffness responded to a strain pulse by a systematic decrease followed by a recovery. Often, the recovery did not reach the pre-shear value. The failure to fully recover is probably due to slow, uncontrolled network reorganization processes, because, independent of the shear pulses, the modulus always exhibited a slow, nearly linear drift (Fig. B in Supporting Information S1). To correct for this “background drift”, the data were parametrized by a linear function 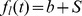 at late times
at late times 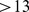 min, where all curves were to a good approximation linear in time. The data were then normalized by this linear asymptote (Fig. C in Supporting Information S1),
min, where all curves were to a good approximation linear in time. The data were then normalized by this linear asymptote (Fig. C in Supporting Information S1), 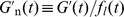 and then averaged over
and then averaged over 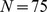 samples.
samples.
Statistical analysis of the recovery data was performed using a Monte-Carlo resampling bootstrapping method, as described in the following. For each time step, the respective values of 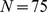 normalized experimental curves were pooled. A resampled curve was created by drawing (with replacement) one value from this pool for every time step. To a total of 1000 resampled recovery curves, exponential functions.
normalized experimental curves were pooled. A resampled curve was created by drawing (with replacement) one value from this pool for every time step. To a total of 1000 resampled recovery curves, exponential functions.
| (1) |
were fitted, with the value  of the normalized stiffness after stimulus cessation and recovery time
of the normalized stiffness after stimulus cessation and recovery time 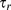 . We obtained
. We obtained 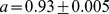 and
and 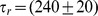 s for 10
s for 10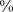 pulse amplitude and
pulse amplitude and 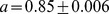 and
and  s for 30
s for 30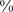 pulse amplitude. Errors are standard errors of the mean. Note that the recovery time for the large pulse is larger than the respective time for the small pulse. This behavior is actually expected from theoretical considerations (Supporting Information S1).
pulse amplitude. Errors are standard errors of the mean. Note that the recovery time for the large pulse is larger than the respective time for the small pulse. This behavior is actually expected from theoretical considerations (Supporting Information S1).
Model
The inelastic glassy wormlike chain (i Gwlc) [25] is an extension of the (equilibrium) glassy wormlike chain (Gwlc) model, which, in turn, is a phenomenological extension of the wormlike chain (Wlc), the standard coarse-grained mathematical description of an individual semiflexible polymer in solution [37]. Beyond the common Wlc, the equilibrium Gwlc phenomenologically accounts for the caging and trapping of a test polymer by the surrounding polymer network. The corresponding slowdown of the long wavelength bending undulations of the polymer backbone is, in mathematical terms, represented by a stretching of the ordinary Wlc relaxation spectrum. Beyond a characteristic minimum interaction wavelength 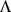 (on the order of the entanglement length) the relaxation times
(on the order of the entanglement length) the relaxation times 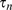 of all Wlc modes
of all Wlc modes  of wavelength
of wavelength 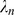 are modified by a mode-dependent Arrhenius factor
are modified by a mode-dependent Arrhenius factor
| (2) |
This modification of the relaxation spectrum gives rise to a dramatic slowdown of the dynamics at long times or small frequencies [37], producing power-law rheology with a small apparent power-law exponent 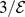 [27], as ubiquitously observed for cells [7].
[27], as ubiquitously observed for cells [7].
A pertinent example for an observable characterizing the mechanical response under an optional prestressing force 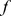 is the complex microscopic susceptibility to transverse displacements [37], given by
is the complex microscopic susceptibility to transverse displacements [37], given by
| (3) |
with the polymer length 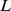 , persistence length
, persistence length 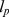 , Euler buckling force
, Euler buckling force 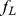 , and thermal energy
, and thermal energy 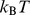 . In the limit of infinitely long polymers, the expression becomes independent of the length and can be converted to an integral. Note that equation (3) implicitly depends on
. In the limit of infinitely long polymers, the expression becomes independent of the length and can be converted to an integral. Note that equation (3) implicitly depends on 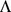 and therefore is better written as
and therefore is better written as 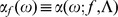 . To evaluate the force response to a given strain stimulus
. To evaluate the force response to a given strain stimulus  in linear response, a superposition principle can be used,
in linear response, a superposition principle can be used,
| (4) |
where 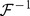 denotes the inverse Fourier transform.
denotes the inverse Fourier transform.
In the inelastic Gwlc (i Gwlc) model, we interpret 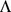 as the average backbone length between adjacent bonds of the test chain with the background network, and
as the average backbone length between adjacent bonds of the test chain with the background network, and 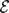 as the height of the free energy barrier (in units of thermal energy) that has to be overcome to break a bond. In contrast to the equilibrium Gwlc,
as the height of the free energy barrier (in units of thermal energy) that has to be overcome to break a bond. In contrast to the equilibrium Gwlc, 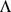 is not assumed to be a fixed equilibrium quantity
is not assumed to be a fixed equilibrium quantity 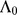 , but is allowed to evolve with time (Fig. D in Supporting Information S1). It is related to the state variable
, but is allowed to evolve with time (Fig. D in Supporting Information S1). It is related to the state variable 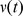 , describing the mean fraction of closed bonds (or “bond fraction”) at a given time
, describing the mean fraction of closed bonds (or “bond fraction”) at a given time  , by
, by 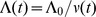 . The equilibrium Gwlc is recovered as the special case of a fixed average bond fraction
. The equilibrium Gwlc is recovered as the special case of a fixed average bond fraction 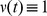 .
.
The bond fraction evolves according to a simple generic first-order kinetic equation,
| (5) |
where 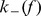 and
and 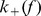 are force-dependent off- and on rates, respectively. The transition rates are taken to depend exponentially on the polymer backbone tension
are force-dependent off- and on rates, respectively. The transition rates are taken to depend exponentially on the polymer backbone tension 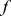 in the standard way [38],
in the standard way [38],
| (6) |
where 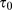 is a characteristic time scale that depends on the properties of the binding potential,
is a characteristic time scale that depends on the properties of the binding potential, 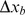 and
and 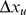 are the widths of potential wells corresponding to the bound and unbound state, respectively, and
are the widths of potential wells corresponding to the bound and unbound state, respectively, and 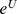 is the relative binding affinity [38], [39].
is the relative binding affinity [38], [39].
To summarize, the model combines two fundamental nonlinear mechanical paradigms, namely single-polymer stiffening and a transient bond softening under load. The resulting nonlinear response is evaluated numerically using a nonlinear update scheme implemented in C++. In brief, in each time step  , the bond fraction
, the bond fraction 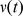 is updated according to equations (5) and (6) and the force history
is updated according to equations (5) and (6) and the force history  . Both
. Both 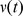 and
and 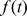 then determine the Gwlc response, at a given time
then determine the Gwlc response, at a given time  , via the Gwlc mode spectrum
, via the Gwlc mode spectrum 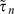 [25].
[25].
Supporting Information
The Supporting Information S1 covers some additional technical details concerning the data analysis and the theoretical model, and auxiliary numerical and experimental data.
(PDF)
Acknowledgments
We thank A. Bausch for helpful and inspiring discussions and for providing lab space and materials, and K. Schmoller, C. Semmrich, and S. Köhler for advice concerning the experiments.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was supported through the Leipzig School of Natural Sciences “Building with molecules and nano-objects” (GSC 185) by the German excellence initiative. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Pourati J, Maniotis A, Spiegel D, Schaffer JL, Butler JP, et al. Is cytoskeletal tension a major determinant of cell deformability in adherent endothelial cells? The American Journal of Physiology. 1998;274:C1283–9. doi: 10.1152/ajpcell.1998.274.5.C1283. [DOI] [PubMed] [Google Scholar]
- 2.Wang N, Tolic-Norrelykke I, Chen J, Mijailovich SM, Butler JP, et al. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. American Journal of Cell Physiology. 2002;282:606–616. doi: 10.1152/ajpcell.00269.2001. [DOI] [PubMed] [Google Scholar]
- 3.Fernández P, Pullarkat P, Ott A. A master relation defines the nonlinear viscoelasticity of single fibroblasts. Biophysical Journal. 2006;90:3796–805. doi: 10.1529/biophysj.105.072215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Trepat X, Deng L, An SS, Navajas D, Tschumperlin DJ, et al. Universal physical responses to stretch in the living cell. Nature. 2007;447:592–5. doi: 10.1038/nature05824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Krishnan R, Park CY, Lin Yc, Mead J, Jaspers RT, et al. Reinforcement versus uidization in cytoskeletal mechanoresponsiveness. PLoS ONE. 2009;4:e5486. doi: 10.1371/journal.pone.0005486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. 1999;402:C47–52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
- 7.Trepat X, Lenormand G, Fredberg JJ. Universality in cell mechanics. Soft Matter. 2008;4:1750. [Google Scholar]
- 8.Fletcher DA, Mullins RD. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–92. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wen Q, Janmey PA. Polymer physics of the cytoskeleton. Current Opinion in Solid State and Materials Science. 2011;15:177–182. doi: 10.1016/j.cossms.2011.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gardel ML, Shin JH, MacKintosh FC, Mahadevan L, Matsudaira P, et al. Elastic behavior of cross-linked and bundled actin networks. Science (New York, NY) 2004;304:1301–5. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 11.Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear elasticity in biological gels. Nature. 2005;435:191–4. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 12.Gardel M, Nakamura F, Hartwig J, Crocker J, Stossel T, et al. Stress-Dependent Elasticity of Composite Actin Networks as a Model for Cell Behavior. Physical Review Letters. 2006;96:12–15. doi: 10.1103/PhysRevLett.96.088102. [DOI] [PubMed] [Google Scholar]
- 13.Fredberg J, Jones K, Nathan MS, Raboudi S, Prakash YS, et al. Friction in airway smooth muscle: mechanism, latch, and implications in asthma. Journal of Applied Physiology. 1996;81:2703–2712. doi: 10.1152/jappl.1996.81.6.2703. [DOI] [PubMed] [Google Scholar]
- 14.Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–89. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 15.Lieleg O, Claessens M, Luan Y, Bausch A. Transient Binding and Dissipation in Cross-Linked Actin Networks. Physical Review Letters. 2008;101:108101. doi: 10.1103/PhysRevLett.101.108101. [DOI] [PubMed] [Google Scholar]
- 16.Xu J, Tseng Y, Wirtz D. Strain hardening of actin filament networks. Regulation by the dynamic cross-linking protein alpha-actinin. The Journal of Biological Chemistry. 2000;275:35886–92. doi: 10.1074/jbc.M002377200. [DOI] [PubMed] [Google Scholar]
- 17.Semmrich C, Larsen RJ, Bausch AR. Nonlinear mechanics of entangled F-actin solutions. Soft Matter. 2008;4:1675. doi: 10.1039/b800989a. [DOI] [PubMed] [Google Scholar]
- 18.MacKintosh F, Käs J, Janmey P. Elasticity of Semiexible Biopolymer Networks. Physical Review Letters. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 19.Ingber DE. Tensegrity I. Cell structure and hierarchical systems biology. Journal of Cell Science. 2003;116:1157–1173. doi: 10.1242/jcs.00359. [DOI] [PubMed] [Google Scholar]
- 20.Broedersz C, Storm C, MacKintosh F. Nonlinear Elasticity of Composite Networks of Stiff Biopolymers with Flexible Linkers. Physical Review Letters. 2008;101:118103. doi: 10.1103/PhysRevLett.101.118103. [DOI] [PubMed] [Google Scholar]
- 21.Morse DC. Viscoelasticity of Concentrated Isotropic Solutions of Semiexible Polymers. 3. Nonlinear Rheology. Macromolecules. 1999;32:5934–5943. [Google Scholar]
- 22.Chaudhuri O, Parekh SH, Fletcher DA. Reversible stress softening of actin networks. Nature. 2007;445:295–8. doi: 10.1038/nature05459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kollmannsberger P, Mierke CT, Fabry B. Nonlinear viscoelasticity of adherent cells is controlled by cytoskeletal tension. Soft Matter. 2011;7:3127–3132. [Google Scholar]
- 24.Lee H, Ferrer J, Lang M, Kamm R. Molecular origin of strain softening in cross-linked F-actin networks. Physical Review E. 2010;82:011919. doi: 10.1103/PhysRevE.82.011919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wolff L, Fernandez P, Kroy K. Inelastic mechanics of sticky biopolymer networks. New Journal of Physics. 2010;12:053024. [Google Scholar]
- 26.Bustamante C, Bryant Z, Smith S. Ten years of tension: single-molecule DNA mechanics. Nature. 2003;421:423–426. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
- 27.Kroy K, Glaser J. Rheological redundancy - from polymers to living cells. AIP Conference Proceedings. 2009;1151:52. [Google Scholar]
- 28.Fantner GE, Oroudjev E, Schitter G, Golde LS, Thurner P, et al. Sacrificial bonds and hidden length: Unraveling molecular mesostructures in tough materials. Biophysical Journal. 2006;90:1411–1418. doi: 10.1529/biophysj.105.069344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen C, Krishnan R, Zhou E, Ramachandran A, Tambe D, et al. Fluidization and resolidification of the human bladder smooth muscle cell in response to transient stretch. PLoS ONE. 2010;5:16–21. doi: 10.1371/journal.pone.0012035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Semmrich C, Storz T, Glaser J, Merkel R, Bausch AR, et al. Glass transition and rheological redundancy in F-actin solutions. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:20199–203. doi: 10.1073/pnas.0705513104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kollmannsberger P, Fabry B. Active soft glassy rheology of adherent cells. Soft Matter. 2009;5:1771–1774. [Google Scholar]
- 32.Fernandez P, Heymann L, Ott A, Aksel N, Pullarkat PA. Shear rheology of a cell monolayer. New Journal of Physics. 2007;9:419–419. [Google Scholar]
- 33.Fabry B, Maksym G, Butler J, Glogauer M, Navajas D, et al. Scaling the Microrheology of Living Cells. Physical Review Letters. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 34.Tharmann R, Claessens MMAE, Bausch AR. Viscoelasticity of isotropically cross-linked actin networks. Physical Review Letters. 2007;98:088103. doi: 10.1103/PhysRevLett.98.088103. [DOI] [PubMed] [Google Scholar]
- 35.Gittes F, Olmsted P, Schnurr B, MacKintosh F, Schmidt C. Microscopic Viscoelasticity: Shear Moduli of Soft Materials Determined from Thermal Fluctuations. Physical Review Letters. 1997;79:3286–3289. [Google Scholar]
- 36.Schmidt C, Baermann M, Isenberg G, Sackmann E. Chain dynamics, mesh size, and diffusive transport in networks of polymerized actin: a quasielastic light scattering and microuorescence study. Macromolecules. 1989;22:3638–3649. [Google Scholar]
- 37.Kroy K, Glaser J. The glassy wormlike chain. New Journal of Physics. 2007;9:416. [Google Scholar]
- 38.Bell G. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 39.Kramers H. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;VII:284–304. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The Supporting Information S1 covers some additional technical details concerning the data analysis and the theoretical model, and auxiliary numerical and experimental data.
(PDF)